1. Introduction
Discrete event systems can be used to study processes that are driven by the occurrence of events. The relevant variables represent times at which events are taking place. An important class of systems consists of min-max-plus systems in which the operations—the maximization, the minimization and the addition, can describe discrete event dynamic systems. The union of two sets of equations describes the min-max-plus systems, where the maximization and addition are contained in one set of equations and the minimization and addition are contained in another set of equations.
Max-plus algebra where , is a set which deals with two main operations—⊕ as maximization and ⊗ as addition. These operations endow with the structure of a commutative semiring.
There are various applications of max-plus algebra in different areas of mathematics [
1]. Max-plus algebra is also considered in traffic control, parallel processing systems, telecommunication networks, manufacturing systems, machine scheduling, and control theory [
2,
3,
4]. In [
5], the author has described the model of all train connections of the whole Dutch railway system with all train types by a max-plus system. Max-plus algebra can be used to model disk events related to synchronization and time delays [
6]. A new steganography method has been proposed to hide an image into another image using matrix multiplication operations on max-plus algebra [
7]. In [
8] the author has shown how max-plus algebra can be helpful for the dynamic programming of algorithms. The primary reason for the utilization of max-plus algebra in different fields is that many equations which are non-linear in conventional algebra become linear in max-plus algebra [
3].
In this paper, we consider the eigenproblems in max-plus algebra. Eigenproblems are the problems of finding an eigenvalue
and an eigenvector
v from an
matrix
M such that
. The algorithm in [
9] can solve these problems.
A novel iterative method is proposed for the computation of eigenvalue and the corresponding eigenvectors in max-plus algebra. To evaluate the eigenvalue and the corresponding eigenvectors of discrete event systems, some algorithms have been established in [
8,
9,
10,
11]. The first algorithm to determine the eigenvalue was given by Karp [
12]. A new algorithm was proposed to solve systems of max-plus linear inequalities [
13]. This algorithm uses the technique of cyclic projectors. In [
14], there is a method for determining the eigenvectors of monotone and homogenous functions.
The paper is structured as follows. In
Section 2, basic results and definitions related to max-plus algebra are described. A new algorithm is proposed to determine the eigenvalue and eigenvectors in an iterative way. In
Section 3, we discuss the Latin squares in max-plus algebra and extend the algorithm for Latin squares. Conclusions are made in
Section 4.
2. Max-Plus Algebra
In this section, we recall some basic results and definitions related to the max-plus algebra. The symbols
denote the algebraic structure of max-plus algebra where
is the set
and
are the binary operations defined as
and
These operations endow with a structure of commutative semiring. Both the operations ⊗ and ⊕ satisfy associativity and commutativity.
So in max-plus algebra, is a null element and 0 is a unit element.
For
and a non-negative integer
n, define
Using the standard multiplication in
, we have
In max-plus algebra,
and
denote the set of all matrices of order
with entries in
, and the set of all
vectors respectively. The set of first
n natural numbers is denoted by
,
,
. Now let
and
be elements of
. The sum of these two matrices
is defined as
Let
and
be two matrices. The product
is defined by the formula
For
, the
power of
M can be defined as
The starting point is the following system of equations describing the time evolution of a discrete event system:
This can be written as
Finally, the previous equation can compactly be written as
where
,
.
System (
1) has an eigenvalue
and the corresponding eigenvector
if
For each matrix
, we can construct a directed graph (digraph)
, where
N is the set of vertices and
E represents the set of edges. There exists an arc
if
; such an arc will be denoted by
. The weight
for each
-arc is defined as
. If
, then there is no
-arc. A path is a sequence of arcs
. If all vertices
are different then the path is called an elementary path. An elementary path of the form
is known as a circuit. A loop is a circuit consisting of an edge that connects a vertex to itself. The weight of a path
, denoted by
, is defined as the sum of weights of each arc. The length of
p, denoted by
, is equal to the number of arcs in the path
p. The average weight of a path
p is defined by
. A critical circuit is a circuit with maximum average weight. If there exists a path from each vertex
i to each vertex
j then the graph is said to be strongly connected. A matrix
M is irreducible if and only if the digraph of
M is strongly connected [
15].
The eigenvalue of a matrix
M is equal to the maximal average weight in
[
16]. The eigenvalue for an irreducible matrix
M, if it exists, is unique [
16]. So, problem of getting the eigenvalue of a matrix
M related to the problem of getting the critical circuits in
.
In this paper, we find the eigenvalue
of a matrix
with the help of the maximal average weight in
as done in [
16]. Then we define the matrix
as
, in other words
. At the end, we define
for
, where
. Using this relation, an algorithm is derived to calculate the associated eigenvectors of a matrix
M.
Theorem 1. Let be a matrix and letfor , where . If there exist some positive integers , such that , thenwhere Proof of Theorem 1. The main task is to prove that
. Indeed, we have
□
The main algorithm of this article stated below (Algorithm 1) gives the eigenvalue and the corresponding eigenvectors. This algorithm consists of the following steps:
| Algorithm 1 Eigenproblems in Max-Plus Algebra |
Compute the maximal circuit mean , in . Define . Define an arbitrary initial vector . Iterate for , until there are positive integers , such that .
|
Each step of the above algorithm is explained with the help of the following example.
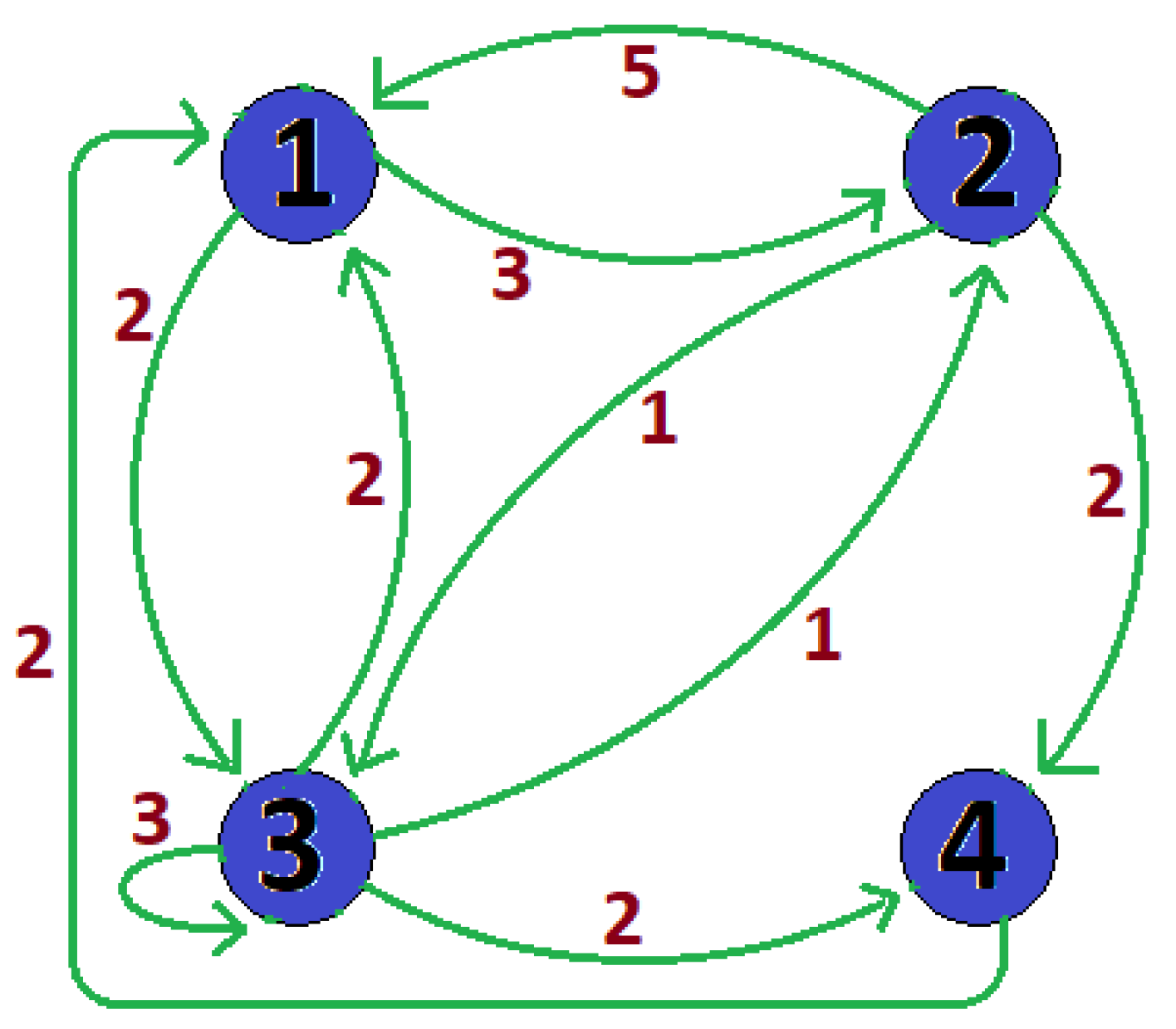
Example 1. Consider the following matrix The corresponding graph is depicted in Figure 1. Since the average weight of the circuit is the maximal circuit mean, the eigenvalue . Now we get Now take the initial vectorThe following sequence is obtained by iterating (3),It follows that . We proceed with the computation of the vector v. It is easy to see that indeedHence for the eigenvalue , the corresponding eigenvector v of the matrix M resulting from the above algorithm is a correct eigenvector. 3. Latin Square
In this section, the proposed algorithm is used to compute the eigenvalue and the corresponding eigenvectors of Latin squares. A Latin square is a square matrix of size
with
n different numbers such that each row and each column contains distinct numbers [
17]. An example of a Latin square is given in the following
The purpose behind considering eigenproblems for Latin squares in max-plus algebra is that similar issues have been examined for different matrices like circulant matrices [
18,
19], Monge matrices [
20] and inverse Monge matrices [
21]. Eigenproblems for these special matrices are more easy to answer. For example, the maximal entry in circulant matrices is its eigenvalue.
Now we will discuss two different types of Latin square.
• The entries of L are .
• The entries of L are .
Let
L be a Latin square with entries in
. Since each entry in
L is finite, the corresponding graph
is strongly connected. Similarly, for a Latin square
L with entries in
, exactly one infinite entry appears in each row and column. So there exists a path of length 2 from each vertex
r to each vertex
s in
. Consequently, the graph
is strongly connected. Hence in both cases, a Latin square is an irreducible matrix. In [
11] authors show that for a Latin square
L, the maximal number in
L is equal to the maximal circuit mean in
. Therefore the eigenvalue of a Latin square
L is equal to the maximal number in
L [
11].
Now using this concept, the proposed algorithm (Algorithm 2) computes the eigenvalue and eigenvectors of Latin square as follows:
| Algorithm 2 Eigenproblems for Latin Square |
Compute the eigenvalue as the maximal number in L. Define . Define an arbitrary initial vector . Iterate for , until there are positive integers , such that .
|
Also, recall the power algorithm presented by Subiono [
9]. This algorithm computes the eigenvalue and corresponding eigenvector for max-plus systems of type
.
Now we illustrate the Algorithms 2 and 3 by means of an example. In the following example, based on Algorithms 2 and 3, M is a Latin square with entries in .
| Algorithm 3 Eigenproblems for Max-Plus Algebra |
Take an arbitrary initial state vector . Iterate until there are integers with and a real number c, such that . Define as eigenvalue (in the conventional sense). Define as eigenvector .
|
Example 2. - 1.
By Algorithm 2, the maximal number in M is the eigenvalue, , Next, consider the initial vector After iterating , the following sequence is obtained: It follows that . To compute a corresponding eigenvector we proceed with the computation of the vector v. It is easy to check whether or not . It follows that Hence for the eigenvalue , the corresponding eigenvector v of the matrix M resulting from the above algorithm is a correct eigenvector.
- 2.
For Algorithm 3, consider the initial vector Iterating , we obtain It follows that . The vector v resulting from Algorithm 3, is given asWhich is the correct eigenvector.
Remark 1. The main purpose of this article is to present an alternative algorithm for the computation of an eigenvalue and the associated eigenvector in max-plus algebra. This algorithm works in an iterative way. Here we give a computational comparison of the Algorithm 2 with the Algorithm 3 given by Subiono and van dar Woude [9]. In the case of a circulant matrix or a Latin square, the maximum value is the eigenvalue. Therefore the Algorithm 2 works quite easily compared to the Algorithm 3 This is because Algorithm 3 ends up in a periodic behavior if there exists a real number c and integers , such that , while in the case of Algorithm 2, we do not need any real number c. Also the Algorithm 3 gives an eigenvector v ashowever, when using the Algorithm 2 one gets an eigenvector v as . Hence the computation of an eigenvector using the Algorithm 2 is quite easy compared to the Algorithm 3.