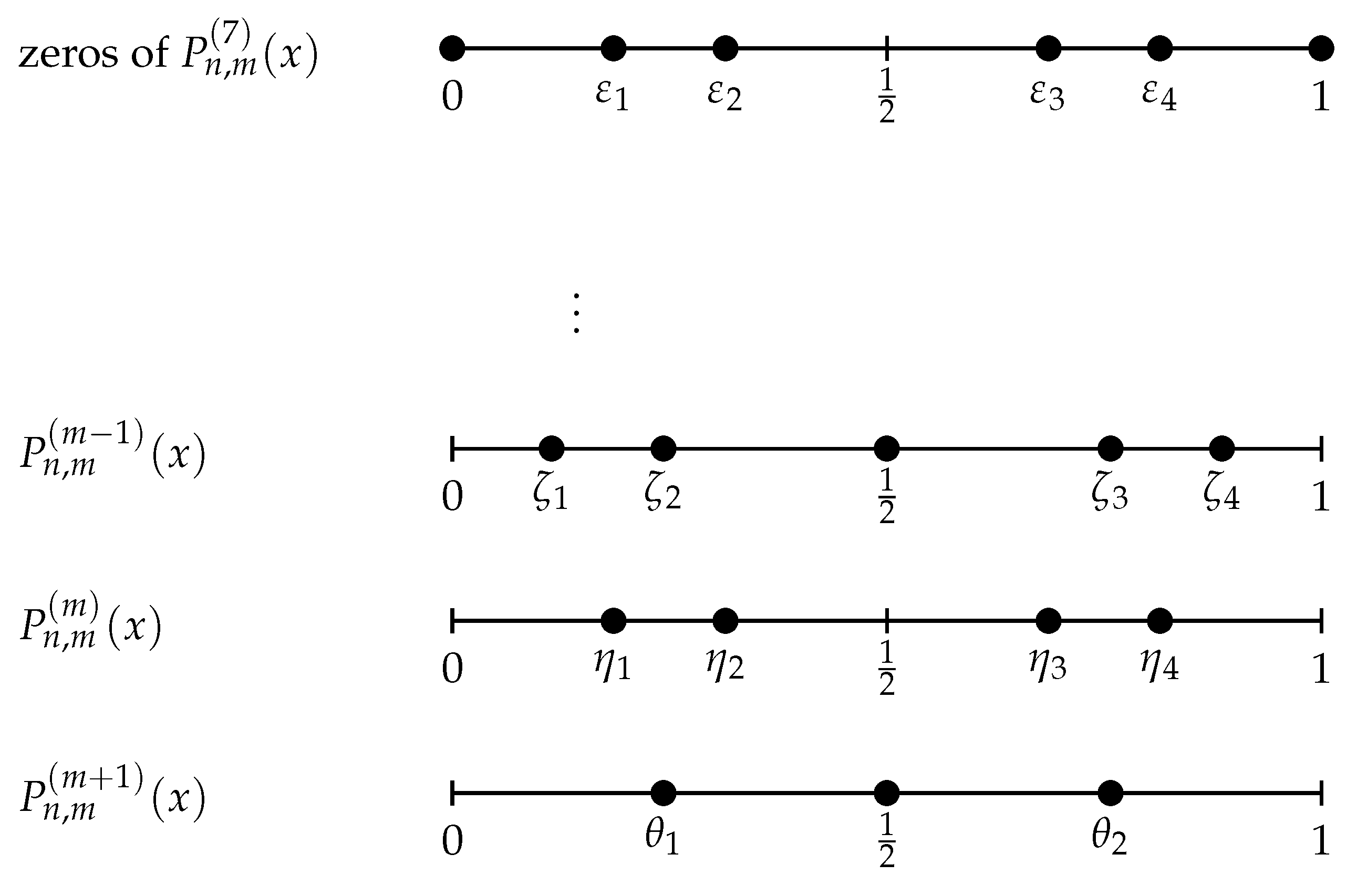1. Introduction
Let
be a field. If
has degree at least 2, we say that
is
decomposable over the field
if we can write
for some nonlinear polynomial
,
. Otherwise, we say that
is
indecomposable over
. Two decompositions
and
are said to be
equivalent over the field
, written
, if there exists a linear polynomial
such that
For a given with degree at least 2, a complete decomposition of over is a decomposition , where the polynomials are indecomposable over for . A polynomial of degree greater than 1 always has a complete decomposition, but it does not need to be unique even up to equivalence.
Euler polynomials are defined by the following generating function
These polynomials play a central role in various branches of mathematics; for example, in various approximation and expansion formulas in discrete mathematics and in number theory (see for instance [
1,
2]), in
p-adic analyis (see [
3], Chapter 2), in statistical physics as well as in semi-classical approximations to quantum probability distributions (see [
4,
5,
6,
7]).
There are several results connected to the decomposability of an infinite family of polynomials, see for instance [
8,
9,
10,
11,
12]. Bilu, Brindza, Kirschenhofer, Pintér and Tichy [
13] gave all the decompositions of Bernoulli polynomials. Kreso and Rakaczki [
14] characterized the all possible decomposations of Euler polynomials with degree even, moreover they showed that every Euler polynomial with odd degree is indecomposable. It is harder to obtain similar results for the sum of polynomials. Pintér and Rakaczki [
15] describe the complete decomposition of linear combinations of the form
of Bernoulli polynomials, where
c is an arbitrary rational number. Later, Pintér and Rakaczki in [
16] proved that for all odd
integer and for all rational number
c the polynomials
are indecomposable.
The main purpose of this paper is to prove that under certain conditions a linear combination with rational coefficients of two Euler polynomials with odd degrees is always indecomposable. We have
Theorem 1. Let , where is an arbitrary rational number, where , , n, m are odd integers with . Then the polynomials are indecomposable over .
2. Auxiliary Results
In the first lemma we collect some well known properties of the Euler polynomials which will be used in the sequel, sometimes without particular reference.
Lemma 1. - (a)
;
- (b)
;
- (c)
;
- (d)
for ;
- (e)
;
The following result is a general theorem from the theory of decomposability.
Lemma 2 (Kreso and Rakaczki [14]). Let be a monic polynomial such that is not divisible by the characteristic of the field . Then for every nontrivial decomposition over any field extension of , there exists a decomposition such that the following conditions are satisfied
and are equivalent over ,
and are monic polynomials with coefficients in
Moreover, such decomposition is unique.
Lemma 3. Let with . If is decomposable over then we can write the polynomial in the form , where u and are relative prime integers, and are primitive polynomials. Moreover, if is a monic polynomial, then .
Proof. Suppose that
, where
,
. Let
Every polynomial with rational coefficients can be written uniquely as a product of a rational number and a primitive polynomial. Hence, we can assume that
and so
The polynomial
can be written in the from
, where
is a primitive polynomial,
,
are relative prime integers. However, then we have
If the polynomial
is monic, then comparing the leading coefficients in (
1) one can deduce that
, where
and
denotes the leading coefficient of the polynomial
and
, respectively. This means that
u divides
v that is
. □
From these definitions it is easy to see that and are subspaces in the vector space .
Lemma 4. Let be a monic polynomial. Assume that and , where , and . Then we can assume that , are monic, and .
The following Lemma is a simple combination of Lemmas 3 and 4.
Lemma 5. Let be a monic polynomial. Assume that and , where , and , . Then we can assume that , where is an integer, and are primitive polynomials, and .
Proof. From Lemma 4 we can assume that and . Using the proof of Lemma 3 and the fact that is a subspace of we get the assertion of our Lemma. □
Lemma 6. Let . Thenfor even index . Proof. Since
we have that
. Computing the coefficient of
on the both sides we obtain that
□
Lemma 7. LetIf k, then the coefficient of the monomial in the polynomial is Proof. It is easy to see that the monomial occurs only in the term . Expanding we simply get the assertion. □
3. Proof of the Theorem
Let
n,
m be odd positive integers with
,
B is an arbitrary integer which is not a power of two. The case of
was treated in [
16]. Suppose that
is decomposable over
. From Lemmas 2 and 5 we can assume that
, where
is an integer,
,
are primitive polynomials and
,
. Let
Using (b) of Lemma 1 one can deduce that
Since
thus
. From (
3) we infer that the polynomial
divides the polynomial
, that is
where
,
and the polynomial
divides the polynomial
in
. We know that
If the polynomial
is a constant polynomial then we have
and so
. It follows from
and (d), (e) of Lemma 1 that the coefficient of
in
equals 0. Applying now Lemma 7 we get that
which is impossible since
by Lemma 6.
In the case when we get , and . Since by assumption , we obtain again that , which is not possible.
Next suppose that
. In this case one can deduce that
s is odd and
. Consider first when
. Then
and
. Let
and
. Then
,
and
Let
Since
we have that
.
Investigate the coefficients of
and
in
Since
in the polynomials
these coefficients are 0. On the other hand, one can observe that
occurs only in the term
and so
. This means that
and so
Since appears only in the term thus .
If
we obtain from (
7) that the coefficients of
,
,
,
and
x in
are zero. This yields that
for
. Further, by Lemma 1
Applying the above, we can study the number of zeros of the polynomials
in the interval [0,1] for
. In the following table we use only the Rolle’s theorem.
![Symmetry 11 00739 i001 Symmetry 11 00739 i001]()
![Symmetry 11 00739 i002 Symmetry 11 00739 i002]()
But
whose the only zero in the interval
is
. This contradiction gives that
.
If
then from
and (
7) one can deduce that
The above argument that we used in the case
shows that this impossible.
Finally, consider the case when
. Let
, where
A and
are relatively prime integers. From (
4) we know that
where the polynomial
is even and divides the polynomial
in
. If we write
as a product of a rational number
and a primitive polynomial
we have that
where
is a primitive polynomial. We obtain from (
8) and (
9) that
Let
,
and
, where
w denotes the greatest common divisor of the integers
,
. Then
which yields that
and
It follows from Lemma 6 that if
p is an odd prime which divides
w then
p divides
,
which is not possible since
is a primitive polynomial. Thus
for some non-negative integer
a. Now assume that
p is a prime which divides
and
is the greatest odd index for which
On the right hand side of (
12) the coefficient of
equals 0 apart from when
or
. Thus
which means that
.
Similarly,
from which we get that
. Continuing the process one can deduce that
Further, if
then
and so
contradicting that the polynomial
is a primitive polynomial. It follows from the above that
j must be 1 and so
If
p is an odd prime then from the above and Lemma 6 we have that
Now let
and
. Then
and for
We know that
and so the coefficients of
,
are zeros in
and so in
Now one can infer from (
16) and (
17) that
mod
which yields
. Comparing coefficient of
we have that
mod
from which we obtain
. Continuing the process it is easy to see that
which contradicts the fact that
is a primitive polynomial. This means that
and
must be powers of two.
Now suppose that
p is a prime with
and
. Using again that on the right hand side of (
12) the coefficient of
equals 0 apart from when
or 1. From
we obtain
p divides
. From
we obtain
p divides
. It follows similarly that
. Finally, from
we get that
p divides
which contradicts that the polynomial
is a primitive polynomial. This means that
must be a power of two. Since
this contradicts to our assumption that
B is not a power of two.