Abstract
The topic “converging shock waves” is quite useful in Inertial Confinement Fusion (ICF). Most of the earlier studies have assumed that the medium of propagation is ideal. However, due to very high temperature at the axis of convergence, the effect of medium on shock waves should be taken in account. We have considered a problem of propagation of cylindrical shock waves in real medium. Magnetic field has been assumed in axial direction. It has been assumed that electrical resistance is zero. The problem can be represented by a system of hyperbolic Partial Differential Equations (PDEs) with jump conditions at the shock as the boundary conditions. The Lie group theoretic method has been used to find solutions to the problem. Lie’s symmetric method is quite useful as it reduces one-dimensional flow represented by a system of hyperbolic PDEs to a system of Ordinary Differential Equations (ODEs) by means of a similarity variable. Infinitesimal generators of Lie’s group transformation have been obtained by invariant conditions of the governing and boundary conditions. These generators involves arbitrary constants that give rise to different possible cases. One of the cases has been discussed in detail by writing reduced system of ODEs in matrix form. Cramer’s rule has been used to find the solution of system in matrix form. The results are presented in terms of figures for different values of parameters. The effect of non-ideal medium on the flow has been studied. Guderley’s rule is used to compute similarity exponents for cylindrical shock waves, in gasdynamics and in magnetogasdynamics (ideal medium), in order to set up a comparison with the published work. The computed values are very close to the values in published articles.
MSC:
35L67; 58J45
1. Introduction
The method of the Lie group of invariance has played a significant role in solving various kinds of systems of PDEs for a long time. In fact, it has become an important tool to deal with a nonlinear system of PDEs. The dimensional analysis gives rise to the natural scaling invariance of a problem. It has presented a way to find a self-similar solution, considered as a specific solution of a governing system of Hyperbolic PDEs, a problem involving symmetry. Point implosion and explosion problems discussed by Taylor [1] and Sedov [2] are the two most common examples of it. Usually, the imposed boundary conditions are not satisfied globally by such types of solutions. However, it can be shown that symmetric solutions can be found using asymptotical analysis in fixed domains. Zeldovich and Raizer [3] have given simple scaling arguments to obtain similarity solutions with an illustration of self-similar or invariant nature of the scaled solutions. Furthermore, the great application of their work is given by Barenblatt [4], giving a clear explanation of the nature of invariant solutions of the first and second kind.
A large number of natural phenomena [5,6,7], magnetized stellar winds, shapes of planetary nebulae, galactic winds, complex filamentary structures in molecular clouds, synchrotron radiation from supernova remnants, gamma-ray bursts, dynamo effects in stars, galaxies and galaxy clusters, structure and interaction of supershells as well as other interesting problems all have important roles in magnetic field. Due to its theoretical and practical importance in the variety of astrophysical situations, plasma physics, nuclear science and engineering physics, analysis of magnetogasdynamics has received more attention from researchers in the fields ranging from condensed matter to gas dynamics. Lie’s approach is applied to estimate the structure of strong imploding shock waves. Guderley [8], Zeldovich and Raizer [3], Sedov [2], Korobeinikov [9] and Arora et al. [10], etc. studied the imploding shock waves and contributed remarkably in this field. Steeb [11] has applied a group theoretic approach to obtain a similarity solution of the Euler equation and the Navier–Stokes equation for incompressible fluid flow. Bluman and Kumei [12], Ovasiannikov [13], Logan [14] and Bluman and Cole [15] have also used the method to study various symmetric flows. Van Dyke and Guttmann [16], Whitham [17], and Halfner [18] have applied other approximation theories to find a solution for the converging shock waves problem. Converging symmetrical waves in real gases have been studied by Madhumita and Sharma [19]. A similarity solution of symmetric shock waves in radiative gas with an axial magnetic field has been analysed by Radha and Sharma [20] using the group theoretic approach.
Pandey et al. [21] obtained the exact solution of magnetogasdynamic equations with cylindrical symmetry using the symmetry analysis. It is worth mentioning the work of Singh et al. [22], Baty and Tucker [23], and Singh and Pandey [24], on magnetogasdynamic equations in both ideal and non-ideal plasma. Chisnell [25] gave an analytical description of flow field. Chisnell [25] has first proposed a technique for the evaluation of exponent in similarity variable. Applying the simple analytic method, a similarity exponent is determined in a non-ideal plasma by Patel and Rao [26]. In the present study, self-similar solutions of a second kind for cylindrical symmetric flow in non-ideal magnetogasdynamics is determined. Lie group of invariance, as presented in Bluman and Cole [15] and Bluman and Kumei [12], has been used to find the solution for the problem.
This paper is organized as follows: Section 2 describes the basic governing equations of the planar and cylindrical symmetric flow in real medium with an axial magnetic field. Boundary conditions at the shock are given by Rankine–Hugoniot conditions. A brief discussion on method of Lie group of invariance is given in Section 3. The method is applied on the earlier described system of PDEs to obtain group of transformations in the section. In Section 4, all possible cases for similarity solutions are discussed in detail and a system of ODEs with an initial condition are obtained in each case. Depending upon the arbitrary constants that appear in the transformations, different possible cases have been constructed in the section. The solution of these systems of ODEs enables us to explore the solution for the considered system of PDEs. In Section 5, a particular case among the possible cases has been studied in detail . Numerical results and discussion are presented in Section 7. A comparison for the exponents of similarity variable by Guderley’s method and our scheme is also presented in the section in Table 1. Flow profiles are drawn in the section to study various effects of parameters on the problem.

Table 1.
Computed values of similarity exponent for different values of , b and in non-ideal magnetogasdynamics for cylindrically symmetric flow.
2. Governing Equations and Shock Conditions
Consider a problem of the propagation of converging symmetric shock waves in a real medium with an axial magnetic field. We assume that the converging shock moves inward in a radial direction. The governing equations for the phenomena may be written as follows [9,17,28,29,30]:
where , u, p are gas density, velocity, pressure and magnetic pressure, respectively. and H denote permeability and magnetic field in transverse direction respectively. m denote the geometry of converging shock. refers to planar shock while refers to cylindrical shock. r is used for radial distance and t refers to time. is the speed of sound in non-ideal plasma, where is the ratio of specific heat at constant pressure and specific heat at constant volume . Equation of state for real gases is taken as follows (Wu and Roberts [31]):
where is the gas constant, T the absolute temperature, and b is the “van der Waals excluded gas volume”; it places a limit , on the density of gas. The temperature T and the gas constant are assumed to obey the thermodynamic relation .
As our aim is to study the converging cylindrical shock waves, we consider the case when the shock is moving with locus in the medium with the propagation velocity of shock front produced by a cylindrical piston with radius initially. Let the initial conditions for the flow variables be specified at the shock front as: , constant, and constant.
All the variables referred as lengths to , speed to V, density to , pressure to , magnetic pressure to , van der Waals excluded gas volume b to and time to are non-dimensional.
At the shock front , the usual Rankine–Hugoniot jump conditions for strong shocks can be written as:
Here, and denotes the cowling number for the shock.
3. Lie Group Analysis
Now, suppose we are able to find a family of curves along which the governing PDEs (1) contain a solution. This solution is known as the similarity solution and the family of curves is known as similarity curves. Actually, our set of partial differential equations reduces to the set of ordinary differential equations along these similarity curves. In order to find the similarity solutions and similarity curves to the system of partial differential Equation (1), we try to find its symmetry group. Symmetry group is a group of transformations under which a corresponding system of partial differential equations remains invariant, which means that the solution of the original system can also be transformed to the solution of the transformed system by this transformation. It makes it easier to find the solution of the original system of equations. With the help of these transformations, we convert the given system of PDEs into system of ODEs. Now, we do some calculations to find a one parameter infinitesimal group of transformations. Consider the following transformations as given in Sharma and Arora [32]:
where the symmetry generators , , U, P, , E are the functions of r, t, u, p, and h. The above one parameter infinitesimal transformation (4) is such that our system of PDEs (1) and its boundary conditions (3) will remain invariant under these transformations. The parameter is considered to be very small so the terms of higher powers of can be considered as negligible. Under the above Lie group transformations, the system of equations are invariant. It gives us a similarity variable that reduces the system of PDEs (1) to much simpler ODEs.
Thus, to proceed further, we use the summation convention and introduce the following notations: and , where i varies from 1 to 4 and j varies from 1 to 2. The system of basic Equation (1) may be represented as
Now, if we consider that the above system is constant conformally invariant under the action of infinitesimal group of transformations, then, for all smooth surfaces, , we must have
where are arbitrary constants and L is the Lie derivative defined as follows:
with , , , , , and
where i, m and k vary from 1 to 4 while l and j from 1 to 2. Here, repetition of indices indicates summation convention and is the notation for generalization of the derivative transformation.
Here, k and n both vary as . Now, a polynomial equation in is obtained from Equation (8) when the value of from (7) is substituted into (8). On comparing all the coefficients of and on both sides of the resulting equation, a system of linear PDEs of the first order is obtained involving the generators . Now, we try to find out a solution of the obtained system, which we call the system of determining equations. A solution of these determining equations forms an invariant group of transformations.
The above procedure is applied on the each equation of the system of PDEs (1). The following system of determining linear PDEs involving generators are obtained from the invariance of first equation in (1):
Invariance of the second equation in (1) under the Lie group transformation gives the following linear PDEs in terms of generators of the Lie group:
Invariance of the third equation in (1) gives the following set of determining equations:
Lastly, invariance of the magnetic field equation in (1) gives:
On solving these determining equations, we obtain the symmetry generators given as under
where , and are the arbitrary constants.
4. Similarity Solutions
On the basis of the values of arbitrary constants, all possibilities are discussed considering the following different cases.
Case I: , .
We convert to () using the following translation:
the system of PDEs (1) remains unaltered. Thus, using the translation (14), the group of transformations (13) can be rewritten as under with a bar sign being suppressed here:
Using the invariant surface condition (see, Logan [14]), we get:
On integrating the set of Equation (16), together with (15), the flow variables are obtained in the following forms:
where
Thus, , , and are functions of dimensionless variable , which is called similarity variable and defined as follows:
A is constant. The dimension of A is such that becomes dimensionless. Since shock must be a similarity curve and remains constant at shock, hence for the sake of simplicity, shock may be normalized at . Therefore, at , we get the following expressions for the path and velocity of shock V
Thus, at shock, the following conditions must be followed by the flow variables:
On applying the condition of invariance on the jump conditions, we obtain the following form of :
where is some reference constants associated with the medium and . The following conditions are imposed on the functions , , and at the position of shock :
On applying (25) and making use of (23), the considered system of PDEs (1) reduces to a system of ODEs in , , and , having as an independent variable for both the cases ideal and non-ideal . Thus, for , the obtained system of ODEs, on suppressing the asterisk sign is given by
and for ,
together with the following initial conditions
Case II: and .
We change the variables to defined as , , which does not make any change in the considered system of PDEs (1). Following the same procedure as above, flow variables readily follow the similarity solutions of the following forms, on suppressing the bar sign:
with the initial density:
where , and V have the same meaning as mentioned earlier and are given as follows:
Here, A is a dimensional constant. On applying the transformations (29) with appropriate use of (31), the considered system of PDEs is converted into the system of ODEs in , , and , which can be expressed as under on suppressing the asterisk sign:
For ,
and for ,
together with the following initial conditions:
Case III: and .
In this case, the study reveals that the similarity solution for the cylindrical symmetric flow does not exist, while it allows the existence of the similarity solution for the planar flow . We change to as follows:
It makes no change in the governing equations of the phenomena. Consequently, on suppressing the bar sign, the flow variables readily follow the similarity solutions of following forms:
where the initial density and initial magnetic pressure are defined as
where , and V are the dimensionless similarity variable, shock location and shock velocity, respectively, and are defined as follows:
Substitution of (36)–(38) in the considered system of PDEs (1) reduces the system (1) into the system of ODEs in , , and . We drop “*” sign for simplicity to get the following ODEs for :
and for ,
together with the following initial conditions:
Case IV: and .
Again as in the previous case, the similarity solution exists only for the planar flow (m = 0), so it does not allow for the existence of similarity solutions in the radially symmetric (m = 1) flows in such a flow configuration. The basic equations in the given system remains unaltered by changing the variables from to defined as
On suppressing the bar sign, the forms of the similarity solutions of the flow variables are given as
The initial density and initial magnetic pressure are defined as under
where , and V have the same meaning as described in earlier cases. These are defined as follows:
Substitution of (43)–(45) in the considered system of PDEs (1) results in the system of ODEs in , , and , which are expressed below on suppression of “*” sign for and , respectively.
For ,
and, for ,
together with the following initial conditions:
5. Imploding Shocks
We elaborate the Case I of the given problem for an imploding shock for which it is assumed that (the speed of sound) in some neighborhood of implosion. In such a case, an imploding shock is about to collapse at the center or axis. We suppose that the time at which converging shock reaches to axis of implosion is . Therefore, for the process of converging shock. We accordingly re-define the similarity variable as follows:
where the interval for the variables r and t is defined as and , which implies that . At any finite radial distance ‘r’, the density, pressure, magnetic pressure, sound speed and the gas velocity are bounded at the instant of collapse . However, it may be noted that ‘’ reaches to ‘∞’ at for any finite value of radial distance. Thus, in order to keep the quantities , p, u and h bounded at the instant of the collapse, we must have to impose the following conditions at :
Thus, Systems (25) and (26) together with (50) form a boundary value problem. We solve this system to get the flow variables behind the shock. Let us consider the system in a non-ideal case (26). Using matrix notation, system (26) can be written as under
where , A is a matrix and C is a matrix. The matrices A and C can be read off by inspecting system (26). Observing system (51), we notice that there exists an unknown parameter , the value of which can not be calculated using energy balance or dimensional considerations. We can compute its value only by solving the nonlinear eigenvalue problem for the system of ODEs. As we discussed above for the converging shocks, similarity variables vary in the range . Now, system (51) would be solved for the variables, , , and using the Cramer’s rule in the following manner:
where , a notation used for the determinant A, may be written as
Notations are used for the determinants that are obtained by replacing the kth column by vector C in . It is obvious that in , and changes its sign from positive to negative in the interval as at and at . Thus, it confirms the existence of a singular solutions of (52) for some due to at . Thus, to obtain a non-zero solution of (51) in interval , we have to choose the value of such that and all vanish simultaneously. To find such an exponent , we define new variable Z as
Taking the first derivative of Z with respect to , and using (52), we obtain
6. Numerical Results and Discussion
To evaluate the numerical results, the fourth order Runge–Kutta method is applied to system (56). For this, we begin with a trial value of and integrate Equation (56) under definite limits to . Integrating (56), we get the values of the generators and at . In order to obtain the correct value of , we have to adopt a hit and trial technique. We are searching for that value of for which the determinant vanishes at . We perform these numerical calculations for with different values of , b and , and obtain the corresponding values of similarity exponent , which is shown in Table 1, which also depicts the comparison with the corresponding values of obtained by Guderley’s rule and Arora and Sharma [27]. It can be seen that the computed results match well with these results.
Magnetic effects in our problem are present in our problem in terms of the parameter (shock cowling number). refers to the phenomena under consideration in gas dynamics with ideal or non-ideal conditions (without magnetic field). The computed values for the similarity exponent match well with earlier values obtained by Arora and Sharma [27]. Furthermore, it is observed that, as we move towards the higher values of the parameter , the obtained values of starts decaying which in turns reduce the velocity of shock as shock moves to axis of convergence. The same observations have been noticed in the case of of parameter ‘b’ which measures the non-ideal gas effect.
The analytical solution of flow variables behind converging shock at the time of collapse (, ( as )) of the shock wave, are of the following forms:
where is a constant.
From the above expressions, it is clearly observed that U, pressure P and E approach ‘0’ as ‘’, due to the value of being smaller than unity at the instant of collapse, whereas the density S remains bounded thereat. The system (52) is integrated over the range , and the values of u, p, and h behind the shock collapse are illustrated in Figure 1, Figure 2 and Figure 3. It is also interesting to note that our computed solutions in vicinity of are found in agreement with the ones that are obtained by the asymptotic relations (57).
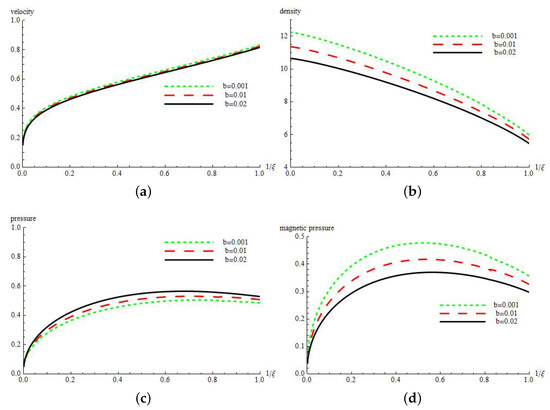
Figure 1.
Flow patterns of non-dimensional (a) velocity (U); (b) density ; (c) pressure (P); and (d) magnetic pressure (E); for cylindrically symmetric flow () with and .
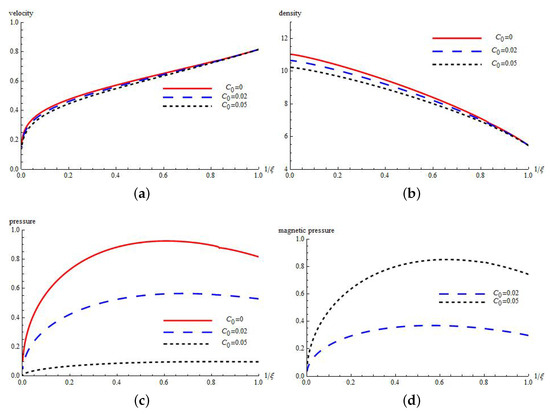
Figure 2.
Flow patterns of non-dimensional (a) velocity (U); (b) density ; (c) pressure (P); and (d) magnetic pressure (E) for cylindrically symmetric flow () with and .
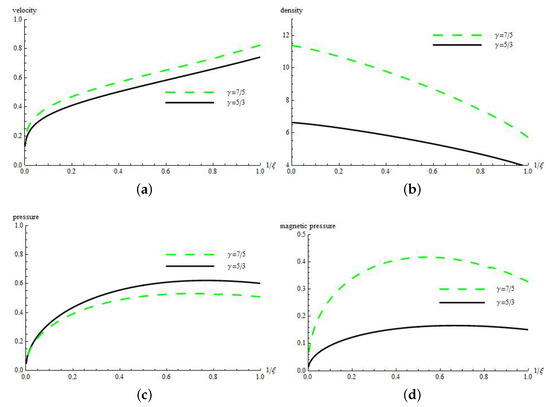
Figure 3.
Flow patterns of non-dimensional (a) velocity (U); (b) density ; (c) pressure (P); and (d) magnetic pressure E for cylindrically symmetric flow () with and .
Figure 1, Figure 2 and Figure 3 show that, as we move to the axis of convergence, i.e., when , there is an increase in density and decrease in velocity. Pressure and magnetic pressure are such that they first increase and attain their maximum values and then start to decrease. Figure 1 shows that, for the fixed values of and , when the value of b increases, the velocity, density and magnetic pressure of the gas decrease, while the pressure increases. Figure 2 shows that, for the fixed values of b and , when the value of increases, the velocity, density and pressure of the gas decrease, while the magnetic pressure increases. Figure 3 shows that, for the fixed values of and b, when the value of increases the velocity, density and magnetic pressure of the gas decrease, while the pressure increases. The reason behind this type of profiles’ behavior is that the particles of gas experience shock compression while moving across it. In fact, this behavior of profiles can also be regarded as the property of geometrical convergence of the shock wave or area contraction.
7. Conclusions
We have used the Lie group theoretic method to find a similarity solution of a problem of converging cylindrical shock in real gases. For most real gases, . The magnetic field is taken in an axial direction and presented in our problem by the parameter . Propagation of cylindrical shocks under these conditions are useful in Inertial Confinement Fusion (ICF). A complete description of Lie group transformations is presented in the article for the problem. Invariance of governing system of PDEs and boundary conditions under the Lie group of transformation is used to obtain the Lie generators and similarity variable. Similarity variable reduces the system of PDEs to the system of ODEs. Furthermore, the arbitrary constants in generators give rise to four different possible cases. One of the cases has been worked out in detail and the effect of magnetic field and non-ideal parameter is studied. Figure 1a–d shows the effect of b on the flow field behind the shock. It can be seen in Figure 1a that velocity decreases with an increase in b. It is a physically correct result as the increase in a non-ideal property will increase the collisions of gas molecules, which, in turn, will reduce the root mean square velocity of the gas molecules. Increased collisions with the increase in a non-ideal property of the medium will create higher pressure behind the converging shock as may be seen in Figure 1c. In Figure 2a,d, the effect of is presented on a flow field behind converging cylindrical shock. It can be seen in Figure 2c that the pressure behind the shock decreases with the increase in . It can be understood as the charged particles are transported away by the strong magnetic field. Different real gases have different values of . Therefore, the effect of on flow profiles has been presented in Figure 3a,d. It can be seen by Figure 3a that velocity decreases with increase in associated with a real gas. However, pressure shows the increment with the increase in .
Author Contributions
All authors contributed equally in the paper.
Funding
This research was funded by the Ministry of Human Resource and Development (MHRD), India.
Acknowledgments
Munesh Devi is thankful to the Ministry of Human Resource and Development (MHRD), India for the financial support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Taylor, G.I. The formation of a blast wave by a very intense explosion, I, Theoretical discussion. Proc. R. Soc. Lond. A 1950, 201, 159–174. [Google Scholar]
- Sedov, L.I. Similarity and Dimensional Methods in Mechanics; Academic Press: New York, NY, USA, 1959. [Google Scholar]
- Zeldovich, Y.B.; Raizer, Y.P. Physics of Shock Waves and High Temperature Hydrodynamic Phenomena; Academic Press: New York, NY, USA, 1967; Volume II. [Google Scholar]
- Barenblatt, G.I. Scaling, Self-Similarity, and Intermediate Asymptotics; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- Rahman, M.M.; Cheng, W.; Samtaney, R.; Urzay, J. Large-Eddy Simulations of Sandstorms as Charged- Particle Suspensions in Turbulent Boundary Layers-Multi-Phase Flows. In Center of Turbulence Research, Stanford, Proceedings of the Summer Program. 2016. Available online: https://stanford.app.box.com/s/bvmv4piwenf3jbe1r4ec17e8lt8c0aam (accessed on 1 September 2019).
- Rahman, M.M.; Samtaney, R. Modeling and analysis of large-eddy simulations of particle-laden turbulent boundary layer flow-RANS and LES Methods. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; pp. 981–992. [Google Scholar]
- Rahman, M.M.; Shevare, G.R. Analysis of Conservation Laws of Non-Linear Springs. In Proceedings of the 13th AeSI CFD Symposium, Indian Institute of Science (IISc), Bangalore, India, 11–12 August 2011. [Google Scholar]
- Guderley, G. Starke kugelige und zylindrische Verdichtungsstosse in der Nahe des Kugelmittelpunktes bzw. Luftfahrt Schung 1942, 19, 302–312. [Google Scholar]
- Korobeinikov, V.P. Problem in the Theory of Point Explosion in Gases; American Math. Soc.: Providence, RI, USA, 1976. [Google Scholar]
- Arora, R.; Siddiqui, M.J.; Singh, V.P. Similarity Method for Imploding Strong Shocks in a Non-Ideal Relaxing Gas. Int. J. Non-Linear Mech. 2013, 57, 1–9. [Google Scholar] [CrossRef]
- Steeb, S. Similarity solutions of the Euler equation and the Navier-Stokes equation in two space dimensions. Int. J. Theor. Phys. 1985, 24, 255–265. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Ovasiannikov, L.V. Group Analysis of Differential Equations; Academic: New York, NY, USA, 1982. [Google Scholar]
- Logan, J.D. Applied Mathematics, A Contemporary Approach; Wiley-Interscience: New York, NY, USA, 1987. [Google Scholar]
- Bluman, G.W.; Cole, J.D. Similarity Methods for Differential Equations; Springer: Berlin, Germany, 1974. [Google Scholar]
- Van Dyke, M.; Guttmann, A.J. The converging shock wave from a spherical or cylindrical piston. J. Fluid Mech. 1982, 120, 451–462. [Google Scholar] [CrossRef]
- Whitham, G.B. Linear and Non-Linear Waves; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Hafner, P. Strong convergent shock waves near the center of convergence: A power series solution. SIAM J. Appl. Math. 1988, 48, 1244–1261. [Google Scholar] [CrossRef]
- Madhumita, G.; Sharma, V.D. Imploding cylindrical and spherical shock waves in a non-ideal medium. J. Hyperb. Differ. Equ. 2004, 1, 521–530. [Google Scholar] [CrossRef]
- Radha, C.; Sharma, V.D. Imploding cylindrical shock in a perfectly conducting and radiating gas. Phys. Fluids Plasma Phys. 1993, 5, 4287. [Google Scholar] [CrossRef]
- Pey, M.; Sharma, V.D.; Radha, R. Symmetry analysis and exact solution of magnetogasdynamic equations. Q. J. Mech. Appl. Math. 2008, 61, 291–310. [Google Scholar]
- Singh, L.P.; Husain, A.; Singh, M. An analytical study of strong non-planar shock waves in magnetogasdynamics. Adv. Theor. Appl. Mech. 2010, 6, 291–297. [Google Scholar]
- Baty, R.S.; Tucker, D.H. Jump conditions for shock waves on the surface of a star. Astrophys. Space Sci. 2009, 319, 23–30. [Google Scholar] [CrossRef]
- Singh, J.B.; Pey, S.K. Analytical solutions of cylindrical shock waves in magnetogasdynamics. Astrophys. Space Sci. 1988, 148, 85–93. [Google Scholar] [CrossRef]
- Chisnell, R.F. An analytic description of converging shock waves. J. Fluid Mech. 1998, 354, 357–375. [Google Scholar] [CrossRef]
- Patel, N.H.; Ranga, M.P. Imploding shocks in a non-ideal medium. J. Eng. Math. 1996, 30, 683–692. [Google Scholar] [CrossRef]
- Arora, R.; Sharma, V.D. Convergence of strong shock in a van der Waals gas. SIAM J. Appl. Math. 2006, 66, 1825–1837. [Google Scholar] [CrossRef]
- Arora, R. Non-planar shock waves in a magnetic field. Comput. Math. Appl. 2008, 56, 2686–2691. [Google Scholar] [CrossRef][Green Version]
- Chauhan, A.; Arora, R.; Tomar, A. Convergence of strong shock waves in non-ideal magnetogasdynamics. Phys. Fluids 2018, 30, 116105. [Google Scholar] [CrossRef]
- Ram, S.D.; Singh, R.; Singh, L.P. An exact analytical solution of the strong shock wave problem in non-ideal magnetogasdynamics. J. Fluids 2013, 2013, 810206. [Google Scholar] [CrossRef]
- Wu, C.C.; Roberts, P.H. Structure and stability of a spherical shock wave in a van der Waals gas. Q. J. Mech. Appl. Math. 1996, 49, 501–543. [Google Scholar] [CrossRef]
- Sharma, V.D.; Arora, R. Similarity solutions for strong shocks in an ideal gas. Stud. Appl. Math. 2005, 114, 375–394. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).