Numerical Solution of Non-Newtonian Fluid Flow Due to Rotatory Rigid Disk
Abstract
1. Introduction
2. Problem Formulation
3. Computational Outline
4. Analysis
5. Closing Remarks
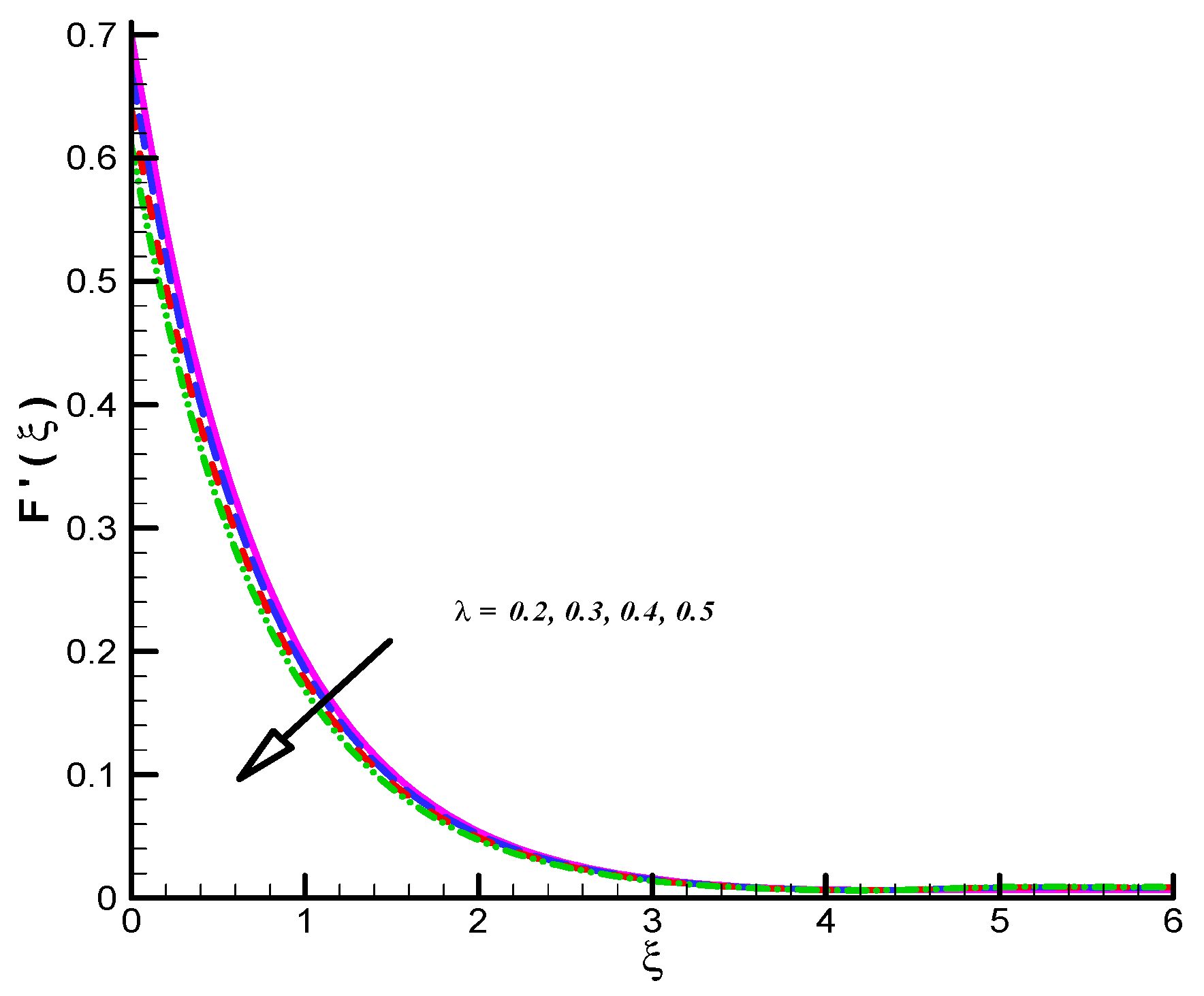
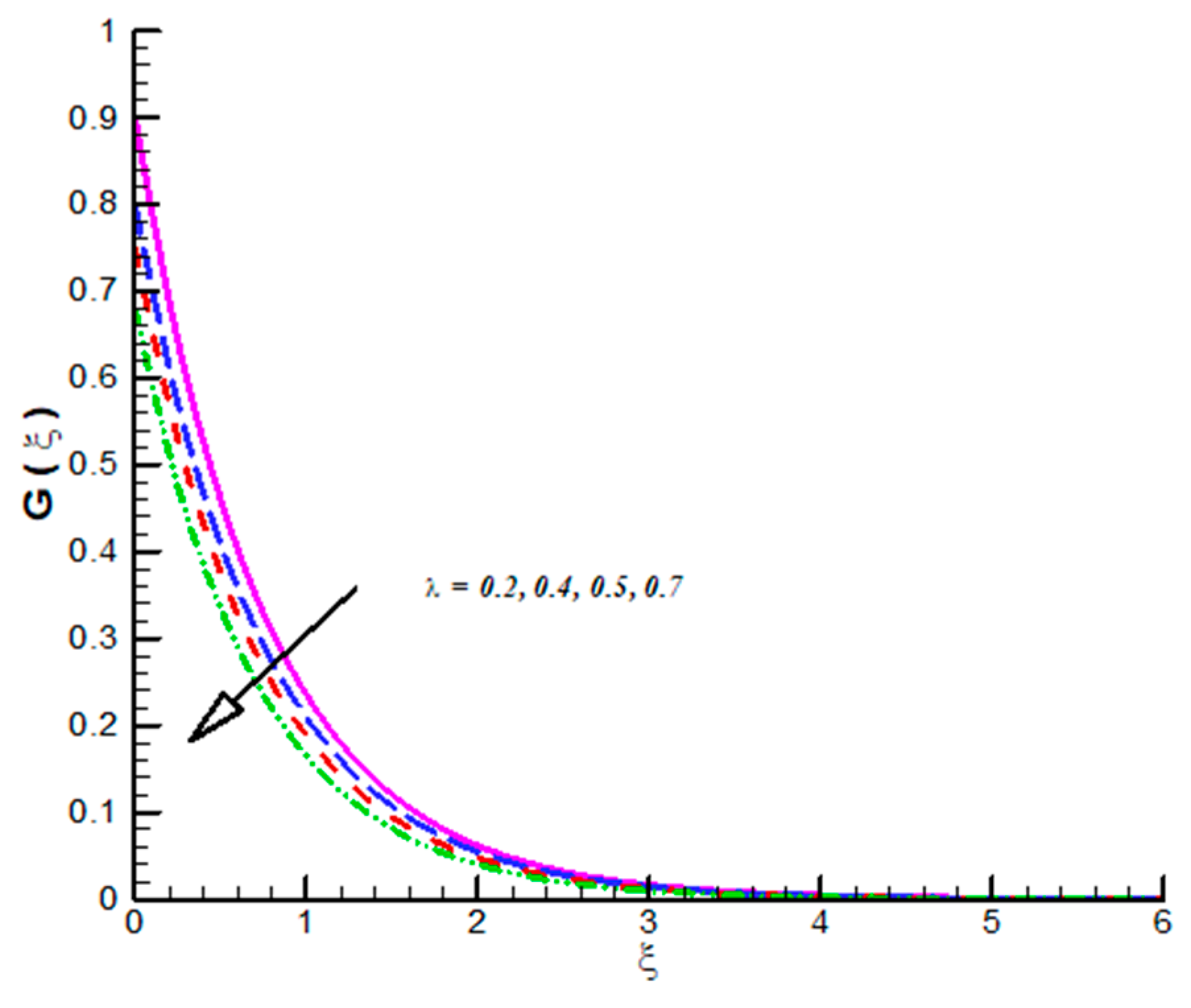
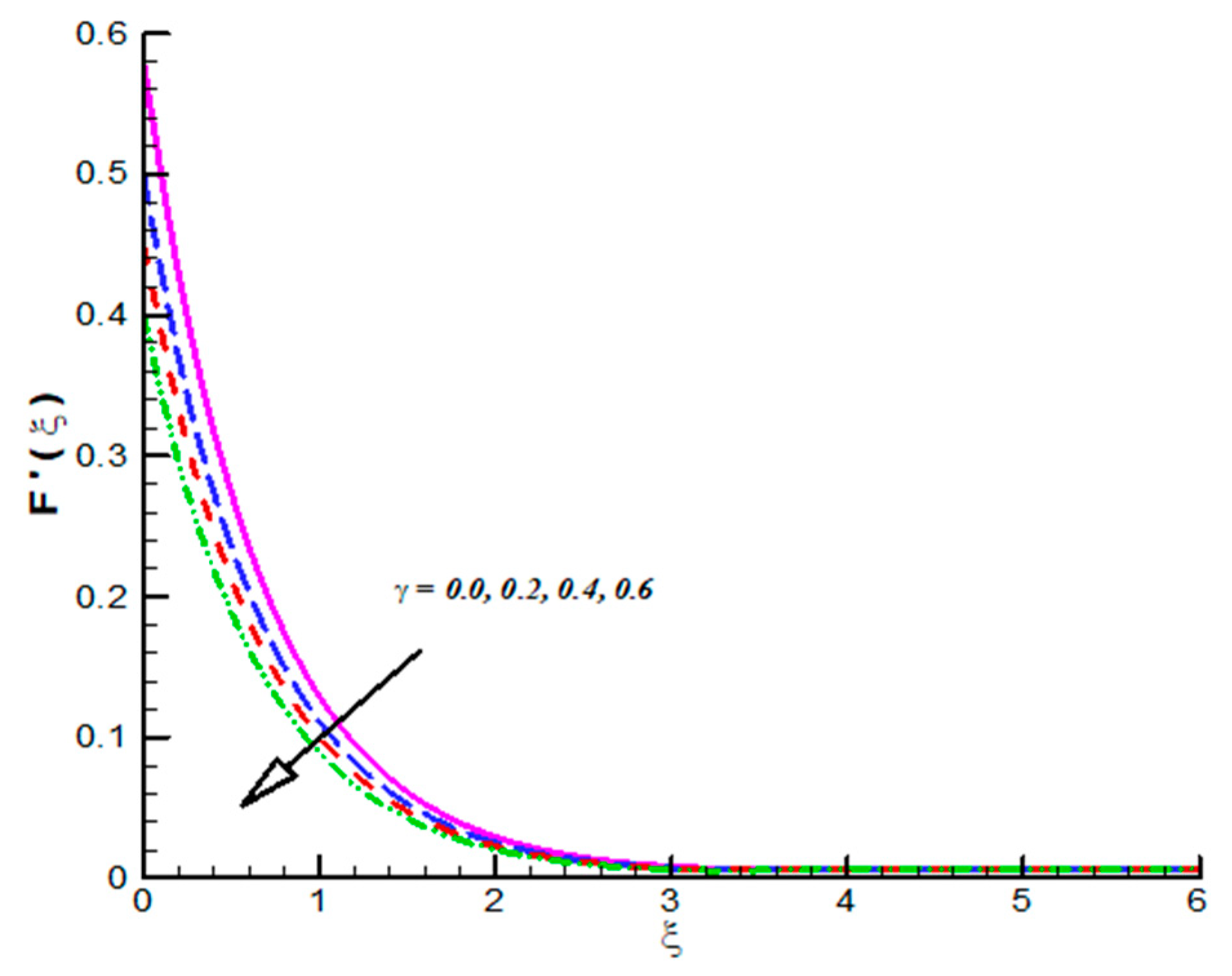
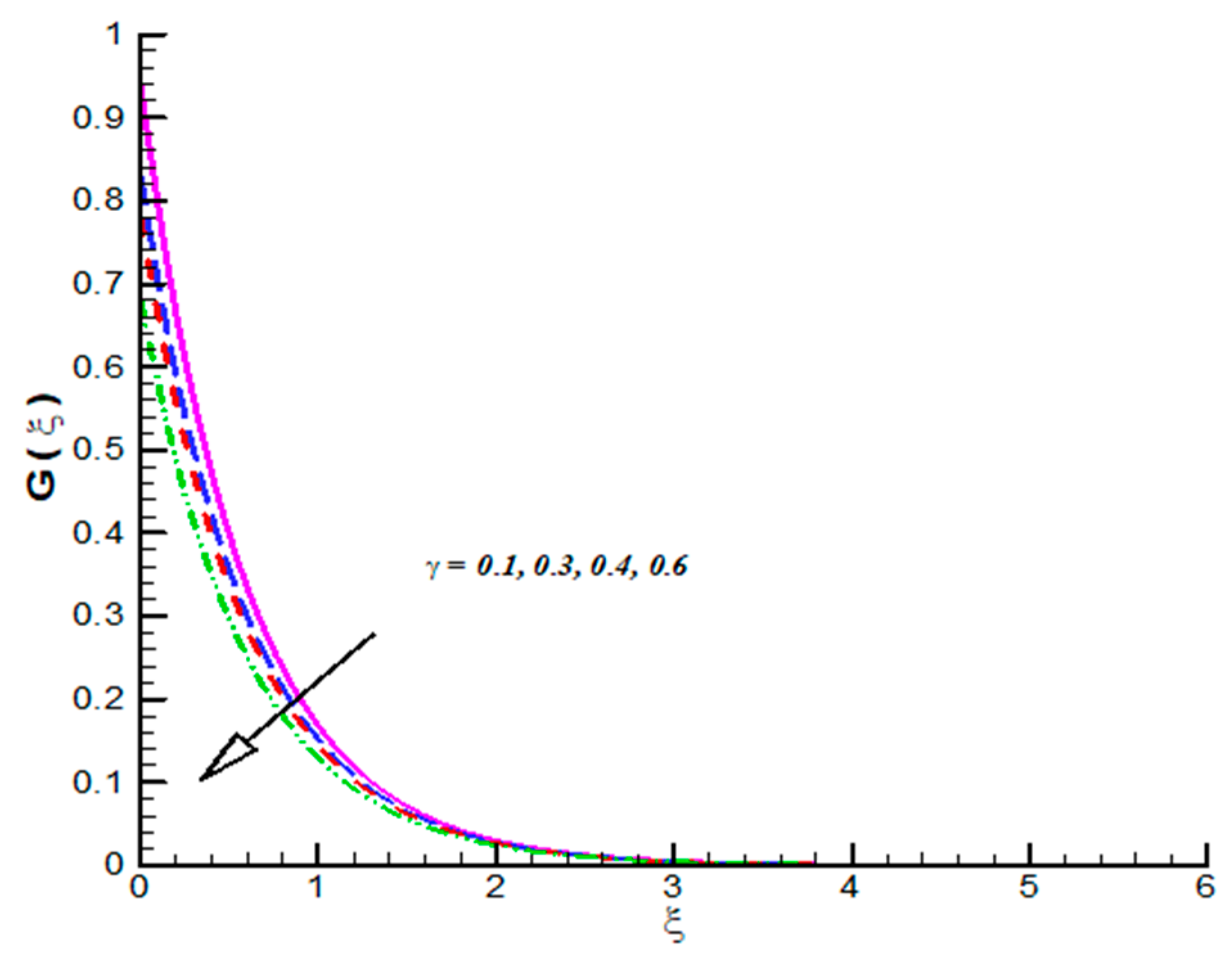
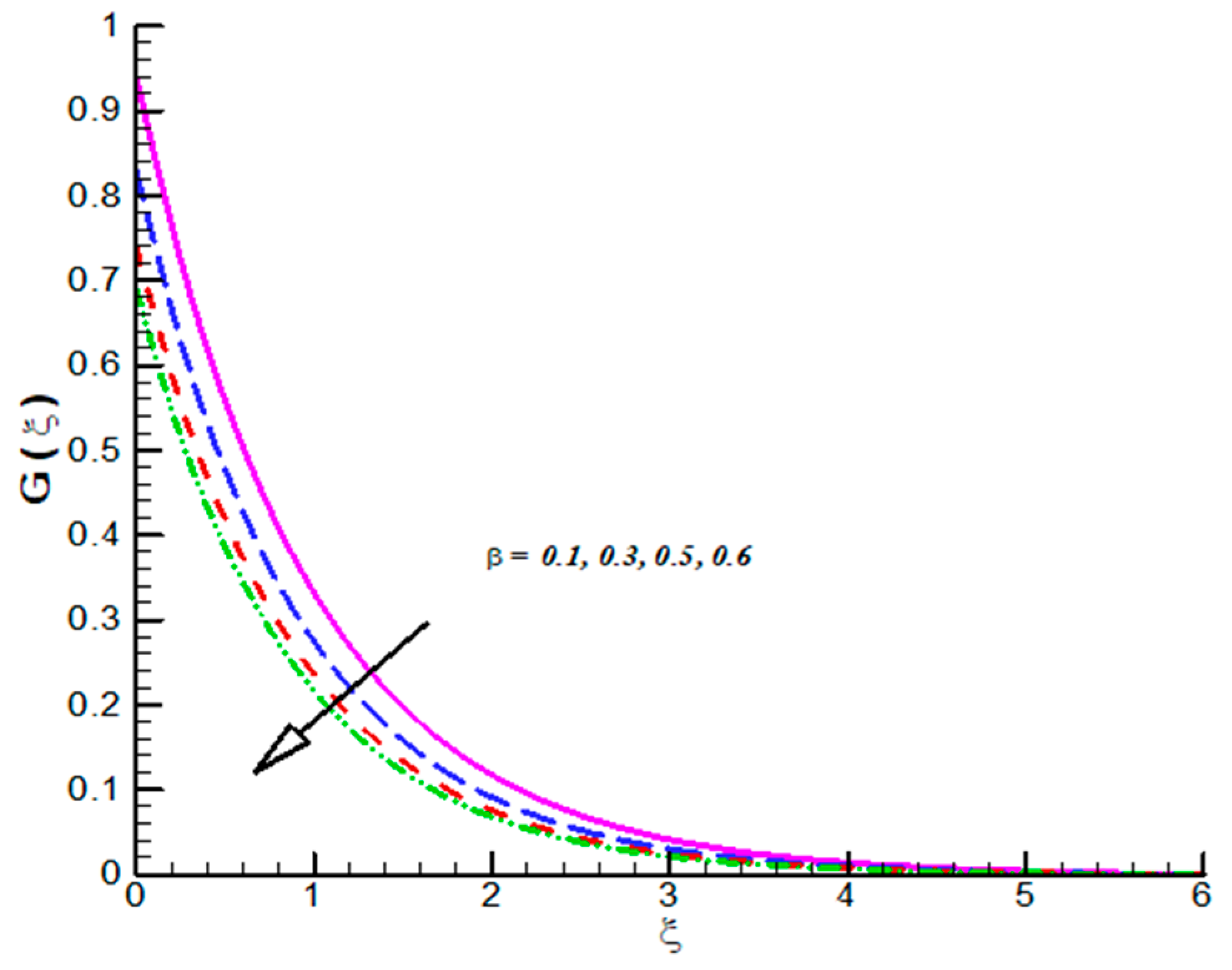
- CF velocities which includes reflects decline trend towards .
- CF velocities are decreasing function of and .
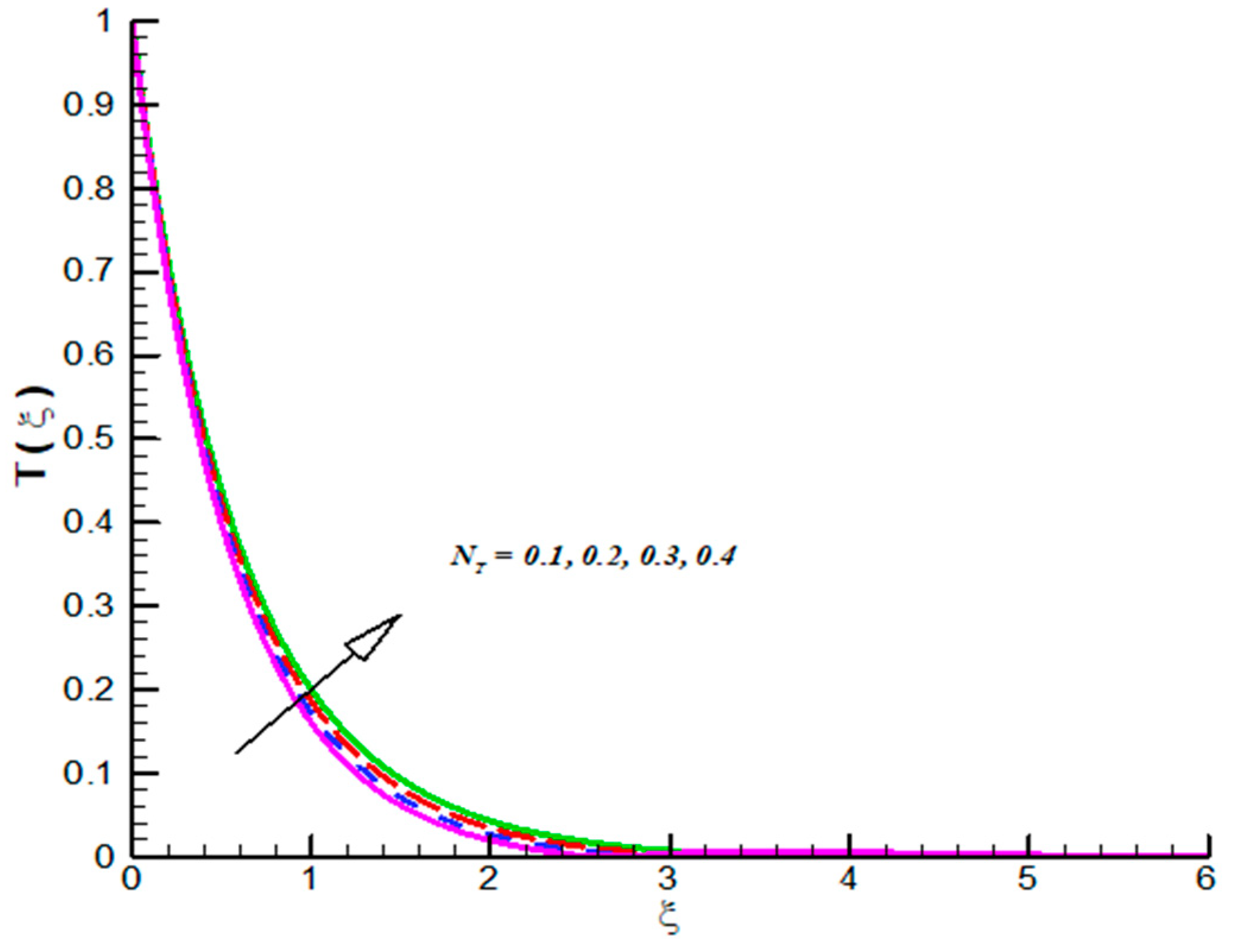
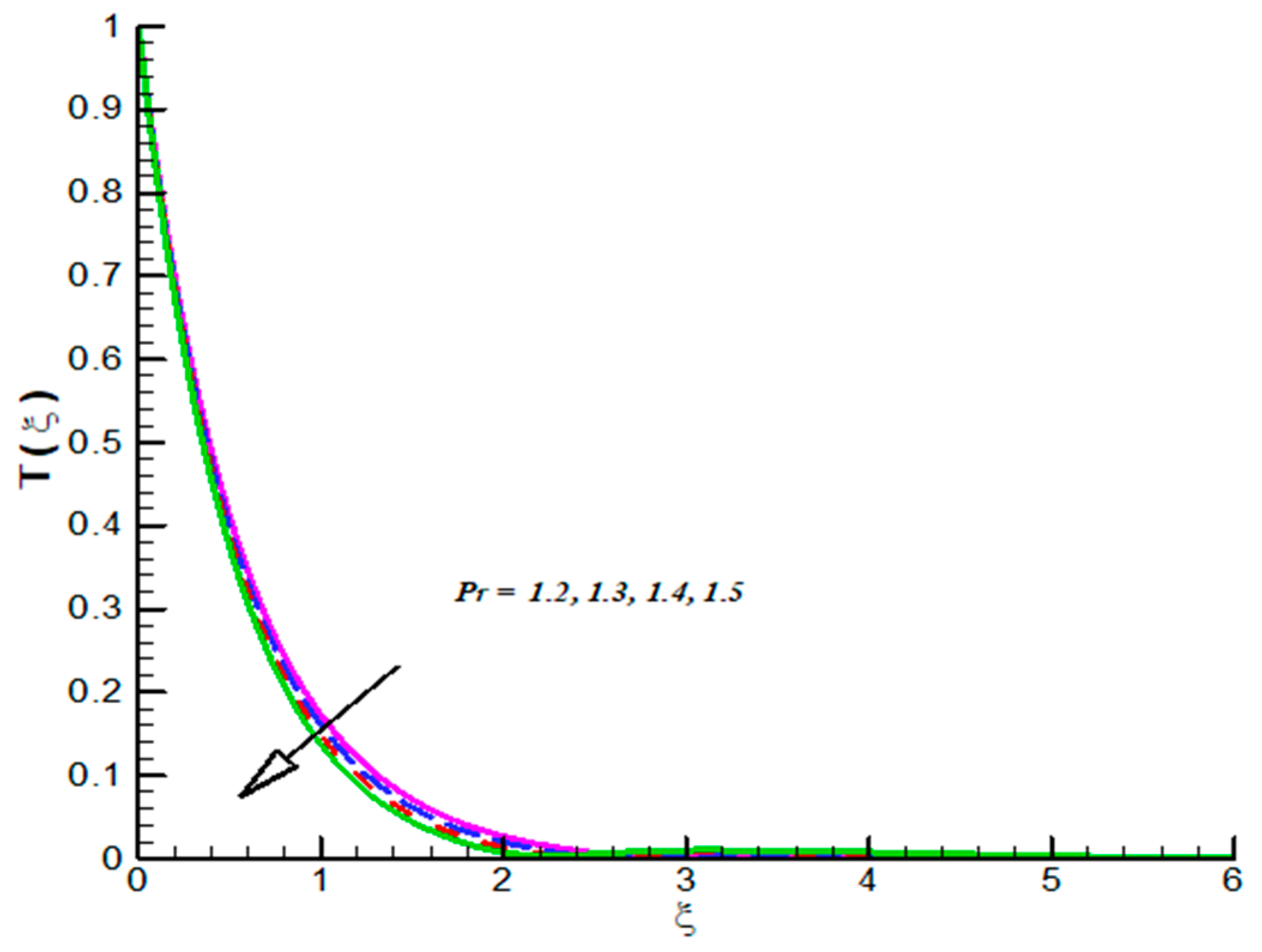
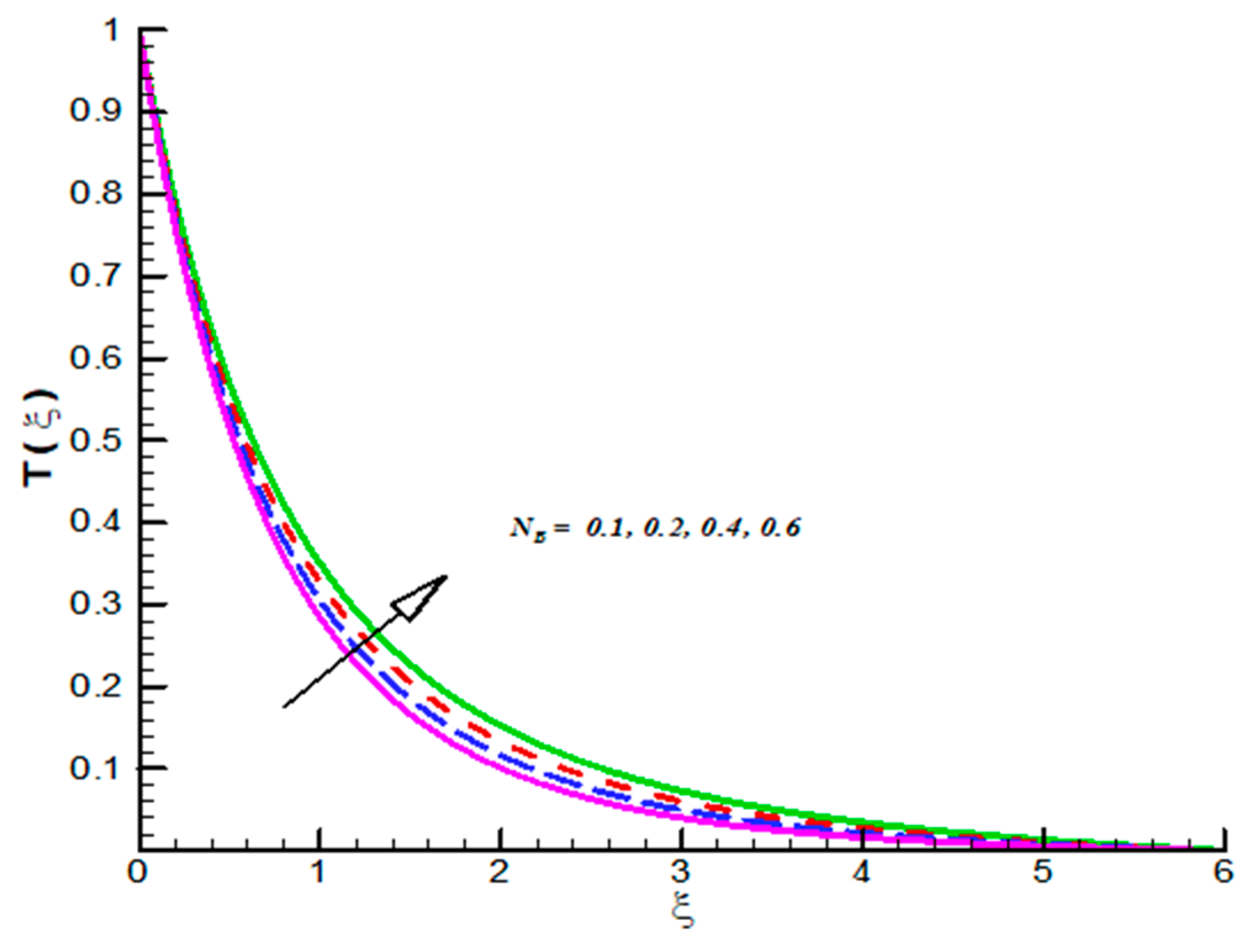
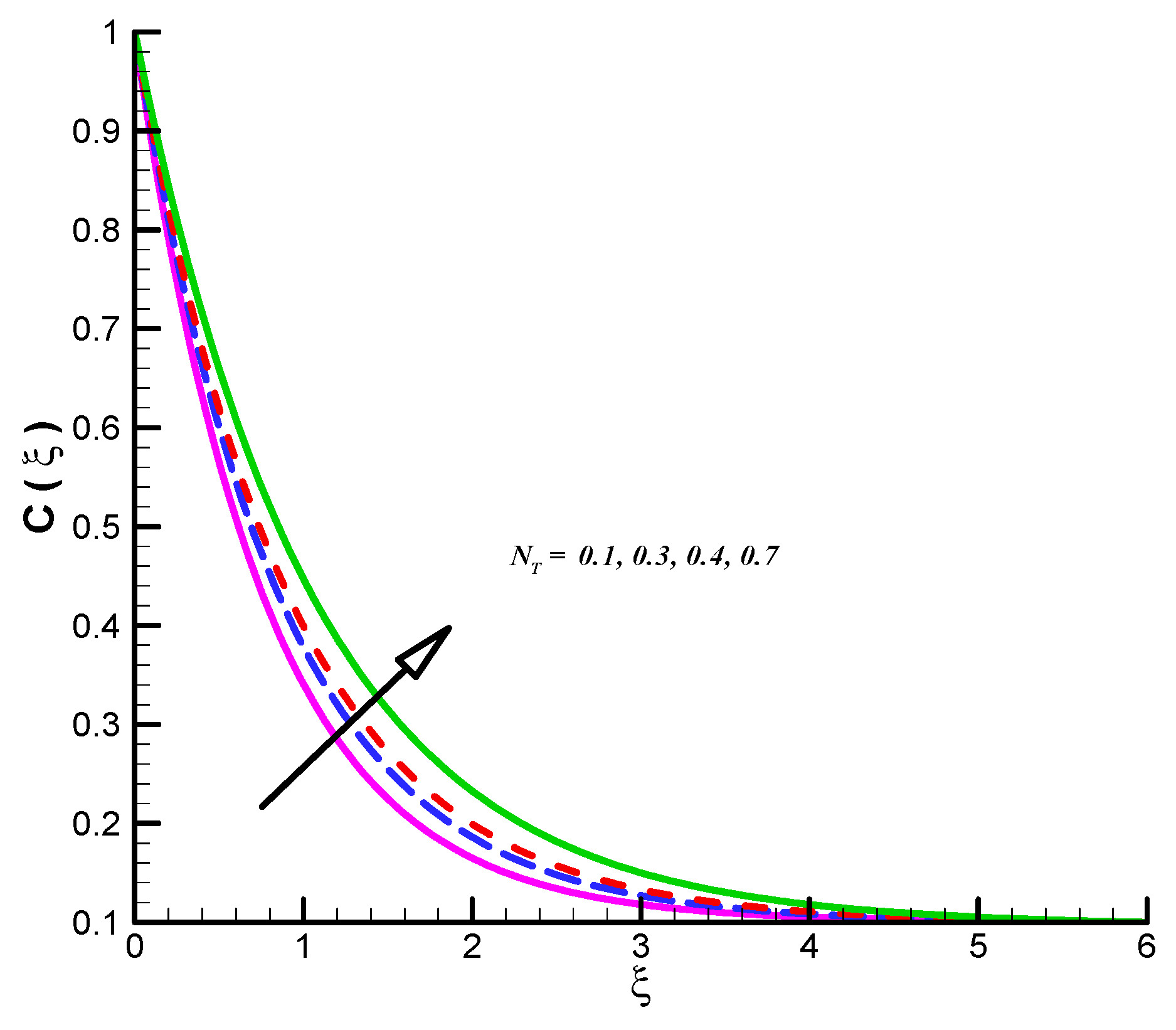
- CFT admits inciting nature towards both and but opposite trend is observed for Pr.
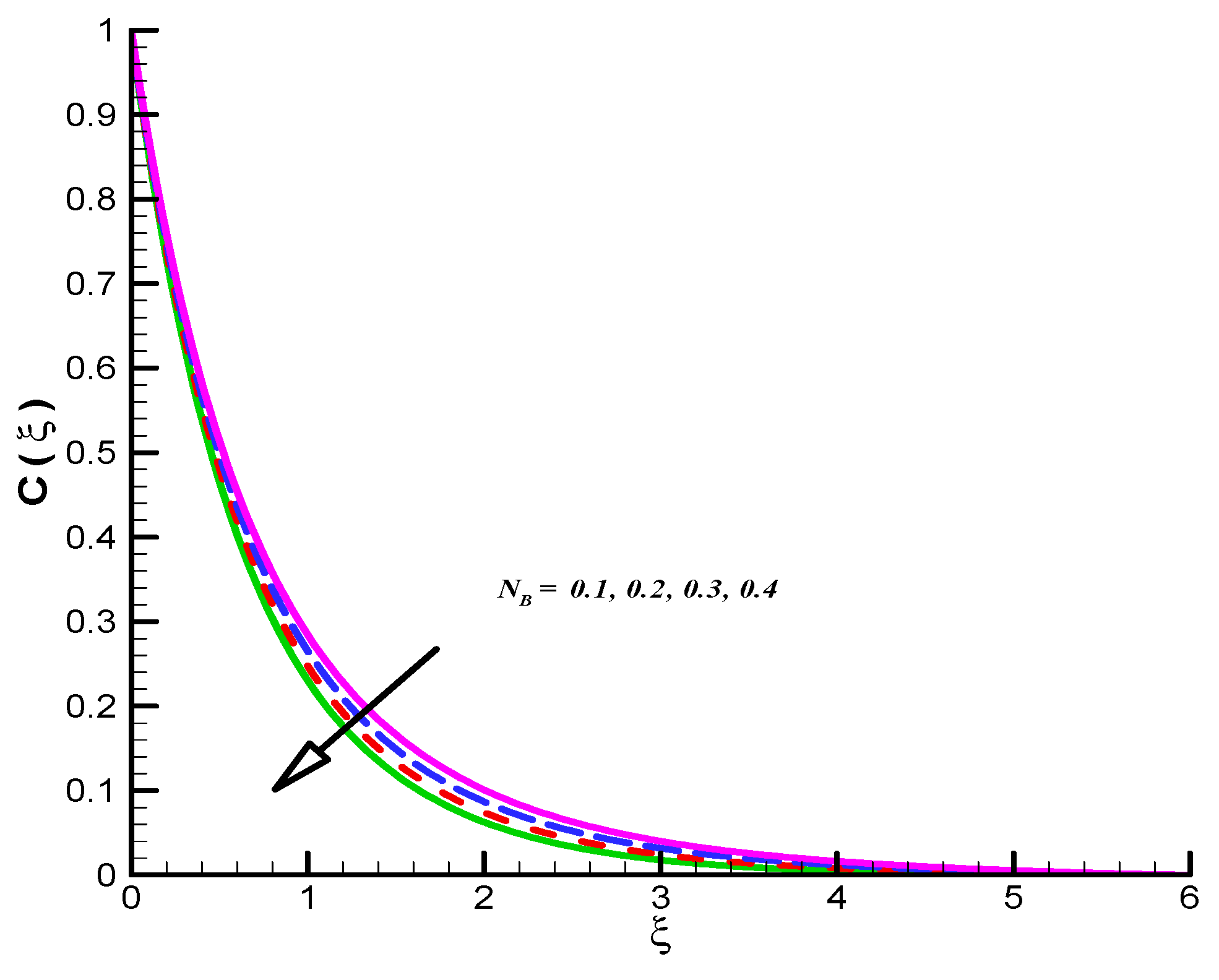
- CFC shows decline values for both Le, and .
- CFC reflect inciting trend for .
- Comparative values of HTR and MTR are provided for involved flow controlling parameters.
Author Contributions
Funding
Acknowledgment
Conflicts of Interest
Nomenclature
| Velocity field | |
| (, , ) | Polar coordinates |
| Kinematic viscosity | |
| Casson fluid parameter | |
| Fluid density | |
| Electrical conductivity | |
| Uniform applied magnetic field | |
| Thermal diffusivity | |
| Brownian diffusion coefficient | |
| Thermophoretic diffusion coefficient | |
| Ambient temperature | |
| Velocity slip parameter | |
| Surface temperature | |
| Surface concentration | |
| Concentration | |
| Dimensionless velocities | |
| Dimensionless temperature | |
| Dimensionless concentration | |
| Magnetic field parameter | |
| Prandtl number | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| Lewis number | |
| Velocity slip parameter | |
| Reynolds number |
References
- Mustafa, M.; Hayat, T.; Pop, I.; Aziz, A. Unsteady boundary layer flow of a Casson fluid due to an impulsively started moving flat plate. Heat Transf. Asian Res. 2011, 6, 563–576. [Google Scholar] [CrossRef]
- Nadeem, S.; Rizwan, U.H.; Lee, C. MHD flow of a Casson fluid over an exponentially shrinking sheet. Sci. Iran. 2012, 19, 1550–1553. [Google Scholar] [CrossRef]
- Mustafa, M.; Tasawar, H.; Pop, I.; Awatif, H. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet. Z. Naturforsch. A 2012, 67, 70–76. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chin. Phys. B 2013, 22, 074701. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Iswar, C.M.; Tasawar, H. MHD boundary layer flow of Casson fluid passing through an exponentially stretching permeable surface with thermal radiation. Chin. Phys. B 2014, 23, 104701. [Google Scholar] [CrossRef]
- Mustafa, M.; Junaid, A.K. Model for flow of Casson nanofluid past a non-linearly stretching sheet considering magnetic field effects. AIP Adv. 2015, 5, 077148. [Google Scholar] [CrossRef]
- Ramesh, K.; Devakar, M. Some analytical solutions for flows of Casson fluid with slip boundary conditions. Ain Shams Eng. J. 2015, 6, 967–975. [Google Scholar] [CrossRef]
- Sandeep, N.; Olubode, K.K.; Isaac, L.A. Modified kinematic viscosity model for 3D-Casson fluid flow within boundary layer formed on a surface at absolute zero. J. Mol. Liq. 2016, 221, 1197–1206. [Google Scholar] [CrossRef]
- Qing, J.; Muhammad, M.B.; Munawwar, A.A.; Mohammad, M.R.; Mohamed, E.-S.A. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy 2016, 18, 123. [Google Scholar] [CrossRef]
- Ali, M.E.; Sandeep, N. Cattaneo-christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: A numerical study. Results Phys. 2017, 7, 21–30. [Google Scholar] [CrossRef]
- Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. Enhanced heat transfer in the flow of dissipative non-Newtonian Casson fluid flow over a convectively heated upper surface of a paraboloid of revolution. J. Mol. Liq. 2017, 229, 380–388. [Google Scholar] [CrossRef]
- Rehman, K.U.; Aneeqa, A.M.; Malik, M.Y.; Sandeep, N.; Saba, N.U. Numerical study of double stratification in Casson fluid flow in the presence of mixed convection and chemical reaction. Results Phys. 2017, 7, 2997–3006. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017, 233, 262–269. [Google Scholar] [CrossRef]
- Ali, F.; Nadeem, A.S.; Ilyas, K.; Muhammad, S. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Mohammad, M.H.; Sivasankar, T. Radiative flow of Casson fluid over a moving wedge filled with gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 575–583. [Google Scholar] [CrossRef]
- Kármán, T.V. Über laminare und turbulente Reibung. ZAMM 1921, 1, 233–252. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Senel, P. Heat and mass transfer of the flow due to a rotating rough and porous disk. Int. J. Therm. Sci. 2013, 63, 146–158. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Kavyani, N.; Abelman, S. Investigation of entropy generation in MHD and slip flow over a rotating porous disk with variable properties. Int. J. Heat Mass Transf. 2014, 70, 892–917. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Nanofluid flow and heat transfer due to a rotating disk. Comput. Fluids 2014, 94, 139–146. [Google Scholar] [CrossRef]
- Griffiths, P.T.; Stephen, J.G.; Stephen, S.O. The neutral curve for stationary disturbances in rotating disk flow for power-law fluids. J. Non Newton. Fluid Mech. 2014, 213, 73–81. [Google Scholar] [CrossRef][Green Version]
- Mustafa, M.; Junaid, A.K.; Hayat, T.; Alsaedi, A. On Bödewadt flow and heat transfer of nanofluids over a stretching stationary disk. J. Mol. Liq. 2015, 211, 119–125. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Hatami, M.; Ganji, D.D. Numerical investigation of nanofluid spraying on an inclined rotating disk for cooling process. J. Mol. Liq. 2015, 211, 577–583. [Google Scholar] [CrossRef]
- Xun, S.; Zhao, J.; Zheng, L.; Chen, X.; Zhang, X. Flow and heat transfer of Ostwald-de Waele fluid over a variable thickness rotating disk with index decreasing. Int. J. Heat Mass Transf. 2016, 103, 1214–1224. [Google Scholar] [CrossRef]
- Latiff, N.A.; Uddin, M.J.; Ismail, A.M. Stefan blowing effect on bioconvective flow of nanofluid over a solid rotating stretchable disk. Propuls. Power Res. 2016, 5, 267–278. [Google Scholar] [CrossRef]
- Ming, C.; Zheng, L.; Zhang, X.; Liu, F.; Anh, V. Flow and heat transfer of power-law fluid over a rotating disk with generalized diffusion. Int. Commun. Heat Mass Transf. 2016, 79, 81–88. [Google Scholar] [CrossRef]
- Imtiaz, M.; Tasawar, H.; Ahmed, A.; Saleem, A. Slip flow by a variable thickness rotating disk subject to magnetohydrodynamics. Results Phys. 2017, 7, 503–509. [Google Scholar] [CrossRef]
- Doh, D.H.; Muthtamilselvan, M. Thermophoretic particle deposition on magnetohydrodynamic flow of micropolar fluid due to a rotating disk. Int. J. Mech. Sci. 2017, 130, 350–359. [Google Scholar] [CrossRef]
- Hayat, T.; Madiha, R.; Maria, I.; Ahmed, A. Nanofluid flow due to rotating disk with variable thickness and homogeneous-heterogeneous reactions. Int. J. Heat Mass Transf. 2017, 113, 96–105. [Google Scholar] [CrossRef]
- Devi, M.; Chitra, L.; Rajendran, A.B.Y.; Fernandez, C. Non-linear differential equations and rotating disc electrodes: Padé approximationtechnique. Electrochim. Acta 2017, 243, 1–6. [Google Scholar] [CrossRef]
- Guha, A.; Sayantan, S. Non-linear interaction of buoyancy with von Kármán’s swirling flow in mixed convection above a heated rotating disc. Int. J. Heat Mass Transf. 2017, 108, 402–416. [Google Scholar] [CrossRef]
- Ellahi, R.; Ahmed, Z.; Farooq, H.; Tehseen, A. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Hayat, T.; Taseer, M.; Sabir, A.S.; Ahmed, A. On magnetohydrodynamic flow of nanofluid due to a rotating disk with slip effect: A numerical study. Comput. Methods Appl. Mech. Eng. 2017, 315, 467–477. [Google Scholar] [CrossRef]
- Vo, T.Q.; Park, B.S.; Park, C.H.; Kim, B.H. Nano-scale liquid film sheared between strong wetting surfaces: Effects of interface region on the flow. J. Mech. Sci. Technol. 2015, 29, 1681–1688. [Google Scholar] [CrossRef]
- Kherbeet, A.; Sh, H.A.; Mohammed, B.H.; Salman, H.E.; Ahmed, O.; Alawi, A.; Rashidi, M.M. Experimental study of nanofluid flow and heat transfer over microscale backward-and forward-facing steps. Exp. Therm. Fluid Sci. 2015, 65, 13–21. [Google Scholar] [CrossRef]
- Abbas, T.; Muhammad, A.; Muhammad, B.; Mohammad, R.; Mohamed, A. Entropy generation on nanofluid flow through a horizontal Riga plate. Entropy 2016, 18, 223. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Abbas, T.; Rashidi, M.M. Numerical study of entropy generation with nonlinear thermal radiation on magnetohydrodynamics non-Newtonian nanofluid through a porous shrinking sheet. J. Magn. 2016, 21, 468–475. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Alper, T.C.; Beskok, A. A phenomenological continuum model for force-driven nano-channel liquid flows. J. Chem. Phys. 2016, 145, 184109. [Google Scholar] [CrossRef]
- Bao, L.; Priezjev, N.V.; Hu, H.; Luo, K. Effects of viscous heating and wall-fluid interaction energy on rate-dependent slip behavior of simple fluids. Phys. Rev. E 2017, 96, 033110. [Google Scholar] [CrossRef]
- Ghorbanian, J.; Beskok, A. Temperature profiles and heat fluxes observed in molecular dynamics simulations of force-driven liquid flows. Phys. Chem. Chem. Phys. 2017, 19, 10317–10325. [Google Scholar] [CrossRef]
- Mohebbi, R.; Rashidi, M.M.; Mohsen, I.; Nor, A.C.S.; Hong, W.X. Forced convection of nanofluids in an extended surfaces channel using lattice Boltzmann method. Int. J. Heat Mass Transf. 2018, 117, 1291–1303. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Iffat, Z.; Alqarni, M.S. Group theoretical analysis for MHD flow fields: A numerical result. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 156. [Google Scholar] [CrossRef]
- Rehman, K.U.; Malik, M.Y.; Mahmood, R.; Kousar, N.; Zehra, I. A potential alternative CFD simulation for steady Carreau–Bird law-based shear thickening model: Part-I. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 176. [Google Scholar] [CrossRef]


| Hayat et al. [32] | Present values | ||||||
| 0.2 | - | - | - | - | - | 0.32655 | 0.326600 |
| 0.5 | - | - | - | - | - | 0.30360 | 0.30363 |
| 0.8 | - | - | - | - | - | 0.28715 | 0.28724 |
| - | 0.0 | - | - | - | - | 0.30494 | 0.30502 |
| - | 0.7 | - | - | - | - | 0.24421 | 0.24434 |
| - | 1.4 | - | - | - | - | 0.17566 | 0.17575 |
| - | - | 0.5 | - | - | - | 0.25913 | 0.25916 |
| - | - | 0.7 | - | - | - | 0.23865 | 0.23879 |
| - | - | 1.0 | - | - | - | 0.21010 | 0.21025 |
| - | - | 0.5 | - | - | 0.29633 | 0.29642 | |
| - | - | 1.0 | - | - | 0.28954 | 0.28963 | |
| - | - | - | 1.5 | - | - | 0.28395 | 0.28398 |
| - | - | - | - | 0.5 | - | 0.24989 | 0.24999 |
| - | - | - | - | 1.0 | - | 0.29211 | 0.29224 |
| - | - | - | - | 1.5 | - | 0.32286 | 0.32294 |
| - | - | - | - | - | 0.5 | 0.26341 | 0.26358 |
| - | - | - | - | - | 0.7 | 0.23677 | 0.23687 |
| - | - | - | - | - | 1.0 | 0.20056 | 0.20068 |
| Hayat et al. [32] | Present values | ||||||
| 0.2 | - | - | - | - | - | 0.27583 | 0.27593 |
| 0.5 | - | - | - | - | - | 0.26933 | 0.26945 |
| 0.8 | - | - | - | - | - | 0.26493 | 0.26498 |
| - | 0.0 | - | - | - | - | 0.27000 | 0.27012 |
| - | 0.7 | - | - | - | - | 0.25387 | 0.25394 |
| - | 1.4 | - | - | - | - | 0.23722 | 0.23735 |
| - | - | 0.5 | - | - | - | 0.22206 | 0.22215 |
| - | - | 0.7 | - | - | - | 0.22539 | 0.22564 |
| - | - | 1.0 | - | - | - | 0.22285 | 0.22288 |
| - | - | 0.5 | - | - | 0.21373 | 0.21380 | |
| - | - | 1.0 | - | - | 0.30132 | 0.30145 | |
| - | - | - | 1.5 | - | - | 0.38690 | 0.38696 |
| - | - | - | - | 0.5 | - | 0.22934 | 0.22944 |
| - | - | - | - | 1.0 | - | 0.26624 | 0.26636 |
| - | - | - | - | 1.5 | - | 0.31262 | 0.31276 |
| - | - | - | - | - | 0.5 | 0.30338 | 0.30342 |
| - | - | - | - | - | 0.7 | 0..31875 | 0..31887 |
| - | - | - | - | - | 1.0 | 0.32959 | 0.32978 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, K.U.; Malik, M.Y.; Khan, W.A.; Khan, I.; Alharbi, S.O. Numerical Solution of Non-Newtonian Fluid Flow Due to Rotatory Rigid Disk. Symmetry 2019, 11, 699. https://doi.org/10.3390/sym11050699
Rehman KU, Malik MY, Khan WA, Khan I, Alharbi SO. Numerical Solution of Non-Newtonian Fluid Flow Due to Rotatory Rigid Disk. Symmetry. 2019; 11(5):699. https://doi.org/10.3390/sym11050699
Chicago/Turabian StyleRehman, Khalil Ur, M. Y. Malik, Waqar A Khan, Ilyas Khan, and S. O. Alharbi. 2019. "Numerical Solution of Non-Newtonian Fluid Flow Due to Rotatory Rigid Disk" Symmetry 11, no. 5: 699. https://doi.org/10.3390/sym11050699
APA StyleRehman, K. U., Malik, M. Y., Khan, W. A., Khan, I., & Alharbi, S. O. (2019). Numerical Solution of Non-Newtonian Fluid Flow Due to Rotatory Rigid Disk. Symmetry, 11(5), 699. https://doi.org/10.3390/sym11050699





