Spin-Boson Model as A Simulator of Non-Markovian Multiphoton Jaynes-Cummings Models
Abstract
:1. Introduction
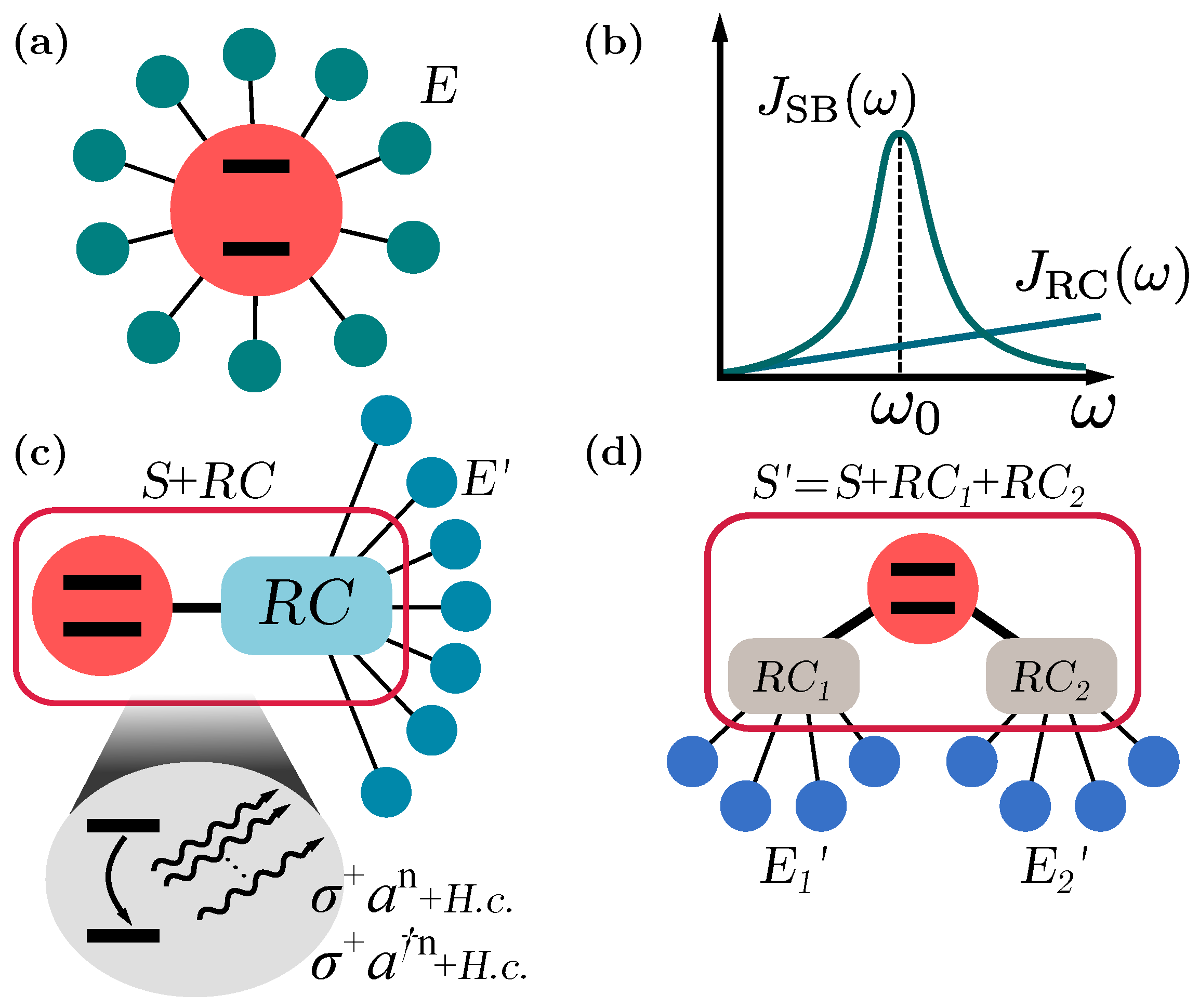
2. The Spin-Boson Model
3. Analogue Simulation of Multiphoton Spin-Boson Interactions
3.1. Reaction Coordinate Mapping
3.2. Structured Environments
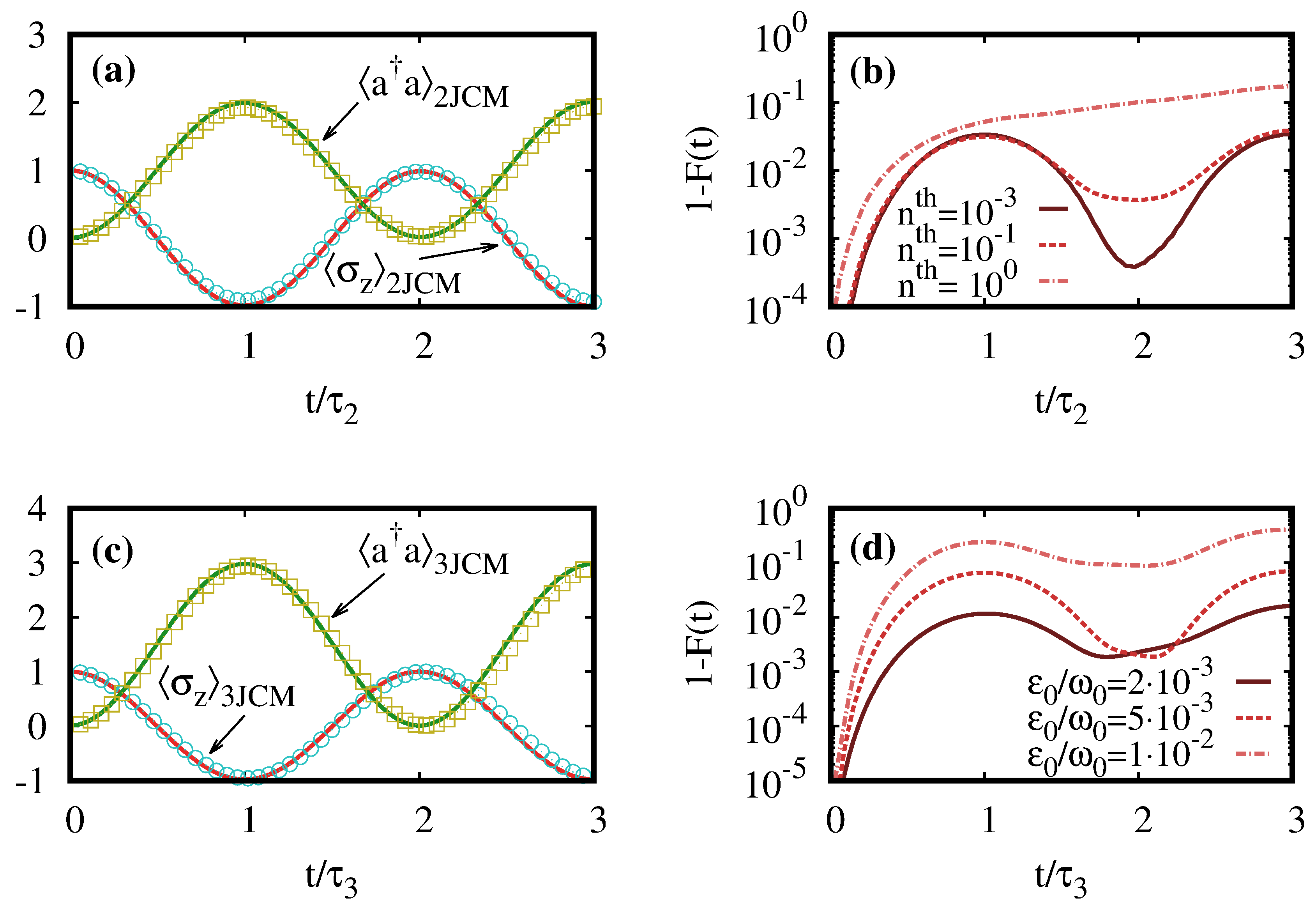
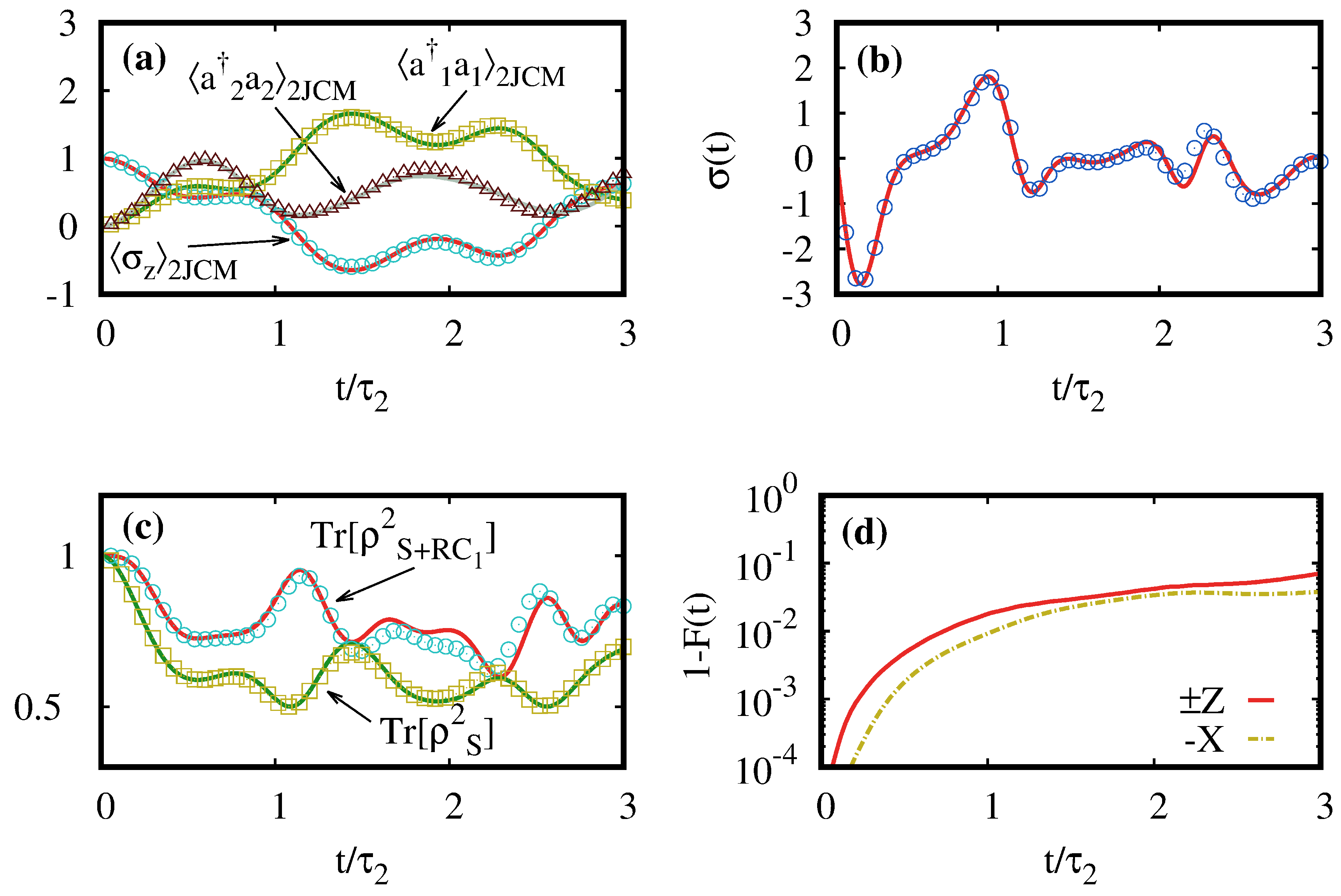
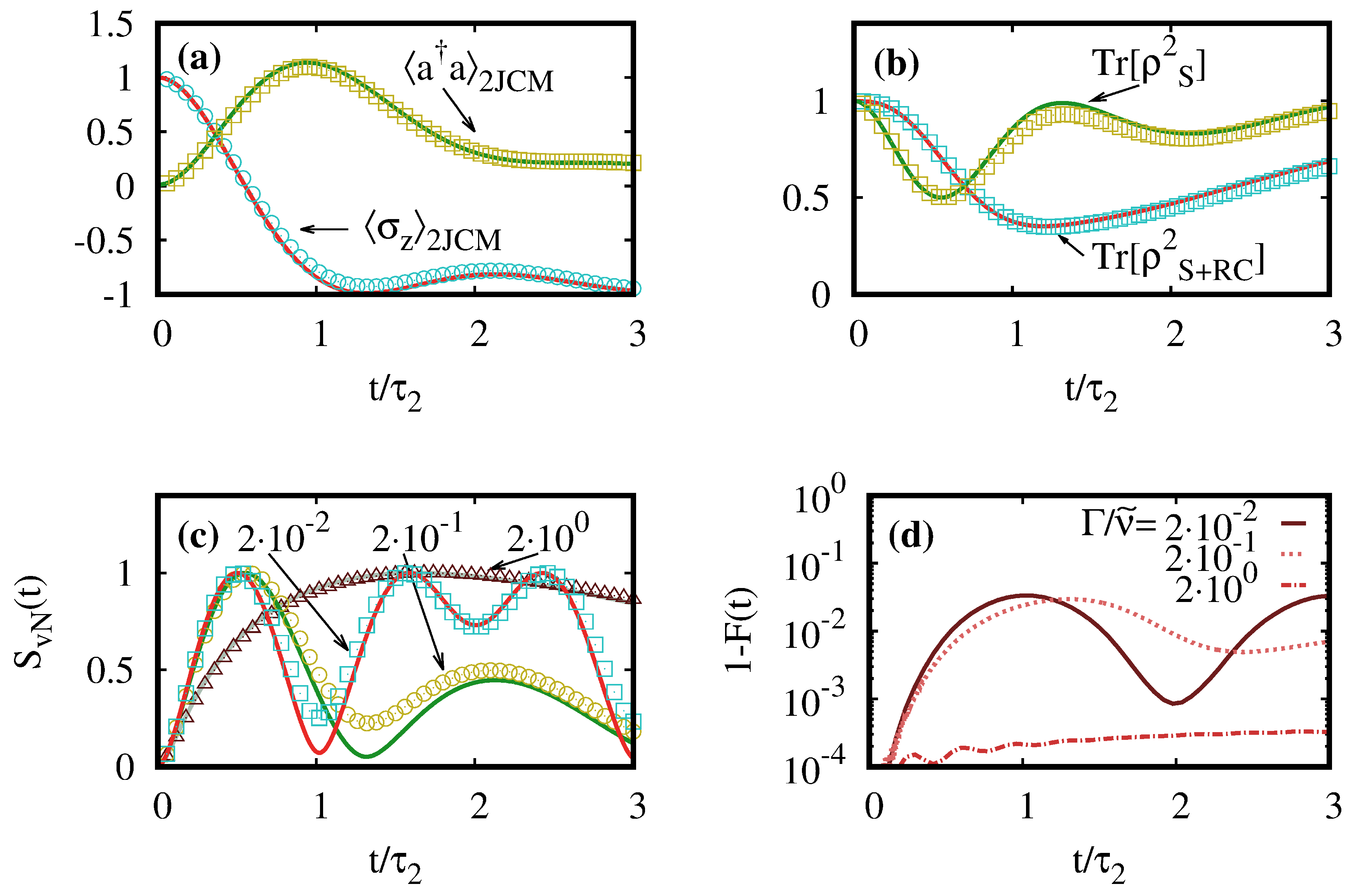
4. Examples and Numerical Simulations
4.1. Dissipationless Multiphoton Jaynes-Cummings Models
4.2. Dissipative Multiphoton Jaynes-Cummings Models
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Reaction Coordinate Mapping
Appendix B. Derivation of and
References
- Dowling, J.P.; Milburn, G.J. Quantum technology: the second quantum revolution. Phil. Trans. R. Soc. A 2003, 361, 1655–1674. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Feynman, R.P. Simulating physics with computers. Int. J. Theor. Phys. 1982, 21, 467–488. [Google Scholar] [CrossRef]
- Johnson, T.H.; Clark, S.R.; Jaksch, D. What is a quantum simulator? EPJ Quantum Technol. 2014, 1, 10. [Google Scholar] [CrossRef]
- Georgescu, I.M.; Ashhab, S.; Nori, F. Quantum simulation. Rev. Mod. Phys. 2014, 86, 153–185. [Google Scholar] [CrossRef]
- Bloch, I.; Dalibard, J.; Nascimbene, S. Quantum simulations with ultracold quantum gases. Nat. Phys. 2012, 8, 267–276. [Google Scholar] [CrossRef]
- Blatt, R.; Roos, C.F. Quantum simulations with trapped ions. Nat. Phys. 2012, 8, 277. [Google Scholar] [CrossRef]
- Leggett, A.J.; Chakravarty, S.; Dorsey, A.T.; Fisher, M.P.A.; Garg, A.; Zwerger, W. Dynamics of the dissipative two-state system. Rev. Mod. Phys. 1987, 59, 1–85. [Google Scholar] [CrossRef]
- Weiss, U. Quantum Dissipative Systems, 3rd ed.; World Scientific: Singapore, 2008. [Google Scholar]
- Rabi, I.I. On the process of space quantization. Phys. Rev. 1936, 49, 324–328. [Google Scholar] [CrossRef]
- Rabi, I.I. Space quantization in a gyrating magnetic field. Phys. Rev. 1937, 51, 652–654. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Scully, M.O.; Zubairy, M.S. Quantum Optics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Huelga, S.F.; Plenio, M.B. Vibrations, quanta and biology. Contemp. Phys. 2013, 54, 181–207. [Google Scholar] [CrossRef]
- Tanimura, Y.; Kubo, R. Time evolution of a quantum system in contact with a nearly gaussian-Markoffian noise Bath. J. Phys. Soc. Jpn. 1989, 58, 101–114. [Google Scholar] [CrossRef]
- Tanimura, Y. Nonperturbative expansion method for a quantum system coupled to a harmonic-oscillator bath. Phys. Rev. A 1990, 41, 6676–6687. [Google Scholar] [CrossRef] [PubMed]
- Prior, J.; Chin, A.W.; Huelga, S.F.; Plenio, M.B. Efficient simulation of strong system-environment interactions. Phys. Rev. Lett. 2010, 105, 050404. [Google Scholar] [CrossRef] [PubMed]
- Dattani, N.S.; Pollock, F.A.; Wilkins, D.M. Analytic Influence Functionals for Numerical Feynman Integrals in Most Open Quantum Systems. Available online: http://www.naturalspublishing.com/files/published/464k51t1luip94.pdf (accessed on 16 April 2019).
- Dattani, N.S. FeynDyn: A MATLAB program for fast numerical Feynman integral calculations for open quantum system dynamics on GPUs. Comput. Phys. Commun. 2013, 184, 2828–2833. [Google Scholar] [CrossRef]
- Wilkins, D.M.; Dattani, N.S. Why quantum coherence is not important in the Fenna-Matthews-Olsen complex. J. Chem. Theor. Comput. 2015, 11, 3411–3419. [Google Scholar] [CrossRef]
- Strathearn, A.; Kirton, P.; Kilda, D.; Keeling, J.; Lovett, B.W. Efficient non-Markovian quantum dynamics using time-evolving matrix product operators. Nat. Commun. 2018, 9, 3322. [Google Scholar] [CrossRef]
- Thoss, M.; Wang, H.; Miller, W.H. Self-consistent hybrid approach for complex systems: Application to the spin-boson model with Debye spectral density. J. Chem. Phys. 2001, 115, 2991–3005. [Google Scholar] [CrossRef]
- Martinazzo, R.; Vacchini, B.; Hughes, K.H.; Burghardt, I. Communication: Universal Markovian reduction of Brownian particle dynamics. J. Chem. Phys. 2011, 134, 011101. [Google Scholar] [CrossRef]
- Iles-Smith, J.; Lambert, N.; Nazir, A. Environmental dynamics, correlations, and the emergence of noncanonical equilibrium states in open quantum systems. Phys. Rev. A 2014, 90, 032114. [Google Scholar] [CrossRef]
- Iles-Smith, J.; Dijkstra, A.G.; Lambert, N.; Nazir, A. Energy transfer in structured and unstructured environments: Master equations beyond the Born-Markov approximations. J. Chem. Phys. 2016, 144, 044110. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Lambert, N.; Brandes, T. Nonequilibrium thermodynamics in the strong coupling and non-Markovian regime based on a reaction coordinate mapping. New J. Phys. 2016, 18, 073007. [Google Scholar] [CrossRef]
- Strasberg, P.; Schaller, G.; Schmidt, T.L.; Esposito, M. Fermionic reaction coordinates and their application to an autonomous Maxwell demon in the strong-coupling regime. Phys. Rev. B 2018, 97, 205405. [Google Scholar] [CrossRef]
- Nazir, A.; Schaller, G. The reaction coordinate mapping in quantum thermodynamics. In Thermodynamics in the Quantum Regime; Binder, F., Correa, L.A., Gogolin, C., Anders, J., Adesso, G., Eds.; Springer International Publishing: New York, NY, USA, 2018; Available online: https://link.springer.com/book/10.1007/978-3-319-99046-0 (accessed on 16 April 2019).
- Chin, A.W.; Rivas, Á.; Huelga, S.F.; Plenio, M.B. Exact mapping between system-reservoir quantum models and semi-infinite discrete chains using orthogonal polynomials. J. Math. Phys. 2010, 51, 092109. [Google Scholar] [CrossRef]
- Woods, M.P.; Groux, R.; Chin, A.W.; Huelga, S.F.; Plenio, M.B. Mappings of open quantum systems onto chain representations and Markovian embeddings. J. Math. Phys. 2014, 55, 032101. [Google Scholar] [CrossRef]
- Mascherpa, F.; Smirne, A.; Tamascelli, D.; Fernández-Acebal, P.; Donadi, S.; Huelga, S.F.; Plenio, M.B. Optimized auxiliary oscillators for the simulation of general open quantum systems. arXiv 2019, arXiv:1904.04822. [Google Scholar]
- Tamascelli, D.; Smirne, A.; Huelga, S.F.; Plenio, M.B. Nonperturbative treatment of non-Markovian dynamics of open quantum systems. Phys. Rev. Lett. 2018, 120, 030402. [Google Scholar] [CrossRef] [PubMed]
- Braak, D.; Chen, Q.H.; Batchelor, M.T.; Solano, E. Semi-classical and quantum Rabi models: in celebration of 80 years. J. Phys. A Math. Theor. 2016, 49, 300301. [Google Scholar] [CrossRef]
- Lloyd, S.; Braunstein, S.L. Quantum computation over continuous variables. Phys. Rev. Lett. 1999, 82, 1784–1787. [Google Scholar] [CrossRef]
- Felicetti, S.; Pedernales, J.S.; Egusquiza, I.L.; Romero, G.; Lamata, L.; Braak, D.; Solano, E. Spectral collapse via two-phonon interactions in trapped ions. Phys. Rev. A 2015, 92, 033817. [Google Scholar] [CrossRef]
- Pedernales, J.S.; Beau, M.; Pittman, S.M.; Egusquiza, I.L.; Lamata, L.; Solano, E.; del Campo, A. Dirac equation in (1+1)-dimensional curved spacetime and the multiphoton quantum Rabi model. Phys. Rev. Lett. 2018, 120, 160403. [Google Scholar] [CrossRef]
- Garbe, L.; Egusquiza, I.L.; Solano, E.; Ciuti, C.; Coudreau, T.; Milman, P.; Felicetti, S. Superradiant phase transition in the ultrastrong-coupling regime of the two-photon Dicke model. Phys. Rev. A 2017, 95, 053854. [Google Scholar] [CrossRef]
- Puebla, R.; Hwang, M.J.; Casanova, J.; Plenio, M.B. Protected ultrastrong coupling regime of the two-photon quantum Rabi model with trapped ions. Phys. Rev. A 2017, 95, 063844. [Google Scholar] [CrossRef]
- Cui, S.; Cao, J.P.; Fan, H.; Amico, L. Exact analysis of the spectral properties of the anisotropic two-bosons Rabi model. J. Phys. A: Math. Theor. 2017, 50, 204001. [Google Scholar] [CrossRef]
- Felicetti, S.; Rossatto, D.Z.; Rico, E.; Solano, E.; Forn-Díaz, P. Two-photon quantum Rabi model with superconducting circuits. Phys. Rev. A 2018, 97, 013851. [Google Scholar] [CrossRef]
- Xie, Y.F.; Duan, L.; Chen, Q.H. Generalized quantum Rabi model with both one- and two-photon terms: A concise analytical study. Phys. Rev. A 2019, 99, 013809. [Google Scholar] [CrossRef]
- Lo, C.F.; Liu, K.L.; Ng, K.M. The multiquantum Jaynes-Cummings model with the counter-rotating terms. Europhys. Lett. 1998, 42, 1. [Google Scholar] [CrossRef]
- Casanova, J.; Puebla, R.; Moya-Cessa, H.; Plenio, M.B. Connecting nth order generalised quantum Rabi models: Emergence of nonlinear spin-boson coupling via spin rotations. npj Quantum Inf. 2018, 4, 47. [Google Scholar] [CrossRef]
- Puebla, R.; Casanova, J.; Houhou, O.; Solano, E.; Paternostro, M. Quantum simulation of multiphoton and nonlinear dissipative spin-boson models. Phys. Rev. A 2019, 99, 032303. [Google Scholar] [CrossRef]
- Breuer, H.P.; Petruccione, F. The Theory of Open Quantum Systems; Oxford University Press: Oxford, UK, 2002. [Google Scholar]
- Vojta, M. Impurity quantum phase transitions. Phil. Mag. 2006, 86, 1807–1846. [Google Scholar] [CrossRef]
- Hur, K.L. Quantum phase transitions in spin-boson systems: Dissipation and light phenomena. In Understanding Quantum Phase Transitions; CRC Press: Boca Raton, FL, USA, 2010; pp. 217–237. Available online: https://www.crcpress.com/Understanding-Quantum-Phase-Transitions/Carr/p/book/9781439802519 (accessed on 16 April 2019).
- Leibfried, D.; Blatt, R.; Monroe, C.; Wineland, D. Quantum dynamics of single trapped ions. Rev. Mod. Phys. 2003, 75, 281–324. [Google Scholar] [CrossRef]
- Pedernales, J.S.; Lizuain, I.; Felicetti, S.; Romero, G.; Lamata, L.; Solano, E. Quantum Rabi model with trapped ions. Sci. Rep. 2015, 5, 15472. [Google Scholar] [CrossRef]
- Lv, D.; An, S.; Liu, Z.; Zhang, J.N.; Pedernales, J.S.; Lamata, L.; Solano, E.; Kim, K. Quantum simulation of the quantum Rabi model in a trapped Ion. Phys. Rev. X 2018, 8, 021027. [Google Scholar] [CrossRef]
- de Matos Filho, R.L.; Vogel, W. Second-sideband laser cooling and nonclassical motion of trapped ions. Phys. Rev. A 1994, 50, R1988–R1991. [Google Scholar] [CrossRef]
- de Matos Filho, R.L.; Vogel, W. Nonlinear coherent states. Phys. Rev. A 1996, 54, 4560–4563. [Google Scholar] [CrossRef]
- Vogel, W.; de Matos Filho, R.L. Nonlinear Jaynes-Cummings dynamics of a trapped ion. Phys. Rev. A 1995, 52, 4214–4217. [Google Scholar] [CrossRef]
- Cheng, X.H.; Arrazola, I.; Pedernales, J.S.; Lamata, L.; Chen, X.; Solano, E. Nonlinear quantum Rabi model in trapped ions. Phys. Rev. A 2018, 97, 023624. [Google Scholar] [CrossRef]
- de Vega, I.; Alonso, D. Dynamics of non-Markovian open quantum systems. Rev. Mod. Phys. 2017, 89, 015001. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puebla, R.; Zicari, G.; Arrazola, I.; Solano, E.; Paternostro, M.; Casanova, J. Spin-Boson Model as A Simulator of Non-Markovian Multiphoton Jaynes-Cummings Models. Symmetry 2019, 11, 695. https://doi.org/10.3390/sym11050695
Puebla R, Zicari G, Arrazola I, Solano E, Paternostro M, Casanova J. Spin-Boson Model as A Simulator of Non-Markovian Multiphoton Jaynes-Cummings Models. Symmetry. 2019; 11(5):695. https://doi.org/10.3390/sym11050695
Chicago/Turabian StylePuebla, Ricardo, Giorgio Zicari, Iñigo Arrazola, Enrique Solano, Mauro Paternostro, and Jorge Casanova. 2019. "Spin-Boson Model as A Simulator of Non-Markovian Multiphoton Jaynes-Cummings Models" Symmetry 11, no. 5: 695. https://doi.org/10.3390/sym11050695
APA StylePuebla, R., Zicari, G., Arrazola, I., Solano, E., Paternostro, M., & Casanova, J. (2019). Spin-Boson Model as A Simulator of Non-Markovian Multiphoton Jaynes-Cummings Models. Symmetry, 11(5), 695. https://doi.org/10.3390/sym11050695






