A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition
Abstract
1. Introduction
2. The Weighted Fourier and Wavelet-Like Descriptor Based on IDSC
2.1. Inner-Distance Shape Context
2.2. Weighted Fourier and Wavelet-Like Descriptor IDSC-wFW
2.2.1. Weighted Fourier Descriptor IDSC-wF
2.2.2. Weight Wavelet-Like Descriptor IDSC-wW
2.2.3. Weighted Fourier and Wavelet-Like Descriptor
2.3. Invariance of IDSC-wFW
2.4. Shape Dissimilarity Measure
3. Computational Complexity
4. Experiments
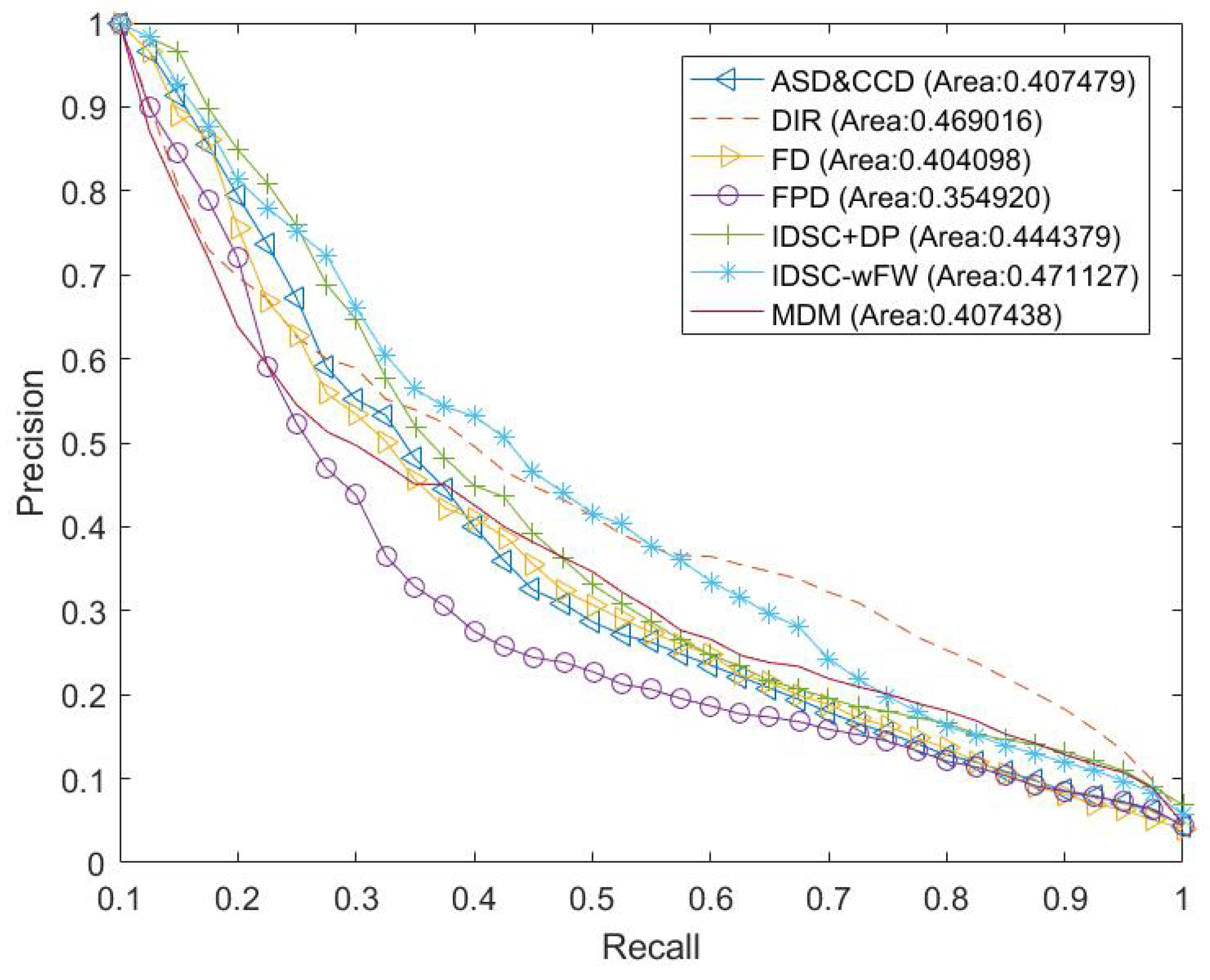
4.1. Experimental Results on the MPEG-7 CE-1 Part B Shape Database
4.2. Experimental Results on the Articulated Database
4.3. Experimental Results on the 270 Plant Leaf Database
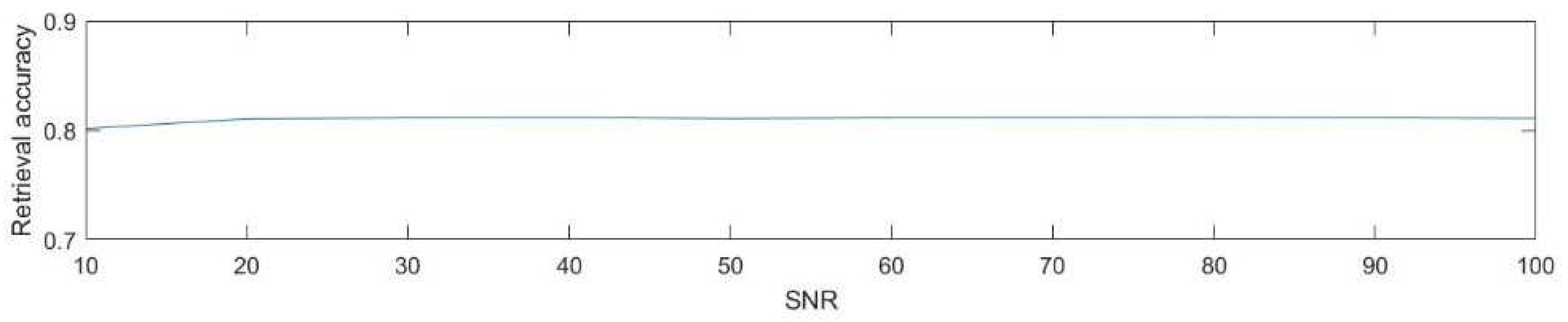
4.4. Experimental Results on Sensitivity to Noise
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Loncaric, S. A survey of shape analysis techniques. Pattern Recognit. 1998, 31, 983–1001. [Google Scholar] [CrossRef]
- Alajlan, N.; El, R.I.; Kamel, M.S.; Freeman, G. Shape retrieval using triangle-area representation and dynamic space warping. Pattern Recognit. 2007, 40, 1911–1920. [Google Scholar] [CrossRef]
- Ling, H.; Jacobs, D.W. Shape classification using the inner-distance. IEEE Trans. Pattern Anal. Mach. Intell. 2007, 29, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Liu, J.; Tang, X. 2D shape matching by contour flexibility. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 180–186. [Google Scholar] [PubMed]
- Belongie, S.; Malik, J.; Puzicha, J. Shape matching and object recognition using shape contexts. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 509–522. [Google Scholar] [CrossRef]
- Grigorescu, C.; Petkov, N. Distance sets for shape filters and shape recognition. IEEE Trans. Image Process. 2003, 12, 1274–1286. [Google Scholar] [CrossRef] [PubMed]
- Felzenszwalb, P.F.; Schwartz, J.D. Hierarchical Matching of Deformable Shapes. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Junior, J.J.D.M.S.; Backes, A.R.; Bruno, O.M. Randomized neural network based descriptors for shape classification. Neurocomputing 2018, 312, 201–209. [Google Scholar] [CrossRef]
- Yang, C.; Hui, W.; Qian, Y.; Yang, C.; Hui, W.; Qian, Y. A Novel Method for 2D Nonrigid Partial Shape Matching. Neurocomputing 2018, 275, 1160–1176. [Google Scholar] [CrossRef]
- Bai, X.; Yang, X.; Latecki, L.J.; Liu, W.; Tu, Z. Learning context-sensitive shape similarity by graph transduction. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 861–874. [Google Scholar] [PubMed]
- El-ghazal, A.; Basir, O.; Belkasim, S. Farthest point distance: A new shape signature for Fourier descriptors. Signal Process. Image Commun. 2009, 24, 572–586. [Google Scholar] [CrossRef]
- Zhang, D.; Lu, G. Study and evaluation of different Fourier methods for image retrieval. Image Vis. Comput. 2005, 23, 33–49. [Google Scholar] [CrossRef]
- Hu, R.; Jia, W.; Ling, H.; Huang, D. Multiscale distance matrix for fast plant leaf recognition. IEEE Trans. Image Process. 2012, 21, 4667–4672. [Google Scholar] [PubMed]
- Yang, H.S.; Lee, S.U.; Lee, K.M. Recognition of 2D object contours using starting-point-independent wavelet coefficient matching. J. Visual Commun. Image Represent. 1998, 9, 171–181. [Google Scholar] [CrossRef]
- Wallace, T.P.; Wintz, P.A. An efficient three-dimensional aircraft recognition algorithm using normalized Fourier descriptors. Comput. Graph. Image Process. 1980, 13, 99–126. [Google Scholar] [CrossRef]
- Kaothanthong, N.; Chun, J.; Tokuyama, T. Distance interior ratio: A new shape signature for 2D shape retrieval. Pattern Recognit. Lett. 2016, 78, 14–21. [Google Scholar] [CrossRef]
- Ling, H.; Jacobs, D.W. Using the inner-distance for classification of articulated shapes. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; pp. 719–726. [Google Scholar]
- Porwik, P.; Lisowska, A. The Haar-wavelet transform in digital image processing: Its status and achievements. Mach. Graph. Vis. 2004, 13, 79–98. [Google Scholar]
- Wang, B.; Gao, Y. Hierarchical string cuts: A translation, rotation, scale, and mirror invariant descriptor for fast shape retrieval. IEEE Trans. Image Process. 2014, 23, 4101–4111. [Google Scholar] [CrossRef] [PubMed]
- Fotopoulou, F.; Economou, G. Multivariate angle scale descriptor of shape retrieval. In Proceedings of the SPAMEC 2011—Signal Processing and Applied Mathematics for Electronics and Communications Workshop, Cluj-Napoca, Romania, 26–28 August 2011; pp. 105–108. [Google Scholar]
- Silva, P.F.; Marcal, A.R.; da Silva, R.M. Evaluation of Features for Leaf Discrimination; Springer: Berlin/Heidelberg, Germany, 2013; pp. 197–204. [Google Scholar]

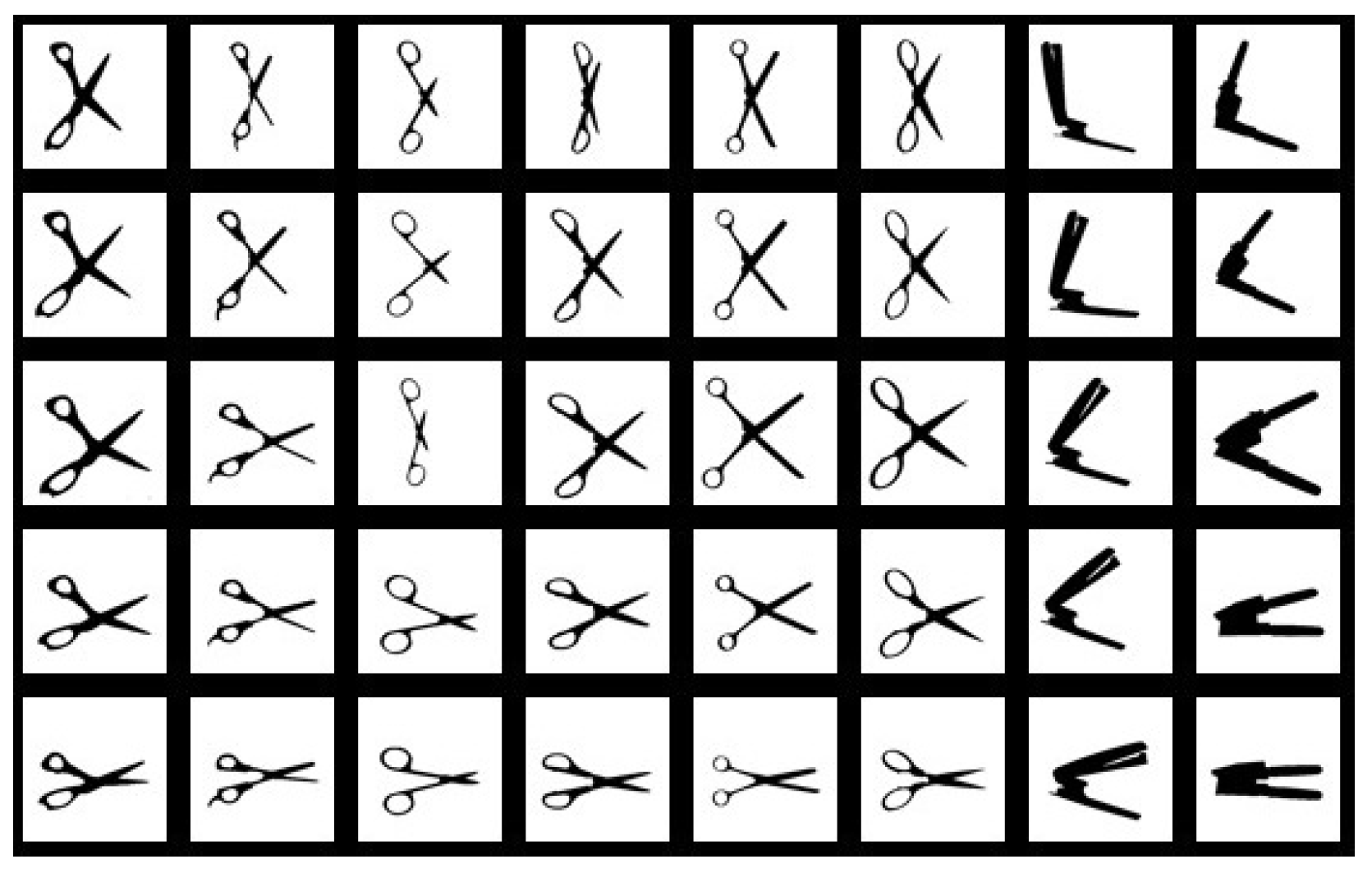


| IDSC-wFW (ours) | IDSC+DP | SC+DP | Shape Tree |
|---|---|---|---|
| M | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
|---|---|---|---|---|---|---|---|---|
| Retrieval Rate (%) | 73.02 | 78.23 | 80.55 | 81.45 | 81.53 | 81.64 | 81.61 | 81.60 |
| J | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Retrieval Rate (%) | 67.81 | 71.87 | 71.83 | 70.91 | 70.27 | 68.44 |
| M, J | 10, 2 | 12, 2 | 14, 2 | 16, 2 | 10, 3 | 12, 3 | 14, 3 | 16, 3 |
|---|---|---|---|---|---|---|---|---|
| Retrieval Rate (%) | 81.52 | 81.65 | 81.67 | 81.64 | 82.12 | 82.34 | 82.33 | 82.31 |
| Method | Retrieval Rate (%) | Matching Time (ms) |
|---|---|---|
| IDSC-wFW (ours) | 82.34 | 11.4 |
| IDSC+DP [3] | 85.40 | 6120.2 |
| DIR [16] | 77.69 | 6.7 |
| MDM [13] | 70.46 | 44.2 |
| ASD&CCD [20] | 76.85 | 27,037.9 |
| FD [12] | 68.14 | 4.1 |
| FPD [11] | 65.52 | 3.3 |
| Methods | 1st (%) | 2nd (%) | 3rd (%) | Average Accuracy (%) | Matching Time () |
|---|---|---|---|---|---|
| IDSC-wFW (ours) | 95.0 | 85.0 | 75.0 | 85.00 | 279.3 |
| IDSC+DP [3] | 97.5 | 87.5 | 67.5 | 84.17 | 149,774.1 |
| DIR [16] | 82.5 | 57.5 | 45.0 | 61.67 | 158.4 |
| ASD&CCD [20] | 80.0 | 50.0 | 32.5 | 54.16 | 735,390.9 |
| FD [12] | 77.5 | 37.5 | 42.5 | 52.50 | 105.6 |
| FPD [11] | 70.0 | 50.0 | 32.5 | 50.83 | 75.7 |
| MDM [13] | 62.5 | 30.0 | 27.5 | 40.00 | 1187.0 |
| SC+DP [10] | 50.0 | 25.0 | 27.5 | 34.17 | 146,203.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Guo, B.; Li, C.; Yan, Y. A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition. Symmetry 2019, 11, 693. https://doi.org/10.3390/sym11050693
Zheng Y, Guo B, Li C, Yan Y. A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition. Symmetry. 2019; 11(5):693. https://doi.org/10.3390/sym11050693
Chicago/Turabian StyleZheng, Yan, Baolong Guo, Cheng Li, and Yunyi Yan. 2019. "A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition" Symmetry 11, no. 5: 693. https://doi.org/10.3390/sym11050693
APA StyleZheng, Y., Guo, B., Li, C., & Yan, Y. (2019). A Weighted Fourier and Wavelet-Like Shape Descriptor Based on IDSC for Object Recognition. Symmetry, 11(5), 693. https://doi.org/10.3390/sym11050693




