Abstract
Recently, symmetry in complex network structures has attracted some research interest. One of the fascinating problems is to give measures of the extent to which the network is symmetric. In this paper, based on the natural action of the automorphism group of on the vertex set V of a given network , we propose three indexes for the characterization of the global symmetry of complex networks. Using these indexes, one can get a quantitative characterization of how symmetric a network is and can compare the symmetry property of different networks. Moreover, we compare these indexes to some existing ones in the literature and apply these indexes to real-world networks, concluding that real-world networks are far from vertex symmetric ones.
Keywords:
complex networks; symmetry index; group action; orbit decomposition; vertex symmetric networks MSC:
05C82; 94C15
1. Introduction
In the past few decades, an array of discoveries has added to our understanding of complex networks [1]. Previous studies were mainly focused on statistical properties of real networks, such as small-world properties [2] and power-law degree distributions [3]. However, one property of the network structure, symmetry, has been rarely studied.
Symmetry, an important concept in many areas of physics [4], can be described explicitly using mathematical tools, namely invariance under a certain group action [5]. Recently, symmetry in network structures has attracted some research interest. In [6], by the analysis of the statistics of local symmetric motifs that contribute to the local symmetry of networks, the authors showed that the symmetry of complex networks is a consequence of a similar linkage pattern. The work in [7] utilized symmetry information to characterize the structural heterogeneity of real networks. In [8,9], Holme proposed ways to measure symmetric properties of vertices and their surroundings in networks. In [10], Garrido managed to show measures of symmetry in complex networks and highlighted their close relation with measures of information and entropy. By considering the size and structure of the automorphism groups of a variety of empirical real-world networks, the authors in [11] found that, in contrast to classical random graph models, many real-world networks are richly symmetric. They also commented on how symmetry can affect network redundancy and robustness in that same paper.
Despite the recent progress in the study of symmetry in network structures, there were few results on the quantitative characterizations of the symmetry of complex networks. We are mainly concerned with giving measurements of the extent to which the network is symmetric. Based on the natural action of the automorphism group on the vertex set V of a given network , we propose three symmetry indexes for the characterization of the symmetry of networks, . Particularly, characterizes how much a network differs from a vertex symmetric one. Recall that vertex symmetric networks, or symmetric interconnection networks in [12], have the property that the network viewed from any vertex of the network looks the same. We take such networks as richly symmetric. In that same paper, based on finite groups and their generators, the authors proposed a group-theoretic model, called the Cayley graph model, for designing, analyzing, and improving such networks. Explicitly, the authors showed that any vertex symmetric network can be represented by a simple extension of this model. Despite the abundance of symmetry in such networks, many real networks are found not to be vertex symmetric. As a result, we introduce the concept of orbit-homogeneous networks, namely all the orbits in the vertex set V under the automorphism group action have the same size. We take such networks as less symmetric than the vertex symmetric ones, and our second symmetry index characterizes how much a network differs from an orbit-homogeneous one. Finally, the third index is the average of the second ones in some sense, which indicates the disparity of sizes between all orbits. Using these three indexes, one can compare the symmetry property of different networks. For more details, see Section 3.2. Moreover, by an analysis of an explicit example in Section 4, we find that our symmetry indexes are much better than the ones in [6,13]. The rest of this paper is organized as follows. In the next section, we recall some basic facts about group actions, which are fundamental to our symmetry indexes. In Section 3, we first introduce the automorphism group action on the vertex set. Based on this group action, we propose three symmetry indexes and discuss their properties. We use a figure to illustrate our definitions. Then, utilizing these indexes, we compare the symmetry property of different networks. In Section 4, these symmetry indexes are compared to those existing in the literature. We apply these symmetry indexes to real-world networks in Section 5. Finally, the following section contains our conclusions, and we summarize the notations appearing in this paper in the last section.
2. Group Actions
In this section, we recall some basic mathematical notions that will be used in this paper. Explicitly, we need the concept of group actions. We shall proceed as elementarily as possible; however, we omit the definition of a group, which can be found in any mathematical textbooks on algebra; see for example [14]. Let G be a group. By a group action, we mean a pair , where S is a set and:
is a map, such that:
- , for and ,
- , where e denotes the identity element of the group G.
When no confusion is possible, we simply write as and omit the symbol f. The action is said to be transitive, if for any two elements , there exists an element , such that . For an element , the orbit of s under the action of G is defined to be the subset of S. Here, we make the convention that if , but , then we count in the orbit of s only once. We will use the notation to denote the orbit of s. Obviously, different orbits have empty intersections, and S is the union of all orbits.
For an element , the stabilizer of s in G is defined as:
It follows easily that is a subgroup of G. Recall that for any subgroup H of G, we define two elements to be equivalent if there exists an element , such that . If and are equivalent, we denote them as . It follows easily that ∼ is an equivalence relation. We denote by the set G modulo the equivalence relation ∼ defined by H. For , we denote by the equivalence class determined by g.
Proposition 1.
The natural map:
is bijective for any .
Proof.
It follows directly from the definitions. □
When G and S as sets are finite, the above proposition will give us an explicit quantity equation. We will use this result in the next section. To get a feeling about group actions, we consider the following example.
Example 1.
Let , the even integers with addition as the group multiplication. Clearly, zero is the identity element of G. We take S to be , and the group action is defined by addition:
For , the orbit , and for , the orbit . Clearly, . For any , the stabilizer . By Proposition 1, the following map:
is bijective, which is obvious.
3. Symmetry Indexes
3.1. Group Actions Arise from Networks
A graph or network is denoted by , where V is the set of vertices and is the set of edges. We only consider graphs that are finite, undirected, loop-free, and devoid of multiple edges in this paper. If , and are adjacent. Denote by the set of all permutations on V, namely all bijective maps from V to itself. is a group under the composition operation of permutations. We call it the permutation group of the vertex set V. It has a natural action on the vertex set V, namely,
where denotes the image of v under the permutation f. We are concerned with those permutations that preserve the adjacency relations of vertices. Explicitly, an automorphism of the graph is a permutation such that, for any vertices u and v, is adjacent to if and only if u is adjacent to v. We denote the set of automorphisms of by . Clearly, G is a subgroup of , and by (2), we have a restricted group action:
It is this natural group action (3) that we will address in this paper.
Let be the orbit set of the action (3), namely each is a G-orbit in V and V is the union of the vertices in these orbits. Vertices in the same orbit have similar properties.
Proposition 2.
Vertices in the same orbit have the same degrees.
Proof.
Let be two vertices in the same orbit with degrees , respectively. By definition, there exists an element such that . Let be the neighbors of . Then, are different neighbors of . Thus, . Similarly, , which forces . □
Recall that two subgroups of G are said to be conjugate if there exists an element , such that . Obviously, conjugate subgroups have the same order, namely they have the same number of elements.
Proposition 3.
Vertices in the same orbit have conjugate stabilizers. Particularly, stabilizers of vertices in the same orbit have the same order.
Proof.
Let be two vertices in the same orbit with stabilizers , respectively. By definition, there exists an element such that . It follows easily that . □
3.2. Symmetry Indexes for Networks
Based on the automorphism group action (3), we will propose several symmetry indexes for the measurement of symmetry of networks in this subsection. Our characterizations of symmetry are focused on the global structure of networks. This is different from Holme’s viewpoint [8,9], which proposed ways to measure symmetric properties of vertices and their surroundings in networks. Our work was inspired by [6], where the authors used graph-oriented symmetry measurements; this allows measurement of the symmetry of the whole network.
For a set S, denote by the number of elements in S. We are mainly concerned with finite sets in this paper. Recall that denote the orbit set under the automorphism group action (3). Consider the ratio of the maximal size of the orbits to the size of the network ; we define:
By Propositions 2 and 3, vertices in the same orbit have similar properties. Thus, networks with all vertices in the same orbit will be considered richly symmetric.
Recall that a graph is said to be vertex symmetric if for every pair of vertices, v and w, there exists an automorphism of the graph that maps v into w. Vertex symmetric graphs have the property that the network viewed from any vertex of it looks the same. In such a network, congestion problems are minimized since the load will be distributed uniformly through all the vertices. Moreover, this symmetry allows for identical processors at every vertex with identical routing algorithms. Vertex symmetric graphs or symmetric interconnection networks were studied by Akers and Krishnamurthy in [12].
Proposition 4.
The graph Γ is vertex symmetric if and only if .
Proof.
By Proposition 4, we can take as the index of how much a network differs from a vertex symmetric one. Generally, . The bigger is, the more symmetric the network is. On the other hand, recall that a network is said to be asymmetric [6,13], if the automorphism group is a trivial group, namely it has only one element. The index also captures information of the asymmetricness of a network.
Proposition 5.
A network Γ is asymmetric if and only if .
Proof.
If is asymmetric, then clearly, reaches its minimum . Conversely, assume that . Then, each orbit under the action (3) is trivial, namely it contains only one element. We conclude that the automorphism group must be a trivial group; otherwise, there will be at least one orbit with more than one vertex. Thus, the network is asymmetric. □
The popular n-cubes, n-dimensional Boolean hypercube, and cube-connected cycles, which have been widely used as processor interconnection networks, are all vertex symmetric networks. However, many real networks are not vertex symmetric; in other words, the symmetric index is less than one. For these graphs, consider the ratio of the minimal size of the orbits to the maximal size of the orbits; we define:
Clearly, . This symmetry index characterizes the maximal size differences of the orbits. Intuitively, we consider graphs with orbits having similar sizes to be more symmetric.
Definition 1.
A graph is said to be orbit-homogeneous if all its orbits have the same size.
By Definition 1, a graph is orbit-homogenous if and only if . In this sense, we can take as the index of how much a network differs from an orbit-homogeneous one. Recall that the stabilizers of vertices under the action (3) have been defined in (1). Using stabilizers, we have another characterization of orbit-homogeneous networks.
Proposition 6.
A network is orbit-homogeneous if and only if the stabilizers and have the same order for any pair of vertices v and w in V.
Proof.
By Proposition 3, the stabilizers of vertices in the same orbit have the same order. Assume and with . By Lagrange’s theorem [15] in group theory and Proposition 1, we have and . Thus, if and only if . Now, the proposition is obvious. □
For the measurement of symmetry of non-orbit-homogeneous networks, we introduce the following:
where denotes the number of orbits in V under the action (3). Different from , which characterizes the maximal size differences of the orbits, detects the average deviation of size of all orbits to the maximal one. This index is more meticulous than the second one. It follows easily that a network is orbit-homogeneous if and only if . The following result gives the relations among the three indexes.
Proposition 7.
For a network Γ, and .
Proof.
This follows directly from the definitions of the indexes. □
To illustrate the above symmetry indexes, we consider the network in Figure 1. This network has ten vertices and twenty edges. Utilizing some tools, such as in [16], we can find all automorphisms for this graph (a total of eight automorphisms can be found). Moreover, we can obtain the orbit decomposition under the action (3) through some computer coding. Vertices in each orbit are marked with the same color in Figure 1. The resulting orbit set is . Thus, , , and .
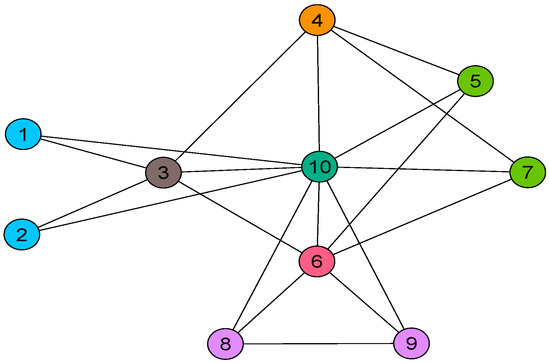
Figure 1.
Illustration of the symmetry indexes. Vertices with the same color belong to the same orbit.
Clearly, implies that (the converse is also true), and implies that . Thus, for detecting the symmetry of a network , we will first consider the first index , then the second one, and finally, the third one.
Given two networks, with these symmetry indexes introduced above, now we can decide which one is more symmetric. What we keep in mind is that vertex symmetric networks are richly symmetric and then are the less symmetric ones, the orbit-homogeneous networks. Explicitly, given two networks and of the same size, namely , if , we consider to be more symmetric than ; if , we compare the second symmetry index. The network with larger will be considered as more symmetric. If the second symmetry indexes are equal, we compare their third symmetry indexes. If the three symmetry indexes are all equal, we will consider the two networks o have the same symmetry property.
Example 2.
Consider two networks and both with 33 vertices. Assume that has four orbits under the action (3) and its orbit sizes are , while has five orbits and its orbit sizes are . Then, and , while ; thus, we conclude that is more symmetric than .
4. Comparison to the Existing Symmetry Index
In their exploration of the origin of symmetry in real networks [6], the authors proposed the following measurement of symmetry in networks:
where N denotes the number of vertices in V. This measurement is based on the intuitive observation that a network having more nontrivial orbits will be more symmetric. We point out that even if reaches its maximal value of one, the network is not as symmetric as indicates that it should be. In other words, the measurement is too coarse. As an example, consider the two networks in Figure 2. Both are with ten vertices and twenty edges. Figure 2a is vertex symmetric, while Figure 2b has three orbits under the automorphism group action, and vertices in the same orbit are marked with the same color. Clearly, , but intuitively, Figure 2a is more symmetric than Figure 2b. Actually, using our symmetry index defined in Section 3.2, . Thus, we conclude that Figure 2a is more symmetric than Figure 2b.
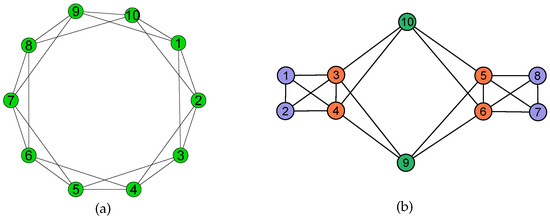
Figure 2.
(a) Vertex symmetric network. (b) Network with three orbits and each orbit is nontrivial.
In [13], the following measurement:
was introduced, which measures the symmetry relative to the maximal number of possible automorphisms of a network with N vertices. This index is also too coarse. Actually, for the two networks in Figure 2, ; however, as we already pointed out, Figure 2a is more symmetric than Figure 2b. Moreover, the order of the automorphism group of a network is not an ideal symmetry index. The more symmetric network Figure 2a has 20 automorphisms, while the less symmetric network Figure 2b has 64 automorphisms.
5. Application to Real-World Networks
In this section, we apply our symmetry indexes together with the indexes in Section 4 to the following real-world network datasets. The first is the social network of friendships between 34 members of a karate club at a U.S. university in the 1970s [17]. We refer to this network as the Karate Club. The second dataset is an undirected social network of frequent associations between 62 dolphins in a community living off Doubtful Sound, New Zealand [18]. We refer to this dataset as Dolphins. The third dataset is the adjacency network of common adjectives and nouns in the novel David Copperfieldby Charles Dickens [19]. We refer to this as Word Adjacency. The fourth dataset is the network of American football games between Division IA colleges during regular season Fall 2000 [20]. We refer to this network as Football Game. The results, including the sizes of the networks and orders of the automorphism groups and five symmetry indexes, are summarized in the following table.
From the above table, we see that the indexes were quite small for these real-world networks. Actually, the maximal orbit in Karate Club had only five vertices, and the maximal orbits of Dolphins and Word Adjacency had two vertices. By the theoretic analysis in Section 3, we conclude that these networks were far from vertex symmetric ones, and the network Football Game was even asymmetric. As the size of the networks in Table 1 increased, the order of the automorphism groups decreased, and the index also decreased, so we conclude that the symmetry of these networks also decreased. Note that when using the three indexes to detect the symmetry of a network, we first considered the first index . Since (actually reaches its minimum, thus asymmetric by Proposition 5) of the Football Game network, we conclude that Football Game was asymmetric, although .

Table 1.
Symmetry indexes for real-world networks.
6. Conclusions
In this paper, based on the orbit decompositions of the vertex set V of a network under the natural action of the automorphism group , we have proposed three indexes for the characterization of the symmetry of network structures. The first one characterized how much a network differs from a vertex symmetric one, which we took as richly symmetric. To address a less symmetric network structure, we introduced the concept of orbit-homogeneous networks. Accordingly, the second symmetry index gives a characterization of how far a network is from an orbit-homogeneous one. Finally, the third symmetry index was the average of the second ones in some sense, which detected the average deviation of the size of all orbits to the maximal one. Using these indexes, one can get quantitative characterization of how symmetric a network is and can compare the symmetry property of different networks. Different from the measurements in [8,9], our symmetry indexes were global and depended on the whole network structure. Therefore, these indexes can measure the symmetry of networks in a gradually relaxed quantitative way, thereby making exact characterization of symmetric structures of a network. As pointed out in Section 4, our symmetry indexes were much better than those in [6,13]. After applying these symmetry indexes to real-world networks in Section 5, we found that real-world networks were far from vertex symmetric ones.
7. Notations
In this section, for the convenience of the reader, we illustrate the notations that appeared in this paper.
: Network with vertex set V and edge set E
: Automorphism group of
: Symmetry indexes for network ,
: Number of elements in the set S
G: Group
: Group action of G on S
: Stabilizer of s in G under the group action
: Orbit of s under the group action
: The set G modulo the equivalence relation defined by the subgroup H of G
: Permutation group of the vertex set V
: Orbit of the automorphism group action on the vertex set
: Symmetry measurements
N: Number of vertices in the vertex set V.
Author Contributions
Conceptualization, Y.C.; investigation and software, X.H.; supervision, Y.Z.; writing, original draft, Y.C.; writing, review and editing, Y.Z.
Funding
This work was supported by the National Natural Science Foundation of China under Project No. 61573119 and the Innovative Projects of Shenzhen under Project No. KQJSCX20180328165509766 and CYJ20170307151312215.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Albert, R.; Barabasi, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef] [PubMed]
- Barabasi, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [PubMed]
- Casterllani, E. On the meaning of symmetry breaking. In Symmetries in Physics: Philosophical Reflections; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Xiao, Y.; Xiong, M.; Wang, W.; Wang, H. Emergence of symmetry in complex networks. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Xiao, Y.; Wu, W.H.; Wang, H.; Xiong, M.; Wang, W. Symmetry-based structure entropy of complex networks. Physica A 2008, 387, 2611–2619. [Google Scholar] [CrossRef]
- Holme, P. Detecting degree symmetries in networks. Phys. Rev. E 2006, 74. [Google Scholar] [CrossRef] [PubMed]
- Holme, P. Local Symmetries in Complex Networks. Available online: https://arxiv.org/pdf/cond-mat/0608695.pdf (accessed on 10 April 2019).
- Garrido, A. Symmetry in complex networks. Symmetry 2011, 3, 1–15. [Google Scholar] [CrossRef]
- MacArthur, B.D.; Sánchez-García, R.J.; Anderson, J.W. Symmetry in complex networks. Discret. Appl. Math. 2008, 156, 3525–3531. [Google Scholar] [CrossRef]
- Akers, S.; Krishnamurthy, B. A group-theoretic model for symmetric interconnection networks. IEEE Trans. Comp. 1989, 38, 555–566. [Google Scholar] [CrossRef]
- MacArthur, B.D.; Anderson, J.W. Symmetry and Self-Organization in Complex Systems. Available online: https://arxiv.org/pdf/cond-mat/0609274.pdf (accessed on 13 April 2019).
- Herstein, I.N. Topics in Algebra; Wiley: Hoboken, NJ, USA, 1975. [Google Scholar]
- Humke, P.D. Lagrange’s Theorem: Statement and Proof. Available online: https://www.stolaf.edu/people/humke/COURSES/AASyllabus/LaGrange.pdf (accessed on 26 April 2019).
- Junttila, T.; Kaski, P. Engineering an efficient canonical labeling tool for large and sparse graphs. In Proceedings of the Ninth Workshop on Algorithm Engineering and Experiments and the Fourth Workshop on Analytic Algorithms and Combinatorics, New Orleans, LI, USA, 6 January 2007. [Google Scholar]
- Zachary, W.W. An information flow model for conflict and fission in small groups. J. Anthropol. Res. 1977, 33, 452–473. [Google Scholar] [CrossRef]
- Lusseau, D.; Schneider, K.; Boisseau, O.J.; Haase, P.; Slooten, E.; Dawson, S.M. The bottlenose dolphin community of Doubtful Sound features a large proportion of long-lasting associations. Behav. Ecol. Sociobiol. 2003, 54, 396–405. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Girvan, M.; Newman, M.E.J. Community structure in social and biological networks. Proc. Natl. Acad. Sci. USA 2002, 99, 7821–7826. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).