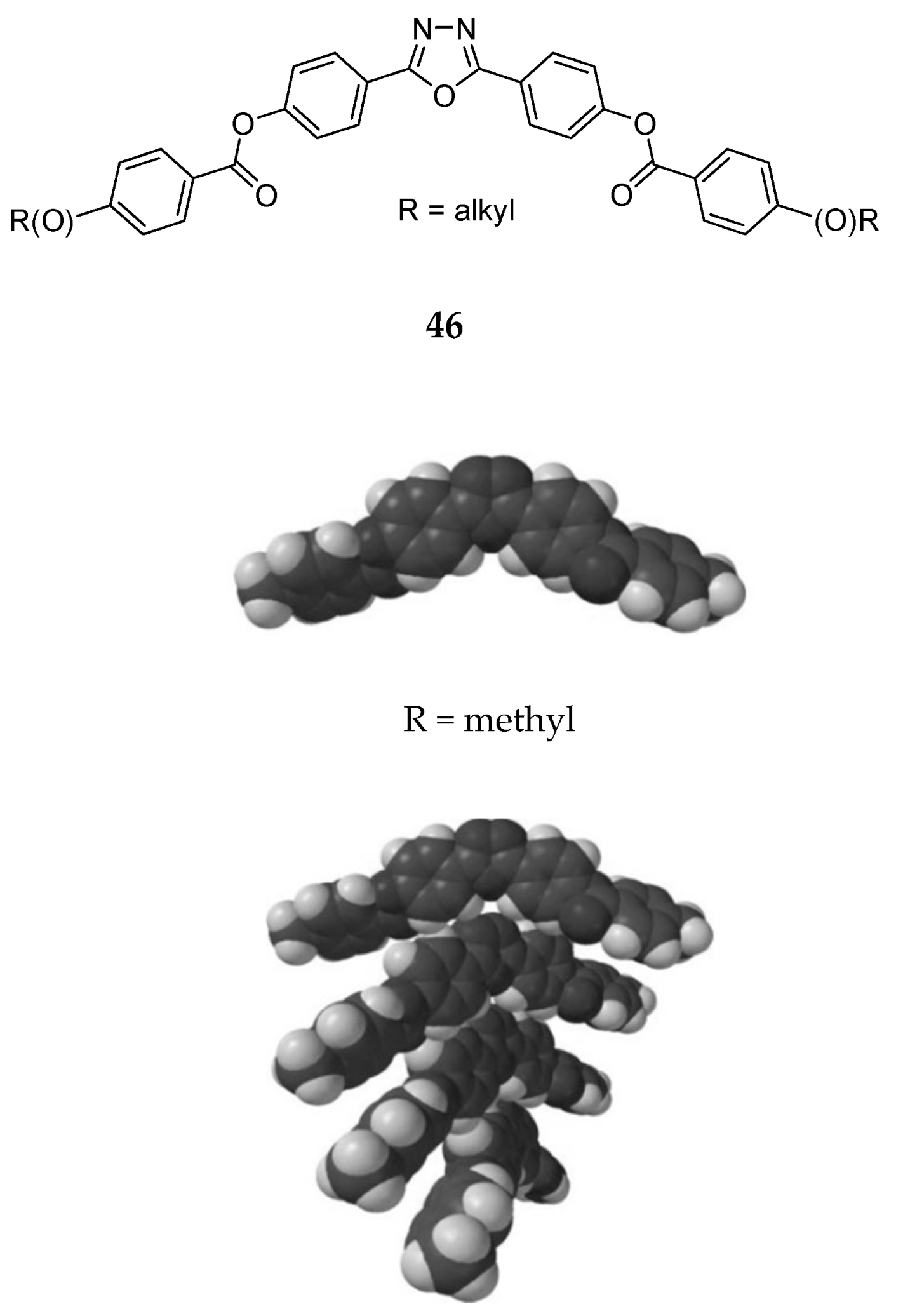
Сhiral and Racemic Fields Concept for Understanding of the Homochirality Origin, Asymmetric Catalysis, Chiral Superstructure Formation from Achiral Molecules, and B-Z DNA Conformational Transition
Abstract
1. Introduction
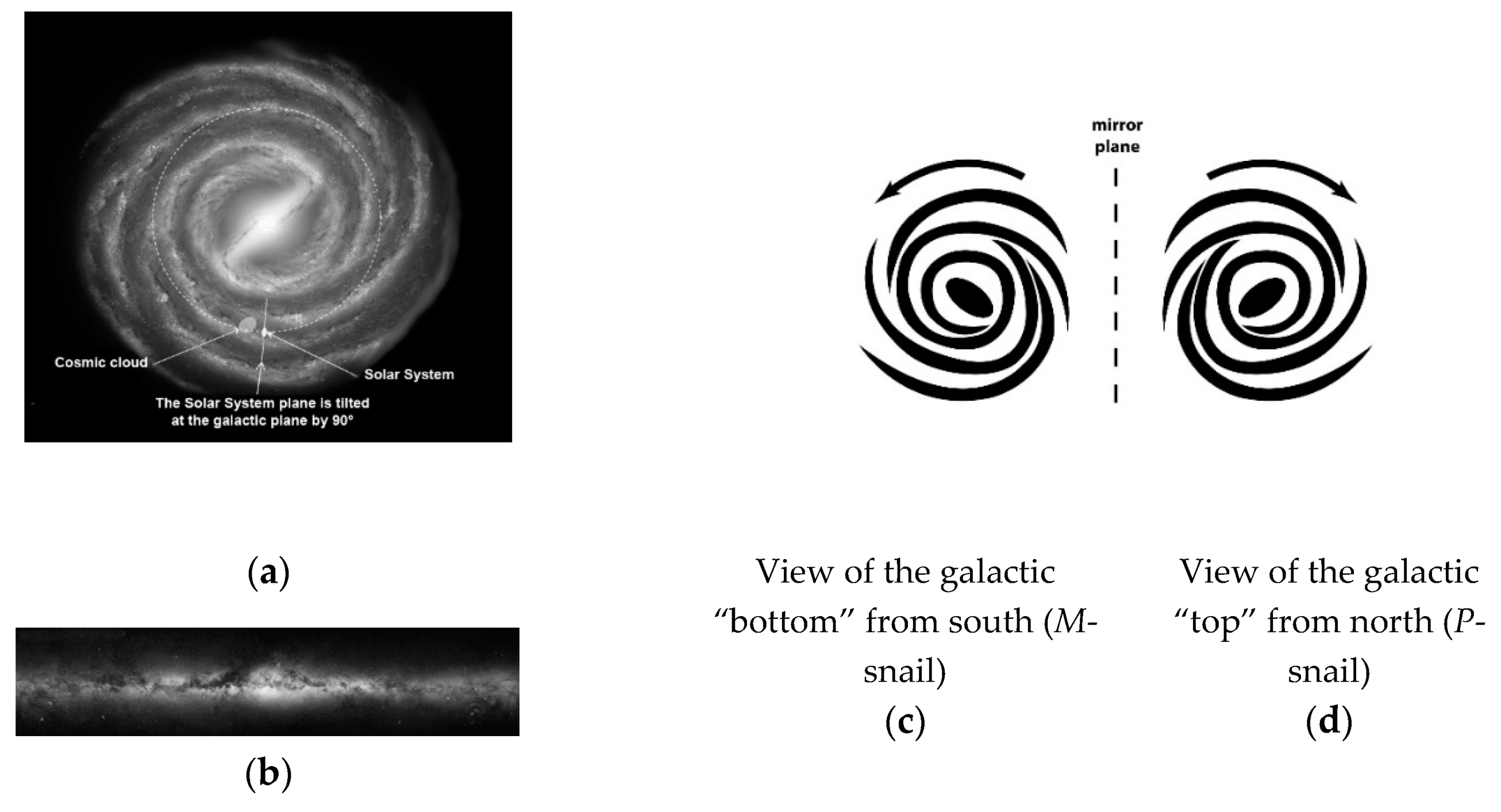
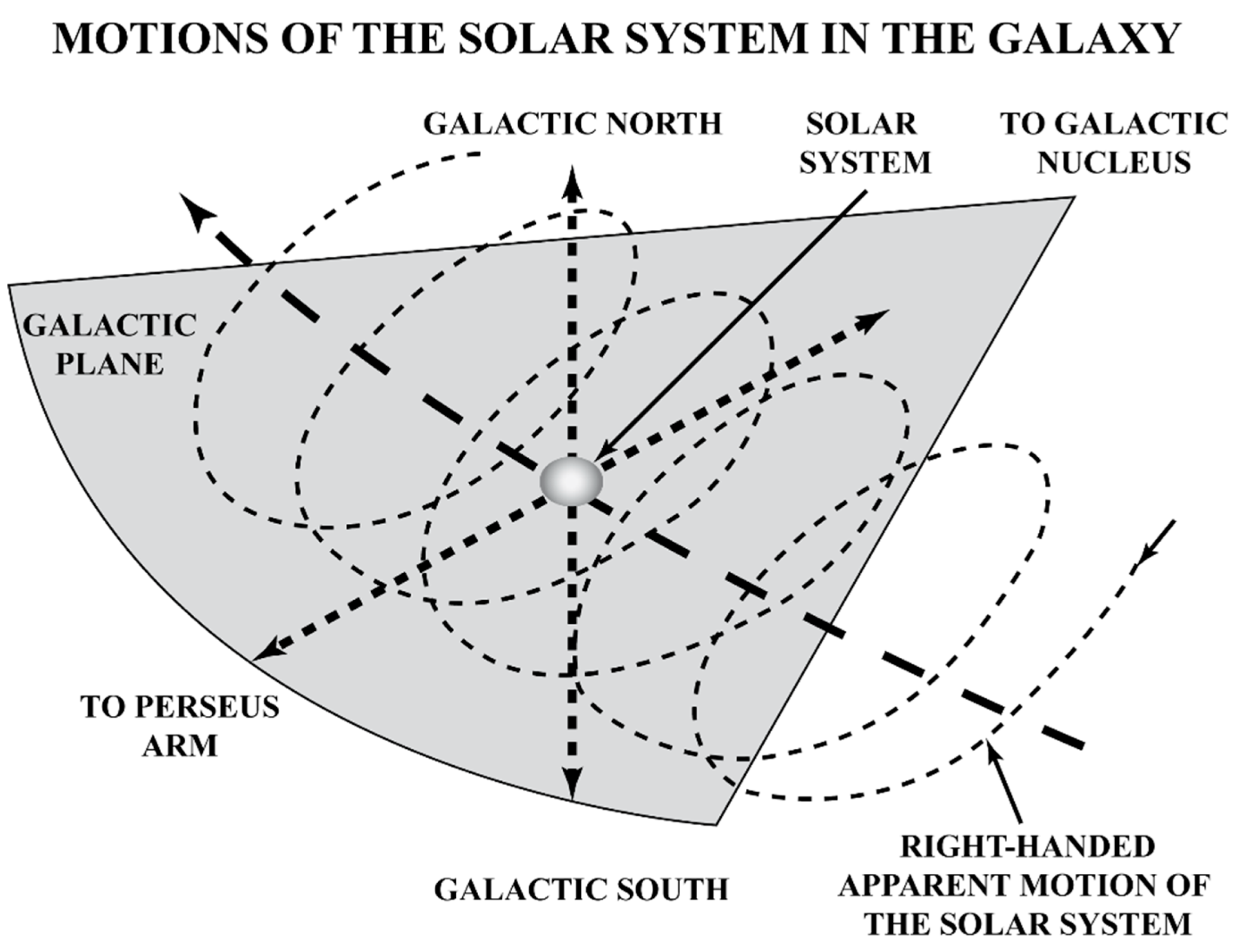
2. Gravity as a Chirality Inductor
3. Gravitational Field Impact on Chemical Reactions
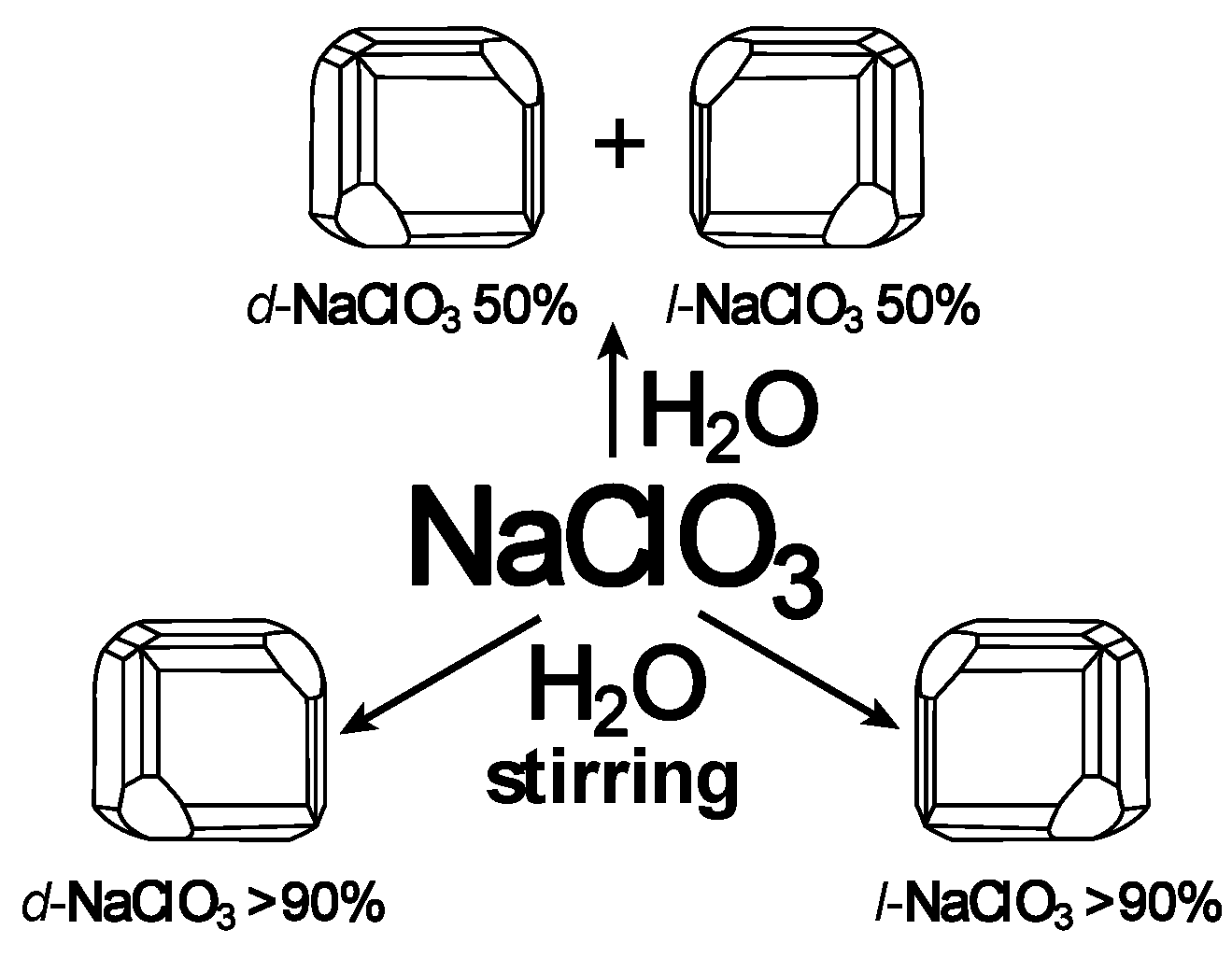
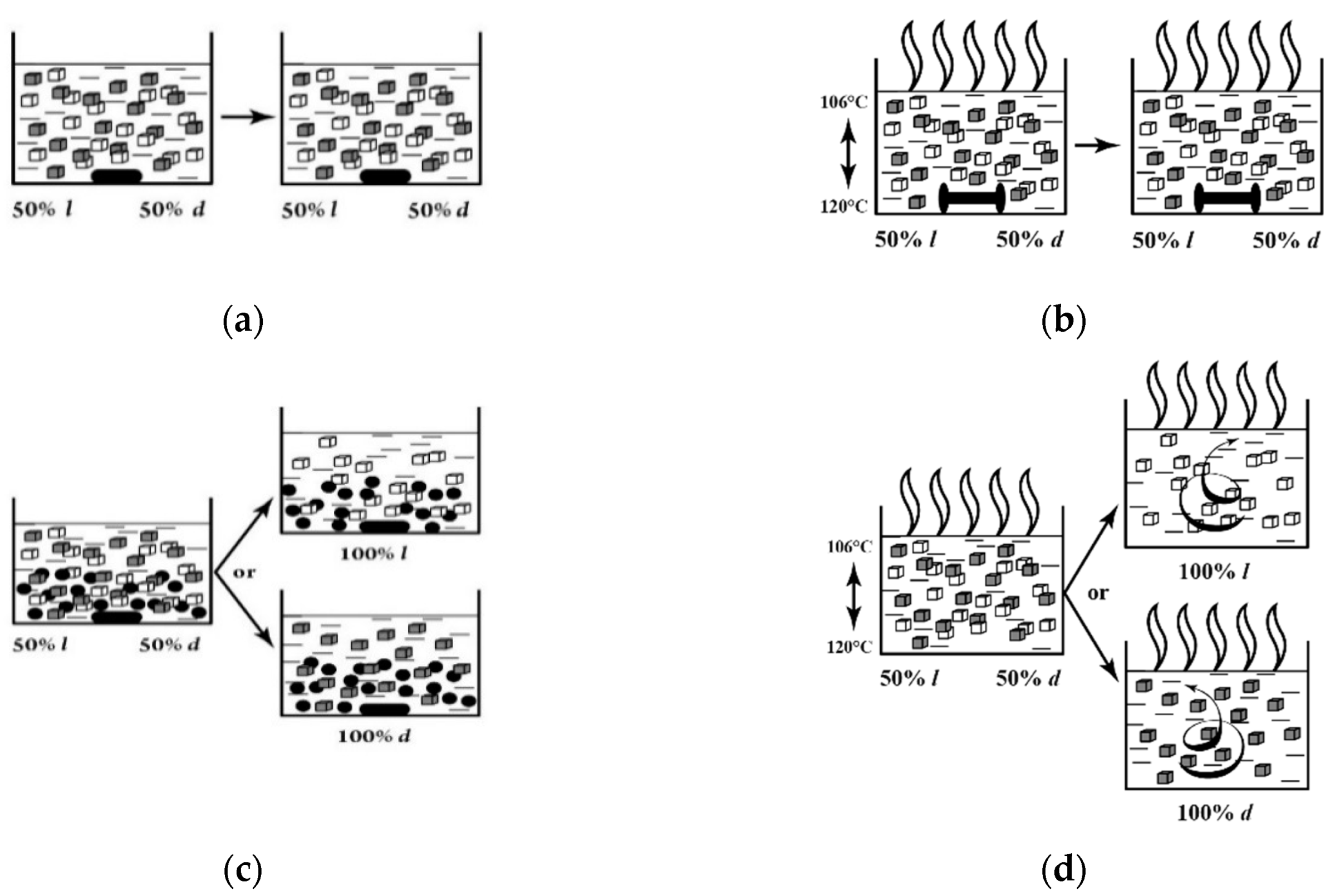
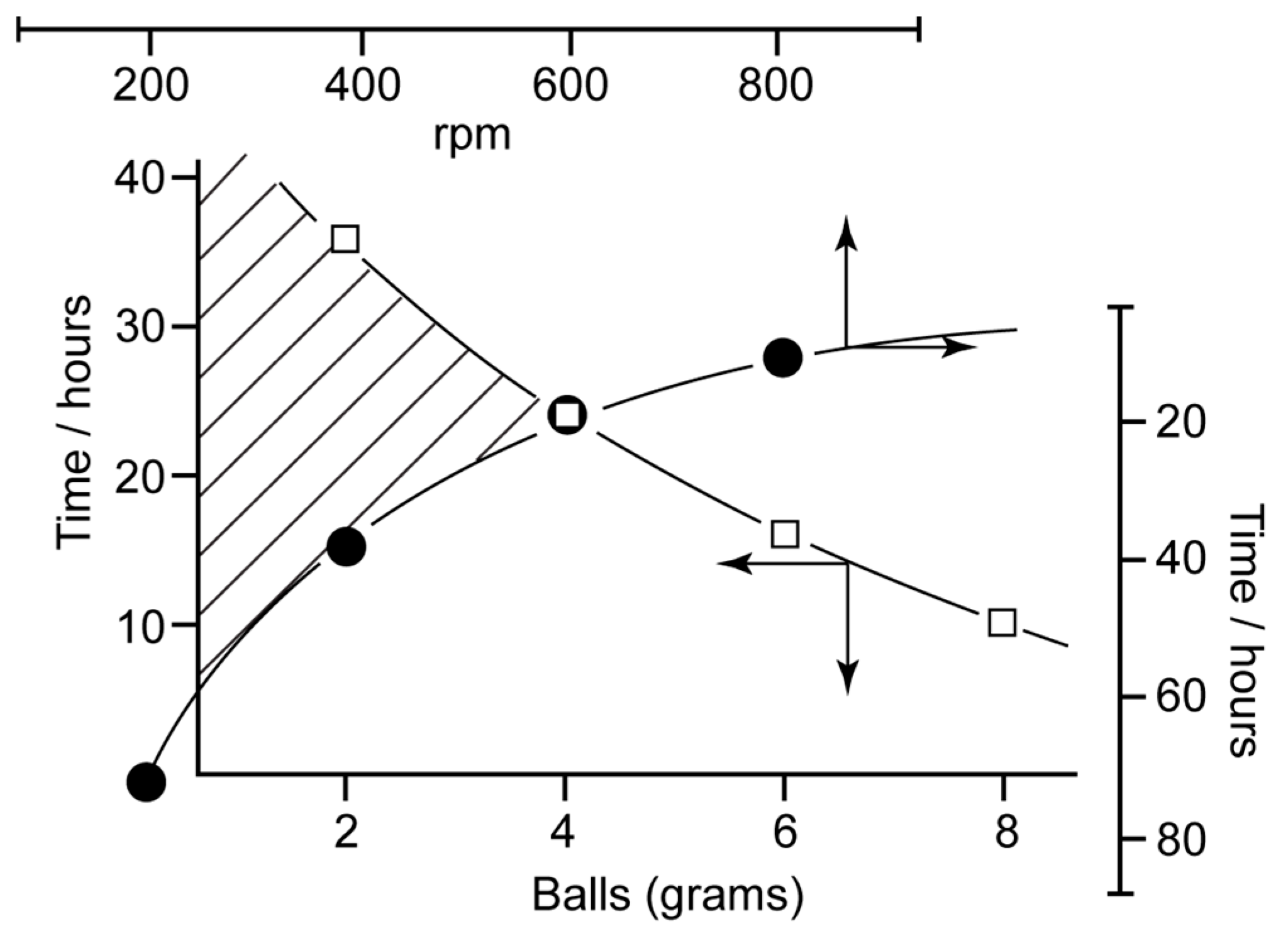
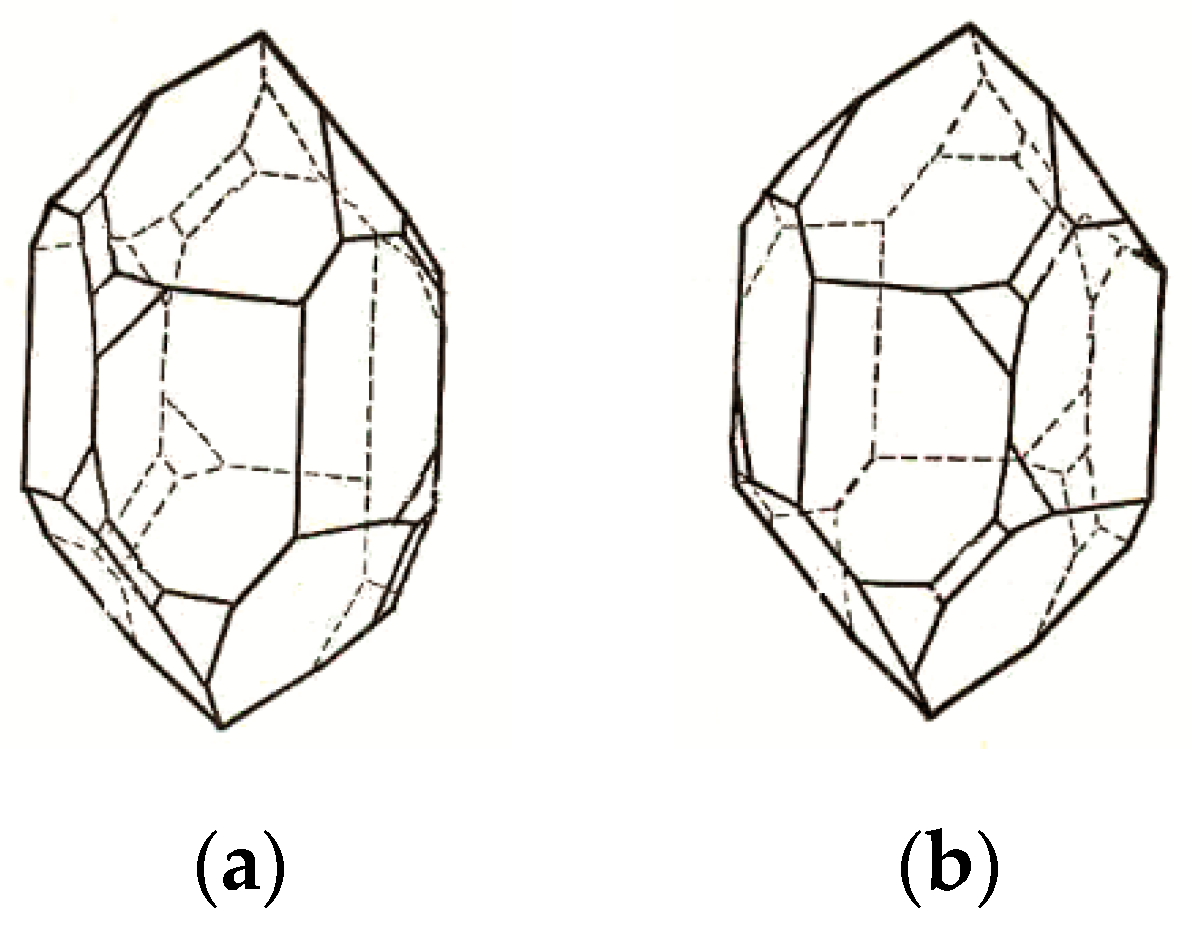
4. Stirring (Helical Flux) of the Reaction Mass as a Chirality Trigger
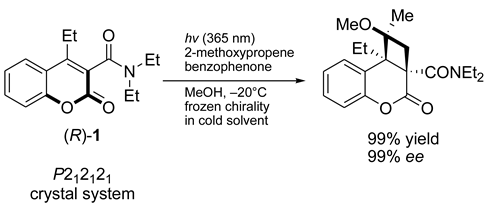

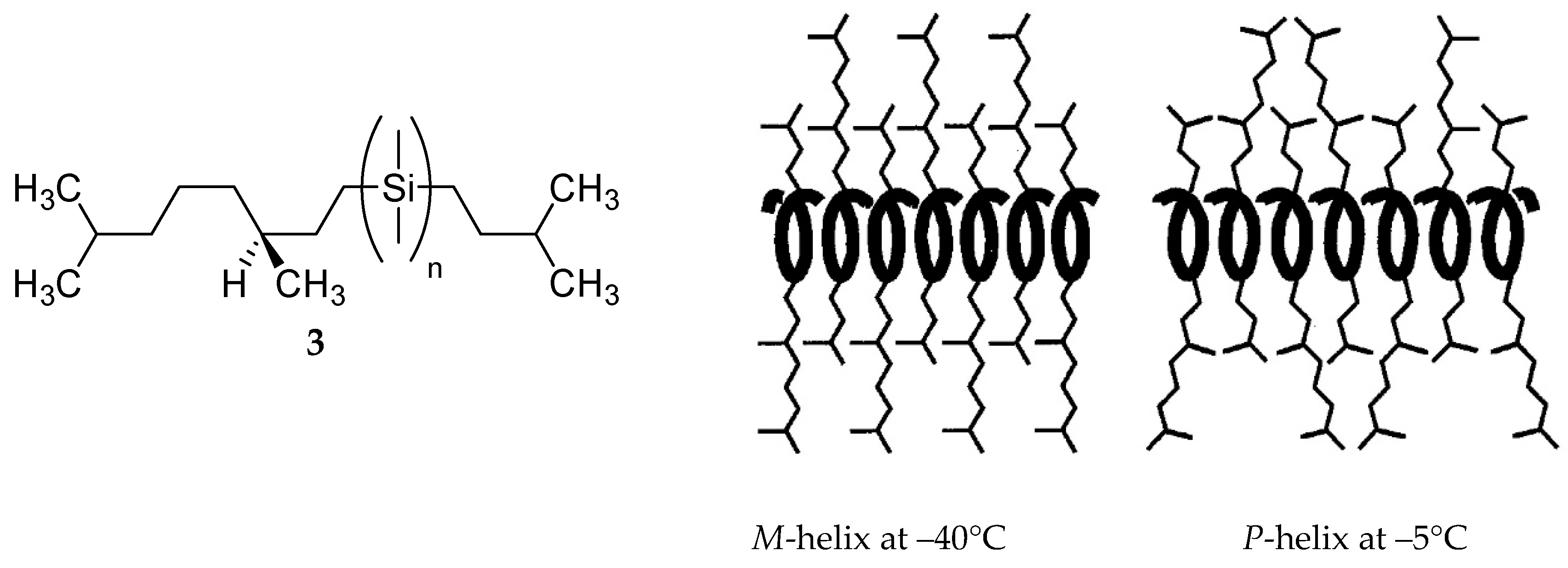
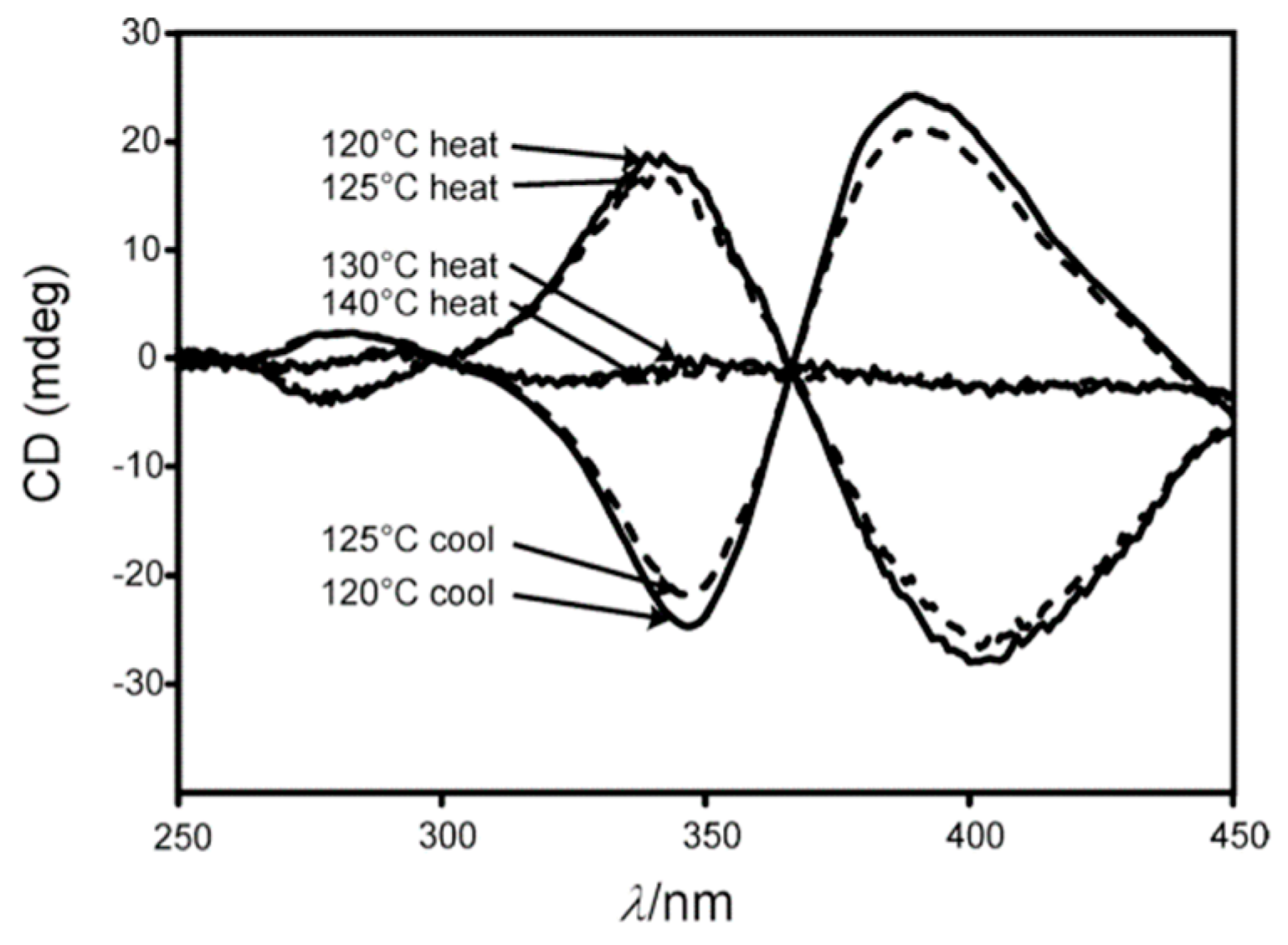
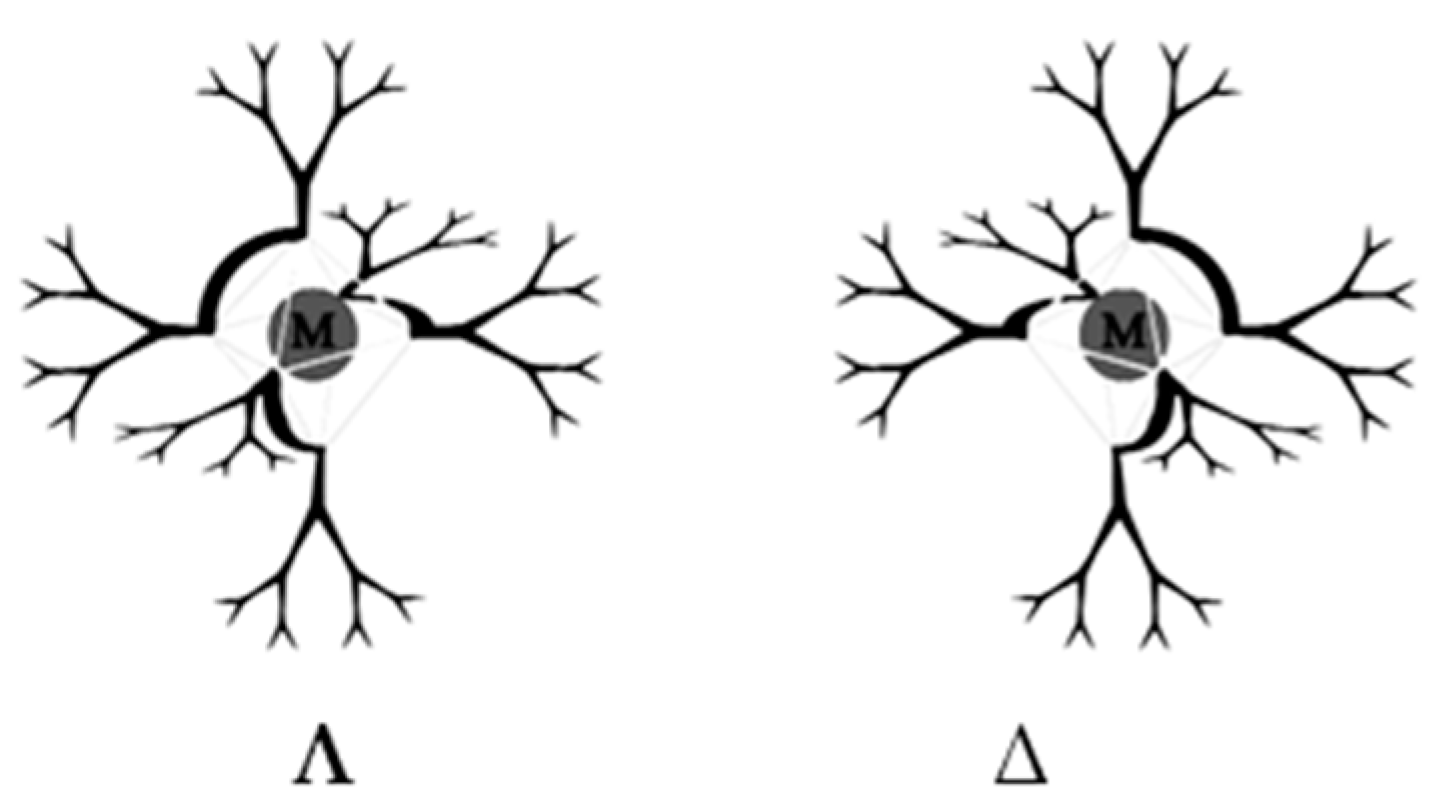
 M transition was observed for other polysilylenes and analogous polymers at different temperatures, with various solvents and varying other reaction conditions [102,103,104,105,106,107].
M transition was observed for other polysilylenes and analogous polymers at different temperatures, with various solvents and varying other reaction conditions [102,103,104,105,106,107]. M conversion of DNA (see Section 8).
M conversion of DNA (see Section 8).
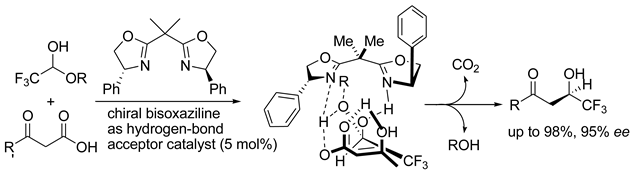
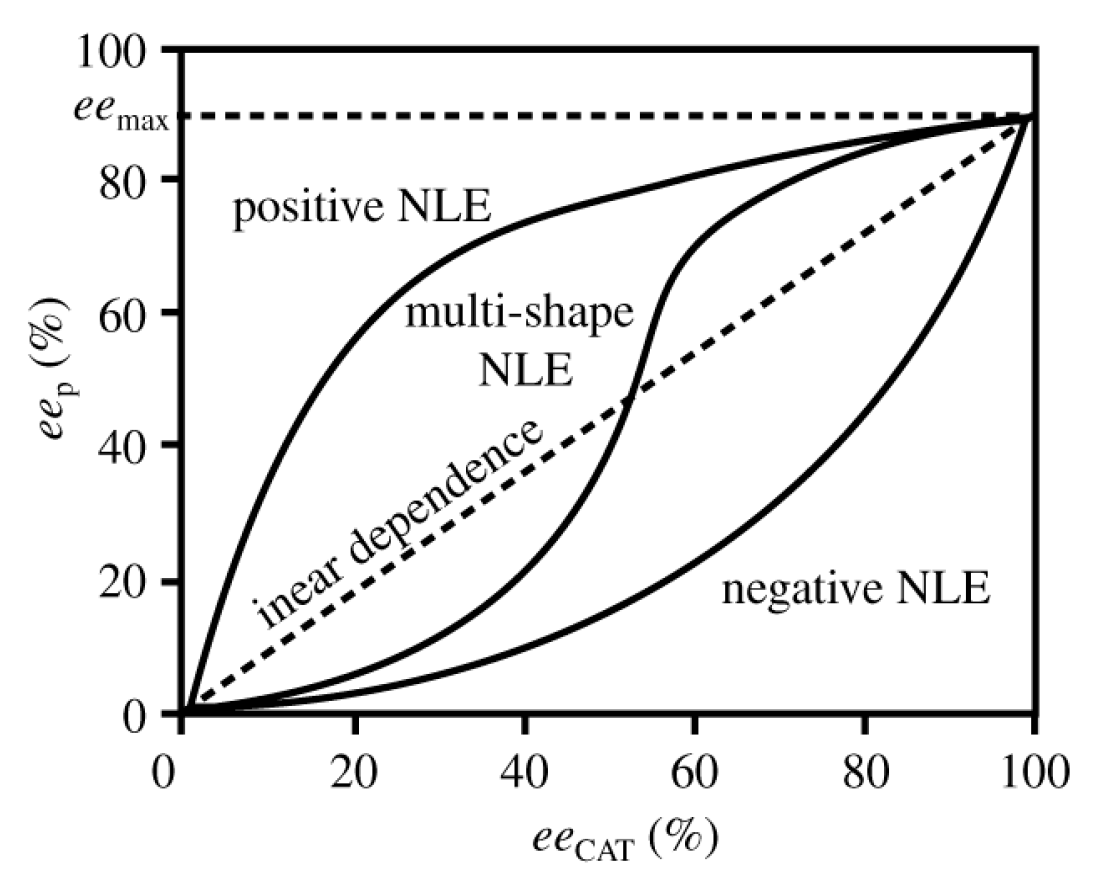
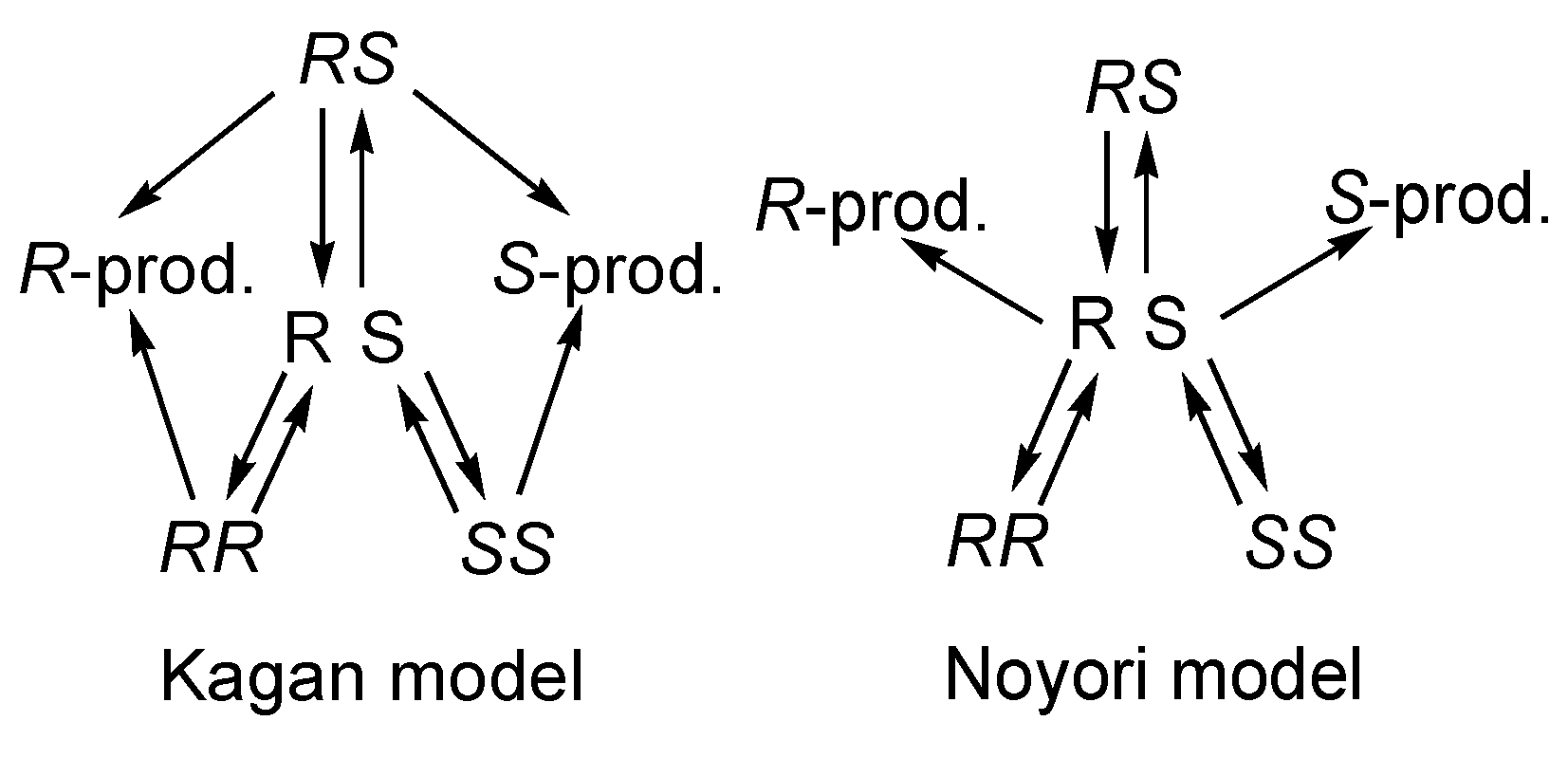
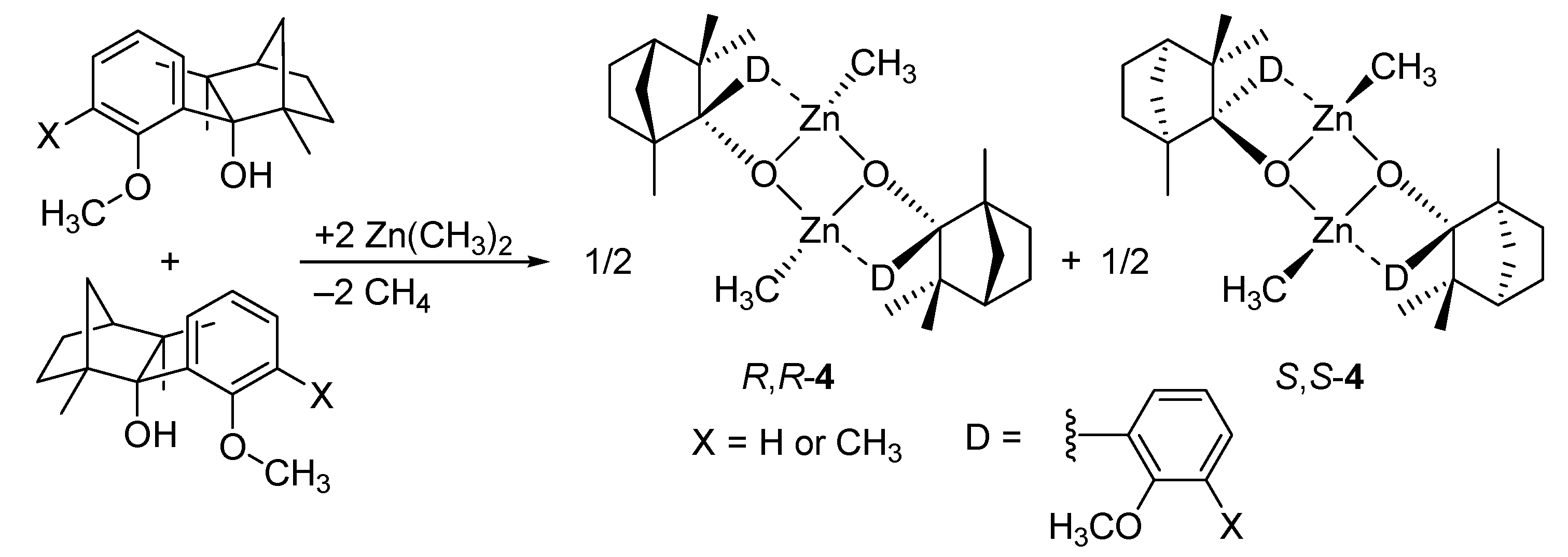
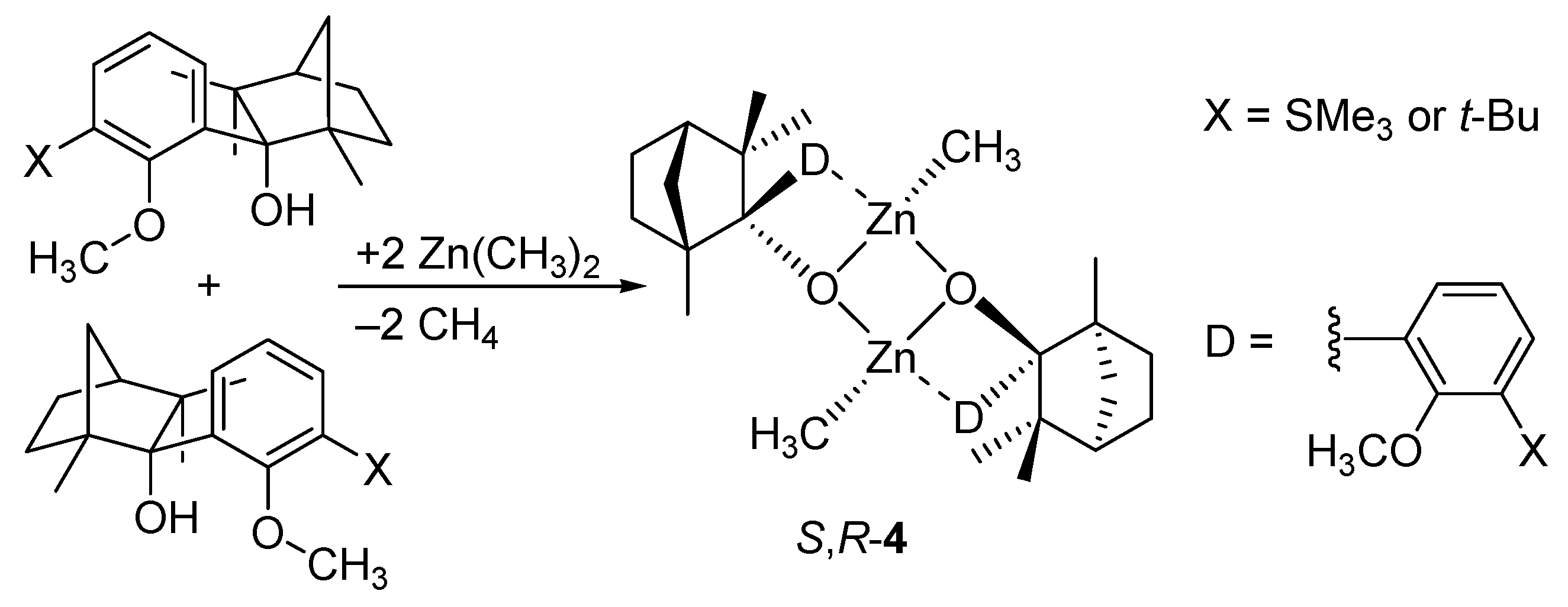
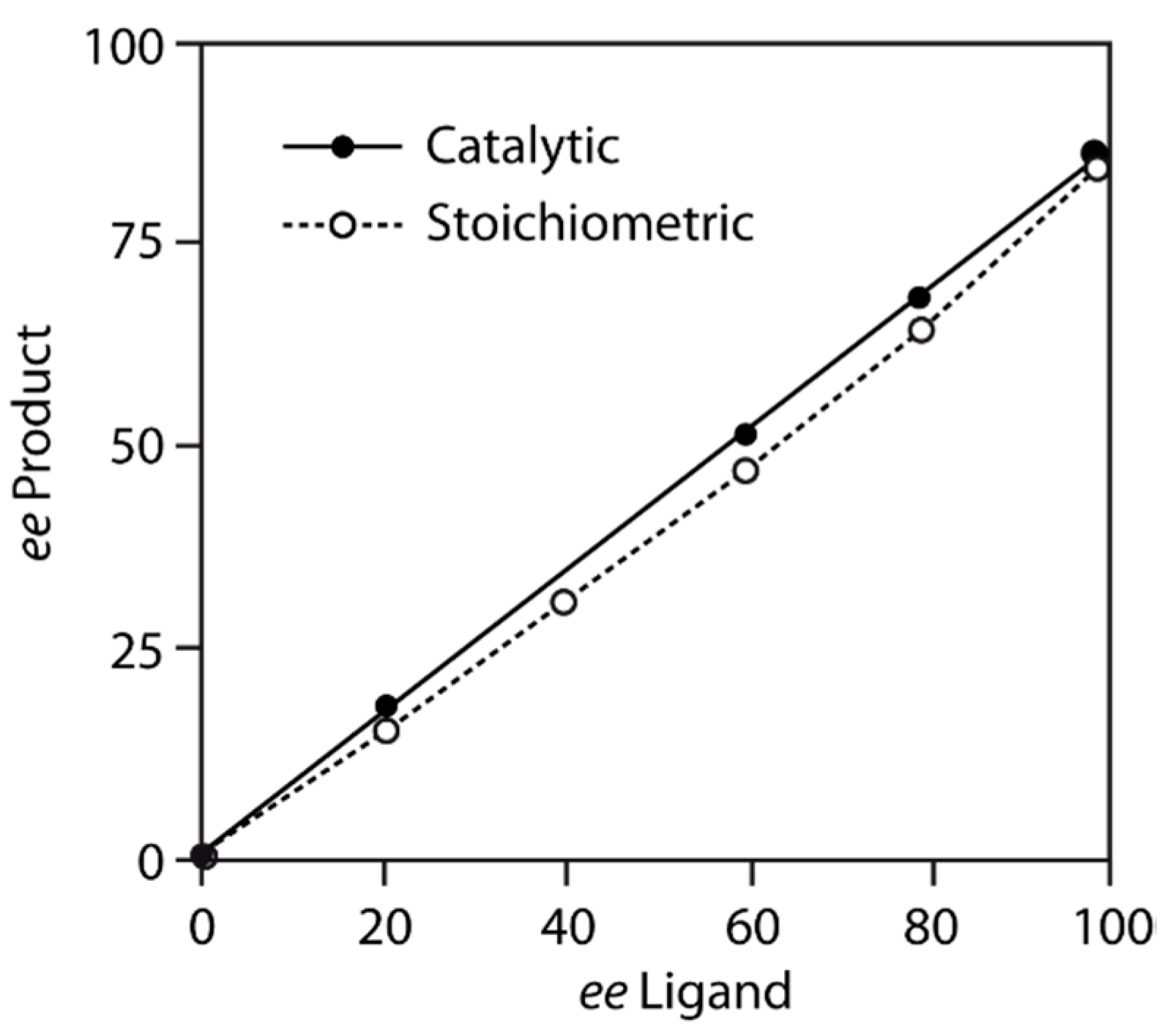
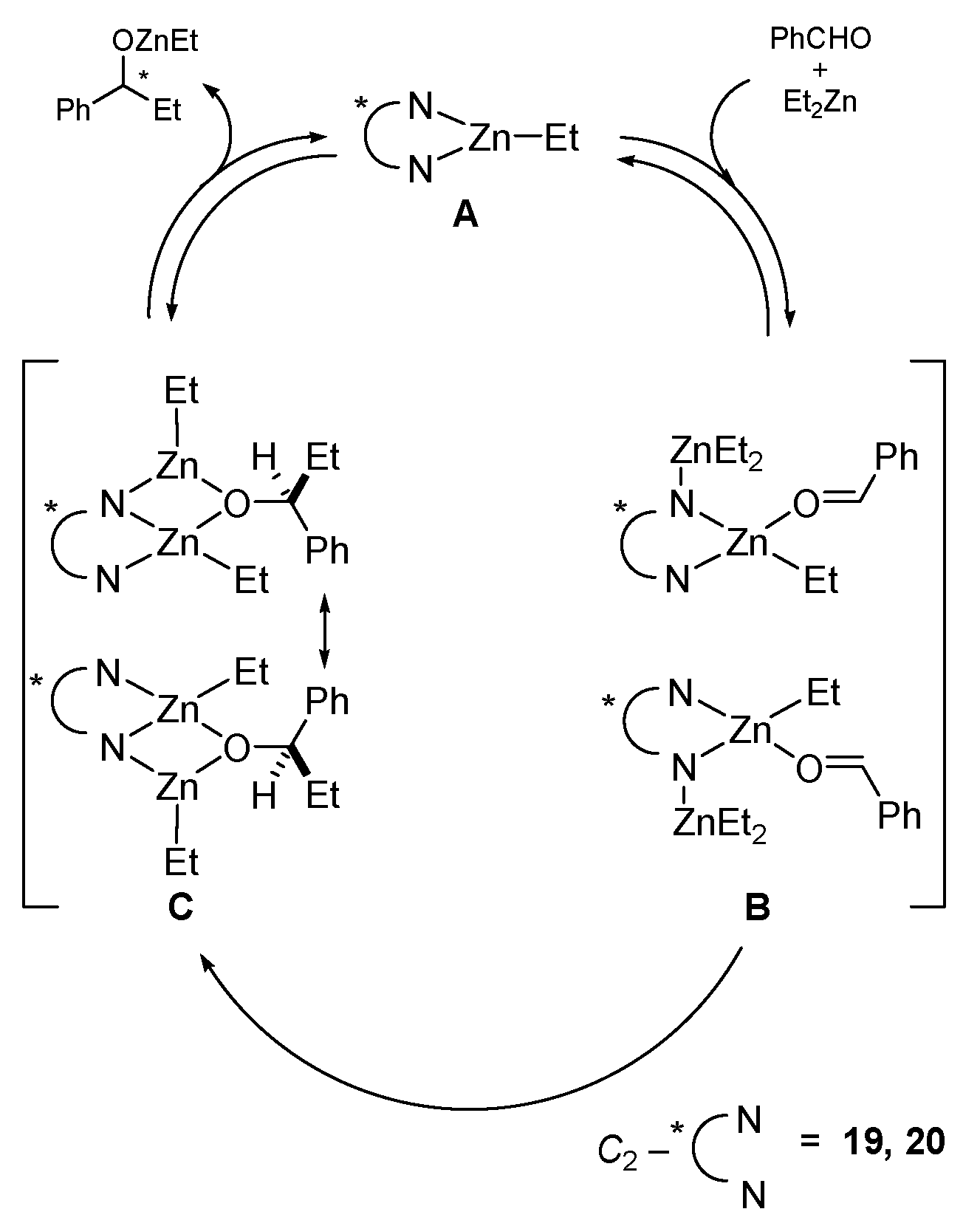
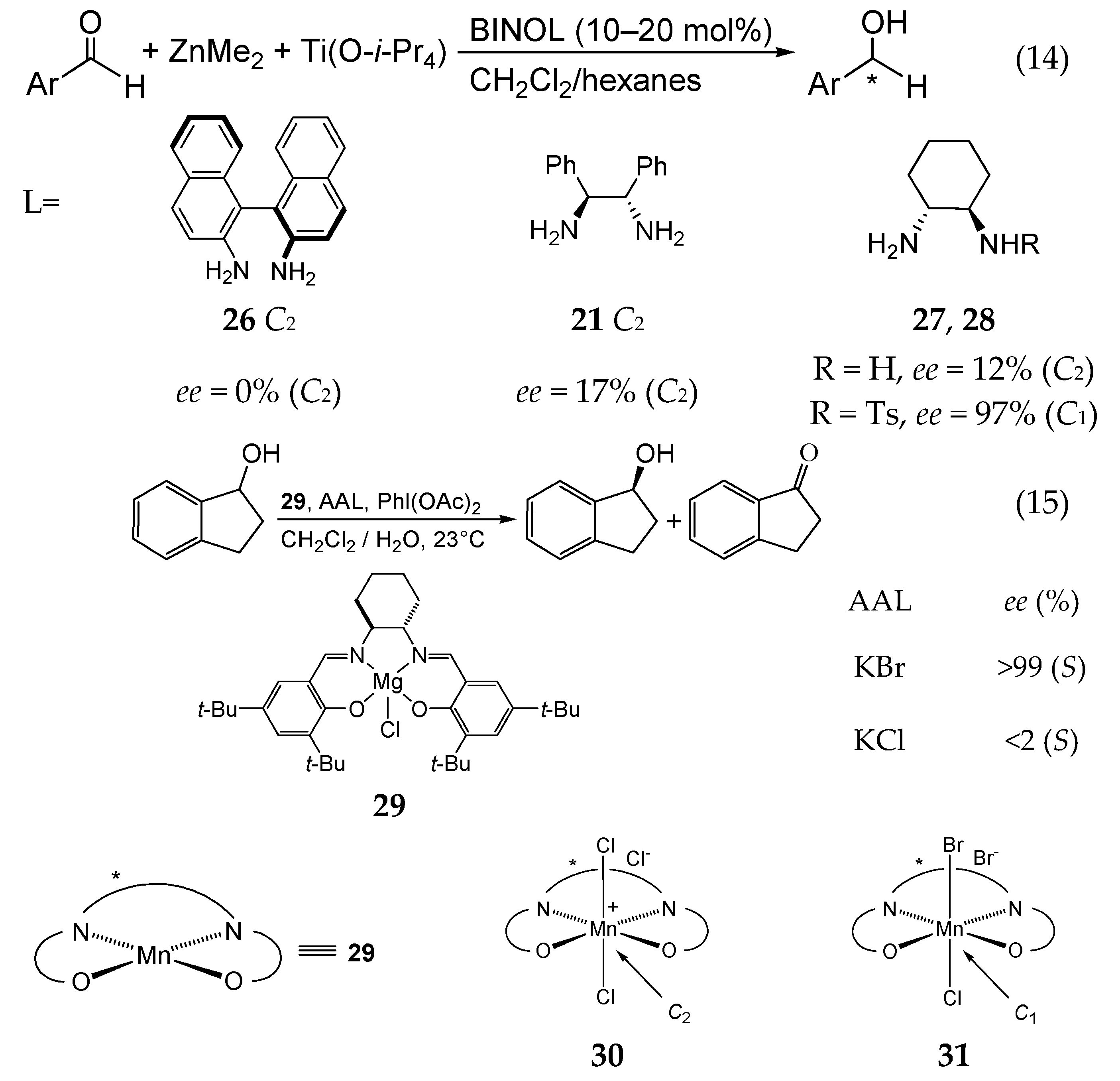
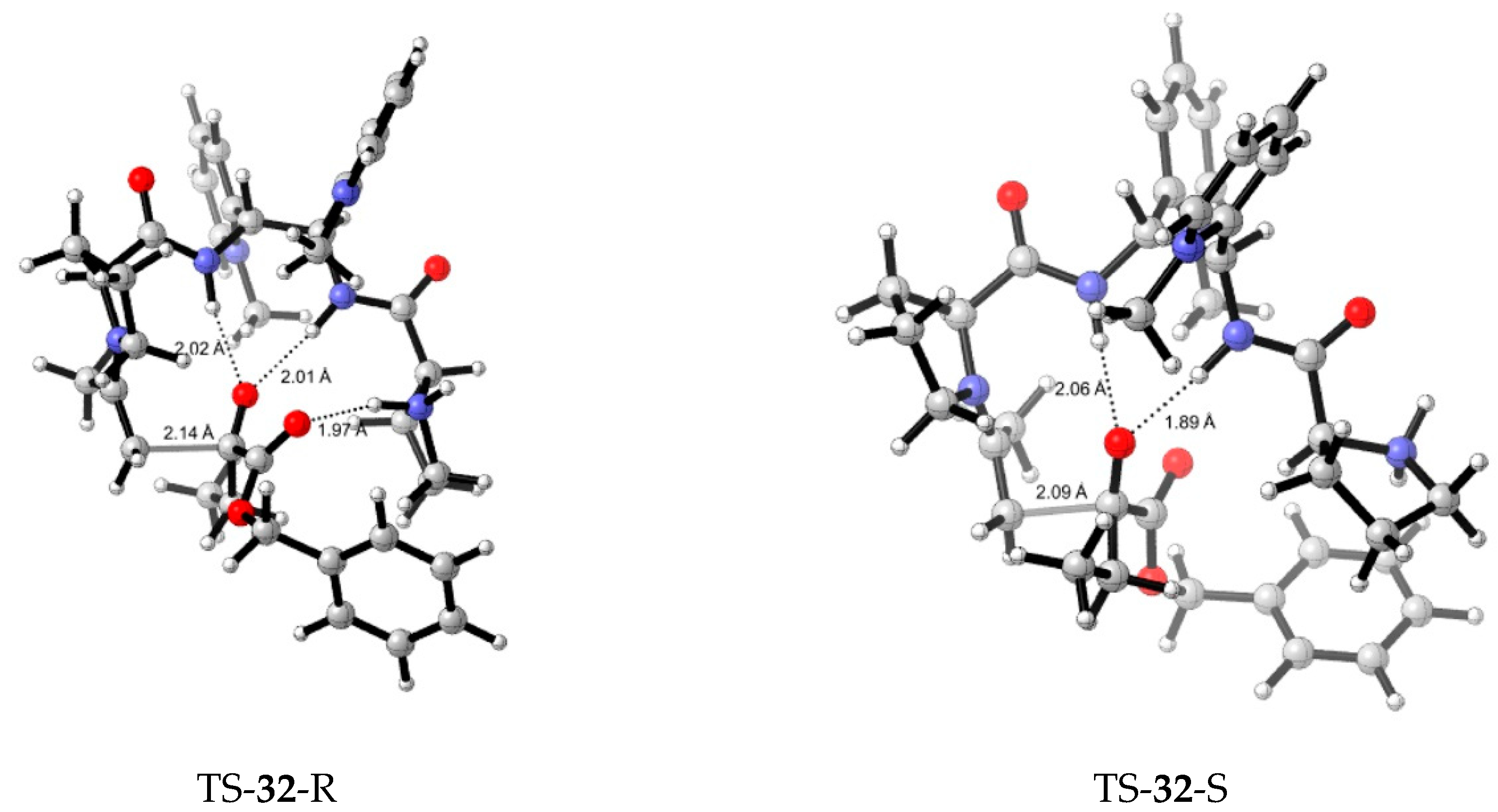
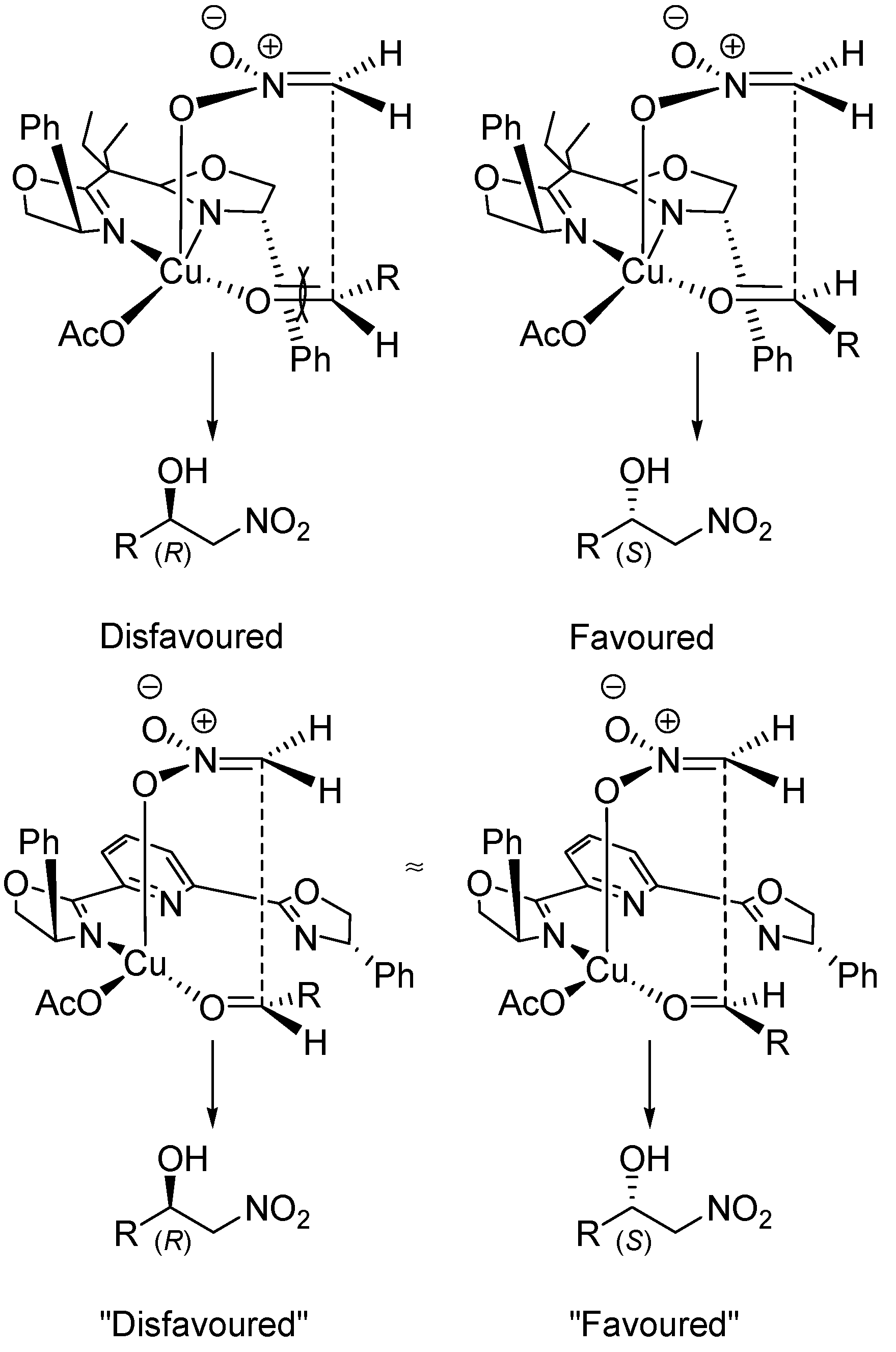
5. Chiral and Racemic Field in Asymmetric Catalysis and Nonlinear Effects

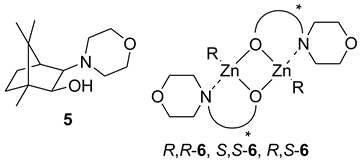
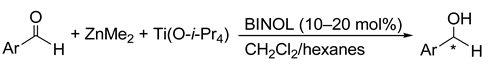
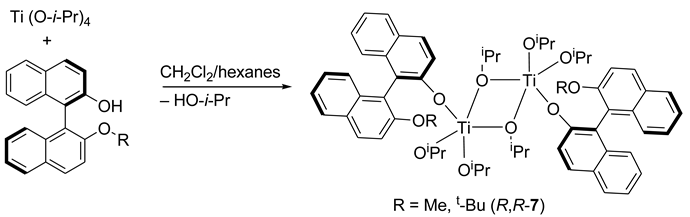
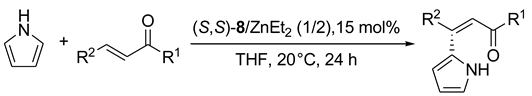

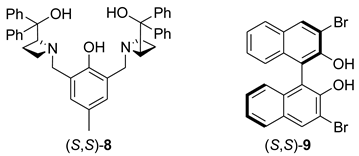
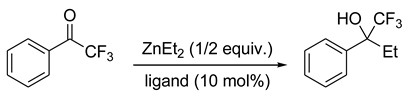
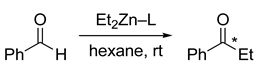
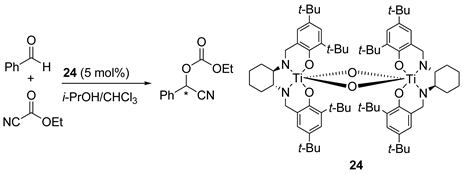
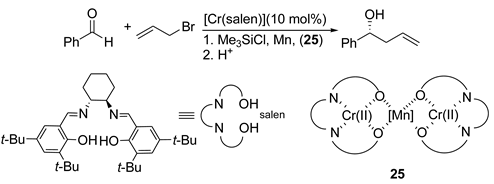
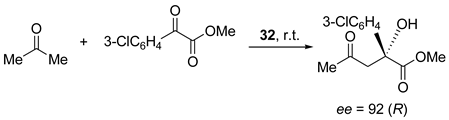
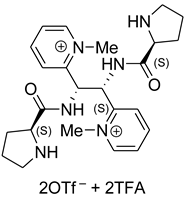
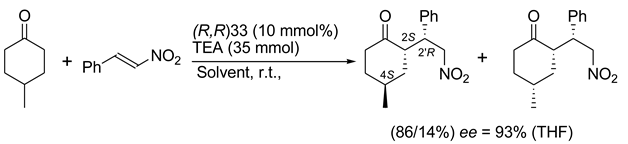

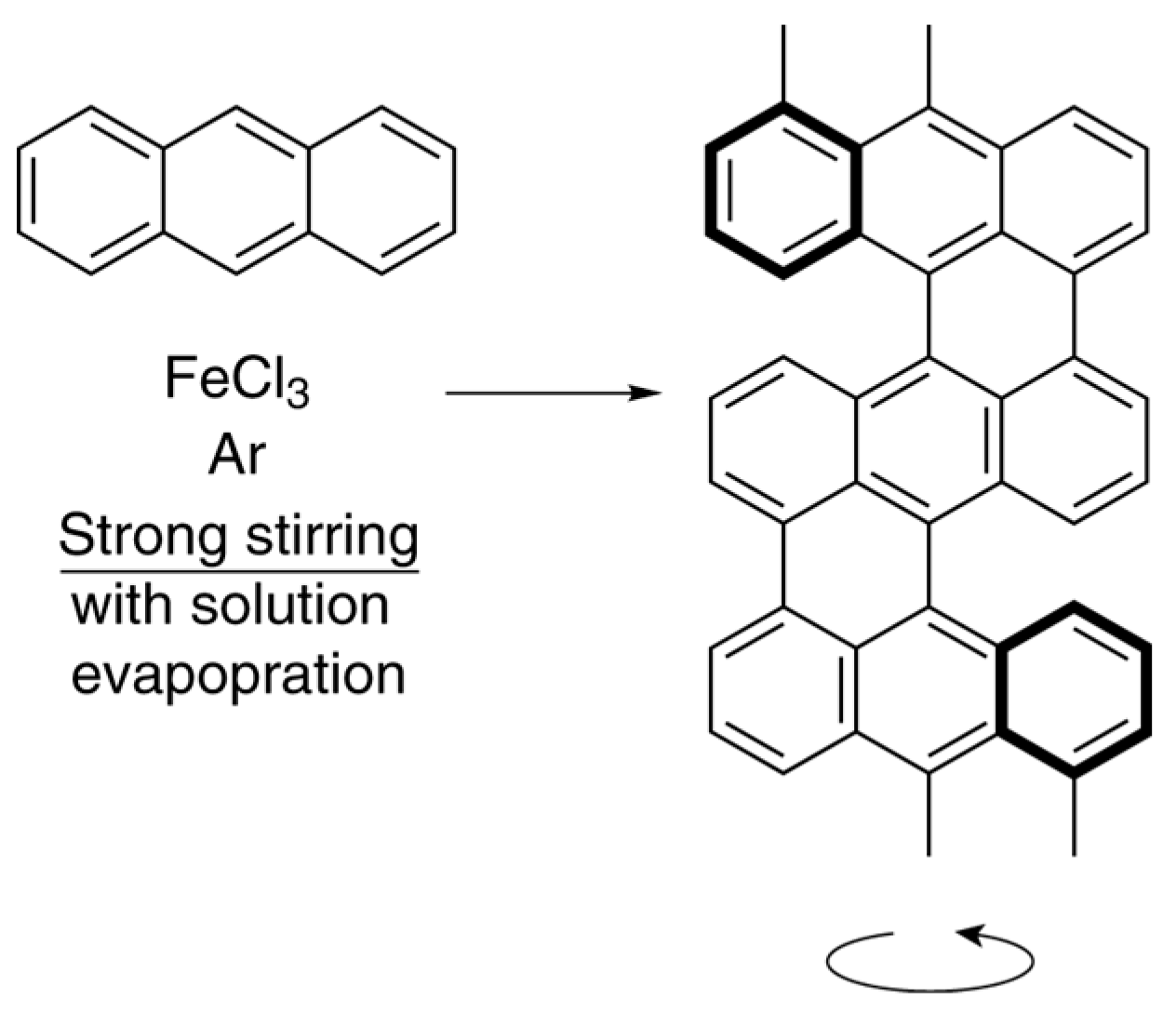
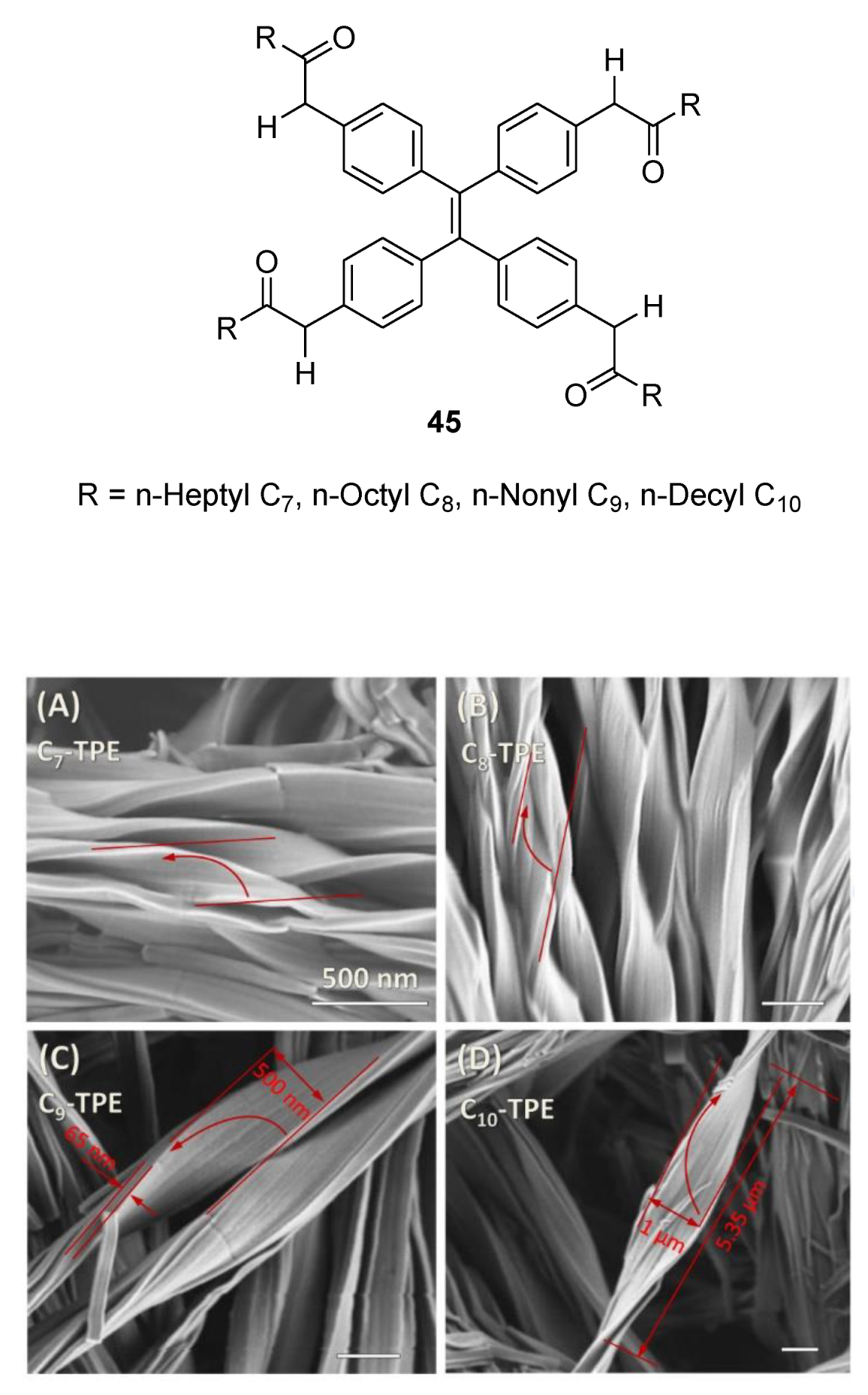
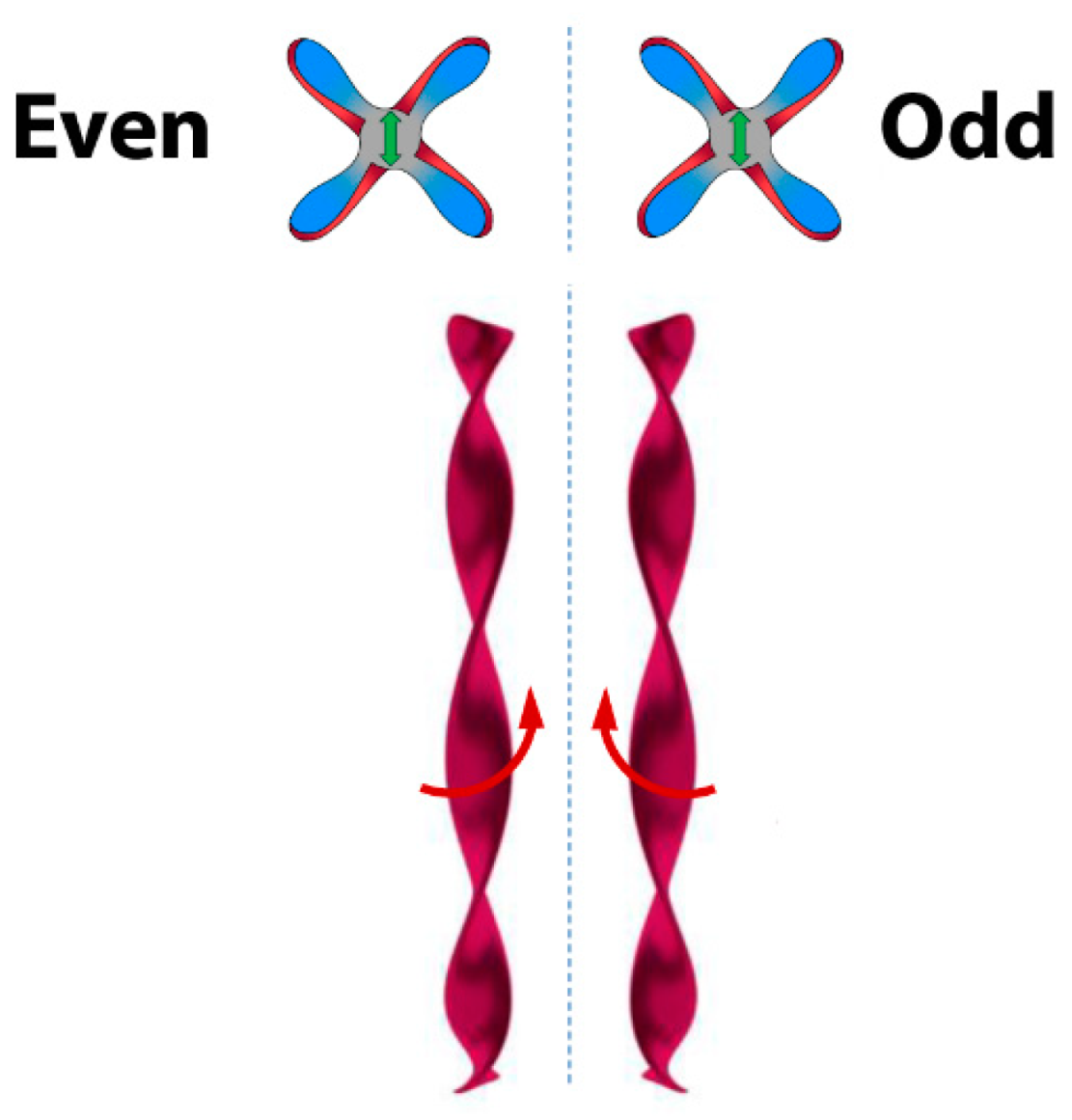
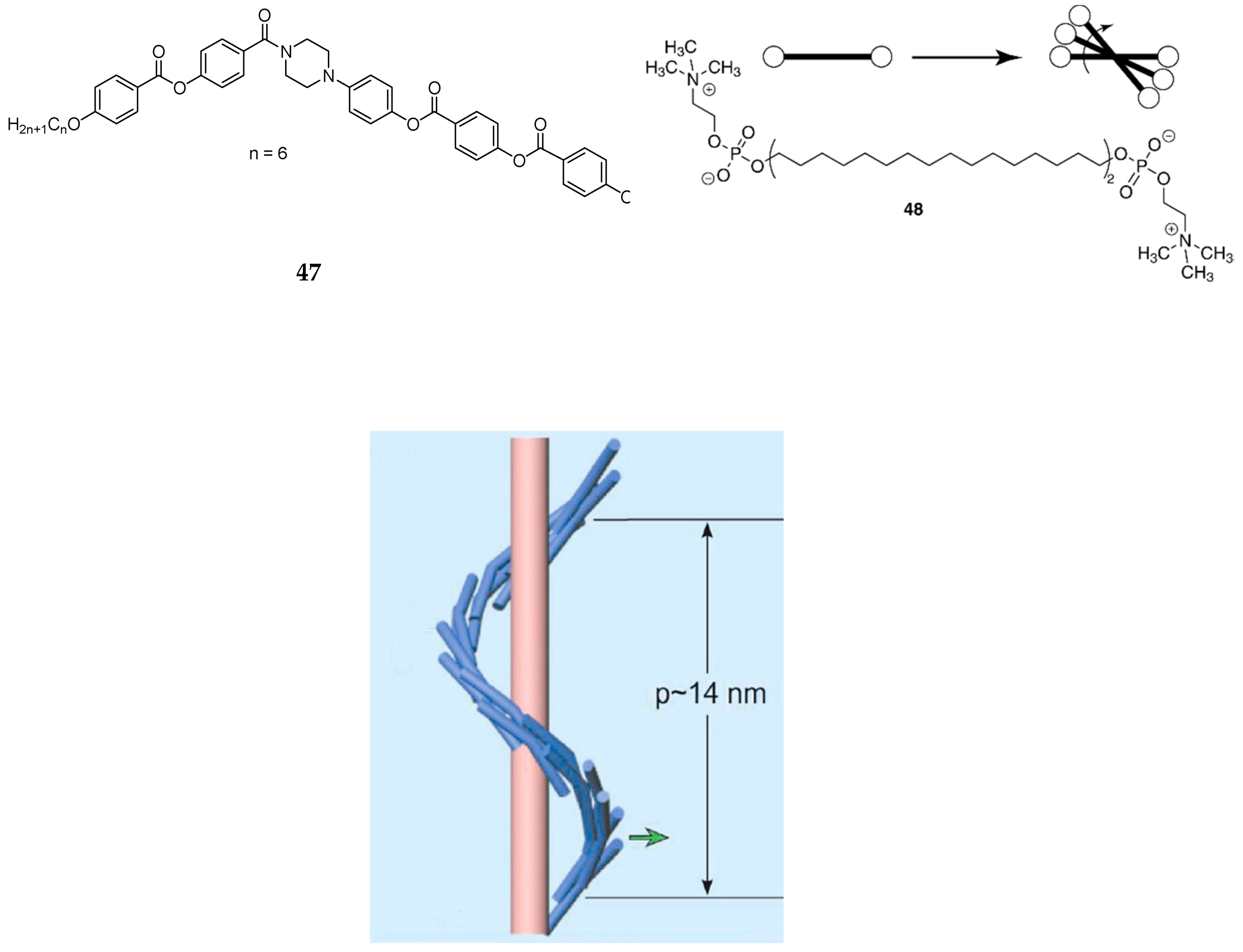
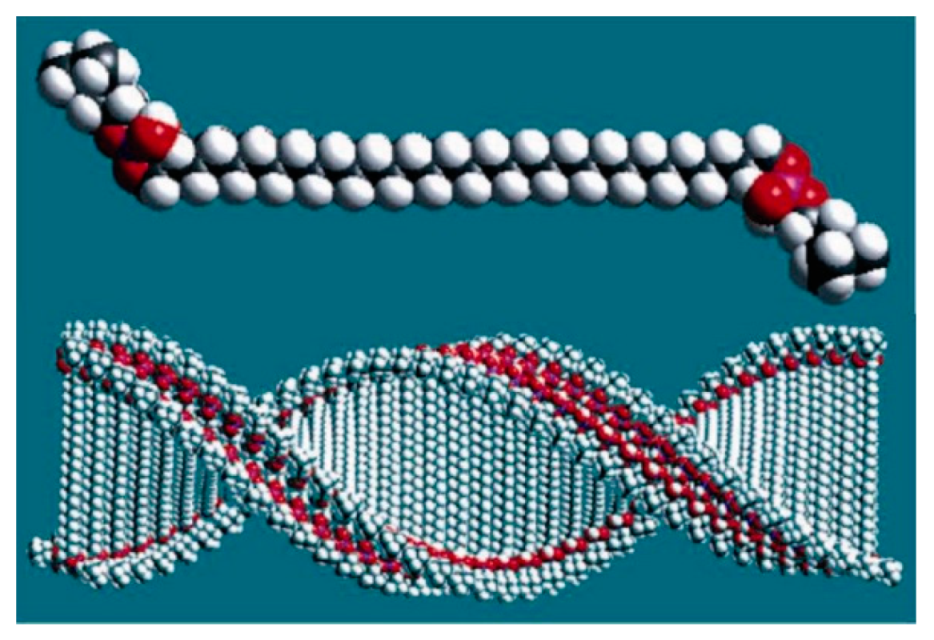
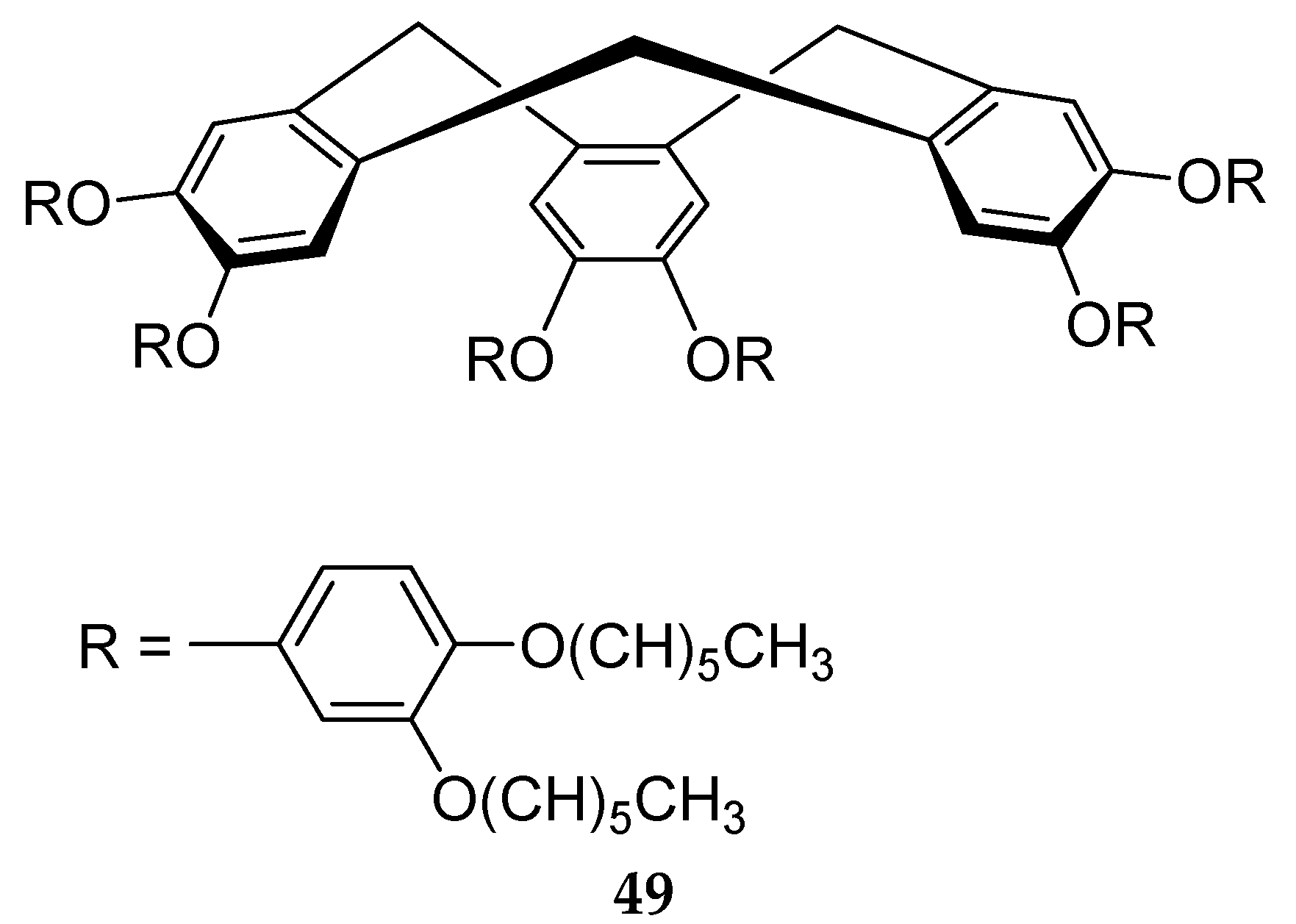
6. Spontaneous Chiral Ordering of Achiral Molecules in Liquid Crystals
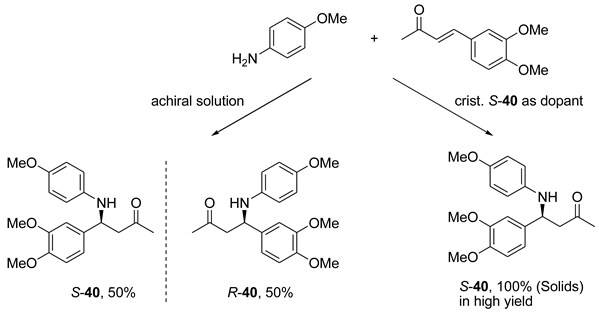
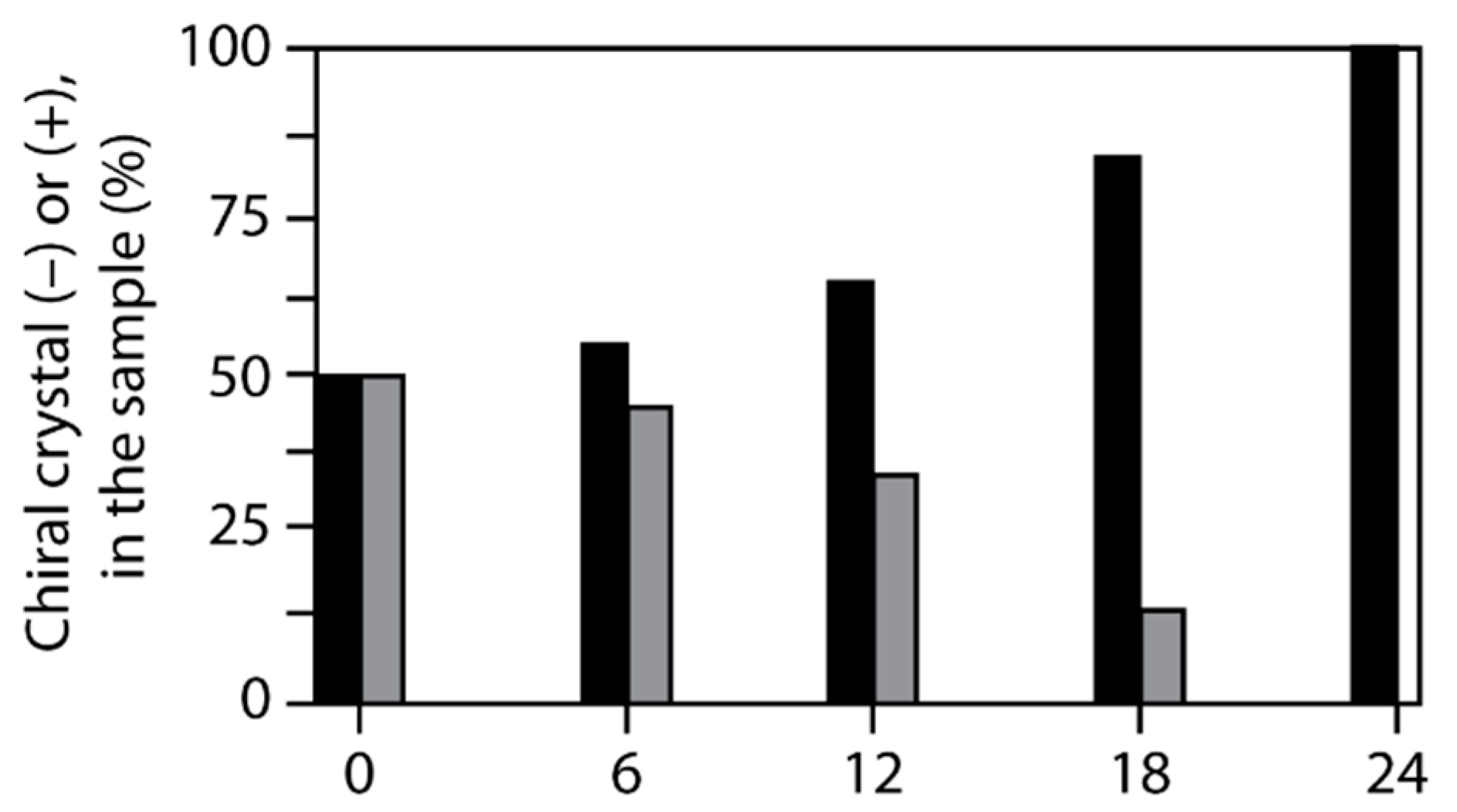
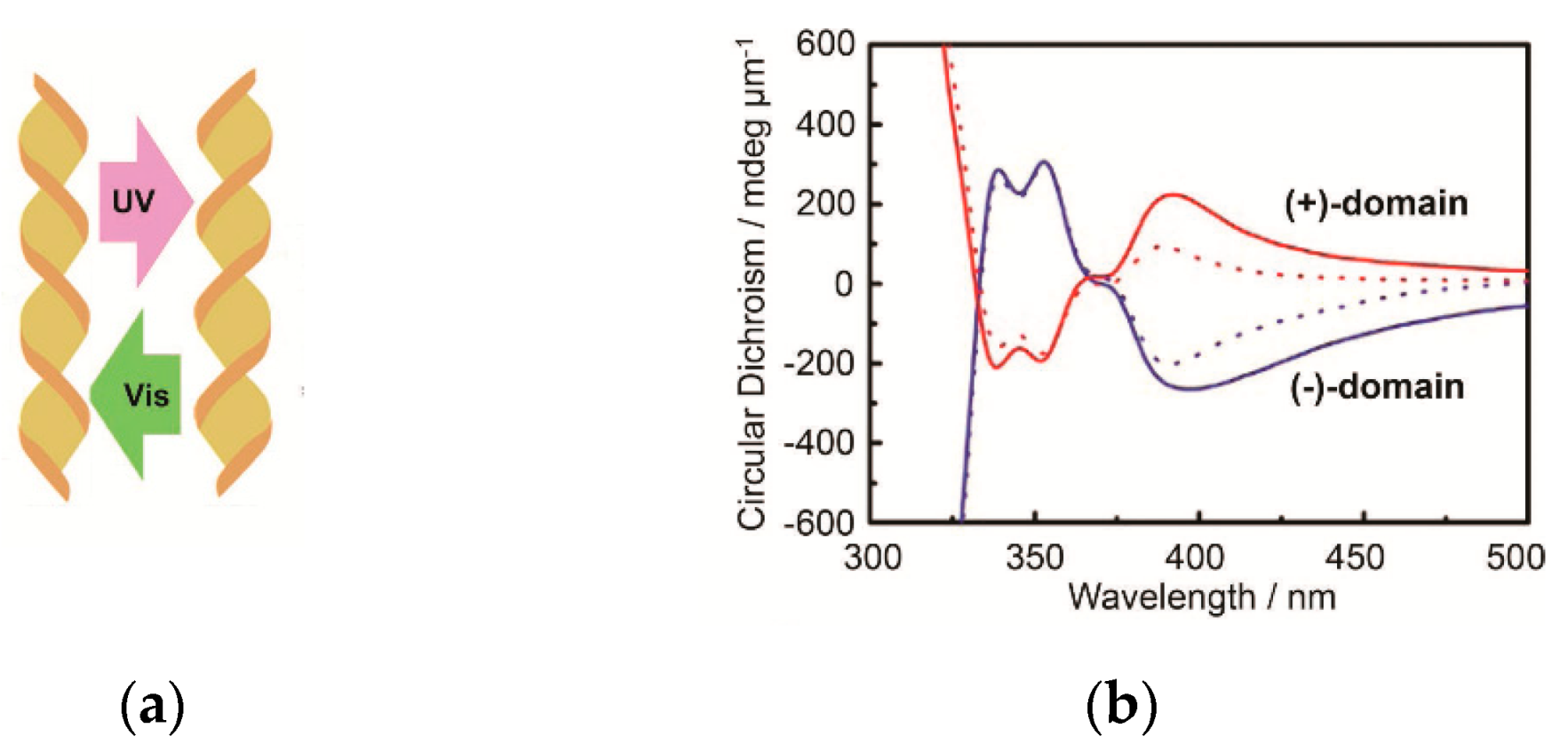
 M enantiomeres was found to be reproducible depending on irradiation [158,162] (Figure 18).
M enantiomeres was found to be reproducible depending on irradiation [158,162] (Figure 18).
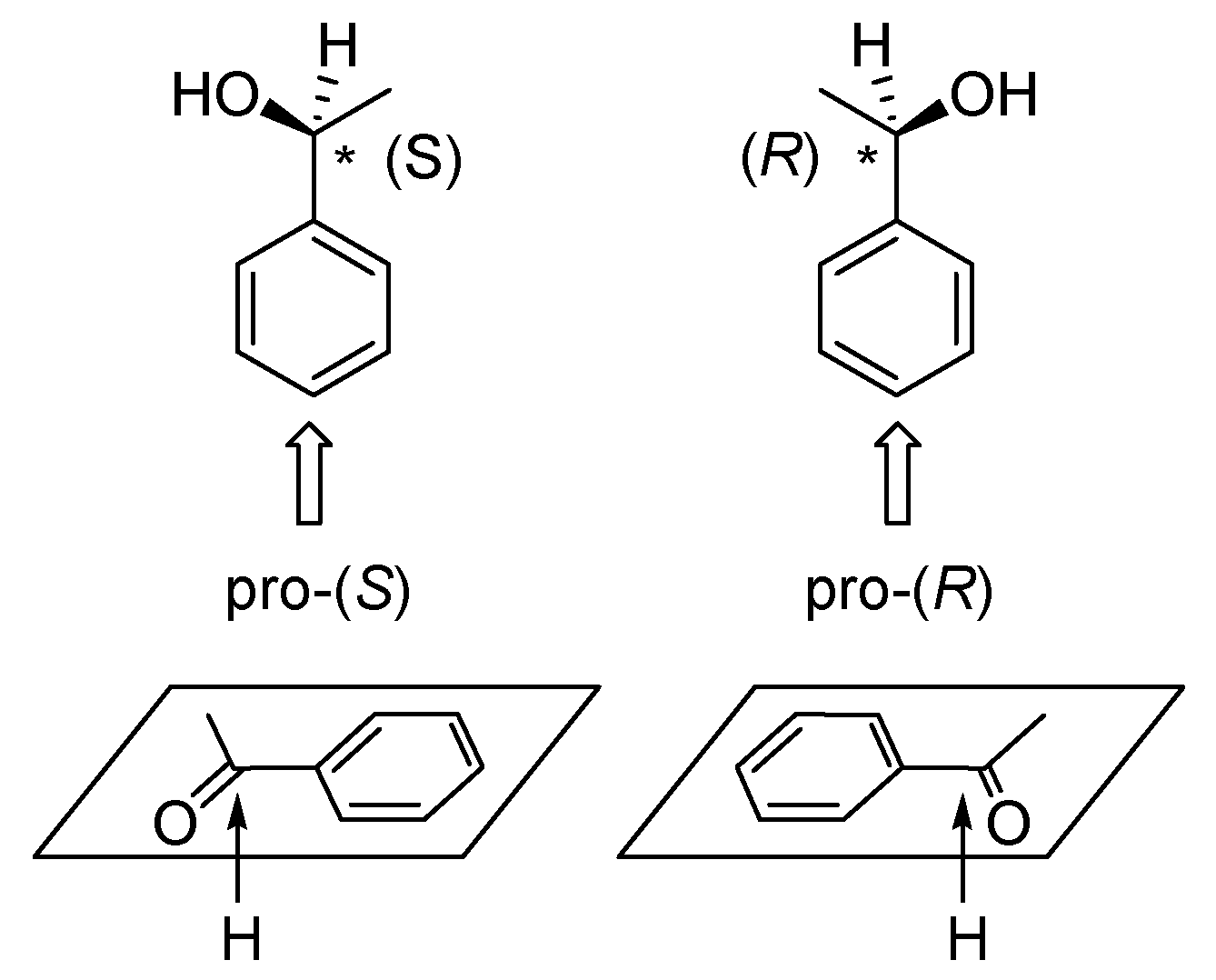
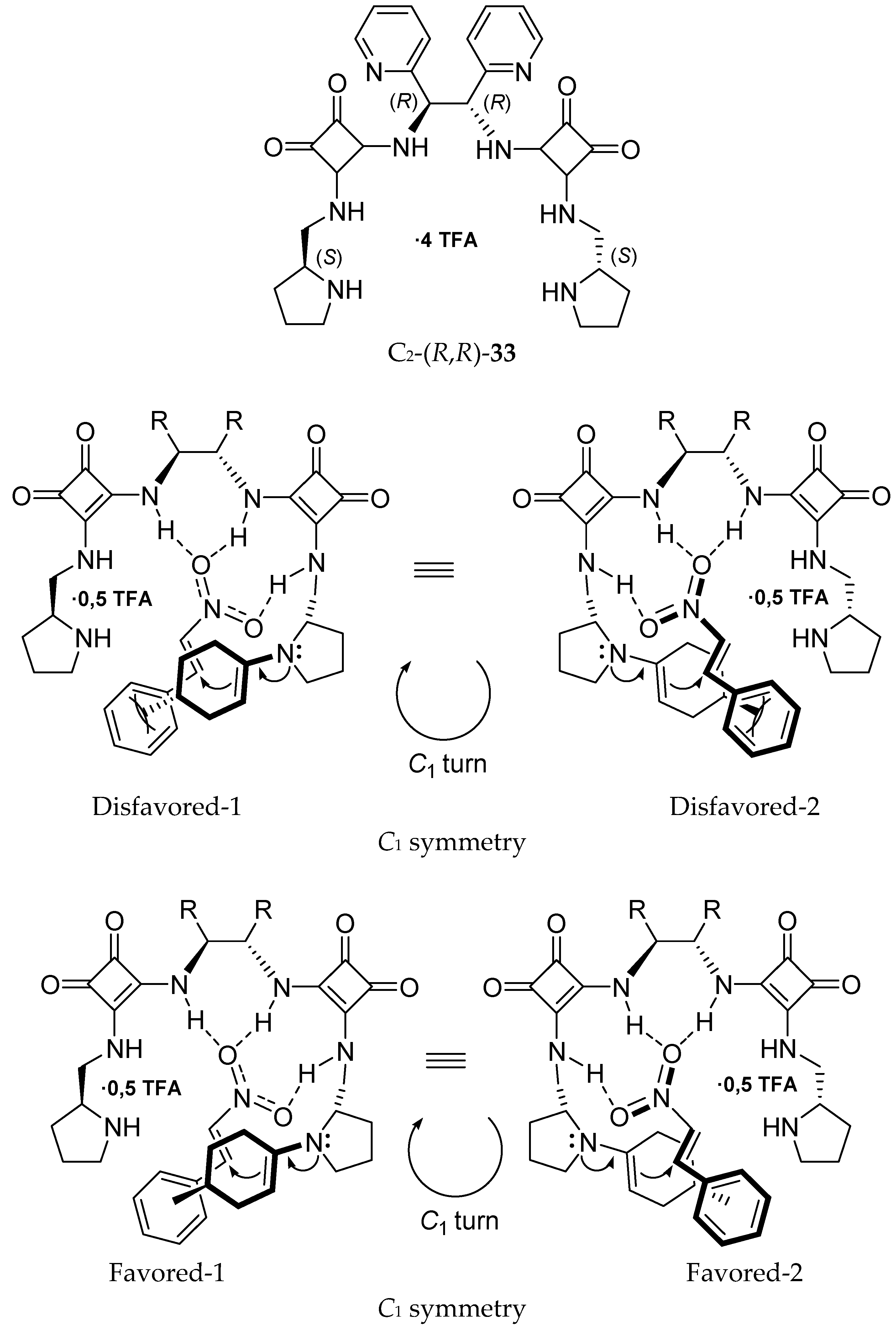
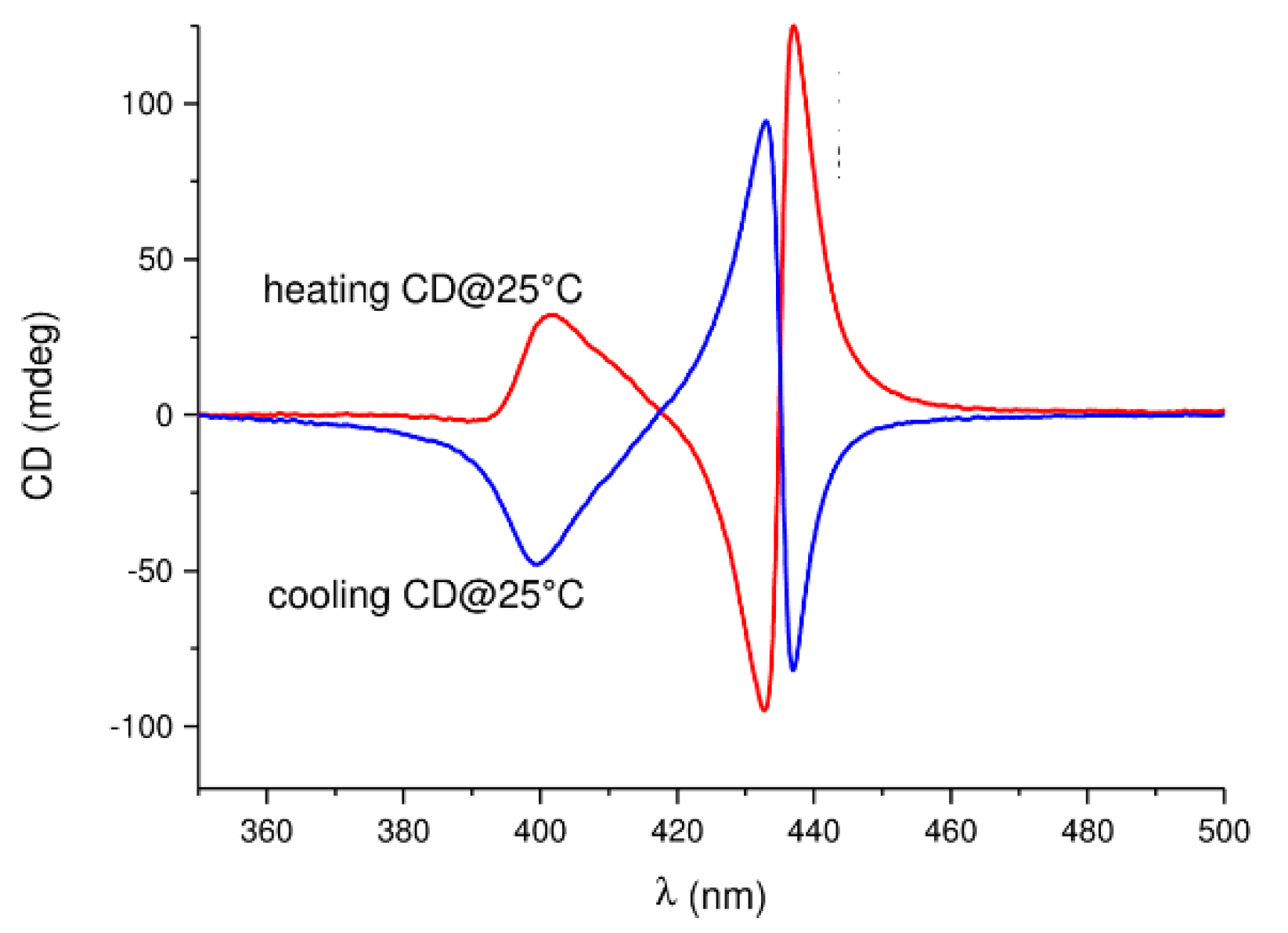
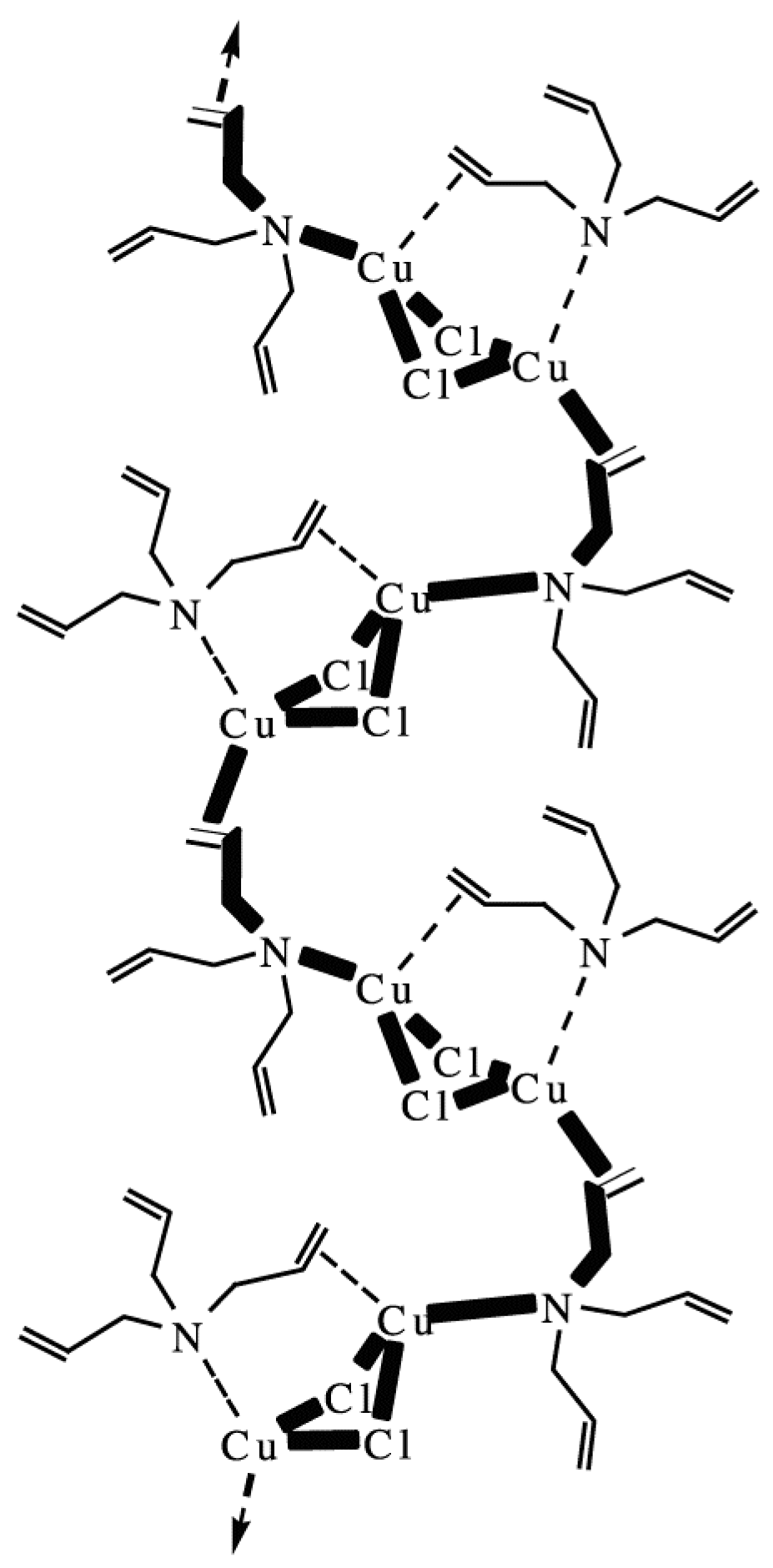
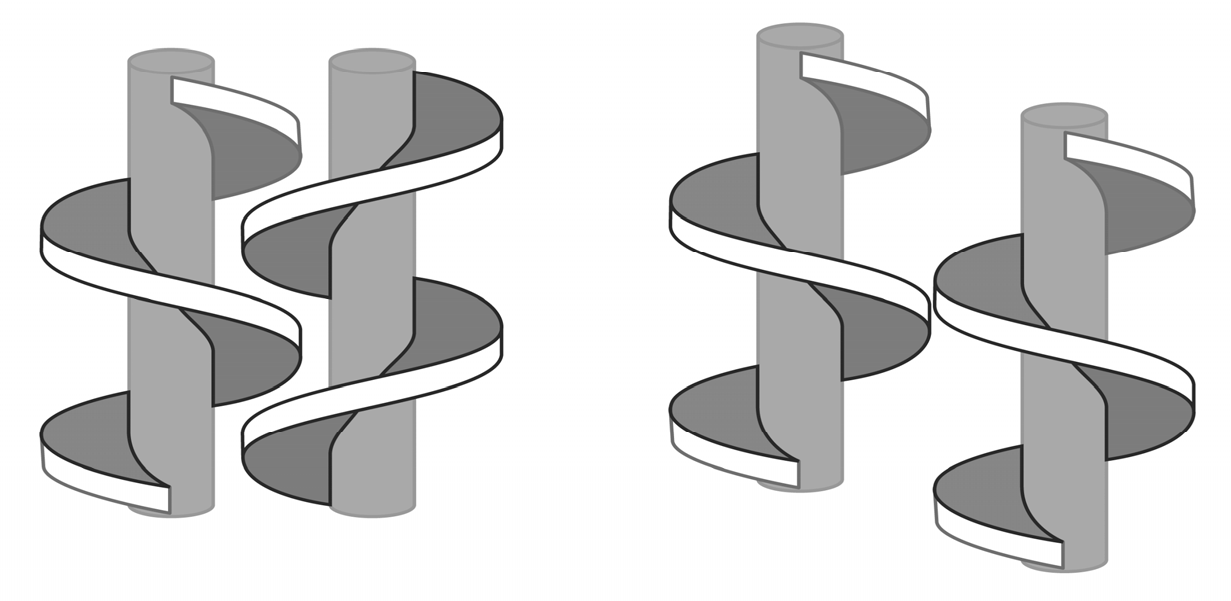
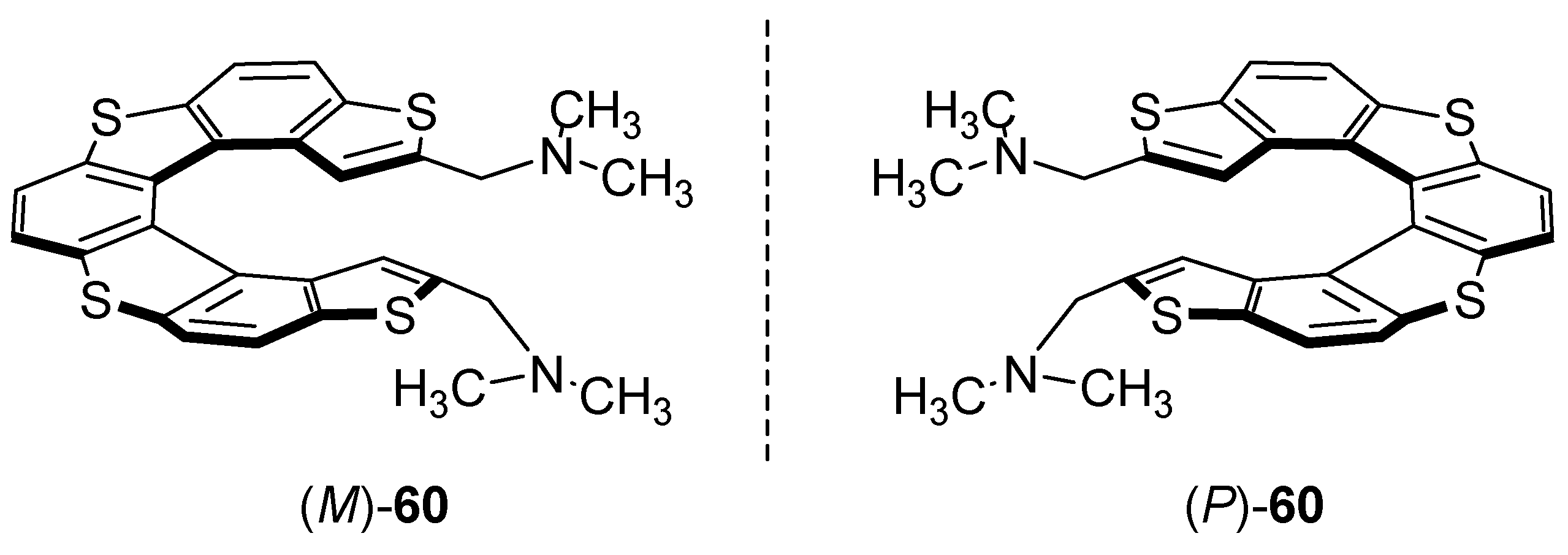
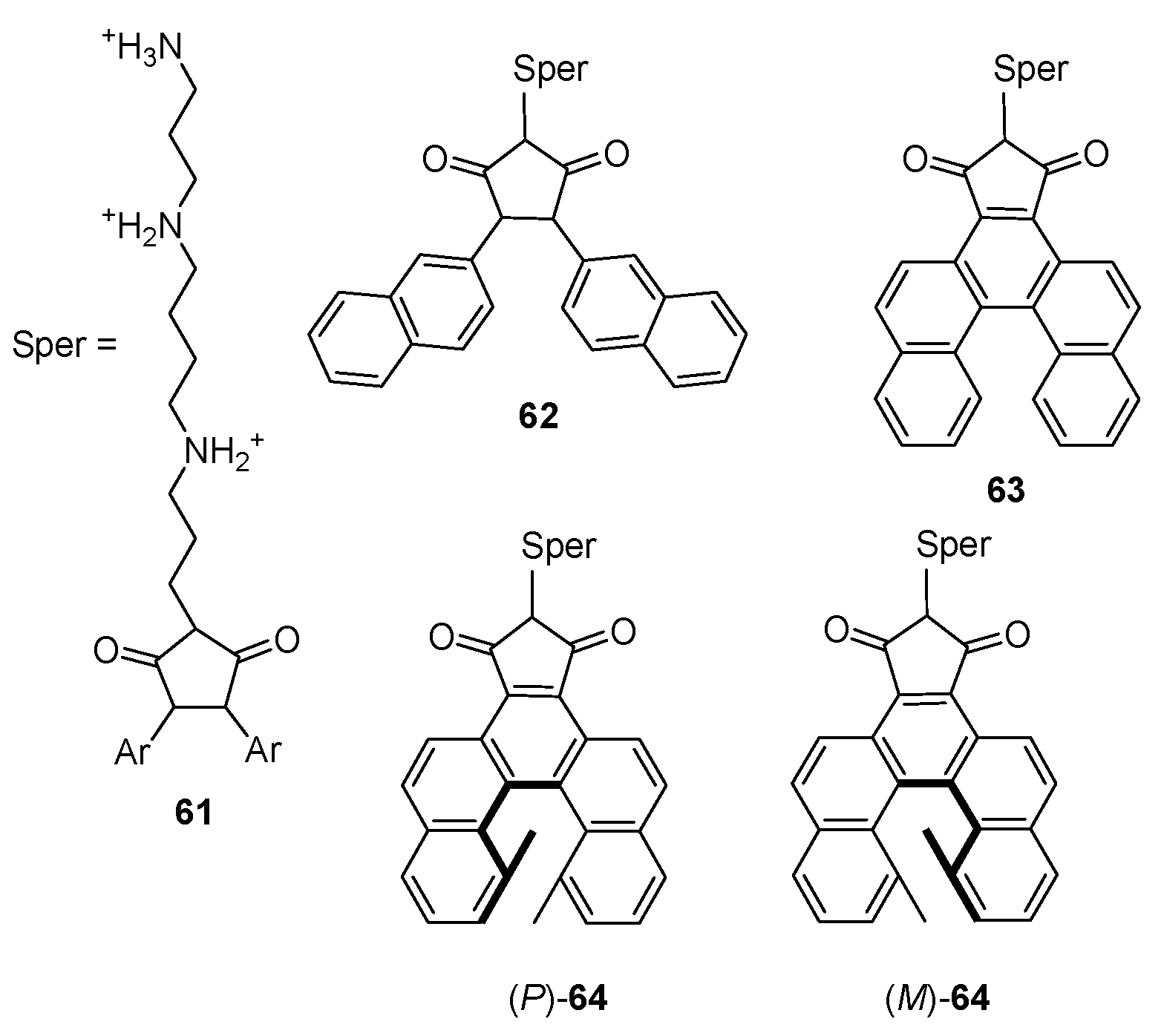
7. Chiral Field (Chiral Memory) and Racemic Field

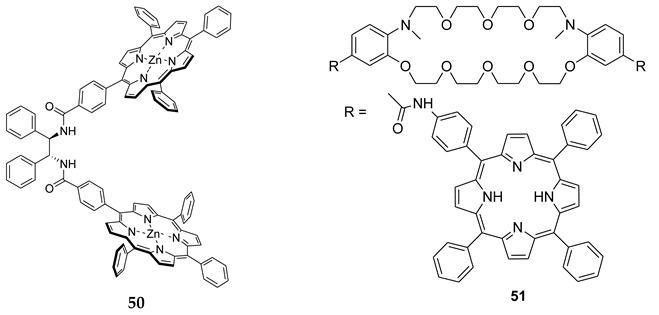
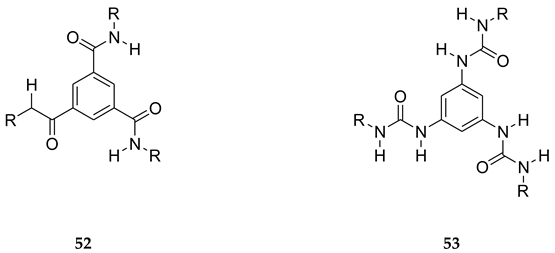
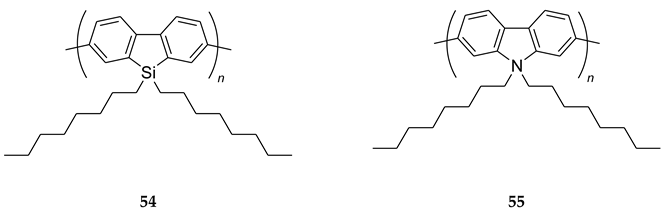
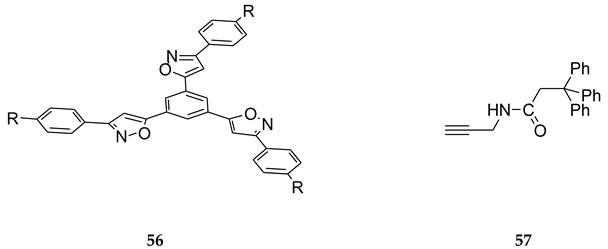
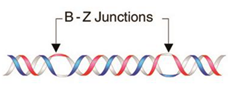
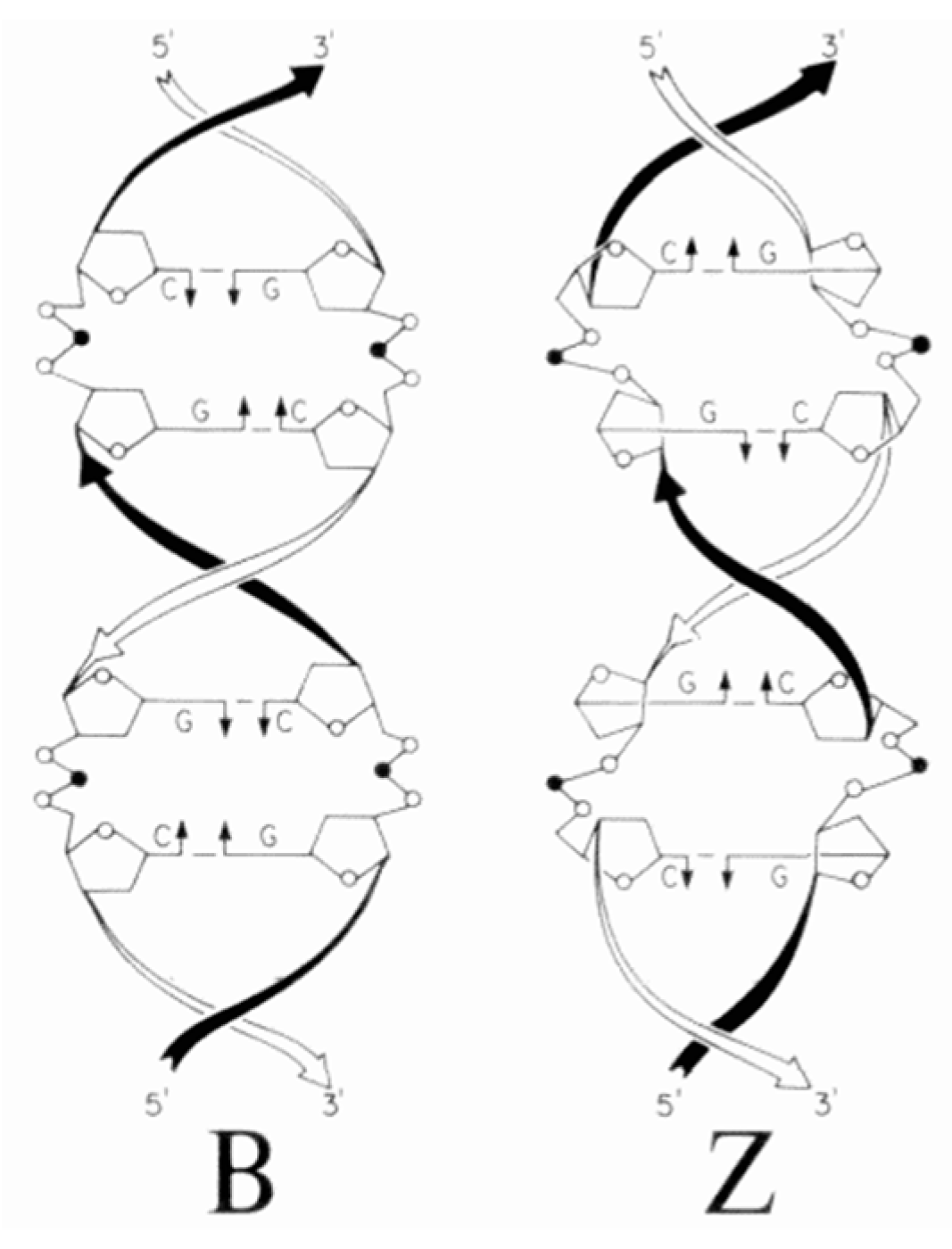
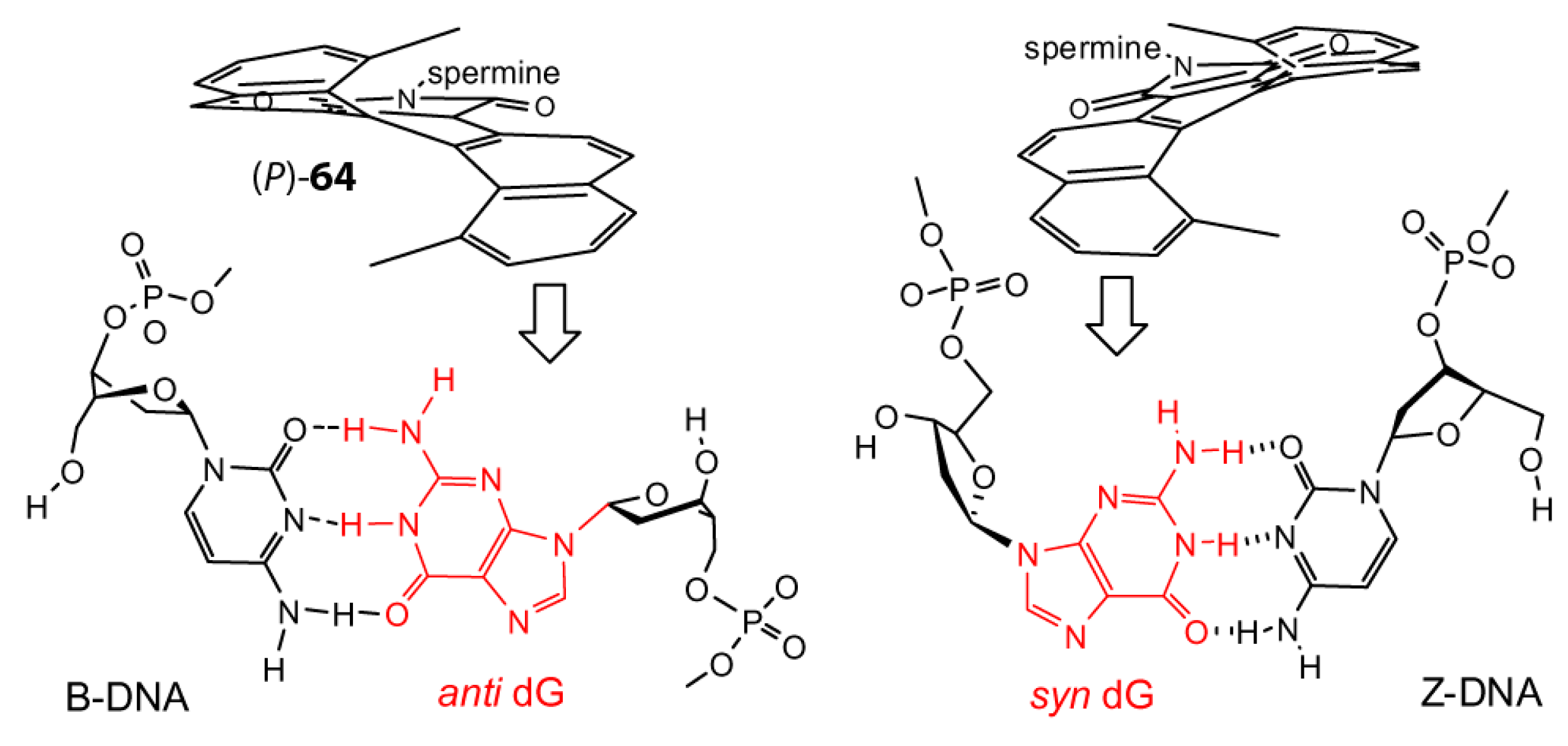
8. B–Z DNA Conformational Transition
 Z equilibrium as well [297,298]. The B–Z DNA transition was also influenced by Co, Mn, Ru and Pt complexes [299,300,301]. Nevertheless, chiral metal complexes failed to convert B-DNA to Z-DNA (see also [302,303,304,305,306]).
Z equilibrium as well [297,298]. The B–Z DNA transition was also influenced by Co, Mn, Ru and Pt complexes [299,300,301]. Nevertheless, chiral metal complexes failed to convert B-DNA to Z-DNA (see also [302,303,304,305,306]).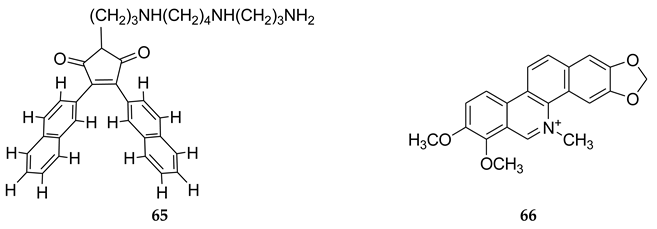
9. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Curie, P. Sur la symétrie dans les phénomènes physiques, symétrie d’un champ électrique et d’un champ magnétique. J. Phys. Theor. Appl. 1894, 3, 393–415. [Google Scholar] [CrossRef]
- Pavlov, V.A. C2 and C1 Symmetry of chiral auxiliaries in catalytic reactions on metal complexes. Tetrahedron 2008, 64, 1147–1179. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Klabunovskii, E.I. The origin of homochirality in nature: A possible version. Russ. Chem. Rev. 2015, 84, 121–133. [Google Scholar] [CrossRef]
- Pavlov, V.; Klabunovskii, E. Homochirality Origin in Nature: Possible Versions. Curr. Org. Chem. 2014, 18, 93–114. [Google Scholar] [CrossRef]
- Breslow, R. Formation of L Amino Acids and D Sugars, and Amplification of their Enantioexcesses in Aqueous Solutions, Under Simulated Prebiotic Conditions. Isr. J. Chem. 2011, 51, 990–996. [Google Scholar] [CrossRef]
- Weissbuch, I.; Lahav, M. Crystalline architectures as templates of relevance to the origins of homochirality. Chem. Rev. 2011, 111, 3236–3267. [Google Scholar] [CrossRef] [PubMed]
- Meierhenrich, U.J. Amino Acids and the Asymmetry of Life. Eur. Rev. 2013, 21, 190–199. [Google Scholar] [CrossRef]
- Lente, G. Open system approaches in deterministic models of the emergence of homochirality. Chirality 2010, 22, 907–913. [Google Scholar] [CrossRef]
- Toxvaerd, S. Origin of homochirality in biosystems. Int. J. Mol. Sci. 2009, 10, 1290–1299. [Google Scholar] [CrossRef] [PubMed]
- Plasson, R.; Kondepudi, D.K.; Bersini, H.; Commeyras, A.; Asakura, K. Emergence of homochirality in far-from-equilibrium systems: Mechanisms and role in prebiotic chemistry. Chirality 2007, 19, 589–600. [Google Scholar] [CrossRef]
- Pizzarello, S. The chemistry of life’s origin: A carbonaceous meteorite perspective. Acc. Chem. Res. 2006, 39, 231–237. [Google Scholar] [CrossRef]
- Jorissen, A.; Cerf, C. Asymmetric Photoreactions as the Origin of Biomolecular Homochirality: A Critical Review. Orig. Life Evol. Biosph. 2002, 32, 129–142. [Google Scholar] [CrossRef]
- Podlech, J. Origin of organic molecules and biomolecular homochirality. Cell Mol. Life Sci. 2001, 58, 44–60. [Google Scholar] [CrossRef]
- Feringa, B.L.; van Delden, R.A. Absolute Asymmetric Synthesis: The Origin, Control, and Amplification of Chirality. Angew. Chem. Int. Ed. 1999, 38, 3418–3438. [Google Scholar] [CrossRef]
- Prelog, V. Chirality in chemistry. Science 1976, 193, 17–24. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Molecular homochirality and the parity-violating energy difference. A critique with new proposals. Chirality 2008, 20, 84–95. [Google Scholar] [CrossRef]
- Carroll, J.D. A new definition of life. Chirality 2009, 21, 354–358. [Google Scholar] [CrossRef] [PubMed]
- Kuttel, M.; Ravenscroft, N.; Foschiatti, M.; Cescutti, P.; Rizzo, R. Conformational properties of two exopolysaccharides produced by Inquilinus limosus, a cystic fibrosis lung pathogen. Carbohydr. Res. 2012, 350, 40–48. [Google Scholar] [CrossRef]
- Hsien-Chih, H.W.; Sarko, A. The double-helical molecular structure of crystalline a-amylose. Carbohydr. Res. 1978, 61, 27–40. [Google Scholar] [CrossRef]
- Hsein-Chih, H.W.; Sarko, A. The double-helical molecular structure of crystalline b-amylose. Carbohydr. Res. 1978, 61, 7–25. [Google Scholar] [CrossRef]
- French, A.; Zaslow, B. Conformation of the “V” amylose helix. J. Chem. Soc. Chem. Commun. 1972, 0, 41–42. [Google Scholar] [CrossRef]
- Sarko, A.; Biloski, A. Crystal structure of the koh-amylose complex. Carbohydr. Res. 1980, 79, 11–21. [Google Scholar] [CrossRef]
- Nishiyama, Y.; Mazeau, K.; Morin, M.; Cardoso, M.B.; Chanzy, H.; Putaux, J.-L. Molecular and Crystal Structure of 7-Fold V-Amylose Complexed with 2-Propanol. Macromolecules 2010, 43, 8628–8636. [Google Scholar] [CrossRef]
- Lopez, C.A.; de Vries, A.H.; Marrink, S.J. Amylose folding under the influence of lipids. Carbohydr. Res. 2012, 364, 1–7. [Google Scholar] [CrossRef]
- Janaswamy, S.; Chandrasekaran, R. Heterogeneity in iota-carrageenan molecular structure: Insights for polymorph II-->III transition in the presence of calcium ions. Carbohydr. Res. 2008, 343, 364–373. [Google Scholar] [CrossRef]
- Matsuda, Y.; Biyajima, Y.; Sato, T. Thermal Denaturation, Renaturation, and Aggregation of a Double-Helical Polysaccharide Xanthan in Aqueous Solution. Polym. J. 2009, 41, 526. [Google Scholar] [CrossRef]
- Sheehan, J.K.; Gardner, K.H.; Atkins, E.D.T. Hyaluronic acid: A double-helical structure in the presence of potassium at low pH and found also with the cations ammonium, rubidium and caesium. J. Mol. Biol. 1977, 117, 113–135. [Google Scholar] [CrossRef]
- Numata, M.; Shinkai, S. ‘Supramolecular wrapping chemistry’ by helix-forming polysaccharides: A powerful strategy for generating diverse polymeric nano-architectures. Chem. Commun. 2011, 47, 1961–1975. [Google Scholar] [CrossRef]
- Pavlov, V.; Pavlova, T. Paradoxes of Symmetry: Homochirality; Cryptochiral Reactions; Chiral Field, Memory, and Induction; Chiral and Racemic Environment. Curr. Org. Chem. 2017, 21, 872–888. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Zhang, Y.; Zhang, L.; Ding, Y. Multiple conformation transitions of triple helical lentinan in DMSO/water by microcalorimetry. J. Phys. Chem. B 2009, 113, 9915–9923. [Google Scholar] [CrossRef]
- Bocchinfuso, G.; Mazzuca, C.; Sandolo, C.; Margheritelli, S.; Alhaique, F.; Coviello, T.; Palleschi, A. Guar gum and scleroglucan interactions with borax: Experimental and theoretical studies of an unexpected similarity. J. Phys. Chem. B 2010, 114, 13059–13068. [Google Scholar] [CrossRef] [PubMed]
- Miyoshi, K.; Uezu, K.; Sakurai, K.; Shinkai, S. Inter-chain and arrayed hydrogen bonds in β-1,3-d-xylan triple helix predicted by quantum mechanics calculation. Carbohydr. Polym. 2006, 66, 352–356. [Google Scholar] [CrossRef]
- Okobira, T.; Miyoshi, K.; Uezu, K.; Sakurai, K.; Shinkai, S. Molecular dynamics studies of side chain effect on the beta-1,3-D-glucan triple helix in aqueous solution. Biomacromolecules 2008, 9, 783–788. [Google Scholar] [CrossRef] [PubMed]
- Villares, A. Polysaccharides from the edible mushroom Calocybe gambosa: Structure and chain conformation of a (1-->4),(1-->6)-linked glucan. Carbohydr. Res. 2013, 375, 153–157. [Google Scholar] [CrossRef]
- Gagnon, M.A.; Lafleur, M. From curdlan powder to the triple helix gel structure: An attenuated total reflection-infrared study of the gelation process. Appl. Spectrosc. 2007, 61, 374–378. [Google Scholar] [CrossRef]
- Harrington, J.C.; Morris, E.R. Conformational ordering and gelation of gelatin in mixtures with soluble polysaccharides. Food Hydrocoll. 2009, 23, 327–336. [Google Scholar] [CrossRef]
- Yanaki, T.; Norisuye, T.; Fujita, H. Triple Helix of Schizophyllum commune Polysaccharide in Dilute Solution. 3. Hydrodynamic Properties in Water. Macromolecules 1980, 13, 1462–1466. [Google Scholar] [CrossRef]
- Yanaki, T.; Ito, W.; Tabata, K.; Kojima, T.; Norisuye, T.; Takano, N.; Fujita, H. Correlation between the antitumor activity of a polysaccharide schizophyllan and its triple-helical conformation in dilute aqueous solution. Biophys. Chem. 1983, 17, 337–342. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Zlotin, S.G. Homochirality, Stochastic Chiral Reactions, Spontaneous Chiral Ordering of Achiral Molecules, and Similar Chiral Effects. Is there a Physical Basis for these Mirror Symmetry Breaking Phenomena? Curr. Org. Chem. 2018, 22, 2029–2054. [Google Scholar] [CrossRef]
- Davankov, V. Chirality as an inherent general property of matter. Chirality 2006, 18, 459–461. [Google Scholar] [CrossRef]
- Kane, A.; Shao, R.-F.; Maclennan, J.E.; Wang, L.; Walba, D.M.; Clark, N.A. Cover Picture: Electric Field-Driven Deracemization (ChemPhysChem 1/2007). ChemPhysChem 2007, 8, 170–174. [Google Scholar] [CrossRef] [PubMed]
- Baranova, N.B.; Zel’dovich, B.Y. Separation of mirror isomeric molecules by radio-frequency electric field of rotating polarization. Chem. Phys. Lett. 1978, 57, 435–437. [Google Scholar] [CrossRef]
- Pavlov, V.A. Mechanisms of asymmetric induction in catalytic hydrogenation, hydrosilylation and cross-coupling on metal complexes. Russ. Chem. Rev. 2002, 71, 33–48. [Google Scholar] [CrossRef]
- Klabunovskii, E.I. Homochirality and its significance for biosphere and the origin of life theory. Russ. J. Org. Chem. 2012, 48, 881–901. [Google Scholar] [CrossRef]
- Takano, Y.; Takahashi, J.-I.; Kaneko, T.; Marumo, K.; Kobayashi, K. Asymmetric synthesis of amino acid precursors in interstellar complex organics by circularly polarized light. Earth Planet. Sci. Lett. 2007, 254, 106–114. [Google Scholar] [CrossRef]
- Managadze, G.G.; Engel, M.H.; Getty, S.; Wurz, P.; Brinckerhoff, W.B.; Shokolov, A.G.; Sholin, G.V.; Terent’ev, S.A.; Chumikov, A.E.; Skalkin, A.S.; et al. Excess of L-alanine in amino acids synthesized in a plasma torch generated by a hypervelocity meteorite impact reproduced in the laboratory. Planet. Space Sci. 2016, 131, 70–78. [Google Scholar] [CrossRef]
- Davankov, V.A. Inherent homochirality of primary particles and meteorite impacts as possible source of prebiotic molecular chirality. Russ. J. Phys. Chem. A 2009, 83, 1247–1256. [Google Scholar] [CrossRef]
- Ivanova, T.A.; Kuznettsov, S.N.; Logachev, Y.I.; Sosnovetc, E.N. North-south asymmetry and anisotropy of solar cosmic rays during the flare of April18, 1972. Kosmicheskie Issledovaniya 1976, 14, 235–238. [Google Scholar]
- Svirzhevsky, N.S.; Svirzhevskaya, A.K.; Bazilevskaya, G.A.; Stozhkov, Y.I. North–South asymmetry in cosmic ray fluxes as measured in the stratosphere and in selected solar wind parameters in the near-Earth space. Adv. Space Res. 2005, 35, 671–676. [Google Scholar] [CrossRef]
- Barron, L.D. True and false chirality and absolute asymmetric synthesis. J. Am. Chem. Soc. 1986, 108, 5539–5542. [Google Scholar] [CrossRef]
- He, Y.J.; Qi, F.; Qi, S.C. Earth’s orbital chirality and driving force of biomolecular evolution. Med. Hypotheses 2001, 56, 493–496. [Google Scholar] [CrossRef]
- Stone, E.C.; Cummings, A.C.; McDonald, F.B.; Heikkila, B.C.; Lal, N.; Webber, W.R. Voyager 1 explores the termination shock region and the heliosheath beyond. Science 2005, 309, 2017–2020. [Google Scholar] [CrossRef]
- Shu, F.H. The Physical Universe: An Introduction to Astronomy; University Science Books, Mill Valley, CA: Sasalito, CA, USA, 1982. [Google Scholar]
- Decker, R.B.; Krimigis, S.M.; Roelof, E.C.; Hill, M.E.; Armstrong, T.P.; Gloeckler, G.; Hamilton, D.C.; Lanzerotti, L.J. Voyager 1 in the foreshock, termination shock, and heliosheath. Science 2005, 309, 2020–2024. [Google Scholar] [CrossRef]
- Vidal-Madjar, A.; Laurent, C.; Bruston, P.; Audouze, J. Is the solar system entering a nearby interstellar cloud. Astrophys. J. 1978, 223. [Google Scholar] [CrossRef][Green Version]
- Grande, C.; Patel, N.H. Nodal signalling is involved in left-right asymmetry in snails. Nature 2009, 457, 1007–1011. [Google Scholar] [CrossRef]
- Mineo, P.; Villari, V.; Scamporrino, E.; Micali, N. New Evidence about the Spontaneous Symmetry Breaking: Action of an Asymmetric Weak Heat Source. J. Phys. Chem. B 2015, 119, 12345–12353. [Google Scholar] [CrossRef]
- Erschov, V.E.; Cantor, J.I. Sea Shells. Concise Guide; “Kursiv”: Moscow, Russia, 2008. [Google Scholar]
- Reiss, H.R. Nuclear beta decay induced by intense electromagnetic fields: Basic theory. Phys. Rev. C 1983, 27, 1199–1228. [Google Scholar] [CrossRef]
- Fischbach, E.; Buncher, J.B.; Gruenwald, J.T.; Jenkins, J.H.; Krause, D.E.; Mattes, J.J.; Newport, J.R. Time-Dependent Nuclear Decay Parameters: New Evidence for New Forces? Space Sci. Rev. 2009, 145, 285–335. [Google Scholar] [CrossRef]
- Fischbach, E.; Chen, K.J.; Gold, R.E.; Goldsten, J.O.; Lawrence, D.J.; McNutt, R.J.; Rhodes, E.A.; Jenkins, J.H.; Longuski, J. Solar influence on nuclear decay rates: Constraints from the MESSENGER mission. Astrophys. Space Sci. 2011, 337, 39–45. [Google Scholar] [CrossRef]
- Sturrock, P.A.; Buncher, J.B.; Fischbach, E.; Javorsek, D., II; Jenkins, J.H.; Mattes, J.J. Concerning the Phases of the Annual Variations of Nuclear Decay Rates. Astrophys. J. 2011, 737. [Google Scholar] [CrossRef]
- Silverman, M.P. Search for anomalies in the decay of radioactive Mn-54. EPL 2016, 114, 62001. [Google Scholar] [CrossRef]
- O’Keefe, D.; Morreale, B.L.; Lee, R.H.; Buncher, J.B.; Jenkins, J.H.; Fischbach, E.; Gruenwald, T.; Javorsek, D.; Sturrock, P.A. Spectral content of 22Na/44Ti decay data: Implications for a solar influence. Astrophys. Space Sci. 2013, 344, 297–303. [Google Scholar] [CrossRef]
- Norman, E.B.; Browne, E.; Shugart, H.A.; Joshi, T.H.; Firestone, R.B. Evidence against correlations between nuclear decay rates and Earth–Sun distance. Astropart. Phys. 2009, 31, 135–137. [Google Scholar] [CrossRef]
- El-Borie, M.A.; El-Abshehy, M.; Talaat, S.; Taleb, W.M.A. North-south asymmetry in solar, interplanetary, and geomagnetic indices. Astrophysics 2012, 55, 127–139. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Kaufman, R.J.; Singh, N. Chiral symmetry breaking in sodium chlorate crystallizaton. Science 1990, 250, 975–976. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Asakura, K. Chiral Autocatalysis, Spontaneous Symmetry Breaking, and Stochastic Behavior. Acc. Chem. Res. 2001, 34, 946–954. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Laudadio, J.; Asakura, K. Chiral Symmetry Breaking in Stirred Crystallization of 1,1’-Binaphthyl Melt. J. Am. Chem. Soc. 1999, 121, 1448–1451. [Google Scholar] [CrossRef]
- Asakura, K.; Soga, T.; Uchida, T.; Osanai, S.; Kondepudi, D.K. Probability distributions of enantiomeric excess in unstirred and stirred crystallization of 1,1’-binaphthyl melt. Chirality 2002, 14, 85–89. [Google Scholar] [CrossRef]
- Cintas, P.; Viedma, C. On the physical basis of asymmetry and homochirality. Chirality 2012, 24, 894–908. [Google Scholar] [CrossRef]
- Viedma, C. Chiral symmetry breaking during crystallization: Complete chiral purity induced by nonlinear autocatalysis and recycling. Phys. Rev. Lett. 2005, 94, 065504. [Google Scholar] [CrossRef]
- Kondepudi, D.K.; Bullock, K.L.; Digits, J.A.; Hall, J.K.; Miller, J.M. Kinetics of chiral symmetry breaking in crystallization. J. Am. Chem. Soc. 1993, 115, 10211–10216. [Google Scholar] [CrossRef]
- McBride, J.M.; Carter, R.L. Spontaneous Resolution by Stirred Crystallization. Angew. Chem. Int. Ed. Engl. 1991, 30, 293–295. [Google Scholar] [CrossRef]
- Tsogoeva, S.B.; Wei, S.; Freund, M.; Mauksch, M. Generation of highly enantioenriched crystalline products in reversible asymmetric reactions with racemic or achiral catalysts. Angew. Chem. Int. Ed. Engl. 2009, 48, 590–594. [Google Scholar] [CrossRef]
- Wei, S.; Mauksch, M.; Tsogoeva, S.B. Autocatalytic enantiomerisation at the crystal surface in deracemisation of scalemic conglomerates. Chemistry 2009, 15, 10255–10262. [Google Scholar] [CrossRef] [PubMed]
- Kondepudi, D.K.; Bullock, K.L.; Digits, J.A.; Yarborough, P.D. Stirring Rate as a Critical Parameter in Chiral Symmetry Breaking Crystallization. J. Am. Chem. Soc. 1995, 117, 401–404. [Google Scholar] [CrossRef]
- Osuna-Esteban, S.; Zorzano, M.P.; Menor-Salvan, C.; Ruiz-Bermejo, M.; Veintemillas-Verdaguer, S. Asymmetric chiral growth of micron-size NaClO3 crystals in water aerosols. Phys. Rev. Lett. 2008, 100, 146102. [Google Scholar] [CrossRef] [PubMed]
- Levilain, G.; Rougeot, C.; Guillen, F.; Plaquevent, J.-C.; Coquerel, G. Attrition-enhanced preferential crystallization combined with racemization leading to redissolution of the antipode nuclei. Tetrahedron Asymmetry 2009, 20, 2769–2771. [Google Scholar] [CrossRef]
- Cartwright, J.H.; Piro, O.; Tuval, I. Ostwald ripening, chiral crystallization, and the common-ancestor effect. Phys. Rev. Lett. 2007, 98, 165501. [Google Scholar] [CrossRef]
- Noorduin, W.L.; Meekes, H.; van Enckevort, W.J.; Millemaggi, A.; Leeman, M.; Kaptein, B.; Kellogg, R.M.; Vlieg, E. Complete deracemization by attrition-enhanced ostwald ripening elucidated. Angew. Chem. Int. Ed. Engl. 2008, 47, 6445–6447. [Google Scholar] [CrossRef] [PubMed]
- Cartwright, J.H.; Garcia-Ruiz, J.M.; Piro, O.; Sainz-Diaz, C.I.; Tuval, I. Chiral symmetry breaking during crystallization: An advection-mediated nonlinear autocatalytic process. Phys. Rev. Lett. 2004, 93, 035502. [Google Scholar] [CrossRef]
- Noorduin, W.L.; van Enckevort, W.J.; Meekes, H.; Kaptein, B.; Kellogg, R.M.; Tully, J.C.; McBride, J.M.; Vlieg, E. The driving mechanism behind attrition-enhanced deracemization. Angew. Chem. Int. Ed. Engl. 2010, 49, 8435–8438. [Google Scholar] [CrossRef]
- Plasson, R.; Kondepudi, D.K.; Asakura, K. Three-dimensional description of the spontaneous onset of homochirality on the surface of a conglomerate crystal phase. J. Phys. Chem. B 2006, 110, 8481–8487. [Google Scholar] [CrossRef]
- El-Hachemi, Z.; Arteaga, O.; Canillas, A.; Crusats, J.; Llorens, J.; Ribo, J.M. Chirality generated by flows in pseudocyanine dye J-aggregates: Revisiting 40 years old reports. Chirality 2011, 23, 585–592. [Google Scholar] [CrossRef]
- Noorduin, W.L.; van der Asdonk, P.; Meekes, H.; van Enckevort, W.J.; Kaptein, B.; Leeman, M.; Kellogg, R.M.; Vlieg, E. Complete chiral resolution using additive-induced crystal size bifurcation during grinding. Angew. Chem. Int. Ed. Engl. 2009, 48, 3278–3280. [Google Scholar] [CrossRef]
- Hein, J.E.; Cao, B.H.; Viedma, C.; Kellogg, R.M.; Blackmond, D.G. Pasteur’s tweezers revisited: On the mechanism of attrition-enhanced deracemization and resolution of chiral conglomerate solids. J. Am. Chem. Soc. 2012, 134, 12629–12636. [Google Scholar] [CrossRef]
- Viedma, C.; Cintas, P. Homochirality beyond grinding: Deracemizing chiral crystals by temperature gradient under boiling. Chem. Commun. 2011, 47, 12786–12788. [Google Scholar] [CrossRef]
- Viedma, C.; Noorduin, W.L.; Ortiz, J.E.; de Torres, T.; Cintas, P. Asymmetric amplification in amino acid sublimation involving racemic compound to conglomerate conversion. Chem. Commun. 2011, 47, 671–673. [Google Scholar] [CrossRef]
- Viedma, C. Selective Chiral Symmetry Breaking during Crystallization: Parity Violation or Cryptochiral Environment in Control? Cryst. Growth Des. 2007, 7, 553–556. [Google Scholar] [CrossRef]
- Steendam, R.R.E.; Harmsen, B.; Meekes, H.; Enckevort, W.J.P.v.; Kaptein, B.; Kellogg, R.M.; Raap, J.; Rutjes, F.P.J.T.; Vlieg, E. Controlling the Effect of Chiral Impurities on Viedma Ripening. Cryst. Growth Des. 2013, 13, 4776–4780. [Google Scholar] [CrossRef]
- Zhang, Q.; Jia, L.; Wang, J.-R.; Mei, X. Absolute asymmetric synthesis of a sanguinarine derivative through crystal–solution interactions. CrystEngComm 2016, 18, 8834–8837. [Google Scholar] [CrossRef]
- Spix, L.; Meekes, H.; Blaauw, R.H.; van Enckevort, W.J.P.; Vlieg, E. Complete Deracemization of Proteinogenic Glutamic Acid Using Viedma Ripening on a Metastable Conglomerate. Cryst. Growth Des. 2012, 12, 5796–5799. [Google Scholar] [CrossRef]
- El-Hachemi, Z.; Crusats, J.; Ribo, J.M.; McBride, J.M.; Veintemillas-Verdaguer, S. Metastability in supersaturated solution and transition towards chirality in the crystallization of NaClO3. Angew. Chem. Int. Ed. Engl. 2011, 50, 2359–2363. [Google Scholar] [CrossRef]
- Medina, D.D.; Gedanken, A.; Mastai, Y. Chiral amplification in crystallization under ultrasound radiation. Chemistry 2011, 17, 11139–11142. [Google Scholar] [CrossRef]
- Han, B.; Shen, F.; Su, H.; Zhang, X.; Shen, Y.; Zhang, T. Self-assembly of achiral monomer into left-handed helical polyanthracene nanofibers. Mater. Express 2016, 6, 88–92. [Google Scholar] [CrossRef]
- Ziach, K.; Jurczak, J. Mirror symmetry breaking upon spontaneous crystallization from a dynamic combinatorial library of macrocyclic imines. Chem. Commun. 2015, 51, 4306–4309. [Google Scholar] [CrossRef]
- Yagishita, F.; Kato, M.; Uemura, N.; Ishikawa, H.; Yoshida, Y.; Mino, T.; Kasashima, Y.; Sakamoto, M. Asymmetric Synthesis Using Chiral Crystals of Coumarin-3-carboxamides and Carbenoids. Chem. Lett. 2016, 45, 1310–1312. [Google Scholar] [CrossRef]
- Sakamoto, M.; Kato, M.; Aida, Y.; Fujita, K.; Mino, T.; Fujita, T. Photosensitized 2 + 2 cycloaddition reaction using homochirality generated by spontaneous crystallization. J. Am. Chem. Soc. 2008, 130, 1132–1133. [Google Scholar] [CrossRef]
- Sakamoto, M.; Yagishita, F.; Ando, M.; Sasahara, Y.; Kamataki, N.; Ohta, M.; Mino, T.; Kasashima, Y.; Fujita, T. Generation and amplification of optical activity of axially chiral N-(1-naphthyl)-2(1H) pyrimidinethione by crystallization. Org. Biomol. Chem. 2010, 8, 5418–5422. [Google Scholar] [CrossRef]
- Fujiki, M. Helix Magic. Thermo-Driven Chiroptical Switching and Screw-Sense Inversion of Flexible Rod Helical Polysilylenes. J. Am. Chem. Soc. 2000, 122, 3336–3343. [Google Scholar] [CrossRef]
- Fujiki, M. Optically Active Polysilylenes: State-of-the-Art Chiroptical Polymers. Macromol. Rapid Commun. 2001, 22, 539–563. [Google Scholar] [CrossRef]
- Fujiki, M. Helix Generation, Amplification, Switching, and Memory of Chromophoric Polymers. In Amplification of Chirality; Soai, K., Ed.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 119–186. [Google Scholar] [CrossRef]
- Tabei, J.; Nomura, R.; Sanda, F.; Masuda, T. Design of Helical Poly(N-propargylamides) that Switch the Helix Sense with Thermal Stimuli. Macromolecules 2004, 37, 1175–1179. [Google Scholar] [CrossRef]
- Koe, J.R.; Fujiki, M.; Nakashima, H.; Motonaga, M. Tempera ture-dependent helix–helix transition of an optically active poly(diarylsilylene). Chem. Commun. 2000, 389–390. [Google Scholar] [CrossRef]
- Watanabe, J.; Okamoto, S.; Satoh, K.; Sakajiri, K.; Furuya, H.; Abe, A. Reversible Helix−Helix Transition of Poly(β-phenylpropyllaspartate) Involving a Screw-Sense Inversion in the Solid State. Macromolecules 1996, 29, 7084–7088. [Google Scholar] [CrossRef]
- Yashima, E.; Maeda, K.; Sato, O. Switching of a Macromolecular Helicity for Visual Distinction of Molecular Recognition Events. J. Am. Chem. Soc. 2001, 123, 8159–8160. [Google Scholar] [CrossRef]
- Green, M.M.; Park, J.-W.; Sato, T.; Teramoto, A.; Lifson, S.; Selinger, R.L.B.; Selinger, J.V. The Macromolecular Route to Chiral Amplification. Angew. Chem. Int. Ed. 1999, 38, 3138–3154. [Google Scholar] [CrossRef]
- Okamoto, Y.; Nakano, T.; Ono, E.; Hatada, K. Synthesis and Reversible Stereomutation of Optically Active Poly[(S)-diphenyl(1-methylpyrrolidin-2-yl)methyl methacrylate]. Chemistry Letters 1991, 20, 525–528. [Google Scholar] [CrossRef]
- Gu, H.; Nakamura, Y.; Sato, T.; Teramoto, A.; Green, M.M.; Andreola, C.; Peterson, N.C.; Lifson, S. Molecular-Weight Dependence of the Optical Rotation of Poly((R)-2-deuterio-n-hexyl isocyanate). Macromolecules 1995, 28, 1016–1024. [Google Scholar] [CrossRef]
- Okamoto, N.; Mukaida, F.; Gu, H.; Nakamura, Y.; Sato, T.; Teramoto, A.; Green, M.M.; Andreola, C.; Peterson, N.C.; Lifson, S. Molecular Weight Dependence of the Optical Rotation of Poly((R)-1-deuterio-n-hexyl isocyanate) in Dilute Solution. Macromolecules 1996, 29, 2878–2884. [Google Scholar] [CrossRef]
- Cai, Y.; Bernasek, S.L. Adsorption-induced asymmetric assembly from an achiral adsorbate. J. Am. Chem. Soc. 2004, 126, 14234–14238. [Google Scholar] [CrossRef]
- Humblot, V.; Lorenzo, M.O.; Baddeley, C.J.; Haq, S.; Raval, R. Local and global chirality at surfaces: Succinic acid versus tartaric acid on Cu110. J. Am. Chem. Soc. 2004, 126, 6460–6469. [Google Scholar] [CrossRef]
- Raval, R. Chiral expression from molecular assemblies at metal surfaces: Insights from surface science techniques. Chem. Soc. Rev. 2009, 38, 707–721. [Google Scholar] [CrossRef]
- Elemans, J.A.; De Cat, I.; Xu, H.; De Feyter, S. Two-dimensional chirality at liquid-solid interfaces. Chem. Soc. Rev. 2009, 38, 722–736. [Google Scholar] [CrossRef]
- Ernst, K.H. Surface chemistry: Single handedness in flatland. Nat. Chem. 2017, 9, 195–196. [Google Scholar] [CrossRef]
- Satyanarayana, T.; Abraham, S.; Kagan, H.B. Nonlinear effects in asymmetric catalysis. Angew. Chem. Int. Ed. Engl. 2009, 48, 456–494. [Google Scholar] [CrossRef]
- Ercolani, G. Principles for designing an achiral receptor promoting asymmetric autocatalysis with amplification of chirality. Tetrahedron Asymmetry 2014, 25, 405–410. [Google Scholar] [CrossRef]
- Steigelmann, M.; Nisar, Y.; Rominger, F.; Goldfuss, B. Homo- and Heterochiral Alkylzinc Fencholates: Linear or Nonlinear Effects in Dialkylzinc Additions to Benzaldehyde. Chem. Eur. J. 2002, 8, 5211–5218. [Google Scholar] [CrossRef]
- Chen, Y.K.; Costa, A.M.; Walsh, P.J. Substrate Dependence of Nonlinear Effects: Mechanistic Probe and Practical Applications. J. Am. Chem. Soc. 2001, 123, 5378–5379. [Google Scholar] [CrossRef]
- Balsells, J.; Davis, T.J.; Carroll, P.; Walsh, P.J. Insight into the Mechanism of the Asymmetric Addition of Alkyl Groups to Aldehydes Catalyzed by Titanium−BINOLate Species. J. Am. Chem. Soc. 2002, 124, 10336–10348. [Google Scholar] [CrossRef]
- Mori, M.; Imma, H.; Nakai, T. Asymmetric Catalytic Cyanosilylation of Aldehydes Using a Chiral Binaphthol-Titanium Complex. Tetrahedron Lett. 1997, 38, 6229–6232. [Google Scholar] [CrossRef]
- Kitamura, M.; Suga, S.; Oka, H.; Noyori, R. Quantitative Analysis of the Chiral Amplification in the Amino Alcohol-Promoted Asymmetric Alkylation of Aldehydes with Dialkylzincs. J. Am. Chem. Soc. 1998, 120, 9800–9809. [Google Scholar] [CrossRef]
- Hua, Y.Z.; Han, X.W.; Yang, X.C.; Song, X.; Wang, M.C.; Chang, J.B. Enantioselective Friedel-Crafts alkylation of pyrrole with chalcones catalyzed by a dinuclear zinc catalyst. J. Org. Chem. 2014, 79, 11690–11699. [Google Scholar] [CrossRef]
- Du, H.; Long, J.; Hu, J.; Li, X.; Ding, K. 3,3’-Br2-BINOL-Zn complex: A highly efficient catalyst for the enantioselective hetero-Diels-Alder reaction. Org. Lett. 2002, 4, 4349–4352. [Google Scholar] [CrossRef]
- Yearick, K.; Wolf, C. Catalytic enantioselective addition of diethylzinc to trifluoromethyl ketones. Org. Lett. 2008, 10, 3915–3918. [Google Scholar] [CrossRef]
- ShengJian, L.; Yaozhong, J.; Aiqiao, M. Asymmetric synthesis XVII. New chiral catalysts for the stereocontrolled addition of benzaldehyde by diethylzinc. Tetrahedron Asymmetry 1992, 3, 1467–1474. [Google Scholar] [CrossRef]
- Soai, K.; Ookawa, A.; Kaba, T.; Ogawa, K. Catalytic asymmetric induction. Highly enantioselective addition of dialkylzincs to aldehydes using chiral pyrrolidinylmethanols and their metal salts. J. Am. Chem. Soc. 1987, 109, 7111–7115. [Google Scholar] [CrossRef]
- Yang, X.; Shen, J.; Da, C.; Wang, R.; Choi, M.C.K.; Yang, L.; Wong, K.-Y. Chiral pyrrolidine derivatives as catalysts in the enantioselective addition of diethylzinc to aldehydes. Tetrahedron Asymmetry 1999, 10, 133–138. [Google Scholar] [CrossRef]
- Ding, K.; Ishii, A.; Mikami, K. Super High Throughput Screening (SHTS) of Chiral Ligands and Activators: Asymmetric Activation of Chiral Diol-Zinc Catalysts by Chiral Nitrogen Activators for the Enantioselective Addition of Diethylzinc to Aldehydes. Angew. Chem. Int. Ed. 1999, 38, 497–501. [Google Scholar] [CrossRef]
- Vyskočil, Š.; Jaracz, S.; Smrčina, M.; Štícha, M.; Hanuš, V.; Polášek, M.; Kočovský, P. Synthesis of N-Alkylated and N-Arylated Derivatives of 2-Amino-2’-hydroxy-1,1’-binaphthyl (NOBIN) and 2,2’-Diamino-1,1’-binaphthyl and Their Application in the Enantioselective Addition of Diethylzinc to Aromatic Aldehydes†. J. Org. Chem. 1998, 63, 7727–7737. [Google Scholar] [CrossRef]
- Le Goanvic, D.; Holler, M.; Pale, P. Chiral tridentate versus bidentate pyridines as catalysts in the enantioselective alkylation of benzaldehyde with diethylzinc. Tetrahedron Asymmetry 2002, 13, 119–121. [Google Scholar] [CrossRef]
- Rosner, T.; Sears, P.J.; Nugent, W.A.; Blackmond, D.G. Kinetic Investigations of Product Inhibition in the Amino Alcohol-Catalyzed Asymmetric Alkylation of Benzaldehyde with Diethylzinc. Org. Lett. 2000, 2, 2511–2513. [Google Scholar] [CrossRef]
- Chen, S.-K.; Peng, D.; Zhou, H.; Wang, L.-W.; Chen, F.-X.; Feng, X.-M. Highly Enantioselective Cyanoformylation of Aldehydes Catalyzed by a Mononuclear Salen-Ti(OiPr)4 Complex Produced In Situ. Eur. J. Org. Chem. 2007, 2007, 639–644. [Google Scholar] [CrossRef]
- Bandini, M.; Cozzi, P.G.; Umani-Ronchi, A. Enantioselective catalytic addition of allyl organometallic reagents to aldehydes promoted by [Cr(Salen)]: The hidden role played by weak Lewis acids in metallo-Salen promoted reactions. Tetrahedron 2001, 57, 835–843. [Google Scholar] [CrossRef]
- Mikami, K.A.; Yamanaka, M. Negative nonlinear effect in aquo palladium catalysis depending on tropos biphenylphosphine ligand chirality controlled by chiral diaminobinaphthyl activator. Pure Appl. Chem. 2004, 76, 537–540. [Google Scholar] [CrossRef]
- Feng, X.; Liu, Y.; Liu, X.; Xin, J. Asymmetric Cyanosilylation of Aldehydes Catalyzed by Novel Chiral Tetraaza-Titanium Complexes. Synlett 2006, 2006, 1085–1089. [Google Scholar] [CrossRef]
- Gamez, P.; Fache, F.; Mangeney, P.; Lamaire, M. Enantioselective catalytic reduction of ketones using C2-symmetric diamines as chiral ligands. Tetrahedron Lett. 1993, 34, 6897–6898. [Google Scholar] [CrossRef]
- Spogliarich, R.; Kašpar, J.; Graziani, M.; Morandini, F. Asymmetric transfer hydrogenation of ketones catalyzed by phosphine-rhodium(I) and -iridium(I) complexes. J. Organomet. Chem. 1986, 306, 407–412. [Google Scholar] [CrossRef]
- Gamez, P.; Fache, F.; Lemaire, M. Asymmetric catalytic reduction of carbonyl compounds using C2 symmetric diamines as chiral ligands. Tetrahedron Asymmetry 1995, 6, 705–718. [Google Scholar] [CrossRef]
- Brown, M.K.; Blewett, M.M.; Colombe, J.R.; Corey, E.J. Mechanism of the enantioselective oxidation of racemic secondary alcohols catalyzed by chiral Mn(III)-salen complexes. J. Am. Chem. Soc. 2010, 132, 11165–11170. [Google Scholar] [CrossRef]
- Zlotin, S.G.; Kochetkov, S.V. C2-Symmetric diamines and their derivatives as promising organocatalysts for asymmetric synthesis. Russ. Chem. Rev. 2015, 84, 1077–1099. [Google Scholar] [CrossRef]
- Kucherenko, A.S.; Siyutkin, D.E.; Nigmatov, A.G.; Chizhov, A.O.; Zlotin, S.G. Chiral Primary Amine Tagged to Ionic Group as Reusable Organocatalyst for Asymmetric Michael Reactions of C-Nucleophiles with α,β-Unsaturated Ketones. Adv. Synth. Catal. 2012, 354, 3078–3086. [Google Scholar] [CrossRef]
- Kucherenko, A.S.; Kostenko, A.A.; Gerasimchuk, V.V.; Zlotin, S.G. Stereospecific diaza-Cope rearrangement as an efficient tool for the synthesis of DPEDA pyridine analogs and related C2-symmetric organo catalysts. Org. Biomol. Chem. 2017, 15, 7028–7033. [Google Scholar] [CrossRef]
- Kucherenko, A.S.; Kostenko, A.A.; Zhdankina, G.M.; Kuznetsova, O.Y.; Zlotin, S.G. Green asymmetric synthesis of Warfarin and Coumachlor in pure water catalyzed by quinoline-derived 1,2-diamines. Green Chem. 2018, 20, 754–759. [Google Scholar] [CrossRef]
- Boucherif, A.; Duan, S.-W.; Yuan, Z.-G.; Lu, L.-Q.; Xiao, W.-J. Catalytic Asymmetric Allylation of 3-Aryloxindoles by Merging Palladium Catalysis and Asymmetric H-Bonding Catalysis. Adv. Synth. Catal. 2016, 358, 2594–2598. [Google Scholar] [CrossRef]
- Nájera, C.; Yus, M. Chiral benzimidazoles as hydrogen bonding organocatalysts. Tetrahedron Lett. 2015, 56, 2623–2633. [Google Scholar] [CrossRef]
- Palomo, C.; Oiarbide, M.; Laso, A. Recent Advances in the Catalytic Asymmetric Nitroaldol (Henry) Reaction. Eur. J. Org. Chem. 2007, 2007, 2561–2574. [Google Scholar] [CrossRef]
- Lisnyak, V.G.; Kucherenko, A.S.; Valeev, E.F.; Zlotin, S.G. (1,2-Diaminoethane-1,2-diyl)bis(N-methylpyridinium) Salts as a Prospective Platform for Designing Recyclable Prolinamide-Based Organocatalysts. J. Org. Chem. 2015, 80, 9570–9577. [Google Scholar] [CrossRef]
- Kucherenko, A.S.; Lisnyak, V.G.; Kostenko, A.A.; Kochetkov, S.V.; Zlotin, S.G. C2-Symmetric pyrrolidine-derived squaramides as recyclable organocatalysts for asymmetric Michael reactions. Org. Biomol. Chem. 2016, 14, 9751–9759. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Zeng, J.L.; Ren, N.; Meng, W.; Nie, J.; Ma, J.A. C2-Symmetric Chiral Bisoxazolines as Hydrogen-Bond-Acceptor Catalysts in Enantioselective Aldol Reaction of beta-Carbonyl Acids with Trifluoroacetaldehyde Hemiacetals. Org. Lett. 2016, 18, 6364–6367. [Google Scholar] [CrossRef]
- Servín, F.A.; Madrigal, D.; Romero, J.A.; Chávez, D.; Aguirre, G.; Anaya de Parrodi, C.; Somanathan, R. Synthesis of C2-symmetric 1,2-diamine-functionalized organocatalysts: Mimicking enzymes in enantioselective Michael addition reactions. Tetrahedron Lett. 2015, 56, 2355–2358. [Google Scholar] [CrossRef]
- Ogasawara, M.; Kotani, S.; Nakajima, H.; Furusho, H.; Miyasaka, M.; Shimoda, Y.; Wu, W.Y.; Sugiura, M.; Takahashi, T.; Nakajima, M. Atropisomeric chiral dienes in asymmetric catalysis: C(2)-symmetric (Z,Z)-2,3-bis[1-(diphenylphosphinyl)ethylidene]tetralin as a highly active Lewis base organocatalyst. Angew. Chem. Int. Ed. Engl. 2013, 52, 13798–13802. [Google Scholar] [CrossRef]
- Gomez-Torres, E.; Alonso, D.A.; Gomez-Bengoa, E.; Najera, C. Conjugate addition of 1,3-dicarbonyl compounds to maleimides using a chiral C2-symmetric bis(2-aminobenzimidazole) as recyclable organocatalyst. Org. Lett. 2011, 13, 6106–6109. [Google Scholar] [CrossRef]
- Delaney, J.P.; Brozinski, H.L.; Henderson, L.C. Synergistic effects within a C2-symmetric organocatalyst: The potential formation of a chiral catalytic pocket. Org. Biomol. Chem. 2013, 11, 2951–2960. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Sohtome, Y.; Hashimoto, Y.; Nagasawa, K. Guanidine-Thiourea Bifunctional Organocatalyst for the Asymmetric Henry (Nitroaldol) Reaction. Adv. Synth. Catal. 2005, 347, 1643–1648. [Google Scholar] [CrossRef]
- Ginotra, S.K.; Singh, V.K. Enantioselective Henry reaction catalyzed by a C2-symmetric bis(oxazoline)Cu(OAc)2. H2O complex. Org. Biomol. Chem. 2007, 5, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Le, K.V.; Takezoe, H.; Araoka, F. Chiral Superstructure Mesophases of Achiral Bent-Shaped Molecules—Hierarchical Chirality Amplification and Physical Properties. Adv. Mater. 2017, 29, 1602737. [Google Scholar] [CrossRef] [PubMed]
- Otani, T.; Araoka, F.; Ishikawa, K.; Takezoe, H. Enhanced optical activity by achiral rod-like molecules nanosegregated in the B4 structure of achiral bent-core molecules. J. Am. Chem. Soc. 2009, 131, 12368–12372. [Google Scholar] [CrossRef] [PubMed]
- Hough, L.E.; Spannuth, M.; Nakata, M.; Coleman, D.A.; Jones, C.D.; Dantlgraber, G.; Tschierske, C.; Watanabe, J.; Korblova, E.; Walba, D.M.; et al. Chiral isotropic liquids from achiral molecules. Science 2009, 325, 452–456. [Google Scholar] [CrossRef]
- Takanishi, Y.; Shin, G.J.; Jung, J.C.; Choi, S.-W.; Ishikawa, K.; Watanabe, J.; Takezoe, H.; Toledano, P. Observation of very large chiral domains in a liquid crystal phase formed by mixtures of achiral bent-core and rod molecules. J. Mater. Chem. 2005, 15. [Google Scholar] [CrossRef]
- Kim, K.; Kim, H.; Jo, S.Y.; Araoka, F.; Yoon, D.K.; Choi, S.W. Photomodulated Supramolecular Chirality in Achiral Photoresponsive Rodlike Compounds Nanosegregated from the Helical Nanofilaments of Achiral Bent-Core Molecules. ACS Appl. Mater. Interfaces 2015, 7, 22686–22691. [Google Scholar] [CrossRef]
- Nagayama, H.; Varshney, S.K.; Goto, M.; Araoka, F.; Ishikawa, K.; Prasad, V.; Takezoe, H. Spontaneous deracemization of disc-like molecules in the columnar phase. Angew. Chem. Int. Ed. Engl. 2010, 49, 445–448. [Google Scholar] [CrossRef]
- Gortz, V.; Goodby, J.W. Enantioselective segregation in achiral nematic liquid crystals. Chem. Commun. 2005, 3262–3264. [Google Scholar] [CrossRef]
- Zhang, C.; Diorio, N.; Lavrentovich, O.D.; Jakli, A. Helical nanofilaments of bent-core liquid crystals with a second twist. Nat. Commun. 2014, 5, 3302. [Google Scholar] [CrossRef]
- Hazen, R.M.; Sholl, D.S. Chiral selection on inorganic crystalline surfaces. Nat. Mater. 2003, 2, 367–374. [Google Scholar] [CrossRef]
- Weissbuch, I.; Addadi, L.; Leiserowitz, L. Molecular recognition at crystal interfaces. Science 1991, 253, 637–645. [Google Scholar] [CrossRef]
- Koretsky, C.M.; Sverjensky, D.A.; Sahai, N. A model of surface site types on oxide and silicate minerals based on crystal chemistry; implications for site types and densities, multi-site adsorption, surface infrared spectroscopy, and dissolution kinetics. Am. J. Sci. 1998, 298, 349–438. [Google Scholar] [CrossRef]
- Dana, E.S. A Text-Book of Mineralogy: With an Extended Treatise on Crystallography and Physical Mineralogy; Wiley: Hoboken, NJ, USA, 1898. [Google Scholar]
- Hazen, R.M.; Filley, T.R.; Goodfriend, G.A. Selective adsorption of L- and D-amino acids on calcite: Implications for biochemical homochirality. Proc. Natl. Acad. Sci. USA 2001, 98, 5487–5490. [Google Scholar] [CrossRef]
- Van Cappellen, P.; Charlet, L.; Stumm, W.; Wersin, P. A surface complexation model of the carbonate mineral-aqueous solution interface. Geochim. Cosmochim. Acta 1993, 57, 3505–3518. [Google Scholar] [CrossRef]
- Stipp, S.L.; Hochella, M.F. Structure and bonding environments at the calcite surface as observed with X-ray photoelectron spectroscopy (XPS) and low energy electron diffraction (LEED). Geochim. Cosmochim. Acta 1991, 55, 1723–1736. [Google Scholar] [CrossRef]
- Bąbel, M. Crystal lography and genesis of the giant intergrowths of gypsum from the Miocene evaporites of Poland. Arch. Miner. 1990, 44, 103–135. [Google Scholar]
- Cody, A.M.; Cody, R.D. Chiral habit modifications of gypsum from epitaxial-like adsorption of stereospecific growth inhibitors. J. Cryst. Growth 1991, 113, 508–519. [Google Scholar] [CrossRef]
- Steendam, R.R.; Verkade, J.M.; van Benthem, T.J.; Meekes, H.; van Enckevort, W.J.; Raap, J.; Rutjes, F.P.; Vlieg, E. Emergence of single-molecular chirality from achiral reactants. Nat. Commun. 2014, 5, 5543. [Google Scholar] [CrossRef]
- Dressel, C.; Liu, F.; Prehm, M.; Zeng, X.; Ungar, G.; Tschierske, C. Dynamic mirror-symmetry breaking in bicontinuous cubic phases. Angew. Chem. Int. Ed. Engl. 2014, 53, 13115–13120. [Google Scholar] [CrossRef]
- Alaasar, M.; Poppe, S.; Dong, Q.; Liu, F.; Tschierske, C. Isothermal Chirality Switching in Liquid-Crystalline Azobenzene Compounds with Non-Polarized Light. Angew. Chem. Int. Ed. Engl. 2017, 56, 10801–10805. [Google Scholar] [CrossRef]
- Alaasar, M.; Prehm, M.; Tschierske, C. Helical Nano-crystallite (HNC) Phases: Chirality Synchronization of Achiral Bent-Core Mesogens in a New Type of Dark Conglomerates. Chemistry 2016, 22, 6583–6597. [Google Scholar] [CrossRef]
- Dressel, C.; Reppe, T.; Prehm, M.; Brautzsch, M.; Tschierske, C. Chiral self-sorting and amplification in isotropic liquids of achiral molecules. Nat. Chem. 2014, 6, 971–977. [Google Scholar] [CrossRef]
- Ueda, T.; Masuko, S.; Araoka, F.; Ishikawa, K.; Takezoe, H. A General Method for the Enantioselective Formation of Helical Nanofilaments. Angew. Chem. 2013, 125, 7001–7004. [Google Scholar] [CrossRef]
- Hu, J.; Gao, L.; Zhu, Y.; Wang, P.; Lin, Y.; Sun, Z.; Yang, S.; Wang, Q. Chiral Assemblies from an Achiral Pyridinium-Tailored Anthracene. Chemistry 2017, 23, 1422–1426. [Google Scholar] [CrossRef]
- Akine, S.; Sairenji, S.; Taniguchi, T.; Nabeshima, T. Stepwise helicity inversions by multisequential metal exchange. J. Am. Chem. Soc. 2013, 135, 12948–12951. [Google Scholar] [CrossRef]
- La, D.D.; Al Kobaisi, M.; Gupta, A.; Bhosale, S.V. Chiral Assembly of AIE-Active Achiral Molecules: An Odd Effect in Self-Assembly. Chem. Eur. J. 2017, 23, 3950–3956. [Google Scholar] [CrossRef]
- Tschierske, C.; Ungar, G. Mirror Symmetry Breaking by Chirality Synchronisation in Liquids and Liquid Crystals of Achiral Molecules. ChemPhysChem 2016, 17, 9–26. [Google Scholar] [CrossRef]
- Chen, D.; Nakata, M.; Shao, R.; Tuchband, M.R.; Shual, M.; Baumeister, U.; Weissflog, W.; Walba, D.M.; Glaser, M.A.; Maclennan, J.E.; Clark, N.A. Twist-bend heliconical chiral nematic liquid crystal phase of an achiral rigid bent-core mesogen. Phys. Rev. E 2014, 89, 022506. [Google Scholar] [CrossRef]
- Kohler, K.; Forster, G.; Hauser, A.; Dobner, B.; Heiser, U.F.; Ziethe, F.; Richter, W.; Steiniger, F.; Drechsler, M.; Stettin, H.; et al. Temperature-dependent behavior of a symmetric long-chain bolaamphiphile with phosphocholine headgroups in water: From hydrogel to nanoparticles. J. Am. Chem. Soc. 2004, 126, 16804–16813. [Google Scholar] [CrossRef]
- Roche, C.; Sun, H.J.; Prendergast, M.E.; Leowanawat, P.; Partridge, B.E.; Heiney, P.A.; Araoka, F.; Graf, R.; Spiess, H.W.; Zeng, X.; et al. Homochiral columns constructed by chiral self-sorting during supramolecular helical organization of hat-shaped molecules. J. Am. Chem. Soc. 2014, 136, 7169–7185. [Google Scholar] [CrossRef]
- Singh, G.; Chan, H.; Baskin, A.; Gelman, E.; Repnin, N.; Kral, P.; Klajn, R. Self-assembly of magnetite n5anocubes into helical superstructures. Science 2014, 345, 1149–1153. [Google Scholar] [CrossRef]
- Pokropivny, V.V. Powder. Metal. Met. Ceram. 2001, 40, 582–594. [Google Scholar] [CrossRef]
- Celik-Aktas, A.; Zuo, J.M.; Stubbins, J.F.; Tang, C.; Bando, Y. Double-helix structure in multiwall boron nitride nanotubes. Acta Crystallogr. A 2005, 61, 533–541. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Tang, C.; Golberg, D. Boron nitride nanotubes. Mater. Sci. Eng. R 2010, 70, 92–111. [Google Scholar] [CrossRef]
- Wang, Z.L. Zinc oxide nanostructures: Growth, properties and applications. J. Phys. Condens. Matter 2004, 16, R829–R858. [Google Scholar] [CrossRef]
- Ma, R.; Bando, Y.; Sato, T. Controlled Synthesis of BN Nanotubes, Nanobamboos, and Nanocables. Adv. Mater. 2002, 14, 366–368. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Spitsina, N.I.; Klabunovsky, E.I. Enantioselective hydrogenation in a cholesteric liquid crystal as a chiral matrix. Bull. Acad. Sci. USSR Div. Chem. Sci. 1982, 31, 2509. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Spitsina, N.I.; Klabunovsky, E.I. Enantioselective hydrogenation in cholesteryl tridecanoate as a chiral liquid-crystalline matrix. Bull. Acad. Sci. USSR Div. Chem. Sci. 1983, 32, 1501–1503. [Google Scholar] [CrossRef]
- Chen, C.W.; Whitlock, H.W. Molecular tweezers: A simple model of bifunctional intercalation. J. Am. Chem. Soc. 1978, 100, 4921–4922. [Google Scholar] [CrossRef]
- Zimmerman, S.C. Rigid Molecular Tweezers as Hosts for the Complexation of Neutral Guests; Springer: Berlin/Heidelberg, Germany, 1993; Volume 165, pp. 70–102. [Google Scholar]
- Harmata, M. Chiral molecular tweezers. Acc. Chem. Res. 2004, 37, 862–873. [Google Scholar] [CrossRef] [PubMed]
- Saha, B.; Ikbal, S.A.; Petrovic, A.G.; Berova, N.; Rath, S.P. Complexation of Chiral Zinc-Porphyrin Tweezer with Achiral Diamines: Induction and Two-Step Inversion of Interporphyrin Helicity Monitored by ECD. Inorg. Chem. 2017, 56, 3849–3860. [Google Scholar] [CrossRef] [PubMed]
- Ouyang, Q.; Zhu, Y.Z.; Li, Y.C.; Wei, H.B.; Zheng, J.Y. Diastereoselective synthesis of chiral diporphyrins via intramolecular meso-meso oxidative coupling. J. Org. Chem. 2009, 74, 3164–3167. [Google Scholar] [CrossRef]
- Ema, T.; Misawa, S.; Nemugaki, S.; Sakai, T.; Utaka, M. New Optically Active Diporphyrin Having a Chiral Cyclophane as a Spacer. Chem. Lett. 1997, 26, 487–488. [Google Scholar] [CrossRef]
- Berova, N.; Pescitelli, G.; Petrovic, A.G.; Proni, G. Probing molecular chirality by CD-sensitive dimeric metalloporphyrin hosts. Chem. Commun. 2009, 5958–5980. [Google Scholar] [CrossRef]
- Borovkov, V.V.; Hembury, G.A.; Inoue, Y. Origin, control, and application of supra molecular chirogenesis in bisporphyrin-based systems. Acc. Chem. Res. 2004, 37, 449–459. [Google Scholar] [CrossRef]
- Huang, X.; Nakanishi, K.; Berova, N. Porphyrins and metalloporphyrins: Versatile circular dichroic reporter groups for structural studies. Chirality 2000, 12, 237–255. [Google Scholar] [CrossRef]
- D’Urso, A.; Nicotra, P.F.; Centonze, G.; Fragala, M.E.; Gattuso, G.; Notti, A.; Pappalardo, A.; Pappalardo, S.; Parisi, M.F.; Purrello, R. Induction of chirality in porphyrin-(bis)calixarene assemblies: A mixed covalent-non-covalent vs a fully non-covalent approach. Chem. Commun. 2012, 48, 4046–4048. [Google Scholar] [CrossRef]
- Gholami, H.; Anyika, M.; Zhang, J.; Vasileiou, C.; Borhan, B. Host-Guest Assembly of a Molecular Reporter with Chiral Cyanohydrins for Assignment of Absolute Stereochemistry. Chemistry 2016, 22, 9235–9239. [Google Scholar] [CrossRef]
- Ikbal, S.A.; Dhamija, A.; Brahma, S.; Rath, S.P. A Nonempirical Approach for Direct Determination of the Absolute Configuration of 1,2-Diols and Amino Alcohols Using Mg(II)bisporphyrin. J. Org. Chem. 2016, 81, 5440–5449. [Google Scholar] [CrossRef]
- Ishii, Y.; Yoshizawa, T.; Kubo, Y. Dibenzodiaza-30-crown-10-appended bis(zinc porphyrin) tweezers: Synthesis and crown-assisted chiroptical behaviour. Org. Biomol. Chem. 2007, 5, 1210–1217. [Google Scholar] [CrossRef]
- Tanasova, M.; Anyika, M.; Borhan, B. Sensing remote chirality: Stereochemical determination of beta-, gamma-, and delta-chiral carboxylic acids. Angew. Chem. Int. Ed. Engl. 2015, 54, 4274–4278. [Google Scholar] [CrossRef]
- Beckett, A.H.; Anderson, P. A Method for the Determination of the Configuration of Organic Molecules using ‘Stereo-selective Adsorbents’. Nature 1957, 179, 1074–1075. [Google Scholar] [CrossRef]
- Bartels, H.; Prijs, B.; Erlenmeyer, H. Über spezifisch adsorbierende Silicagele V. Helv. Chim. Acta 1966, 49, 1621–1625. [Google Scholar] [CrossRef]
- Erlenmeyer, H.; Bartels, H. Über das Problem der Ähnlichkeit in der Chemie Über spezifisch adsorbierende Silikagele II [1]. Helv. Chim. Acta 1964, 47, 1285–1288. [Google Scholar] [CrossRef]
- Bartels, H.; Erlenmeyer, H. Über das Problem der Ähnlichkeit in der Chemie Über spezifisch adsorbierende Silicagele III. Helv. Chim. Acta 1965, 48, 285–290. [Google Scholar] [CrossRef]
- Ducos, P.; Liautard, V.; Robert, F.; Landais, Y. Chiral Memory in Silylium Ions. Chemistry 2015, 21, 11573–11578. [Google Scholar] [CrossRef]
- Miyabe, T.; Iida, H.; Ohnishi, A.; Yashima, E. Enantioseparation on poly(phenyl isocyanide)s with macromolecular helicity memory as chiral stationary phases for HPLC. Chem. Sci. 2012, 3, 863–867. [Google Scholar] [CrossRef]
- Huang, H.; Deng, J.; Shi, Y. Optically Active Physical Gels with Chiral Memory Ability: Directly Prepared by Helix-Sense-Selective Polymerization. Macromolecules 2016, 49, 2948–2956. [Google Scholar] [CrossRef]
- Zhao, Y.; Abdul Rahim, N.A.; Xia, Y.; Fujiki, M.; Song, B.; Zhang, Z.; Zhang, W.; Zhu, X. Supramolecular Chirality in Achiral Polyfluorene: Chiral Gelation, Memory of Chirality, and Chiral Sensing Property. Macromolecules 2016, 49, 3214–3221. [Google Scholar] [CrossRef]
- Yang, D.; Zhao, Y.; Lv, K.; Wang, X.; Zhang, W.; Zhang, L.; Liu, M. A strategy for tuning achiral mainchain polymers into helical assemblies and chiral memory systems. Soft. Matter. 2016, 12, 1170–1175. [Google Scholar] [CrossRef]
- Sobczuk, A.A.; Tsuchiya, Y.; Shiraki, T.; Tamaru, S.; Shinkai, S. Creation of chiral thixotropic gels through a crown-ammonium interaction and their application to a memory-erasing recycle system. Chemistry 2012, 18, 2832–2838. [Google Scholar] [CrossRef]
- De Jong, J.J.; Lucas, L.N.; Kellogg, R.M.; van Esch, J.H.; Feringa, B.L. Reversible optical transcription of supramolecular chirality into molecular chirality. Science 2004, 304, 278–281. [Google Scholar] [CrossRef]
- Inoue, K.; Ono, Y.; Kanekiyo, Y.; Ishii, T.; Yoshihara, K.; Shinkai, S. Chiroselective re-binding of saccharides to the fibrous aggregates prepared from organic gels of cholesterylphenylboronic acid. Tetrahedron Lett. 1998, 39, 2981–2984. [Google Scholar] [CrossRef]
- Gural’skiy, I.y.A.; Reshetnikov, V.A.; Szebesczyk, A.; Gumienna-Kontecka, E.; Marynin, A.I.; Shylin, S.I.; Ksenofontov, V.; Fritsky, I.O. Chiral spin crossover nanoparticles and gels with switchable circular dichroism. J. Mater. Chem. C 2015, 3, 4737–4741. [Google Scholar] [CrossRef]
- Duan, P.; Zhu, X.; Liu, M. Isomeric effect in the self-assembly of pyridine-containing L-glutamic lipid: Substituent position controlled morphology and supramolecular chirality. Chem. Commun. 2011, 47, 5569–5571. [Google Scholar] [CrossRef]
- Van Gorp, J.J.; Vekemans, J.A.J.M.; Meijer, E.W. C3-Symmetrical Supramolecular Architectures: Fibers and Organic Gels from Discotic Trisamides and Trisureas. J. Am. Chem. Soc. 2002, 124, 14759–14769. [Google Scholar] [CrossRef]
- Tobe, Y.; Utsumi, N.; Kawabata, K.; Nagano, A.; Adachi, K.; Araki, S.; Sonoda, M.; Hirose, K.; Naemura, K. m-Diethynylbenzene Macrocycles: Syntheses and Self-Association Behavior in Solution. J. Am. Chem. Soc. 2002, 124, 5350–5364. [Google Scholar] [CrossRef]
- Lahiri, S.; Thompson, J.L.; Moore, J.S. Solvophobically Driven π-Stacking of Phenylene Ethynylene Macrocycles and Oligomers. J. Am. Chem. Soc. 2000, 122, 11315–11319. [Google Scholar] [CrossRef]
- Xing, P.; Zhao, Y. Controlling Supramolecular Chirality in Multicomponent Self-Assembled Systems. Acc. Chem. Res. 2018, 51, 2324–2334. [Google Scholar] [CrossRef]
- Haino, T.; Tanaka, M.; Fukazawa, Y. Self-assembly of tris(phenylisoxazolyl)benzene and its asymmetric induction of supramolecular chirality. Chem. Commun. 2008, 468–470. [Google Scholar] [CrossRef]
- Edwards, W.; Smith, D.K. Enantioselective component selection in multicomponent supramolecular gels. J. Am. Chem. Soc. 2014, 136, 1116–1124. [Google Scholar] [CrossRef]
- Molla, M.R.; Das, A.; Ghosh, S. Chiral induction by helical neighbour: Spectroscopic visualization of macroscopic-interaction among self-sorted donor and acceptor pi-stacks. Chem. Commun. 2011, 47, 8934–8936. [Google Scholar] [CrossRef]
- Tanaka, M.; Ikeda, T.; Mack, J.; Kobayashi, N.; Haino, T. Self-assembly and gelation behavior of tris(phenylisoxazolyl)benzenes. J. Org. Chem. 2011, 76, 5082–5091. [Google Scholar] [CrossRef]
- Smith, D.K. Lost in translation? Chirality effects in the self-assembly of nanostructured gel-phase materials. Chem. Soc. Rev. 2009, 38, 684–694. [Google Scholar] [CrossRef]
- Shen, Z.; Wang, T.; Liu, M. Macroscopic chirality of supramolecular gels formed from achiral tris(ethyl cinnamate) benzene-1,3,5-tricarboxamides. Angew. Chem. Int. Ed. Engl. 2014, 53, 13424–13428. [Google Scholar] [CrossRef]
- Yu, X.; Wang, Z.; Li, Y.; Geng, L.; Ren, J.; Feng, G. Fluorescent and Electrochemical Supramolecular Coordination Polymer Hydrogels Formed from Ion-Tuned Self-Assembly of Small Bis-Terpyridine Monomer. Inorg. Chem. 2017, 56, 7512–7518. [Google Scholar] [CrossRef]
- Jin, W.; Fukushima, T.; Niki, M.; Kosaka, A.; Ishii, N.; Aida, T. Self-assembled graphitic nanotubes with one-handed helical arrays of a chiral amphiphilic molecular graphene. Proc. Natl. Acad. Sci. USA 2005, 102, 10801–10806. [Google Scholar] [CrossRef]
- Onouchi, H.; Miyagawa, T.; Morino, K.; Yashima, E. Assisted formation of chiral porphyrin homoaggregates by an induced helical poly(phenylacetylene) template and their chiral memory. Angew. Chem. Int. Ed. Engl. 2006, 45, 2381–2384. [Google Scholar] [CrossRef]
- Mammana, A.; D’Urso, A.; Lauceri, R.; Purrello, R. Switching off and on the supramolecular chiral memory in porphyrin assemblies. J. Am. Chem. Soc. 2007, 129, 8062–8063. [Google Scholar] [CrossRef]
- Randazzo, R.; Mammana, A.; D’Urso, A.; Lauceri, R.; Purrello, R. Reversible “chiral memory” in ruthenium tris(phenanthroline)-anionic porphyrin complexes. Angew. Chem. Int. Ed. Engl. 2008, 47, 9879–9882. [Google Scholar] [CrossRef]
- Gaeta, M.; Oliveri, I.P.; Fragala, M.E.; Failla, S.; D’Urso, A.; Di Bella, S.; Purrello, R. Chirality of self-assembled achiral porphyrins induced by chiral Zn(ii) Schiff-base complexes and maintained after spontaneous dissociation of the templates: A new case of chiral memory. Chem. Commun. 2016, 52, 8518–8521. [Google Scholar] [CrossRef]
- Lauceri, R.; Raudino, A.; Scolaro, L.M.; Micali, N.; Purrello, R. From Achiral Porphyrins to Template-Imprinted Chiral Aggregates and Further. Self-Replication of Chiral Memory from Scratch. J. Am. Chem. Soc. 2002, 124, 894–895. [Google Scholar] [CrossRef]
- Yashima, E.; Maeda, K.; Okamoto, Y. Memory of macromolecular helicity assisted by interaction with achiral small molecules. Nature 1999, 399, 449. [Google Scholar] [CrossRef]
- Hase, Y.; Mitsutsuji, Y.; Ishikawa, M.; Maeda, K.; Okoshi, K.; Yashima, E. Unexpected thermally stable, cholesteric liquid-crystalline helical polyisocyanides with memory of macromolecular helicity. Chem. Asian J. 2007, 2, 755–763. [Google Scholar] [CrossRef]
- Ishikawa, M.; Maeda, K.; Mitsutsuji, Y.; Yashima, E. An unprecedented memory of macromolecular helicity induced in an achiral polyisocyanide in water. J. Am. Chem. Soc. 2004, 126, 732–733. [Google Scholar] [CrossRef]
- Takashima, S.; Abe, H.; Inouye, M. Unexpected chain length dependence on a chiral memory effect of ‘meta-ethynylpyridine’ oligomers. Tetrahedron Asymmetry 2013, 24, 527–531. [Google Scholar] [CrossRef]
- Ishidate, R.; Shimomura, K.; Ikai, T.; Kanoh, S.; Maeda, K. Macromolecular helicity induction and memory in a poly(biphenylylacetylene) bearing an ester group and its application to a chiral stationary phase for high-performance liquid chromatography. Chem. Lett. 2015, 44, 946–948. [Google Scholar] [CrossRef]
- Rosaria, L.; D’Urso, A.; Mammana, A.; Purrello, R. Chiral memory: Induction, amplification, and switching in porphyrin assemblies. Chirality 2008, 20, 411–419. [Google Scholar] [CrossRef]
- Sung, B.; de la Cotte, A.; Grelet, E. Chirality-controlled crystallization via screw dislocations. Nat. Commun. 2018, 9, 1405. [Google Scholar] [CrossRef]
- Thomas, C.W.; Tor, Y. Dendrimers and chirality. Chirality 1998, 10, 53–59. [Google Scholar] [CrossRef]
- Vestergren, M.; Johansson, A.; Lennartson, A.; Håkansson, M. Non-stochastic homochiral helix crystallization: Cryptochirality in control? Mendeleev Commun. 2004, 14, 258–260. [Google Scholar] [CrossRef]
- Wallach, O. Zur Kenntniss der Terpene und der ätherischen Oele. Justus Liebig’s Ann. Chem. 1895, 286, 90–118. [Google Scholar] [CrossRef]
- Dunitz, J.D.; Gavezzotti, A. Proteogenic amino acids: Chiral and racemic crystal packings and stabilities. J. Phys. Chem. B 2012, 116, 6740–6750. [Google Scholar] [CrossRef]
- Brock, C.P.; Schweizer, W.B.; Dunitz, J.D. On the validity of Wallach’s rule: On the density and stability of racemic crystals compared with their chiral counterparts. J. Am. Chem. Soc. 1991, 113, 9811–9820. [Google Scholar] [CrossRef]
- Slepukhin, P.A.; Gruzdev, D.A.; Chulakov, E.N.; Levit, G.L.; Krasnov, V.P.; Charushin, V.N. Structures of the racemate and (S)-enantiomer of 7,8-difluoro-3-methyl-2,3-dihydro-4H-[1,4]benzoxazine. Russ. Chem. Bull. 2011, 60, 955–960. [Google Scholar] [CrossRef]
- Navare, P.S.; MacDonald, J.C. Investigation of Stability and Structure in Three Homochiral and Heterochiral Crystalline Forms of 3-Phenyllactic Acid. Cryst. Growth Des. 2011, 11, 2422–2428. [Google Scholar] [CrossRef]
- Sørensen, H.O.; Larsen, S. Hydrogen bonding in enantiomericversusracemic mono-carboxylic acids; a case study of 2-phenoxypropionic acid. Acta Crystallogr. B Struct. Sci. 2003, 59, 132–140. [Google Scholar] [CrossRef]
- Assaad, T.; Rukiah, M. Powder X-ray study of racemic (2RS,3RS)-5-amino-3-[4-(3-methoxyphenyl)piperazin-1-yl]-1,2,3,4-tetrahydronaphtha len-2-ol. Acta Crystallogr. C 2011, 67, o469–o472. [Google Scholar] [CrossRef]
- Husin, H.; Leong, Y.-K.; Liu, J. Molecular attributes of an effective steric agent: Yield stress of dispersions in the presence of pure enantiomeric and racemate malic acids. Adv. Powder Technol. 2012, 23, 459–464. [Google Scholar] [CrossRef]
- Sanabria, C.M.; Gomez, S.L.; Palma, A.; Cobo, J.; Glidewell, C. Four 1-naphthyl-substituted tetrahydro-1,4-epoxy-1-benzazepines: hydrogen bonded structures in one, two and three dimensions. Acta Crystallogr. C 2010, 66, o540–o546. [Google Scholar] [CrossRef]
- Marthi, K.; Larsen, S.; Ács, M.; Fogassy, E. Enantiomer associations in the crystal structures of racemic and (2S,3S)-(+)-3-hydroxy-2-(4-methoxyphenyl)-2,3-dihydro-1,5-benzothiazepin-4(5H)-one. J. Mol. Struct. 1996, 374, 347–355. [Google Scholar] [CrossRef]
- Luger, P.; Weber, M. DL-Cysteine at 298K. Acta Crystallogr. C Cryst. Struct. Commun. 1999, 55, 1882–1885. [Google Scholar] [CrossRef]
- Krishnaswamy, S.; Patil, M.T.; Shashidhar, M.S. Comparison of racemic epi-inosose and (-)-epi-inosose. Acta Crystallogr. C 2011, 67, o435–o438. [Google Scholar] [CrossRef]
- Kitoh, S.-I.; Kunimoto, K.-K.; Funaki, N.; Senda, H.; Kuwae, A.; Hanai, K.J. Crystal structures and vibrational spectra of racemic and chiral 4-phenyl-1,3-oxazolidine-2-thione. Chem. Crystallogr. 2002, 32, 547–553. [Google Scholar] [CrossRef]
- Pella, E.; Restelli, R. Binary phase diagram of the enantiomers of indoprofen. Mikrochim. Acta 1983, 79, 65–74. [Google Scholar] [CrossRef]
- Xie, S.; Nusbaum, D.A.; Stein, H.J.; Pink, M. 4-(3-Methoxy-phen-yl)-2,6-dimethyl-cyclo-hex3-enecarboxylic acid. Acta Crystallogr. E Struct. Rep. Online 2010, 66, o1443–o1449. [Google Scholar] [CrossRef]
- Blazis, V.J.; Koeller, K.J.; Rath, N.P.; Spilling, C.D. Application of Wallach’s Rule in a Comparison of the X-ray Crystal Structures of the Racemate and the (S) Enantiomer of (1-Hydroxy3-phenyl-2-propenyl) Dimethylphosphonate. Acta Crystallogr. B Struct. Sci. 1997, 53, 838–842. [Google Scholar] [CrossRef]
- Simonov, Y.; Bourosh, P.; Kravtsov, V.; Gdanets, М.; Semenishyna, K.; Pavlovsky, V.; Kabanova, T.; Khalimova, O.; Andronati, S. A comparative analysis of the crystal structure of r,s-racemate and r-enantiomer of 7-bromo-3-(2-methoxy)ethoxy-5-phenyl-1,2-dihydro- h-1,4-benzodiazepine-2-one exhibiting a high analgesic activity. Zhurnal Organichnoi ta Farmatsevtichnoi Khimi 2011, 9, 70–73. [Google Scholar]
- Patrick, B.O.; Brock, C.P. S,S-1,2-Dicyclohexylethane-1,2-diol and its racemic compound: A striking exception to Wallach’s rule. Acta Crystallogr. B 2006, 62, 488–497. [Google Scholar] [CrossRef]
- Benson, N.; Snelder, N.; Ploeger, B.; Napier, C.; Sale, H.; Birdsall, N.J.; Butt, R.P.; van der Graaf, P.H. Estimation of binding rate constants using a simultaneous mixed-effects method: Application to monoamine transporter reuptake inhibitor reboxetine. Br. J. Pharmacol. 2010, 160, 389–398. [Google Scholar] [CrossRef]
- Xu, F.; Khan, I.J.; McGuinness, K.; Parmar, A.S.; Silva, T.; Murthy, N.S.; Nanda, V. Self-assembly of left- and right-handed molecular screws. J. Am. Chem. Soc. 2013, 135, 18762–18765. [Google Scholar] [CrossRef]
- Kwon, S.; Shin, H.S.; Gong, J.; Eom, J.H.; Jeon, A.; Yoo, S.H.; Chung, I.S.; Cho, S.J.; Lee, H.S. Self-assembled peptide architecture with a tooth shape: Folding into shape. J. Am. Chem. Soc. 2011, 133, 17618–17621. [Google Scholar] [CrossRef]
- Chen, C.C.; Hsu, W.; Hwang, K.C.; Hwu, J.R.; Lin, C.C.; Horng, J.C. Contributions of cation-pi interactions to the collagen triple helix stability. Arch. Biochem. Biophys. 2011, 508, 46–53. [Google Scholar] [CrossRef]
- Brown, E.M. Development and utilization of a bovine type I collagen microfibril model. Int. J. Biol. Macromol. 2013, 53, 20–25. [Google Scholar] [CrossRef]
- Miyoshi, K.; Uezu, K.; Sakurai, K.; Shinkai, S. Proposal of a new hydrogen-bonding form to maintain curdlan triple helix. Chem. Biodivers. 2004, 1, 916–924. [Google Scholar] [CrossRef]
- Ishikawa, T.; Morita, T.; Kimura, S. Unique Helical Triangle Molecular Geometry Induced by Dipole–Dipole Interactions. Bull. Chem. Soc. Jpn. 2007, 80, 1483–1491. [Google Scholar] [CrossRef]
- Kony, D.B.; Damm, W.; Stoll, S.; van Gunsteren, W.F.; Hunenberger, P.H. Explicit-solvent molecular dynamics simulations of the polysaccharide schizophyllan in water. Biophys. J. 2007, 93, 442–455. [Google Scholar] [CrossRef]
- Wells, R.D. Non-B DNA conformations, mutagenesis and disease. Trends Biochem. Sci. 2007, 32, 271–278. [Google Scholar] [CrossRef] [PubMed]
- Wells, R.D.; Dere, R.; Hebert, M.L.; Napierala, M.; Son, L.S. Advances in mechanisms of genetic instability related to hereditary neurological diseases. Nucleic Acids. Res. 2005, 33, 3785–3798. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, H.; Ren, J.; Qu, X. Reversible B/Z-DNA transition under the low salt condition and non-B-form polydApolydT selectivity by a cubane-like europium-L-aspartic acid complex. Biophys. J. 2006, 90, 3203–3207. [Google Scholar] [CrossRef]
- Mirkin, S.M. DNA structures, repeat expansions and human hereditary disorders. Curr. Opin. Struct. Biol. 2006, 16, 351–358. [Google Scholar] [CrossRef]
- Bacolla, A.; Wells, R.D. Non-B DNA conformations, genomic rearrangements, and human disease. J. Biol. Chem. 2004, 279, 47411–47414. [Google Scholar] [CrossRef]
- Lupski, J.R. Genomic disorders: Structural features of the genome can lead to DNA rearrangements and human disease traits. Trends Genet. 1998, 14, 417–422. [Google Scholar] [CrossRef]
- Lupski, J.R.; Stankiewicz, P. Genomic Disorders: The Genomic BAsis of Desease; Humana Press: New York, NY, USA, 2006. [Google Scholar]
- Genetic Instabilities and Neurological Diseases; Academic Press: Houston, TX, USA, 2006.
- Harvey, S.C. DNA structural dynamics: Longitudinal breathing as a possible mechanism for the B ⇄ Z transition. Nucleic Acids Res. 1983, 11, 4867–4878. [Google Scholar] [CrossRef]
- Green, M.M.; Peterson, N.C.; Sato, T.; Teramoto, A.; Cook, R.; Lifson, S. A helical polymer with a cooperative response to chiral information. Science 1995, 268, 1860–1866. [Google Scholar] [CrossRef] [PubMed]
- Lifson, S.; Felder, C.E.; Green, M.M. Helical conformations, internal motion, and helix sense reversal in polyisocyanates and the preferred helix sense of an optically active polyisocyanate. Macromolecules 1992, 25, 4142–4148. [Google Scholar] [CrossRef]
- Lee, J.; Kim, Y.G.; Kim, K.K.; Seok, C. Transition between B-DNA and Z-DNA: Free energy landscape for the B-Z junction propagation. J. Phys. Chem. B 2010, 114, 9872–9881. [Google Scholar] [CrossRef]
- Pohl, F.M.; Jovin, T.M. Salt-induced co-operative conformational change of a synthetic DNA: Equilibrium and kinetic studies with poly(dG-dC). J. Mol. Biol. 1972, 67, 375–396. [Google Scholar] [CrossRef]
- Zacharias, W.; Martin, J.C.; Wells, R.D. A condensed form of (dG-dC)n.cntdot.(dG-dC)n as an intermediate between the B- and Z-conformations induced by sodium acetate. Biochemistry 2002, 22, 2398–2405. [Google Scholar] [CrossRef]
- Wang, A.J.; Quigley, G.J.; Kolpak, F.J.; van der Marel, G.; van Boom, J.H.; Rich, A. Left-handed double helical DNA: Variations in the backbone conformation. Science 1981, 211, 171–176. [Google Scholar] [CrossRef] [PubMed]
- Wang, A.H.; Quigley, G.J.; Kolpak, F.J.; Crawford, J.L.; van Boom, J.H.; van der Marel, G.; Rich, A. Molecular structure of a left-handed double helical DNA fragment at atomic resolution. Nature 1979, 282, 680–686. [Google Scholar] [CrossRef] [PubMed]
- Behe, M.; Felsenfeld, G. Effects of methylation on a synthetic polynucleotide: The B--Z transition in poly(dG-m5dC).poly(dG-m5dC). Proc. Natl. Acad. Sci. USA 1981, 78, 1619–1623. [Google Scholar] [CrossRef]
- Russell, W.C.; Precious, B.; Martin, S.R.; Bayley, P.M. Differential promotion and suppression of Z leads to B transitions in poly[d(G-C)] by histone subclasses, polyamino acids and polyamines. EMBO J. 1983, 2, 1647–1653. [Google Scholar] [CrossRef] [PubMed]
- Pohl, F.M. Polymorphism of a synthetic DNA in solution. Nature 1976, 260, 365–366. [Google Scholar] [CrossRef]
- Feigon, J.; Wang, A.H.; van der Marel, G.A.; van Boom, J.H.; Rich, A. A one- and two-dimensional NMR study of the B to Z transition of (m5dC-dG)3 in methanolic solution. Nucleic Acids Res. 1984, 12, 1243–1263. [Google Scholar] [CrossRef]
- Zimmer, C.; Tymen, S.; Marck, C.; Guschlbauer, W. Conformational transitions of poly(dA-dC). poly(dG-dT) induced by high salt or in ethanolic solution. Nucleic Acids Res. 1982, 10, 1081–1091. [Google Scholar] [CrossRef][Green Version]
- Van de Sande, J.H.; McIntosh, L.P.; Jovin, T.M. Mn2+ and other transition metals at low concentration induce the right-to-left helical transformation of poly[d(G-C)]. EMBO J. 1982, 1, 777–782. [Google Scholar] [CrossRef]
- Pohl, F.M.; Jovin, T.M.; Baehr, W.; Holbrook, J.J. Ethidium Bromide as a Cooperative Effector of a DNA Structure. Proc. Natl. Acad. Sci. USA 1972, 69, 3805–3809. [Google Scholar] [CrossRef] [PubMed]
- Mirau, P.A.; Kearns, D.R. The effect of Intercalating drugs on the kinetics of the B to Z transition of poly(dG–dC). Nucleic Acids Res. 1983, 11, 1931–1941. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Zacharias, W.; Larson, J.E.; Klysik, J.; Stirdivant, S.M.; Wells, R.D. Conditions which cause the right-handed to left-handed DNA conformational transitions. Evidence for several types of left-handed DNA structures in solution. J. Biol. Chem. 1982, 257, 2775–2782. [Google Scholar]
- Wu, Z.; Tian, T.; Yu, J.; Weng, X.; Liu, Y.; Zhou, X. Formation of sequence-independent Z-DNA induced by a ruthenium complex at low salt concentrations. Angew. Chem. Int. Ed. Engl. 2011, 50, 11962–11967. [Google Scholar] [CrossRef]
- Johnson, A.; Qu, Y.; Van Houten, B.; Farrell, N. B↑ Z DNA conformational changes induced by a family of dinuclear bis(platinum) complexes. Nucleic Acids Res. 1992, 20, 1697–1703. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nordén, B.; Lincoln, P.; Akerman, B.; Tuite, E. DNA interactions with substitution-inert transition metal ion complexes. Met. Ions. Biol. Syst. 1996, 33, 177–252. [Google Scholar] [PubMed]
- Nordén, B.; Tjerneld, F. Binding of inert metal complexes to deoxyribonucleic acid detected by linear dichroism. FEBS Lett. 1976, 67, 368–370. [Google Scholar] [CrossRef]
- Barton, J.K. Tris (phenanthroline) metal complexes: Probes for DNA helicity. J. Biomol. Struct. Dyn. 1983, 1, 621–632. [Google Scholar] [CrossRef]
- Chow, C.S.; Barton, J.K. Transition metal complexes as probes of nucleic acids. Methods Enzymol. 1992, 212, 219–242. [Google Scholar]
- Xu, Y.; Zhang, Y.X.; Sugiyama, H.; Umano, T.; Osuga, H.; Tanaka, K. (P)-helicene displays chiral selection in binding to Z-DNA. J. Am. Chem. Soc. 2004, 126, 6566–6567. [Google Scholar] [CrossRef]
- Tsuji, G.; Kawakami, K.; Sasaki, S. Enantioselective binding of chiral 1,14-dimethyl[5]helicene-spermine ligands with B- and Z-DNA. Bioorg. Med. Chem. 2013, 21, 6063–6068. [Google Scholar] [CrossRef]
- Qu, X.; Trent, J.O.; Fokt, I.; Priebe, W.; Chaires, J.B. Allosteric, chiral-selective drug binding to DNA. Proc. Natl. Acad. Sci. USA 2000, 97, 12032–12037. [Google Scholar] [CrossRef]
- Doi, I.; Tsuji, G.; Kawakami, K.; Nakagawa, O.; Taniguchi, Y.; Sasaki, S. The spermine-bisaryl conjugate as a potent inducer of B- to Z-DNA transition. Chemistry 2010, 16, 11993–11999. [Google Scholar] [CrossRef]
- Haque, L.; Pradhan, A.B.; Bhuiya, S.; Das, S. Structural conversion of left handed protonated form of calf thymus DNA to right handed B-DNA by the alkaloid chelerythrine. J. Lumin. 2016, 173, 44–51. [Google Scholar] [CrossRef]
- Kim, J.; Ha, C.S.; Lee, H.J.; Song, K. Repetitive exposure to a 60-Hz time-varying magnetic field induces DNA double-strand breaks and apoptosis in human cells. Biochem. Biophys. Res. Commun. 2010, 400, 739–744. [Google Scholar] [CrossRef]
- Lopez-Diaz, B.; Mercado-Saenz, S.; Martinez-Morillo, M.; Sendra-Portero, F.; Ruiz-Gomez, M.J. Long-term exposure to a pulsed magnetic field (1.5 mT, 25 Hz) increases genomic DNA spontaneous degradation. Electromagn. Biol. Med. 2014, 33, 228–235. [Google Scholar] [CrossRef]
- Ruiz-Gomez, M.J.; Martinez-Morillo, M. Enhancement of the cell-killing effect of ultraviolet-C radiation by short-term exposure to a pulsed magnetic field. Int. J. Radiat. Biol. 2005, 81, 483–490. [Google Scholar] [CrossRef]
- Ivancsits, S.; Diem, E.; Pilger, A.; Rüdiger, H.W.; Jahn, O. Induction of DNA strand breaks by intermittent exposure to extremely-low-frequency electromagnetic fields in human diploid fibroblasts. Mutat. Res. Genet. Toxicol. Environ. Mutagen. 2002, 519, 1–13. [Google Scholar] [CrossRef]
- Wolf, F.I.; Torsello, A.; Tedesco, B.; Fasanella, S.; Boninsegna, A.; D’Ascenzo, M.; Grassi, C.; Azzena, G.B.; Cittadini, A. 50-Hz extremely low frequency electromagnetic fields enhance cell proliferation and DNA damage: Possible involvement of a redox mechanism. Biochim. Biophys. Acta. 2005, 1743, 120–129. [Google Scholar] [CrossRef]
- Scarfí, M.R.; Sannino, A.; Perrotta, A.; Sarti, M.; Mesirca, P.; Bersani, F. Evaluation of Genotoxic Effects in Human Fibroblasts after Intermittent Exposure to 50 Hz Electromagnetic Fields: A Confirmatory Study. Radiat. Res. 2005, 164, 270–276. [Google Scholar] [CrossRef]
- Igarashi, A.; Kobayashi, K.; Matsuki, H.; Endo, G.; Haga, A. Evaluation of damage in DNA molecules resulting from very-low-frequency magnetic fields by using bacterial mutation repairing genetic system. IEEE Trans. Magn. 2005, 41, 4368–4370. [Google Scholar] [CrossRef]
- Lai, H.; Singh, N.P. Magnetic-field-induced DNA strand breaks in brain cells of the rat. Environ. Health Perspect. 2004, 112, 687–694. [Google Scholar] [CrossRef]
- Zheng, Y.; Sanche, L. Influence of organic ions on DNA damage induced by 1 eV to 60 keV electrons. J. Chem. Phys. 2010, 133, 155102. [Google Scholar] [CrossRef]
- Zmyslony, M.; Palus, J.; Dziubaltowska, E.; Politanski, P.; Mamrot, P.; Rajkowska, E.; Kamedula, M. Effects of in vitro exposure to power frequency magnetic fields on UV-induced DNA damage of rat lymphocytes. Bioelectromagnetics 2004, 25, 560–562. [Google Scholar] [CrossRef]
- Williams, P.A.; Ingebretsen, R.J.; Dawson, R.J. 14.6 mT ELF magnetic field exposure yields no DNA breaks in model system Salmonella, but provides evidence of heat stress protection. Bioelectromagnetics 2006, 27, 445–450. [Google Scholar] [CrossRef]
- McNamee, J.P.; Bellier, P.V.; Chauhan, V.; Gajda, G.B.; Lemay, E.; Thansandote, A. Evaluating DNA Damage in Rodent Brain after Acute 60 Hz Magnetic-Field Exposure. Radiat. Res. 2005, 164, 791–797. [Google Scholar] [CrossRef]
- Li, S.H.; Chow, K.C. Magnetic field exposure induces DNA degradation. Biochem. Biophys. Res. Commun. 2001, 280, 1385–1388. [Google Scholar] [CrossRef]
- Ruiz-Gómez, M.J.; Martínez-Morillo, M. Electromagnetic fields and the induction of DNA strand breaks. Electromagn. Biol. Med. 2009, 28, 201–214. [Google Scholar] [CrossRef]
- Aydin, M.; Taspinar, M.S.; Cakmak, Z.E.; Dumlupinar, R.; Agar, G. Static magnetic field induced epigenetic changes in wheat callus. Bioelectromagnetics 2016, 37, 504–511. [Google Scholar] [CrossRef]
- Potenza, L.; Cucchiarini, L.; Piatti, E.; Angelini, U.; Dacha, M. Effects of high static magnetic field exposure on different DNAs. Bioelectromagnetics 2004, 25, 352–355. [Google Scholar] [CrossRef]
- Zhang, Q.M.; Tokiwa, M.; Doi, T.; Nakahara, T.; Chang, P.W.; Nakamura, N.; Hori, M.; Miyakoshi, J.; Yonei, S. Strong static magnetic field and the induction of mutations through elevated production of reactive oxygen species in Escherichia coli soxR. Int. J. Radiat. Biol. 2003, 79, 281–286. [Google Scholar] [CrossRef]
- Boulikas, T. Evolutionary consequences of nonrandom damage and repair of chromatin domains. J. Mol. Evol. 1992, 35, 156–180. [Google Scholar] [CrossRef]
- Villarini, M.; Moretti, M.; Scassellati-Sforzolini, G.; Boccioli, B.; Pasquini, R. Effects of co-exposure to extremely low frequency (50 Hz) magnetic fields and xenobiotics determined in vitro by the alkaline comet assay. Sci. Total Environ. 2006, 361, 208–219. [Google Scholar] [CrossRef]

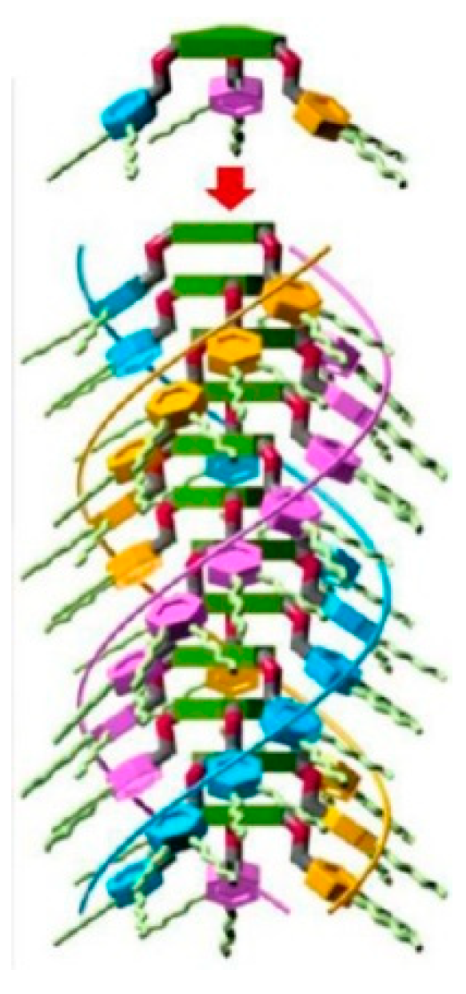

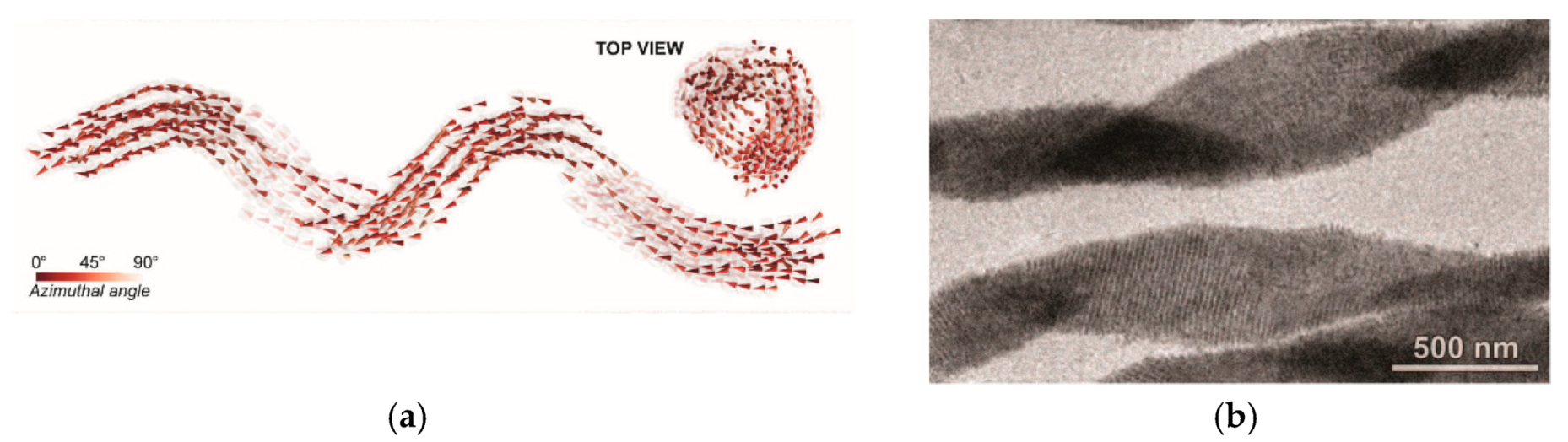


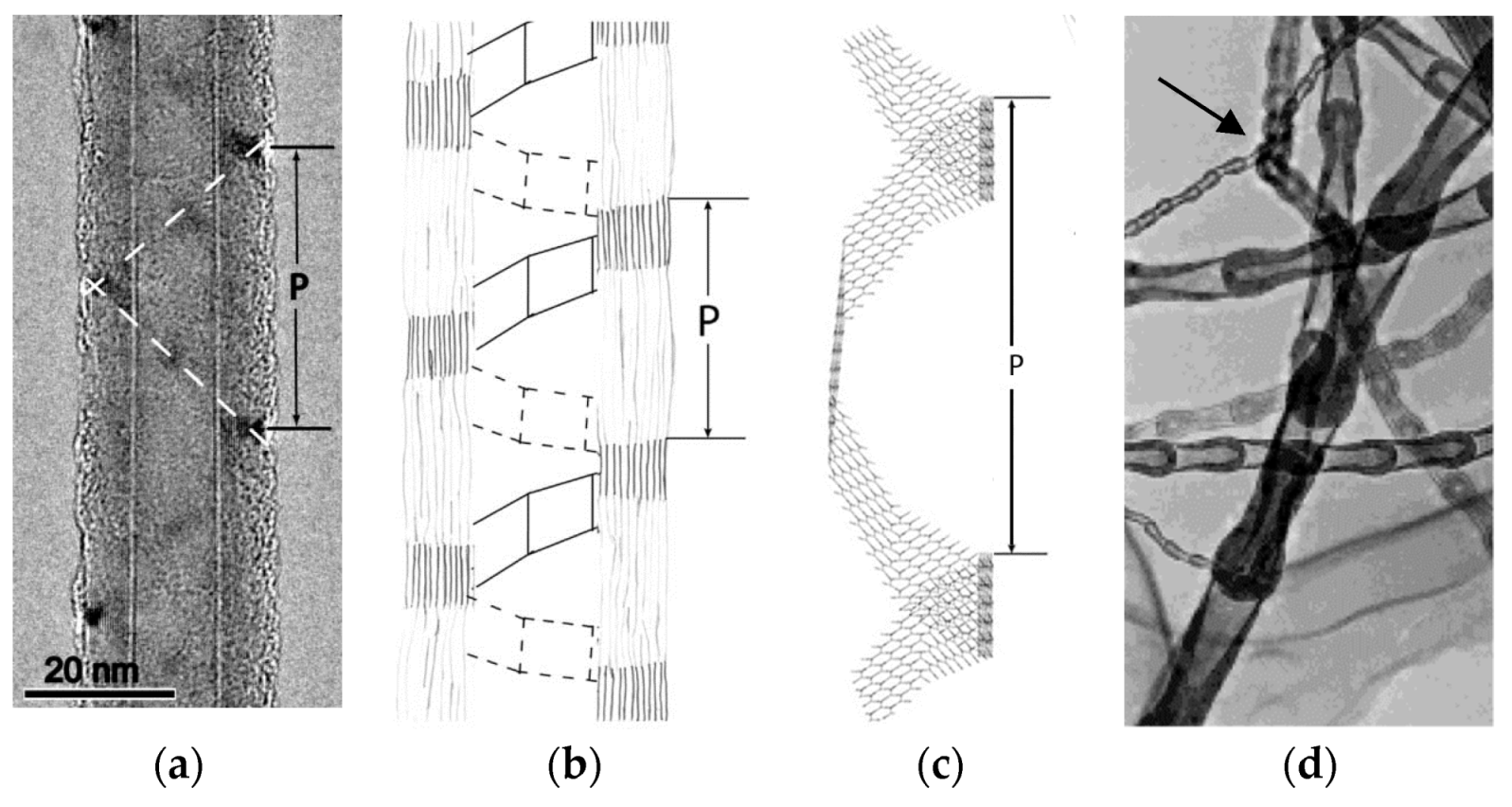
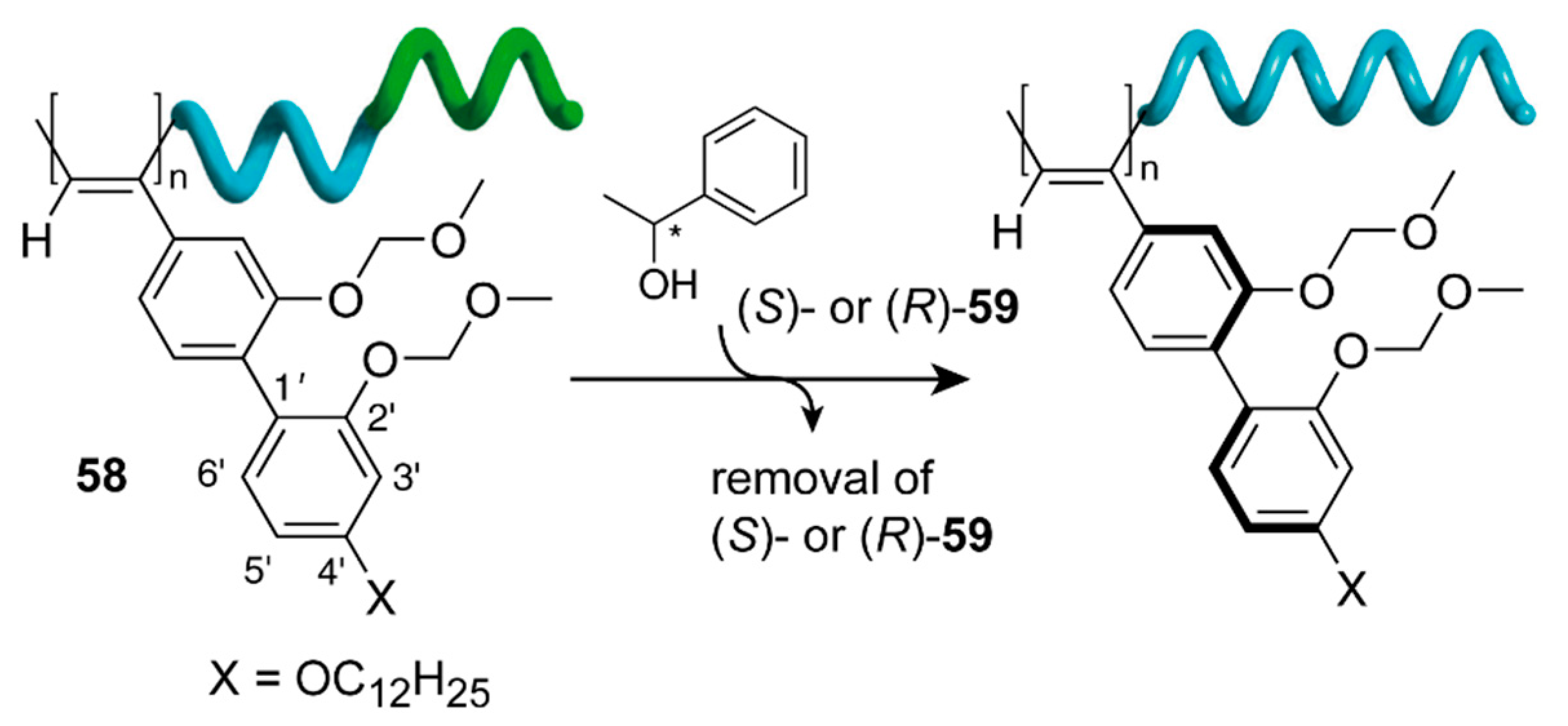

| № | Amylose | Solvent | Helix | Reference |
|---|---|---|---|---|
| 1 | Amylose A 1 | water | P | [19] |
| 2 | Amylose B 1 | water | P | [20] |
| 3 | Amylose V | – | M | [21] |
| 4 | KOH-Amylose | water, KOH | M | [22] |
| 5 | Amylose Vpropan-2-ol | propan-2-ol, water | M | [23] |
| 6 | Amylose | water | M | [24] |
| Starting Racemate in VPR | Number of VPR Experiments | Final Chirality Purity | ||
|---|---|---|---|---|
| l-Crystals | d-Crystals | % of l-Crystals | ||
| NaClO3 | 200 | 160 | 40 | 79.5 |
| 240 | 236 | 4 | 98.3 | |
| 200 | 102 | 98 | 51.0 | |
| 100 | 83 | 17 | 83.0 | |
| 100 | 49 | 51 | 49.0 | |
| 100 | 73 | 27 | 73.0 | |
| NaBrO3 | 260 | 258 | 2 | 99.2 |
| 280 | 274 | 6 | 97.8 | |
| 200 | 89 | 111 | 44.5 | |
| 100 | 80 | 20 | 80.0 | |
| 100 | 52 | 48 | 52.0 | |
| 100 | 68 | 32 | 68.0 | |
| Entry | Temp./°C | Conv. of 1/% | Yield of 2/% | ee of 2/% |
|---|---|---|---|---|
| 1 | 20 | 69 | 37 | 0 |
| 2 | 0 | 38 | 53 | 50 |
| 3 | −20 | 27 | 65 | 67 |
| 4 | −40 | 16 | 93 | 97 |
| Ligand | ee % | |||
|---|---|---|---|---|
| 10 | 37 | 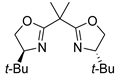 | 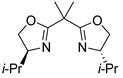 | 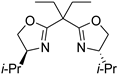 |
| 11 | 8 | |||
| 12 | 1 | 10 | 11 | 12 |
| 13 | 7 | 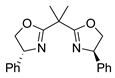 | 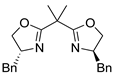 | 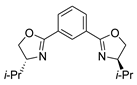 |
| 14 | 0 | |||
| 15 | 0 | 13 | 14 | 15 |
| L | ee % | Config Product | Ref. |
|---|---|---|---|
| 16 | 97 | R | [127] |
| 17 | 100 | R | [128] |
| 18 | 99 | R | [129] |
| 19 | 8 | S | [130] |
| 21 | 26 | S | [130] |
| 20 | 8 | R | [131] |
| 22 | 20 | R | [130] |
| 23 | 4 | S | [132] |
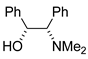 | 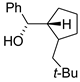 | 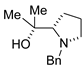 | |
| 16 (C1) | 17 (C1) | 18 (C1) | |
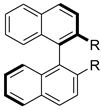 |  | 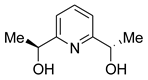 | |
| 19 R = OH (C2) 20 R = NMePh (C2) | 21 R = NH2 (C2) 22 R = OH (C2) | 23 (C2) | |
| Ligand | Product ee% | ||
|---|---|---|---|
| 34 35 36 37 38 39 | 69 71 67 0 2 0 | 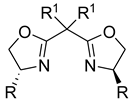 34 R1 = Et, R = Bn 35 R1 = Et, R = Ph 36 R1 = Me, R = iPr | 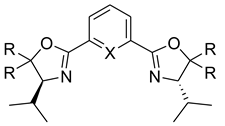 37 X = N, R = H 38 X = N, R = Ph 39 X = C, R = iPr |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavlov, V.A.; Shushenachev, Y.V.; Zlotin, S.G. Сhiral and Racemic Fields Concept for Understanding of the Homochirality Origin, Asymmetric Catalysis, Chiral Superstructure Formation from Achiral Molecules, and B-Z DNA Conformational Transition. Symmetry 2019, 11, 649. https://doi.org/10.3390/sym11050649
Pavlov VA, Shushenachev YV, Zlotin SG. Сhiral and Racemic Fields Concept for Understanding of the Homochirality Origin, Asymmetric Catalysis, Chiral Superstructure Formation from Achiral Molecules, and B-Z DNA Conformational Transition. Symmetry. 2019; 11(5):649. https://doi.org/10.3390/sym11050649
Chicago/Turabian StylePavlov, Valerii A., Yaroslav V. Shushenachev, and Sergey G. Zlotin. 2019. "Сhiral and Racemic Fields Concept for Understanding of the Homochirality Origin, Asymmetric Catalysis, Chiral Superstructure Formation from Achiral Molecules, and B-Z DNA Conformational Transition" Symmetry 11, no. 5: 649. https://doi.org/10.3390/sym11050649
APA StylePavlov, V. A., Shushenachev, Y. V., & Zlotin, S. G. (2019). Сhiral and Racemic Fields Concept for Understanding of the Homochirality Origin, Asymmetric Catalysis, Chiral Superstructure Formation from Achiral Molecules, and B-Z DNA Conformational Transition. Symmetry, 11(5), 649. https://doi.org/10.3390/sym11050649