Overview of Low-Temperature Heat Capacity Data for Zn2(C8H4O4)2.C6H12N2 and the Salam Hypothesis
Abstract
1. Introduction
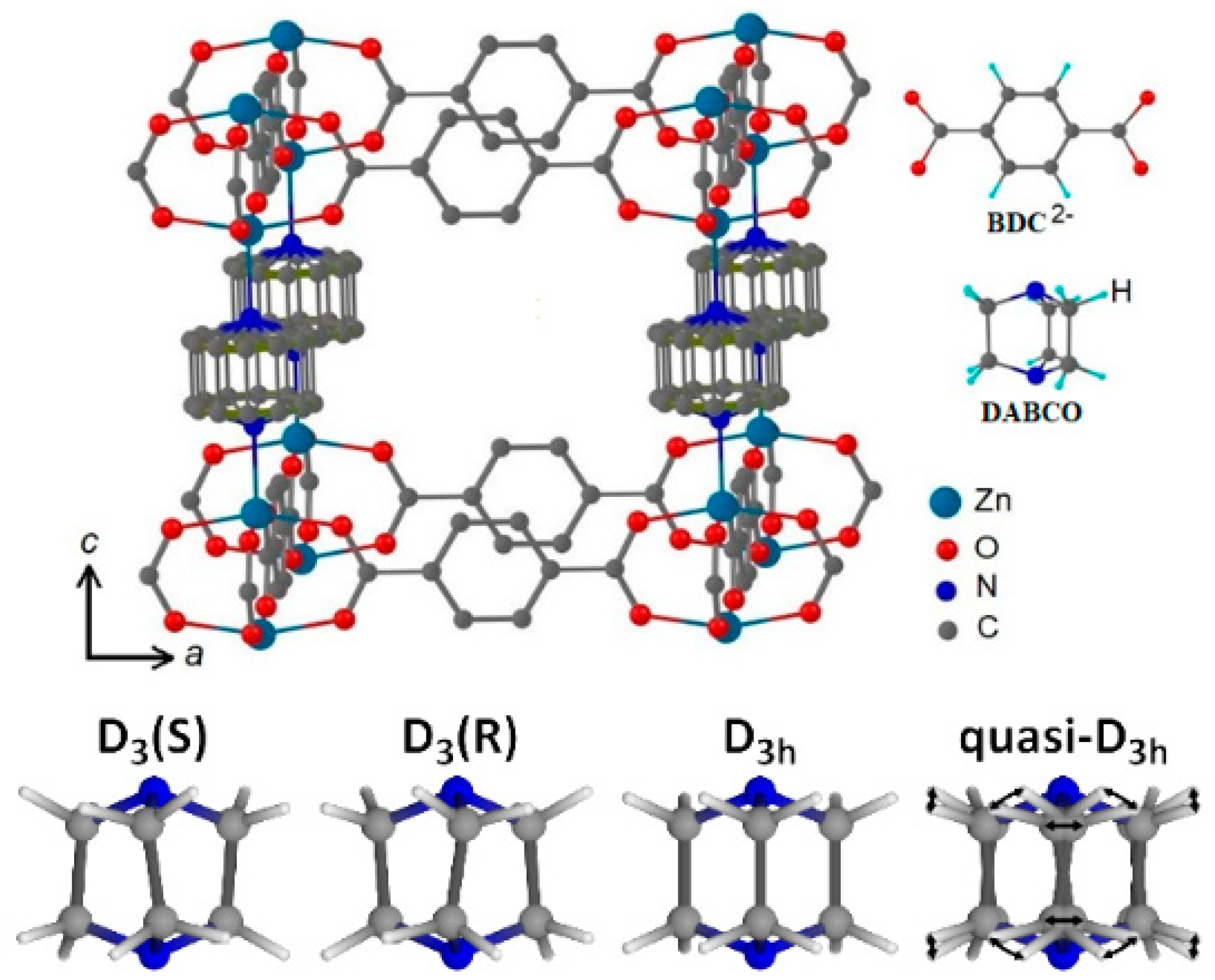
2. Structure of DABCO Molecule in Zn2(C8H4O4)2·C6H12N2
3. Mobility of DABCO Molecules in Zn2(C8H4O4)2·C6H12N2
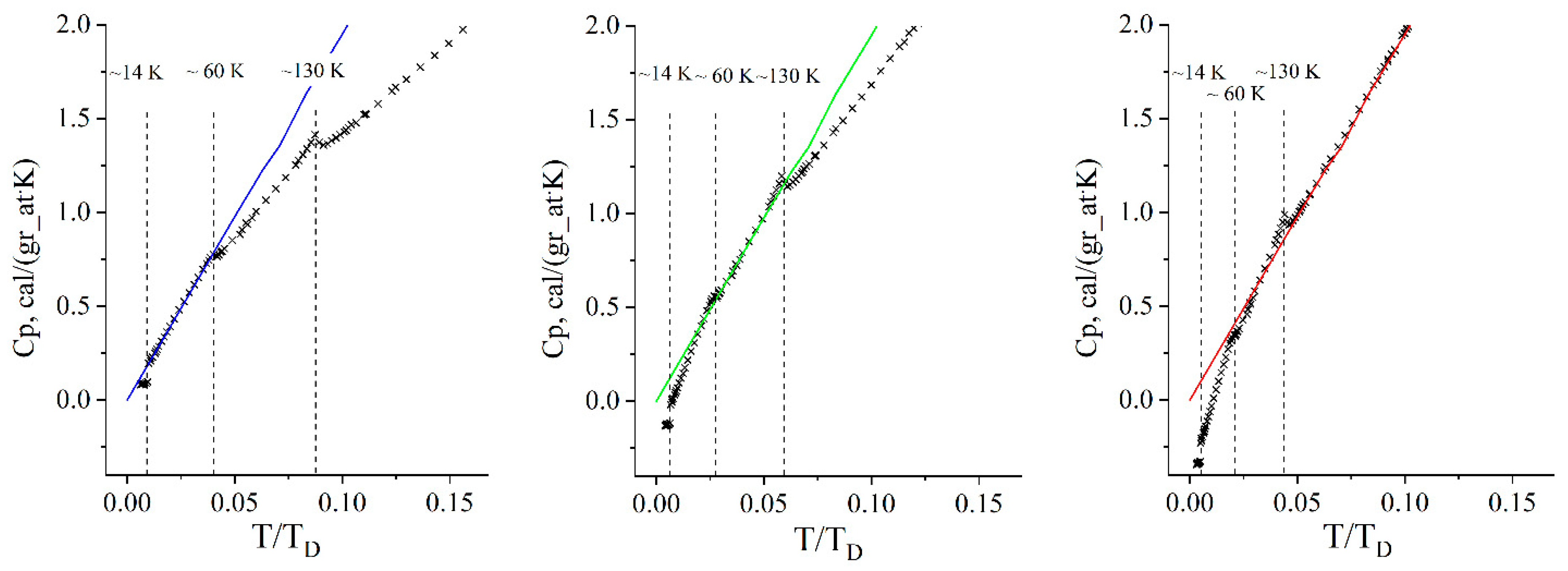
4. Low-Temperature Heat Capacity in Zn2(C8H4O4)2·C6H12N2
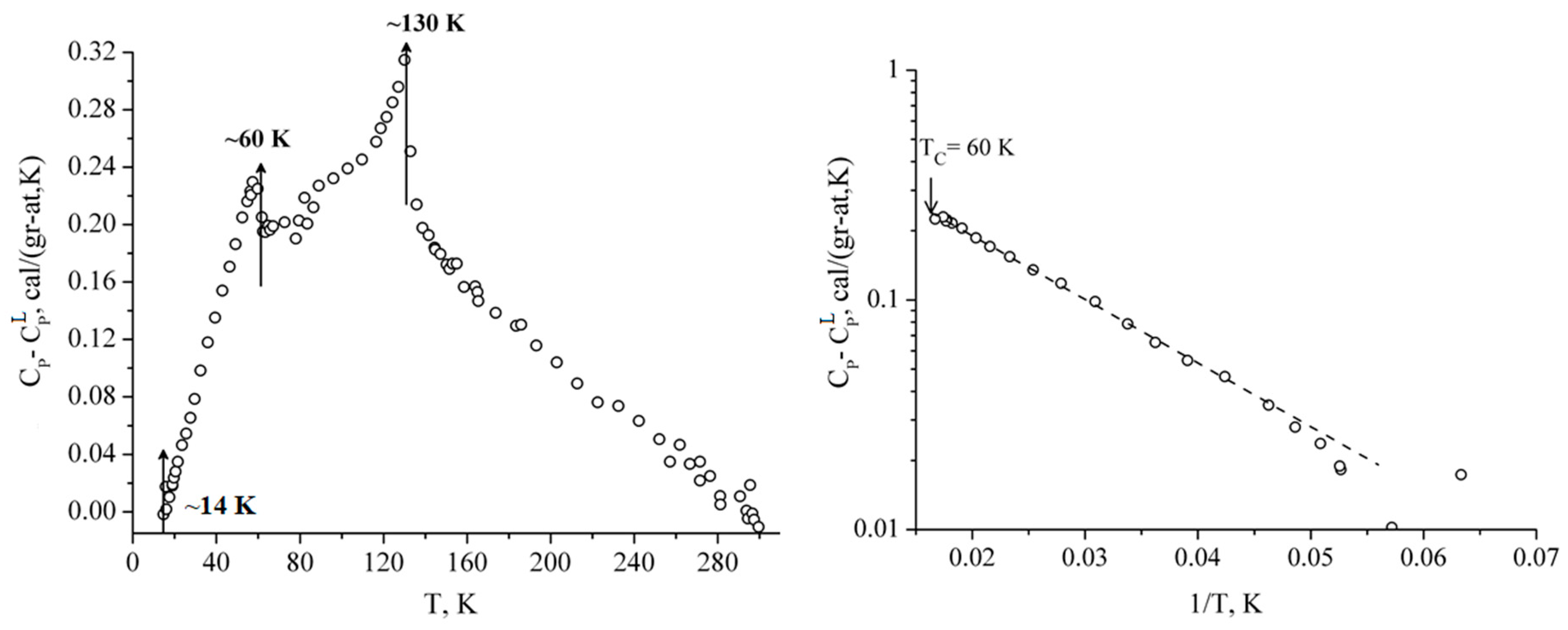
5. Heat Capacity Behavior during the Phase Transition at 60 K and the Salam Hypothesis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Salam, A. The role of chirality in the origin of life. J. Mol. Evol. 1992, 33, 105–113. [Google Scholar] [CrossRef]
- Salam, A. Chirality, phase transitions and their induction in amino acids. Phys. Lett. B 1992, 288, 153–160. [Google Scholar] [CrossRef]
- Bargueňo, P.; Perez de Tudela, R.; Miret-Artes, S.; Gonzalo, I. An alternative route to detect parity violating energy differences through Bose–Einstein condensation of chiral molecules. Phys. Chem. Chem. Phys. 2011, 13, 806–810. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, S.G.; Mirzaeva, I.V.; Ryzhikov, M.R. DABCO molecule in the M2(C8H4O4)2·C6H12N2 (M = Co, Ni, Cu, Zn) metal-organic frameworks. Coord. Chem. Rev. 2018, 376, 62–74. [Google Scholar] [CrossRef]
- Dybtsev, D.N.; Chun, H.; Kim, K. Rigid and flexible: A highly porous metal–organic framework with unusual guest-dependent dynamic behavior. Angew. Chem. Int. Ed. 2004, 43, 5033–5036. [Google Scholar] [CrossRef]
- Kozlova, S.G.; Gabuda, S.P. Thermal properties of Zn2(C8H4O4)2•C6H12N2 metal-organic framework compound and mirror symmetry violation of dabco molecules. Sci. Rep. 2017, 7, 11505. [Google Scholar] [CrossRef]
- Gabuda, S.P.; Kozlova, S.G.; Samsonenko, D.G.; Dybtsev, D.N.; Fedin, V.P. Quantum Rotations and Chiral Polarization of Qubit Prototype Molecules in a Highly Porous Metal–Organic Framework: 1H NMR T1 Study. J. Phys. Chem. C 2011, 115, 20460–20465. [Google Scholar] [CrossRef]
- Paukov, I.E.; Samsonenko, D.G.; Pishchur, D.P.; Kozlova, S.G.; Gabuda, S.P. Phase transitions and unusual behavior of heat capacity in metal organic framework compound Zn2(C8H4O4)2 N2(CH2)6. J. Solid State Chem. 2014, 220, 254–258. [Google Scholar] [CrossRef]
- Kim, Y.; Haldar, R.; Kim, H.; Koo, J.; Kim, K. The guest-dependent thermal response of the flexible MOF Zn2(BDC)2(DABCO). Dalton Trans. 2016, 45, 4187–4192. [Google Scholar] [CrossRef] [PubMed]
- Pishchur, D.P.; Kompankov, N.B.; Lysova, A.A.; Kozlova, S.G. Order-disorder phase transitions in Zn2(C8H4O4)2·C6H12N2 in atmospheres of noble gases. J. Chem. Thermodyn. 2019, 130, 147–153. [Google Scholar] [CrossRef]
- Gabuda, S.P.; Kozlova, S.G. Chirality-related interactions and a mirror symmetry violation in handed nano structures. J. Chem. Phys. 2014, 141, 044701. [Google Scholar] [CrossRef]
- Gabuda, S.P.; Kozlova, S.G. Abnormal difference between the mobilities of left- and right-twisted conformations of C6H12N2 roto-symmetrical molecules at very low temperatures. J. Chem. Phys. 2015, 142, 234302. [Google Scholar] [CrossRef]
- Sabylinskii, A.V.; Gabuda, S.P.; Kozlova, S.G.; Dybtsev, D.N.; Fedin, V.P. 1H NMR refinement of the structure of the guest sublattice and molecular dynamics in the ultrathin channels of [Zn2(C8H4O4)2(C6H12N2)]·n(H3C)2NCHO. J. Struct. Chem. 2009, 50, 421–428. [Google Scholar] [CrossRef]
- Gallyamov, M.R.; Moroz, N.K.; Kozlova, S.G. NMR line shape for a rectangular configuration of nuclei. Appl. Magn. Reson. 2011, 41, 477–482. [Google Scholar] [CrossRef]
- Khudozhitkov, A.E.; Kolokolov, D.I.; Stepanov, A.G.; Bolotov, V.A.; Dybtsev, D.N. Metal-cation-independent dynamics of phenylene ring in microporous MOFs: A 2H solid-state NMR study. J. Phys. Chem. C 2015, 119, 28038–28045. [Google Scholar] [CrossRef]
- Kozlova, S.G.; Pishchur, D.P.; Dybtsev, D.N. Phase transitions in a metal–organic coordination polymer: [Zn2(C8H4O4)2(C6H12N2)]·with guest molecules. Thermal effects and molecular mobility. Phase Trans. 2017, 90, 628–636. [Google Scholar] [CrossRef]
- Burtch, N.C.; Torres-Knoop, A.; Foo, G.S.; Leisen, J.; Sievers, C.; Ensing, B.; Dubbeldam, D.; Walton, K.S. Understanding DABCO nanorotor dynamics in isostructural metal–organic frameworks. J. Phys. Chem. Lett. 2015, 6, 812–816. [Google Scholar] [CrossRef] [PubMed]
- Lemouchi, C.; Mézière, C.; Zorina, L.; Simonov, S.; Rodríguez-Fortea, A.; Canadell, E.; Wzietek, P.; Auban-Senzier, P.; Pasquier, C.; Giamarchi, T.; et al. Design and evaluation of a crystalline hybrid of molecular conductors and molecular rotors. J. Am. Chem. Soc. 2012, 134, 7880–7891. [Google Scholar] [CrossRef]
- Lemouchi, C.; Iliopoulos, K.; Zorina, L.; Simonov, S.; Wzietek, P.; Cauchy, T.; Rodríguez-Fortea, A.; Canadell, E.; Kaleta, J.; Michl, J.; et al. Crystalline arrays of pairs of molecular rotors: Correlated motion, rotational barriers, and space-inversion symmetry breaking due to conformational mutations. J. Am. Chem. Soc. 2013, 135, 9366–9376. [Google Scholar] [CrossRef]
- Shi, X.; Luo, J.; Sun, Z.; Li, S.; Ji, C.; Li, L.; Han, L.; Zhang, S.; Yuan, D.; Hong, M. Switchable dielectric phase transition induced by ordering of twisting motion in 1,4-diazabicyclo[2.2.2]octane chlorodifluoroacetate. Cryst. Growth Des. 2013, 13, 2081–2086. [Google Scholar] [CrossRef]
- Yao, Z.-S.; Yamamoto, K.; Cai, H.-L.; Takahashi, K.; Sato, O. Above room temperature organic ferroelectrics: Diprotonated 1,4-diazabicyclo[2.2.2] octane shifts between two 2-chlorobenzoates. J. Am. Chem. Soc. 2016, 138, 12005–12008. [Google Scholar] [CrossRef]
- Chen, L.-Z.; Huang, D.-D.; Ge, J.-Z.; Pan, Q.-J. Reversible ferroelastic phase transition of N-chloromethyl-1,4-diazabicyclo[2.2.2]octonium trichlorobromoaquo copper(II). Inorg. Chem. Commun. 2014, 45, 5–9. [Google Scholar] [CrossRef]
- Nizovtsev, A.S.; Ryzhikov, M.R.; Kozlova, S.G. Structural flexibility of DABCO. Ab initio and DFT benchmark study. Chem. Phys. Lett. 2017, 667, 87–90. [Google Scholar] [CrossRef]
- Mathivon, K.; Linguerri, R.; Hochlaf, M. Systematic theoretical studies of the interaction of 1,4-diazabicyclo [2.2.2]octane (DABCO) with rare gases. J. Chem. Phys. 2013, 139, 164306. [Google Scholar]
- Tarasov, V.V. Heat Capacity of Anisotropic Solids. Zhurnal Fiz. Khimii 1950, 24, 111–128. (In Russian) [Google Scholar]
- Wunderlich, B.; Baur, H. Heat Capacities of Liner High Polymers; Springer: Berlin, Germany, 1970. [Google Scholar]
- Stockmayer, W.H.; Hecht, C.E. Heat capacity of chain polymeric crystals. J. Chem. Phys. 1953, 21, 1954–1958. [Google Scholar] [CrossRef]
- Tan, K.; Nijem, N.; Canepa, P.; Gong, Q.; Li, J.; Thonhauser, T.; Chabal, Y.J. Stability and hydrolyzation of metal organic frameworks with paddle-wheel SBUs upon hydration. Chem. Mater. 2012, 24, 3153–3167. [Google Scholar] [CrossRef]
- Mirzaeva, I.V.; Kozlova, S.G. Computational estimation of parity violation effects in a metal-organic framework containing DABCO. Chem. Phys. Lett. 2017, 687, 110–115. [Google Scholar] [CrossRef]
- Mirzaeva, I.V.; Kozlova, S.G. Parity violating energy difference for mirror conformers of DABCO linker between two M2+ cations (M = Zn, Cd, Hg). J. Chem. Phys. 2018, 149, 214302. [Google Scholar] [CrossRef] [PubMed]
- Kozlova, S.G. Behavior of the heat capacity at second-order phase transitions in the [Zn2(C8H4O4)2·C6H12N2] metal-organic framework compound. JETP Lett. 2016, 104, 253–256. [Google Scholar] [CrossRef]
- Sullivan, R.; Pyda, M.; Pak, J.; Wunderlich, B.; Thompson, J.R.; Pagni, R.; Pan, H.J.; Barnes, C.; Schwerdtfeger, P.; Compton, R. Search for electroweak interactions in amino acid crystals. II. The Salam hypothesis. J. Phys. Chem. A 2003, 107, 6674–6680. [Google Scholar] [CrossRef]
- Tanaka, Y.; Kojima, T.; Takata, Y.; Chainani, A.; Lovesey, S.W.; Knight, K.S.; Takeuchi, T.; Oura, M.; Senba, Y.; Ohashi, H.; et al. Determination of structural chirality of berlinite and quartz using resonant x-ray diffraction with circularly polarized x-rays. Phys. Rev. B 2010, 81, 144104. [Google Scholar] [CrossRef]

| P | ~14 K | ~60 K | ~130 K |
|---|---|---|---|
| 0.51 | 6.0 ± 0.4 | 8.0 ± 0.2 | 23.0 ± 0.3 |
| 1.52 | 5.0 ± 0.4 | 11.0 ± 0.2 | 23.0 ± 0.3 |
| Tc | ~14 | ~60 | ~130 |
|---|---|---|---|
| P | ΔS/R | ΔS/R | ΔS/R |
| 0.51 | 0.42 ± 0.05 | 0.14 ± 0.02 | 0.30 ± 0.04 |
| 1.52 | 0.28 ± 0.04 | 0.23 ± 0.02 | 0.30 ± 0.04 |
| Region of Fit, K | 299.6–141.6 | 130.1–72.6 | 57.4–14.7 |
|---|---|---|---|
| νm, cm−1 | 1250 | 765 | 285 |
| N | ~38.5 | ~28.9 | ~12.0 |
| 1 | ~0.75 | ~0.31 | |
| 1 | ~0.67 | ~0.33 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozlova, S.; Ryzhikov, M.; Pishchur, D.; Mirzaeva, I. Overview of Low-Temperature Heat Capacity Data for Zn2(C8H4O4)2.C6H12N2 and the Salam Hypothesis. Symmetry 2019, 11, 657. https://doi.org/10.3390/sym11050657
Kozlova S, Ryzhikov M, Pishchur D, Mirzaeva I. Overview of Low-Temperature Heat Capacity Data for Zn2(C8H4O4)2.C6H12N2 and the Salam Hypothesis. Symmetry. 2019; 11(5):657. https://doi.org/10.3390/sym11050657
Chicago/Turabian StyleKozlova, Svetlana, Maxim Ryzhikov, Denis Pishchur, and Irina Mirzaeva. 2019. "Overview of Low-Temperature Heat Capacity Data for Zn2(C8H4O4)2.C6H12N2 and the Salam Hypothesis" Symmetry 11, no. 5: 657. https://doi.org/10.3390/sym11050657
APA StyleKozlova, S., Ryzhikov, M., Pishchur, D., & Mirzaeva, I. (2019). Overview of Low-Temperature Heat Capacity Data for Zn2(C8H4O4)2.C6H12N2 and the Salam Hypothesis. Symmetry, 11(5), 657. https://doi.org/10.3390/sym11050657





