1. Introduction
Frequency hopping communication is a kind of spread spectrum communication, which is the main communication mode in the field of military communication, and has been widely used in military communication and civil communication [
1]. Frequency hopping communication is widely used in the field of aerospace communication, such as Link16, and military satellites etc., because of its good confidentiality, strong anti-jamming ability, strong networking ability, anti-frequency selective fading, low requirements for channel phase frequency distortion characteristics, and easy compatibility with traditional communication systems [
2,
3]. Since frequency hopping communication has been used in the military, deployed for the purposes of interference and anti-interference, anti-sabotage and destruction has not stopped. In the actual communication, especially in short-wave band, the electromagnetic environment is very complex. Dense fixed-frequency signals, noise signals, external interference signals and various burst signals interweave with each other, which makes the detection of frequency-hopping signals very difficult, and also poses a severe challenge to communication investigation.
Frequency communication is the abbreviation of frequency hopping extended spectrum communication system, and the frequency hopping signal has a time-varying and pseudo-random carrier frequency [
4]. It uses a binary pseudo-random code sequence to control the frequency of the output signal of the RF carrier oscillator, so that the carrier frequency of the transmitting signal jumps with the change of the pseudo-random code. Frequency hopping signal parameter recognition is of great significance; through it, the information of the enemy can be obtained by the military, so as to gain the first chance in warfare, and to design our own frequency hopping radio to prevent many kinds of interference and tracking by the enemies. Frequency hopping parameter identification also provides an important basis for signal demodulation and information acquisition. The frequency hopping parameters mainly include the frequency hopping rate, the frequent set and the frequency hopping width [
5]. The frequency hopping sequence and frequency hopping DOA for frequency hopping radio sorting, in which the frequency hopping rate refers to the number of frequencies per second change, now frequency hopping communication is generally changed thousands of times per second. Frequency hopping refers to the frequency hopping set used in the frequency hopping communication system. Hopping bandwidth is the difference between the maximum and minimum frequency hopping. By estimating these parameters, the identification of frequency hopping signal and the sorting of frequency hopping radio can be completed, which lays a good foundation for the sorting of the frequency hopping signal in a communication reconnaissance system.
In addition to these signal physical parameters, signal wave direction (DOA) is also a very key parameter in frequency hopping communication reconnaissance, which plays an important supporting role in the task of sorting and signal recognition of FH network [
6,
7]. Because the carrier frequency of the hopping signal is not fixed, it changes randomly with time, so the DOA estimation method of a narrowband signal can’t be used directly for frequency hopping signal, which also brings some difficulties to the DOA estimation of frequency hopping signal. The frequency hopping signal is an instantaneous narrowband and macroscopic wideband signal.
At present, most of the detection and processing of frequency hopping signals focus on signal detection and parameter estimation in a time-frequency domain, but there are a few researches on the spatial information of frequency hopping signals. The mainstream method of time-frequency domain parameter estimation for frequency hopping signal is the time-frequency analysis method, as well as the compression perception and sparse Bayesian learning methods developed in recent years. The time-Frequency analysis method has a good processing ability for time-varying signals, which can’t be replaced by other methods, and the common time-frequency analysis is mainly divided into linear time-frequency analysis and quadratic time-frequency analysis. Linear time-frequency analysis mainly has a short-time Fourier transform [
8], Gabor transformation and wavelet transform.Among them, discrete wavelet transform (DWT) is the most effective time-frequency analysis tool. The 1D and 2D DWT introduced in the literature [
9] are often used for digital signal processing. Bilinear time-frequency representations include spectral graphs, Wigner-Wille distribution (WVD), pseudo-Wigner distribution (PWVD), smooth pseudo-Wigner distribution (SPWVD) [
10,
11,
12], Margenau-Hill and so on. Chaos, entropy and fractals have drawn the interest of many researchers due to their mathematical modeling ability to solve a wide variety of real problems [
13], and we can also use entropy theory and fractals for time-varying signal processing. Linear time-frequency transformation is easy to be affected by time-frequency resolution, and bilinear frequency distribution has a good time-frequency focus, but for multi-component signal, there is a serious time-frequency crossover [
14,
15,
16], generating false signals. Because the received frequency hopping signal contains multiple components, it can’t be directly applied to the frequency hopping signal parameter identification. The spatial information of a frequency hopping signal, such as the direction of the wave, plays an important role in the sorting, signal tracking and interference of the network platform. The concept of space-time-frequency was first proposed in the literature [
17,
18], and the space-time frequency processing method was applied to blind source signal separation and DOA estimation, which achieved better performance than the traditional method. The paper [
19,
20,
21] uses the space-time frequency method to carry on the direction finding and the signal separation to some non-stationary signals (such as linear FM, sound signal), but does not use the space time frequency to measure the frequency hopping signal direction. Multi-signal separation correlation research [
2,
22,
23] has combined space-time frequency analysis with other algorithms including MUSIC, influence function, etc., used in DOA recognition, to achieve good results, but these algorithms are only applicable to narrowband signals, and not suitable for frequency hopping signals such as broadband signal, because of its terrible effect.
This article is mainly divided into five parts. The first part is the introduction of frequency hopping signal parameter estimation and is mainly concerned about frequency hopping signal jump frequent set rate, frequency hopping period, frequency hopping sequence, etc. Frequency hopping radio separation frequency hopping signal DOA is included too. The second part is the system model and frequency hopping parameters. Herein is introduced the frequency hopping signal model and linear array receiving model, and the construction of the space-time frequency matrix of each hop. The third part is parameter estimation of frequency hopping signal. It mainly introduces joint diagonalization algorithm of space-time-frequency matrix and root-MUSIC algorithm of frequency hopping DOA estimation to realize parameter estimation of multi-frequency hopping signal. In the fourth part, simulation experiments are designed to verify the effectiveness of the proposed algorithm. The last step is a summary of the proposed algorithm.
2. System Model and Frequency Hopping Parameters
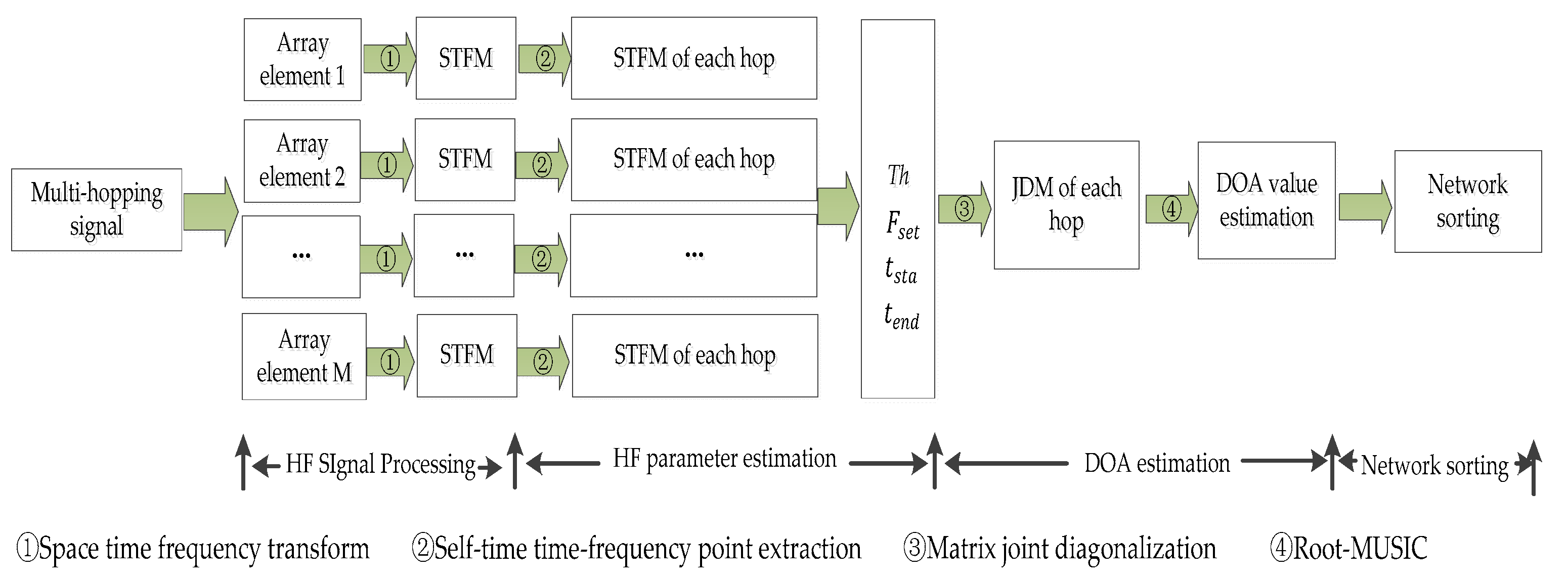
In this section, we mainly introduce the multi-component frequency hopping signal model, and the description of the signal acceptance by the linear array. We combined the time-frequency distribution to describe the space-time-frequency distribution transformation process. In this paper, a linear array is used to receive the frequency hopping signal, and then the time domain signals received by each array element are processed to complete the parameter estimation of the multi-hopping frequency signal and the sorting task of the frequency hopping radio station. The parameter estimation process in the paper is shown in
Figure 1.
Firstly, the hybrid multi-frequency hopping signals received by each array element are subjected to space-time-frequency conversion to obtain a space-time-frequency matrix (STFM) containing all signal space-time-frequency information, and denoising processing is performed on the space-time-frequency domain. The algorithm of finding the island is used to estimate the number of hops and extract the time-frequency points of each hop. The STFM of each hop is constructed and the frequency hopping period (Th), frequency hopping frequency set (), start time () and deadline () of each hop are completed. Joint diagonalization the STFM of the same hop received by different array elements to obtain a joint diagonalization matrix (JDM), using this JDM to complete the DOA estimation of the frequency hopping signal, and using the DOA value to complete the frequency hopping radio sorting.
2.1. Frequency Hopping Signal Model
With the change of pseudo-random code, the frequency of hopping signal changes randomly, and the pseudo-random code sequence is used to control the carrier frequency sequence. The frequency hopping signal model in this paper as follows, assuming that there are
frequency hopping signals entering the receiver during the observation time
, and the central frequency of the receiving machine is
, with the bandwidth
. Assuming the period of the nth frequency hopping signal
be
, there are K hops in the observation time
, and the carrier frequency and initial phase of the kth hop are
and
, then the expression of
as shown in Formula (1).
which
,
is the baseband envelope of the signal
, and
rect represents a unit rectangular pulse.
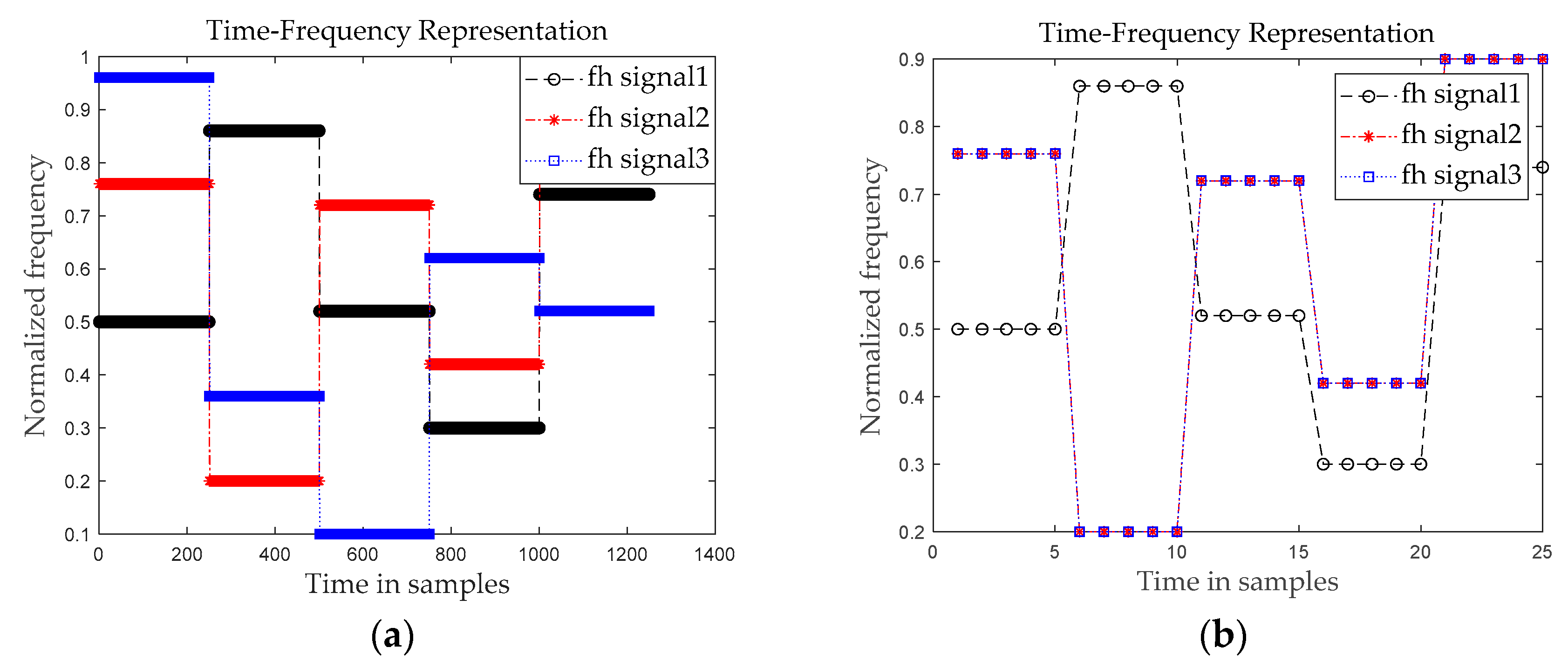
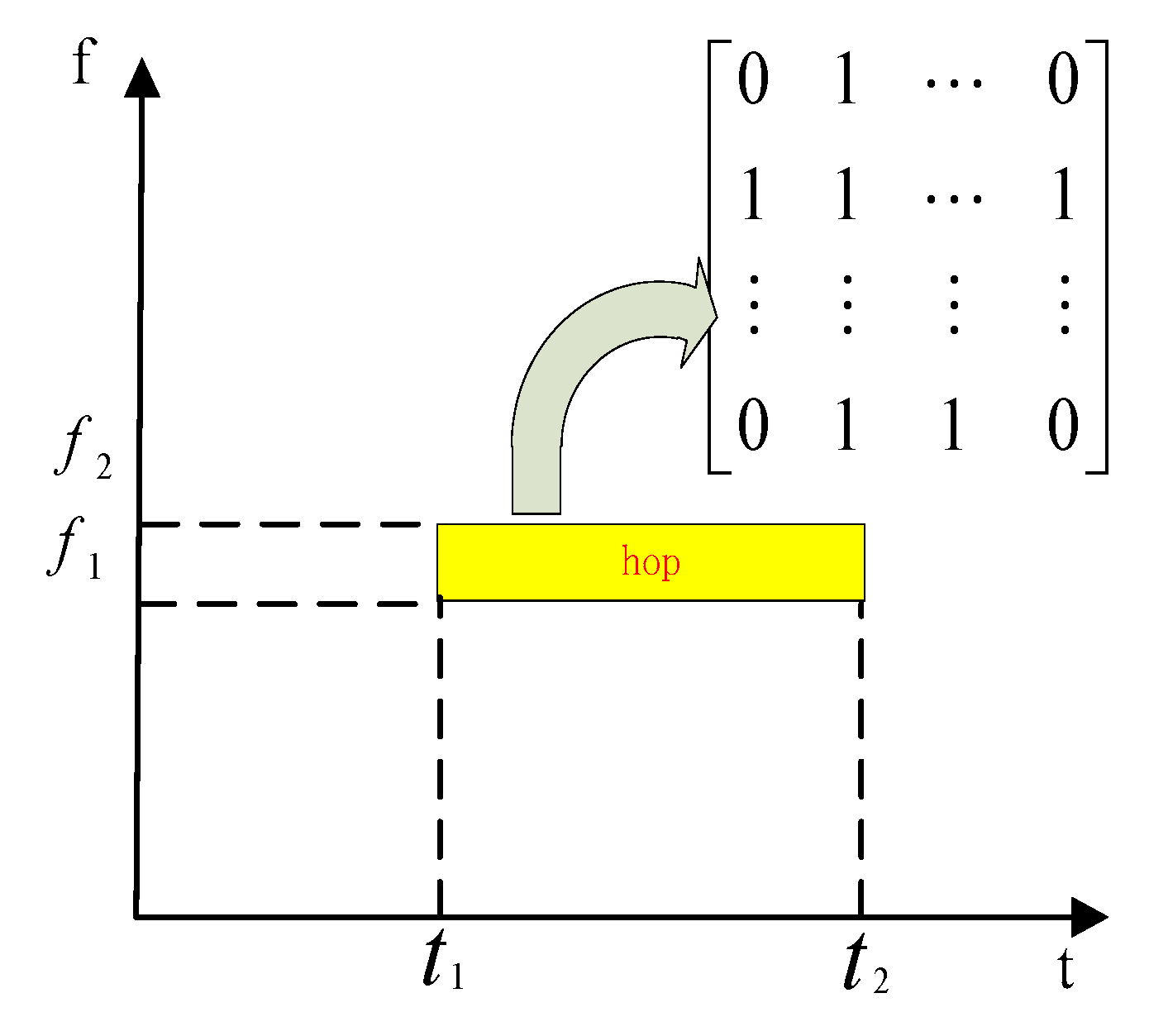
Actually, sampling frequency hopping signal is about
, then sampling frequency obtained in this paper
, and Frequency hopping frequency in this paper is approximately
. The time-frequency diagram of the frequency hopping signal is shown in
Figure 2. In order to normalize the frequency, the normalization formula
is adopted, which is
. In this paper, the frequency hopping sequence is expressed as the Formula (2).
in the upper formula,
represents the number of frequency hopping signals and
k represents the
kth hop of the
nth signal.
2.2. Space-Time Frequency Distribution of Frequency Hopping Signal
The frequency of frequency hopping signal varies nonlinearly with time, which is a temporal signal and belongs to a typical non-stationary signal. The time-Frequency analysis method is the most common and effective method for analyzing time-varying signals. For example, the literature [
22] uses time-frequency analysis and wavelet transform for medical time-varying signal processing, and achieved good results. Commonly used short-time Fourier transformations can be expressed as Formula (3).
Commonly used QTFD can be expressed as Formula (4).
which
is the time delay kernel function. The QTFD possesses desirable properties such as local energy concentration IF, first moment visualization and reduced interference.
In this paper, a linear uniform array is used to receive the frequency hopping signal. Assuming that the array has an M array element, and the first array is located at the origin, and the spacing of each array is
, and
is the azimuth of each signal. The source is located in the far field, and the array noise is additive Gauss white noise. There is no correlation between the array elements, and the signal is not correlated with the noise. Thus, the array direction vector is expressed as Formula (5).
among them,
,
for signal carrier frequency. The time-domain signal received by the array is represented as Formula (6).
which
,
,
, M represents the number of array elements, and N representing the number of frequency hopping signals.
Through (5) Formula, we can see that the array direction vector and manifold matrix are related to the carrier frequency and jump with the frequency hopping of the carrier, when the carrier frequency changes, corresponding to the array direction of the vector changes also occur. Frequency hopping communication carrier frequency has been changed; it can’t be fixed directly to the fixed-frequency signal processing method applied to the frequency hopping communication. We know that the frequency of FH communication is fixed in a hop duration, that is, the direction vector of the array is unchanged during this hop duration, and it can be used as narrowband signal processing. Based on this, the frequency hopping signal can be decomposed into one hop, so that the analysis object can be simplified to a narrowband model.
Frequency hopping signals received by antenna arrays contain abundant spatial information in the direction matrix. The space-time-frequency analysis used in this paper is to extend the research object of traditional space-time processing to time-frequency domain, that is, to analyze the signal in time-frequency domain first, then to select effective time-frequency points in time-frequency domain, and to use these time-frequency data to form space-time-frequency matrix. The benefits of STFD over the spatial correlation matrix in a nonstationary signal environment is the direct exploitation of the information [
24,
25]. We first review the definition and basic properties of the STFDs. STFDs based on Cohen’s class of TFD were introduced in [
17], and its applications to direction finding and blind source separation have been discussed in [
25,
26,
27].
The discrete form of the smoothed pseudo Wegener Ville distribution can be expressed as Formula (7).
where * indicates complex conjugate, the space-time-frequency distribution is to process the snapshot vectors
received by the array. The space-time-frequency distribution matrix is defined as Formula (8).
to bring (6) into Formula (8).
the noise is zero mean Gaussian white noise and is not related to the signal. To expect (9) form, then
, Then Formula (9) is as Formula (10).
2.3. Frequency Hopping Hop Extraction and Space Time Frequency Matrix Construction
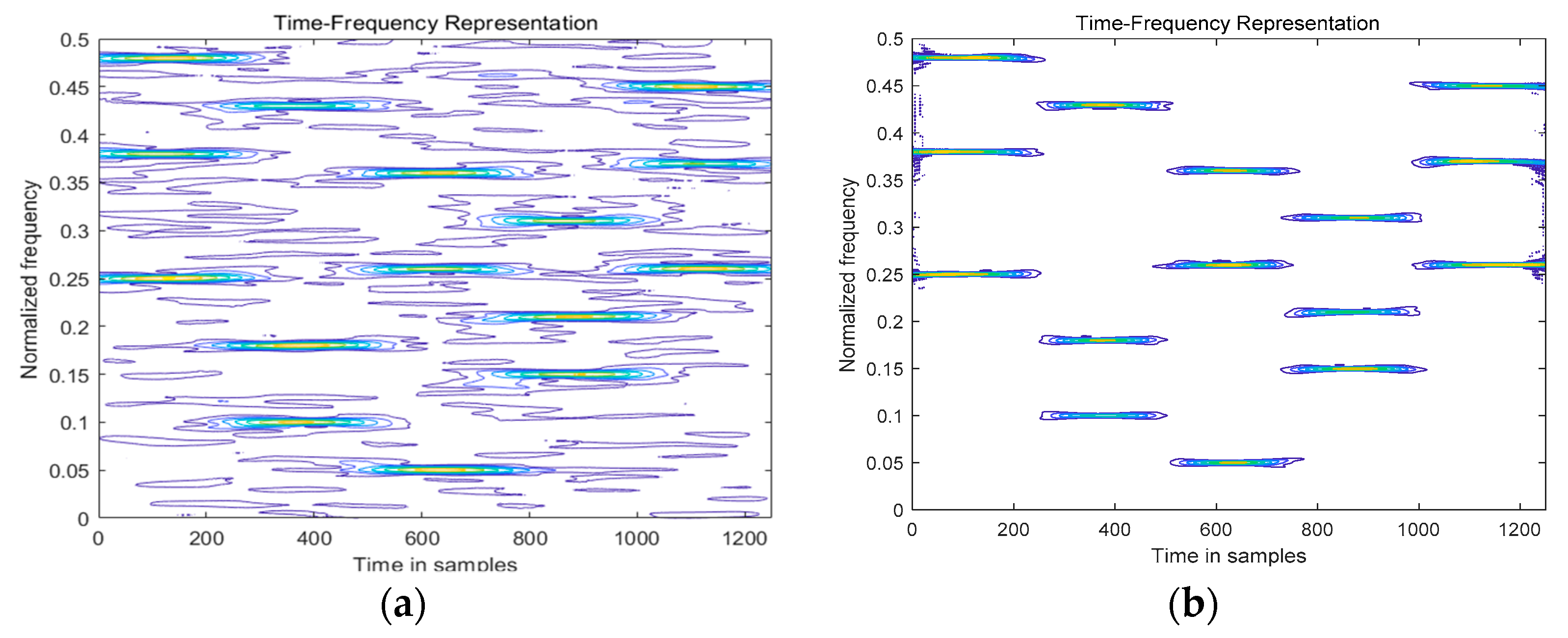
On the basis of the space-time frequency distribution graph obtained in the previous section, this section mainly completes the time-frequency point extraction and the space-time frequency matrix construction of each hop. Since the space-time frequency values are plural, it is not convenient to find the self-item frequency point of each hop directly on the space-time frequency distribution map, so this paper first converts all values to 0 and 1 by threshold, and then finds a position on the space time-frequency distribution that contains only 0, 1, and the value corresponding to the position of 1 is the value of the time-frequency point.
(a) Construct 0, 1 space-time frequency distribution matrix.
Step1: The array receiving signal is made of linear space-time frequency transformation and bilinear space-time frequency transformation to obtain
and
as shown in
Figure 3 and
Figure 4, which do point multiplication, and the space-time frequency combination Matrix
is obtained,
, and the “
” is Hadamard product.
Step2: The
is truncated to get the self-time frequency graph
as Formula (11).
which
is Cut-off threshold and
, the
is threshold factor. Through the above operation, a matrix
containing only 0 and 1 elements is obtained.
(b) Self time and frequency point extraction.
Each hop is extracted on the space-time frequency graph, and its corresponding time-frequency value is formed to form the space-time frequency matrix of each hop. In this paper, we use the method of finding “islands” to traverse the
obtained by Formula (11) and find out the number
N of all “islands” in the space-time-frequency matrix. As shown in the
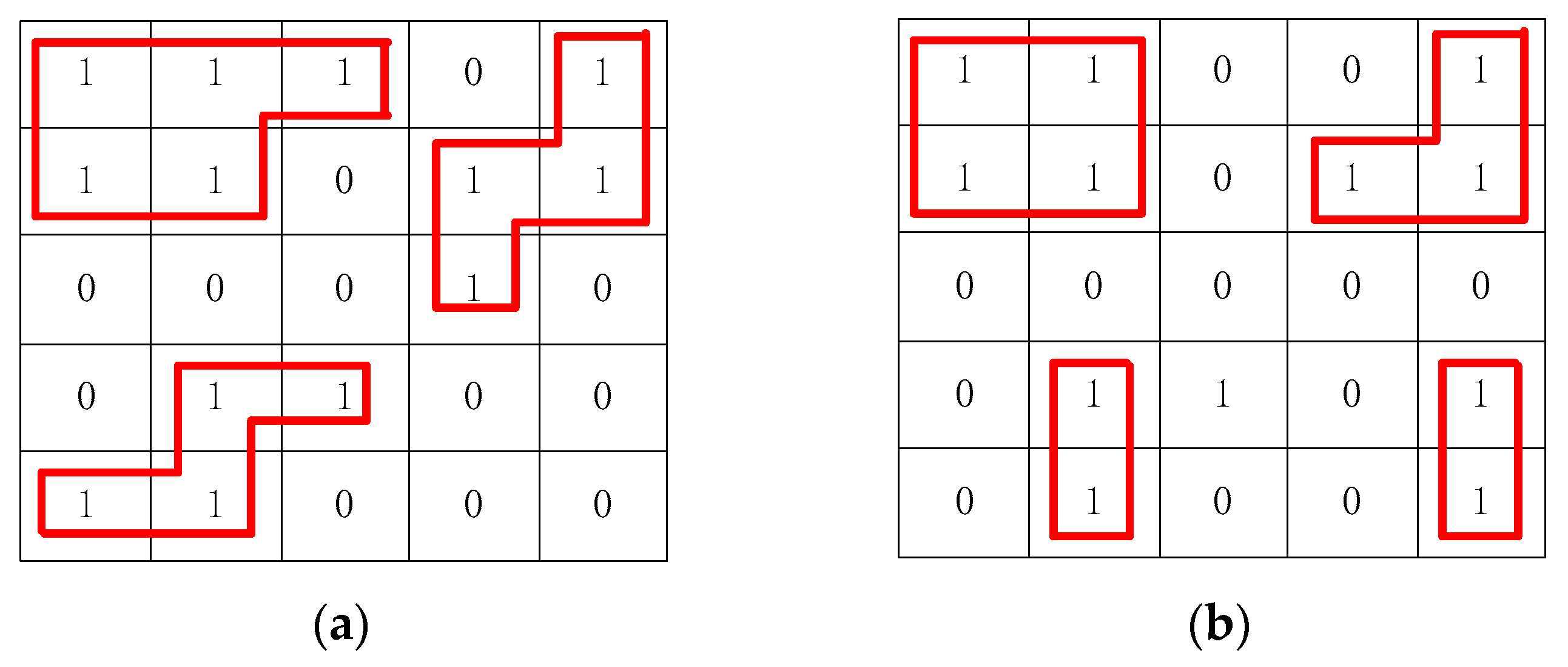
Figure 5, in a matrix, surrounded by red rectangular frames is called “islands”, and the number of islands is the number of hops. The observation found that there are three islands in the
Figure 5, a total of four islands in the right image, that is, three hops on the left and four hops on the right.
Each of these “island” corresponds to a hop in the frequency hopping signal, only need to find the islands in the matrix, you can extract the time frequency point of each hop from the space-time frequency matrix, these self-entry time frequency points to form the hop’s space-time frequency matrix. The matrix obtained by the Formula (11) is “C” that contains only two elements of 0,1 and traverses the matrix. The interconnected element 1 is called an island, and find all the islands in the matrix. The total number of islands is recorded
, and the coordinates of the element 1 in each island are recorded. If the Element 1 in the island
is taken as the location of the element. The coordinates of the hop self-term time point can be expressed as Formula (12).
Finding 1 of each island in Matrix C, recording its position in the form of an island. According to this method, the location of 1 in all islands is found, and the time-frequency points of self-term are extracted.
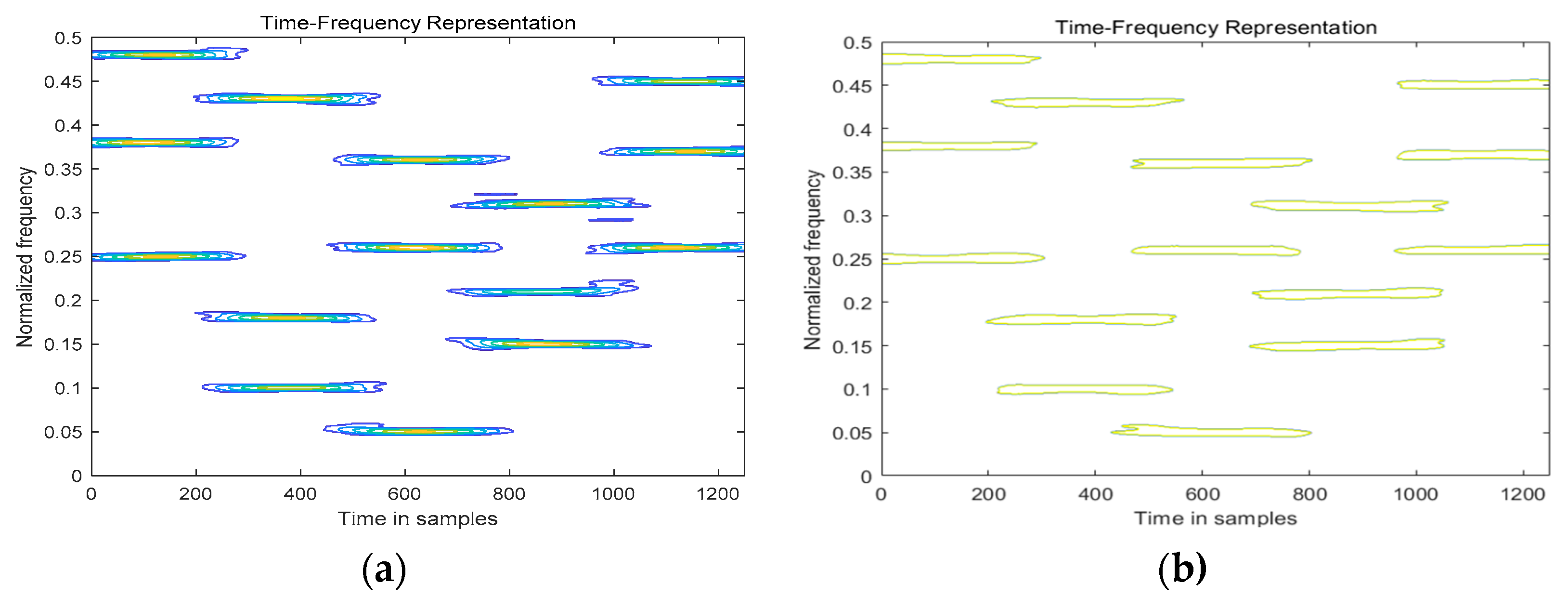
The space-time frequency matrix obtained after the (11) transformation is recorded as , according to the coordinate value of each island obtained by Formula (12), the corresponding position is found in Matrix , the space-time frequency value of the corresponding position is taken out, and the space time frequency value in the same block is recorded as Y according to the principle that the corresponding position remains unchanged. Each space-time frequency matrix corresponds to a hop, then all hops corresponding to the space-time frequency matrix are recorded as .
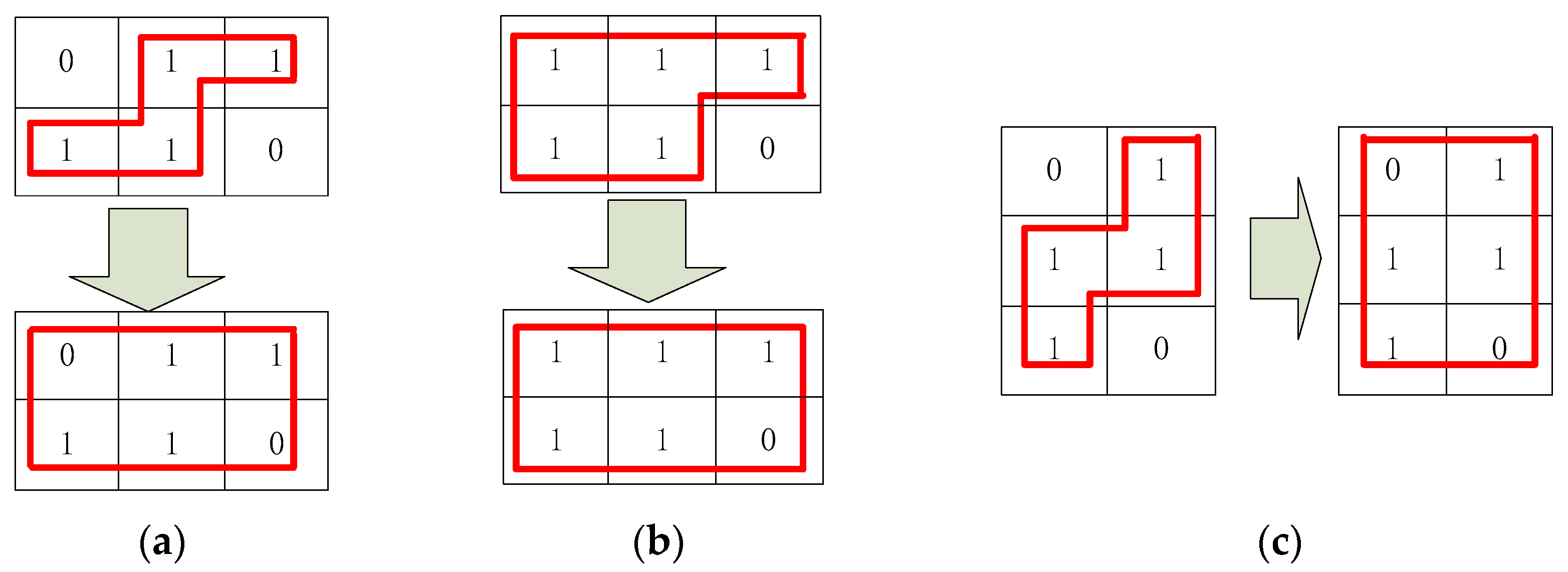
The position composition of the self-term time-frequency points extracted from each island may not be a rectangular shape. At this time, it needs to be adjusted accordingly. Without destroying the whole structure, the corresponding position is complemented by 0, so that each hop constitutes a matrix. There are three hops in the left graph of the
Figure 4. They are hop1, hop2 and hop3 from left to right and from top to bottom. By doing the following transformation, the space-time-frequency values of all hops can be changed into the space-time-frequency matrix shown in the
Figure 6.
3. Frequency Hopping Signal Parameter Estimation
This part is mainly based on the space-time frequency matrix of each hop extracted in the second part to estimate the frequency hopping parameters. The first section is the basic parameter estimation of the frequency hopping signal, including the frequency hopping frequency sets, hopping period, jump time, etc. the second section of the frequency hopping signal DOA estimation. Firstly, the matrix joint diagonalization algorithm based on the minimum mean square error is used to diagonalize the space-time-frequency matrix of the same hop received by different array elements, and a joint diagonalization matrix is obtained. Then the root-MUSIC algorithm is used to complete the DOA estimation of each hop. Finally, the DOA values of all hop estimates are clustering according to the clustering algorithm.
3.1. Hopping Basic Parameter Estimation
This section mainly estimates the parameters based on the coordinates of the elements in the space-time frequency matrix of each hop obtained in the original space-time frequency matrix, where it is assumed that the sampling frequency of the signal is known, and when the scale value of each hop self-entry frequency point along the timeline and frequency axis on the space-time frequency graph is found. The scale values of each hop on the space-time frequency axis can be obtained by averaging the parameters corresponding to the same hop in different arrays.
The time
t in
Figure 7 is replaced by a number of points. For this hop,
Th can expressed as Formula (13).
where
denotes the nth signal, m denotes the
m-th element, and
K denotes the kth hop of the frequency hopping signal, and the start time of the frequency hopping signal
, and the cutoff time for the hop is
, and The carrier frequency of the hop can be expressed as Formula (14).
Then the carrier frequency of the
k-th hop of the
n-th FH signal can be expressed as
, The starting time of the K hop of the nth frequency hopping signal is expressed as
. The deadline is expressed as
, The frequency hopping period
of the
nth frequency hopping signal is expressed as Formula (15).
The jump frequency rate is expressed as .
3.2. Joint Diagonalization of Space-Time-Frequency Matrix Based on Minimum Mean Square Error
Matrix joint diagonalization was first proposed mainly for signal blind separation (BSS) and independent component analysis (ICA) [
28]. Joint diagonalization is mainly to find a diagonal matrix to replace a matrix set, which contains many sub-matrices. Mathematical formulas can be expressed as: Assuming that set
contains
matrix
, joint diagonalization is to find a diagonal matrix
and
related diagonal matrix
to make
achieve the minimum value as Formula (16).
Considering that the multiple hops of the same frequency hopping signal received by each array element, many space-time frequency matrices are obtained, and the information of each space-time frequency matrix cannot be synthesized separately. In this paper, the joint diagonalization algorithm based on the minimum mean square error is used to estimate the parameter of frequency hopping signal. If there are M elements
in an array, and the received signal of
element is expressed as
after space-time-frequency transformation, then the received signal of
element is expressed as
, where
is the
k-th hop space-time-frequency matrix of the frequency hopping signal received by the first element of
K. If the same hop received by different elements is recorded as a set of
,
expressed as Formula (17).
Then is , so that the space-time-frequency matrix of the same hop received by different elements can be formed into a set. Then a diagonal matrix is found according to the principle of minimum mean square error, and the set of hop space-time-frequency matrices is represented by the diagonal matrix . In order to find the diagonal matrix , making the Formula (16) the smallest, it is mainly divided into the following two steps:
Step1: Change the diagonal matrix
and take the target matrix
as the variable. First initialize a diagonal matrix
of the same size as the
, assuming that the size of
is
, then
is represented as a column
, and (16) the formula can be expressed as Formula (18).
where
is the element at the coordinate position (
n,
n) of the diagonal matrix
,
representing conjugate transposition, recorded as
, then Formula (18) can be expressed as Formula (19).
where
denotes the trace of matrix, we can find that
is a constant value and the value of
is independent of
. If
is expressed as
, where
b is a real number greater than 0,
is a unit normal vector and
, the expression can be expressed as Formula (20).
where
is a constant and
is a square matrix of
size, the Formula (20) is equal to zero. If we derive
b, we can get b = 0 or
and replace it with Formula (20), because
, then
we can know that when
is the eigenvector corresponding to the largest eigenvalue of
, the above Formula (21) achieves the minimum.
Step2: With diagonal matrix
as
a variable, the corresponding
is updated when the minimum value of Formula (18) is obtained. Formula (18) is decomposed into
independent linear minimization problems as Formula (22).
Here we do the following transformation: making the parameter vector is
, and the
columns are stitched together
(
is a column mosaic function), then the formula can be reduced to a linear minimization problem as Formula (23).
where
H is defined as
, L is
the unit vector, then the linear minimization problem is transformed into the Formula (24).
Through the above operation, the Formula (16) obtains the minimum value, then replacing the original with and alternating the operation between the two Steps (1) and (2), when the minimum mean square error satisfies a certain threshold condition, and the matrix at this time is the space-time frequency combined diagonalization matrix of the asked hop.
3.3. FH Signal DOA Estimation
This section is based on each hop joint diagonalization matrix obtained in the previous section, using the spatial information it contains to complete the wave direction (DOA) estimation of each hop. Because the expansion subspace by the signal feature vector is consistent with the expansion subspace by the array guide vector, and according to the orthogonality of the signal subspace and the noise subspace, the MUSIC algorithm can be used for DOA estimation of the joint diagonalization matrix. Because the MUSIC algorithm needs spectral peak search, the complexity is high. In this paper the root-MUSIC algorithm, which does not need spectral peak search, is used to estimate the DOA of the hop, and the root MUSIC algorithm is a polynomial root finding form of the MUSIC algorithm. The time-frequency MUSIC space spectrum of the signal can be obtained by replacing the covariance matrix in the traditional algorithm with the modified space-time frequency matrix. Thus, the DOA estimation of the signal is obtained. Define a polynomial as Formula (25).
where
is the
lth eigenvector of matrix R, and in order to extract information from all noise eigenvectors at the same time, we hope to find the zero point of MUSIC. Because the former is also a polynomial of
z, there exists a power term of
. Because only interested in the
z value on the unit circle and replaced
by
, the polynomial of root MUSIC is obtained as Formula (26).
where
is the
quadratic polynomial, when its root and unit circle are mirrored, the phase of the
K roots
with the maximum amplitude in the unit circle is given to estimate the direction of the wave,
can be expressed as Formula (27).
the DOA estimate obtained by each hop is expressed as
.
3.4. Frequency Hopping Network Table Sorting
In this subsection, on the basis of the DOA estimation of each hop obtained in the previous section, the K-means clustering algorithm is used to identify the number of frequency hopping signals and sort the frequency hopping radio. The paper’s main research focus is synchronous networking radio, which changes the carrier frequency at the same time with each station in the network, and the hop time is basically the same, so a hop can be divided into several networks according to DOA parameters. The traditional K-means algorithm is completely random for K initial centroids, which results in slow convergence. The k-means++ algorithm is used to optimize the method of K-means random initial centroids, which is divided into two steps: K value determination and DOA estimation clustering.
Step1: The
K value of clustering center is determined by contour coefficient method. The contour coefficient combines the condensation degree and the separation degree of the cluster, which is determined by the cluster non-similarity
and the non-similarity
between the clusters, as Formula (28).
the mean value of
for all samples is called the contour coefficient. By enumerating, the
K is from 2 to a fixed value, repeatedly running several times on each
K value (avoiding the local optimal solution), and calculating the average contour coefficient of the current
k, and finally selecting
K corresponding to the value of the maximum contour coefficient as the final number of clusters.
Step2:
K-means++ algorithm is used to complete DOA clustering. By randomly selecting the first clustering center
and calculating
, the algorithm chooses
K maximum values and finds the corresponding clustering center, which is the number of frequency hopping signals, and the corresponding hop of DOA clustered to the same clustering center is the frequency hopping signal of the same network. In combination with
Section 3.1, the frequency hopping set of the frequency hopping signal, the frequency hopping sequence of the frequency hopping signal and the frequency hopping time can be estimated, and the parameters of the frequency hopping signal can be estimated.
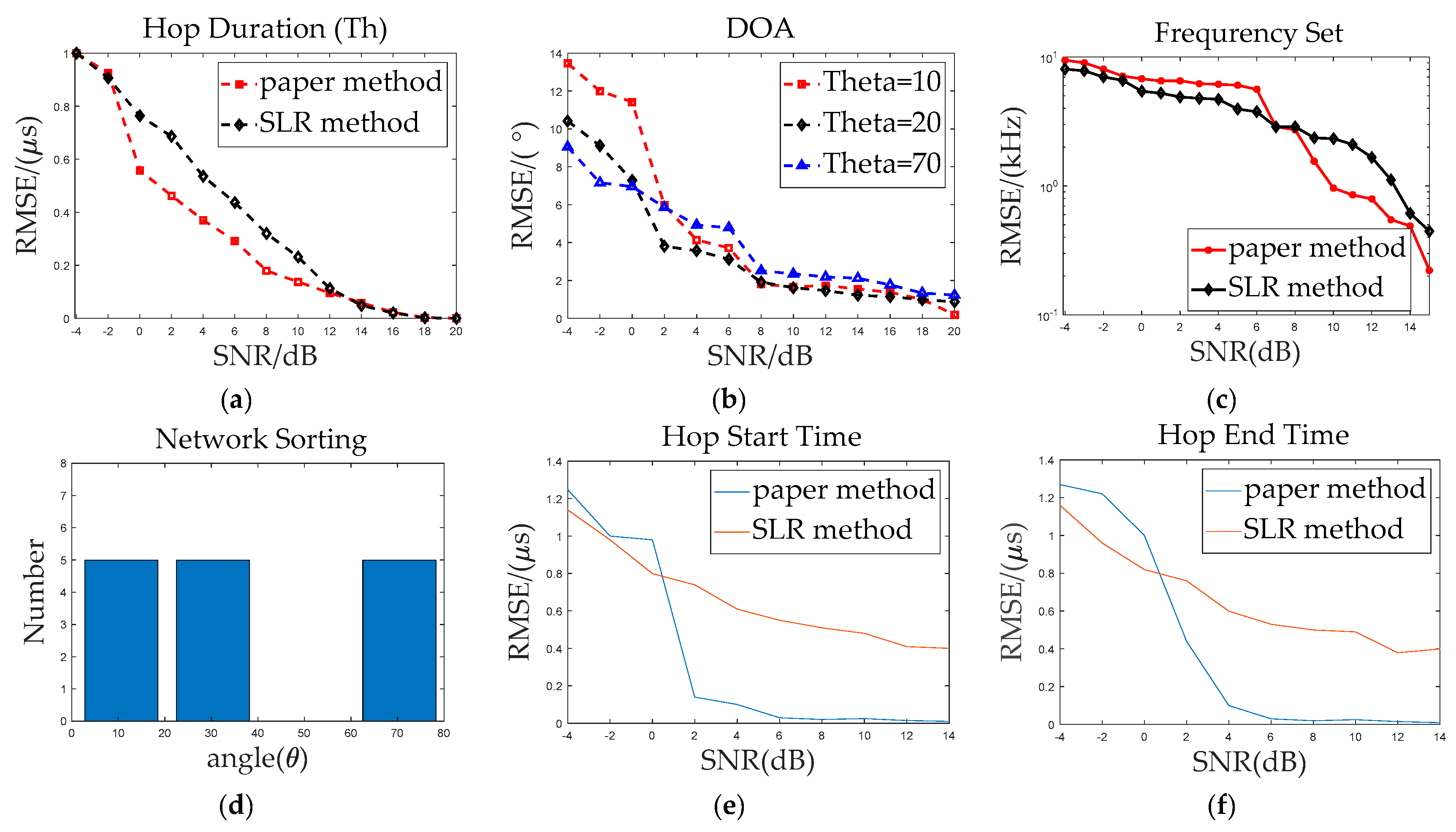
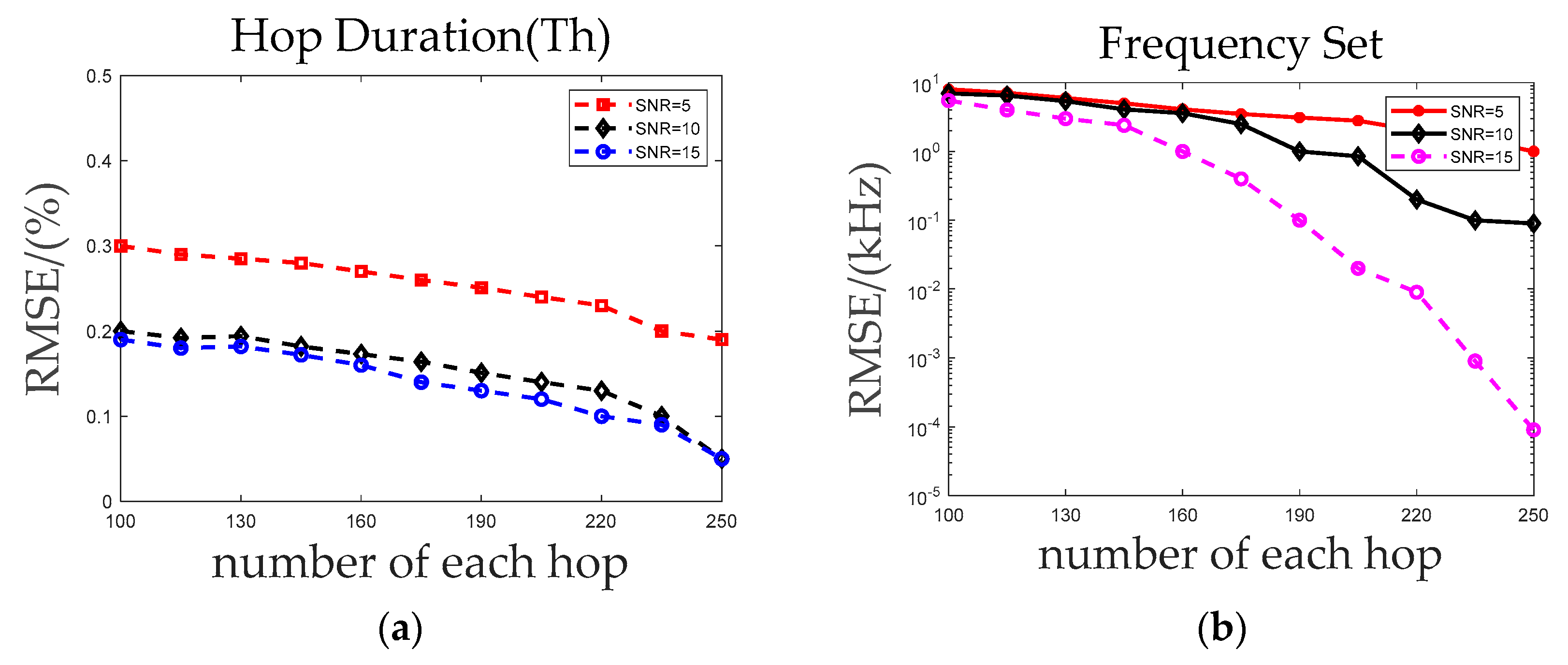
5. Conclusions
In order to adapt to the parameter estimation of multi-frequency hopping signals in more and more complex electromagnetic environment, based on the research of predecessors, this paper makes full use of the spatial domain information of array received signals. On the basis of the obtained matrix distribution of the space-time-frequency distribution, the matrix joint diagonalization algorithm is innovatively applied to the parameter estimation of multi-frequency hopping signals, and the root-MUSIC algorithm is used to complete the multi-frequency hopping signals. According to the estimated DOA of each hop, the k-means++ algorithm is used to complete the sorting of frequency hopping network stations. By setting up three sets of simulation experiments, the effectiveness of the proposed algorithm, the accuracy of the estimation and the robustness of the algorithm are verified. Through experimental simulation, it is found that when the SNR is −4 dB, the proposed finding “island” algorithm can correctly complete the estimation of the number of hops and the extract the self-terms time-frequency points, and the estimated accuracy is 70.43%, which is set for the text simulation conditions. the estimation error Th reaches 1.2 μs, and the estimated accuracy rate reaches 62%, which the DOA estimation error averages , the estimated accuracy rate reaches 71%. The jump start time and the jump end time accuracy rate are 75.42% and 74.48%, and the frequency hopping frequency set estimation error is 1 MHz, which the accuracy rate reaches 73.26%. the average accuracy of the frequency hopping parameter estimation reaches 70.42%; when the SNR = 0 dB, the estimation accuracy reaches 82.46%. When the SNR = 5 dB, Th estimation error decreases to 0.025 μs, for which the accuracy rate is 94.5%; the DOA estimation error is , which the accuracy rate is 94.28; the frequency hopping frequency set estimation error is reduced to 0.76 MHz, which the accuracy rate is 93.26%; the jump start time and the end time estimation accuracy rate are 96.12% and 95.96%, then the accuracy of the frequency hopping parameter estimation is 94.74%. As the signal-to-noise ratio increases, the estimation accuracy becomes higher and higher, and the proposed algorithm can be found to be effective for multi-hopping parameter estimation.