Singly Diagonally Implicit Block Backward Differentiation Formulas for HIV Infection of CD4+T Cells
Abstract
:1. Introduction
2. Singly Diagonally Implicit Block Backward Differentiation Formulas
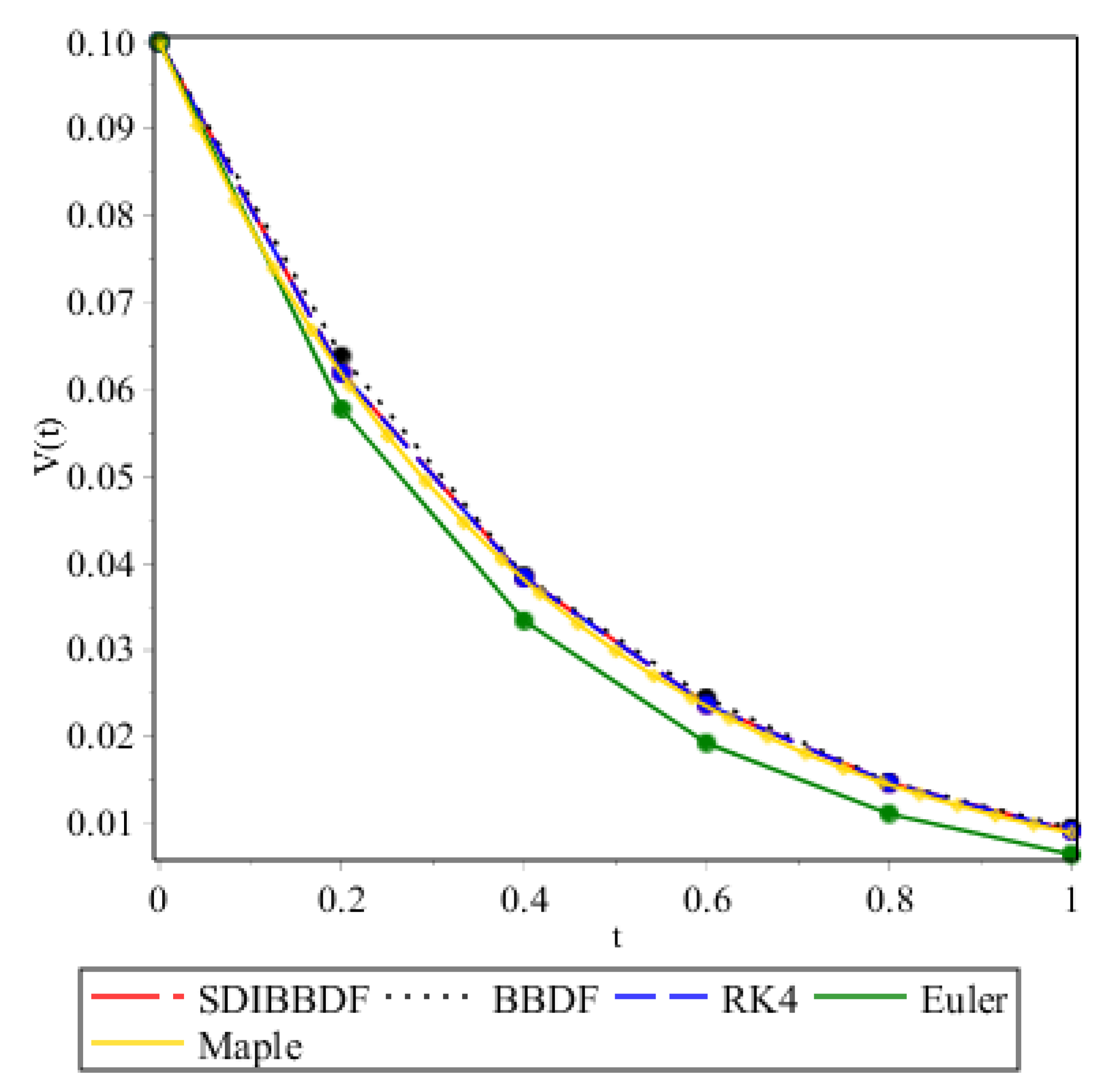
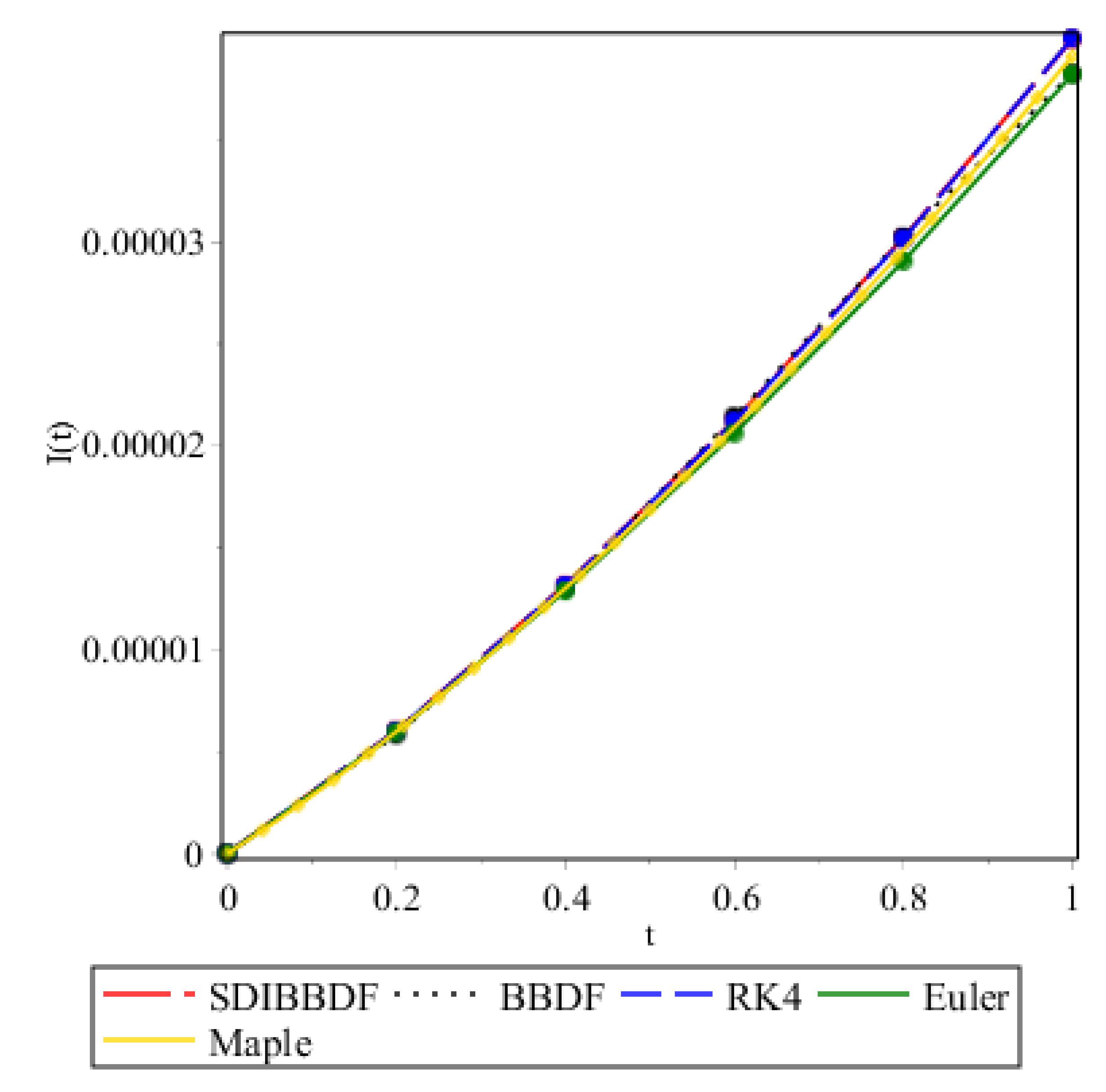
3. Results of Numerical Simulation
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- UNAIDS, Global HIV and AIDS Statistics—2018 Sheet. 2019. Available online: http://www.unaids.org/en/resources/fact-sheet (accessed on 15 January 2019).
- U.S. Department of Veterans Affairs. HIV/AIDS CD4 Count or T-Cell Count. 2005. Available online: https://www.hiv.va.gov/patient/diagnosis/labs-CD4-count.asp (accessed on 16 January 2019).
- Perelson, A.S. Modeling the interaction of the immune system with HIV. In Lecture Notes in Biomathematics; Castillo-Chavez, C., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; Volume 83, pp. 350–370. [Google Scholar] [CrossRef]
- Perelson, A.S.; Kirschner, D.E.; Boer, R.D. Dynamics of HIV infection CD4+T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Culshaw, R.V.; Ruan, S. A delay-differential equation model of HIV infection of CD4+T-cells. Math. Biosci. 2000, 165, 27–39. [Google Scholar] [CrossRef]
- Ibrahim, Z.B. Block Multistep Methods for Solving Ordinary Differential Dquations. Ph.D. Thesis, Universiti Putra Malaysia, Selangor, Malaysia, 2006. [Google Scholar]
- Norsett, S.P. Semi-Explicit Runge-Kutta Methods; Report Mathematics and Computation No. 6/74; Department of Mathematics, University of Trondheim: Trondheim, Norway, 1974. [Google Scholar]
- Stal, J. Implementation of Singly Diagonally Implicit Runge-Kutta Methods with Constant Step Sizes. Bachelor’s Thesis, Lund University, Lund, Sweden, 2015. [Google Scholar]
- Milne, W.E. Numerical Solution of Differential Equations; John Wiley & Sons: New York, NY, USA, 1953. [Google Scholar]
- Suleiman, M.B. Generalized Multistep Adams and Backward Differentiation Methods for the Solution of Stiff and Non-Stiff Ordinary Differential Equations. Ph.D. Thesis, Universiti Putra Malaysia, Selangor, Malaysia, 1979. [Google Scholar]
- Khalid, M.; Sultana, M.; Zaidi, F.; Khan, F.S. A numerical solution of a model for HIV infection CD4+T-cells. Int. J. Innov. Sci. Res. 2015, 16, 79–85. [Google Scholar]
- Klatzmann, D.; Barre-Sinoussi, F.; Nugeyre, M.T.; Danquet, C.; Vilmer, E.; Griscelli, C.; Brun-Veziret, F.; Rouzioux, C.; Gluckman, J.C.; Chermann, J.C. Selective tropism of lymphadenopathy associated virus (LAV) for helper-inducer T lymphocytes. Science 1984, 225, 59–63. [Google Scholar] [CrossRef] [PubMed]
- Masur, H.; Ognibene, F.P.; Yarchoan, R.; Shelhamer, J.H.; Baird, B.F.; Travis, W.; Suffredini, A.F.; Deyton, L.; Kovacs, J.A.; Falloon, J.; et al. CD4 counts as predictors of opportunistic pneumonias in human immunodeficiency virus (HIV) infection. Ann. Intern. Med. 1989, 111, 223–231. [Google Scholar] [CrossRef] [PubMed]
- Okoye, A.A.; Picker, L.J. CD4+T-cell depletion in HIV infection: Mechanisms of immunological failure. Immun. Rev. 2013, 254, 54–64. [Google Scholar] [CrossRef] [PubMed]

| Dependent variables | ||
|---|---|---|
| T | Uninfected CDT cells population size | |
| I | Infected CDT cells density | |
| V | Initial density of HIV RNA | |
| Parameters & constants | ||
| Source term for uninfected CDT cells | day mm | |
| Natural death rate of CDT cells | day | |
| r | Growth rate of CDT cells population | 3 day |
| Maximal population level of CDT cells | mm day | |
| k | Rate of CDT cells become infected with virus | mm |
| Blanket death rate of infected CDT cells | day | |
| N | Number of virions produced by infected CDT cells | 10 mm |
| Death rate of free virus | day |
| t | SDIBBDF | BBDF | RK4 | EULER |
|---|---|---|---|---|
| 0.0 | 0.1000000000000000 | 0.1000000000000000 | 0.1000000000000000 | 0.1000000000000000 |
| 0.2 | 0.2090205532222125 | 0.2162665954333766 | 0.2087297222454430 | 0.2066396850000000 |
| 0.4 | 0.4065545236060797 | 0.4050981887697551 | 0.4059409955447710 | 0.3455020000000000 |
| 0.6 | 0.7648420298033937 | 0.7365813304773389 | 0.7635801781341750 | 0.6050020000000000 |
| 0.8 | 1.4145067965307667 | 1.3965775540613832 | 1.4119574363577000 | 1.0420600000000000 |
| 1.0 | 2.5840259154129843 | 2.3865826219889092 | 2.5867778755778800 | 1.7779900000000000 |
| t | SDIBBDF | BBDF | RK4 | EULER |
|---|---|---|---|---|
| 0.0 | 0.1000000000000000 | 0.1000000000000000 | 0.1000000000000000 | 0.1000000000000000 |
| 0.2 | 0.0619225726474935 | 0.0638429946616157 | 0.0618798121706440 | 0.0577610000000000 |
| 0.4 | 0.0383177394040220 | 0.0385396728096125 | 0.0382948730759080 | 0.0333660000000000 |
| 0.6 | 0.0237164781782014 | 0.0244736504530348 | 0.0237045402752520 | 0.0192790000000000 |
| 0.8 | 0.0146863853079351 | 0.0147827377616151 | 0.0146803506585660 | 0.0111450000000000 |
| 1.0 | 0.0091490338084673 | 0.0094989136071827 | 0.0091008270878710 | 0.0064500000000000 |
| t | SDIBBDF | BBDF | RK4 | EULER |
|---|---|---|---|---|
| 0.0 | 0.0000000000000000 | 0.0000000000000000 | 0.0000000000000000 | 0.0000000000000000 |
| 0.2 | 0.0000060459344453 | 0.0000058406917327 | 0.0000060315204770 | 0.0000059531387000 |
| 0.4 | 0.0000131823896412 | 0.0000130303451230 | 0.0000131530315000 | 0.0000128846300000 |
| 0.6 | 0.0000212573455944 | 0.0000214442550764 | 0.0000212106240460 | 0.0000206134400000 |
| 0.8 | 0.0000302184570008 | 0.0000302550927739 | 0.0000301518386990 | 0.0000290605600000 |
| 1.0 | 0.0000399547343565 | 0.0000382633892925 | 0.0000399942614780 | 0.0000382160400000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jana Aksah, S.; Ibrahim, Z.B. Singly Diagonally Implicit Block Backward Differentiation Formulas for HIV Infection of CD4+T Cells. Symmetry 2019, 11, 625. https://doi.org/10.3390/sym11050625
Jana Aksah S, Ibrahim ZB. Singly Diagonally Implicit Block Backward Differentiation Formulas for HIV Infection of CD4+T Cells. Symmetry. 2019; 11(5):625. https://doi.org/10.3390/sym11050625
Chicago/Turabian StyleJana Aksah, Saufianim, and Zarina Bibi Ibrahim. 2019. "Singly Diagonally Implicit Block Backward Differentiation Formulas for HIV Infection of CD4+T Cells" Symmetry 11, no. 5: 625. https://doi.org/10.3390/sym11050625
APA StyleJana Aksah, S., & Ibrahim, Z. B. (2019). Singly Diagonally Implicit Block Backward Differentiation Formulas for HIV Infection of CD4+T Cells. Symmetry, 11(5), 625. https://doi.org/10.3390/sym11050625





