1. Introduction
Shepard and Metzler [
1] reported that latencies for making same/different decisions about simultaneously presented pairs of rotated but identically shaped objects increased linearly with the angular distance between the two objects in three-dimensional space within the range of 0° to 180°. Because this linearity of latencies was evident across stimuli and participants, the researchers assumed that the process of making identity decisions about the rotated objects involved “mental rotation in three-dimensional space” (p. 703). This assumption implies that the recognition of rotated objects is on the basis of the non-analytical process of normalization by rotation. In contrast, Corballis [
2] proposed that people recognize a figure by extracting its coordinate-independent descriptions (later defined as invariant features) which could be used for its identification regardless of its orientations or of outline deformation (e.g., the letter “A” could be identified as such because of having a closed sequence of three line segments attached with roughly codirected two line segments even when its size, orientation, and aspect ratio are modestly altered).
More detailed examinations of the phenomenon of mental rotation has revealed that the slopes of the latencies against the angular distances between the two disoriented figures of identical pairs vary according to the experimental conditions. Mental rotation slopes are generally steep for complex stimuli, including Shepard’s block figures [
1], stimuli involving extended blocks of Shepard’s figures [
3], random polygons with varied numbers of flections [
4], and complex random matrices [
5]. The slopes for these stimuli are typically >20 ms/°. However, for normal versus mirror-reflected decisions about memorized letter-like symbols [
6], memorized Shepard’s blocks [
7], and memorized random polygons [
8], slopes are reported to be in the rage of 1 ms/° and 5 ms/°. These results indicate that mental rotation is involved in the recognition of both 3D and 2D stimuli. As a reference, Cohen and Kubovy [
9] claimed that slopes shallower than 1 ms/° are thought to be too shallow for mental rotation to occur.
Another group of tasks that might be associated with increased slope are tasks requiring same/mirror-reflected discriminations of unfamiliar stimuli [
1,
10,
11]. Förster, Gebhardt, Lindlar, Siemann, and Delius [
12] presented participants with triplets of random polygons and instructed them to choose which of the flanking polygons were identical in shape to the central polygon regardless of its orientation. The results revealed that the slopes for discriminating mirror-reflected polygons were similar to slopes for polygons that were difficult to discriminate. The researchers suggested that mirror-reflected stimuli may be a special case of hard-to-discriminate stimuli.
Regarding the recognition of mirror-reflected figures, Corballis [
2] proposed that mental rotation would be necessary if the recognition of a figure requires either the discrimination from its mirror-reflected counterpart regardless of its orientation or the discrimination of its left side from the right side (i.e., handedness) [
13,
14].
In the current study, (
6 point,
n line) figures (or a (
6,
n) figure) were used as stimuli for the figure recognition experiments. A (
6,
n) figure consists of
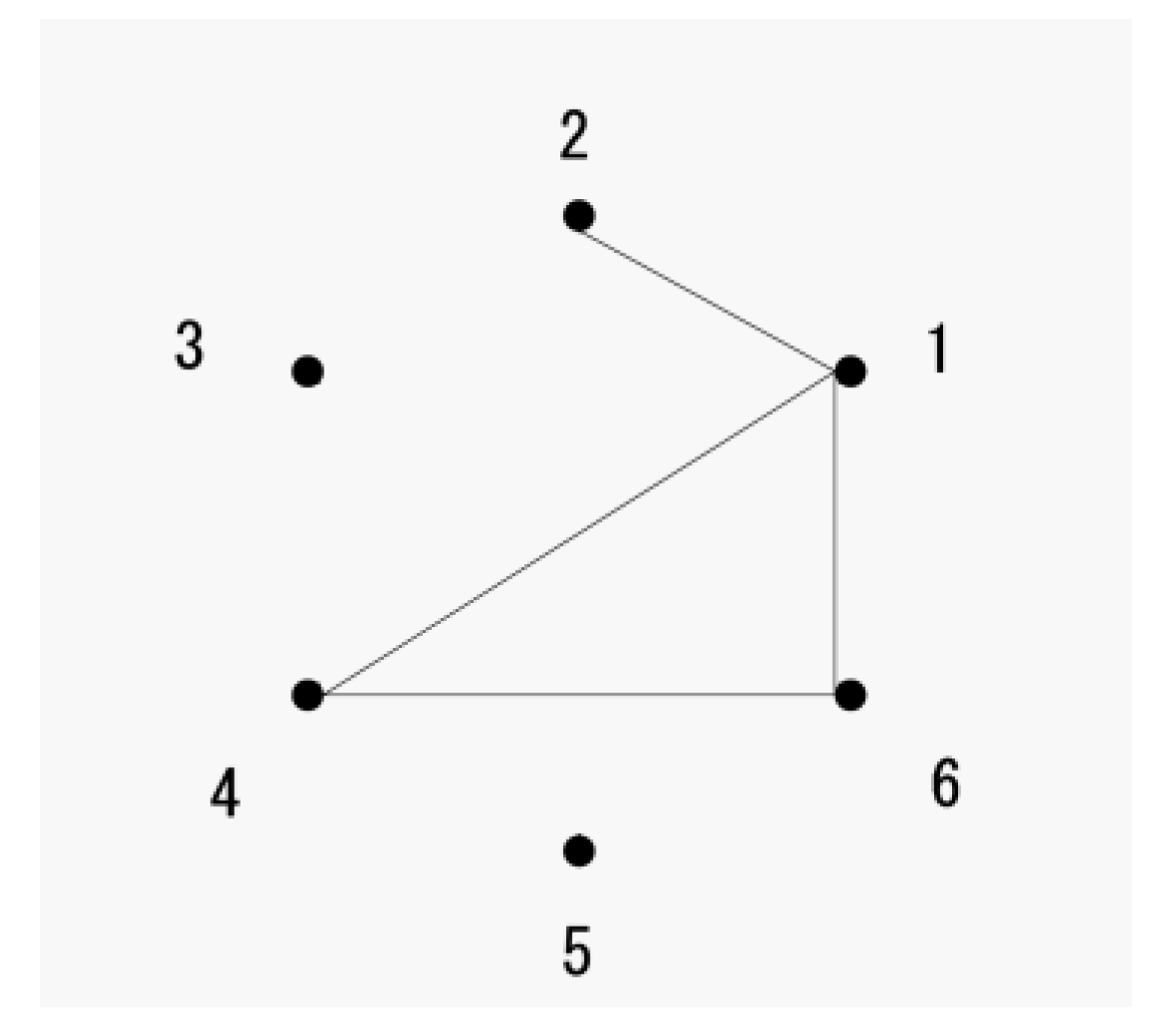
n line segments, each of which is connected between a distinct pair of points located at the vertices of a regular hexagon (
Figure 1). According to graph theory, if the line segments connecting
n pairs of points in one figure are identical to those connecting
n pairs of points in another figure, regardless of the locations of the points, the two figures are mutually isomorphic [
15].
For clarity, in the current study, a descriptive element (or property) of a figure is hereafter referred to as a feature. Features can be classified into two categories: (a) features describing structural aspects of a figure (invariant features), and (b) features describing non-structural aspects (superficial features). Here, the definition of invariant features was based on the definition of graph invariants [
15]. Among an isomorphic set of figures, all invariant feature values are the same, and only the values of superficial features differ. It must also be noted in the more general setting of graphons, this is still true. Importantly, two figures of an identically shaped pair as well as those of a mirror-reflected pair are both mutually isomorphic. In the current study, identical figure pairs, regardless of their orientation, are hereafter referred to as rotated-to-be-identical (Id
r) pairs, and mirror-reflected pairs are referred to as axisymmetric (Ax) pairs.
The latencies required to discriminate non-identical, non-axisymmetric (Nd) pairs are generally shorter than the latencies required to identify Id
r pairs [
16,
17,
18,
19]. This phenomenon could be interpreted as indicating that feature values of an Nd pair of figures are more varied compared with those of an Id
r pair, and their value differences would be readily available in cases where the decision “different” is made. Specifically, it has been reported that detection of a difference in invariant feature values is prioritized compared with detection of a difference in superficial feature values [
17,
20]. Although Ax pairs are a special case of Nd pairs, the latencies for Ax pairs tend to be longer than those for Id
r pairs [
18,
19].
Because there is no difference in invariant feature values between Idr and Ax figure pairs, it is important to understand differences in how the values of superficial features behave between the two pair types. The shapes are the same for the two figures of an Idr pair. Thus, there is no difference in corresponding line lengths and included angles between the two figures. In addition, such superficial feature values, either a clockwise or counterclockwise direction from one base location to a specific location in one figure, are identical to the direction from the base location to the corresponding location in the other figure, and the shortest angular distances from respective locations of one figure to the corresponding locations of the other figure are constant when the centers of the two figures are superposed. Regarding Ax pairs, the corresponding line lengths and included angles are the same as those in an Idr pair, but the direction from one base location to another location by the shortest angular distance in one figure is opposite to the corresponding direction in the other figure, except for the angular distance between the two locations, which is 180° in both figures. Moreover, the shortest angular distances from respective locations of one figure to the corresponding locations of the other figure are twice the distance from a location to an axis of symmetry in one figure when the centers of the two figures are superposed.
Thus, two superficial features could cause the difficulty for Ax pairs: difficulty detecting a difference in the clockwise or counterclockwise direction from a base location to another location between the two figures of a pair and difficulty detecting a difference in the shortest angular distances from respective locations of one figure to the corresponding locations of the other figure.
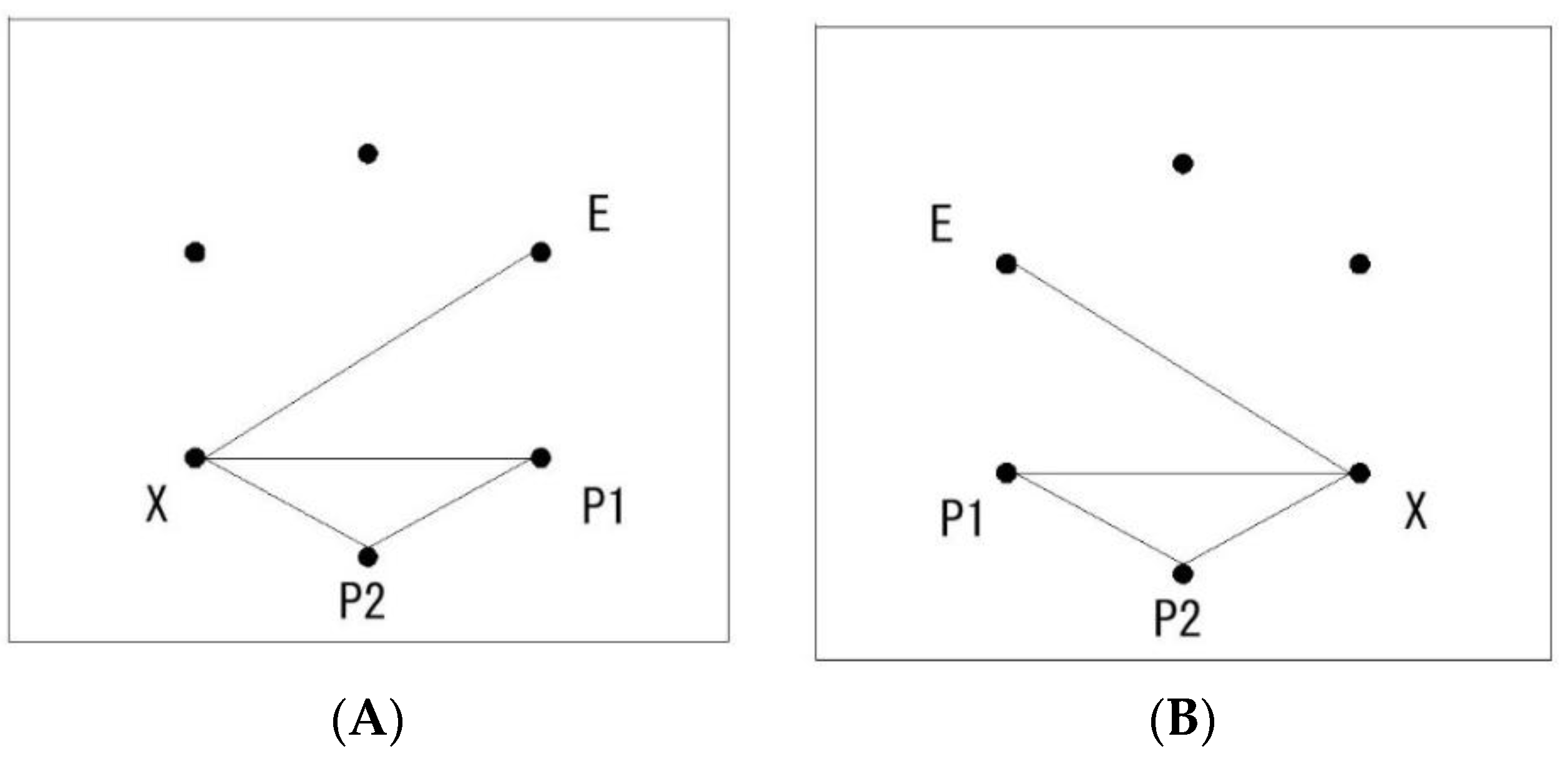
In the current study, information concerning either a clockwise or counterclockwise direction from the location of a base point to the location of another point by the shortest angular distance in a figure was referred to as the handedness of the location [
21], and the angular distances between the corresponding locations of two figures of a pair, either in a clockwise or a counterclockwise direction, when the centers of the two figures are superposed, were referred to as a shift of locations. In short, the lengths, angles, and respective handedness were all identical, and the shifts of locations were all constant for an Id
r pair. In contrast, the lengths and angles were identical, but respective handedness was mainly opposite, and the shifts of locations were variable for an Ax pair.
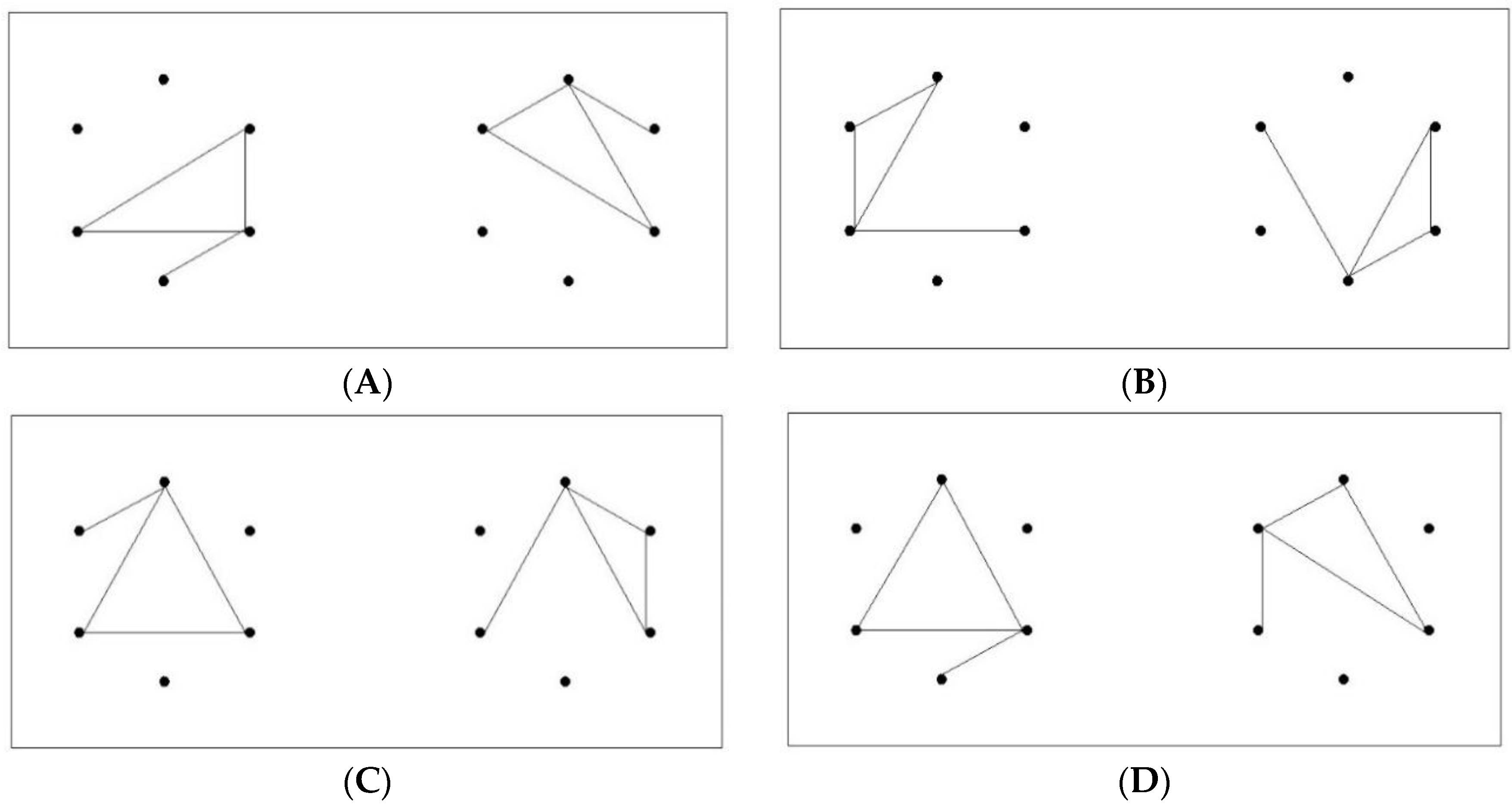
Figure 2 shows the characteristics of the superficial features of handedness and shifts in Id
r and Ax pairs.
In an earlier study by the author [
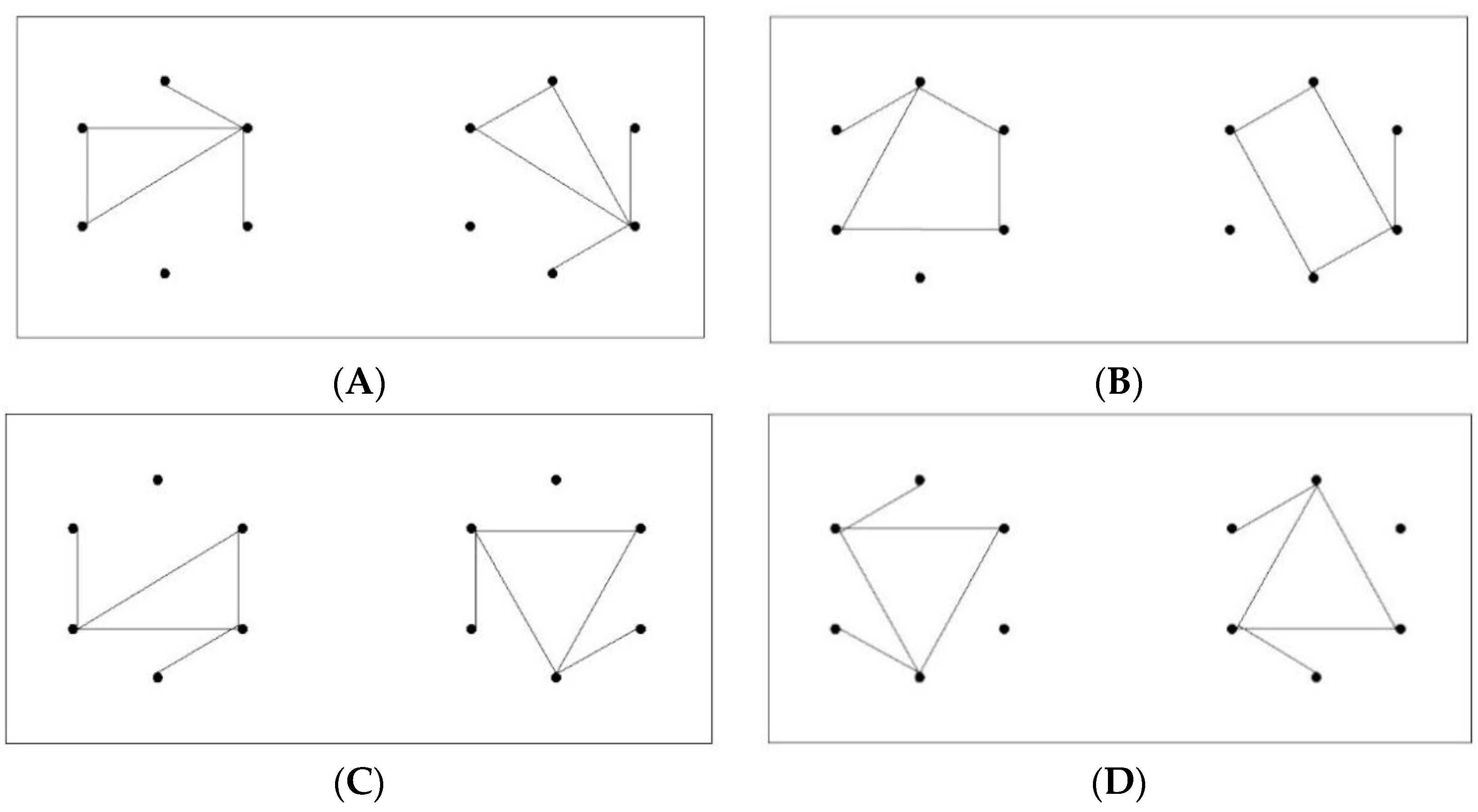
18], it was presumed that complex shifting patterns of locations caused the discrimination of the two figures of an Ax pair to be difficult. Specifically, it was hypothesized that discrimination latencies of Nd pairs would become similar to those of Ax pairs when both types of pairs had the same extent of complexity in the shifting pattern of invariant feature locations. In a task used to determine whether a presented pair of figures were identical in shape regardless of their orientation, three main types of (
6,
5) figure pairs were prepared: Id
r, Ax, and mutually isomorphic Nd pairs.
In each figure, the locations of four invariant features (i.e., an endpoint, a cycle, an isolated point, and maximum degree point) were calculated. Concerning Nd pairs, they were further categorized according to the extent of deviation from a constant shift of four invariant locations of one figure to the other figure in a pair: Nd 1/4, Nd 2/4, and Nd 4/4 pairs with the numerators indicating the number of the deviant locations from a constant shift. Axisymmetric (Ax) pairs with their number of deviations from a constant shift other than 2/4 were discarded from the stimuli, and thus, Ax pairs were all Ax 2/4 pairs. The results revealed that the latencies were significantly different between every pair with an ascending order as Nd 4/4, Nd 2/4, Nd 1/4, Idr, and Ax 2/4 pairs. The results, thus, did not support the hypothesis that the complex shifting pattern of invariant feature locations in Ax pairs alone caused the difficulty in distinguishing Ax pairs.
The current study sought to examine the importance of handedness of figure pairs in the recognition of figures. Provided that the lack of sensitivity to opposite handedness between the two figures of Ax pairs causes difficulties in discrimination, it was hypothesized that the discrimination difficulty of non-identical pairs with opposite handedness would be critical in the discrimination difficulty of Ax pairs. Three pair types were generated: Idr, Ax, and Nd pairs. And Nd pairs were further classified into two categories: pairs in which two figures had the same handedness (Nd sm) and pairs in which two figures had opposite handedness (Nd op).
Previous studies reporting the importance of handedness information for the occurrence of mental rotation have tended to use familiar stimuli such as disoriented (b versus d) and (p versus q) decisions [
14] or left versus right side decisions about an asterisk in a nearby disoriented letter [
22]. The stimuli in these studies were overlearned, and handedness information was stereotypically presented to participants. In contrast, the present stimuli were randomly generated, and the presentation of handedness information varied from trial to trial. Thus, the current results could be more generalizable.
Given the evidence suggesting that the detection of differences in invariant feature values is prioritized over the detection of differences in superficial features [
17,
20,
23], all stimulus figure pairs were set to be mutually isomorphic to prevent the effect of invariant features being confounded with the effect of handedness. Because some researchers have insisted that the presence of intersections of line segments are detected preattentively [
24], figures with one or more intersections of line segments were discarded from the stimulus figures.
Several previous studies indicated that the presence of closure is critical in figure recognition [
16,
25,
26], while Julesz [
27] claimed that line terminators (i.e., endpoints) were detected at an early stage of figure recognition. Thus, figures consisting of a cycle and endline(s) were selected as stimulus figures. The number of lines incident with a point is referred to as the degree of the point [
15]. An endpoint is a point whose degree is 1 (also called a pendant vertex [
28]), an endline is a line segment with at least one endpoint at its ends, and a cycle is a closed sequence of points and line segments that starts and ends at the same point. Finally, handedness is defined here as either a clockwise or counterclockwise direction from a maximum degree point to an endpoint.
4. General Discussion
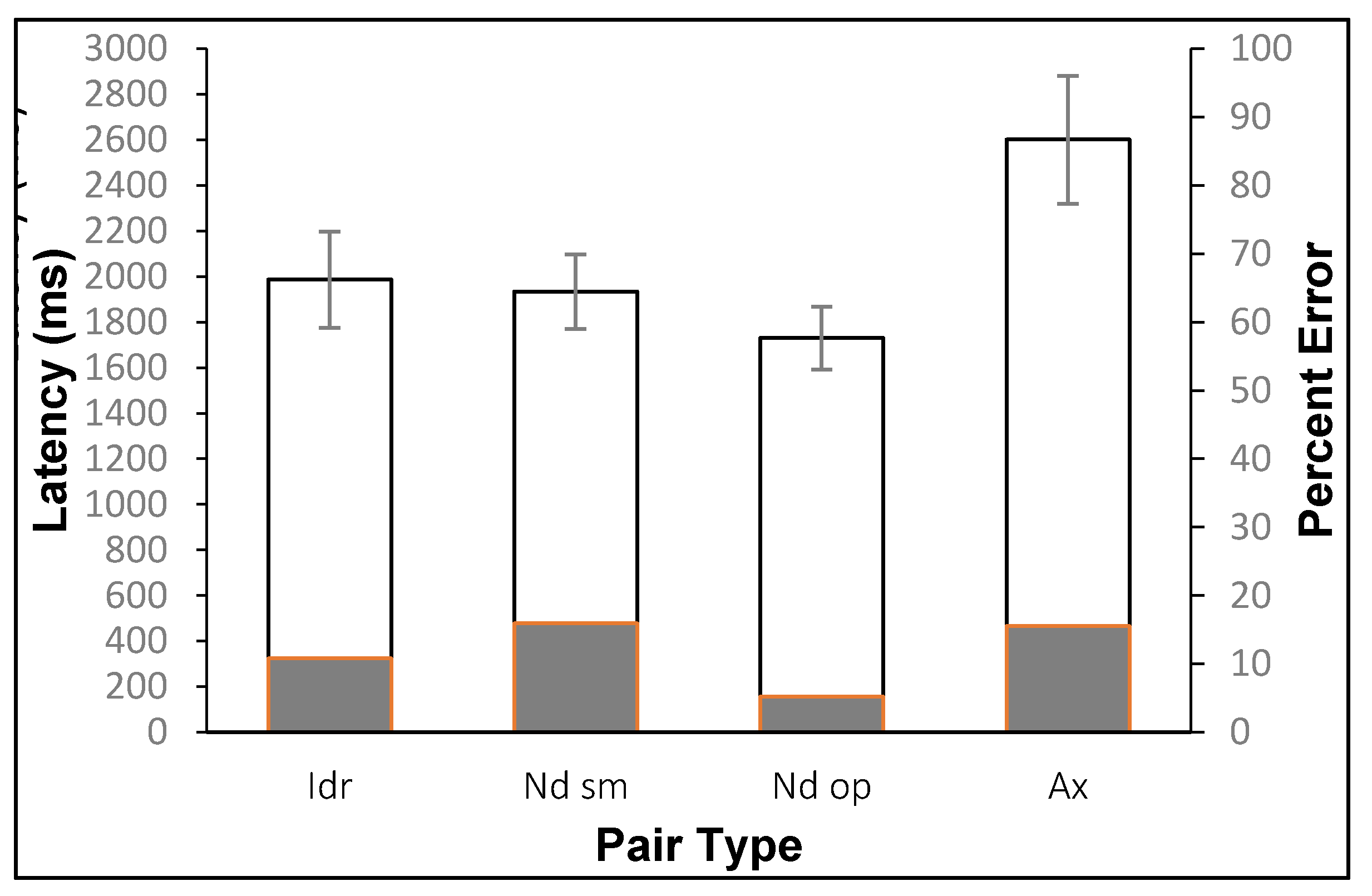
Because the latencies for Nd op pairs were shorter than those for Ax pairs, but no latency difference was found between Nd op and Nd sm pairs in the two experiments, handedness information did not appear to be a critical superficial feature for figure recognition. The difficulty in discriminating Ax pairs from Idr pairs supports this conclusion because figures of Idr pairs have the same handedness, but figures of Ax pairs had opposite handedness.
Thus, other superficial features may play a critical role in discriminating mutually isomorphic pairs of figures. As mentioned in the Introduction, the lengths of respective line segments and the angles formed by any two adjacent line segments were identical both for Id
r and Ax pairs. In contrast, no experimental control was applied to the lengths of line segments for both types of Nd pairs during the process of pair generation in the current experiments. Thus, the lengths of endlines and the shapes of a cycle (i.e., a triangle or a rectangle) could be different between the two figures of Nd pairs. It is likely that participants made use of superficial feature differences, such as the shapes of the cycle and differences in endline lengths, to discriminate the figures of Nd pairs. In a previous study by the author [
19], when equalizing the total lengths of triangles between the two (
6,
4) figures in Nd pairs, the latencies to reject identities in Nd pairs of figures with the same endline length became almost equal to those for Ax pairs. Because any triangles existing in (
6,
n) figures with an equal total length have either the same or axisymmetric shapes, the result strongly suggests that line length is a critical superficial feature in figure recognition. However, the length of a line segment is constrained by a pair of points between which the segment spans. The angle formed between two adjacent line segments is also constrained by two pairs of points, and thus, the lengths and angles are confounded. It will be necessary for future studies to examine the importance of lengths and angles independently without the two variables confounding each other.
The present study was designed on the basis of the premise that the detection of invariant features precedes the detection of superficial features in figure recognition [
17,
20]. This raises the question of which superficial features are critical in discrimination of figures when figures share the same invariant feature values. Several superficial features could potentially play this role, including the location, distance (or length), angle, direction, and shape of a figure. One previous study by the author [
18] suggested that shifting patterns of feature locations were not critical. The present study also indicated that participants were neither sensitive to nor attaching importance to the direction of feature locations (or handedness) for the discrimination of non-identical pairs. Moreover, another study by the author [
19] revealed that differences in the lengths of a line segment could be critical in the discrimination of figures. However, line length was confounded by angle. In addition, the shapes of cycles (specifically quadrilaterals) were found to be easily discriminable [
20]. Based on these previous findings and the current results, I propose that the abstract (invisible) relationships between feature locations (e.g., shifting patterns and handedness) do not play a critical role in figure recognition, whereas concrete (visible) relationships between feature locations (e.g., the length of a line segment) appear to play a critical role. A small number of cycles may be interpreted as well-known closed shapes rather than closed sequences of line segments with specific lengths. At the same time, it should be noted that some superficial feature values could be critical in the discrimination of figures, although the robustness of discriminability of superficial features may be less than that of invariant features.
Despite the claim by Corballis [
12] that mental rotation must be induced to determine the handedness of a given figure, the current results indicated that participants’ sensitivity to handedness was weak. However, the current results indicated that mental rotation did occur when identification of Id
r pairs was required. Mental rotation is thought to constitute internal processes and representations that are analogous to the external operations and objects [
7]. Thus, mental rotation is essentially a continuous process of recognizing figures by matching a transformed image of an object with the object’s percept. However, there is substantial evidence that people make use of invariant and superficial feature value differences for the discrimination of figures [
17,
18,
19,
20]. Thus, it is theoretically necessary to reconcile the distinct characteristics of the non-analytical mental rotation hypothesis and the analytical feature comparison hypothesis, which may coexist in the processes underlying figure recognition.