2. Cylinder Grid Graph
The Cartesian product
of two graphs
and
, is the graph with vertex set
, and any two vertices
and
are adjacent in
whenever
and
or
and
. The cylinder grid graph
is the graph formed from the Cartesian product
of the path graph
and the cycle graph
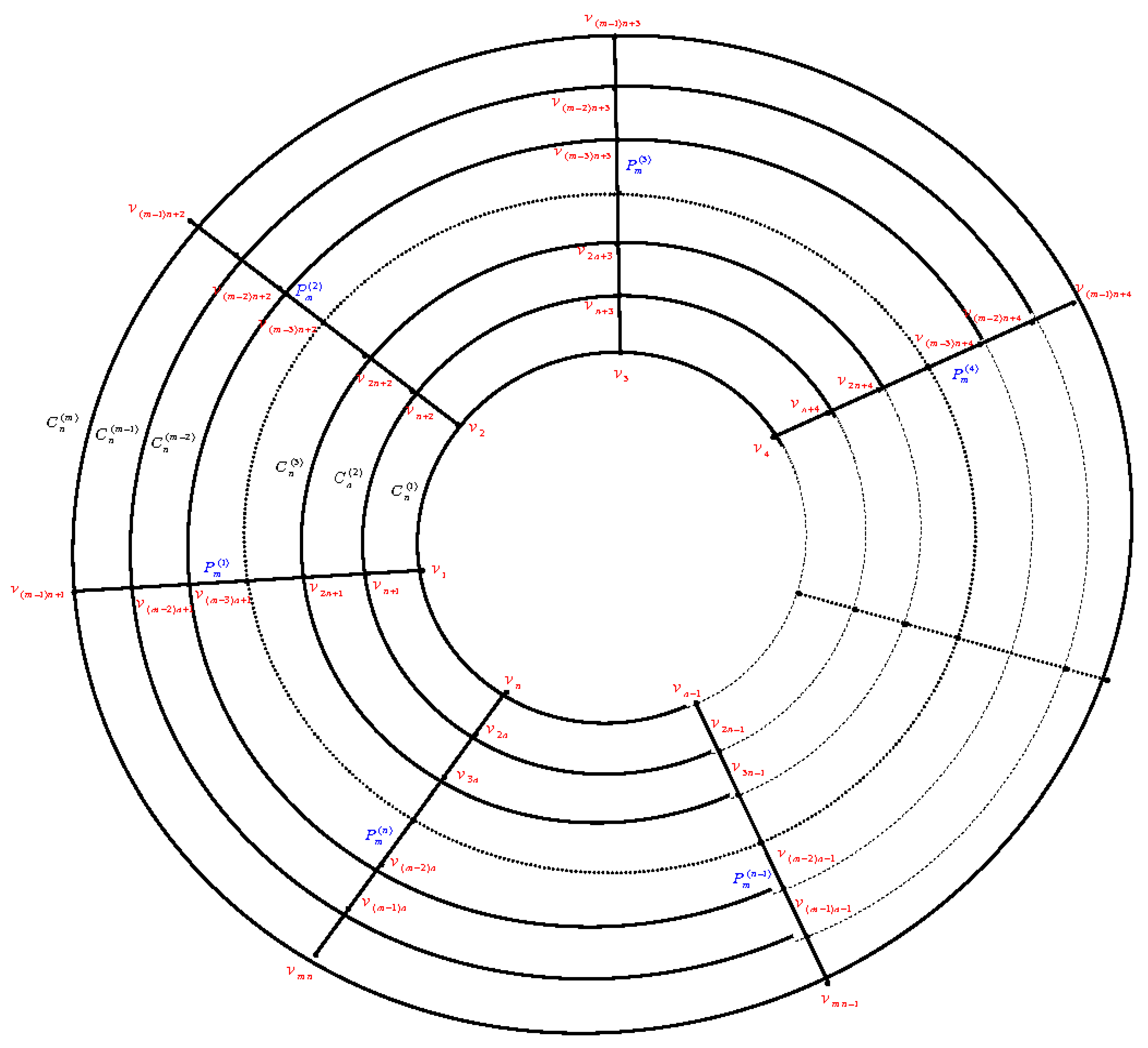
. That is, the cylinder grid graph consists of
copies of
represented by circles, and will be numbered from the innermost circle to the outer circle as
and we call them simply circles;
copies of
represented by paths transverse the
circles and will be numbered clockwise as
and we call them paths (see
Figure 1).
Theorem 1. If is an even positive integer greater than or equal and , then the cylinder grid graph , is an edge even graceful graph.
Proof. Using standard notation
,
and
and
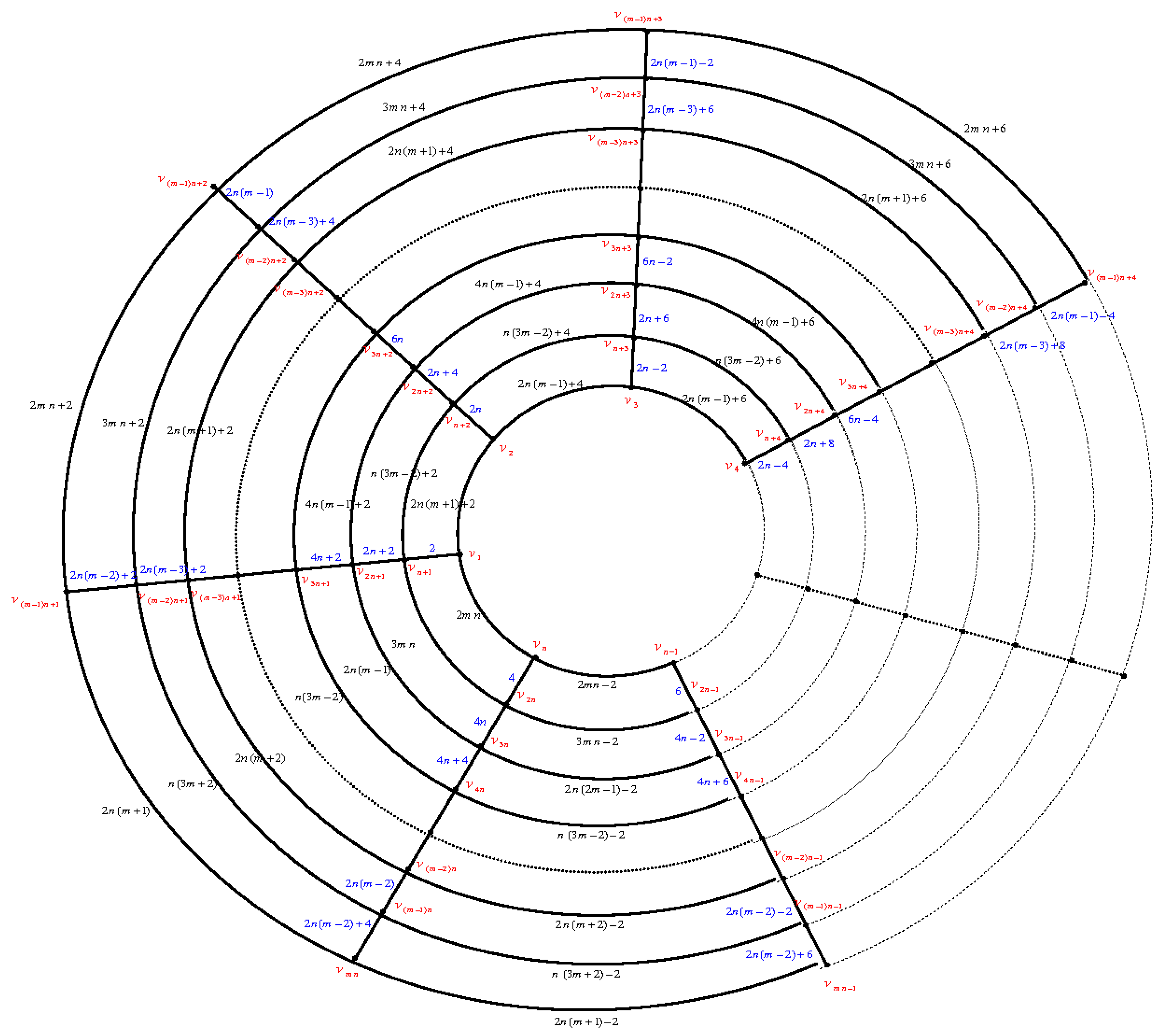
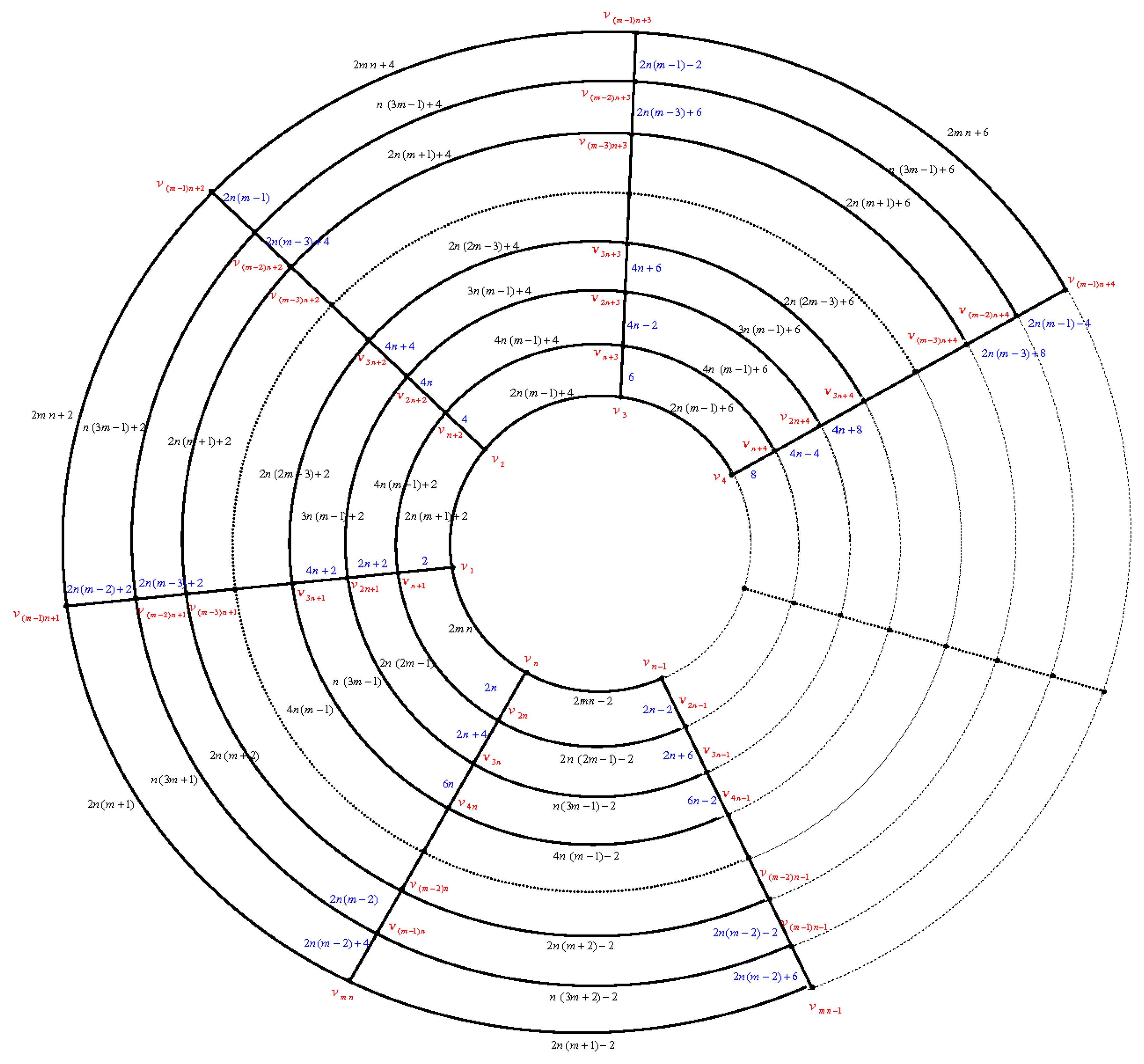
Let the cylinder grid graph
be as in
Figure 2. □
First, we label the edges of the paths beginning with the edges of the path as follows: Move anticlockwise to label the edges by then move clockwise to label the edges , by , then move anticlockwise to label the edges by and so on. Finally, move anticlockwise to label the edges , by
Secondly, we label the edges of the circles beginning with the edges of the innermost circle then the edges of outer circle , then the edges of the circles
Finally, we label the edges of the circles as follows: , is odd.
Thus, the labels of corresponding vertices will be:
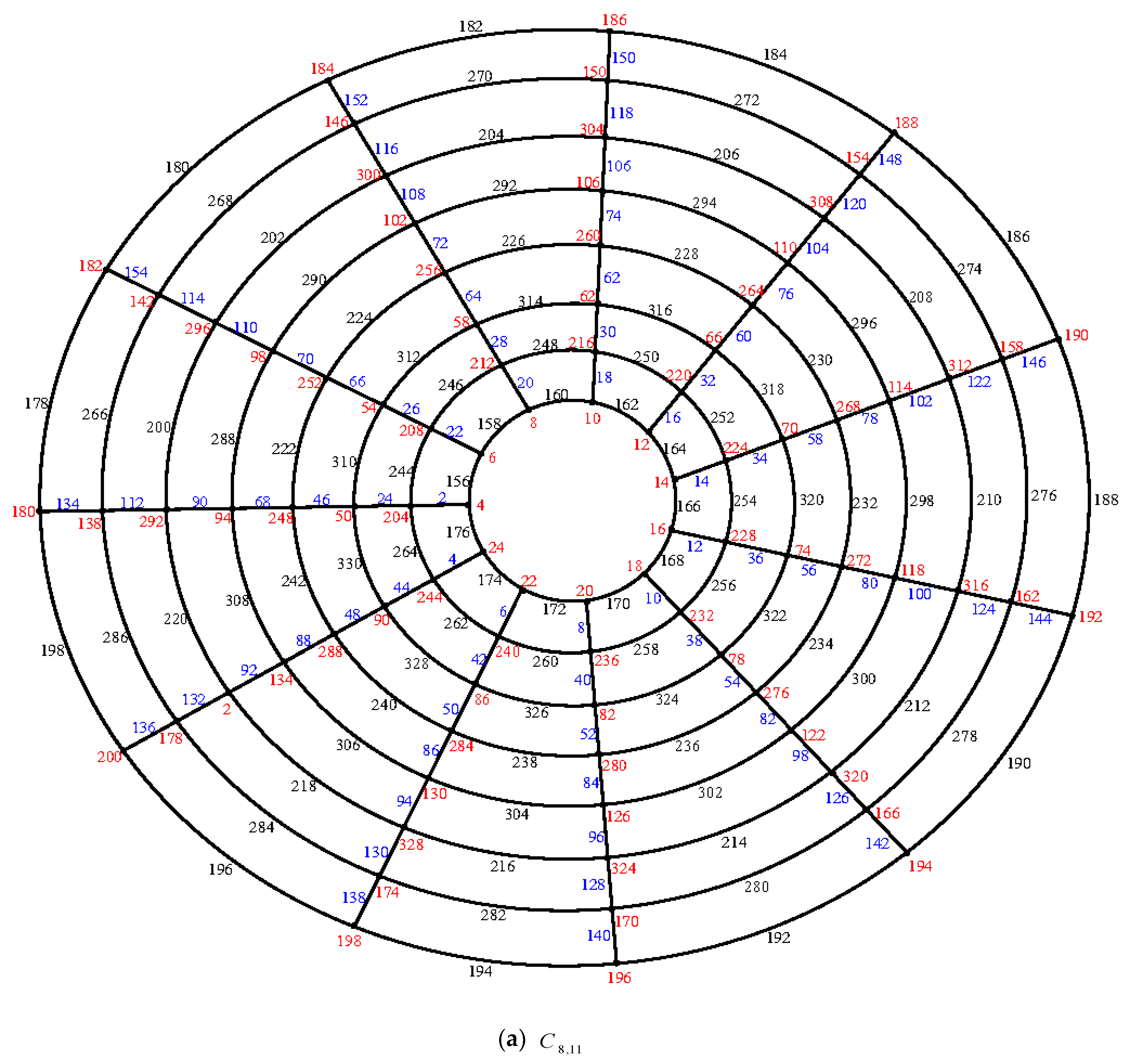
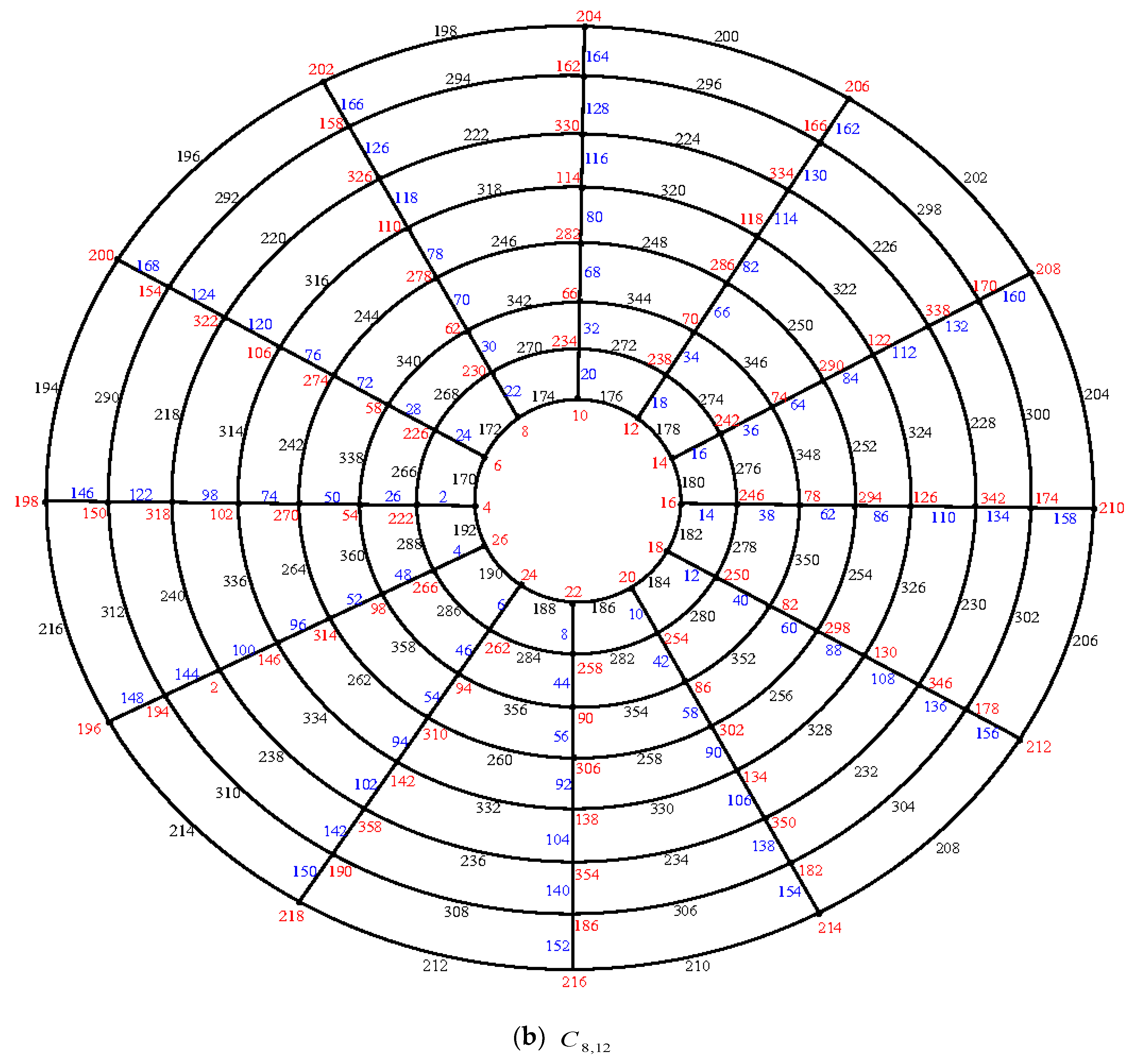
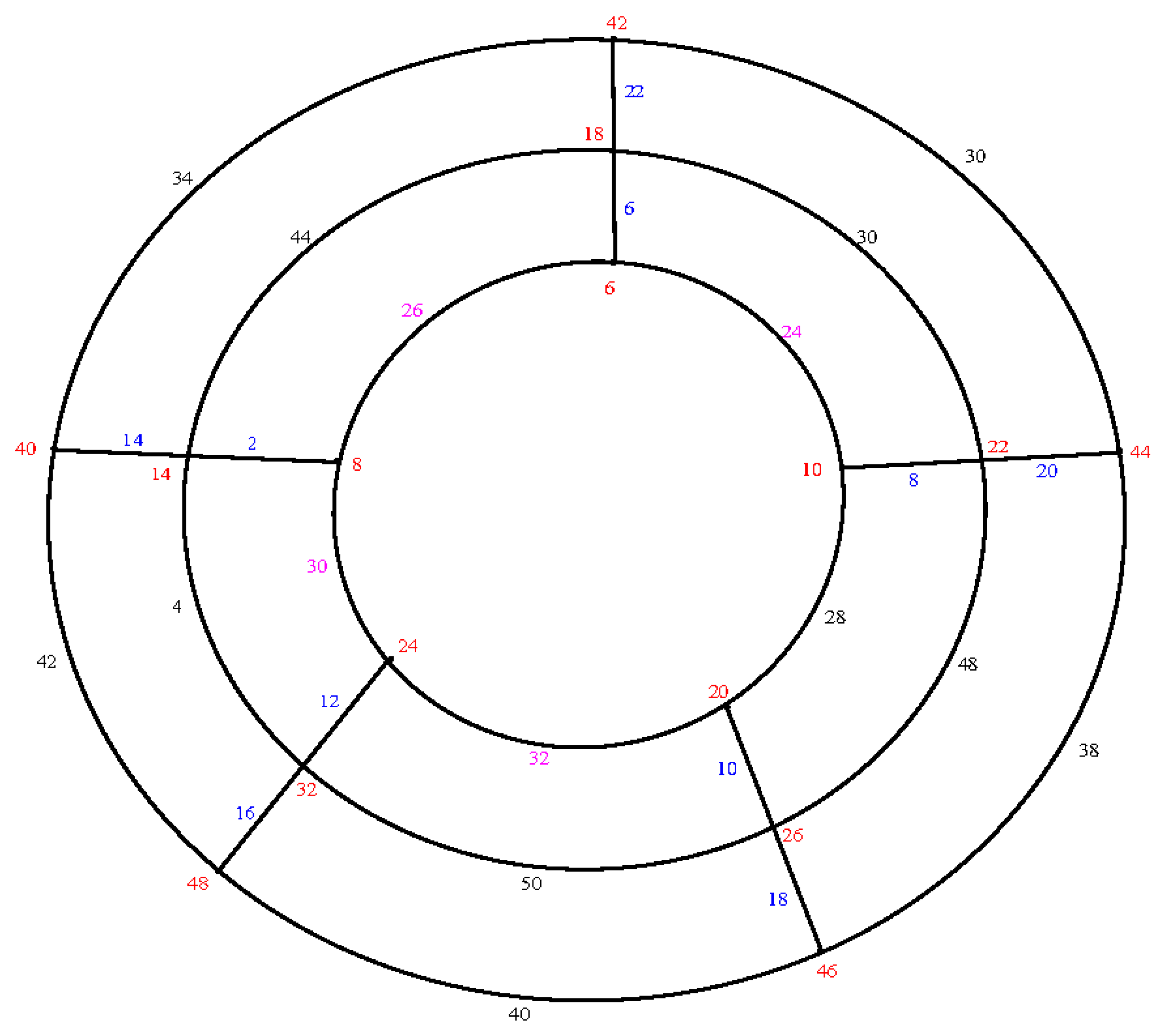
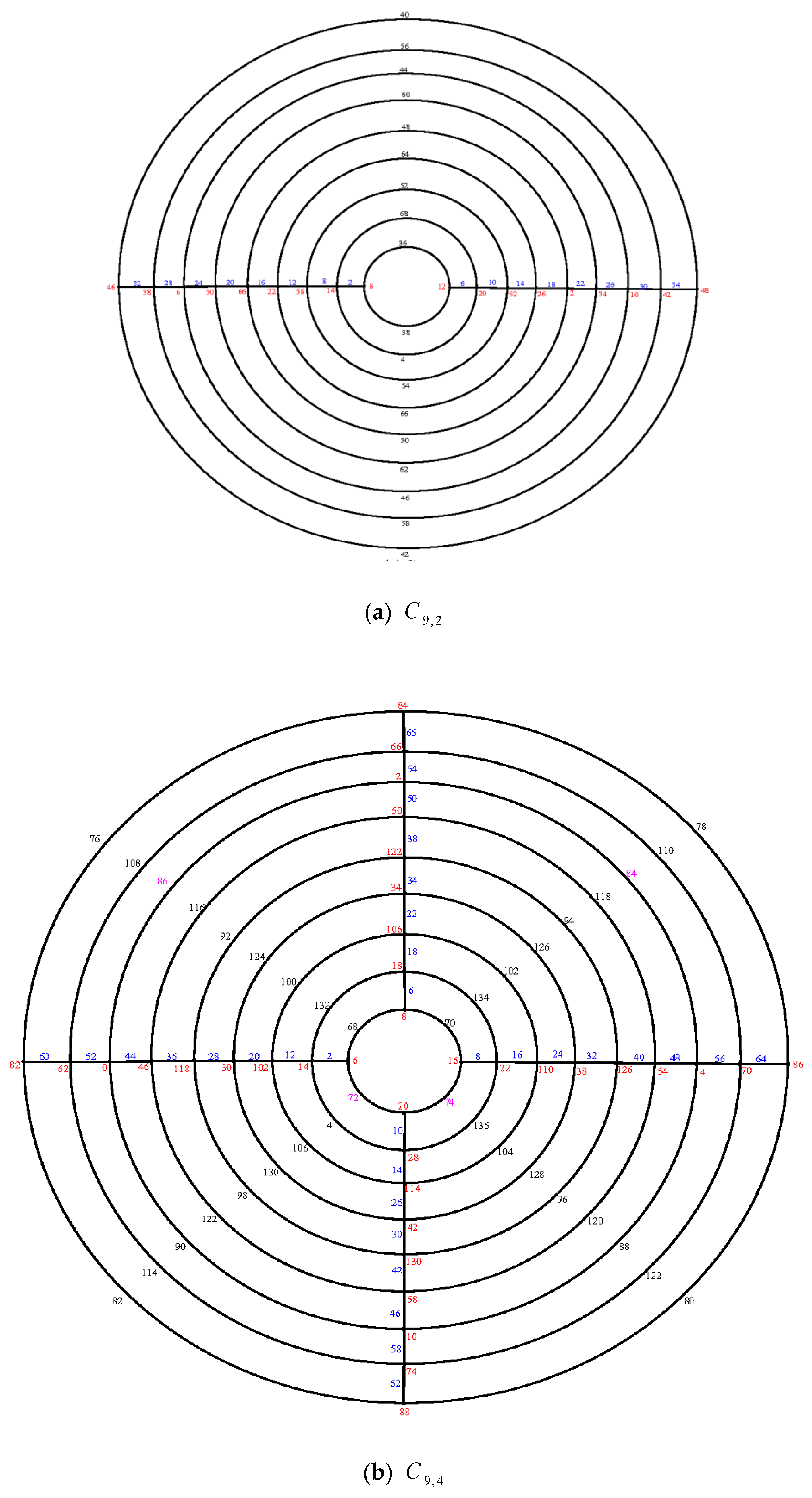
Illustration: An e.e.g., l, of the cylinder grid graphs
and
are shown in
Figure 3.
Theorem 2. If and is an odd positive integer greater than , then the cylinder grid graph , is an edge even graceful graph.
Proof. Using standard notation , , , and There are three cases:
Case (1): If
, let the cylinder grid graph
be as in
Figure 4.
First, we label the edges of the paths beginning with the edges of the path as follows: Move clockwise to label the edges Then, move anticlockwise to label the edges ,
Secondly, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circle . Label the edges of the circle as follows: , , , , , □
Label the edges of the circle as follows:
Label the edges of the circle as follows:
The labels of corresponding of vertices are as follows:
The labels of vertices of the circle are as follows: , , , ,
The labels of vertices of the circle are
The labels of vertices of the circle are
Case (2): If
, let the cylinder grid graph
be as in
Figure 5.
First, we label the edges of the paths beginning with the edges of the path as the same in case (1).
Secondly, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circle .
Label the edges of the circle as follows: , , , , , ,
The labels of corresponding vertices are as follows: The label of vertices of the circle are , ,
The labels of vertices of the circles and are the same as in case (1).
Case (3): If
, let the cylinder grid graph
be as in
Figure 6.
First, we label the edges of the paths beginning with the edges of the path as the same in case (1). Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circle .
Label the edges of the circle as follows: , , , , ,
The labels of corresponding vertices are as follows: The labels of vertices of the circle : , , ,
The labels of vertices of the circles and are the same as in case (1).
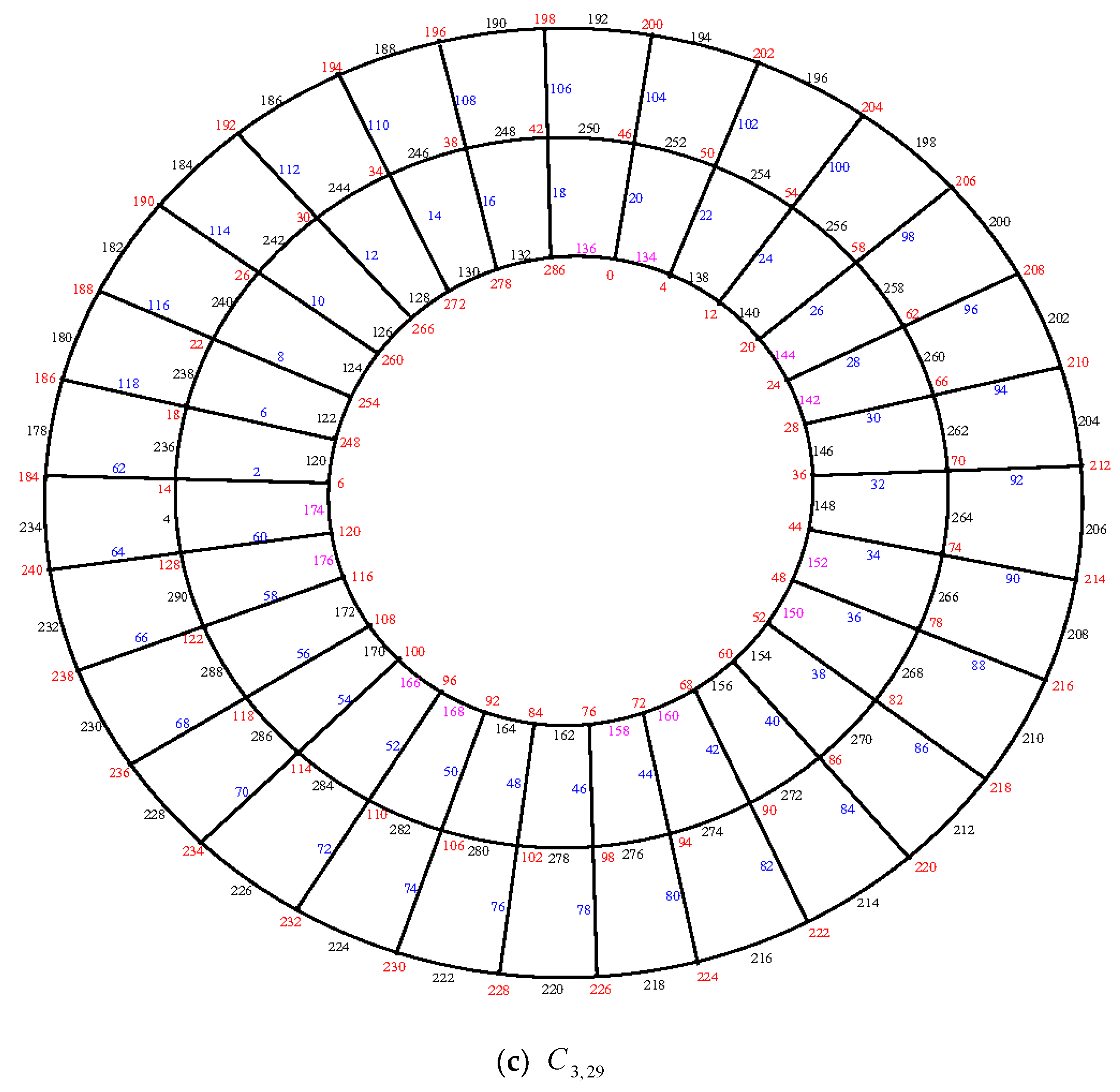
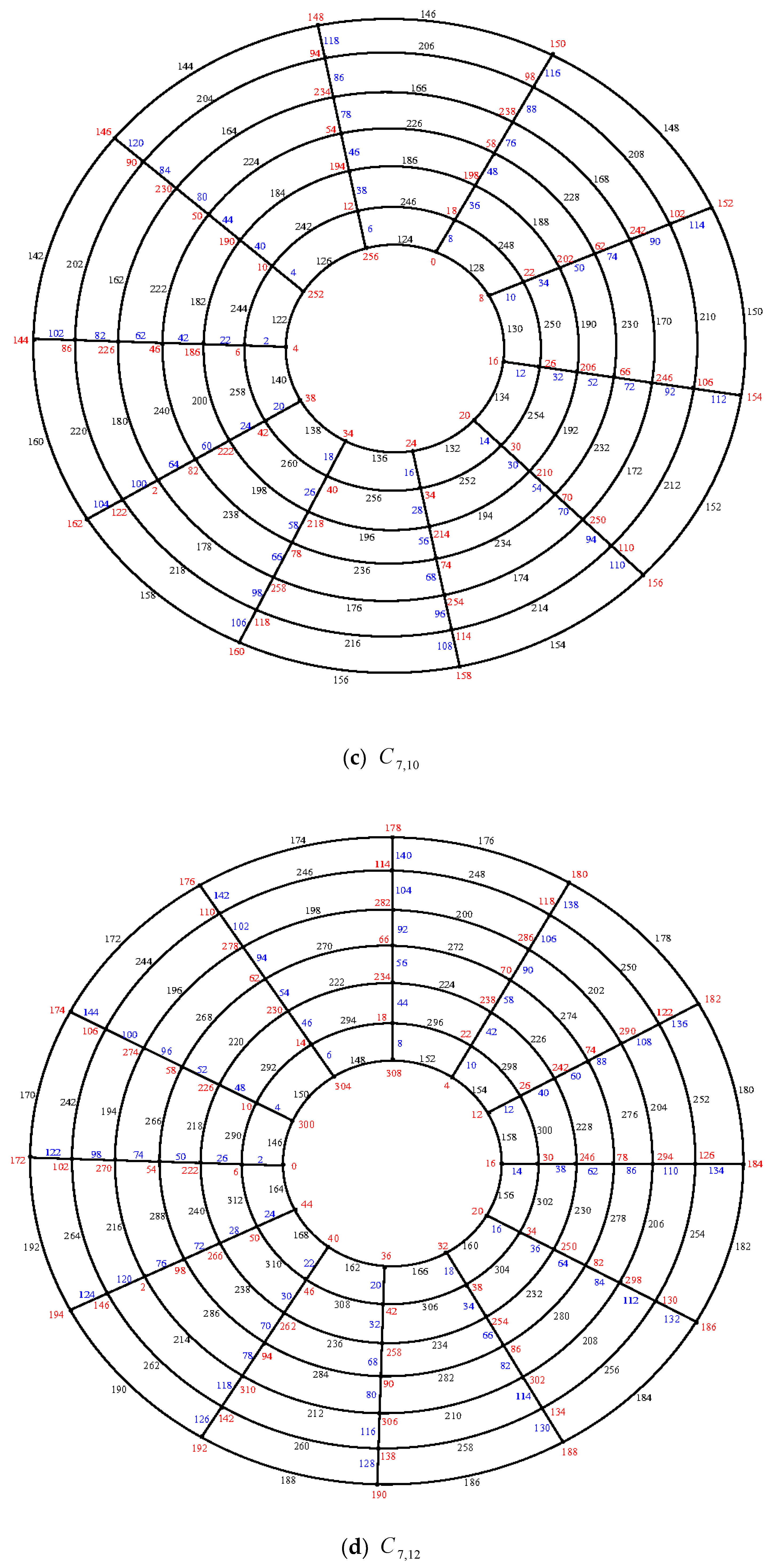
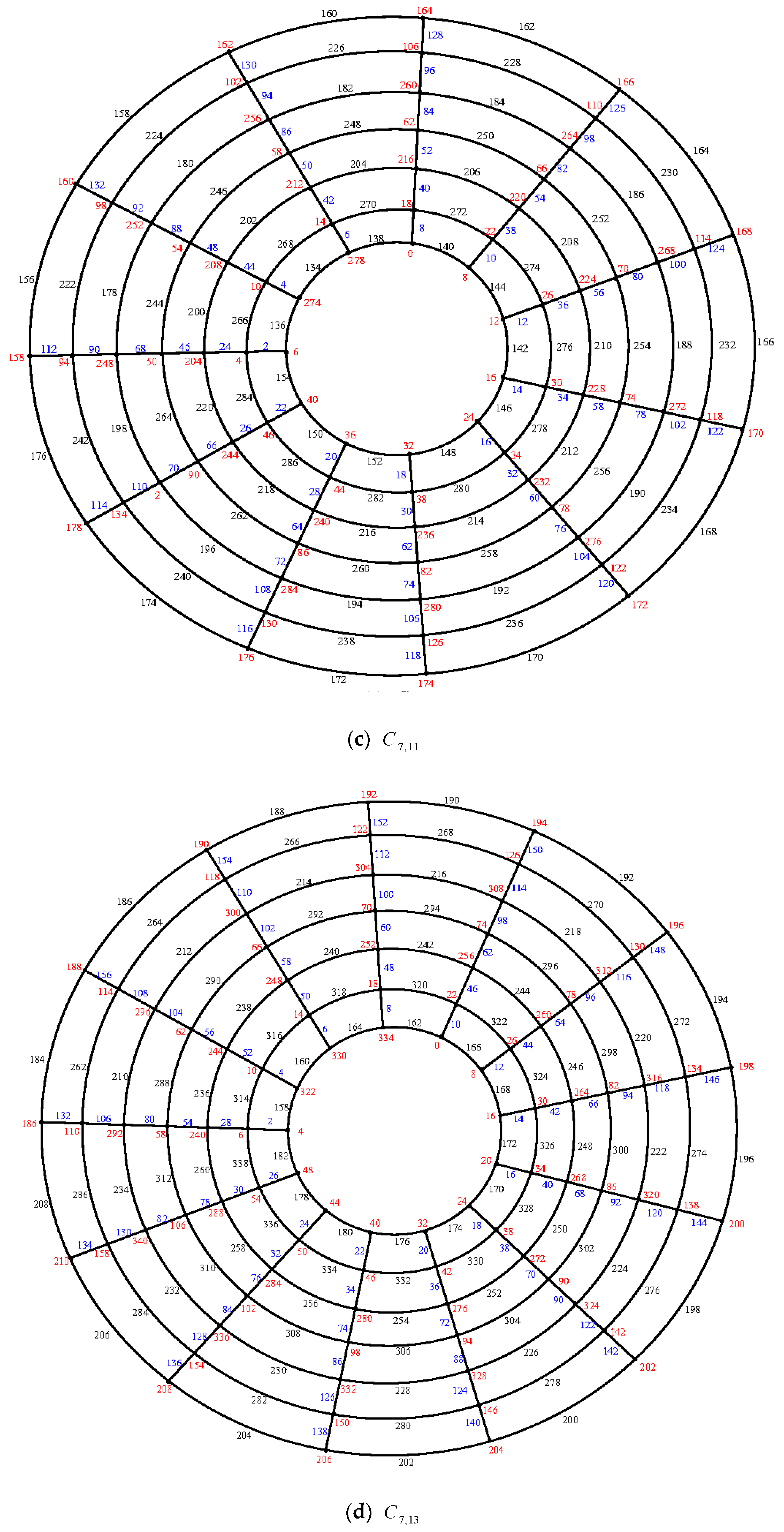
Illustration: An e.e.g., l. of the cylinder grid graphs
and
are shown in
Figure 7.
Remark 1. Note that is an edge even graceful graph but it does not follow the pervious rule (see Figure 8). Theorem 3. If is an odd positive integer greater than and is an even positive integer, , then the cylinder grid graph , is an edge even graceful graph.
Proof. Using standard notation , and and □
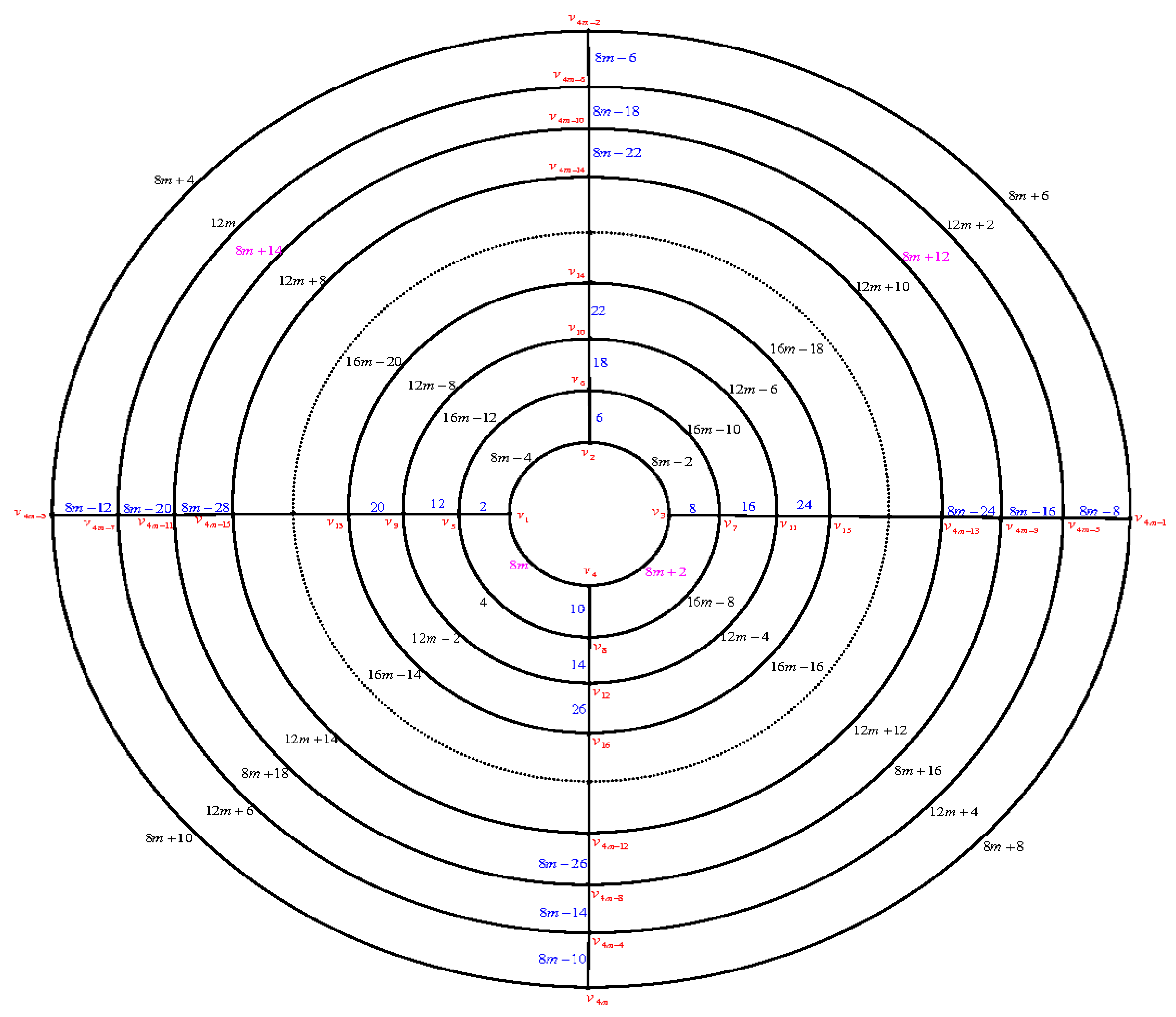
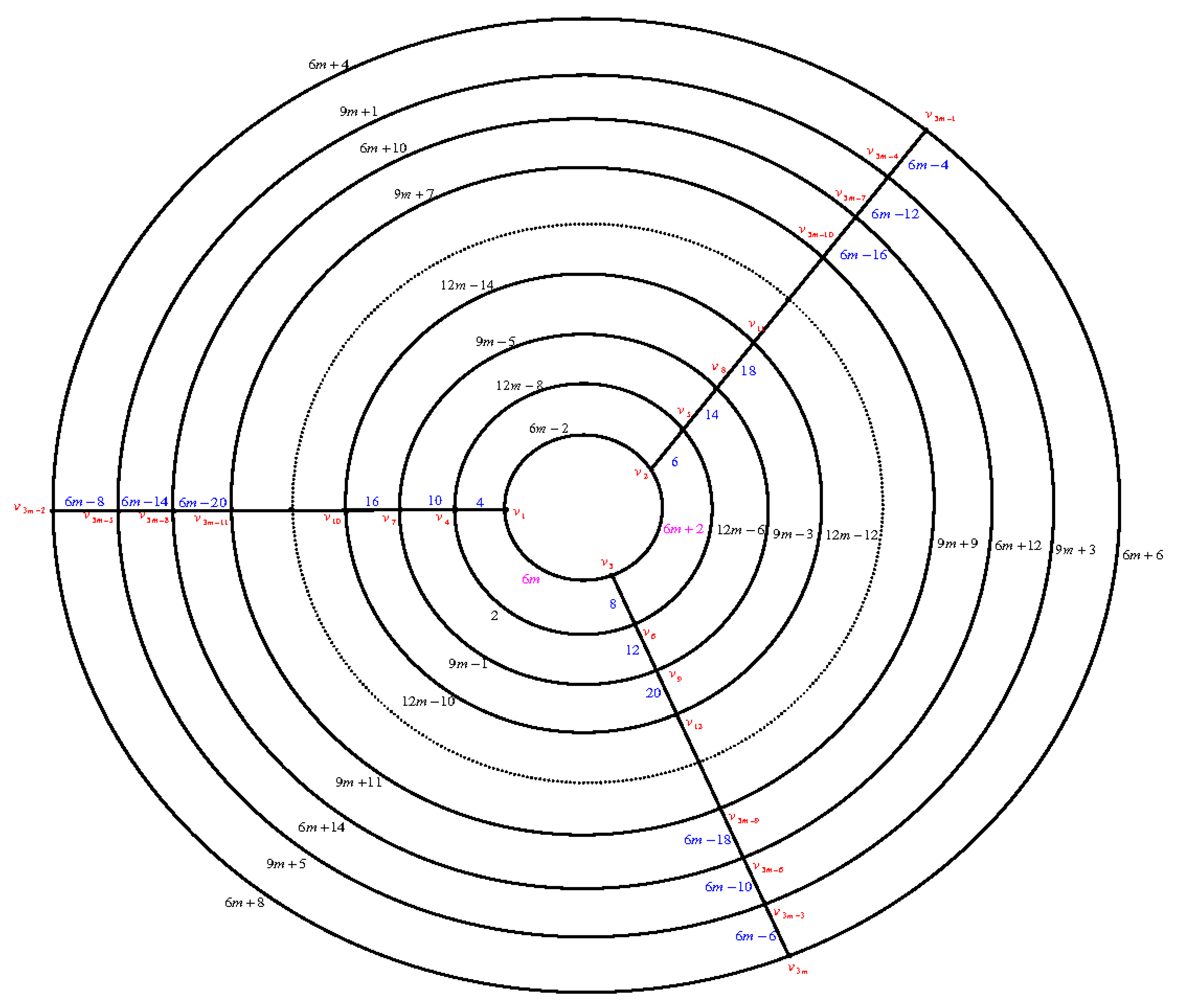
Let the cylinder grid graph
be as in
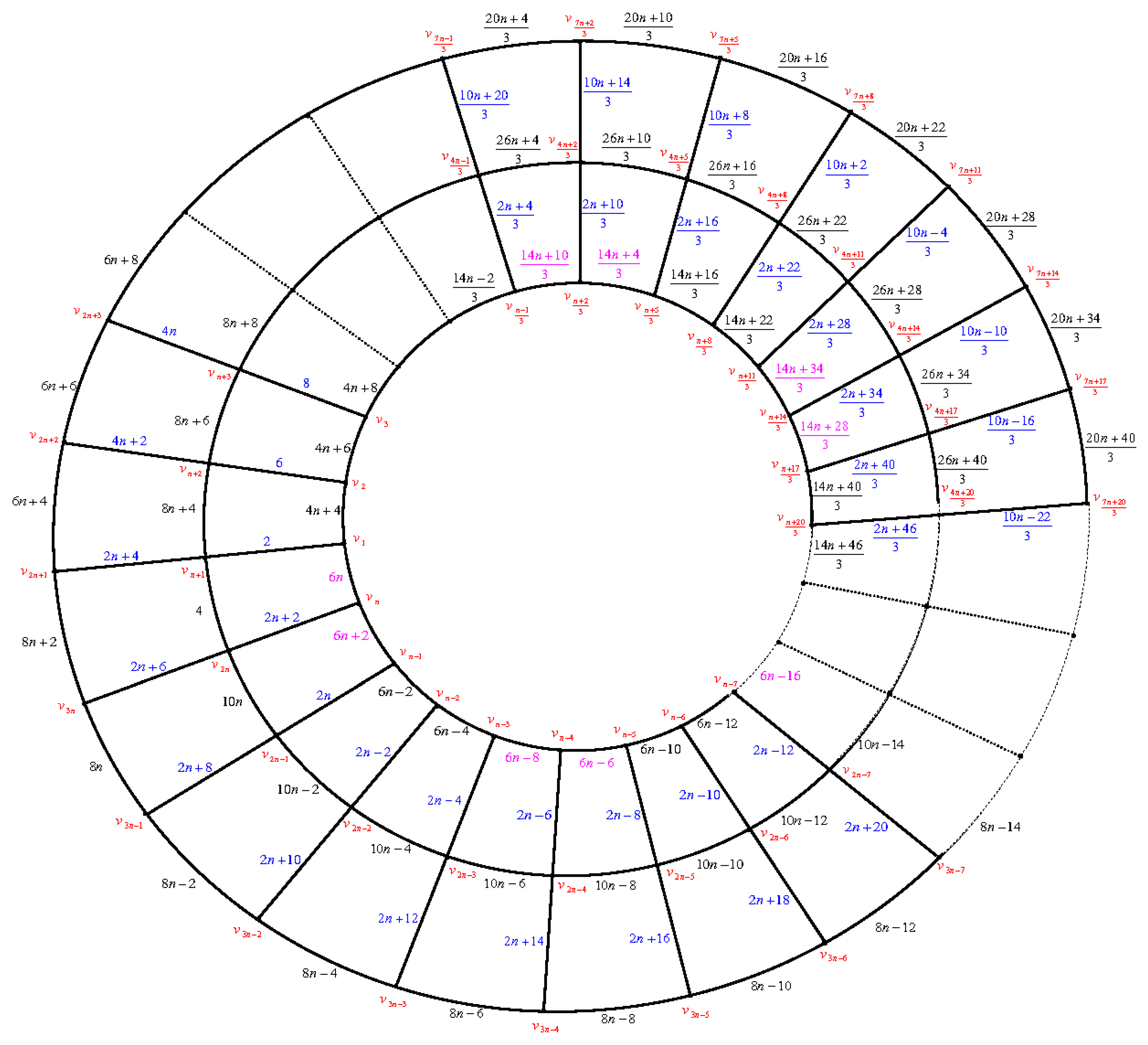
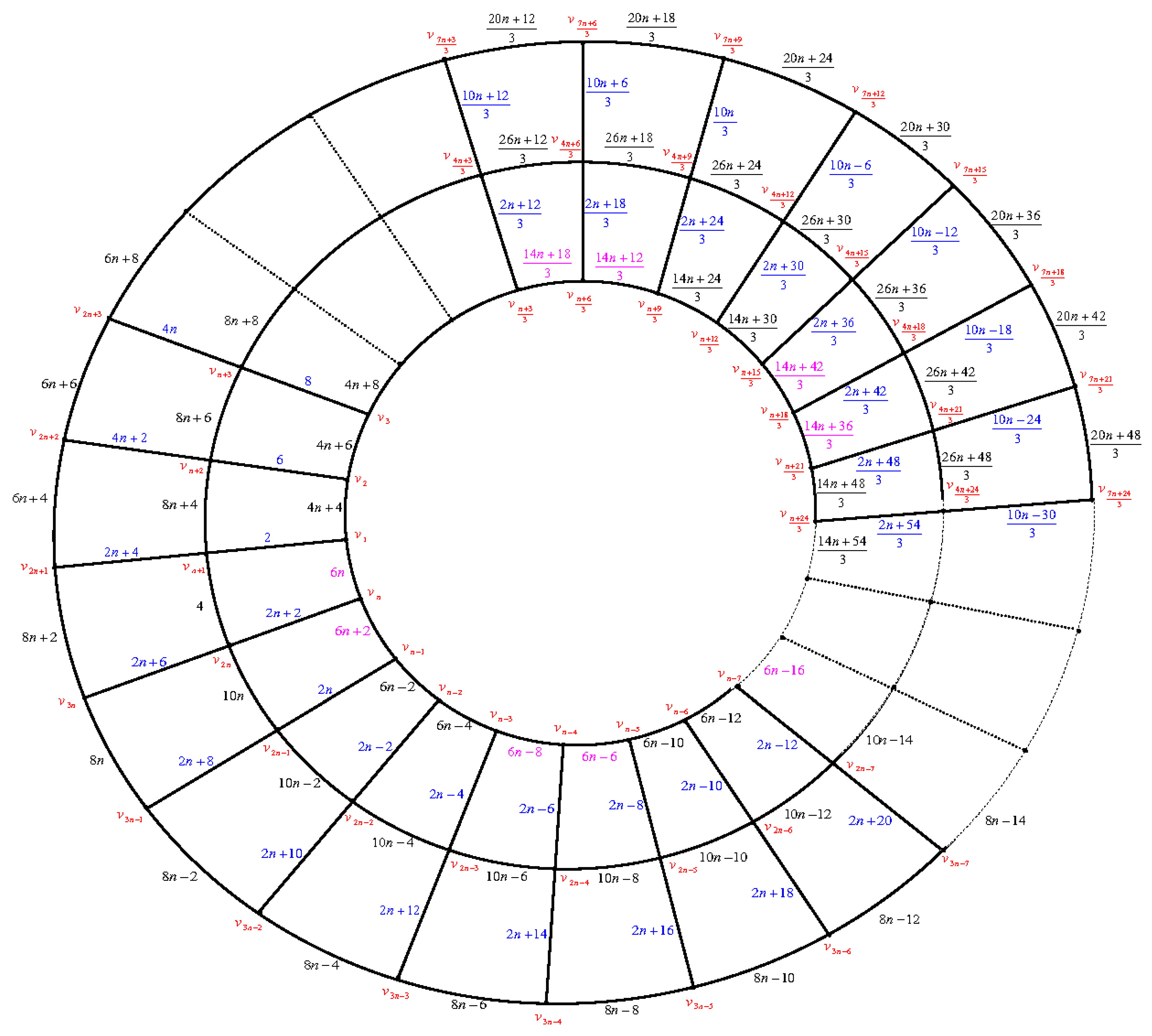
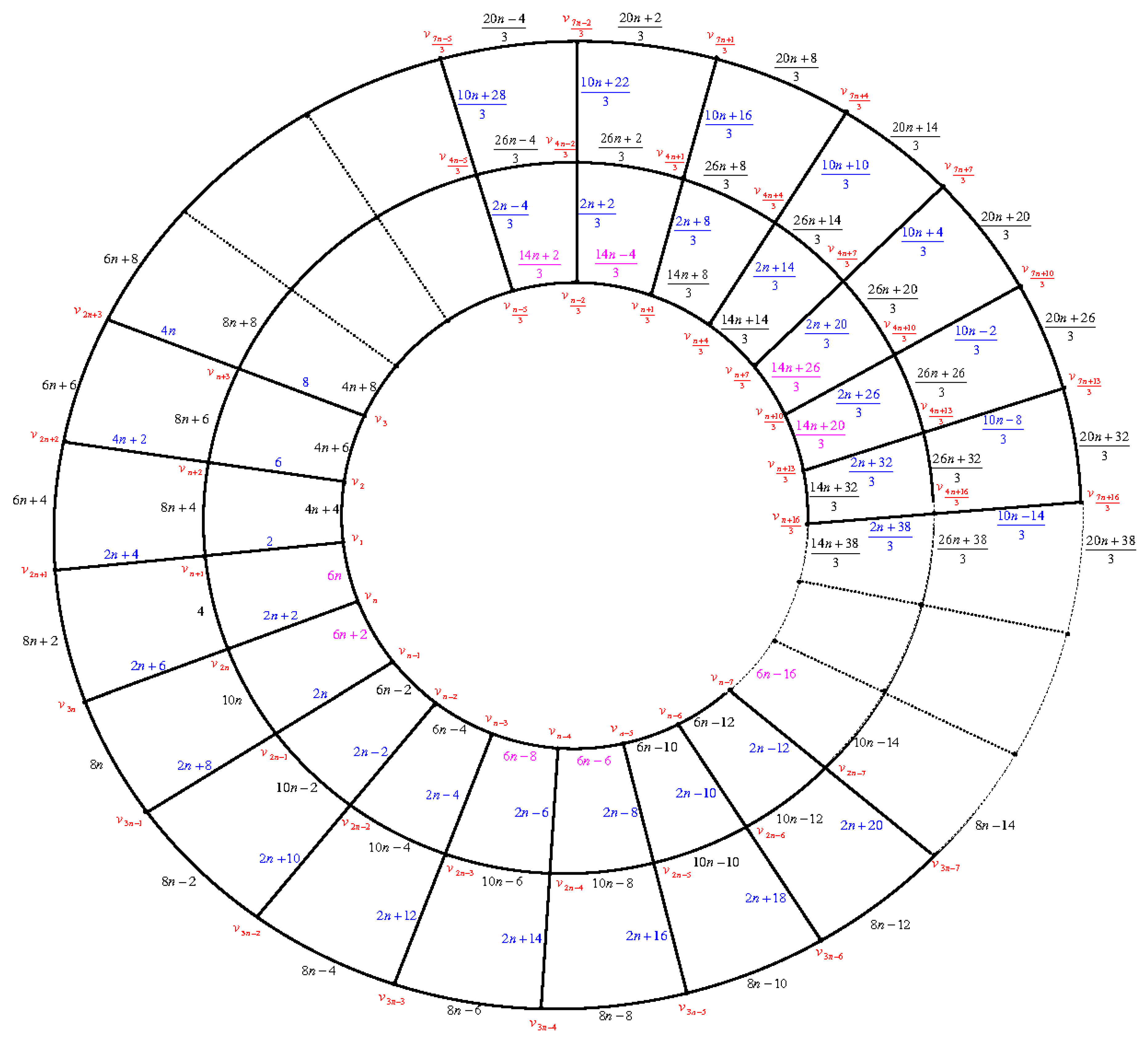
Figure 9. There are six cases:
Case (1): . First, we label the edges of the paths beginning with the edges of the path as follows: Move clockwise to label the edges by then move anticlockwise to label the edges by then move clockwise to label the edges by and so on.
Finally, move anticlockwise to label the edges by
Secondly, we label the edges of the circles beginning with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles . Finally, we label the edges of the circles .
Label the edges of the circle as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows: and so on.
Label the edges of the circle as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows: and so on.
Label the edges of the circle as follows:
Label the edges of as follows:
Thus, the labels of corresponding vertices will be:
The label the vertices of are: ; ; ;
The label the vertices of respectively are: ;
Case (2): .
First, we label the edges of the paths begin with the edges of the path as the same in case (1).
Secondly, we label the edges of the circles begin with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , ,
Label the edges of the circle as follows: , Label the edges of and as in case (1).
Thus, the labels of corresponding vertices will be:
The label the vertices of are: , , ,
The label the vertices of the circle are: , .
The label the vertices of respectively are as the same as in case (1).
Remark 2. In case . Let the edges of the cylinder grid graph are labeled as shown in Figure 10. The corresponding labels of vertices are as follows: ; Case (3): .
First we label the edges of the paths begin with the edges of the path as the same in case (1).
Second we label the edges of the circles begin with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles
Finally we label the edges of the circles .
Label the edges of the circle as follows: , , , and
Label the edges of and as in case (1).
Thus we have the labels of corresponding vertices of the circle will be:
The label the vertices of respectively are as same in case (1)
Remark 3. In case . Let the the edges of the cylinder grid graph are labeled as shown in Figure 11. The corresponding labels of vertices are as follows: , Case (4): .
First, we label the edges of the paths begin with the edges of the path as the same in case (1).
Secondly, we label the edges of the circles begin with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , , ,
Label the edges of and as in case (1).
Label the edges of the circle as follows: ,
Label the edges of the circle as follows:
Thus we have the labels of corresponding vertices will be:
The labels the vertices of the circle are: , , , ,
The labels the vertices of the circle are:
The labels the vertices of respectively are the same as in case (1).
The labels the vertices of are: Case (5): .
First, we label the edges of the paths begin with the edges of the path as the same in case (1).
Secondly, we label the edges of the circles begin with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles
Finally we label the edges of the circles
Label the edges of the circle as follows: , , , , ,
Label the edges of the circle as follows ,
Label the edges of and as the same in case (1).
Thus we labels of corresponding vertices of the circle will be: , , , ,
The labels the vertices of the circle are: The labels the vertices of respectively are as the same in case (1).
Case (6): . First we label the edges of the paths begin with the edges of the path as the same as in case (1).
Second we label the edges of the circles begin with the edges of the inner most circle , then the edges of outer circle , then the edges of the circles
Finally we label the edges of the circles .
Label the edges of the circle as follows: , , , , ,
Label the edges of the circle as follows: ,
Label the edges of and as in case (1).
Thus we have the labels of corresponding vertices will be:
The labels the vertices of the circle are as follows: , , , ,
The labels the vertices of the circle are as follows: Label the vertices of respectively are as the same as in case (1).
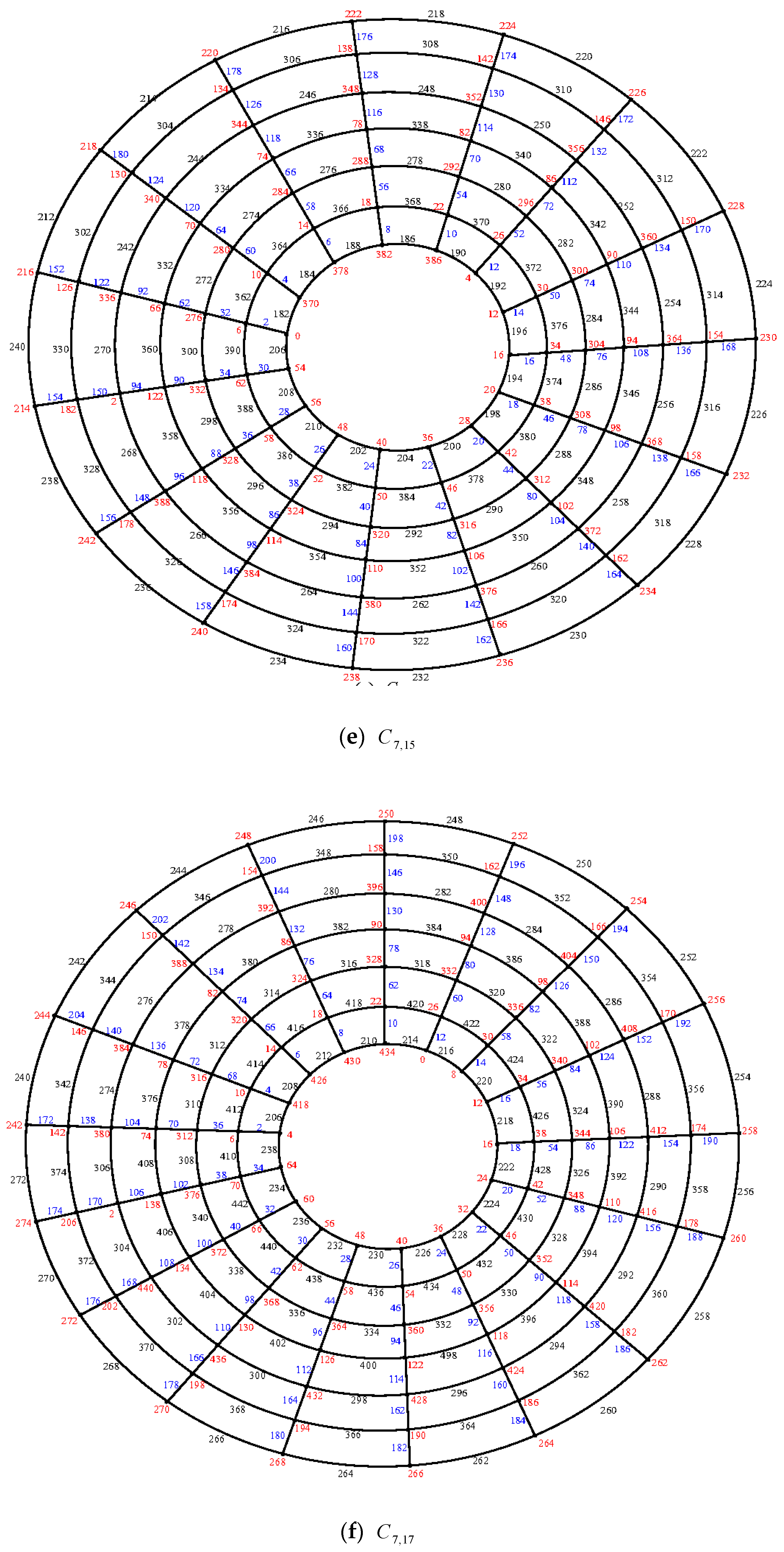
Illustration: The edge even graceful labeling of the cylinder grid graphs
and
are shown in
Figure 12.
Theorem 4. If is an odd positive integer greater than and is an odd positive integer, , then the cylinder grid graph , is an edge even graceful graph.
Proof. Using standard notation , , , and □
Let the cylinder grid graph
be as in
Figure 9. There are six cases:
Case (1): .
First, we label the edges of the paths beginning with the edges of the path as follows: Move clockwise to label the edges by then move anticlockwise to label the edges by then move clockwise to label the edges by , and so on.
Finally, move anticlockwise to label the edges , by
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of as follows: , , , ,
Then, label the edges of and as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows: and so on.
Label the edges of the circle as follows:
Label the edges of the circle as follows:
Label the edges of the circle as follows: and so on.
Label the edges of the circle as follows:
Label the edges of as follows:
Thus, the labels of corresponding vertices of the circle will be: , ,
The labels of the vertices of , respectively, are as follows: ;
Case (2): .
First, we label the edges of the paths beginning with the edges of the path as the same in case (1).
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , ,
Label the edges of the circle as follows: , ,
Label the edges of and as in case (1).
Thus, the labels of corresponding vertices will be:
The labels of the vertices of are as follows: , , ,
The labels of the vertices of the circle are as follows: ,
The labels of the vertices of , respectively, are the same as in case (1).
Remark 4. In case and is odd, .
Let the label of edges of the cylinder grid graph be as in Figure 13. Thus, the labels of corresponding vertices are as follows:
The labels of the vertices of the circle are
The labels of the vertices of the circle are
The labels of the vertices of the circles are , is odd.
The labels of the vertices of the circles are , is even.
Case (3): .
First, we label the edges of the paths beginning with the edges of the path the same as in case (1).
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , , , Label the edges of and as in case (1).
Thus, the labels of corresponding vertices of the circle will be: , , , ,
The labels of the vertices of , respectively, are the same as in case (1).
Case (4): .
First, we label the edges of the paths beginning with the edges of the path the same as in case (1).
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , , ,
Label the edges of the circle as follows: , , ,
Label the edges of and as in case (1).
Thus, the labels of corresponding vertices will be:
The labels of the vertices of the circle are as follows: , , , ,
The labels of the vertices of the circle are as follows: ,
The labels of the vertices of , respectively, are as in case (1).
Case (5): .
First, we label the edges of the paths beginning with the edges of the path the same as in case (1).
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , , ,
Label the edges of the circle as follows: , ,
Label the edges of and as in case (1).
Thus, the labels of corresponding vertices will be:
The labels of the vertices of the circle are as follows: , , , ,
The labels of the vertices of the circle are as follows: ,
The labels of the vertices of , respectively, are as in case (1).
Case (6): .
First, we label the edges of the paths beginning with the edges of the path the same as in case (1).
Second, we label the edges of the circles beginning with the edges of the innermost circle , then the edges of outer circle , and then the edges of the circles
Finally, we label the edges of the circles .
Label the edges of the circle as follows: , , , , ,
Label the edges of the circle as follows:
Label the edges of and as in case (1).
Thus, the labels of corresponding vertices will be:
The labels of the vertices of the circle are as follows: , , , ,
The labels of the vertices of the circle are as follows:
The labels of the vertices of , respectively, are as the same as in case (1).
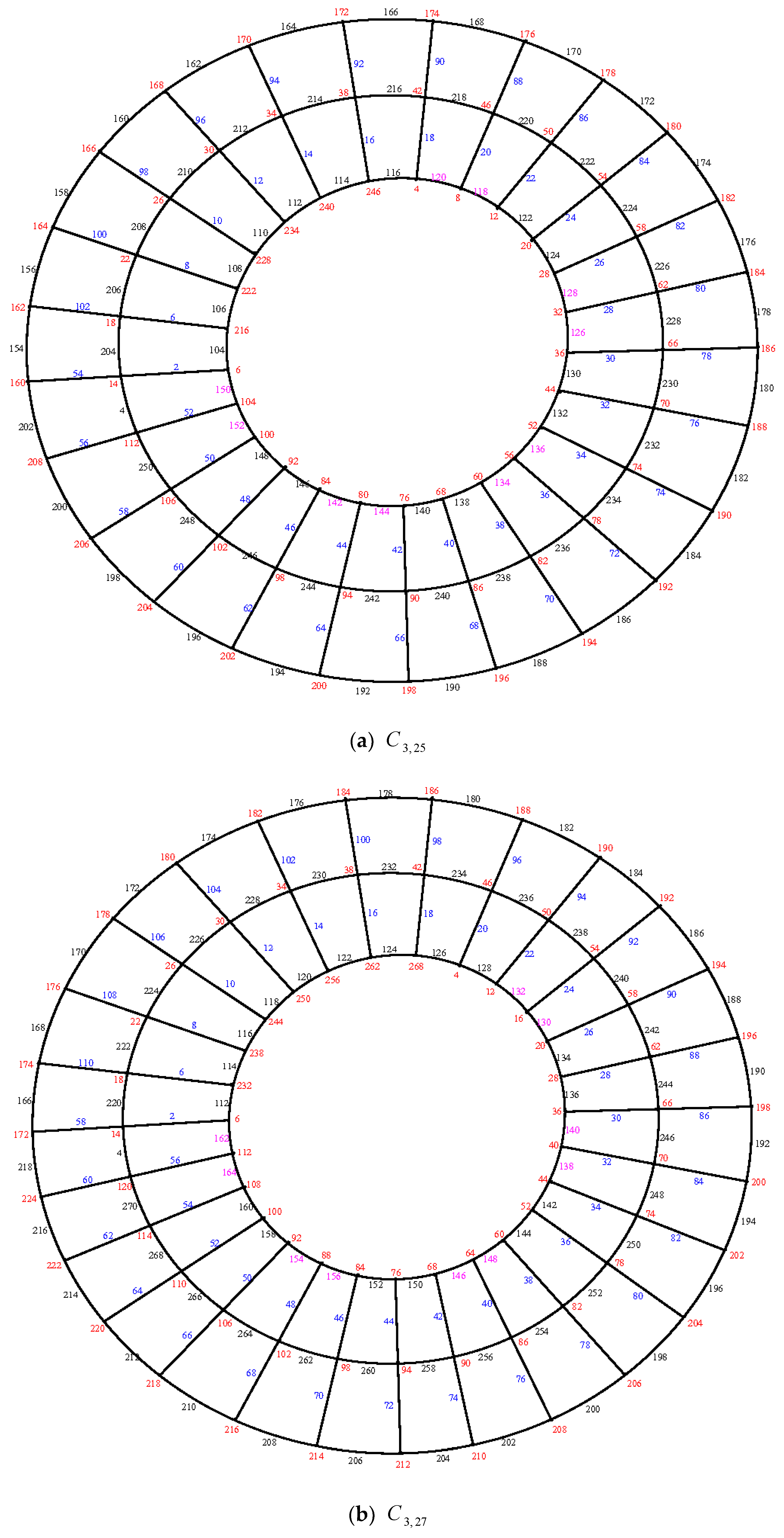
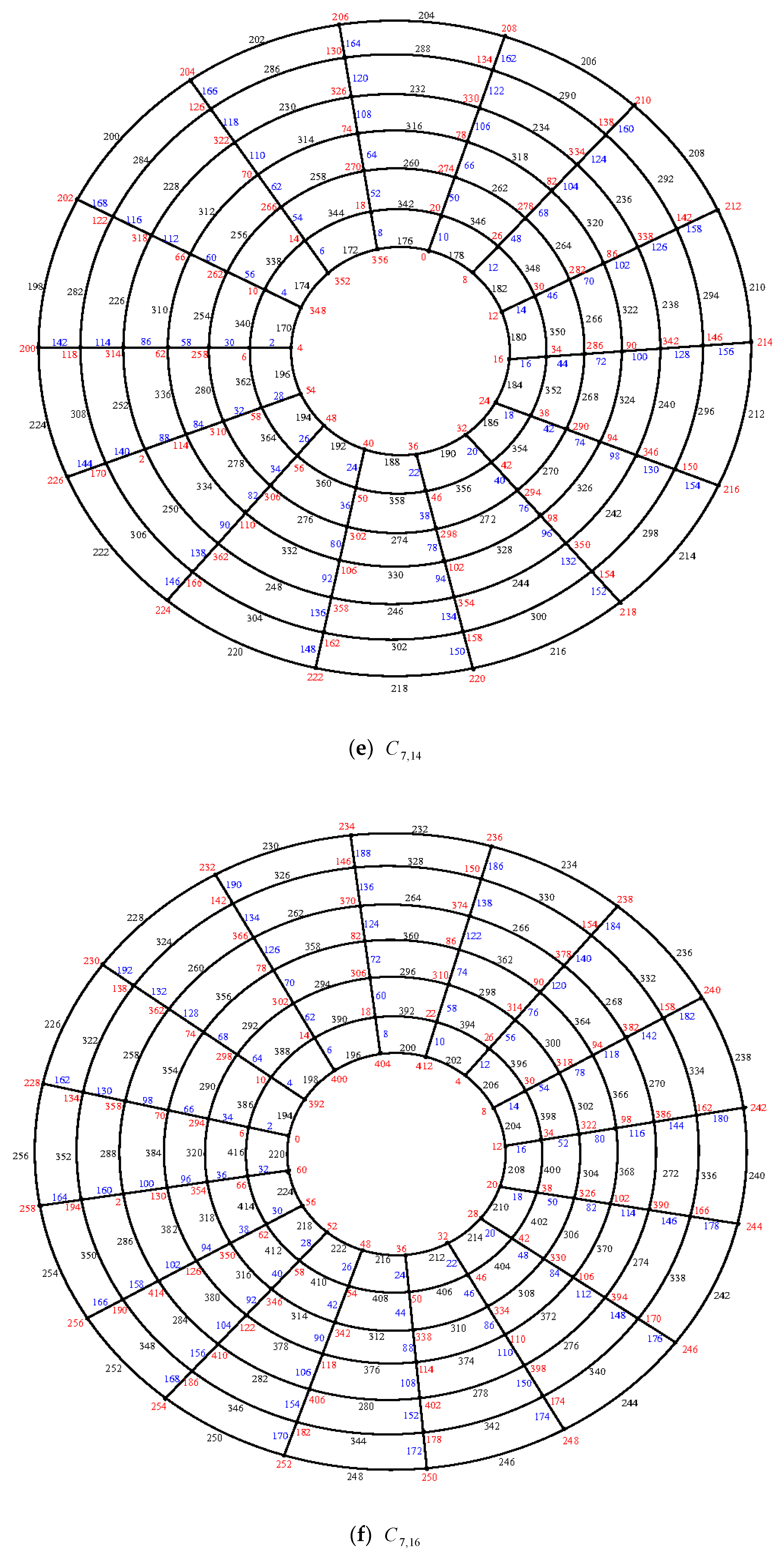
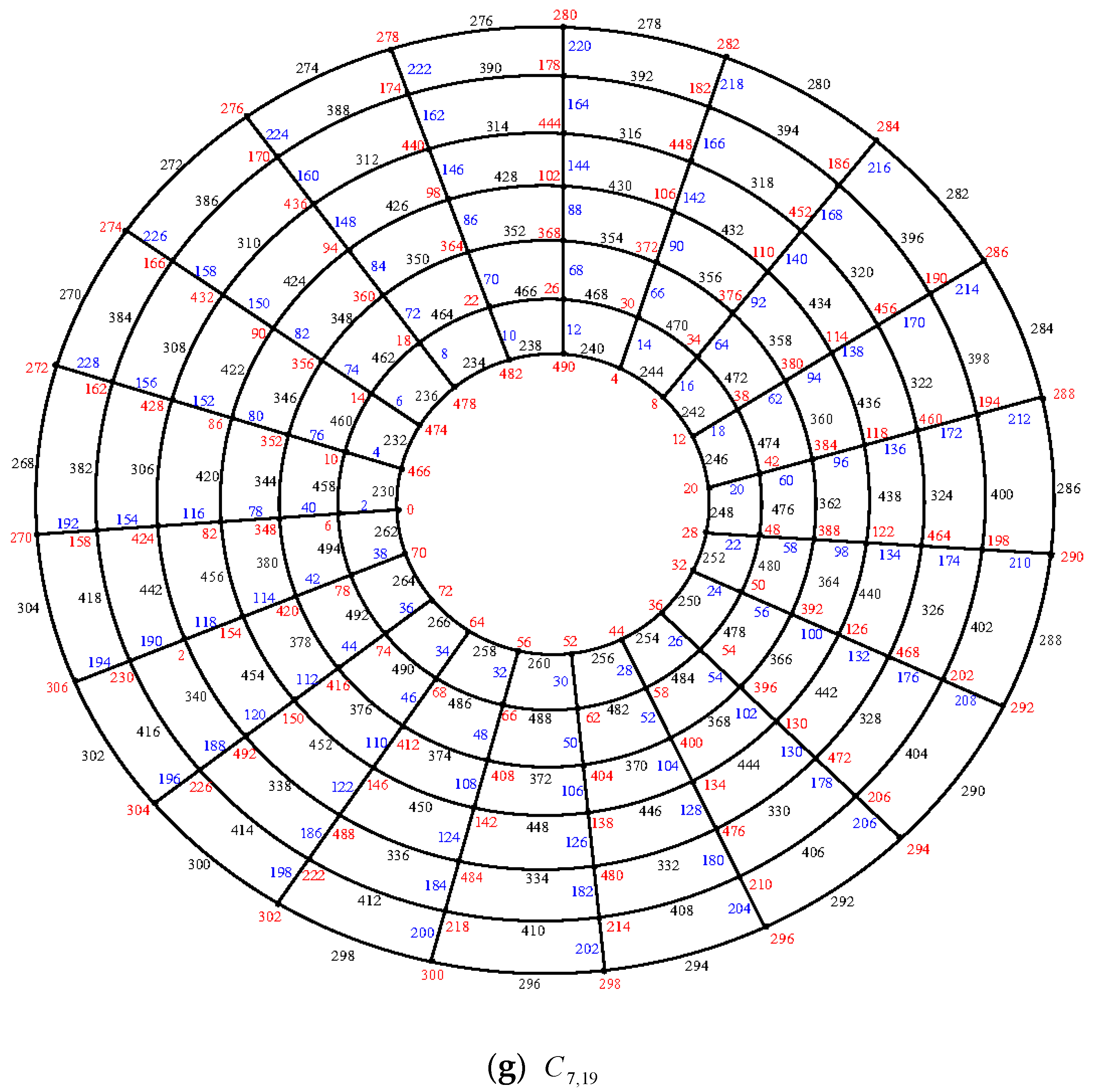
Illustration: An e.e.g.l. of the cylinder grid graphs
and
is shown in
Figure 14.