Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators
Abstract
1. Introduction
2. Results
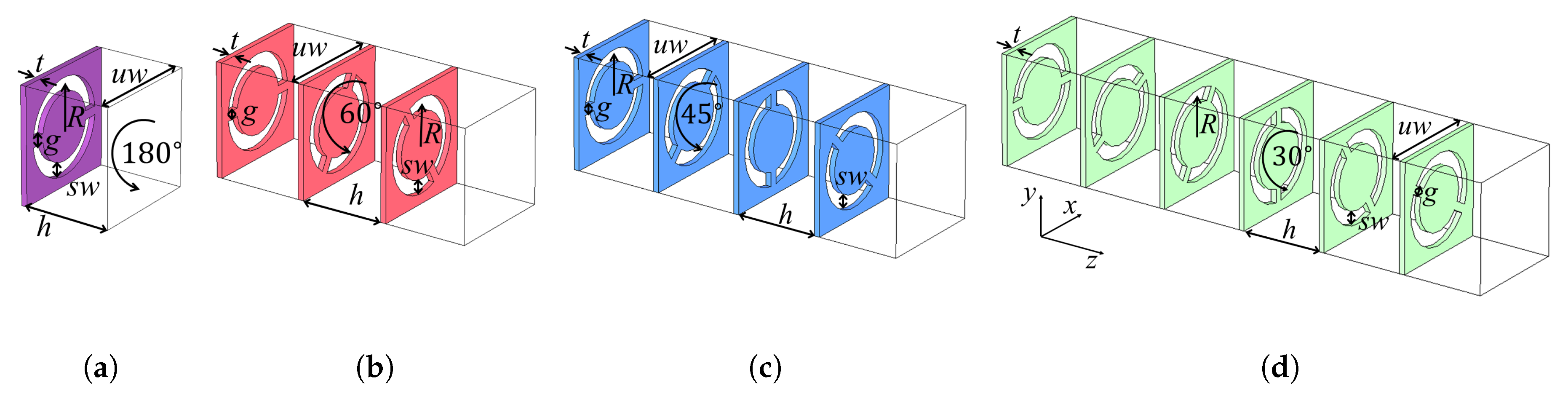
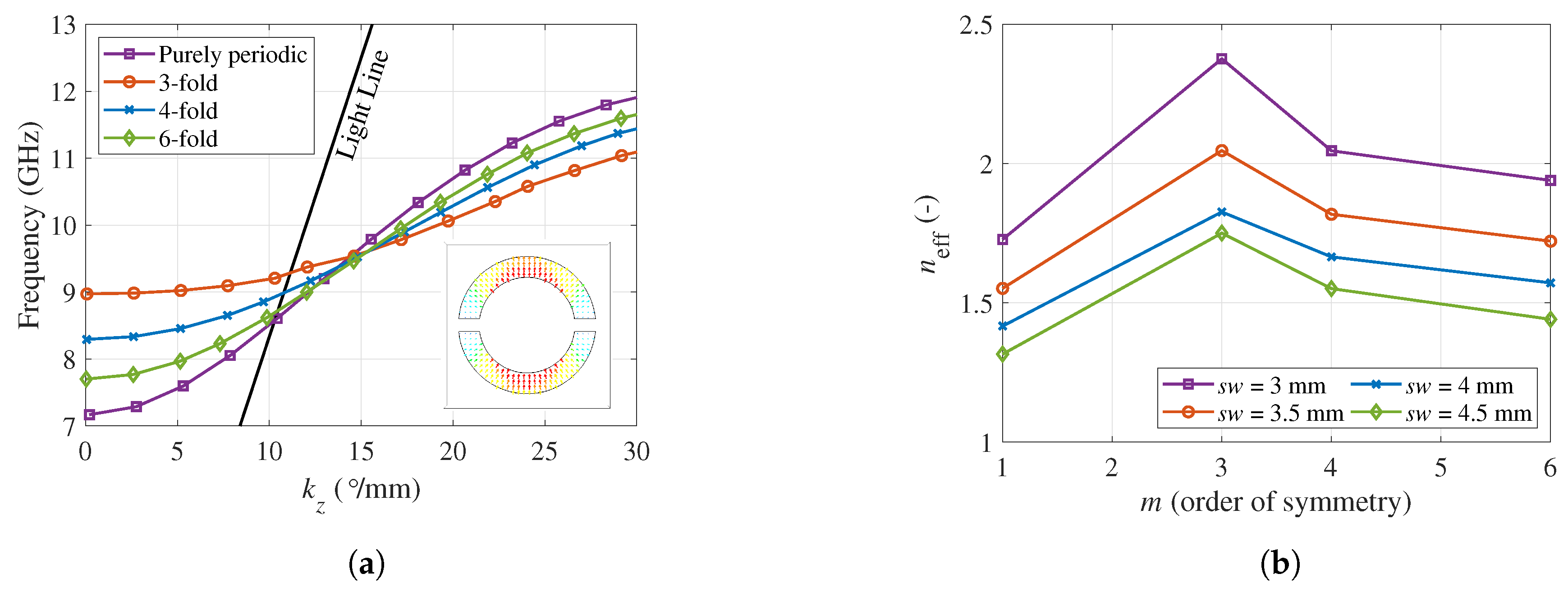
2.1. Study of Twist-Symmetric Complementary Split Ring Resonators
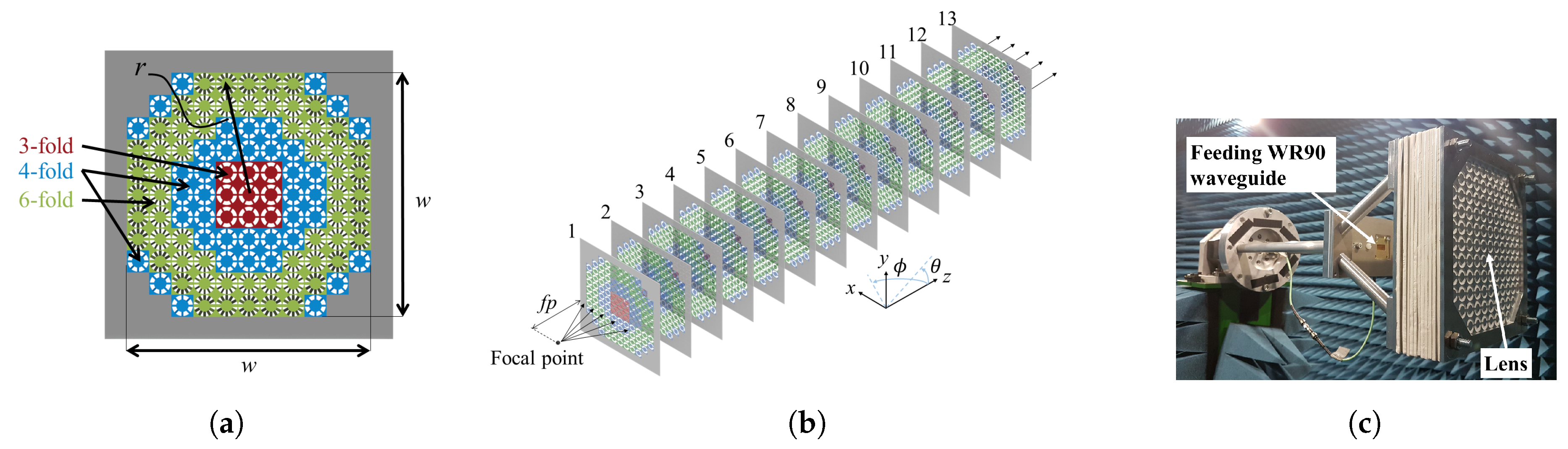
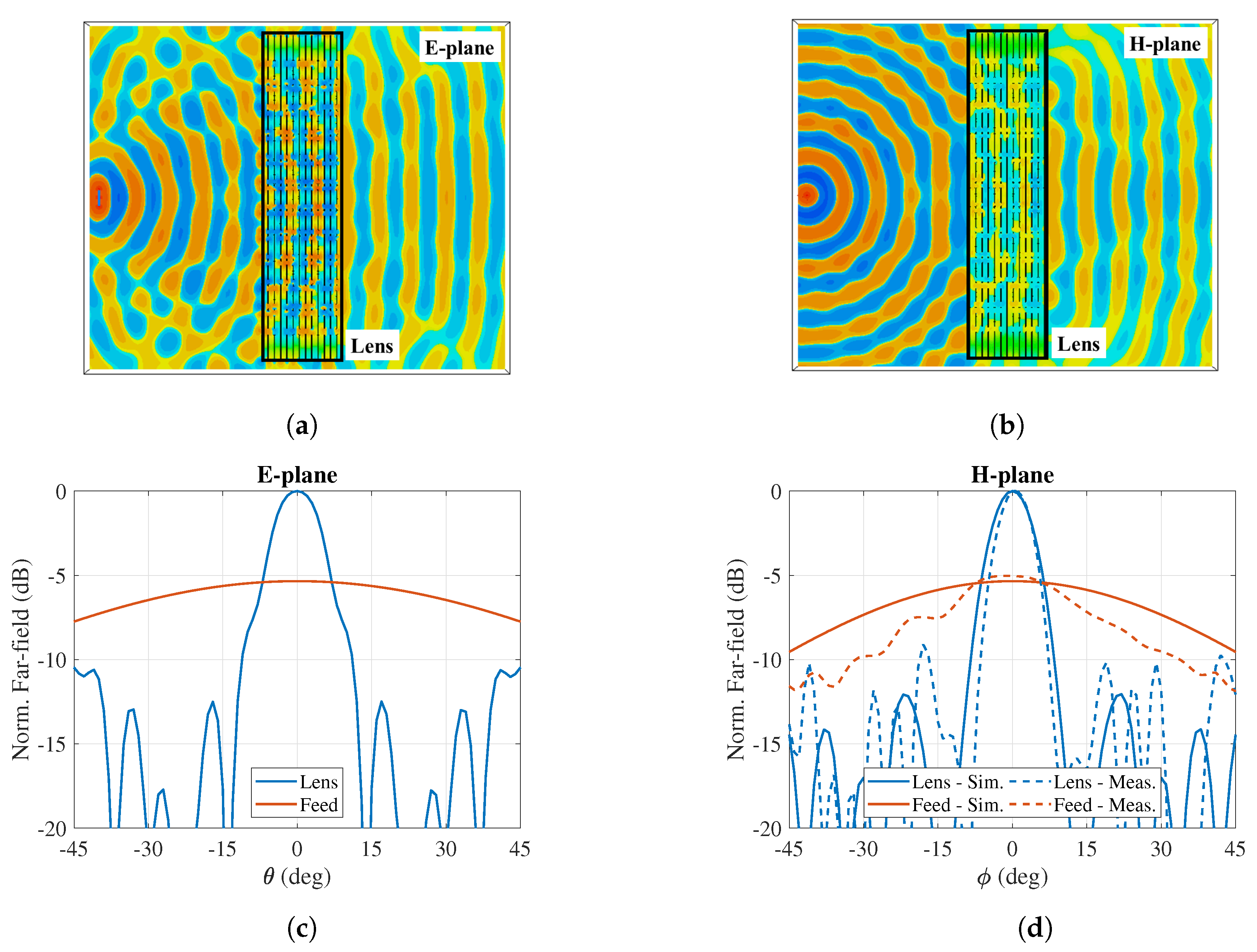
2.2. Lens Design Using CSRRs
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Conflicts of Interest
References
- Hessel, A.; Chen, M.H.; Li, R.C.M.; Oliner, A.A. Propagation in Periodically Loaded Waveguides with Higher Symmetries. Proc. IEEE 1973, 61, 183–195. [Google Scholar] [CrossRef]
- Crepeau, P.J.; McIsaac, P.R. Consequences of Symmetry in Periodic Structures. Proc. IEEE 1963, 52, 33–43. [Google Scholar] [CrossRef]
- Mittra, R.; Laxpati, S. Propagation in a Wave Guide with Glide Reflection Symmetry. Can. J. Phys. 1965, 43, 353–372. [Google Scholar] [CrossRef]
- Kieburtz, R.; Impagliazzo, J. Multimode Propagation on Radiating Traveling-Wave Structures with Glide-Symmetric Excitation. IEEE Trans. Antennas Propag. 1970, 18, 3–7. [Google Scholar] [CrossRef]
- Cao, W.; Chen, Z.N.; Hong, W.; Zhang, B.; Liu, A. A Beam Scanning Leaky-Wave Slot Antenna with Enhanced Scanning Angle Range and Flat Gain Characteristic Using Composite Phase-Shifting Transmission Line. IEEE Trans. Antennas Propag. 2014, 62, 5871–5875. [Google Scholar] [CrossRef]
- Wu, J.J.; Wu, C.J.; Hou, D.J.; Liu, K.; Yang, T.J. Propagation of Low-Frequency Spoof Surface Plasmon Polaritons in a Bilateral Cross-Metal Diaphragm Channel Waveguide in The Absence of Bandgap. IEEE Photonics J. 2015, 7, 1–8. [Google Scholar] [CrossRef]
- Lyu, Y.L.; Liu, X.X.; Wang, P.Y.; Erni, D.; Wu, Q.; Wang, C.; Kim, N.Y.; Meng, F.Y. Leaky-Wave Antennas Based on Noncutoff Substrate Integrated Waveguide Supporting Beam Scanning From Backward To Forward. IEEE Trans. Antennas Propag. 2016, 64, 2155–2164. [Google Scholar] [CrossRef]
- Quesada, R.; Martín-Cano, D.; García-Vidal, F.; Bravo-Abad, J. Deep-Subwavelength Negative-Index Waveguiding Enabled By Coupled Conformal Surface Plasmons. Opt. Lett. 2014, 39, 2990–2993. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Kehn, M.N.M. Ultrawideband Metasurface Lenses Based on Off-Shifted Opposite Layers. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 484–487. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Miao, J.; Mattsson, M.; Algaba-Brazalez, A.; Johansson, M.; Manholm, L. Glide-Symmetric Fully Metallic Luneburg Lens for 5G Communications at Ka-Band. IEEE Antennas Wirel. Propag. Lett. 2018, 17, 1588–1592. [Google Scholar] [CrossRef]
- Padilla, P.; Herrán, L.; Tamayo-Domínguez, A.; Valenzuela-Valdés, J.; Quevedo-Teruel, O. Glide Symmetry to Prevent The Lowest Stopband of Printed Corrugated Transmission Lines. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Quevedo-Teruel, O.; Rajo-Iglesias, E. Design Guidelines for Gap Waveguide Technology Based on Glide-Symmetric Holey Structures. IEEE Microw. Wirel. Compon. Lett. 2017, 27, 542–544. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Brazalez, A.A.; Manholm, L.; Quevedo-Teruel, O. Using Glide-Symmetric Holes to Reduce Leakage Between Waveguide Flanges. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 473–475. [Google Scholar] [CrossRef]
- Ebrahimpouri, M.; Rajo-Iglesias, E.; Sipus, Z.; Quevedo-Teruel, O. Cost-Effective Gap Waveguide Technology Based on Glide-Symmetric Holey EBG Structures. IEEE Trans. Microw. Theory Tech. 2018, 66, 927–934. [Google Scholar] [CrossRef]
- Rajo-Iglesias, E.; Ebrahimpouri, M.; Quevedo-Teruel, O. Wideband Phase Shifter in Groove Gap Waveguide Technology Implemented With Glide-Symmetric Holey EBG. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 476–478. [Google Scholar] [CrossRef]
- Dahlberg, O.; Mitchell-Thomas, R.; Quevedo-Teruel, O. Reducing the Dispersion of Periodic Structures with Twist and Polar Glide Symmetries. Sci. Rep. 2017, 7, 10136. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Twist and Polar Glide Symmetries: An Additional Degree of Freedom to Control The Propagation Characteristics of Periodic Structures. Sci. Rep. 2018, 8, 11266. [Google Scholar] [CrossRef]
- Dahlberg, O.; Ghasemifard, F.; Valerio, G.; Quevedo-Teruel, O. Propagation Characteristics of Periodic Structures Possessing Twist and Polar Glide Symmetries. EPJ Appl. Metamater. 2019, in pressing. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Dahlberg, O.; Valerio, G. Propagation in Waveguides With Transversal Twist-Symmetric Holey Metallic Plates. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Quevedo-Teruel, O.; Ebrahimpouri, M.; Ghasemifard, F. Lens Antennas for 5G Communications Systems. IEEE Commun. Mag. 2018, 56, 36–41. [Google Scholar] [CrossRef]
- Cavallo, D.; Felita, C. Analytical Formulas for Artificial Dielectrics with Nonaligned Layers. IEEE Trans. Antennas Propag. 2017, 65, 5303–5311. [Google Scholar] [CrossRef]
- Cavallo, D. Dissipation Losses in Artificial Dielectric Layers. (Early Access) IEEE Trans. Antennas Propag. 2018, 66. [Google Scholar] [CrossRef]
- Chang, T.; Kim, J.U.; Kang, S.K.; Kim, H.; Kim, D.K.; Lee, Y.H.; Shin, J. Broadband Giant-Refractive-Index Material Based on Mesoscopic Space-Filling Curves. Nat. Commun. 2016, 7, 12661. [Google Scholar] [CrossRef][Green Version]
- Chen, Q.; Ghasemifard, F.; Valerio, G.; Quevedo-Teruel, O. Modeling and Dispersion Analysis of Coaxial Lines With Higher Symmetries. IEEE Trans. Microw. Theory Tech. 2018, 66, 1–8. [Google Scholar] [CrossRef]
- Valerio, G.; Sipus, Z.; Grbic, A.; Quevedo-Teruel, O. Accurate Equivalent-Circuit Descriptions of Thin Glide-Symmetric Corrugated Metasurfaces. IEEE Trans. Antennas Propag. 2017, 65, 2695–2700. [Google Scholar] [CrossRef]
- Valerio, G.; Ghasemifard, F.; Sipus, Z.; Quevedo-Teruel, O. Glide-Symmetric All-Metal Holey Metasurfaces for Low-Dispersive Artificial Materials: Modeling and Properties. IEEE Trans. Microw. Theory Tech. 2018, 66, 1–14. [Google Scholar] [CrossRef]
- Ghasemifard, F.; Norgren, M.; Quevedo-Teruel, O. Dispersion Analysis of 2-D Glide-Symmetric Corrugated Metasurfaces Using Mode-Matching Technique. IEEE Microw. Wirel. Compon. Lett. 2018, 28, 1–3. [Google Scholar] [CrossRef]
- Mesa, F.; Rodríguez-Berral, R.; Medina, F. On the Computation of the Dispersion Diagram of Symmetric One-Dimensionally Periodic Structures. Symmetry 2018, 10, 307. [Google Scholar] [CrossRef]
- Palomares-Caballero, A.; Padilla, P.; Valenzuela-Valdes, J.; Quevedo-Teruel, O. Twist and Glide Symmetries for Helix Antenna Design and Miniaturization. Symmetry 2019, 11, 349. [Google Scholar] [CrossRef]
- Wei, Z.; Cao, Y.; Fan, Y.; Yu, X.; Li, H. Broadband Polarization Transformation via Enhanced Asymmetric Transmission Through Arrays of Twisted Complementary Split-Ring Resonators. Appl. Phys. Lett. 2011, 99, 221907. [Google Scholar] [CrossRef]
- Pfeiffer, C.; Grbic, A. Millimeter-Wave Transmitarrays for Wavefront and Polarization Control. IEEE Trans. Microw. Theory Tech. 2013, 61, 4407–4417. [Google Scholar] [CrossRef]
- Pfeiffer, C.; Grbic, A. Bianisotropic Metasurfaces for Optimal Polarization Control: Analysis and Synthesis. Phys. Rev. Appl. 2014, 2, 044011. [Google Scholar] [CrossRef]
- Padilla, P.; Muñoz-Acevedo, A.; Sierra-Castañer, M. Passive Planar Transmit-Array Microstrip Lens for Microwave Purpose. Microw. Opt. Technol. Lett. 2010, 52, 940–947. [Google Scholar] [CrossRef]
- Yeap, S.B.; Qing, X.; Chen, Z.N. 77-GHz Dual-Layer Transmit-Array for Automotive Radar Applications. IEEE Trans. Antennas Propag. 2015, 63, 2833–2837. [Google Scholar] [CrossRef]
- CST Microwave Studio, Version: 2017. Available online: http://www.cst.com/ (accessed on 20 February 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dahlberg, O.; Valerio, G.; Quevedo-Teruel, O. Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators. Symmetry 2019, 11, 581. https://doi.org/10.3390/sym11040581
Dahlberg O, Valerio G, Quevedo-Teruel O. Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators. Symmetry. 2019; 11(4):581. https://doi.org/10.3390/sym11040581
Chicago/Turabian StyleDahlberg, Oskar, Guido Valerio, and Oscar Quevedo-Teruel. 2019. "Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators" Symmetry 11, no. 4: 581. https://doi.org/10.3390/sym11040581
APA StyleDahlberg, O., Valerio, G., & Quevedo-Teruel, O. (2019). Fully Metallic Flat Lens Based on Locally Twist-Symmetric Array of Complementary Split-Ring Resonators. Symmetry, 11(4), 581. https://doi.org/10.3390/sym11040581





