Green Simulation of Pandemic Disease Propagation
Abstract
1. Introduction
2. Efficient Bernoulli Generation
- Within a particular simulation run, one could use a binomial random variable instead of a series of Bern(p) random variables to determine the number of new infections. For instance, if an infective walks into a room with n susceptibles, and is “small,” then it may more efficient to (i) generate one Bin() random variate X representing in one fell swoop the number of susceptibles who will become infected than to instead (ii) sample n individual Bern(p) trials corresponding to the n susceptibles. If one were to take the Bin() route, one could sample a single Unif(0,1) PRN and use the discrete distribution version of the inverse-transform method to do a table look-up or instead use a normal distribution approximation to the binomial to generate the corresponding value for X (see, e.g., Law [14]). If , we would then have to randomly reassign x susceptibles to the infected state, which would take a little bit more work—though the expected number of assignments is only .
- Within a particular simulation run, we could work with a single “super-infective” individual rather than multiple infectives. Consider the scenario above, except that k infectives walk into the room containing n susceptibles. Assuming that all of the infectives interact with all of the susceptibles in the form of Bern(p) trials, an easy calculation shows that the probability that a particular susceptible will become infected that day is , where . Then, instead of performing Bern(p) trials with the individual infectives, we might equivalently perform only n Bern() trials using a“super-infective” entity—or even a single Bin() trial; see Section 4 or references such as Tsai et al. [15].
- Consider driving the simulation from different points of view. For example, is it more efficient to (i) generate each infected individual and see which susceptibles he infects as he proceeds through his day, or (ii) generate each susceptible individual and see if he gets infected as he proceeds through his day? See Shen et al. [16] and Tsai et al. [15] for insights and recommendations.
- When re-running a simulation but with different input parameters, we might reuse from one simulation to the next as many of the random numbers as possible. This is the goal of the current paper. To illustrate, again consider the situation in which one infectious individual walks into a room with n susceptibles. Suppose that we perform n Bern() trials to determine who, if anyone, becomes infected. Now suppose we run another simulation, but this time with a new probability of infection . We will show how to reuse many of the PRNs from the initial simulation to do the version of the job with less effort.
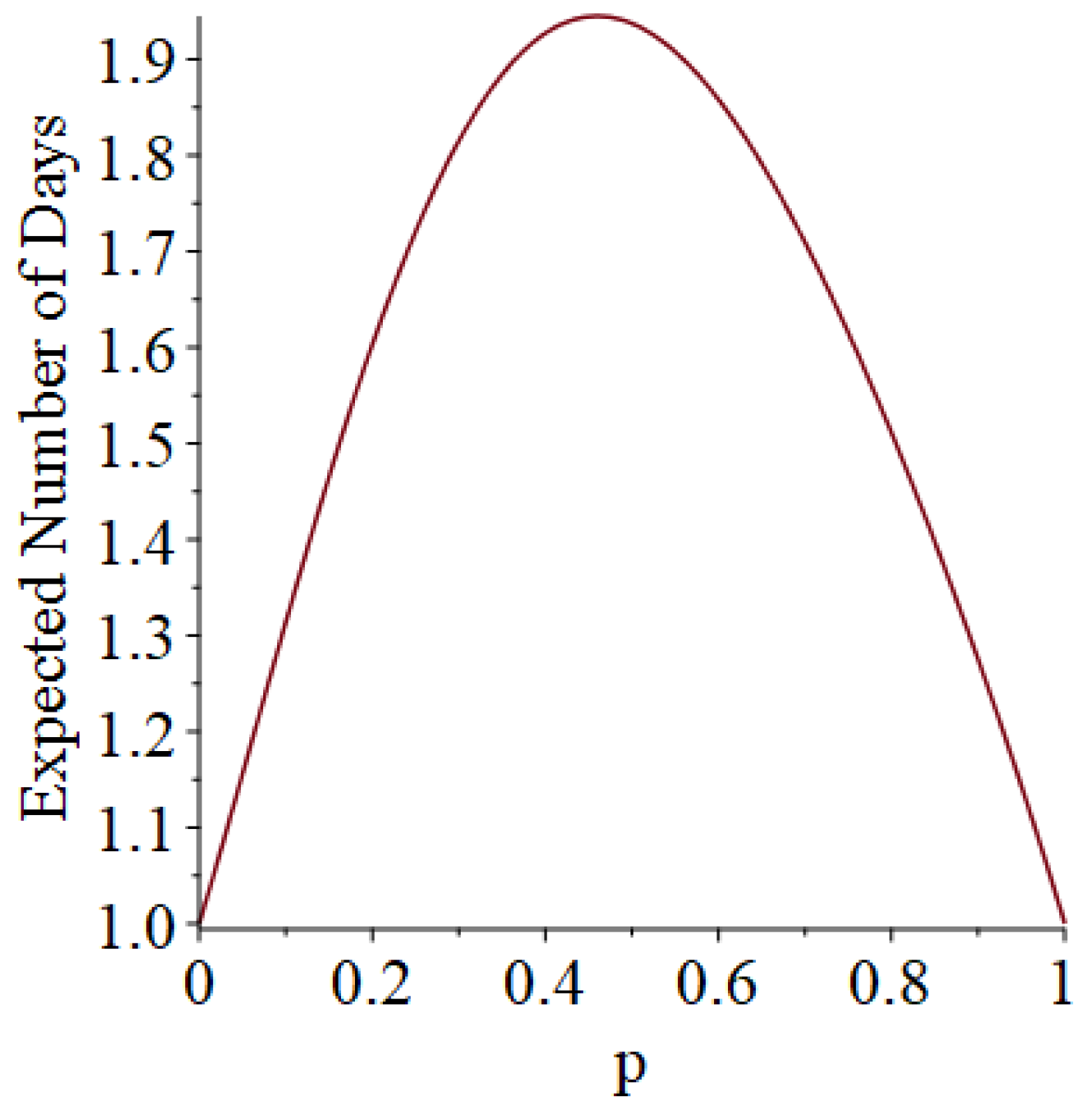
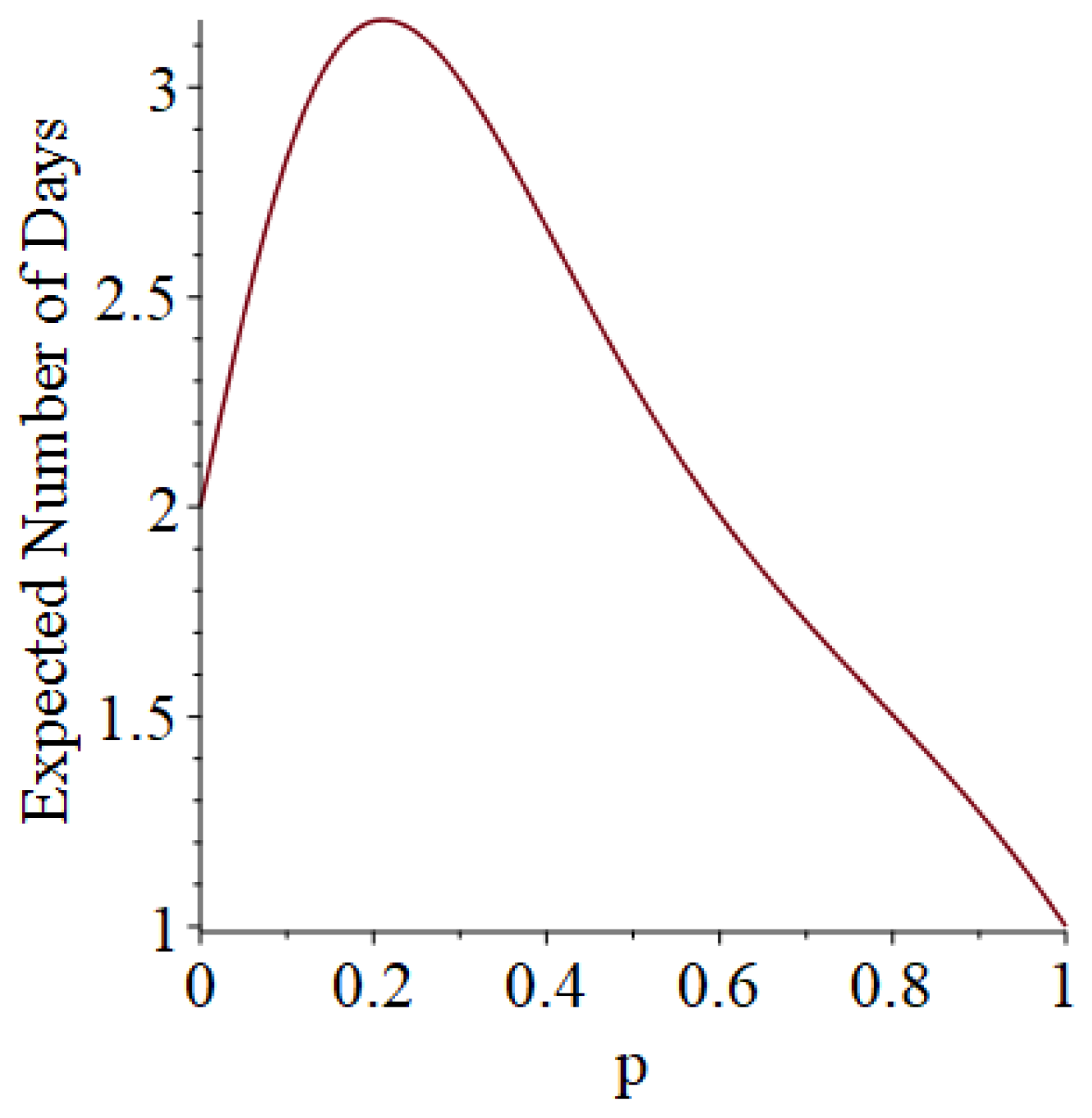
- Generally speaking, the pandemic progresses quickly if p is very small (in which case the pandemic dies out rapidly) or very large (in which case the pandemic rapidly infects many people). Thus, for p very small or very large, we would expect to use only a small number of PRNs. Intermediate values of p might require more PRNs. See Section 3, Example 1.
- How many PRNs will we need to generate in order to simulate multiple scenarios involving the same n susceptible individuals, with each scenario having a different parameter value, for instance, ? With Remark 1.1 in mind, it might be prudent to generate an initial set of PRNs for possible use in any of the scenarios, where T is the maximum time horizon of interest. It is almost certain that many of the PRNs will never be used if, e.g., T is conservatively chosen to be so high as to guarantee that the pandemic will have run its course. However, if we are running a large number of scenarios, then the expected savings garnered by the use of green simulation would likely mitigate the conservativeness of T and the corresponding one-time charge of generating PRNs. For example, for the scenarios presented in Table 1 and Table 2, the maximum possible number of days for the scenarios to run is 15, in which case would be a conservative choice. See Section 4 for more insight on this matter.
- It is possible (in rare cases) to obtain sample paths in which an individual becomes infectious on a certain day when simulating the Bernoulli trials for a particular probability parameter , but remains susceptible on that day when the simulation is re-run under a scenario with a larger probability parameter . For such an anomalous example, see the sample paths of Individual 3 in Table 3 and Table 4 for the cases and 0.25, respectively; and see Section 4 for additional discussion.
3. Examples
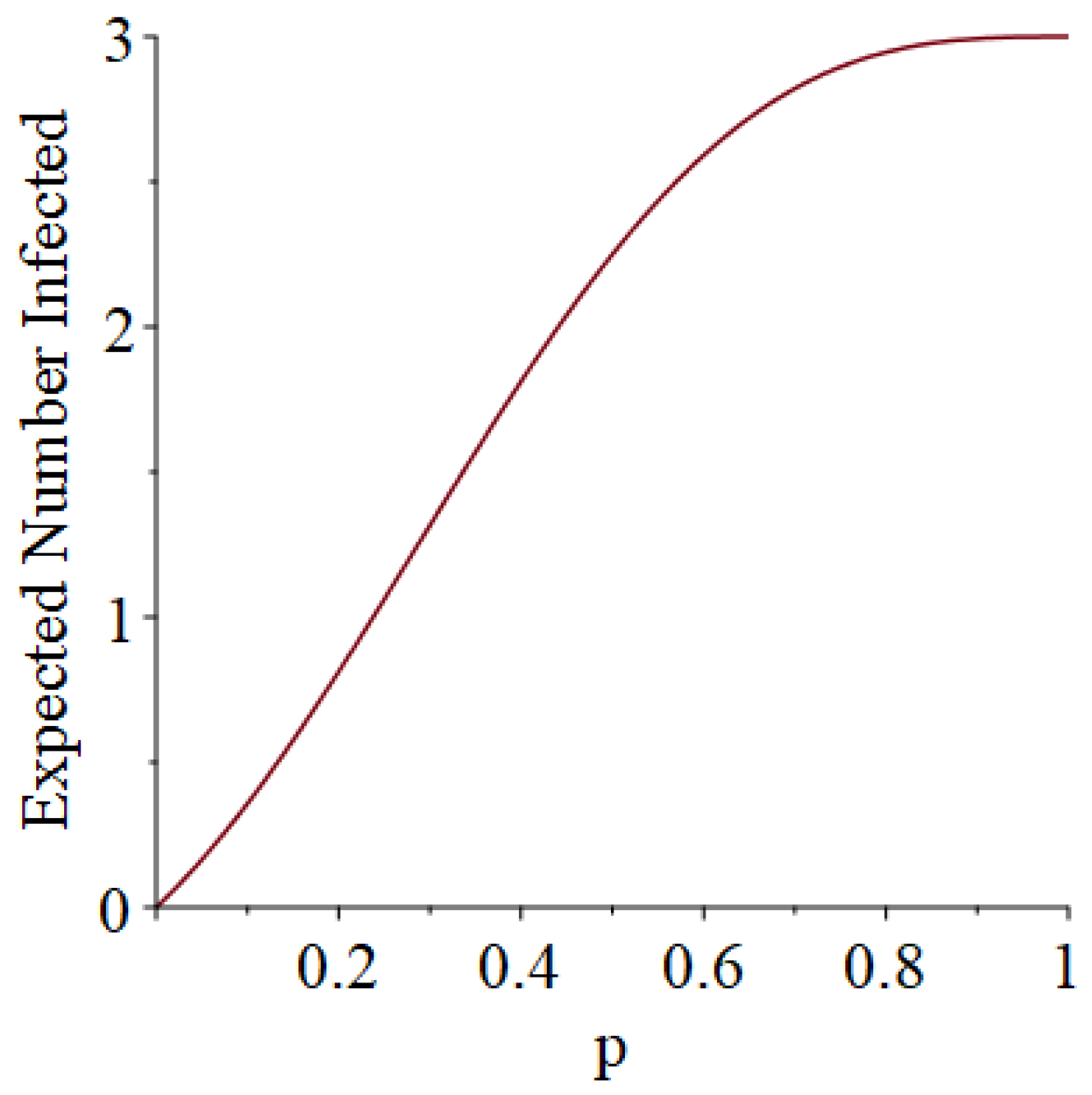
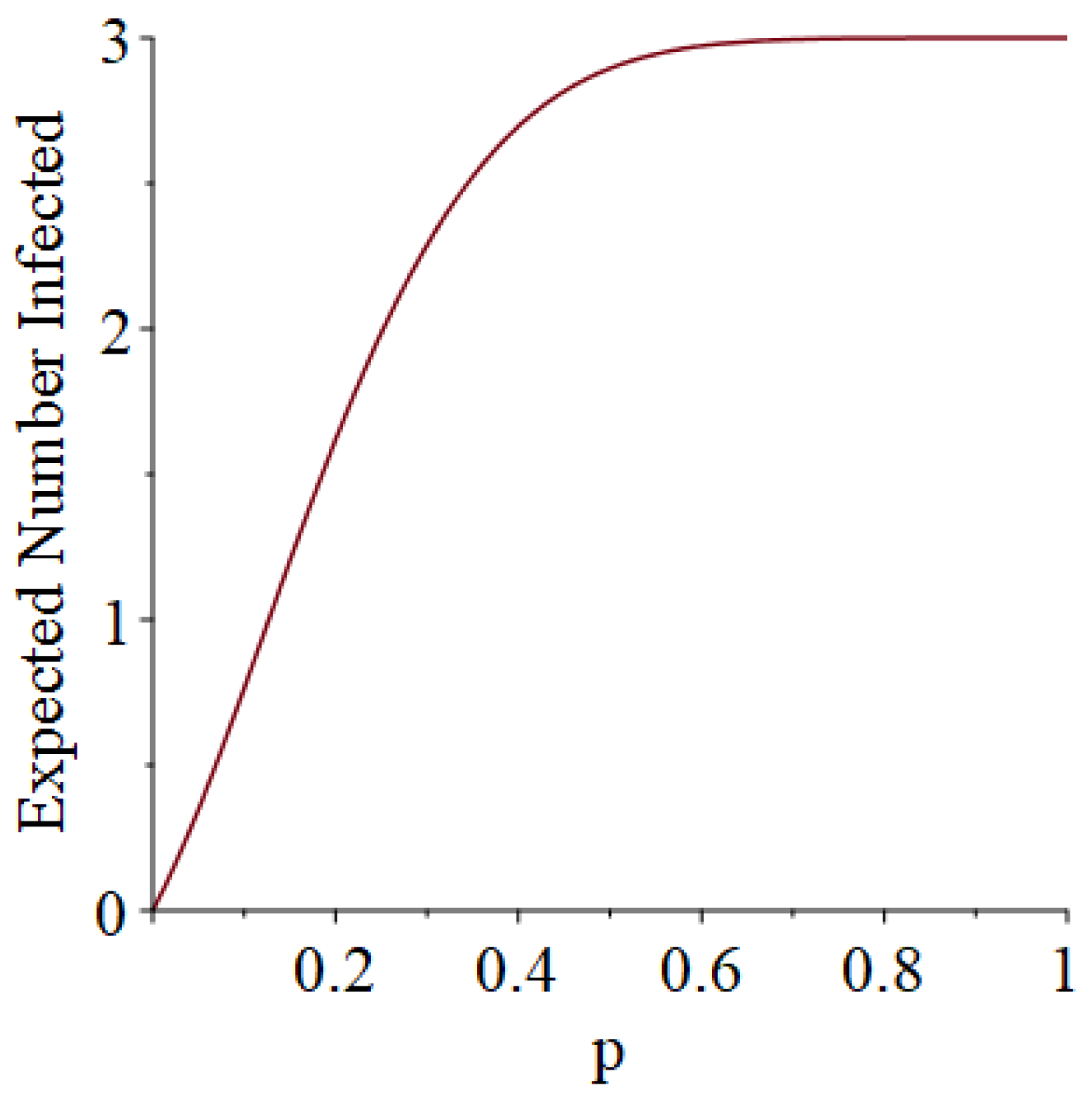
3.1. Some Small-Sample Exact Results
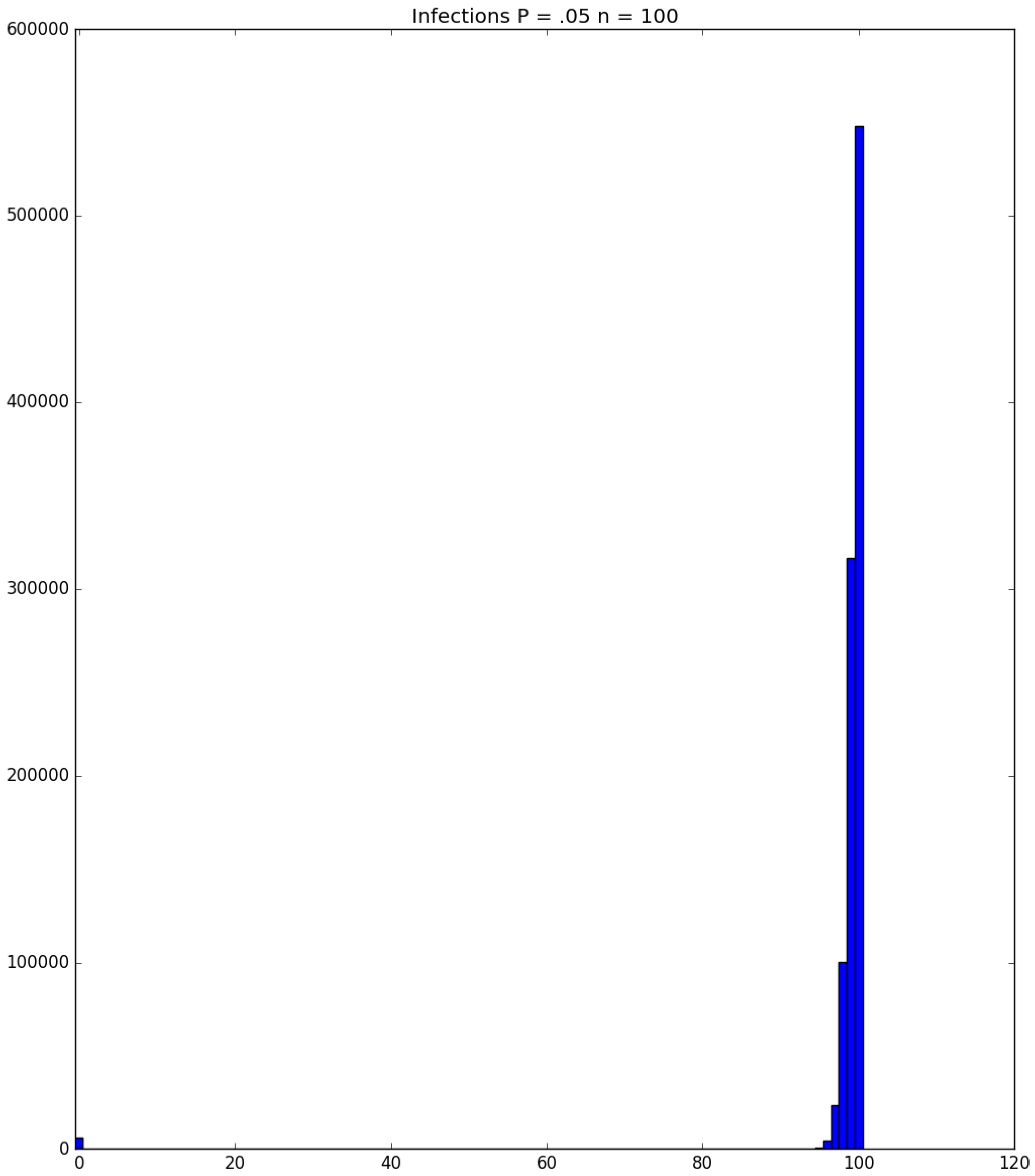
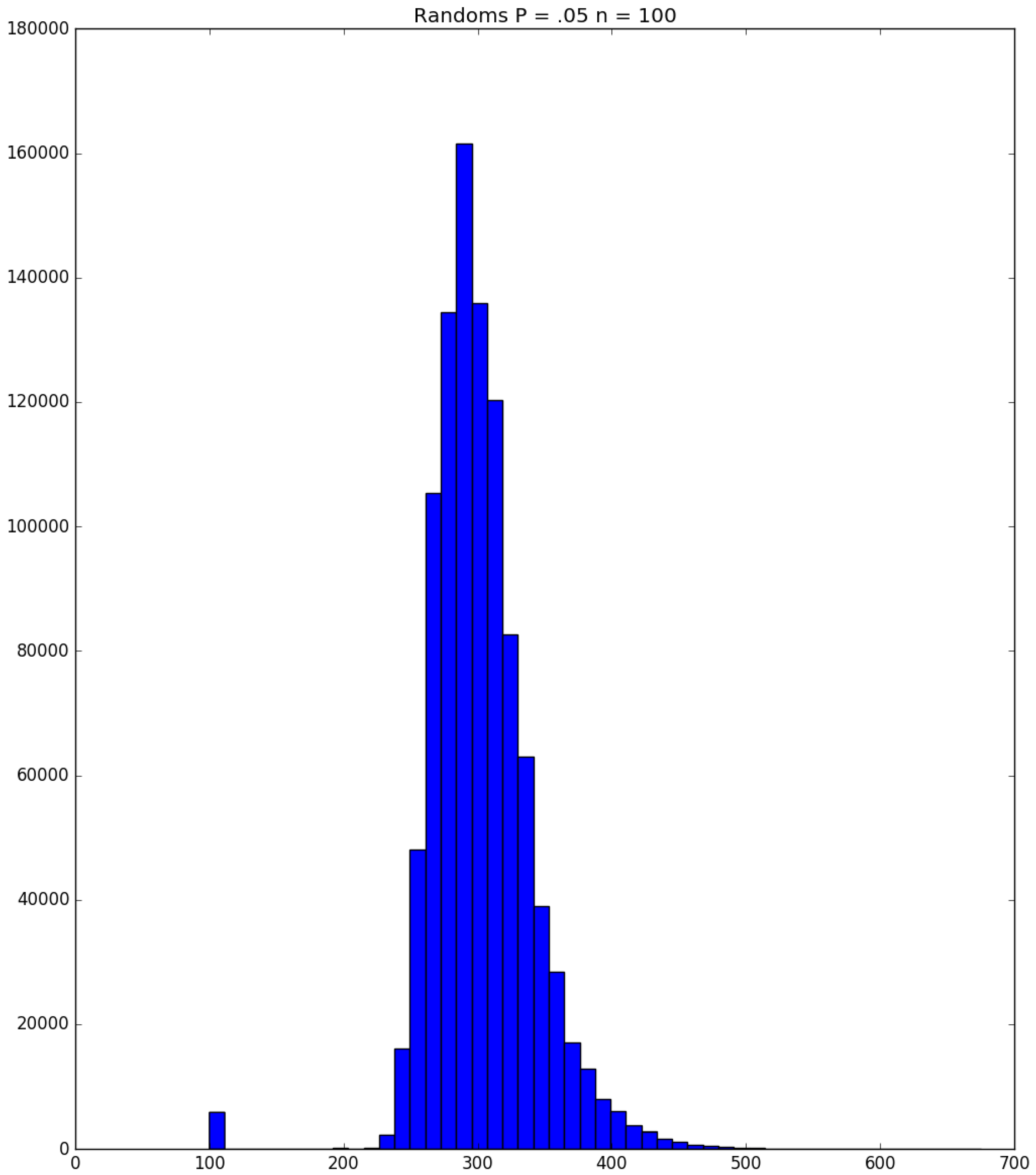
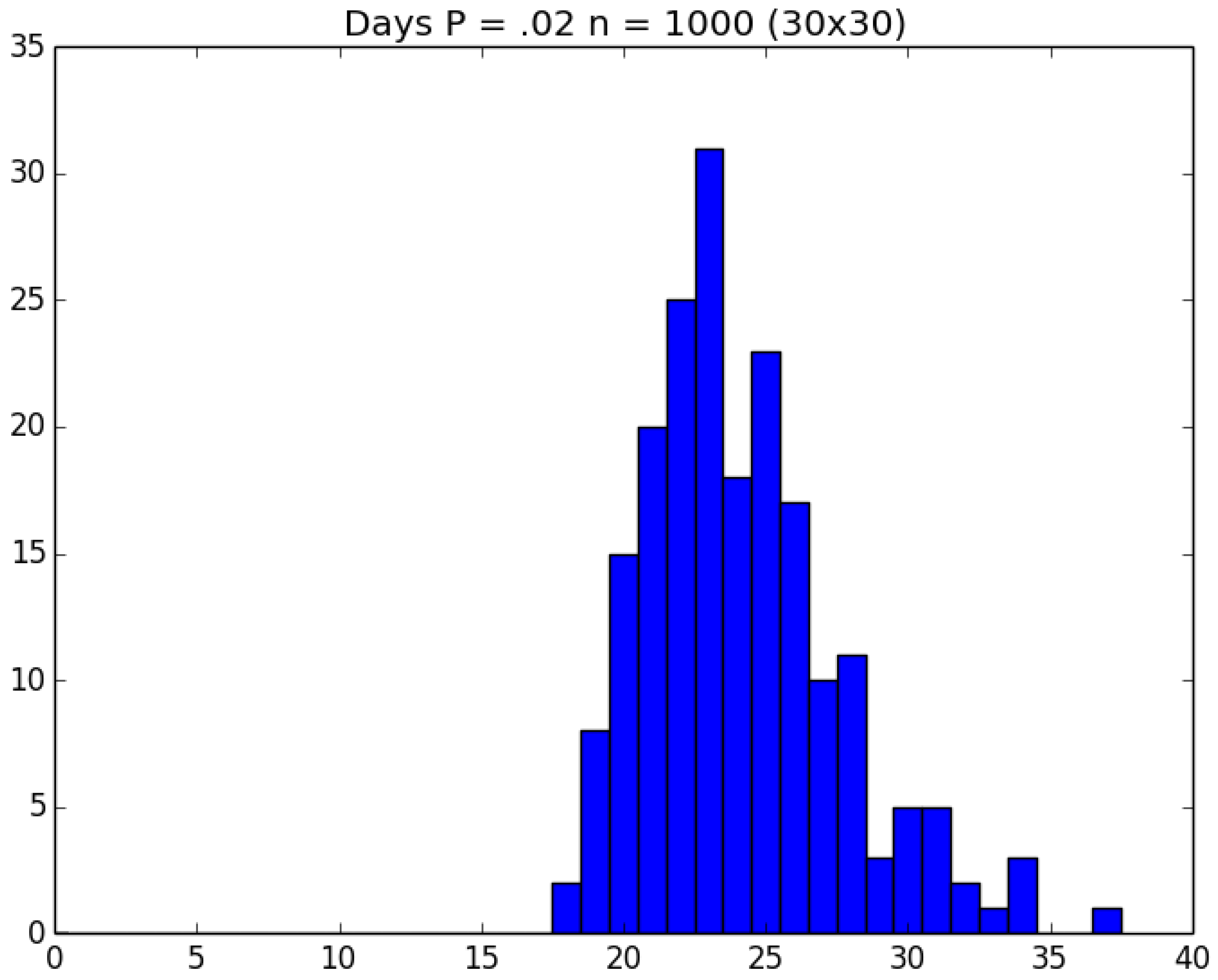
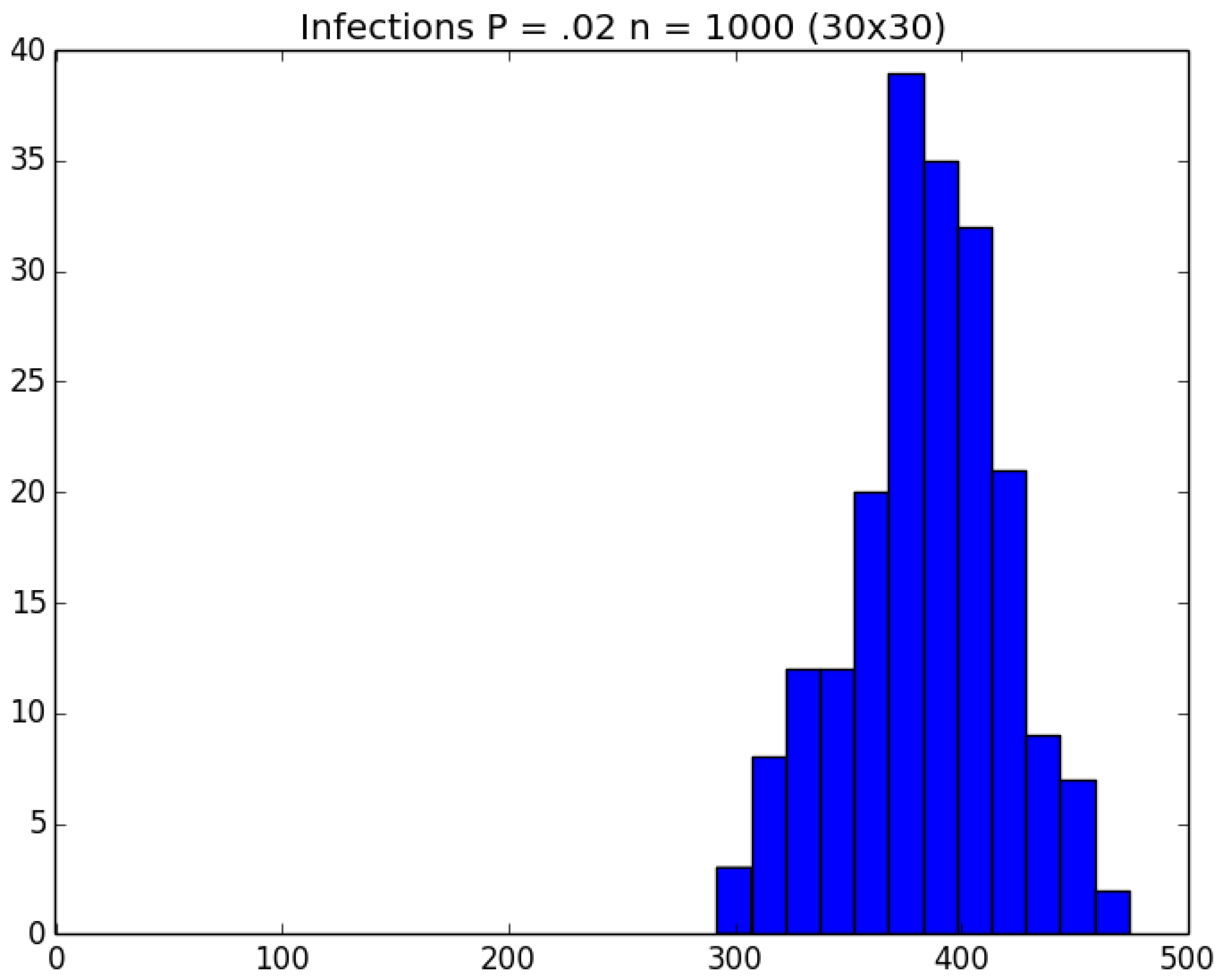
3.2. Simulation
3.3. Run Time and Efficiency Considerations
4. Conclusions and Future Work
- Item 1 of Section 2 discusses the use of a single Bin() random variable instead of n Bern(p) trials to determine the number of infections that occur on a given day. We can immediately implement efficient methods for generating the Bin() random variables (Kachitvichyanukul and Schmeiser [17,18]), but we might also apply our green technology for Bin() generation across scenarios involving different values of p.
- Remark 1.2 in Section 2 suggests that one could pre-generate PRNs to be used on all scenarios of the simulation, but that may be a needlessly high number. In fact, one might instead generate each PRN only on a strict as-needed basis.
- Remark 1.3 notes that it is possible (because of how we handle “super-infectives”) for an individual who is infected on a certain day under the scenario to at least temporarily escape infection for the () scenario. We are currently investigating ways to identify and take advantage of these (rare) events.
- We are in the process of performing expanded analyses (i) on much larger population sizes, (ii) with a greater variety of parameter choices (including different probabilities of infection for different sets of infectives and susceptibles), and (iii) under more-general compartmental environments (e.g., individuals can move between home, school, and work on any given day).
- The common random variates variance reduction technique is one of several that are popular in the literature. A worthy endeavor is that of incorporating other such methods in the context of disease propagation simulation.
- Ultimately, we will use our efficient simulations to evaluate the effects of various mitigation strategies on outbreaks.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Bern | Bernoulli random variable |
| Bin | Binomial random variable |
| p.m.f. | probability mass function |
| PRN | Pseudo-Random Number |
| SIR | Susceptible-Infected-Recovered |
| Unif | Uniform random variable |
References
- Abbott, A.; Pearson, H. Fear of human pandemic grows as bird flu sweeps through Asia. Nature 2004, 427, 472–473. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Cummings, D.A.; Cauchemez, S.; Fraser, C.; Riley, S.; Meeyai, A.; Iamsirithaworn, S.; Burke, D.S. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 2015, 437, 209–214. [Google Scholar] [CrossRef] [PubMed]
- Andradóttir, S.; Chiu, W.; Goldsman, D.; Lee, M.L.; Tsui, K.-L.; Sander, B.; Fisman, D.N.; Nizam, A. Reactive strategies for containing developing outbreaks of pandemic influenza. BMC Public Health 2011, 11, S1. [Google Scholar] [CrossRef] [PubMed]
- Kermack, W.O.; McKendrick, A.G. Contributions of mathematical theory to epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Elveback, L.R.; Fox, J.P.; Ackerman, E.; Langworthy, A.; Boyd, M.; Gatewood, L. An influenza simulation model for immunization studies. Am. J. Epidemiol. 1976, 103, 152–165. [Google Scholar] [CrossRef] [PubMed]
- Halloran, M.E.; Longini, I.M.; Nizam, A.; Yang, Y. Containing bioterrorist smallpox. Science 2002, 128, 1428–1432. [Google Scholar] [CrossRef] [PubMed]
- Kelso, J.; Milne, G.; Kelly, H. Simulation suggests that rapid activation of social distancing can arrest epidemic development due to a novel strain of influenza. BMC Public Health 2009, 9, 117. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.Y.; Brown, S.T.; Cooley, P.C.; Zimmerman, R.K.; Wheaton, W.D.; Zimmer, S.M.; Grefenstette, J.J.; Assi, T.-M.; Furphy, T.J.; Wagener, D.K.; et al. A computer simulation of employee vaccination to mitigate an influenza epidemic. Am. J. Prev. Med. 2010, 38, 247–257. [Google Scholar] [CrossRef] [PubMed]
- Longini, I.M.; Halloran, M.E.; Nizam, A.; Yang, Y. Containing pandemic influenza with antiviral agents. Am. J. Epidemiol. 2004, 159, 623–633. [Google Scholar] [CrossRef] [PubMed]
- Longini, I.M.; Nizam, A.; Xu, S.; Ungchusak, K.; Hanshaoworakul, W.; Cummings, D.A.; Halloran, M.E. Containing pandemic influenza at the source. Science 2005, 309, 1083–1087. [Google Scholar] [CrossRef] [PubMed]
- Andradóttir, S.; Chiu, W.; Goldsman, D.; Lee, M.L. Simulation of influenza propagation: Model development, parameter estimation, and mitigation strategies. IIE Trans. Healthc. Syst. Eng. 2014, 4, 27–48. [Google Scholar] [CrossRef]
- Feng, M.; Staum, J. Green simulation designs for repeated experiments. In Proceedings of the 2015 Winter Simulation Conference; Yilmaz, L., Chan, W.K.V., Moon, I., Roeder, T.M.K., Macal, C., Rossetti, M.D., Eds.; Institute of Electrical and Electronics Engineers: Piscataway, NJ, USA, 2015; pp. 403–413. [Google Scholar]
- Meterelliyioz, M.; Alexopoulos, C.; Goldsman, D. Folded overlapping variance estimators for simulation. Eur. J. Oper. Res. 2012, 220, 135–146. [Google Scholar] [CrossRef]
- Law, A.M. Simulation Modeling and Analysis, 5th ed.; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Tsai, M.T.; Chern, T.C.; Chuang, J.H.; Hsueh, C.W.; Kuo, H.S.; Liau, C.J.; Riley, S.; Shen, B.J.; Shen, C.H.; Wang, D.W.; et al. Efficient simulation of the spatial transmission dynamics of influenza. PLoS ONE 2010, 5, e13292. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Wong, Z.S.-Y.; Ling, M.-H.; Goldsman, D.; Tsui, K.-L. Comparison of algorithms to simulate disease transmission. J. Simul. 2017, 11, 285–294. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V.; Schmeiser, B.W. Binomial random variate generation. Commun. ACM 1988, 31, 216–222. [Google Scholar] [CrossRef]
- Kachitvichyanukul, V.; Schmeiser, B.W. Algorithm 678 BTPEC: Sampling from the binomial dstribution. ACM Trans. Math. Softw. 1989, 15, 394–397. [Google Scholar] [CrossRef]
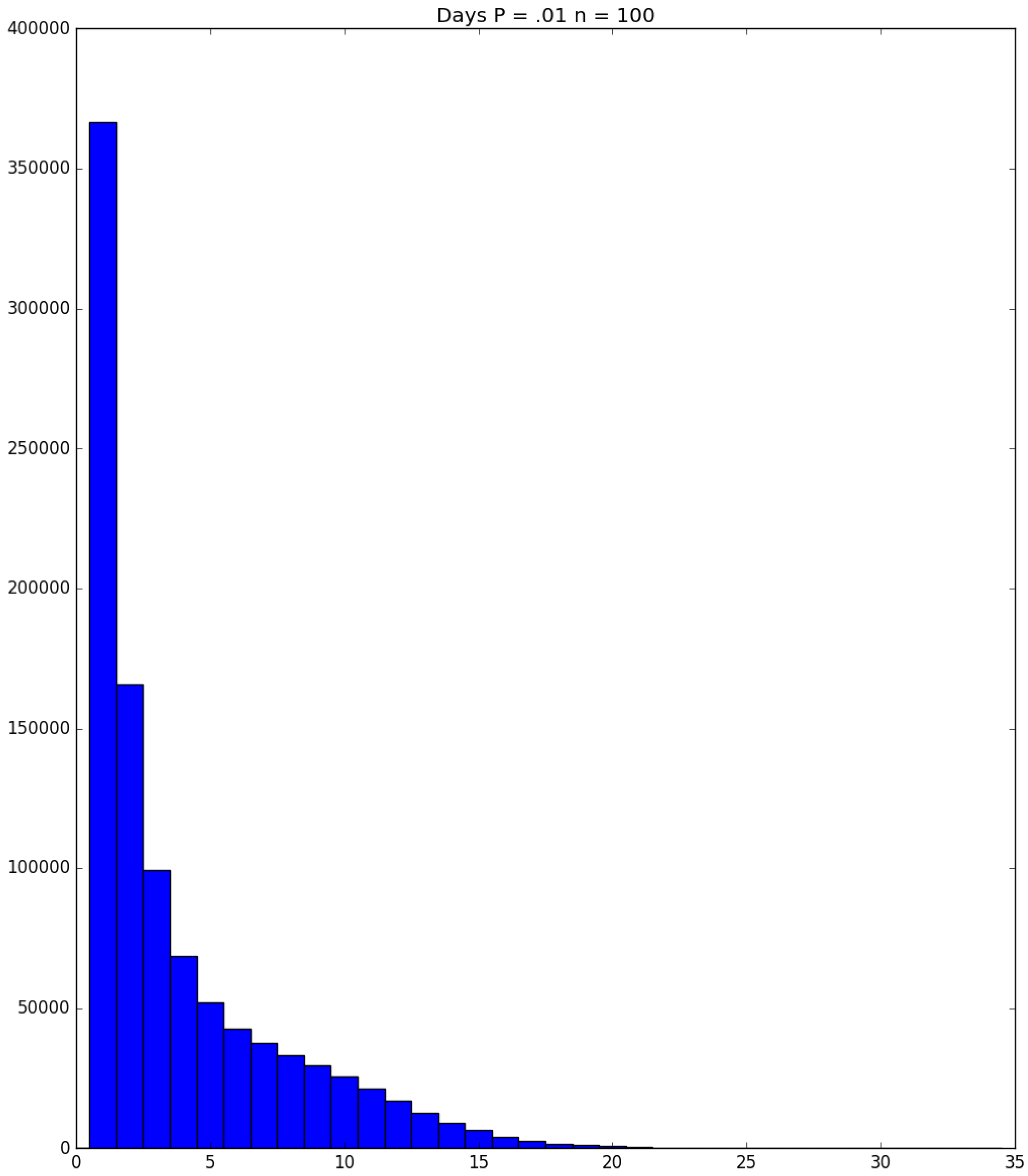
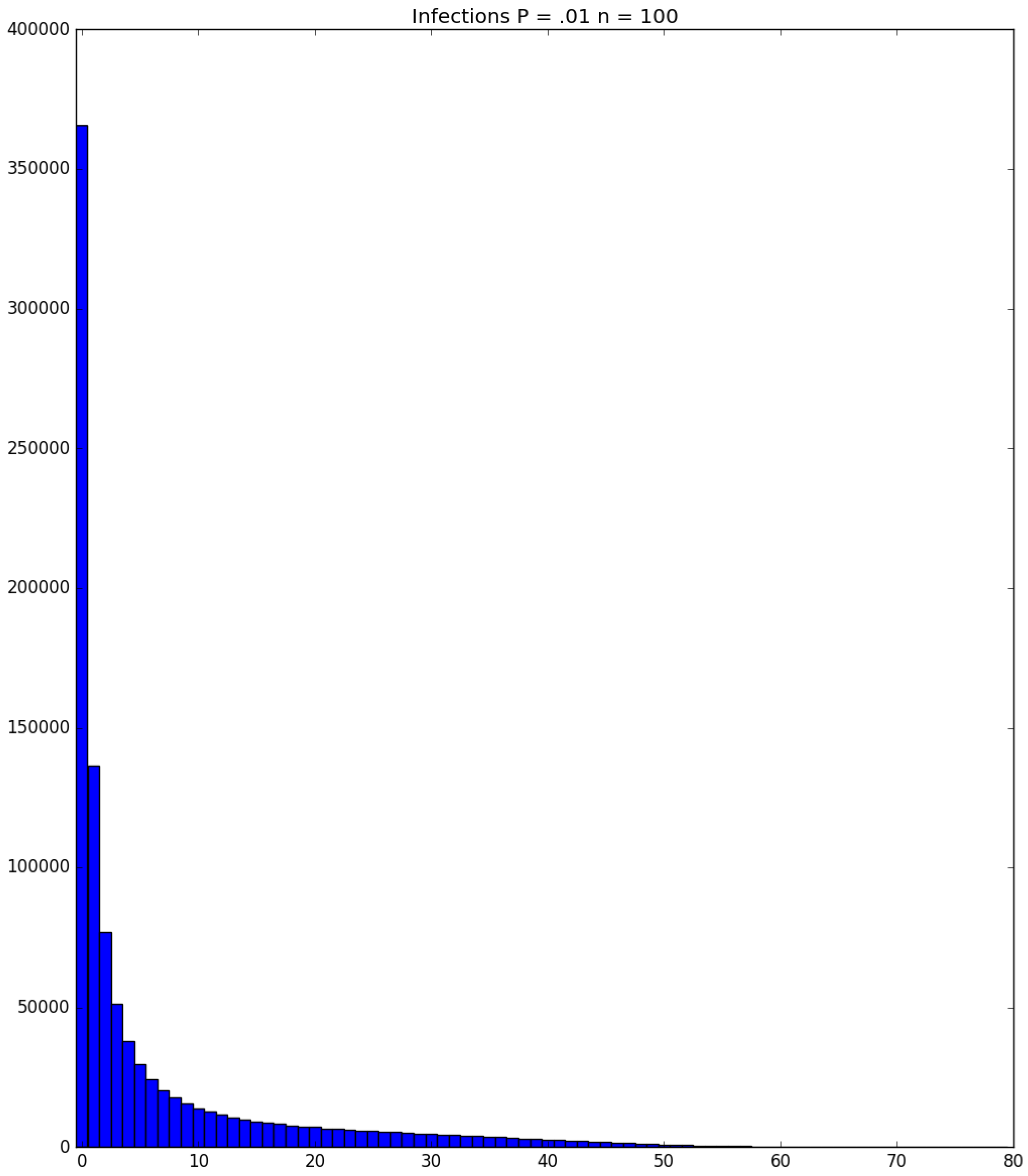
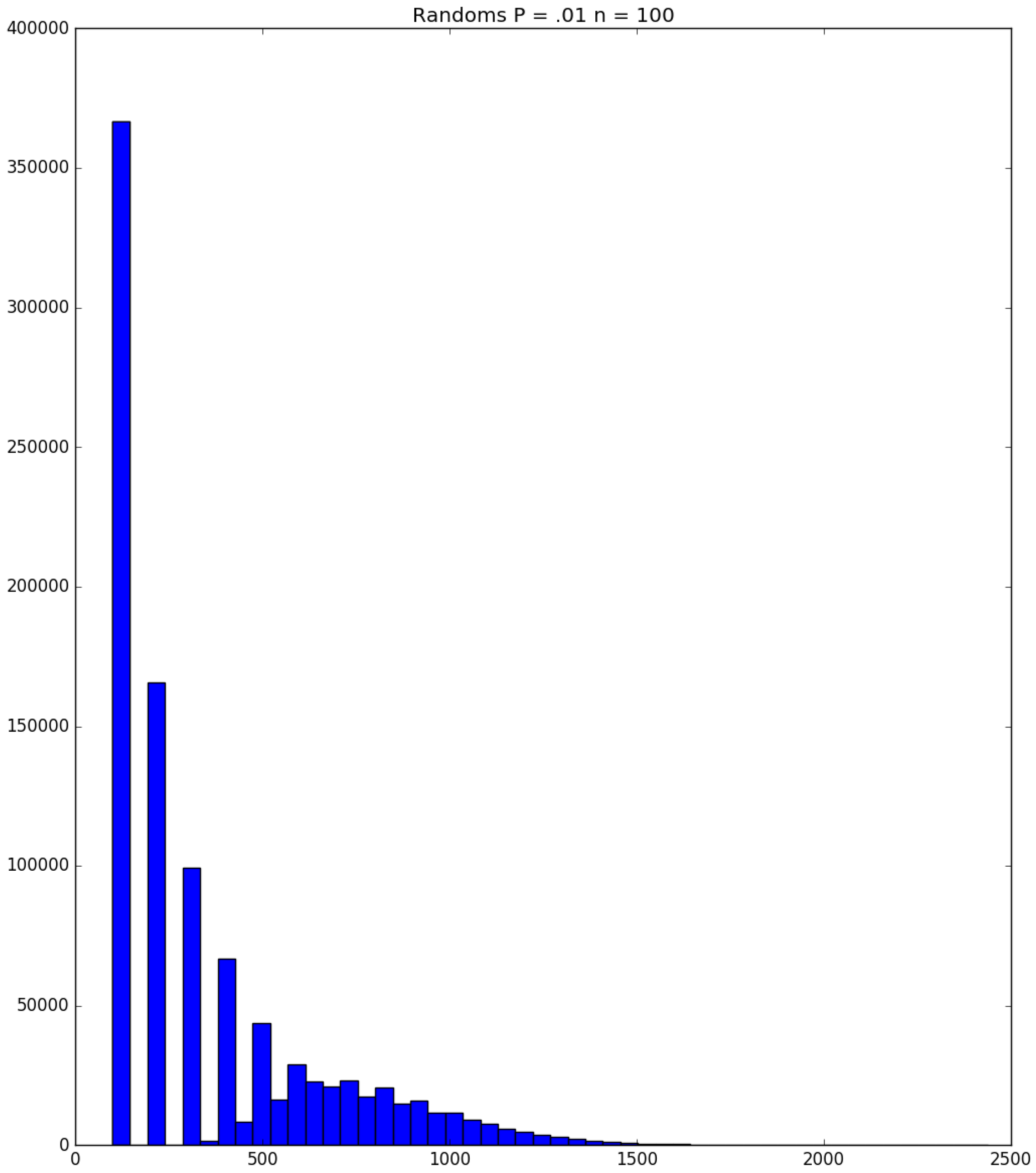
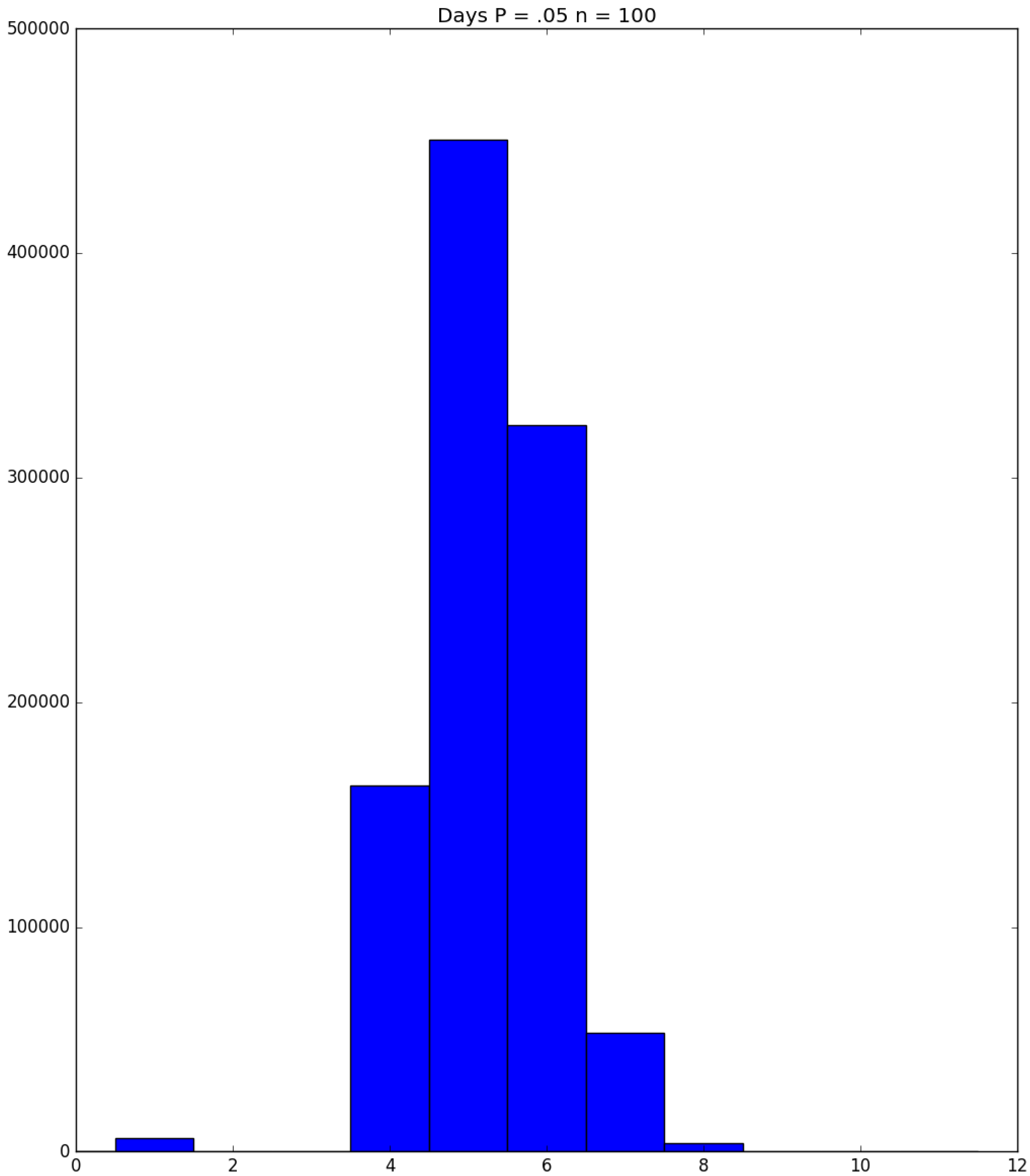
| Day t | 1 | 2 | 3 | 4 | 5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.488 | 0.67232 | 0.67232 | 0.2 | ||||||
| Individual | PRN/State | PRN/State | PRN/State | PRN/State | PRN/State | |||||
| 1 | 0.637 | S | 0.886 | S | 0.855 | S | 0.975 | S | 0.828 | S |
| 2 | 0.992 | S | 0.986 | S | 0.688 | S | 0.335 | I | R | |
| 3 | 0.262 | S | 0.027 | I | R | R | R | |||
| 4 | 0.244 | S | 0.877 | S | 0.145 | I | R | R | ||
| 5 | 0.700 | S | 0.101 | I | R | R | R | |||
| 6 | 0.082 | I | R | R | R | R | ||||
| 7 | 0.136 | I | R | R | R | R | ||||
| 8 | 0.857 | S | 0.372 | I | R | R | R | |||
| 9 | 0.513 | S | 0.045 | I | R | R | R | |||
| 10 | 0.333 | S | 0.496 | S | 0.039 | I | R | R | ||
| 11 | 0.978 | S | 0.546 | S | 0.148 | I | R | R | ||
| 12 | 0.980 | S | 0.567 | S | 0.147 | I | R | R | ||
| 13 | 0.253 | S | 0.011 | I | R | R | R | |||
| 14 | 0.253 | S | 0.965 | S | 0.658 | I | R | R | ||
| 15 | 0.200 | I | R | R | R | R | ||||
| 12 | 7 | 2 | 1 | 1 | ||||||
| 3 | 5 | 5 | 1 | 0 | ||||||
| 0 | 3 | 8 | 13 | 14 | ||||||
| # PRNs | 15 | 12 | 7 | 2 | 1 | |||||
| Day t | 1 | 2 | 3 | 4 | ||||
|---|---|---|---|---|---|---|---|---|
| 0.3 | 0.91765 | 0.91765 | 0.3 | |||||
| Individual | PRN/State | PRN/State | PRN/State | PRN/State | ||||
| 1 | 0.637 | S | 0.886 | I | R | R | ||
| 2 | 0.992 | S | 0.986 | S | 0.688 | I | R | |
| 3 | 0.262 | I | R | R | R | |||
| 4 | 0.244 | I | R | R | R | |||
| 5 | 0.700 | S | 0.101 | I | R | R | ||
| 6 | 0.082 | I | R | R | R | |||
| 7 | 0.136 | I | R | R | R | |||
| 8 | 0.857 | S | 0.372 | I | R | R | ||
| 9 | 0.513 | S | 0.045 | I | R | R | ||
| 10 | 0.333 | S | 0.496 | I | R | R | ||
| 11 | 0.978 | S | 0.546 | I | R | R | ||
| 12 | 0.980 | S | 0.567 | I | R | R | ||
| 13 | 0.253 | I | R | R | R | |||
| 14 | 0.253 | I | R | R | R | |||
| 15 | 0.200 | I | R | R | R | |||
| 8 | 1 | 0 | 0 | |||||
| 7 | 7 | 1 | 0 | |||||
| 0 | 7 | 14 | 15 | |||||
| # PRNs | 15 | 8 | 1 | 0 | ||||
| Day | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| 0.2 | 0.2 | 0.36 | ||||
| Individual | PRN/State | PRN/State | PRN/State | |||
| 1 | 0.24 | S | 0.44 | S | 0.72 | S |
| 2 | 0.23 | S | 0.19 | I | R | |
| 3 | 0.65 | S | 0.95 | S | 0.29 | I |
| 4 | 0.18 | I | R | R | ||
| 5 | 0.21 | S | 0.18 | I | R | |
| 6 | 0.42 | S | 0.55 | S | 0.38 | S |
| Day | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| 0.25 | 0.6836 | 0.25 | ||||
| Individual | PRN/State | PRN/State | PRN/State | |||
| 1 | 0.24 | I | R | R | ||
| 2 | 0.23 | I | R | R | ||
| 3 | 0.65 | S | 0.95 | S | 0.29 | S |
| 4 | 0.18 | I | R | R | ||
| 5 | 0.21 | I | R | R | ||
| 6 | 0.42 | S | 0.55 | I | R | |
| Set | Case A (Indep Scenarios) | Case B (Green Scenarios) | ||||||
|---|---|---|---|---|---|---|---|---|
| 1 | 20.5945 | 21.0066 | 412 | 20.5593 | 20.9086 | 349 | ||
| 2 | 20.5325 | 20.8906 | 358 | 20.5773 | 20.9409 | 364 | ||
| 3 | 20.5611 | 20.8921 | 331 | 20.5604 | 20.9071 | 347 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilson, S.; Alabdulkarim, A.; Goldsman, D. Green Simulation of Pandemic Disease Propagation. Symmetry 2019, 11, 580. https://doi.org/10.3390/sym11040580
Wilson S, Alabdulkarim A, Goldsman D. Green Simulation of Pandemic Disease Propagation. Symmetry. 2019; 11(4):580. https://doi.org/10.3390/sym11040580
Chicago/Turabian StyleWilson, Spencer, Abdullah Alabdulkarim, and David Goldsman. 2019. "Green Simulation of Pandemic Disease Propagation" Symmetry 11, no. 4: 580. https://doi.org/10.3390/sym11040580
APA StyleWilson, S., Alabdulkarim, A., & Goldsman, D. (2019). Green Simulation of Pandemic Disease Propagation. Symmetry, 11(4), 580. https://doi.org/10.3390/sym11040580





