When Considering More Elements: Attribute Correlation in Unsupervised Data Cleaning under Blocking
Abstract
:1. Introduction
1.1. Problem Description
1.2. Research Status
1.3. Purpose and Structure of This Paper
2. Materials and Methods
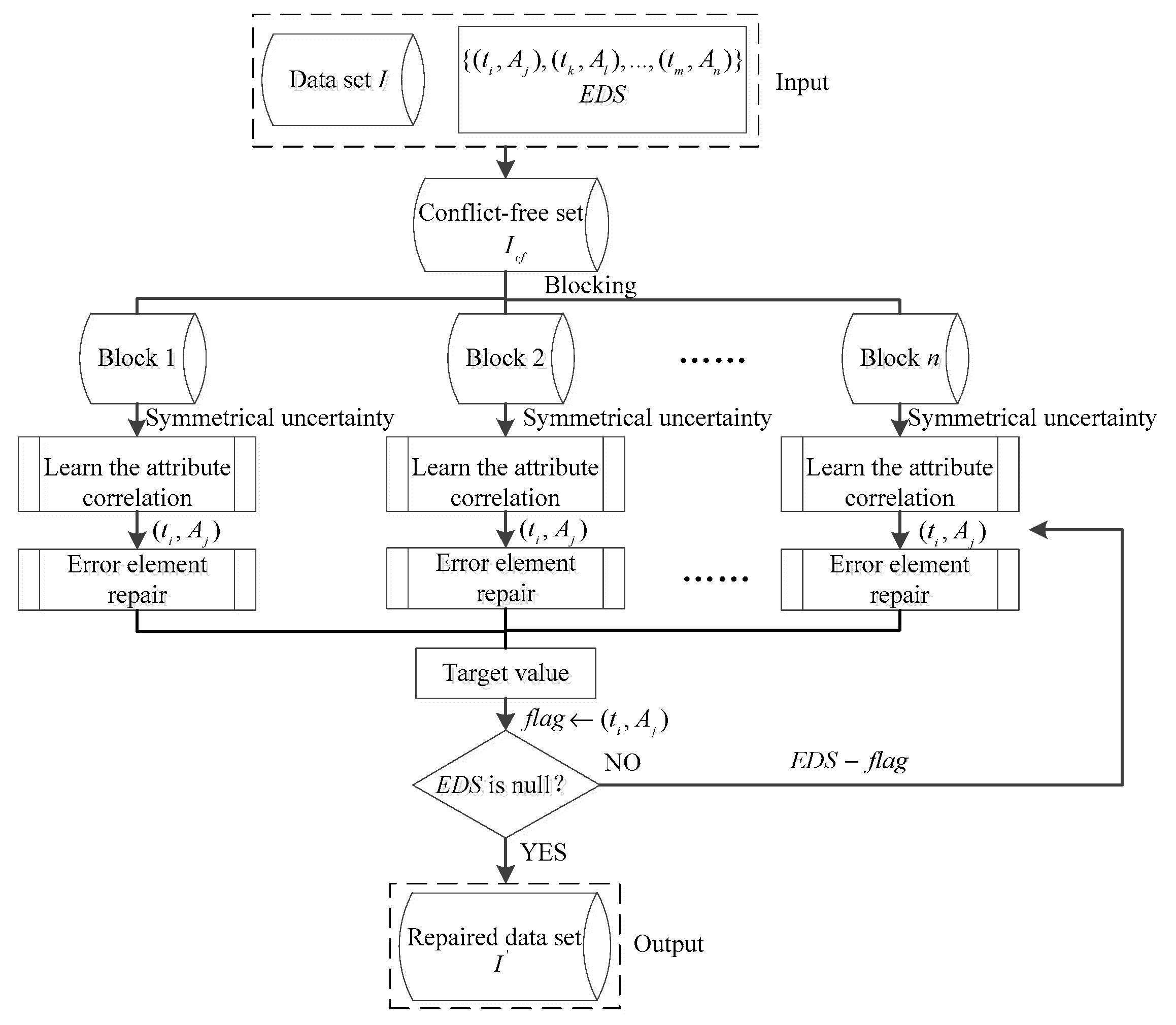
2.1. Design of the ACB-Framework
2.2. The Blocking Module
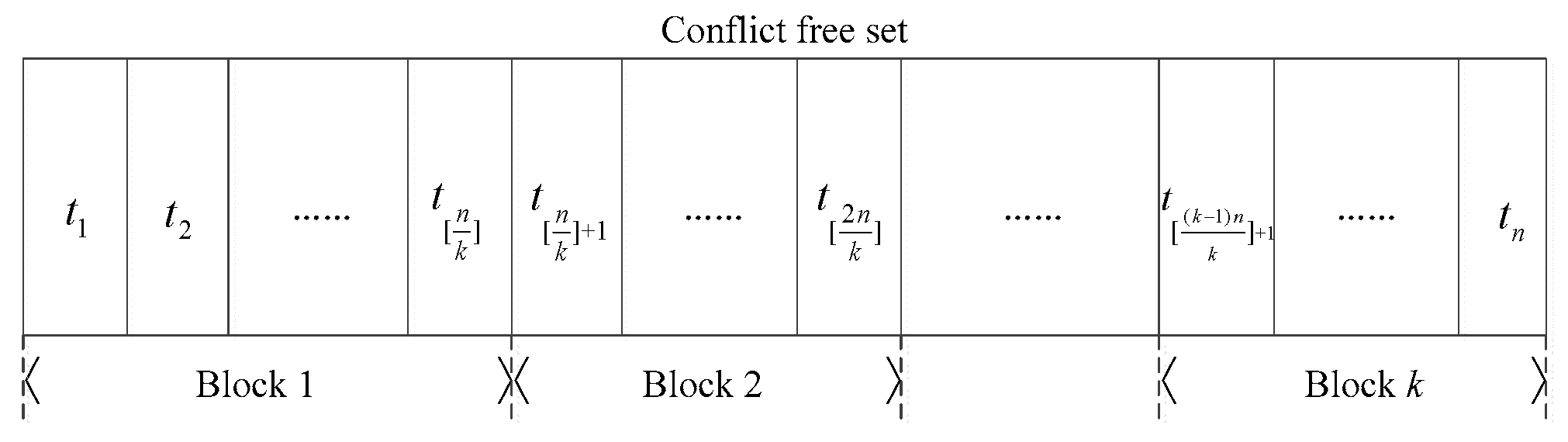
2.2.1. Design of Blocking Algorithms
- (1)
- Blocking is a pretreatment process in data cleaning to reduce the time complexity, so we should choose algorithms with low complexity.
- (2)
- The repair ability of data cleaning algorithms cannot be significantly reduced after blocking.
- (3)
- Blocking algorithms should improve the repair speed of erroneous data in datasets.
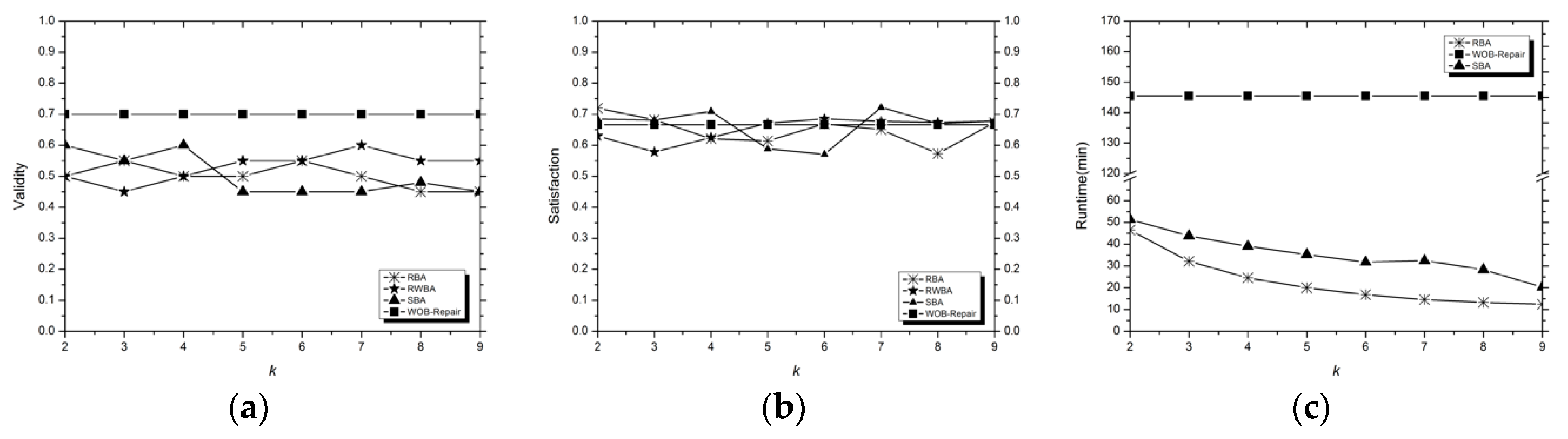
Random Blocking Algorithm (RBA)
| Algorithm 1. The Random Blocking Algorithm (RBA) flow. |
| Input: conflict-free dataset , blocks amounts k Output: blocking results of RBA |
|
Similarity Blocking Algorithm, SBA
| Algorithm 2. The Similarity Blocking Algorithm (SBA) flow. |
| Input: conflict-free dataset , threshold Output: blocking results of SBA |
|
Random Walk Blocking Algorithm, RWBA
| Algorithm 3. The Random Walk Blocking Algorithm (RWBA) flow. |
| Input: conflict-free dataset , threshold Output: blocking results of RWBA |
|
2.2.2. The Convergence and Complexity Analysis of the Blocking Methods
Convergence Analysis
Complexity Analysis
2.3. The Data Cleaning Module
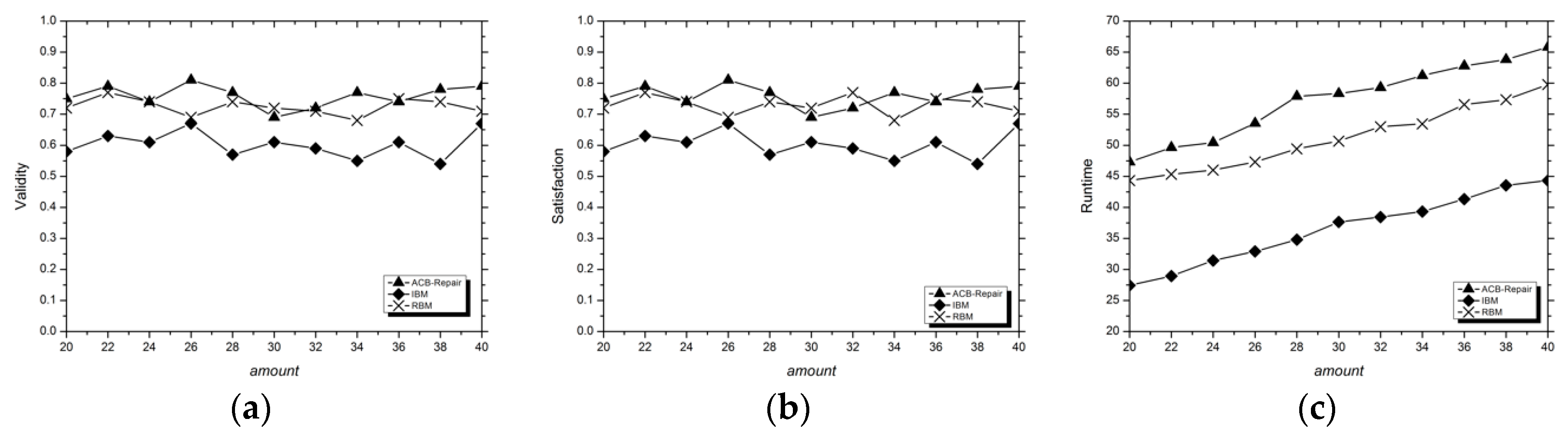
2.3.1. Design of the ACB-Repair
Attribute Correlation Learning
Erroneous Elements Reparation
| Algorithm 4. The ACB-Repair flow. |
| Input: Blocks for , EDS Output: repaired dataset I′ |
|
2.3.2. The Convergence and Complexity Analysis of ACB-Repair
Convergence Analysis
Complexity Analysis
3. Results
3.1. Experimental Configuration
3.1.1. Experimental Environment
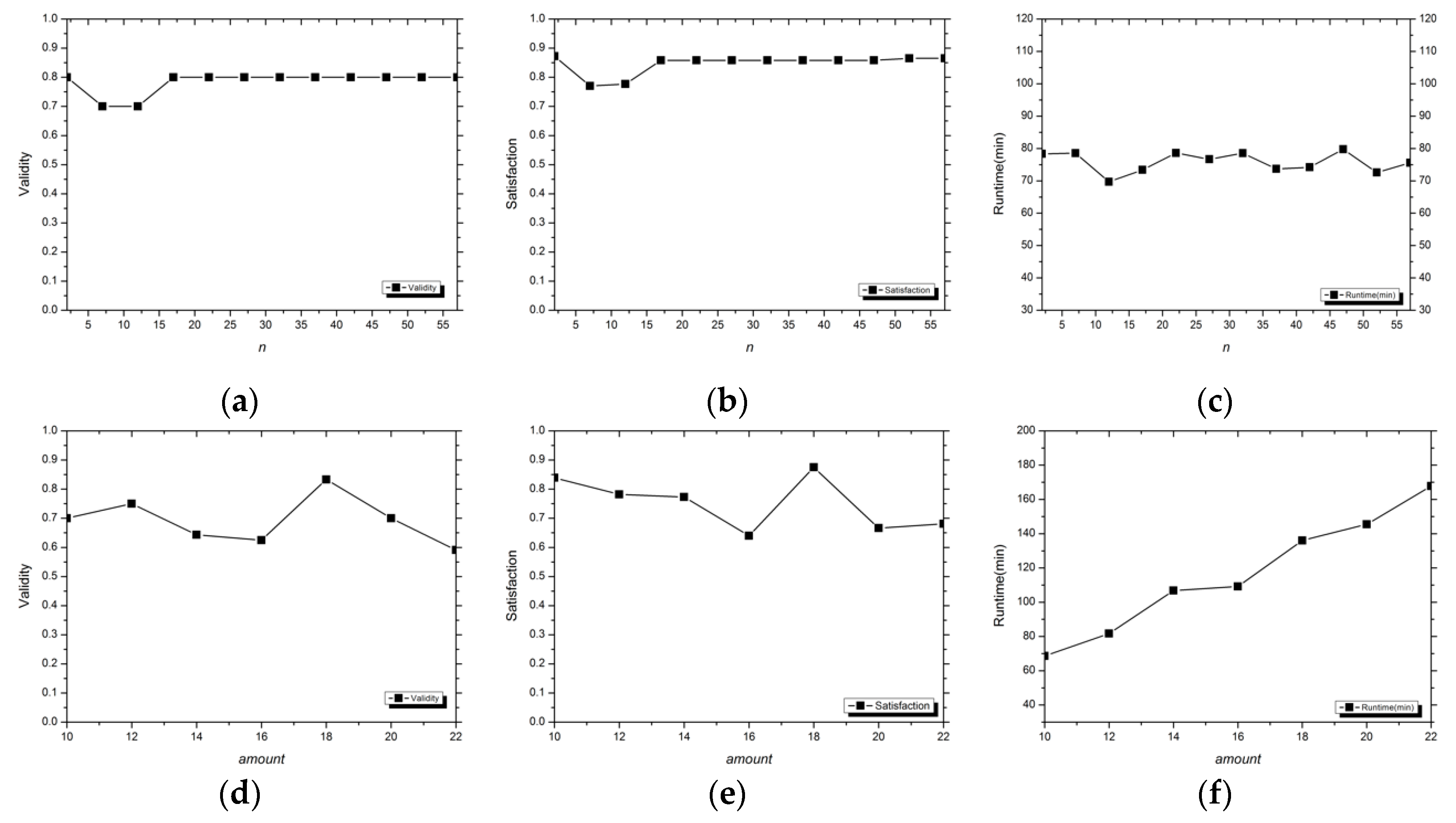
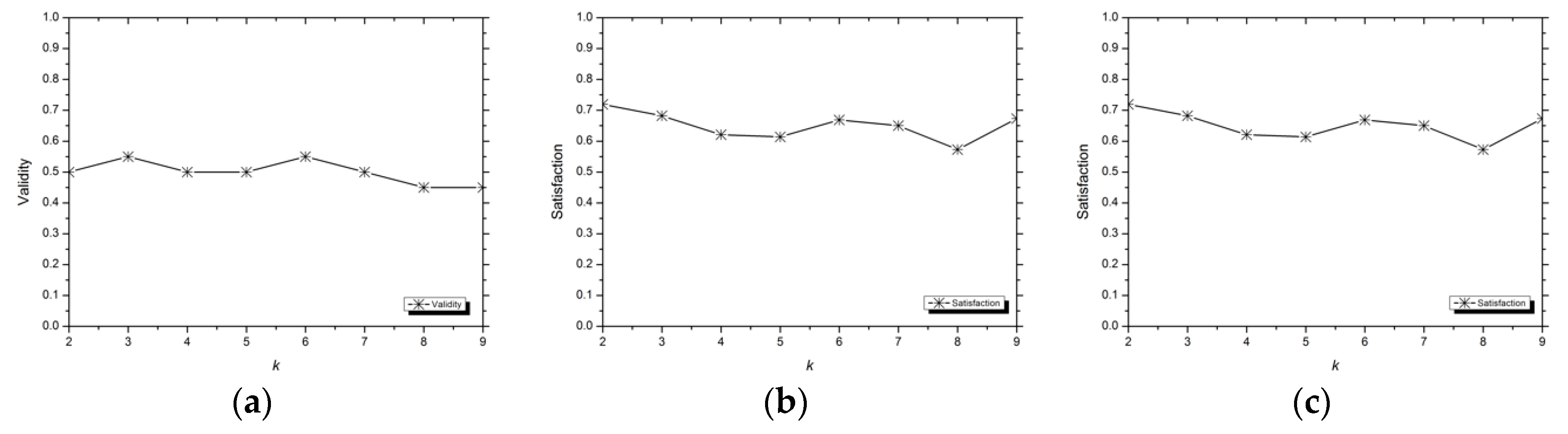
3.1.2. Experimental Datasets
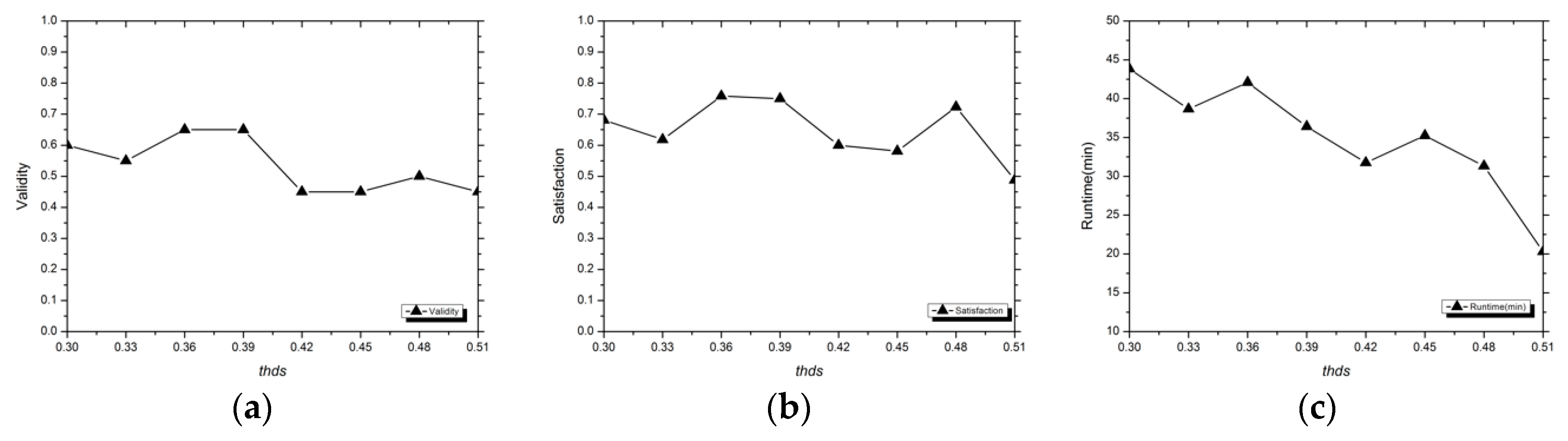
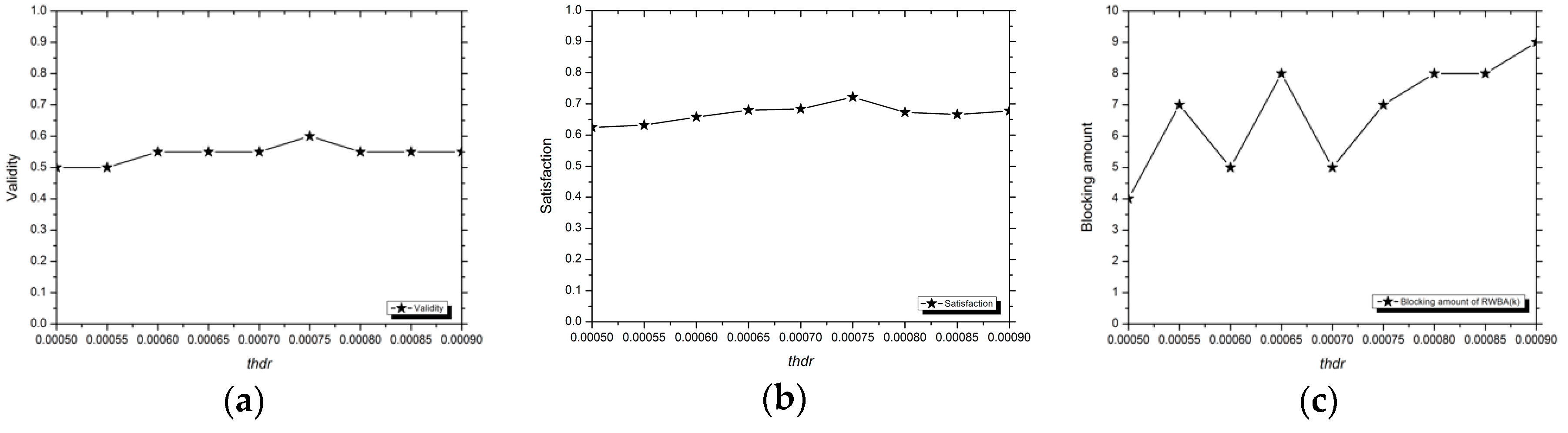
3.1.3. Evaluation Indexes
Validity
Satisfaction
Runtime
3.2. Analysis of Experimental Results
4. Discussion
- (1)
- How to design better repair methods in unsupervised data cleaning?
- (2)
- How to further reduce the cleaning time while better maintaining its cleaning ability?
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, H.Z.; Li, M.D.; Bu, Y.Y.; Li, J.Z.; Gao, H.; Zhang, J.C. Cleanix: A Parallel Big Data Cleaning System. SIGMOD Rec. 2015, 44, 35–40. [Google Scholar] [CrossRef]
- Xu, S.; Lu, B.; Baldea, M.; Edgar, T.F.; Wojsznis, W.; Blevins, T.; Nixon, M. Data cleaning in the process industries. Rev. Chem. Eng. 2015, 31, 453–490. [Google Scholar] [CrossRef]
- Liu, X.L.; Li, J.Z. Consistent Estimation of Query Result in Inconsistent Data. Chin. J. Comput. 2015, 9, 1727–1738. [Google Scholar]
- Fujii, T.; Ito, H.; Miyoshi, S. Statistical-Mechanical Analysis Connecting Supervised Learning and Semi-Supervised Learning. J. Phys. Soc. Jpn. 2017, 86, 6. [Google Scholar] [CrossRef]
- Fabris, F.; de Magalhes, J.P.; Freitas, A.A. A review of supervised machine learning applied to ageing research. Biogerontology 2017, 18, 171–188. [Google Scholar] [CrossRef]
- Xu, S.L.; Wang, J.H. Classification Algorithm Combined with Unsupervised Learning for Data Stream. Pattern Recognit. Artif. Intell. 2016, 29, 665–667. [Google Scholar]
- Kim, J.; Jang, G.J.; Lee, M. Investigation of the Efficiency of Unsupervised Learning for Multi-task Classification in Convolutional Neural Network. In Proceedings of the International Conference on Neural Information Processing, Kyoto, Japan, 16–21 October 2016; pp. 547–554. [Google Scholar]
- Can, B.; Manandhar, S. Methods and Algorithms for Unsupervised Learning of Morphology. In Proceedings of the International Conference on Intelligent Text Processing and Computational, Kathmandu, Nepal, 6–12 April 2014; pp. 177–205. [Google Scholar]
- Zhou, J.L.; Diao, X.C.; Cao, J.J.; Pan, Z.S. An Optimization Strategy for CFDMiner: An Algorithm of Discovering Constant Conditional Functional Dependencies. IEICE Trans. Inf. Syst. 2016, E99.D, 537–540. [Google Scholar] [CrossRef]
- Li, M.H.; Li, J.Z.; Cheng, S.Y.; Sun, Y.B. Uncertain Rule Based Method for Determining Data Currency. IEICE Trans. Inf. Syst. 2018, E101-D, 2447–2457. [Google Scholar] [CrossRef]
- Mcgilvray, D. Executing Data Quality Projects; Elsevier LTD Press: Oxford, UK, 2008. [Google Scholar]
- Zhang, L.; Zhao, Y.; Zhu, Z.F.; Shen, D.G.; Ji, S.W. Multi-View Missing Data Completion. IEEE Trans. Knowl. Data Eng. 2018, 30, 1296–1309. [Google Scholar] [CrossRef]
- Diao, Y.L.; Sheng, W.X.; Liu, K.Y.; He, K.Y.; Meng, X.L. Research on Online Cleaning and Repair Methods of Large-Scale Distribution Network Load Data. Power Syst. Technol. 2015, 11, 3134–3140. [Google Scholar]
- Benbernou, S.; Ouziri, M. Enhancing Data Quality by Cleaning Inconsistent Big RDF Data. In Proceedings of the 2017 IEEE International Conference on Big Data (Big Data), Boston, MA, USA, 11–14 December 2017; pp. 74–79. [Google Scholar]
- Fisher, J.; Christen, P.; Wang, Q.; Rahm, E. A Clustering-Based Framework to Control Block Sizes for Entity Resolution. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 279–288. [Google Scholar]
- Ahmad, H.A.; Wang, H. An effective weighted rule-based method for entity resolution. Distrib. Parallel Databases 2018, 36, 593–612. [Google Scholar] [CrossRef]
- Wang, H.Z.; Li, J.Z.; Gao, H. Efficient entity resolution based on subgraph cohesion. Knowl. Inf. Syst. 2016, 46, 285–314. [Google Scholar] [CrossRef]
- Brisaboa, N.R.; Rodriguez, M.A.; Seco, D.; Troncoso, R.A. Rank-based strategies for cleaning inconsistent spatial databases. Int. J. Geogr. Inf. Sci. 2015, 29, 280–304. [Google Scholar] [CrossRef]
- Xu, Y.L.; Li, Z.H.; Chen, Q.; Zhong, P. Repairing Inconsistent Relational Data Based on Possible World Model. J. Softw. 2016, 27, 1685–1699. [Google Scholar]
- Martin, D.; Rosete, A.; Alcala-Fdez, J.; Herrera, F. A New Multiobjective Evolutionary Algorithm for Mining a Reduced Set of Interesting Positive and Negative Quantitative Association Rules. IEEE Trans. Evol. Comput. 2014, 18, 54–69. [Google Scholar] [CrossRef]
- Perez-Alonso, A.; Medina, I.J.B.; Gonzalez-Gonzalez, L.M.; Chica, J.M.S. Incremental maintenance of discovered association rules and approximate dependencies. Int. Data Anal. 2017, 21, 117–133. [Google Scholar] [CrossRef]
- Zhang, X.J.; Wang, M.; Meng, X.F. An Accurate Method for Mining top-k Frequent Pattern under Differential Privacy. J. Comput. Res. Dev. 2014, 51, 104–114. [Google Scholar]
- Zhang, C.S.; Diao, Y.F. Conditional Functional Dependency Discovery and Data Repair Based on Decision Tree. In Proceedings of the 2015 12th International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Zhangjiajie, China, 15–17 August 2015; pp. 864–868. [Google Scholar]
- Yadav, M.L.; Roychoudhury, B. Handling missing values: A study of popular imputation packages in R. Knowl.-Based Syst. 2018, 160, 104–118. [Google Scholar] [CrossRef]
- Krishnan, S.; Franklin, M.J.; Goldberg, K.; Wu, E. Boostclean: Automated error detection and repair for machine learning. arXiv 2017, arXiv:1711.01299. [Google Scholar]
- Li, L.; Hanson, T.E. A Bayesian semiparametric regression model for reliability data using effective age. Comput. Stat. Data Anal. 2014, 73, 177–188. [Google Scholar] [CrossRef]
- Karakasidis, A.; Koloniari, G.; Verykios, V.S. Scalable Blocking for Privacy Preserving Record Linkage. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 527–536. [Google Scholar]
- Papadakis, G.; Papastefanatos, G.; Koutrika, G. Supervised Meta-blocking. Proc. VLDB Endow. 2014, 7, 1929–1940. [Google Scholar] [CrossRef]
- Kim, J.S.; Sim, J.Y.; Kim, C.S. Multiscale Saliency Detection Using Random Walk with Restart. IEEE Trans. Circuits Syst. Video Technol. 2014, 24, 198–210. [Google Scholar]
- Sun, C.C.; Shen, D.R.; Kou, Y.; Nie, T.Z.; Yu, G. Entity Resolution Oriented Clustering Algorithm. J. Softw. 2016, 27, 2303–2319. [Google Scholar]
- Tong, H.H.; Faloutsos, C.; Pan, J.Y. Fast random walk with restart and its applications. In Proceedings of the Sixth International Conference on Data Mining, Hong Kong, China, 18–22 December 2006. [Google Scholar]
- Le, H.T.; Urruty, T.; Gbehounou, S.; Lecellier, F.; Martinet, J.; Fernandez-Maloigne, C. Improving retrieval framework using information gain models. Signal Image Video Process. 2017, 11, 309–316. [Google Scholar] [CrossRef]
- Ye, M.Q.; Gao, L.Y.; Wu, C.R.; Wan, C.Y. Informative Gene Selection Method Based on Symmetric Uncertainty and SVM Recursive Feature Elimination. Pattern Recognit. Artif. Intell. 2017, 30, 429–438. [Google Scholar]
| Attributes | Meanings | Value Types | Abbreviations |
|---|---|---|---|
| Id | the building number | numeric | ID |
| MSSubClass | the building class | numeric | MC |
| MSZoning | the general zoning classification | text | MZ |
| Street | type of road access | text | ST |
| LotShape | general shape of property | text | LS |
| CentralAir | central air conditioning | Boolean | CA |
| BldgType | type of dwelling | text | BT |
| SalePrice | the property’s sale price in dollars | numeric | SP |
| ID | MC | MZ | ST | LS | CA | BT | SP |
|---|---|---|---|---|---|---|---|
| 1 | 60 | RL | Pave | Reg | Y | 1Fam | 200,000 |
| 2 | 20 | RL | Pave | Reg | * | 1Fam | 181,500 |
| 3 | 60 | RM | Pave | IR1 | Y | 1Fam | 140,000 |
| 4 | * | RL | Grvl | IR1 | Y | * | 250,000 |
| 5 | 60 | FV | Pave | IR1 | N | 1Fam | 140,000 |
| 6 | 50 | RM | Pave | Reg | N | 1Fam | 307,000 |
| 7 | 20 | * | Pave | IR2 | Y | Duplex | 200,000 |
| 8 | 60 | RM | Grvl | IR2 | Y | 1Fam | 129,500 |
| 9 | 50 | FV | Pave | Reg | Y | Duplex | 129,500 |
| 10 | 20 | RL | Pave | IR1 | N | 1Fam | 345,000 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Dai, C.; Wang, W. When Considering More Elements: Attribute Correlation in Unsupervised Data Cleaning under Blocking. Symmetry 2019, 11, 575. https://doi.org/10.3390/sym11040575
Li P, Dai C, Wang W. When Considering More Elements: Attribute Correlation in Unsupervised Data Cleaning under Blocking. Symmetry. 2019; 11(4):575. https://doi.org/10.3390/sym11040575
Chicago/Turabian StyleLi, Pei, Chaofan Dai, and Wenqian Wang. 2019. "When Considering More Elements: Attribute Correlation in Unsupervised Data Cleaning under Blocking" Symmetry 11, no. 4: 575. https://doi.org/10.3390/sym11040575
APA StyleLi, P., Dai, C., & Wang, W. (2019). When Considering More Elements: Attribute Correlation in Unsupervised Data Cleaning under Blocking. Symmetry, 11(4), 575. https://doi.org/10.3390/sym11040575




