Abstract
In this paper, we present a new model for simulating an interesting class of Islamic design. Based on periodic sequences on the one-dimensional manifolds, and from emerging numbers, we construct closed graphs with edges on the unit circle. These graphs build very nice shapes and lead to a symmetrical class of geometric patterns of so-called Islamic design. Moreover, we mathematically characterize and analyze some convergence properties of the used up-down sequences. Finally, four planar type of patterns are simulated.
MSC:
34A08; 34B10
1. Motivation
The art in the Islamic culture is very rich in spiritual and meditative messages. It uses complex geometric patterns and shapes; see Figure 1. For instance, in wood for ornamental patterns, in bricks of buildings, in brass for decorations, paper, tiling, plaster, glass, etc. Islamic design can be found mainly in three distinct geometrical patterns, namely rectangular Kufic fonts, arabesque shapes, and polygonal designs [1]. The largest class of Islamic design employs, in general, complex and symmetrical polygons, where, in each polygonal graph, the starting design is a cell in the form of a symmetrical shape. The creation of the symmetrical rectangular, triangular, and circular patterns leads to beautiful ornamental patterns [2,3,4,5]. The mathematical modeling of these cells is based on iterative techniques for generating beautiful and colored patterns. Different methods were used for seeking explicit relationships between a simple single cell and the corresponding complex multiplicity, either for constructing symmetrical groups for infinite periodic patterns form the 17 classes of the two-dimensional crystallographic groups [6] or by using planar geometrical transformations, translations, rotations, reflections, and glide reflections for rearranging and space filling. The modeling of symmetries in nature and sciences brought together the interest of many scientists [7,8,9,10] for developing several techniques. In [11,12], the authors used the logistic mapping for generating and describing pictures created by merging symmetry and chaos.

Figure 1.
Examples of geometric patterns in Islamic design.
In [13], we studied the existence and the symmetry of the multiple barycenters, especially in the unit circle considered as one-dimensional manifold. The generated vertices are, for special values of n, the so-called multiple barycenters on . Moreover, since mapping circular patterns on curved surfaces in a three-dimensional space is in general a nontrivial task—see [14,15,16]—we propose a new algorithm for generating planar and isometric patterns. We construct and characterize vertices on the unit circle similar to the multiple barycenters using repeated iterations of emerged numbers. Thereafter, connecting these barycenters as vertices with finite number of edges describes and classifies special periodic sequences. These sequences are the main source for constructing symmetrical designs, especially Islamic design.
This paper is organized as follows: In Section 2, we introduce the periodic sequences on the unit circle, and we present necessary analytical properties. Based on the results presented in the previous section, we define and construct, in Section 3, the Islamic design. In Section 4, we present some numerical simulations of different types of designs and patterns. Conclusions and future works are listed in Section 5.
2. Periodic Sequences on the Unit Circle
Let a be a real number in and be the unit circle considered as one-dimensional manifold. For a given starting value , we define the real iterative sequence with values on modulo by:
The up-down behavior of the sequence will be observed as emerging numbers on the unit circle, considered as a one-dimensional manifold (see Appendix A). In this example, we compute some special cases of the sequence (1) for the initial guess . The following table presents the first eight values of the up-down sequence:
From our experiments, we observed that the sequence is periodic for special values of the parameter a only. Therefore, we assign to the clockwise rotation a negative direction (negative integer ) and we assign the positive direction to any rotation in the counterclockwise direction (i.e., ). Furthermore, we are interested to characterizing the minimal number of rotations till the first-come-back . In the following, let us denote by , the range of the up-down sequence for a given parameter .
Definition 1.
A sequence is called Alternating sequence if the corresponding range set contains exactly two elements. Otherwise, we call it a Loop-sequence.
Lemma 1.
The sequence is an Alternating sequence for and 1 and a Loop-sequence for .
Proof.
In the bullet diagram below, we illustrate the results of the lemma above:
- For , we needed one rotation in the counterclockwise direction and four iteration to reach the first-come-back for and (see Table 1 and Figure 2a).
 Table 1. Value of the up-down sequence using different values of the parameter a.
Table 1. Value of the up-down sequence using different values of the parameter a.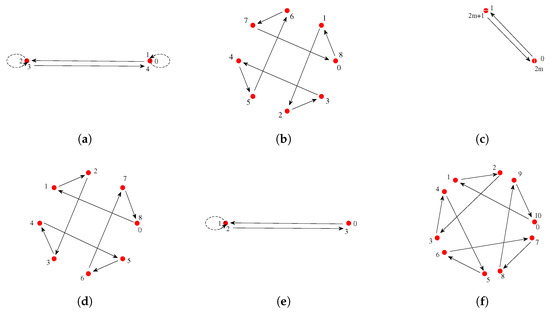 Figure 2. The path of the periodic sequence on . (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
Figure 2. The path of the periodic sequence on . (a) ; (b) ; (c) ; (d) ; (e) ; (f) .
It should be stressed that for , the up-down sequence rotate in the counterclockwise direction (i.e., positive direction ) and if it rotates in the clockwise direction (negative direction ). In the following, we are looking for a relationship between a and the minimal index such that .
It is important to note that the graphs in the Figure 2b,d,f are closed and lead to the construction symmetric areas. While the path trajectory in the Figure 2a,c,e represents a segment. Moreover, in the Figure 2c, the up-down sequence oscillates between the origin and .
According to the results in the example above, it should be stressed that for a certain value of a one can find the pair satisfying the first-come-back property. In the same context, the following theorem characterize the parameter using, in somehow, Archimedean principle applied to a circle. In other words, we determine a necessary and sufficient condition for constructing the minimal number of loops till the first-come-back :
Theorem 1.
For any rational number and any initial value , there exists n such that and if , we have for all .
Proof.
Let us assume that . If , then . Therefore, we restrict the proof for to the case and we distinguish between the following two cases:
- Case 1:
- n even In this case, we haveLet us consider the number the integer k as the number of complete rotations. From (11) it follows thatthus, the parameter a, could be written as
- Case 2:
- n odd means that is evenSimilar to the previous case, from (11) we haveThus, the parameter a, could be written as follows:
In general, we distinguish between the odd and the even come-back events, therefore we define the following mappings.
Definition 2.
According to Theorem 1, we define the come-back mappings (for construction of the parameter a) as
and
Lemma 2.
Let and n be an even natural number, then the following identities hold
- 1.
- .
- 2.
- .
Proof.
For 1 using the definition of the mapping e,
For 2: similar to 1, we can easily prove that the following identity is true:
The geometrical interpretation of the results (17) and (19) leads to an interesting observation about the up-down behavior of the sequence , namely if the first-come-back n is even, making k loops in the positive direction or in the negative one have the same path (i.e., the same range). While if the first-come-back n is odd, the direction affects the range of the up-down sequence. However, we could admit similar result in the even case for large n only.
Lemma 3.
Let us consider and n in , then the following identities hold
- 1.
- for all .
- 2.
- for all odd such that .
Proof.
For 1 using the definition of the mapping e,
For 2 we have
The results in Lemma 3 mean that the range of and are identical for all but and are identical only for all odd such that .
Theorem 2.
If and , then the first-come-back of is given by
Proof.
Suppose that , then the 1st and the 2nd values of the sequence are given by
Per recurrence, we deduce the and the values of the sequence :
Thus, we can define the first come-back, if at least one of the following conditions is satisfied
Since per definition the natural numbers and represent the number of loops needed till the first-come-back, numbers
Thus, according to (22) and (23), we can determine the first come-back as a function of the minimal number of loops needed as follows:
According to the result of the theorem above, we remarked that the range of the sequence contains exactly elements if . However, if , then the range of the sequence contains at least element.
- (i)
- If , then is an even number, it followsBy this way, we construct all previous elements and , .
- (ii)
- If , then is an odd number, it followsTherefore, we can construct other elements , which are not necessary in the set . To make the following observations clear, we consider the following examples.
Definition 3.
We define the following indices:
- (i)
- The first-come-back index is defined as .
- (ii)
- If Range, then we denote by , the maximal index in the range of the sequence R.
- (iii)
- The cardinal number of the range of the sequence is defined by Range .
Example 1.


For , we compute the values of the first 15 elements of the sequence :We deduce the indices , and (see below Table 2). Similarly, we compute the same indices for different parameters a. We also must mention that an interesting open question could be deduced from the results in Table 2 and Table 3. Namely, the relationship between the three indices and .

Table 2.
Value of the up-down sequence using different values of the parameter a.

Table 3.
Examples of values of and using different values of the parameters a.
3. Construction of Geometric Patterns in Islamic Design
In general, the Islamic design employs complex polygons with vertices on a circle. In our case, these polygons represent connected graphs with vertices and edges , where represents the initial value of the sequence . For a given parameter a and an initial value , the vertices set is defined as spatial points in by:
where for
The set of edges of the closed graph is
where denotes the range number and a is rational number in .
Definition 4 (single cell).
A cell defining a design is a graph with colored sub-areas generated by a sequence on a circle with radius and a center . We denote by , the set of all possible geometric patterns of the Islamic designs in . (see Figure 2b,d,f).
Throughout this paper, starting from a single cell, we construct special class of Islamic designs and patterns. Any geometrical transformation of a single cell leads to the formation of symmetrical patterns. Therefore, geometric patterns in the Islamic design, at least in the context of this work, is a repeated and/or modified planar transformation of a single cell.
Definition5 (Planar transformations).
For a given , we define the vertical translation mapping as
The horizontal translation mapping is defined by
The diagonal translation mapping is defined by
where and .
The Design (space filling) mapping is defined by
where , are positive constants.
The radial translation mapping is defined by
To construct designs according to all constructions presented in this paper, we suggest the following mathematical definition of geometric patterns in Islamic designs:
Definition6 (Geometric Patterns in Islamic Design).
A Circular Islamic Design with elements is a symmetrical repeated placement of circular cells of the form .
Please note that any single cell from represents the class of geometric patterns in Islamic design. Moreover, any composite cell could be considered as a single cell, thus it is also an element of the Circular Islamic design. The mathematical construction of the circle-based class of geometric patterns in Islamic design is then achieved by using the geometrical translational and transformation mappings given by (29)–(33). More details are presented in the following section.
4. Numerical Simulation Islamic Geometric Patterns
In this work, we discuss four classes of circular Islamic designs, namely:
- Modeling of Circular Islamic Design using single cells (see Appendix B).
- Modeling of Circular Islamic Design using composite cells.
- Modeling of Circular Islamic Design using circular cells.
- Modeling of Circular Islamic Design using overlapping cells.
4.1. Modeling with Single Cells
The first class of Islamic designs presented in this work is achieved by arranging single symmetrical cells in vertical and horizontal forms. For any even number n, representing the first-come-back and any integer k representing the number of loops needed, we construct a sequence using the Formula (12). Thus, we can generate Islamic designs using single cells using vertical and horizontal translation as follows:
see Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 (left and middle figures). To generate cells in the vertical direction and cells in the horizontal direction, we use the following algorithmic translations:
where the distance needed for constructing non-overlapping shapes are given by for the vertical direction and by for the horizontal direction.

Figure 3.
Single cells Patterns for and .
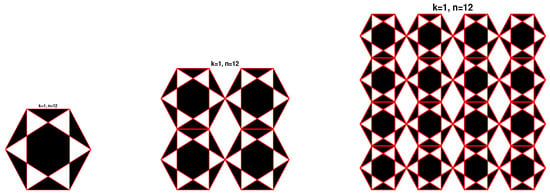
Figure 4.
Single cells Patterns for and .

Figure 5.
Single cells Patterns for and .

Figure 6.
Single cells Patterns for and .
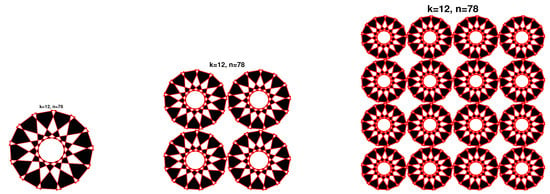
Figure 7.
Single cells Patterns for and .
For even number n and for different values of k, according to theorem 1, we construct different symmetrical single cells. We show the resulting shapes in the first column of Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. In the second column, we plot a design and in the third column we present the result of designs. Moreover, between the design, we observe the presence of the contour of a new design; see the second column.
It is important to note that changing the initial value leads to other designs, especially with totally different contours between the single cells. Moreover, it should be stressed that all our simulations are presented as the output of mathematical function without any modifications. For more interesting definition and historical evolution of the Islamic arts we refer to [1]. In Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7, we show five different designs using even numbers n and different number of loops: (a) , (b) , (c) , (d) and (e) .
4.2. Modeling with Composite Cells
The second class of Islamic designs is achieved by arranging four single non-symmetrical cells in vertical and horizontal forms. In this case, the number n is odd. Because of the non-symmetry of the cells, we can construct a composite cell using four identical cells, using four different initial values of the same sequence given the Formula (12), where is given by . The governing function generating symmetrical shapes using composite cells is defined by
where , r a constant radius of the circle and .
After the construction of the composite single cells (36) for a satisfying the theorem 1, we use different initial values for , for instance , , and and similar to the first case, we use vertical and horizontal translation to simulate the patterns showed in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, second and third column. For cells in the vertical direction and cells in the horizontal direction, we use the following translations; see the third column in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12. To generate cells in the vertical direction and cells in the horizontal direction, we use the following algorithmic translations:
where the distance needed for constructing non-overlapping four cells shapes are given by for the vertical directions and by for the horizontal direction. For an odd number n and for different values of k, according to theorem 1, we construct different non-symmetrical single cells using odd numbers n and different number of loops: (a) , (b) , (c) , (d) and (e) . In the first column of the Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12, we show the resulting shapes of sequences with odd numbers and different initial values. In the second column, we plot the corresponding composite cell. In the third column, we present the result of designs. Moreover, between the designs, we remarked the presence new shapes; see the second column in Figure 8, Figure 9, Figure 10, Figure 11 and Figure 12.

Figure 8.
Composite cells Patterns for and .
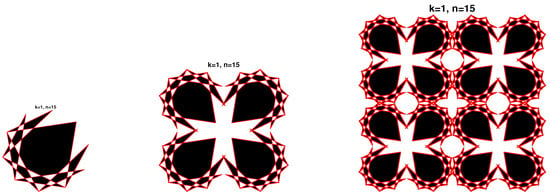
Figure 9.
Composite cells Patterns for and .
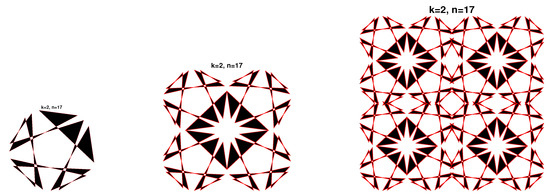
Figure 10.
Composite cells Patterns for and .
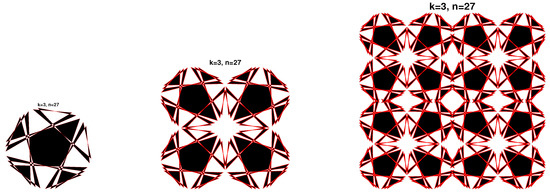
Figure 11.
Composite cells Patterns for and .
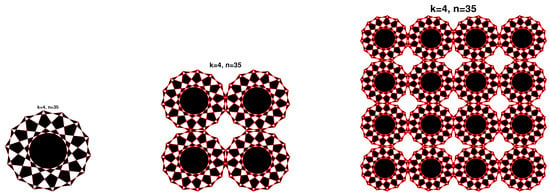
Figure 12.
Composite cells Patterns for and .
4.3. Modeling with Circular Composite Cells
The third class of Islamic designs is the composition of symmetrical cells in circular forms and a centered design. For even numbers , , we construct composite design using single cells only. Because of the non-symmetry of the cells, we can construct a composite cell using four identical cells, using four different initial values of the same sequence given by Formula (12), where is given by . This could be clearly seen in the first row of Figure 13. The governing function generating symmetrical composite cell is defined by:
where refers to the number of surrounded circles, is the center of the centered design, the coordinates represent the centers of surrounded circles and is the corresponding radius for . Similar to the first and second cases, we use vertical and horizontal translation to simulate the patterns showed in Figure 13.
where represents the number of composite cells in the vertical direction and the number of composite cells in the horizontal direction (see the third column in Figure 13).
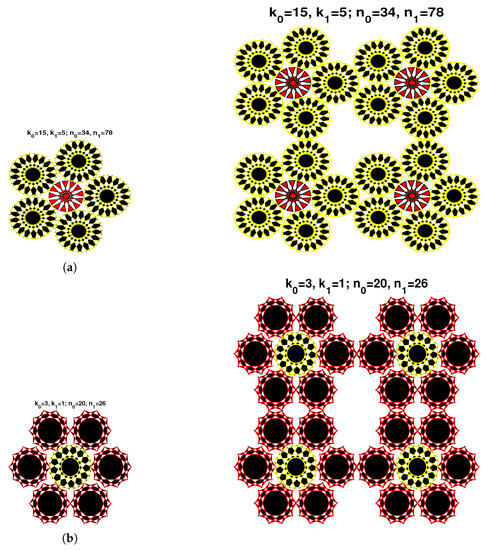
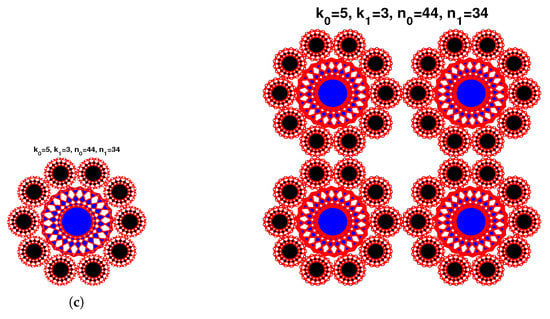
Figure 13.
Circular composite Patterns.
In the first row of the Figure 13, we plot the design using , . For the case (a), we have and . In the second row, we simulate a different design using , . For the case (b), and . In the third row, case (c), we use , , and .
For these three designs, we remarked the presence of three different contours between the circles (see the second row of Figure 13).
4.4. Modeling with Overlapping Cells
The fourth class of Islamic designs is constructed by using overlapping single cells with the same center and increasing radius. Because of the symmetry of the cells, the number n should be an even number. Thus, we can construct overlapping cells with non-necessary identical sequences with different initial values and parameters . The governing function generating symmetrical overlapping cells is defined by:
where is the center of the second centered design, the coordinates, . To construct more overlapping designs, we apply the radial transformation mapping several times. For , the governing function generating this type of designs is given as follows:
where for , the positive decreasing sequence represents the radius of the overlapping circles. In Figure 14, we see six different overlapping designs for , . In Figure 15, we present repeated overlapping designs using different colors with different parameters, (see the titles of the Figure 15). For Figure 14, the following entries are implemented:

Figure 14.
Overlapping Patterns for loops and come-backs.

Figure 15.
Repeated overlapping patterns for loops and come-backs.
- a.
- b.
- and
- c.
- and
- d.
- and
- e.
- and
- f.
- and
5. Concluding Remarks and Future Outlook
Using the geometrical properties of connected and closed graphs with vertices on the unit circle, we presented a new mathematical approach for modeling an interesting class of geometric patterns in Islamic design. The symmetries of vertices on the one-dimensional manifold leads to the construction of two-dimensional planar patterns, which are in the literature well known as a part of Islamic design. The resulting designs define beautiful fine arts and are, in general, expressed using basic mathematical transformations. Moreover, we believe that the class of geometric patterns presented in this work could be seen as a starting point for advanced studies in modeling of other classes of Islamic design using advanced techniques in Graph Theory, in modeling of more complex designs, or in characterizing the symmetry phenomenon in nature. In light of the simple techniques used here, the present geometrical framework can also serve as a valuable exercise in mathematics education. Furthermore, a generalization of the proposed work to curved surface inputs is an interesting avenue for future research works, in particular for developing similar and easy models to contribute to making mathematics more attractive for students as well as for non-mathematician researchers.
Funding
This work is supported by the University of Sharjah (UOS), Research group MASEP, RGS-2018-2019, No. 1802144062-P and Research project No. 1802144069.
Acknowledgments
I would like to thank Prof. Madjid Merabti and Prof. Abdelaziz Soufyane for their fruitful and valuable comments. In addition, I would like to thank the anonymous reviewers for their comments and suggestions.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A. The Sequence
%% The sequence function sequenceID.m
function f = sequenceID(n,x0,a)
ff = zeros(n,1);
ff(1) = x0;
for k = 1:n
p=mod(k,2);
if(p==1)
ff(k+1) = ff(k)+a*pi;
else
ff(k+1) = ff(k)+(a-1)*pi ;
end
end
f=ff;
%---------------------------------------------
Appendix B. The Main Code for Generating Islamic Geometric Patterns
function ID=IslamicDesignE(k,N,x0,mv,mh)
% N should even, for the odd case use the thm formula
% construction the parameter of the sequence
a=((4*k)/N+1)/2;
% construction of the sequence
X=sequenceID(N,x0,a);
% adapting the distance between the cells
tx=2; ty=1.85;
% generating designs
for r=1:mv
for t=1:mh
A=tx*t+cos(X);
B=ty*r+sin(X);
hold on; fill(A,B,’k’);
hold on; plot(A,B,’r’);
axis off; axis equal;
end
end
ID=a;
%---------------------------------------------
Compile: IslamicDesignE(1,20,0,5,5)
References
- Abas, S.J.; Salman, A.S. Symmetries of Islamic Geometrical Patterns; World Scientific Publishing Company: Singapore, 1994. [Google Scholar]
- Denny, W.B. The Ceramics of the Mosque of Rüstem Pasha and the Environment of Change; Garland Publishers, Inc.: New York, NY, USA, 1977. [Google Scholar]
- Grube, E.J. Islamic Pottery; Faber & Faber, Ltd.: London, UK, 1976. [Google Scholar]
- Humbert, C. Islamic Ornamental Design; Faber & Faber, Ltd.: London, UK, 1980. [Google Scholar]
- van der Hoop, A.N.J.Th.àTh. Indonesian Ornamental Design; A.C. Nix & Co.: Bandoeng, Indonesia, 1949. [Google Scholar]
- Tennant, R.F. Subgroup Lattices for Crystallografic Groups. Vis. Math. Art Sci. Electron. J. 2002, 4, 4. [Google Scholar]
- Arnone, S.; Falcolini, C.; Moauro, F.; Siccardi, M. On Numbers in Different Bases: Symmetries and a Conjecture. Exp. Math. 2017, 26, 197–209. [Google Scholar] [CrossRef]
- Chossat, P.; Golubitsky, M. Symmetry increasing bifurcations of chaotic attractors. Physica D 1988, 32, 423–436. [Google Scholar] [CrossRef]
- Hodgson, C.D.; Weeks, J.R. Symmetries, Isometries and Length Spectra of Closed Hyperbolic Three-Manifolds. Exp. Math. 1994, 3, 261–274. [Google Scholar] [CrossRef]
- Weyl, H. Symmetry; Princeton University Press: Princeton, NJ, USA, 1952. [Google Scholar]
- Field, M.; Golubitsky, M. Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature; SIAM: Philadelphia, PA, USA, 2009. [Google Scholar]
- Metzler, W.; Beau, W.; Frees, W.; Ueberla, A. Symmetry and Self-Similarity with Coupled Logistic Maps. Zeitschrift für Naturforschung 1987, 42, 310–318. [Google Scholar] [CrossRef]
- Zahri, M.; Khallaf, N. Some Results on Riemannean Multiple Barycenters. J. Appl. Math. Phys. 2014, 2, 503–509. [Google Scholar] [CrossRef][Green Version]
- Barton, M.; Shi, L.; Kilian, M.; Wallner, J.; Pottmann, H. Circular arc snakes and kinematic surface generation. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2013; Volume 32, pp. 1–10. [Google Scholar]
- Bo, P.; Pottmann, H.; Kilian, M.; Wang, W.; Wallner, J. Circular Arc Structures; Association for Computing Machinery: New York, NY, USA, 2011; Volume 30, p. 101. [Google Scholar]
- Song, X.; Aigner, M.; Chen, F.; Jüttler, B. Circular spline fitting using an evolution process. J. Comput. Appl. Math. 2009, 231, 423–433. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).