Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise
Abstract
1. Introduction
2. Related Works
2.1. CEEMDAN Algorithm
- (1)
- Apply EMD to decompose signal () to extract the first IMF;Here, is white noise with unit variance, and is the corresponding amplitude.
- (2)
- Obtain the differential signal by Equation (2);
- (3)
- Extract the first mode by decompose and appoint the second IMF using Equation (3);
- (4)
- Decompose the -th residue and extract the first mode, and the -th mode can be obtained using the following equation ():Here, indicates the symbol function of the k-th IMF.
- (5)
- Obtain last mode by Equation (5) when the residue has fewer than (or equal to) two extrema by repeating step,Signal is decomposed using equation,
2.2. De-Trended Fluctuation Algorithm (DFA)
- (1)
- Divide the following series into integrated time:Here, indicates the mean of the series .
- (2)
- Slice into n length sub-section;
- (3)
- Apply least square method fitting to obtain the local trend ;
- (4)
- Extract from the to obtain fluctuation function ;
- (5)
- Obtain different by different length segments;
- (6)
- Calculate the slope (fractal scaling index) between and ; the bigger slope of signal, the smoother time series (as shown in Equation (9)):
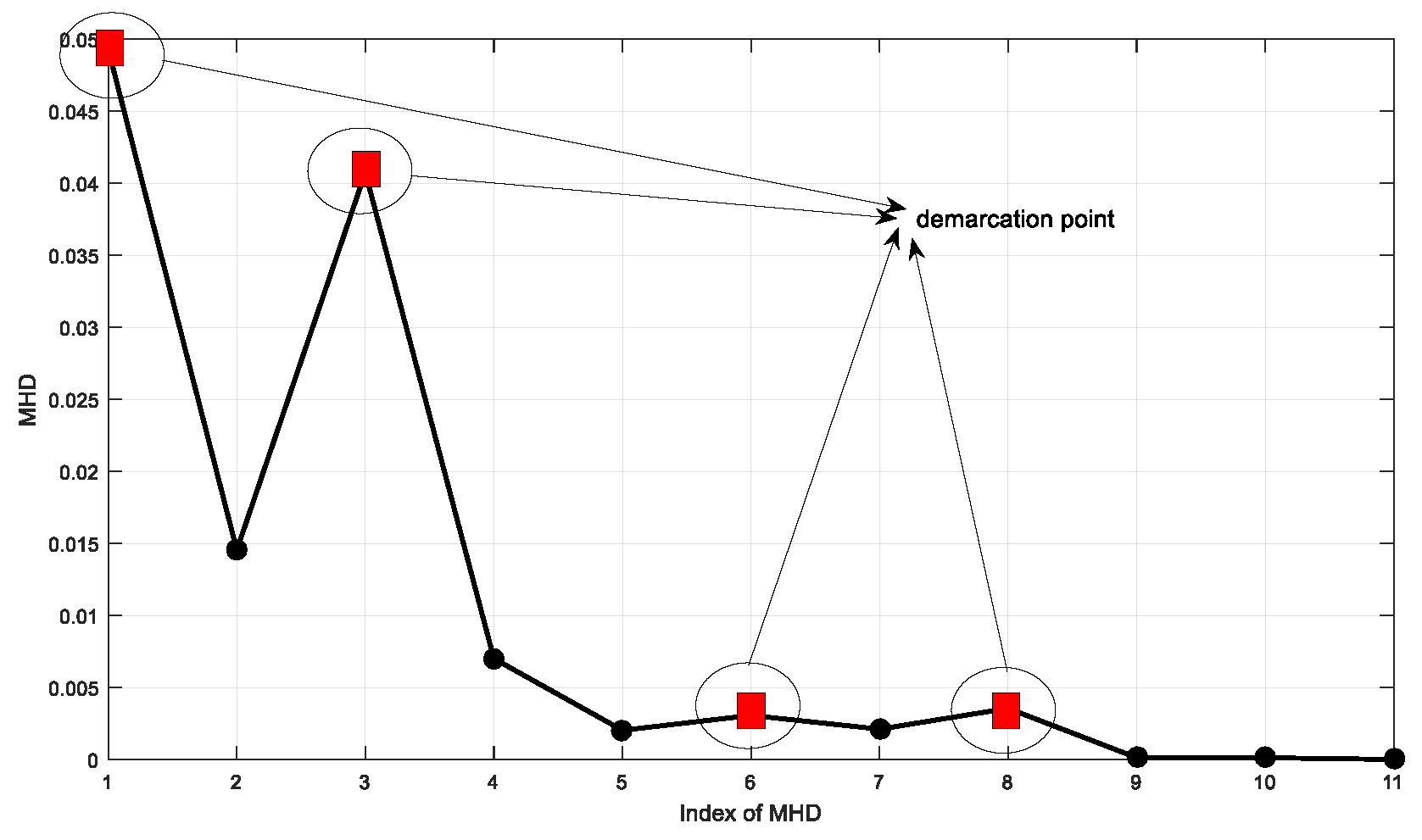
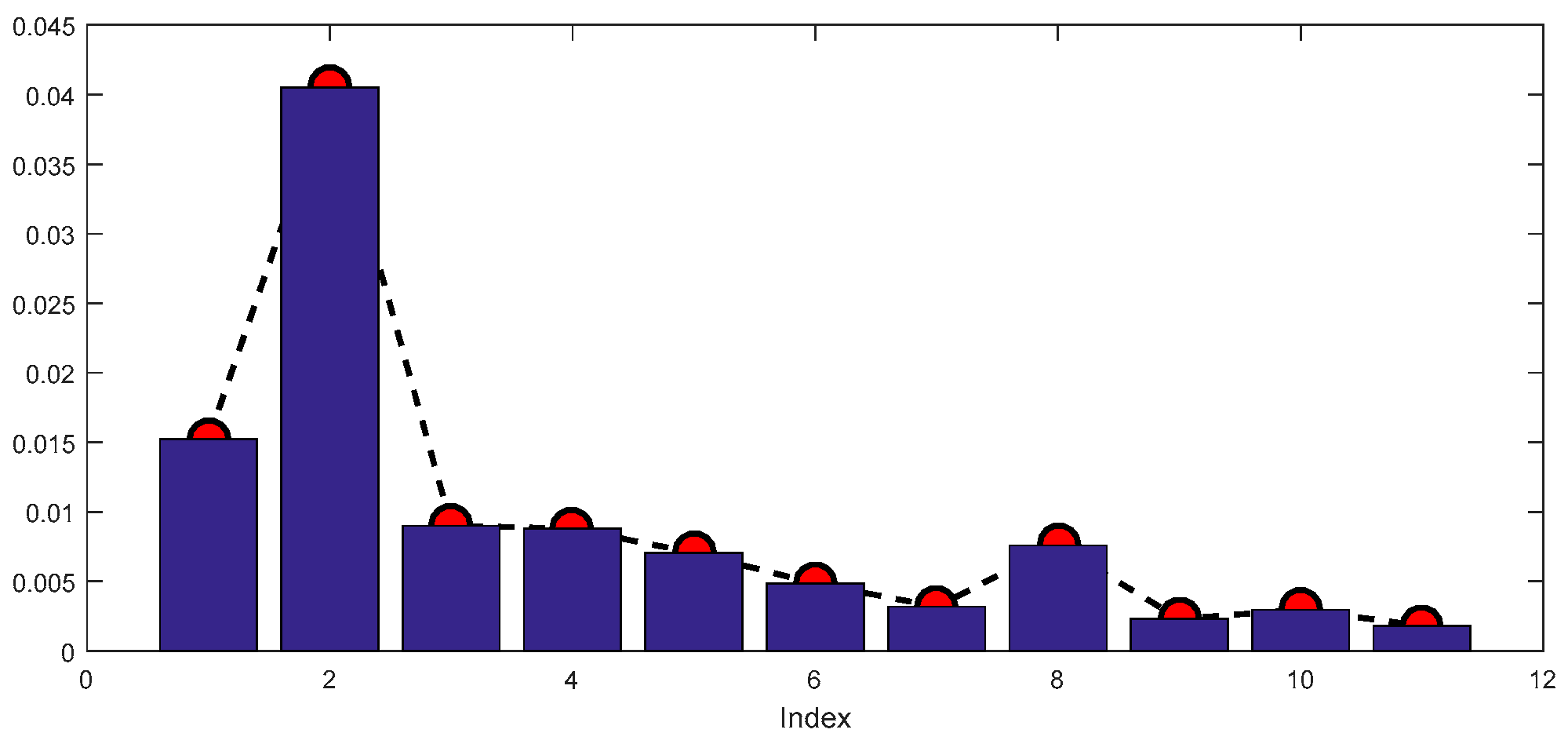
2.3. Modified Hausdorff Distance (MHD)
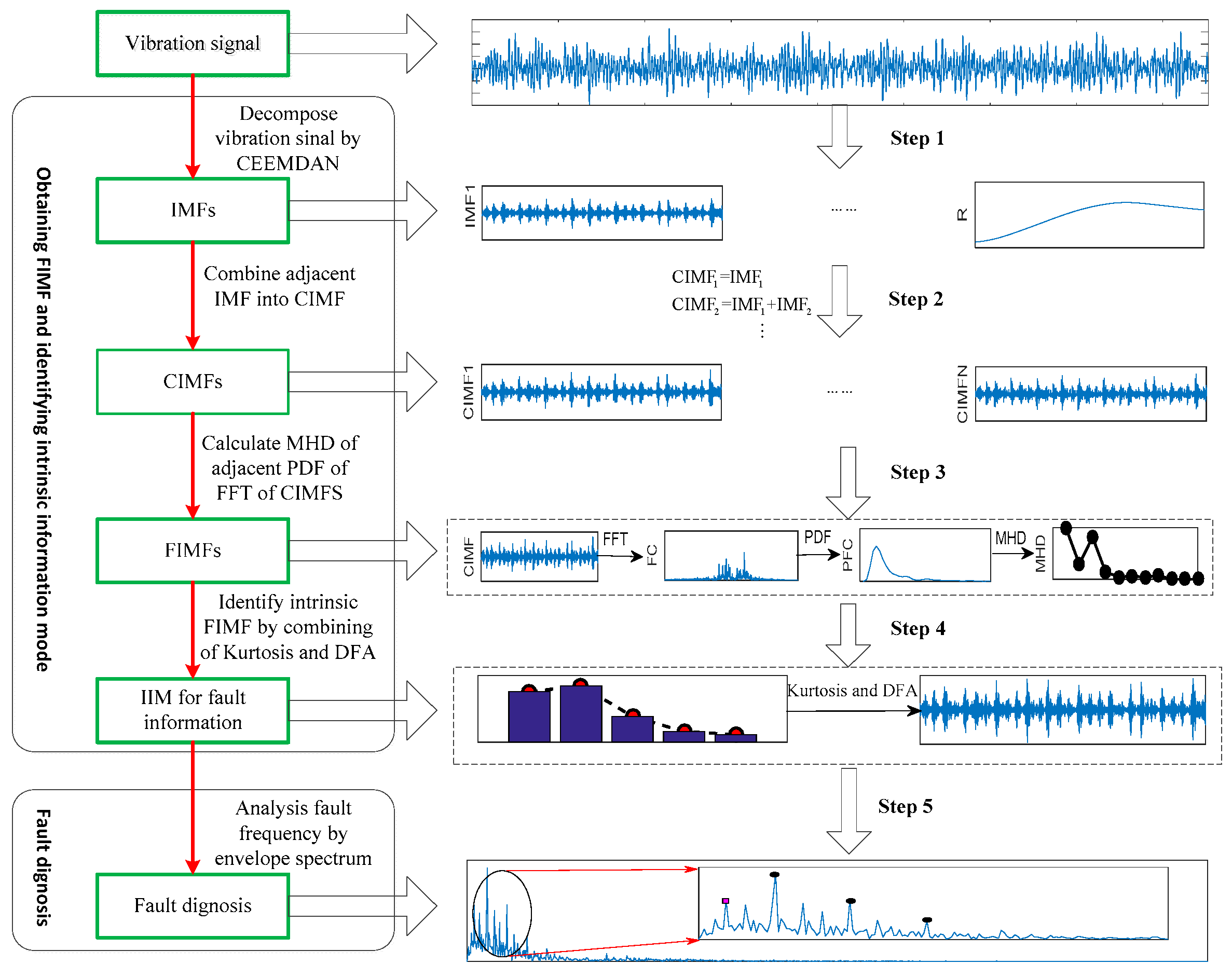
3. Proposed Works
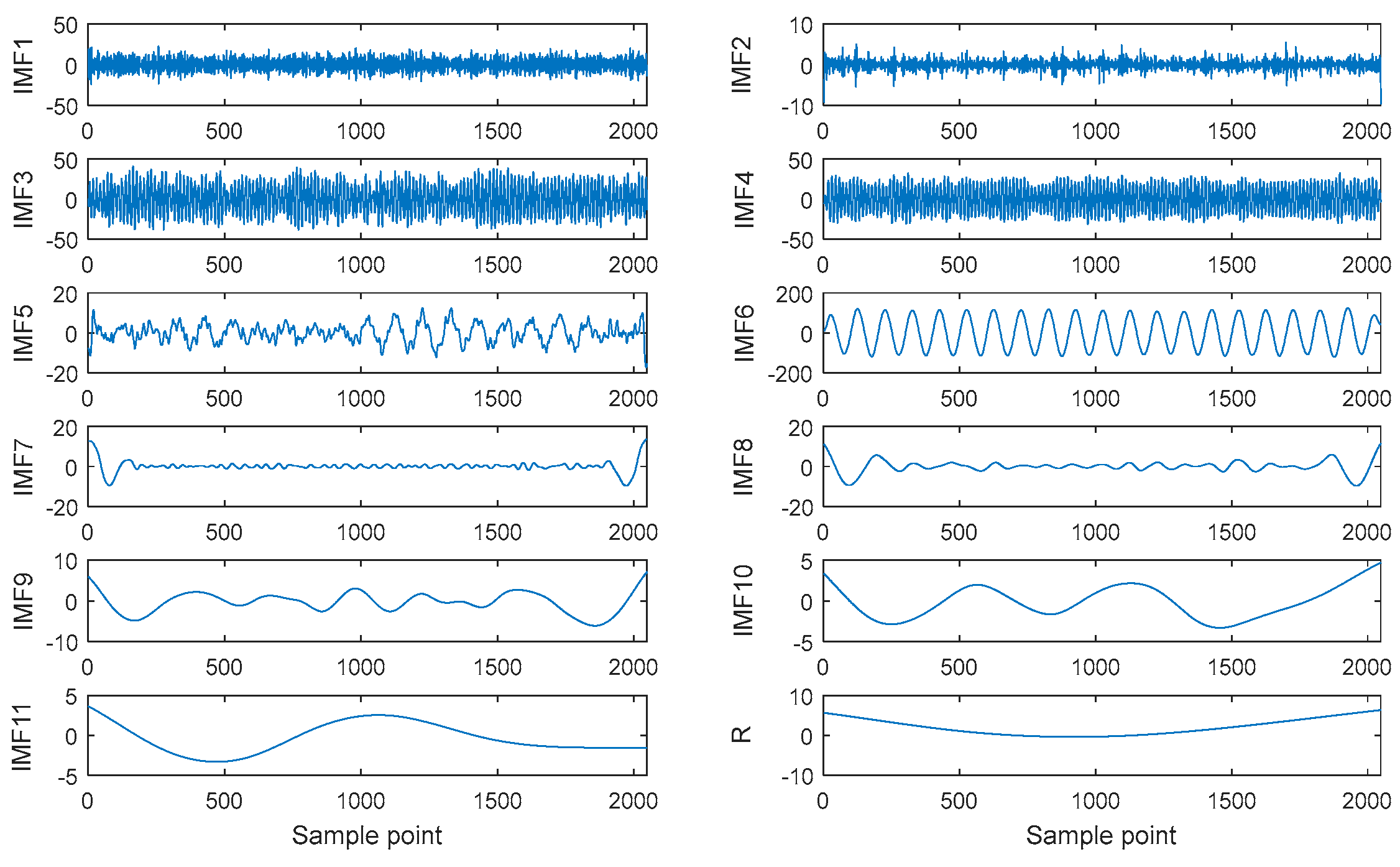
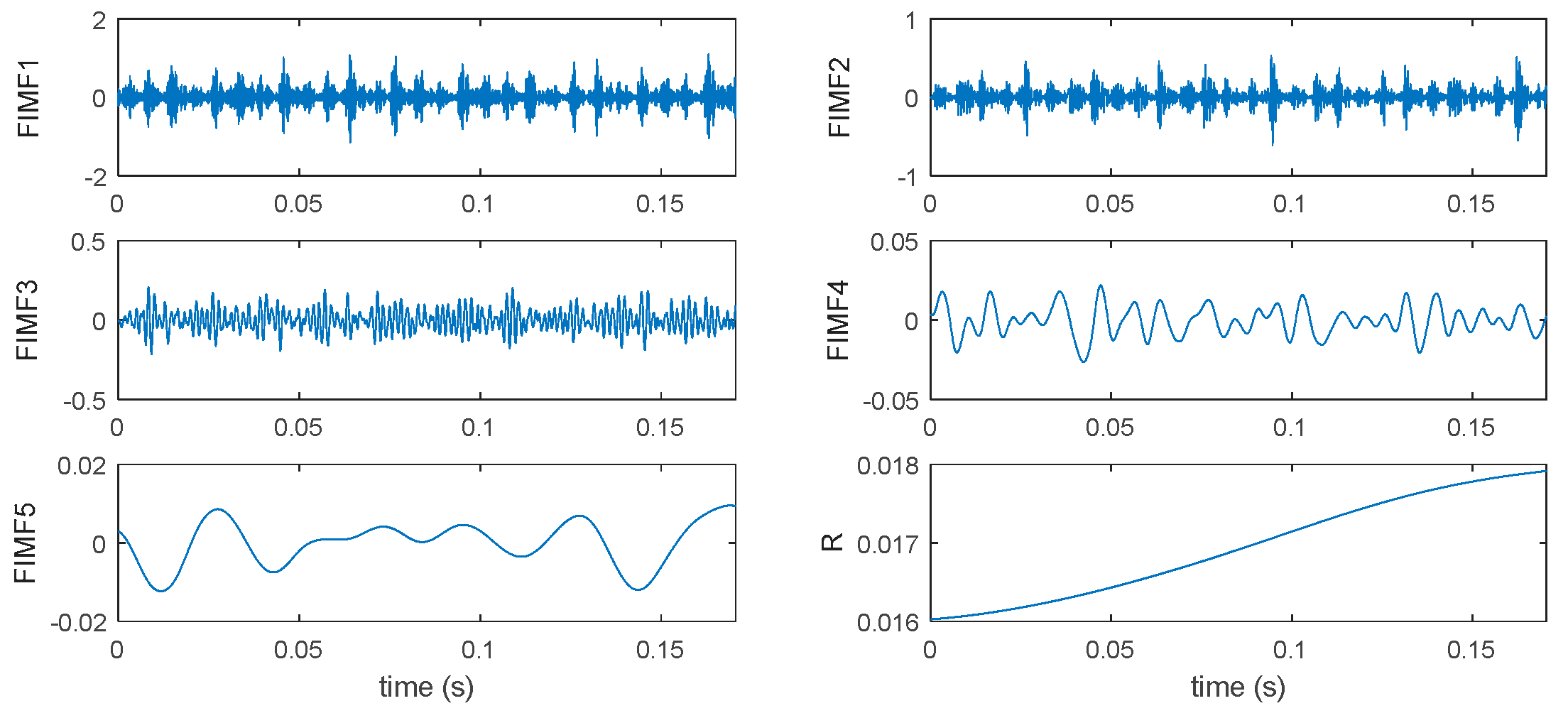
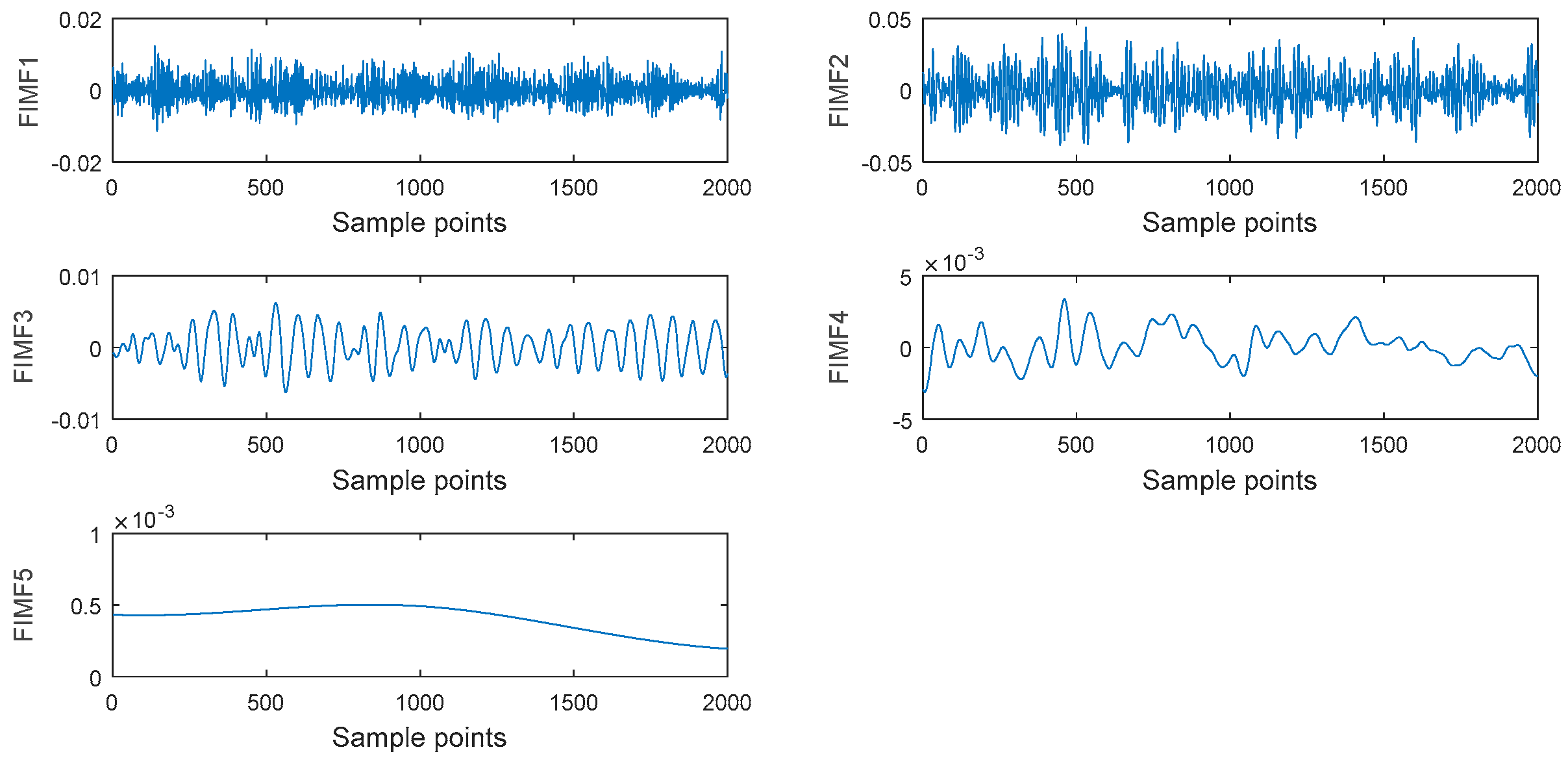
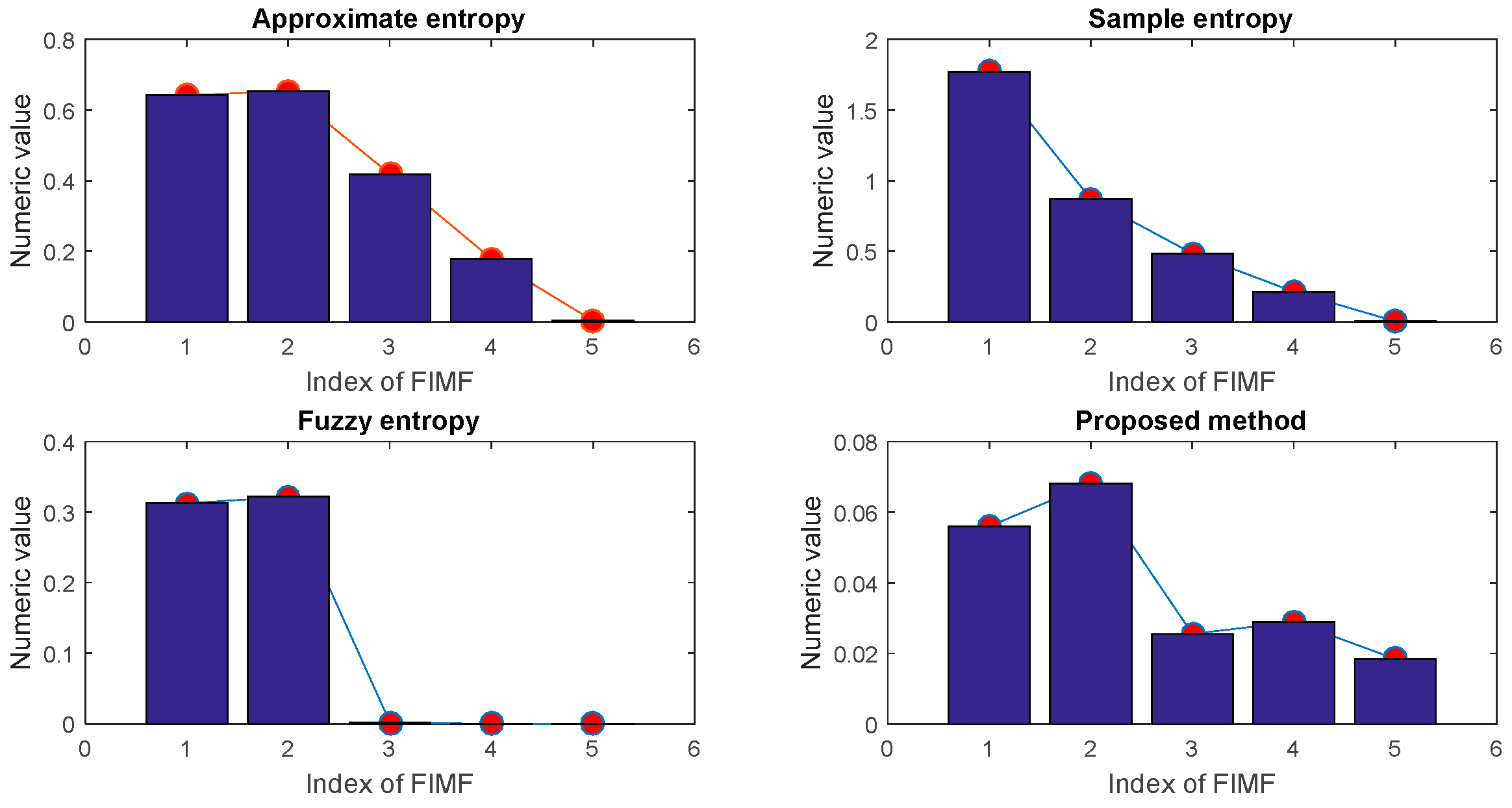
3.1. Identifying of IMF with Minimum Number and Physical Meaning
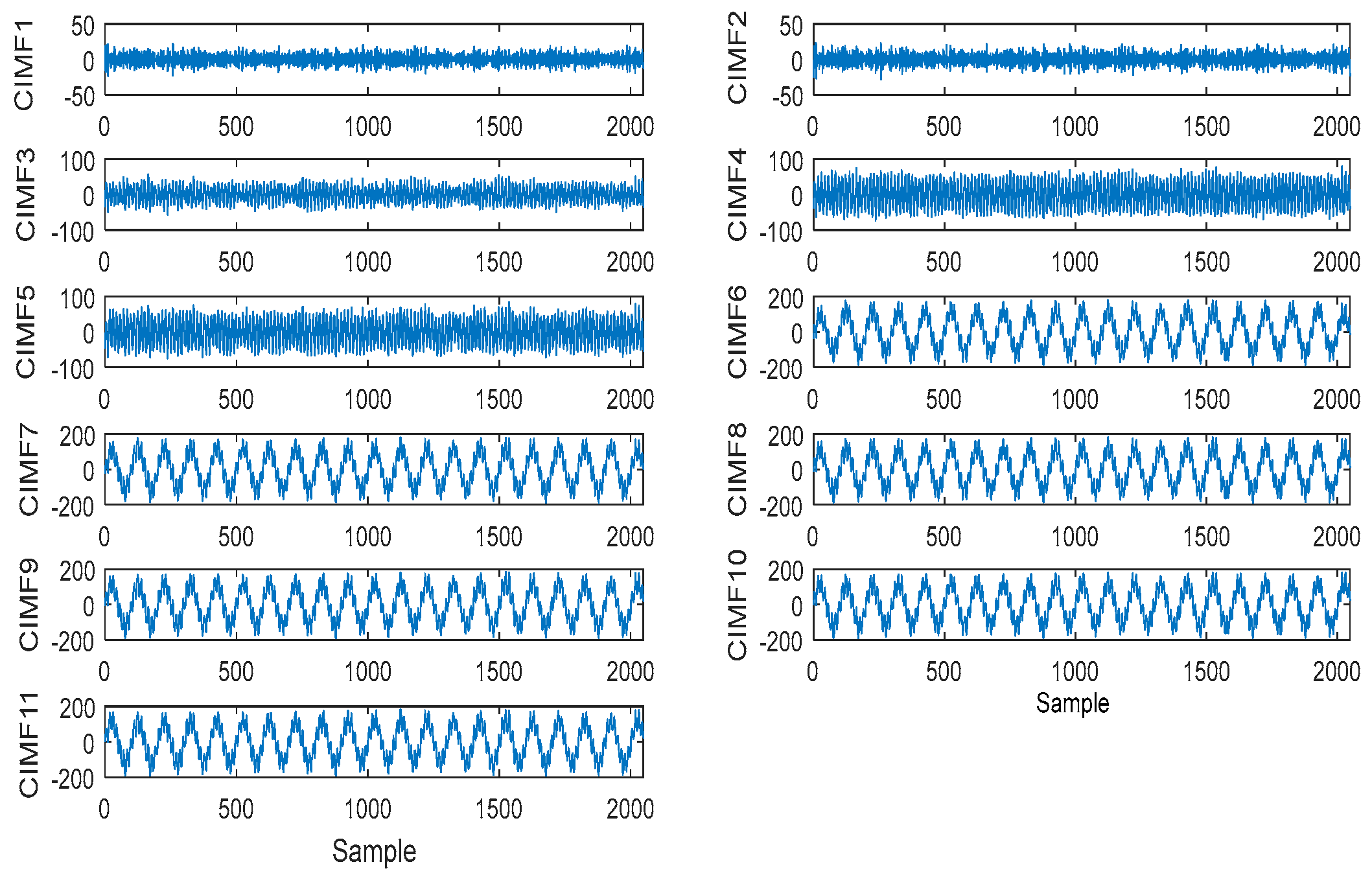
3.2. Selection of Intrinsic Information Mode
- (1)
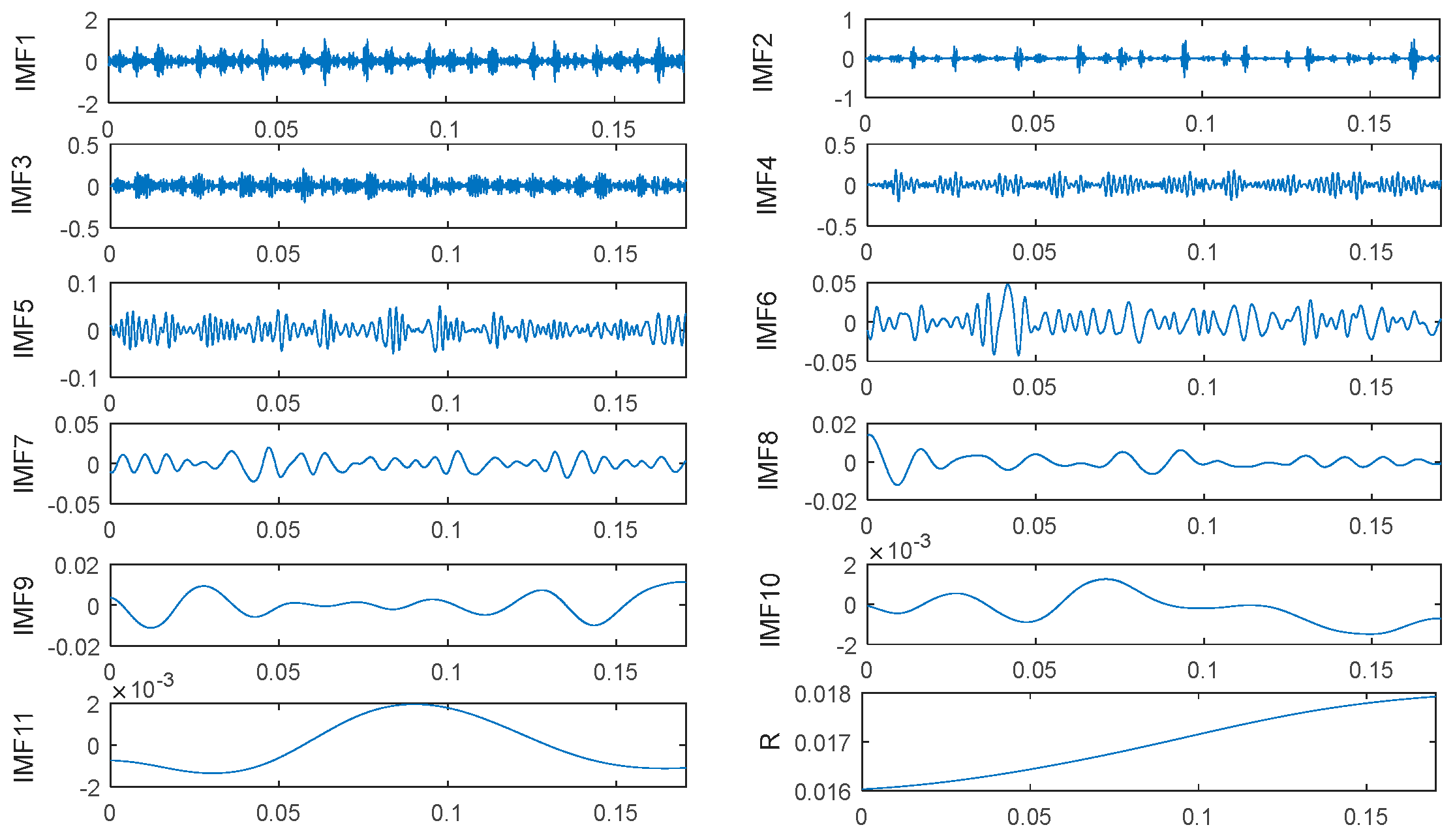
- Decompose the vibration signal into sets of IMFs by CEEMDAN;
- (2)
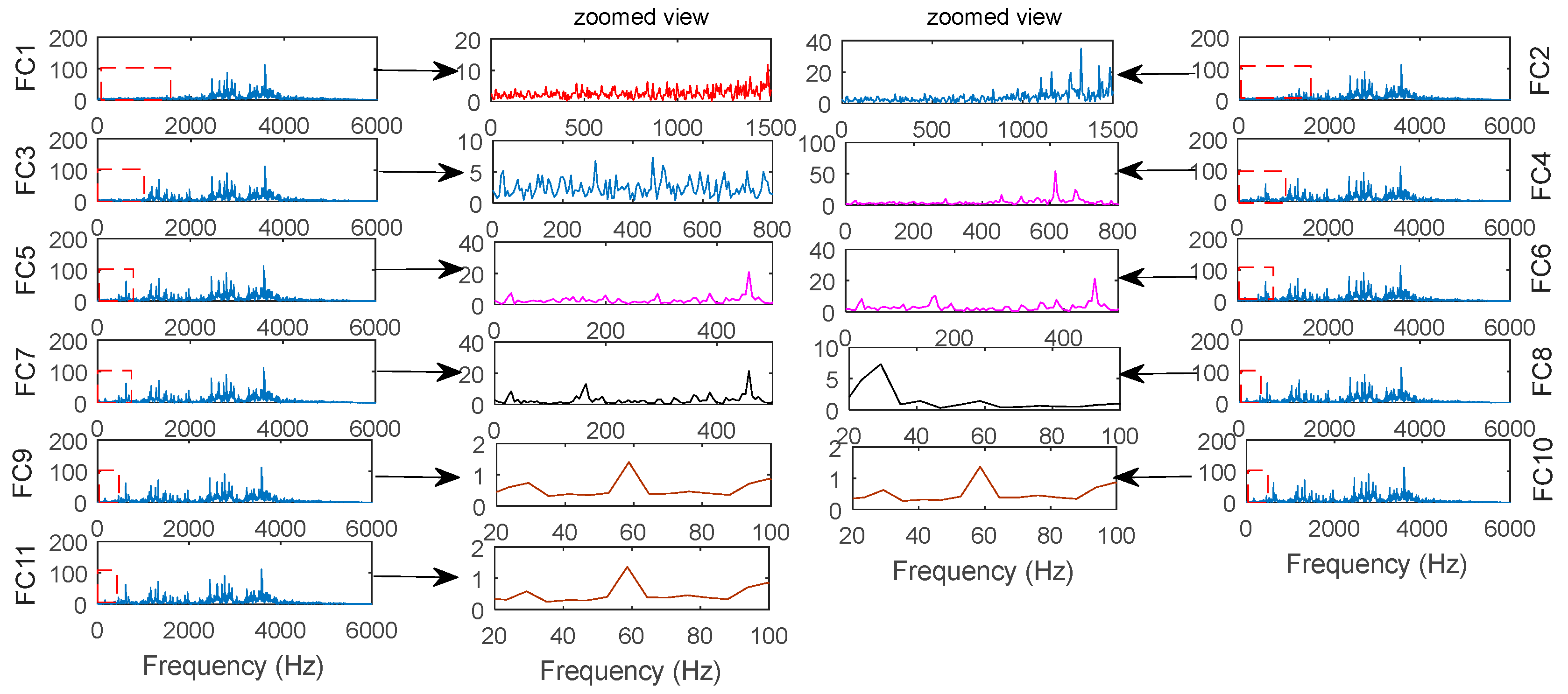
- Combine the adjacent IMFs into CIMF;
- (3)
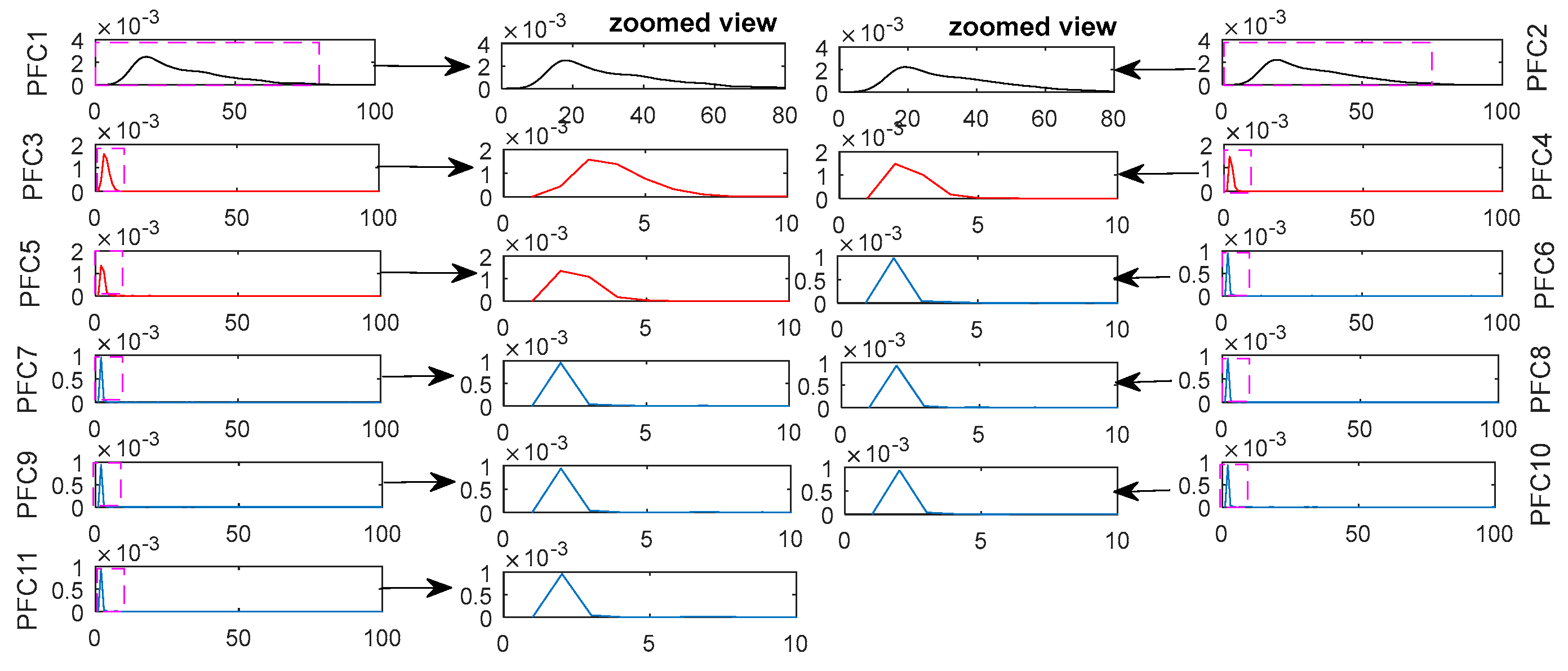
- Obtain the FC by calculating the FFT of each CIMF;
- (4)
- Get PFC by estimating the PDF of each FFT;
- (5)
- Obtain the FIMF by calculating the MHD of adjacent PDF;
- (6)
- Obtain the minimum amount of mode information with physical meanings;
- (7)
- Identify the IIM by comprehensive evaluate index;
- (8)
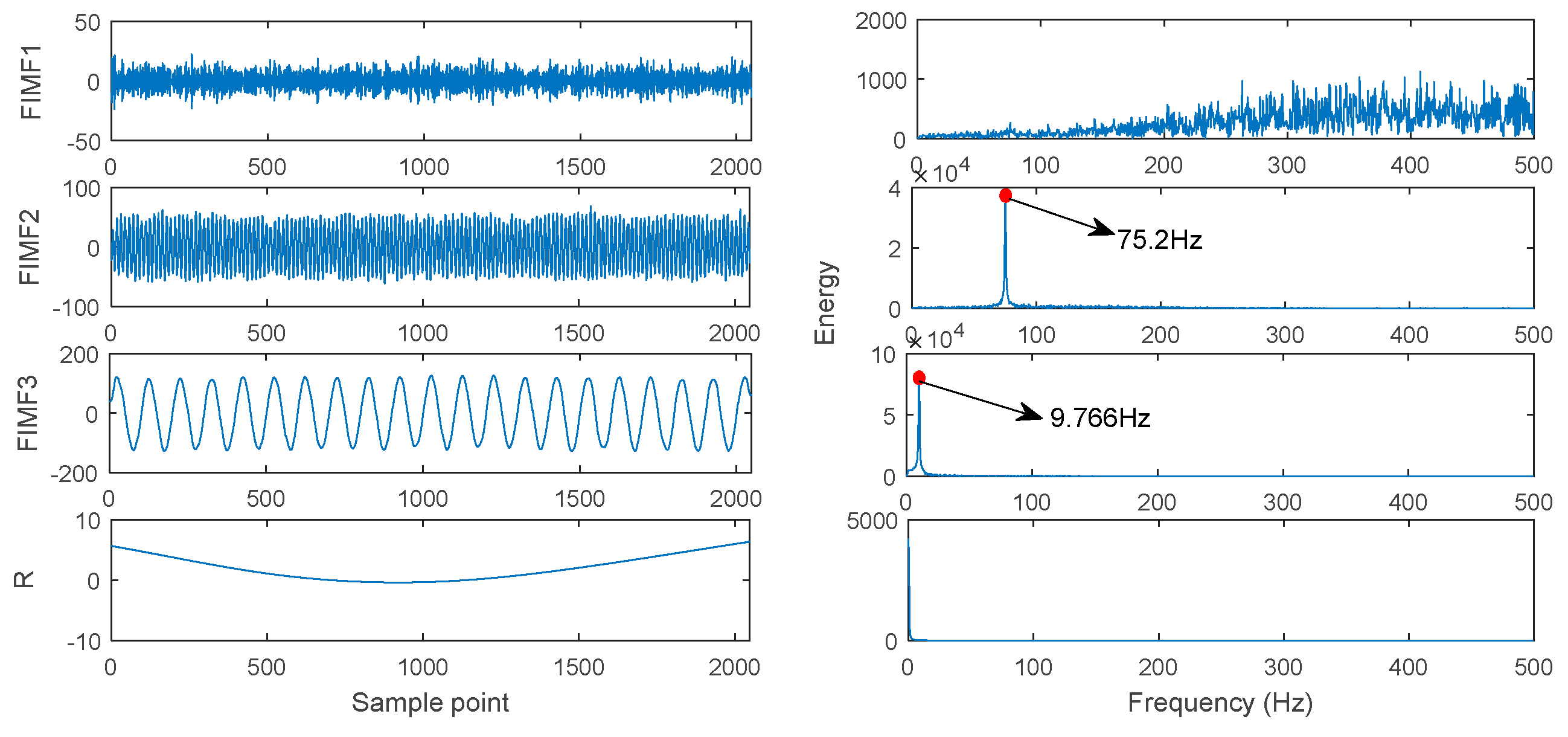
- Identify the feature frequency of rolling bearings using the IIM envelope.
4. Results and Discussions
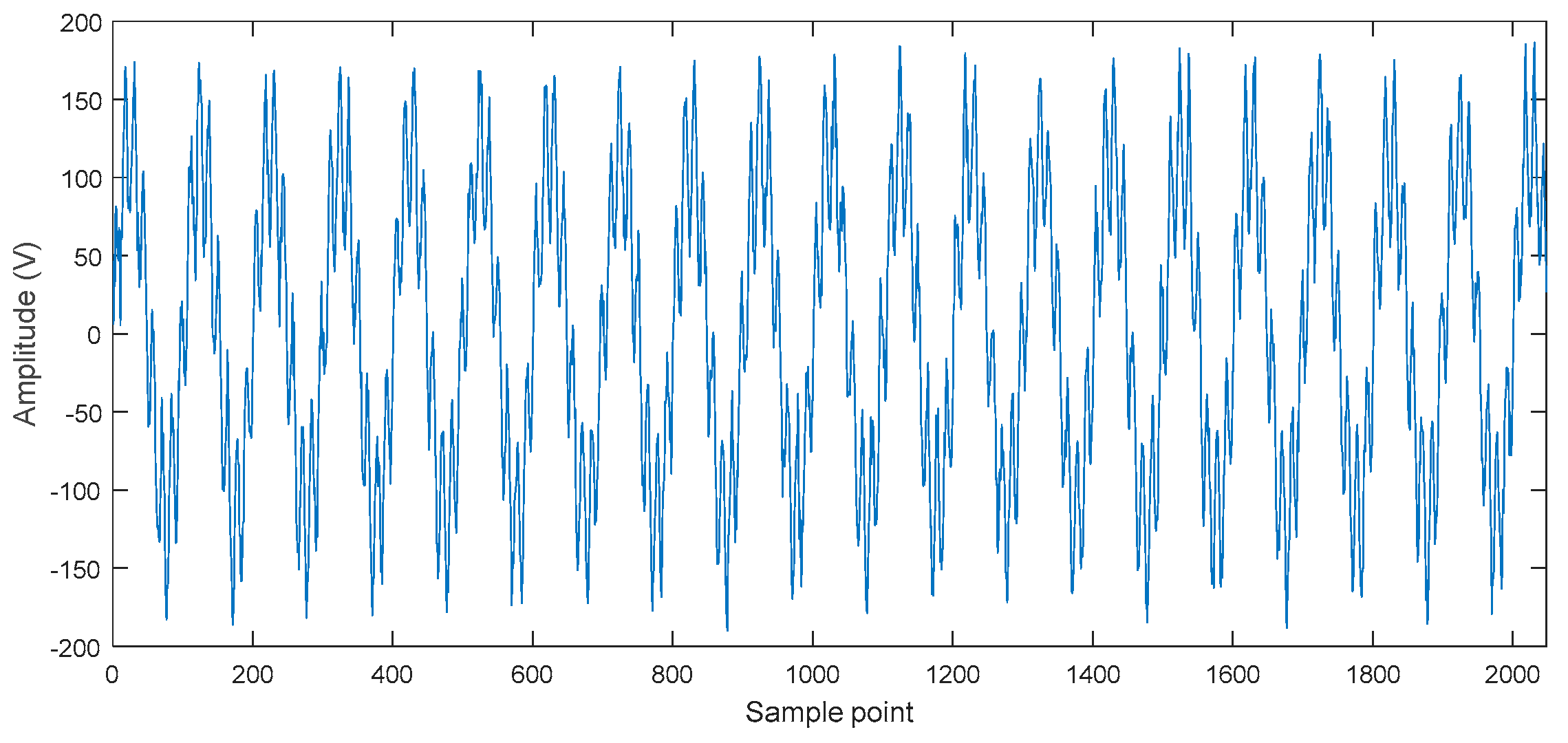
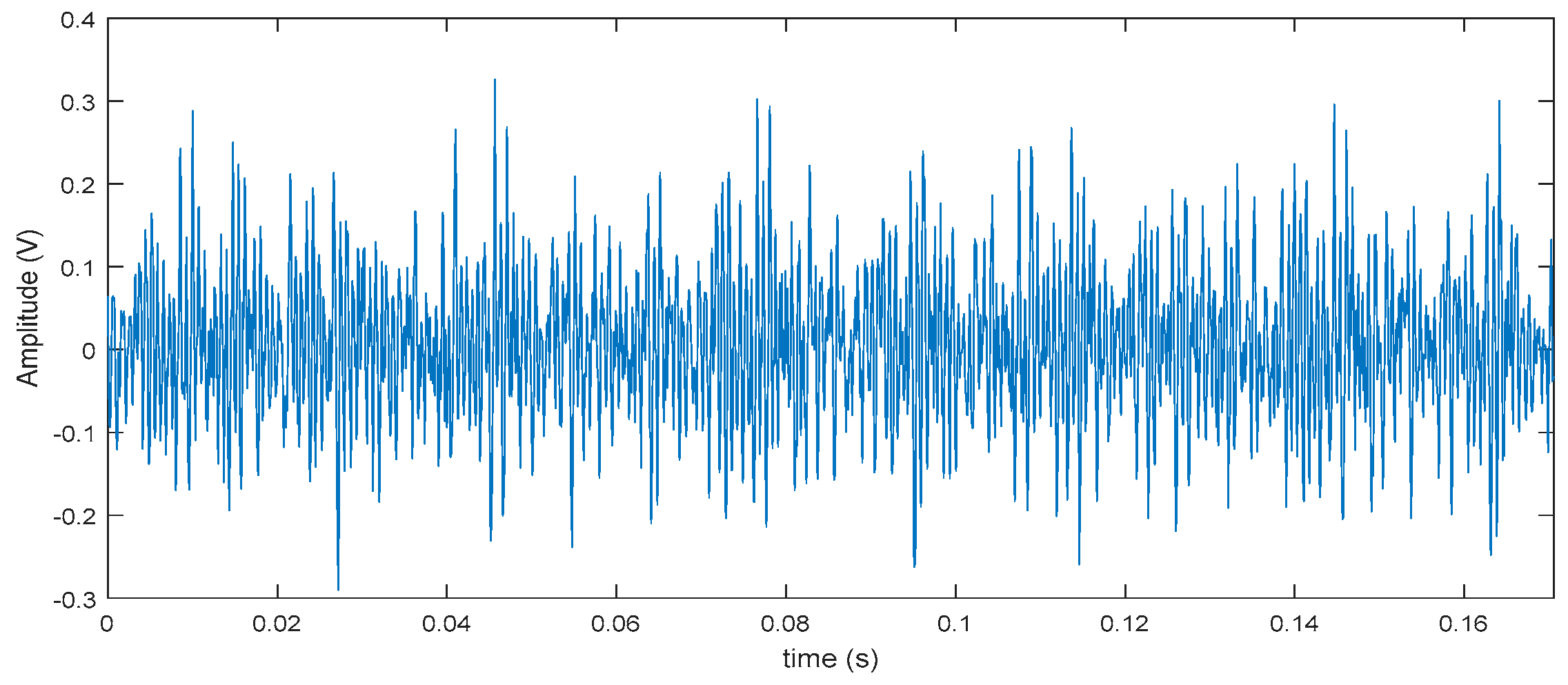
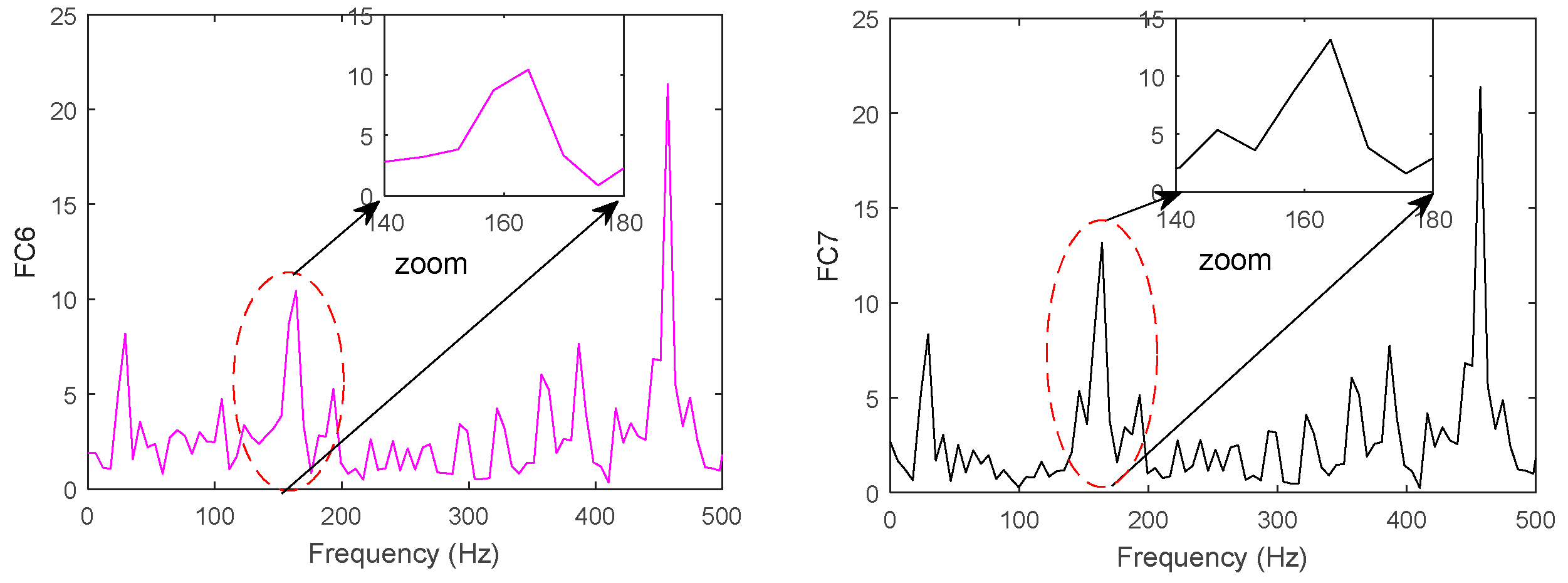
4.1. Diagnose Inner Raceway Fault of Rolling Bearing
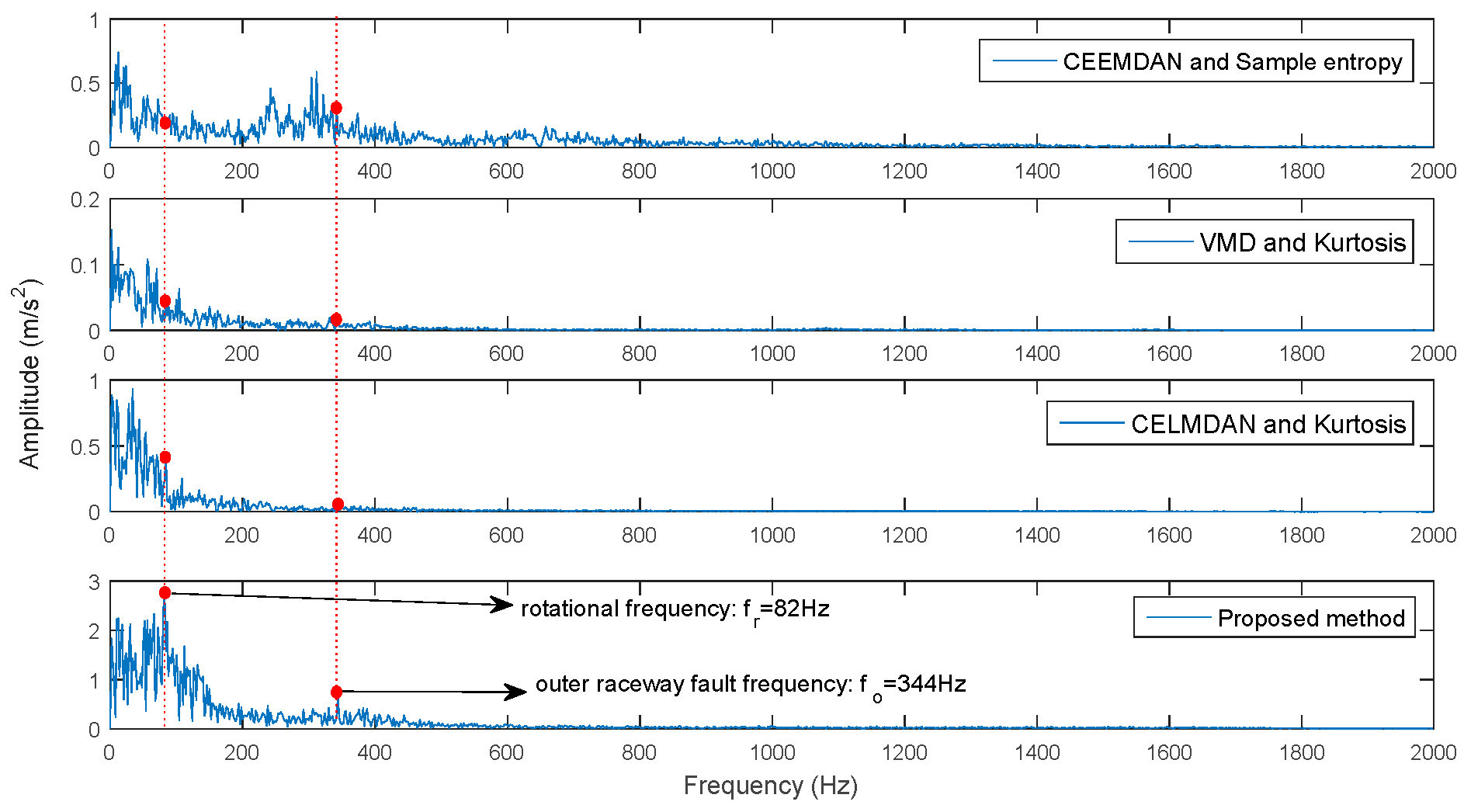
4.2. Diagnose Outer Raceway Fault of Rolling Bearing
5. Conclusions
- (1)
- Our research introduces a method which combines adjacent IMFs into a novel mode function (CIMF) to enhance difference characteristics among IMFs (as shown in step 2).
- (2)
- It proposes a method of combing FFT, PDF and MHD to obtain final intrinsic information mode (FIMF) of minimum number and with physical meanings (as shown in step 3).
- (3)
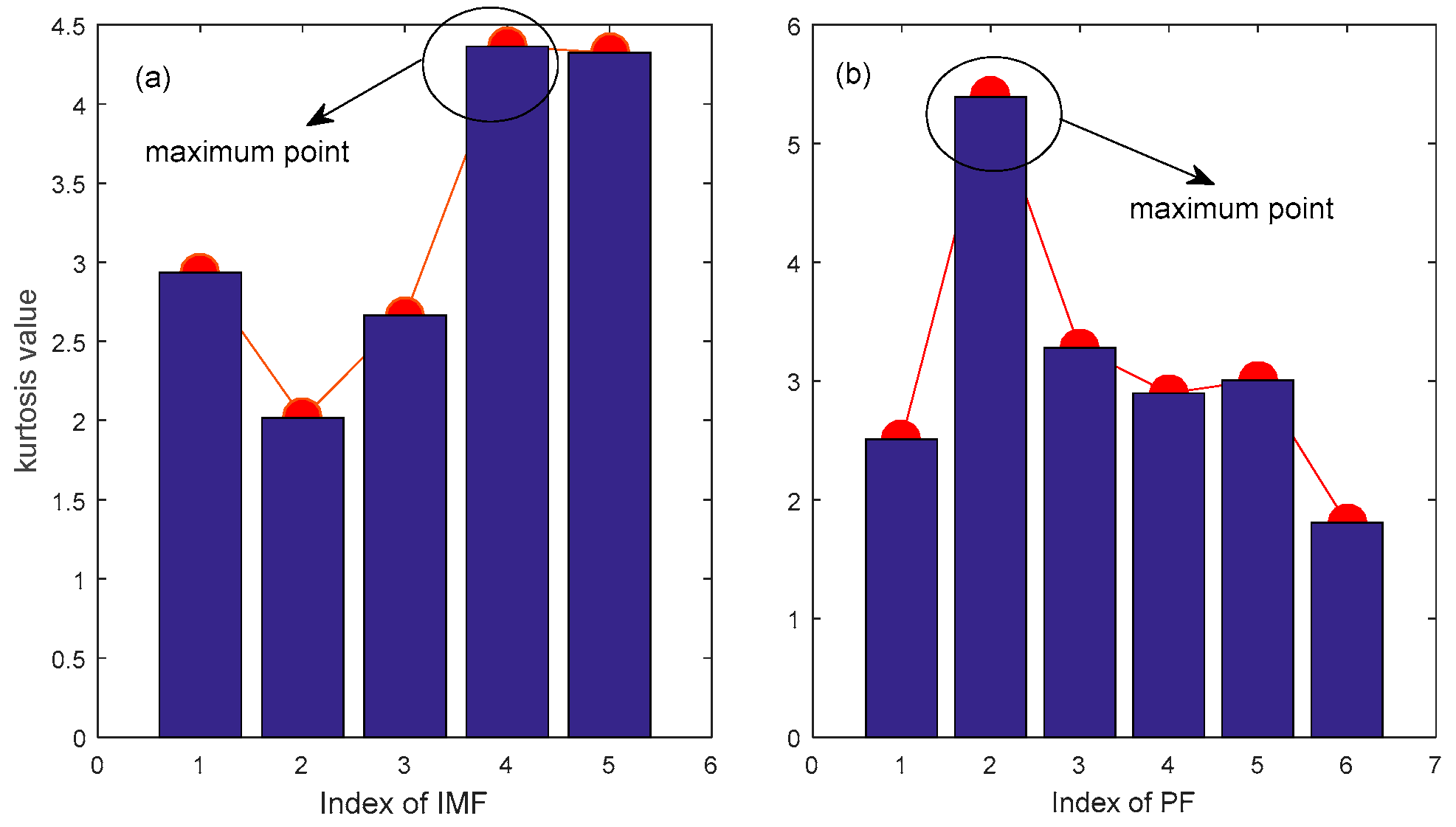
- It introduces a comprehensive evaluate index (DFA and Kurtosis) to identify intrinsic information mode (IIM) to extract the feature frequencies of rolling bearings (as shown in step 4).
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| CEEMDAN | complete ensemble empirical mode decomposition with adaptive noise | IMFs | intrinsic mode functions |
| CIMFs | Combined mode functions | FFT | Fast Fourier Transform |
| probability density function | MHD | modified Hausdorff distance | |
| FIMFs | final intrinsic mode functions | DFA | de-trended fluctuation analysis |
| EMD | empirical mode decomposition | EEMD | ensemble EMD |
| CEEMD | Complementary EEMD | ELMD | ensemble local mean decomposition |
| CELMDAN | complete ensemble local mean decomposition with adaptive noise | K-L | Kullback-Leibler |
| LMD | local mean decomposition | HD | Hausdorff distance |
| FFT of CIMF | FC | PDF of FC | PFC |
| IIM | intrinsic information mode | AE | approximate entropy |
| SE | Sample entropy | FE | Fuzzy entropy |
| VMD | variational mode decomposition |
References
- Zhao, S.; Liang, L.; Xu, G.; Wang, J.; Zhang, W. Quantitative diagnosis of a spall-like fault of a rolling element bearing by empirical mode decomposition and the approximate entropy method. Mech. Syst. Signal Process. 2013, 40, 154–177. [Google Scholar] [CrossRef]
- Yang, H.; Mathew, J.; Ma, L. Fault diagnosis of rolling element bearings using basis pursuit. Mech. Syst. Signal Process. 2005, 19, 341–356. [Google Scholar] [CrossRef]
- Kang, M.; Kim, J.; Kim, J.-M.; Tan, A.C.C.; Kim, E.Y.; Choi, B.-K.; Kim, J. Reliable Fault Diagnosis for Low-Speed Bearings Using Individually Trained Support Vector Machines With Kernel Discriminative Feature Analysis. Power Electron. IEEE Trans. 2015, 30, 2786–2797. [Google Scholar] [CrossRef]
- Bluestein, L.I. A linear filtering approach to the computation of discrete Fourier transform. Audio Electroacoust. IEEE Trans. 1970, 18, 451–455. [Google Scholar] [CrossRef]
- Wang, T.; Lin, J. Fault Diagnosis of Rolling Bearings Based on Wavelet Packet and Spectral Kurtosis. In Proceedings of the Fourth International Conference on Intelligent Computation Technology and Automation, Guangdong, China, 28–29 March 2011; pp. 665–669. [Google Scholar]
- Wang, J.; He, Q. Wavelet Packet Envelope Manifold for Fault Diagnosis of Rolling Element Bearings. IEEE Trans. Instrum. Meas. 2016, 65, 2515–2526. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar]
- Pittman-Polletta, B.; Hsieh, W.H.; Kaur, S.; Lo, M.T.; Hu, K. Detecting phase-amplitude coupling with high frequency resolution using adaptive decompositions. J. Neurosci. Methods 2014, 226, 15–32. [Google Scholar] [CrossRef]
- Yeh, C.H.; Lo, M.T.; Hu, K. Spurious cross-frequency amplitude-amplitude coupling in nonstationary, nonlinear signals. Phys. A Stat. Mech. Its Appl. 2016, 454, 143–150. [Google Scholar]
- Yeh, C.H.; Shi, W. Identifying Phase-Amplitude Coupling in Cyclic Alternating Pattern using Masking Signals. Sci. Rep. 2018, 8, 2649. [Google Scholar]
- Deering, R.; Kaiser, J.F. The use of a masking signal to improve empirical mode decomposition. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, 23–23 March 2005. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assissted Data Analysis Method. Adv. Adapt. Data Anal. 2011, 1, 1–41. [Google Scholar]
- Yeh, J.-R.; Shieh, J.-S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Lei, Y.; He, Z.; Zi, Y. Application of the EEMD method to rotor fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2009, 23, 1327–1338. [Google Scholar] [CrossRef]
- Lei, Y.; Zuo, M.J. Fault diagnosis of rotating machinery using an improved HHT based on EEMD and sensitive IMFs. Meas. Sci. Technol. 2009, 20, 125701. [Google Scholar] [CrossRef]
- Zhou, Y.; Tao, T.; Mei, X.; Jiang, G.; Sun, N. Feed-axis gearbox condition monitoring using built-in position sensors and EEMD method. Robot. Comput.-Integr. Manuf. 2011, 27, 785–793. [Google Scholar] [CrossRef]
- Chang, K.M.; Liu, S.H. Gaussian Noise Filtering from ECG by Wiener Filter and Ensemble Empirical Mode Decomposition. J. Signal Process. Syst. 2011, 64, 249–264. [Google Scholar] [CrossRef]
- Zhang, J.; Yan, R.; Gao, R.X.; Feng, Z. Performance enhancement of ensemble empirical mode decomposition. Mech. Syst. Signal Process. 2010, 24, 2104–2123. [Google Scholar]
- Žvokelj, M.; Zupan, S.; Prebil, I. Non-linear multivariate and multiscale monitoring and signal denoising strategy using Kernel Principal Component Analysis combined with Ensemble Empirical Mode Decomposition method. Mech. Syst. Signal Process. 2011, 25, 2631–2653. [Google Scholar]
- Žvokelj, M.; Zupan, S.; Prebil, I. Multivariate and multiscale monitoring of large-size low-speed bearings using Ensemble Empirical Mode Decomposition method combined with Principal Component Analysis. Mech. Syst. Signal Process. 2010, 24, 1049–1067. [Google Scholar]
- Colominas, M.A.; Schlotthauer, G.; Torres, M.E. Improved complete ensemble EMD: A suitable tool for biomedical signal processing. Biomed. Signal Process. Control 2014, 14, 19–29. [Google Scholar]
- Yang, Y.; Cheng, J.; Zhang, K. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems. Measurement 2012, 45, 561–570. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.; Miao, Q.; Zhang, X. Complete ensemble local mean decomposition with adaptive noise and its application to fault diagnosis for rolling bearings. Mech. Syst. Signal Process. 2018, 106, 24–39. [Google Scholar] [CrossRef]
- Gao, Q.; Duan, C.; Fan, H.; Meng, Q. Rotating machine fault diagnosis using empirical mode decomposition. Mech. Syst. Signal Process. 2008, 22, 1072–1081. [Google Scholar] [CrossRef]
- Laha, S.K. Enhancement of fault diagnosis of rolling element bearing using maximum kurtosis fast nonlocal means denoising. Measurement 2017, 100, 157–163. [Google Scholar]
- Cheng, J.; Ma, X.; Yang, Y. The Rolling Bearing Fault Diagnosis Method Based on Correlation Coefficient of Independent Component Analysis and VPMCD. J. Vib. Meas. Diagn. 2015, 35, 645–648. [Google Scholar]
- Jin, P.; Wang, W.; Wang, H.; Tang, X. Fault diagnosis method of wind turbine’s bearing based on EEMD kurtosis-correlation coefficients criterion and multiple features. Renew. Energy Resour. 2016, 34, 1481–1490. [Google Scholar]
- Harmouche, J.; Delpha, C.; Diallo, D. Faults diagnosis and detection using principal component analysis and Kullback-Leibler divergence. In Proceedings of the Conference of the IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012. [Google Scholar]
- Woo, W.; Gao, B.; Bouridane, A.; Ling, B.; Chin, C. Unsupervised Learning for Monaural Source Separation Using Maximization–Minimization Algorithm with Time–Frequency Deconvolution. Sensors 2018, 18, 1371. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, Y.; Chen, C.; Li, Y.F.; Huang, H.Z. Fault diagnosis of rotating machinery based on kernel density estimation and Kullback-Leibler divergence. J. Mech. Sci. Technol. 2014, 28, 4441–4454. [Google Scholar]
- Shang, D.; Xu, M.; Shang, P. Generalized sample entropy analysis for traffic signals based on similarity measure. Phys. A Stat. Mech. Its Appl. 2017, 474, 1–7. [Google Scholar]
- Deng, F.; Tang, G. An intelligent method for rolling element bearing fault diagnosis based on time-wavelet energy spectrum sample entropy. J. Vib. Shock 2017, 36, 28–34. [Google Scholar]
- Yan, R.; Gao, R.X. Approximate Entropy as a diagnostic tool for machine health monitoring. Mech. Syst. Signal Process. 2007, 21, 824–839. [Google Scholar] [CrossRef]
- Li, X.; He, N.; He, K. Cylindrical Roller Bearing Diagnosis Based on Wavelet Packet Approximate Entropy and Support Vector Machines. J. Vib. Meas. Diagn. 2015, 35, 1031–1036. [Google Scholar]
- Luukka, P. Feature selection using fuzzy entropy measures with similarity classifier. Expert Syst. Appl. 2011, 38, 4600–4607. [Google Scholar] [CrossRef]
- Chen, W.; Wang, Z.; Xie, H.; Yu, W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007, 15, 266–272. [Google Scholar] [CrossRef]
- Cerrada, M.; Ren, S. A review on data-driven fault severity assessment in rolling bearings. Mech. Syst. Signal Process. 2018, 99, 169–196. [Google Scholar]
- Gao, Z.; Cecati, C.; Ding, S.X. A Survey of Fault Diagnosis and Fault-Tolerant Techniques—Part I: Fault Diagnosis With Model-Based and Signal-Based Approaches. IEEE Trans. Ind. Electron. 2015, 62, 3757–3767. [Google Scholar]
- Nguyen, T.L.; Djeziri, M.; Ananou, B.; Ouladsine, M.; Pinaton, J. Fault prognosis for batch production based on percentile measure and gamma process: Application to semiconductor manufacturing. J. Process Control 2016, 48, 72–80. [Google Scholar]
- Benmoussa, S.; Djeziri, M.A. Remaining useful life estimation without needing for prior knowledge of the degradation features. IET Sci. Meas. Technol. 2017, 11, 1071–1078. [Google Scholar]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. Application of EEMD and improved frequency band entropy in bearing fault feature extraction. ISA Trans. 2018. [Google Scholar] [CrossRef]
- Dubuisson, M.P.; Jain, A.K. A modified Hausdorff distance for object matching. In Proceedings of the International Conference on Pattern Recognition, Jerusalem, Israel, 9–13 October 2002; Volume 1, pp. 566–568. [Google Scholar]
- Chen, Z.; Hu, K.; Carpena, P.; Bernaola-Galván, P.; Stanley, H.E.; Ivanov, P.C. Effect of nonlinear filters on detrended fluctuation analysis. Phy. Rev. E 2005, 71, 011104. [Google Scholar] [CrossRef]
- Chen, Z.; Ivanov, P.C.; Hu, K.; Stanley, H.E. Effect of nonstationarities on detrended fluctuation analysis. Phys. Rev. E 2002, 65, 041107. [Google Scholar] [CrossRef]
- Horvatic, D.; Stanley, H.E.; Podobnik, B. Detrended cross-correlation analysis for non-stationary time series with periodic trends. Europhys. Lett. 2011, 94, 18007. [Google Scholar] [CrossRef]
- Lv, Y.; Yuan, R.; Wang, T.; Li, H.; Song, G. Health Degradation Monitoring and Early Fault Diagnosis of a Rolling Bearing Based on CEEMDAN and Improved MMSE. Materials 2018, 11, 1009. [Google Scholar]
- Bouhalais, M.L.; Djebala, A.; Ouelaa, N.; Babouri, M.K. CEEMDAN and OWMRA as a hybrid method for rolling bearing fault diagnosis under variable speed. Int. J. Adv. Manuf. Technol. 2017, 94, 2475–2489. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar]
- Zhao, C.; Shi, W.; Deng, Y. A New Hausdorff Distance for Image Matching; Elsevier Science Inc.: New York, NY, USA, 2005. [Google Scholar]
- Schutze, O.; Esquivel, X.; Lara, A.; Coello, C.A.C. Using the Averaged Hausdorff Distance as a Performance Measure in Evolutionary Multiobjective Optimization. IEEE Trans. Evol. Comput. 2012, 16, 504–522. [Google Scholar]
- Loparo, K.A. Bearing Data Center. Case Western Reserve University, 2000. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 10 February 2019).
- Zhao, H.; Li, L. Fault diagnosis of wind turbine bearing based on variational mode decomposition and Teager energy operator. IET Renew. Power Gener. 2016, 11, 453–460. [Google Scholar] [CrossRef]














| Bearing Type | (mm) | (mm) | (°) | |
|---|---|---|---|---|
| 6205-2RS | 9 | 52 | 8 | 0 |
| (mm) | (mm) | (°) | |
|---|---|---|---|
| 10 | 46 | 7.9 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Zhan, L.; Li, C.; Li, Z.; Wang, T. Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Symmetry 2019, 11, 513. https://doi.org/10.3390/sym11040513
Ma F, Zhan L, Li C, Li Z, Wang T. Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Symmetry. 2019; 11(4):513. https://doi.org/10.3390/sym11040513
Chicago/Turabian StyleMa, Fang, Liwei Zhan, Chengwei Li, Zhenghui Li, and Tingjian Wang. 2019. "Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise" Symmetry 11, no. 4: 513. https://doi.org/10.3390/sym11040513
APA StyleMa, F., Zhan, L., Li, C., Li, Z., & Wang, T. (2019). Self-Adaptive Fault Feature Extraction of Rolling Bearings Based on Enhancing Mode Characteristic of Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. Symmetry, 11(4), 513. https://doi.org/10.3390/sym11040513





