Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem
Abstract
1. Introduction
2. Preliminaries
2.1. Hesitant Fuzzy Set (HFS)
2.2. Hesitant Fuzzy Linguistic Term Sets (HFLTSs)
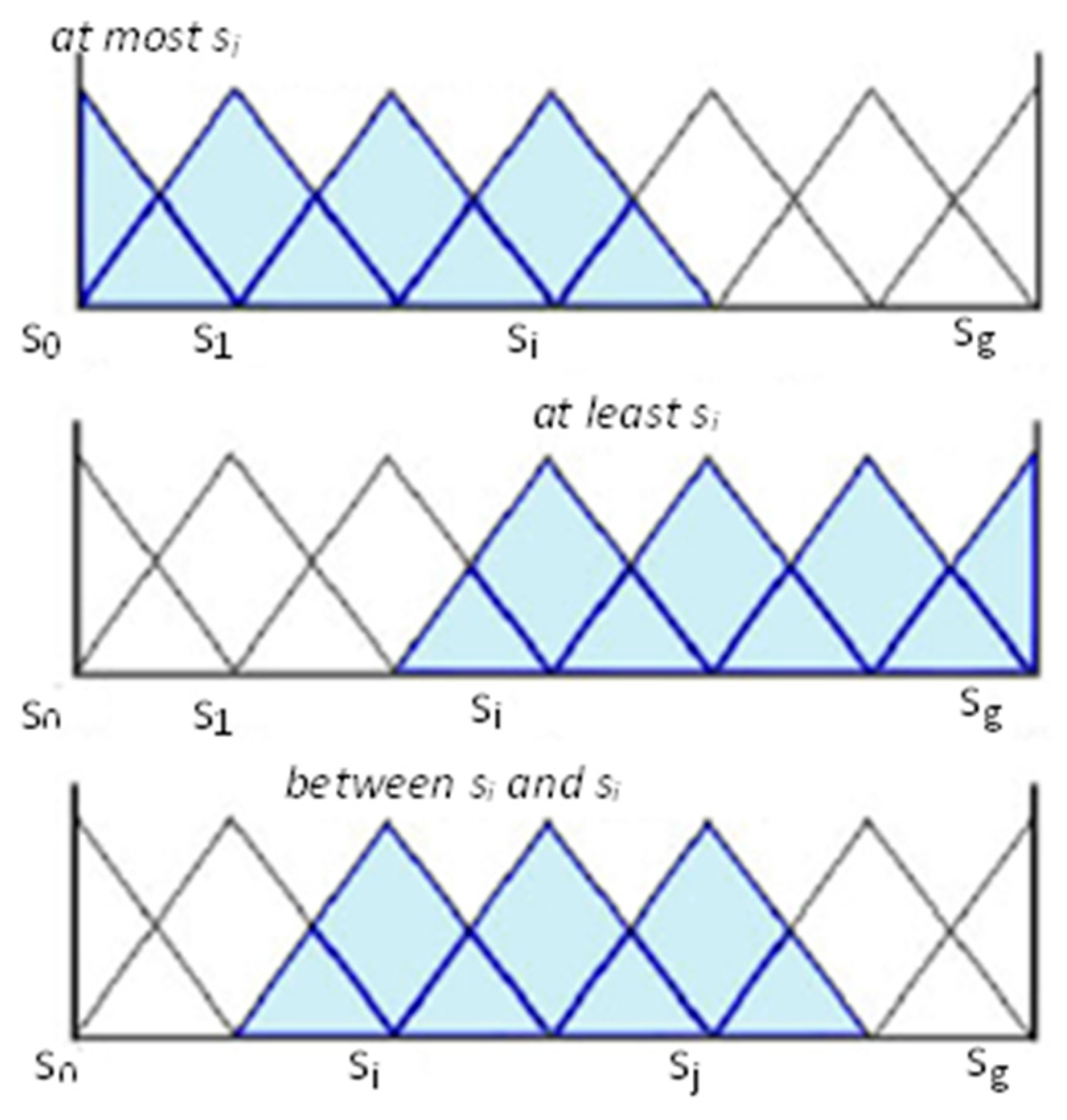
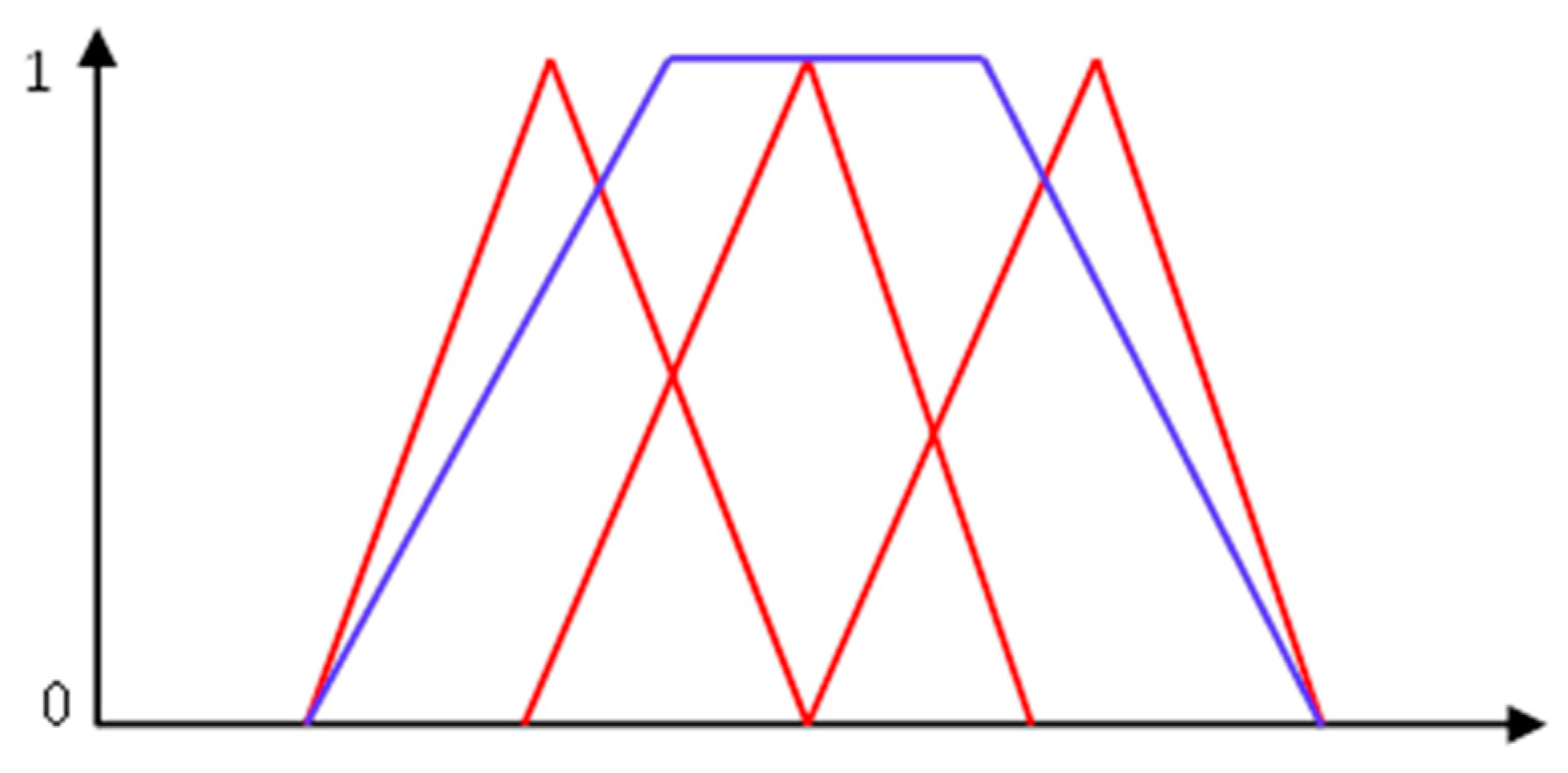
2.3. Fuzzy Envelope for HFLTSs
2.4. Trapezoidal Fuzzy Numbers
3. Proposed Methodology
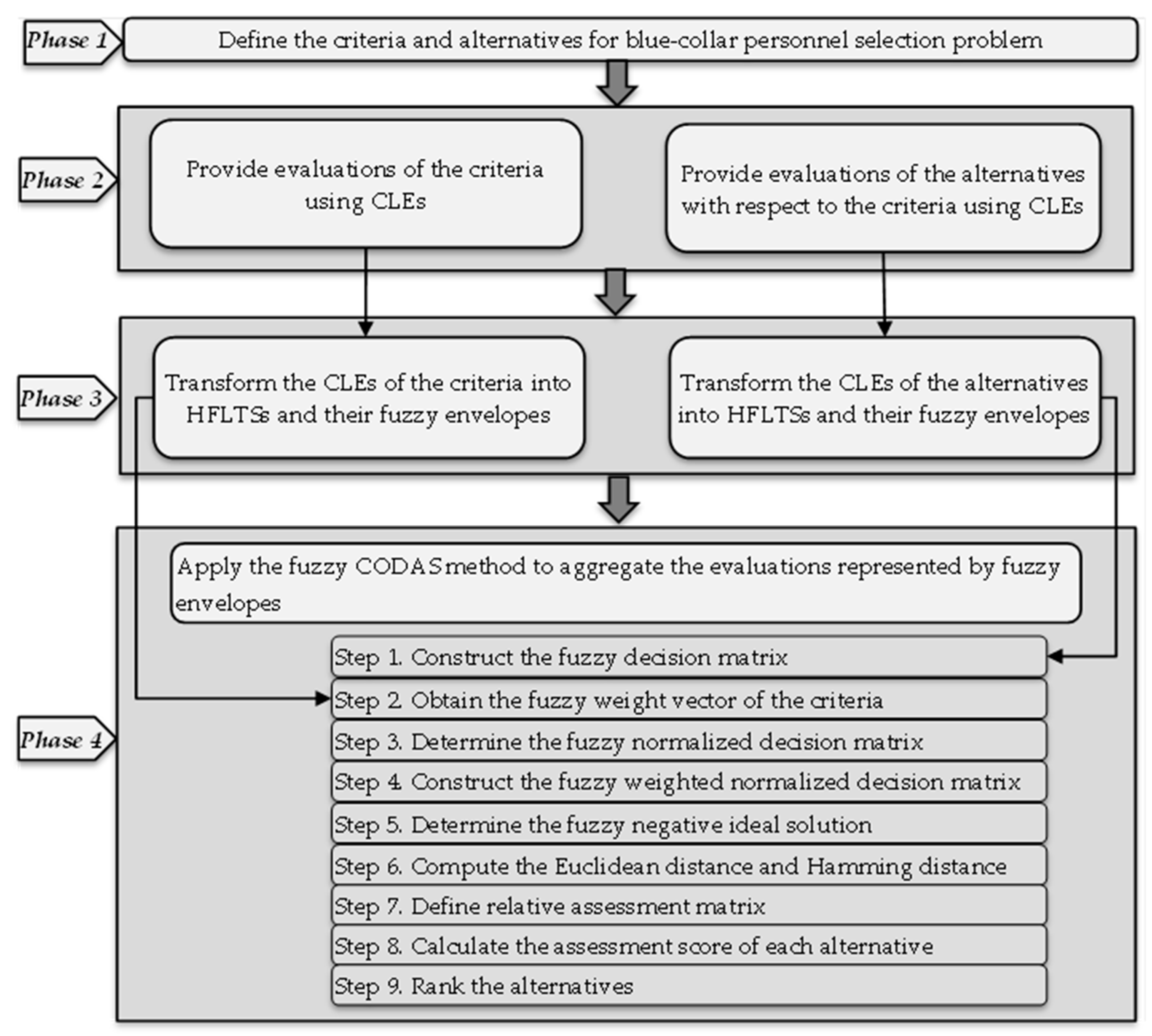
3.1. Representation of the Proposed Methodology
3.2. The Fuzzy CODAS Method
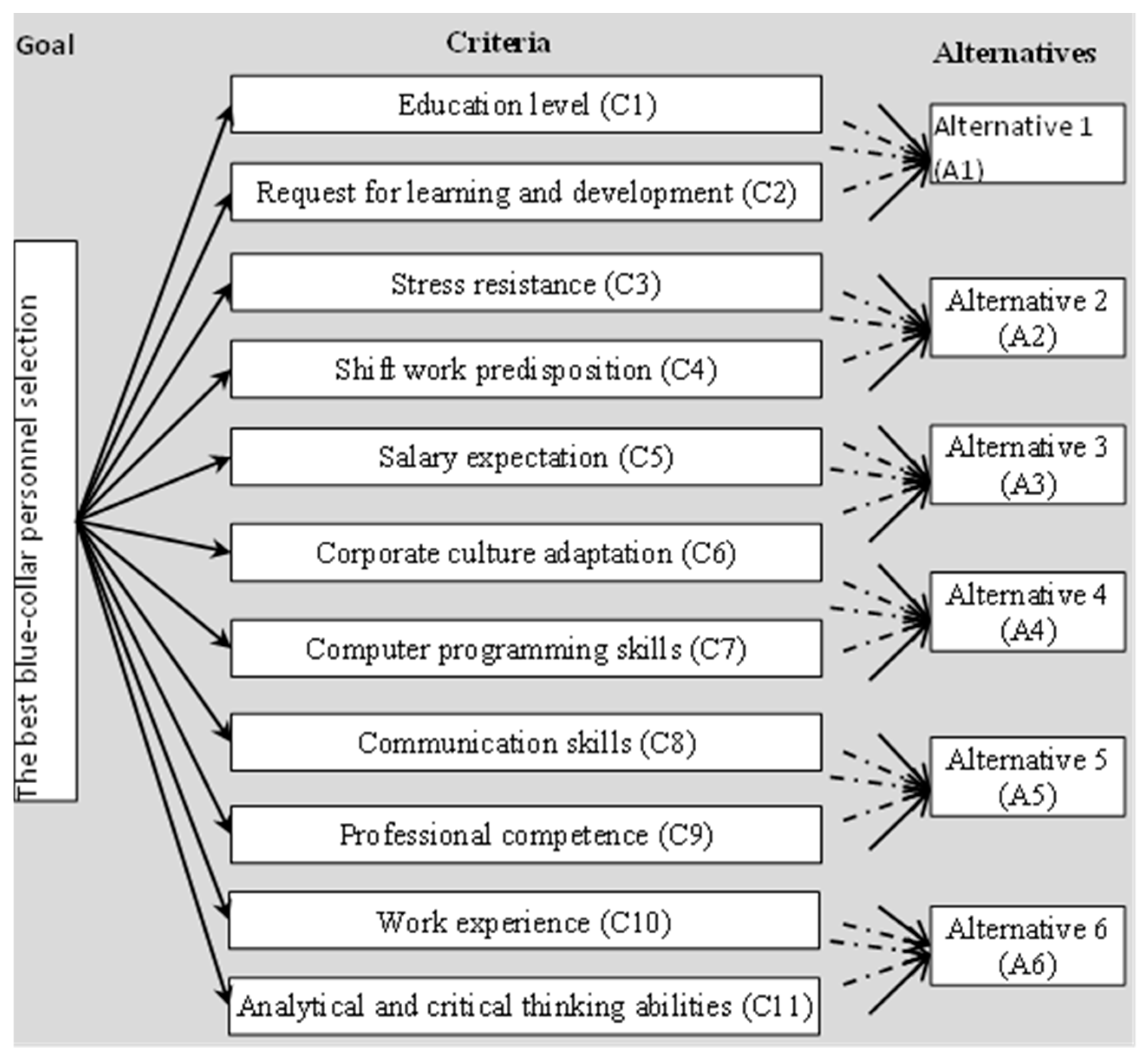
4. A Case Study of a Blue-Collar Personnel Selection Problem
4.1. Application of the Proposed Methodology
4.2. Sensitivity Analysis
4.3. Comparative Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Dursun, M.; Karsak, E.E. A fuzzy MCDM approach for personnel selection. Expert Syst. Appl. 2010, 37, 4324–4330. [Google Scholar]
- Heidary Dahooie, J.; Beheshti Jazan Abadi, E.; Vanaki, A.S.; Firoozfar, H.R. Competency-based IT personnel selection using a hybrid SWARA and ARAS-G methodology. Hum. Factors Ergon. Manuf. Serv. Ind. 2018, 28, 5–16. [Google Scholar] [CrossRef]
- Lin, H.-T. Personnel selection using analytic network process and fuzzy data envelopment analysis approaches. Comput. Ind. Eng. 2010, 59, 937–944. [Google Scholar] [CrossRef]
- MacCrimmon, K.R. Decision Making among Multiple-Attribute Alternatives: A Survey and Consolidated Approach; RAND Memorandum RM-4823-ARPA; The RAND Corporation: Santa Monica, CA, USA, 1968. [Google Scholar]
- Saaty, T.L. The Analytical Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Saaty, T.L. Decision Making with Dependence and Feedback: The Analytical Network Process; RWS Publications: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making-Methods and Applications: A State-of-the-Art Survey; Springer: New York, NY, USA, 1981. [Google Scholar]
- Roy, B. The outranking approach and the foundation of ELECTRE methods. Theor. Decis. 1991, 31, 49–73. [Google Scholar] [CrossRef]
- Brans, J.P.; Vincke, P. Apreference ranking organization method: The PROMETHEE method for MCDM. Manag. Sci. 1985, 31, 647–656. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Kaklauskas, A.; Sarka, V. The new method of multicriteria complex proportional assessment of projects. Technol. Econ. Dev. Econ. 1994, 1, 131–139. [Google Scholar]
- Opricovic, S. Multicriteria Optimization of Civil Engineering Systems; Faculty of Civil Engineering: Belgrade, Serbia, 1998. [Google Scholar]
- Brauers, W.K.M.; Zavadskas, E.K. Project management by MULTIMOORA as an instrument for transition economies. Technol. Econ. Dev. Econ. 2010, 16, 5–24. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J.; Zakarevicius, A. Optimization of Weighted Aggregated Sum Product Assessment. Electron. Electr. Eng. 2012, 6, 3–6. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Turskis, Z. A new additive ratio assessment (ARAS) method in multi-criteria decision-making. Technol. Econ. Dev. Econ. 2010, 16, 159–172. [Google Scholar]
- Gomes, L.F.A.M.; Lima, M.M.P.P. TODIM: Basics and application to multicriteria ranking of projects with environmental impacts. Found. Comput. Dec. Sci. 1992, 16, 113–127. [Google Scholar]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Olfat, L.; Turskis, Z. Multi-criteria inventory classification using a new method of evaluation based on distance from average solution (EDAS). Informatica 2015, 26, 435–451. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Turskis, Z.; Antucheviciene, J. A new combinative distance-based assessment (CODAS) method for multi-criteria decision-making. Econ. Comput. Econ. Cyb. 2016, 50, 25–44. [Google Scholar]
- Gibney, R.; Shang, J. Decision making in academia: A case of the dean selection process. Math. Comp. Model. 2007, 46, 1030–1040. [Google Scholar] [CrossRef]
- Afshari, A.R.; Mojahed, M.; Yusuf, R.M. Simple Additive Weighting approach to Personnel Selection problem. Int. J. Innovat. Manag. Tech. 2010, 1, 511–515. [Google Scholar]
- Boran, F.E.; Genc, S.; Akay, D. Personnel Selection Based on Intuitionistic Fuzzy Sets. Hum. Factors Ergon. Manuf. Serv. Ind. 2011, 21, 493–503. [Google Scholar] [CrossRef]
- Shih, H.S.; Shyur, H.J.; Lee, E.S. An extension of TOPSIS for group decision making. Math. Comput. Modell. 2007, 45, 801–814. [Google Scholar] [CrossRef]
- Bogdanovic, D.; Miletic, S. Personnel evaluation and selection by multicriteria decision making method. Econ. Comput. Econ. Cybern. Stud. Res. 2014, 48, 179–196. [Google Scholar]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Afshari, A.R.; Nikolić, M.; Ćoćkalo, D. Applications of Fuzzy Decision Making for Personnel Selection Problem—A Review. J. Eng. Manag. Compet. 2014, 4, 68–77. [Google Scholar] [CrossRef]
- Liang, G.S.; Wang, M.J.J. Personnel selection using fuzzy MCDM algorithm. Eur. J. Oper. Res. 1994, 78, 22–33. [Google Scholar] [CrossRef]
- Yaakob, S.B.; Kawata, S. Workers’ placement in an industrial environment. Fuzzy Sets Syst. 1999, 106, 289–297. [Google Scholar] [CrossRef]
- Chen, C.T. Extensions of the TOPSIS for Group Decision-Making under Fuzzy Environment. Fuzzy Sets Syst. 2000, 114, 1–9. [Google Scholar] [CrossRef]
- Tsao, C.-T.; Chu, T.-C. Personnel selecting using an improved fuzzy MCDM algorithm. J. Inf. Optim. Sci. 2001, 22, 521–536. [Google Scholar]
- Karsak, E.E. Personnel Selection Using a Fuzzy MCDM Approach Based on Ideal and Anti-ideal Solutions. In Multiple Criteria Decision Making in the New Millennium. Lecture Notes in Economics and Mathematical Systems; Köksalan, M., Zionts, S., Eds.; Springer: Heidelberg, Germany, 2001; pp. 393–402. [Google Scholar]
- Capaldo, G.; Zollo, G. Applying fuzzy logic to personnel assessment: A case study. Omega 2001, 29, 585–597. [Google Scholar] [CrossRef]
- Huang, L.C.; Huang, K.S.; Huang, H.P.; Jaw, B.S. Applying fuzzy neural network in human resource selection system. In Proceedings of the 2004 IEEE Annual Meeting of the Fuzzy Information (NAFIPS’04), Banff, AB, Canada, 27–30 June 2004. [Google Scholar]
- Saghafian, S.; Hejazi, S.R. Multi-criteria group decision making using a modified fuzzy TOPSIS procedure. In Proceedings of the International Conference on Computational Intelligence for Modeling, Control and Automation, and International Conference on Intelligent Agents, Web Technologies and Internet Commerce (CIMCA-IAWTIC’05), Vienna, Austria, 28–30 November 2005; pp. 215–221. [Google Scholar]
- Golec, A.; Kahya, E. A fuzzy model for competency-based employee evaluation and selection. Comput. Ind. Eng. 2007, 52, 143–161. [Google Scholar] [CrossRef]
- Mahdavi, I.; Mahdavi-Amiri, N.; Heidarzade, A.; Nourifar, R. Designing a model of fuzzy TOPSIS in multiple criteria decision making. Appl. Math. Comput. 2008, 206, 607–617. [Google Scholar] [CrossRef]
- Güngör, Z.; Serhadlıoğlu, G.; Kesen, S.E. A fuzzy AHP approach to personnel selection problem. Appl. Soft Comput. 2009, 9, 641–646. [Google Scholar] [CrossRef]
- Ayub, M.; Kabir, M.J.; Alam, M.G.R. Personnel selection method using Analytic Network Process (ANP) and fuzzy concept. In Proceedings of the 12th International Conference on Computers and Information Technology (ICCIT’09), Dhaka-Bangladesh, Bangladesh, 21–23 December 2009; pp. 373–378. [Google Scholar]
- Polychroniou, P.V.; Giannikos, I. A fuzzy multi criteria decision-making methodology for selection of human resources in a Greek private bank. Career Dev. Int. 2009, 14, 372–387. [Google Scholar] [CrossRef]
- Kelemenis, A.; Askounis, D. A new TOPSIS-based multi-criteria approach to personnel selection. Expert Syst. Appl. 2010, 37, 4999–5008. [Google Scholar] [CrossRef]
- Kelemenis, A.; Ergazakis, K.; Askounis, D. Support managers’ selection using an extension of fuzzy TOPSIS. Expert Syst. Appl. 2011, 38, 2774–2782. [Google Scholar] [CrossRef]
- Balezěntis, A.; Balezěntis, T.; Brauers, W.K.M. Personnel selection based on computing with words and fuzzy MULTIMOORA. Expert Syst. Appl. 2012, 39, 7961–7967. [Google Scholar] [CrossRef]
- Kabak, M.; Burmaoğlu, S.; Kazançoğlu, Y. A fuzzy hybrid MCDM approach for professional selection. Expert Syst. Appl. 2012, 39, 3516–3525. [Google Scholar] [CrossRef]
- Rouyendegh, B.D.; Erkan, T.E. An Application of the Fuzzy ELECTRE Method for Academic Staff Selection. Hum. Factors Ergon. Manuf. Serv. Ind. 2013, 23, 107–115. [Google Scholar] [CrossRef]
- Aggarwal, R. Identifying and Prioritizing Human Capital Measurement Indicators for Personnel Selection Using Fuzzy MADM. In Advances in Intelligent Systems and Computing, Proceedings of the Third International Conference on Soft Computing for Problem Solving, Berkeley, CA, USA, 26–28 December 2013; Pant, M., Deep, K., Nagar, A., Bansal, J.C., Eds.; Springer: New Delhi, India, 2014; pp. 427–439. [Google Scholar]
- Keršulienė, V.; Turskis, Z. A hybrid linguistic fuzzy multiple criteria group selection of a chief accounting officer. J. Bus. Econ. Manag. 2014, 15, 232–252. [Google Scholar] [CrossRef][Green Version]
- Sang, X.; Liu, X.; Qin, J. An analytical solution to fuzzy TOPSIS and its application in personnel selection for knowledge-intensive enterprise. Appl. Soft Comput. 2015, 30, 190–204. [Google Scholar] [CrossRef]
- Chang, K.-L. The use of a hybrid MCDM model for public relations personnel selection. Informatica 2015, 26, 389–406. [Google Scholar] [CrossRef]
- Mizumoto, M.; Tanaka, K. Some properties of fuzzy sets of type 2. Inf. Control 1976, 31, 312–340. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.I.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Mendel, J.M.; Wu, H. Type-2 fuzzistics for symmetric interval type-2 fuzzy sets: Part 1, forward problems. IEEE Trans. Fuzzy Syst. 2006, 14, 781–792. [Google Scholar] [CrossRef]
- Dubois, D.; Prade, H. Fuzzy Sets and Systems: Theory and Applications; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. More on intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 33, 37–45. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Gau, W.L.; Buehrer, D.J. Vague sets. IEEE Trans. Syst. Man. Cybern. 1993, 23, 610–614. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Vague sets are intuitionistic fuzzy sets. Fuzzy Sets Syst. 1996, 79, 403–405. [Google Scholar] [CrossRef]
- Yager, R.R. On the theory of bags. Int. J. Gen. Syst. 1986, 13, 23–37. [Google Scholar] [CrossRef]
- Miyamoto, S. Remarks on basics of fuzzy sets and fuzzy multisets. Fuzzy Sets Syst. 2005, 156, 427–431. [Google Scholar]
- Garibaldi, J.M.; Jaroszewski, M.; Musikasuwan, S. Nonstationary fuzzy sets. IEEE Trans. Fuzzy Syst. 2008, 16, 1072–1086. [Google Scholar] [CrossRef]
- Smarandache, F. A Unifying Field in Logics. Neutrosophy: Neutrosophic Probability, Set and Logic; American Research Press: Rehoboth, DE, USA, 1999. [Google Scholar]
- Torra, V.; Narukawa, Y. On hesitant fuzzy sets and decision. In Proceedings of the IEEE International Conference on Fuzzy Systems, Jeju Island, Korea, 20–24 August 2009; pp. 1378–1382. [Google Scholar]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Kwong, C.K.; Bai, H. Determining the importance weights for the customer requirements in QFD using a Fuzzy AHP with an extent analysis approach. IIE Trans. 2003, 35, 619–626. [Google Scholar] [CrossRef]
- Calabrese, A.; Costa, R.; Menichini, T. Using fuzzy AHP to manage intellectual capital assets: An application to the ICT service industry. Expert Syst. Appl. 2013, 40, 3747–3755. [Google Scholar]
- Zhang, S.F.; Liu, S.Y. AGRA-based intuitionistic fuzzy multi-criteria group decision making method for personnel selection. Expert Syst. Appl. 2011, 38, 11401–11405. [Google Scholar] [CrossRef]
- Boran, S.; Göztepe, K.; Yavuz, E. A study on Election of Personnel Based on Performance Measurement by Using Analytic Network Process (ANP). Int. J. Comput. Sci. Netw. Secur. 2008, 8, 333–338. [Google Scholar]
- Wan, S.-P.; Wang, Q.-Y.; Dong, J.-Y. The extended VIKOR method for multi-attribute group decision making with triangular intuitionistic fuzzy numbers. Knowl.-Based Syst. 2013, 52, 65–77. [Google Scholar] [CrossRef]
- Yu, D.; Zhang, W.; Xu, Y. Group decision making under hesitant fuzzy environment with application to personnel evaluation. Knowl.-Based Syst. 2013, 52, 1–10. [Google Scholar] [CrossRef]
- Liu, H.; Qin, J.; Mao, L.; Zhang, Z. Personnel Selection Using Interval 2-Tuple Linguistic VIKOR Method. Hum. Factors Ergon. Manuf. Serv. Ind. 2015, 25, 370–384. [Google Scholar] [CrossRef]
- Ji, P.; Zhang, H.-Y.; Wang, J.-Q. A projection-based TODIM method under multi-valued neutrosophic environments and its application in personnel selection. Neural Comput. Appl. 2016, 29, 221–234. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. Frank aggregation operators and their application to hesitant fuzzy multiple attribute decision making. Appl. Soft Comput. 2016, 41, 428–452. [Google Scholar]
- Efe, B.; Kurt, M. A systematic approach for an application of personnel selection in assembly line balancing problem. Int. Tran. Oper. Res. 2018, 25, 1001–1025. [Google Scholar] [CrossRef]
- Yeni, F.B.; Özçelik, G. Interval-Valued Atanassov Intuitionistic Fuzzy CODAS Method for Multi Criteria Group Decision Making Problems. Group Decis. Negot. 2019, 28, 433–452. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Labella, Á.; Martínez, L. An overview on fuzzy modelling of complex linguistic preferences in decision making. Int. J. Comput. Intell. Syst. 2016, 9, 81–94. [Google Scholar]
- Keshavarz Ghorabaee, M.; Amiri, M.; Zavadskas, E.K.; Hooshmand, R.; Antuchevičienė, J. Fuzzy Extension of the CODAS Method for Multi-Criteria Market Segment Evaluation. J. Bus. Econ. Manag. 2017, 18, 1–19. [Google Scholar] [CrossRef]
- Xia, M.; Xu, Z. Hesitant fuzzy information aggregation in decision making. Int. J. Approx. Reason. 2011, 52, 395–407. [Google Scholar] [CrossRef]
- Rodríguez, R.M.; Martínez, L.; Torra, V.; Xu, Z.S.; Herrera, F. Hesitant fuzzy sets: State of the art and future directions. Int. J. Intell. Syst. 2014, 29, 495–524. [Google Scholar] [CrossRef]
- Xu, Z. Hesitant Fuzzy Sets Theory; Springer: New York, NY, USA, 2014. [Google Scholar]
- Song, Y.; Wang, X.; Quan, W.; Huang, W. A new approach to construct similarity measure for intuitionistic fuzzy sets. Soft Comp. 2019, 23, 1985–1998. [Google Scholar] [CrossRef]
- Ren, F.; Kong, M.; Pei, Z. A New Hesitant Fuzzy Linguistic TOPSIS Method for Group Multi-Criteria Linguistic Decision Making. Symmetry 2017, 9, 289. [Google Scholar] [CrossRef]
- Liu, P.; Mahmood, T.; Khan, Q. Multi-Attribute Decision-Making Based on Prioritized Aggregation Operator under Hesitant Intuitionistic Fuzzy Linguistic Environment. Symmetry 2017, 9, 270. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Qian, L. An Improved A* Algorithm Based on Hesitant Fuzzy Set Theory for Multi-Criteria Arctic Route Planning. Symmetry 2018, 10, 765. [Google Scholar] [CrossRef]
- Liao, H.; Si, G.; Xu, Z.; Fujita, H. Hesitant Fuzzy Linguistic Preference Utility Set and Its Application in Selection of Fire Rescue Plans. Int. J. Environ. Res. Public Health 2018, 15, 664. [Google Scholar] [CrossRef]
- Chen, S.-M.; Hong, J.-A. Multi-criteria linguistic decision making based on hesitant fuzzy linguistic term sets and the aggregation of fuzzy sets. Inf. Sci. 2014, 286, 63–74. [Google Scholar] [CrossRef]
- Liu, Y.; Rodríguez, R.M.; Hagras, H.; Liu, H.; Qin, K.; Martínez, L. Type-2 fuzzy envelope of hesitant fuzzy linguistic term set: A new representation model of comparative linguistic expression. IEEE Trans. Fuzzy Syst. 2019, in press. [Google Scholar] [CrossRef]
- Liu, H.; Rodriguez, R.M. A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making. Inf. Sci. 2014, 258, 220–238. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Z.; Zeng, X.-J. Modeling complex linguistic expressions in qualitative decision making: An overview. Knowl.-Based Syst. 2018, 144, 174–187. [Google Scholar] [CrossRef]
- Keshavarz Ghorabaee, M.; Zavadskas, E.K.; Amiri, M.; Turskis, Z. Extended EDAS method for fuzzy multi-criteria decision-making: An application to supplier selection. Int. J. Comput. Commun. 2016, 11, 358–371. [Google Scholar] [CrossRef]
- Bolturk, E.; Kahraman, C. Interval-valued intuitionistic fuzzy CODAS method and its application to wave energy facility location selection problem. J. Intell. Fuzzy Syst. 2018, 35, 4865–4877. [Google Scholar] [CrossRef]
- Panchal, D.; Chatterjee, P.; Shukla, R.K.; Choudhury, T.; Tamosaitiene, J. Integrated fuzzy AHP-CODAS framework for maintenance decision in urea fertilizer industry. Econ. Comput. Econ. Cybern. Stud. Res. 2017, 51, 179–196. [Google Scholar]
- Bolturk, E. Pythagorean fuzzy CODAS and its application to supplier selection in a manufacturing firm. J. Enterp. Inform. Manag. 2018, 31, 550–564. [Google Scholar] [CrossRef]
- Mathew, M.; Sahu, S. Comparison of new multi-criteria decision making methods for material handling equipment selection. Manag. Sci. Lett. 2018, 8, 139–150. [Google Scholar] [CrossRef]
- Peng, X.; Garg, H. Algorithms for interval-valued fuzzy soft sets in emergency decision making based on WDBA and CODAS with new information measure. Comput. Ind. Eng. 2018, 119, 439–452. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K.; Antucheviciene, J.; Kosareva, N. A hybrid model based on fuzzy AHP and fuzzy WASPAS for construction site selection. Int. J. Comput. Commun. 2015, 10, 113–128. [Google Scholar] [CrossRef]
- Turskis, Z.; Zavadskas, E.K. A new fuzzy additive ratio assessment method (ARAS-F). Case study: The analysis of fuzzy multiple criteria in order to select the logistic centers location. Transport 2010, 25, 423–432. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Antucheviciene, J. Multiple criteria evaluation of rural building’s regeneration alternatives. Build. Environ. 2007, 42, 436–451. [Google Scholar] [CrossRef]
- Yazdani, M.; Alidoosti, A.; Zavadskas, E.K. Risk analysis of critical infrastructures using fuzzy COPRAS. Econ. Res. 2011, 24, 27–40. [Google Scholar] [CrossRef]
| Author(s) | Applied Method(s) |
|---|---|
| Liang and Wang [26] | A two-stage fuzzy MCDM |
| Yaakob and Kawata [27] | A fuzzy linguistic evaluation |
| Chen [28] | Fuzzy TOPSIS |
| Tsao and Chue [29] | Improved fuzzy MCDM algorithm |
| Karsak [30] | A distance-based fuzzy TOPSIS |
| Capaldo and Zollo [31] | A fuzzy logic evaluation method |
| Huang et al. [32] | Fuzzy AHP, Fuzzy Neural Networks, and SAW |
| Saghafian and Hejazi [33] | A modified Fuzzy TOPSIS |
| Golec and Kahya [34] | A fuzzy rule base approach |
| Mahdavi et al. [35] | Fuzzy TOPSIS |
| Güngör et al. [36] | Fuzzy AHP |
| Ayub et al. [37] | Fuzzy ANP |
| Polychroniou and Giannikos [38] | Fuzzy TOPSIS |
| Kelemenis and Askounis [39] | Fuzzy TOPSIS |
| Kelemenis et al. [40] | A novel fuzzy TOPSIS |
| Balezěntis et al. [41] | Fuzzy MULTIMOORA |
| Kabak et al. [42] | Fuzzy ANP, Fuzzy TOPSIS and Fuzzy ELECTRE |
| Rouyendegh and Erkan [43] | Fuzzy ELECTRE |
| Aggarwal [44] | Fuzzy-Delphi and Fuzzy AHP |
| Keršulienė and Turskis [45] | A hybrid linguistic fuzzy multiple criteria |
| Sang et al. [46] | Karnik–Mendel algorithm-based fuzzy TOPSIS |
| Chang [47] | Fuzzy Delphi, ANP, and TOPSIS |
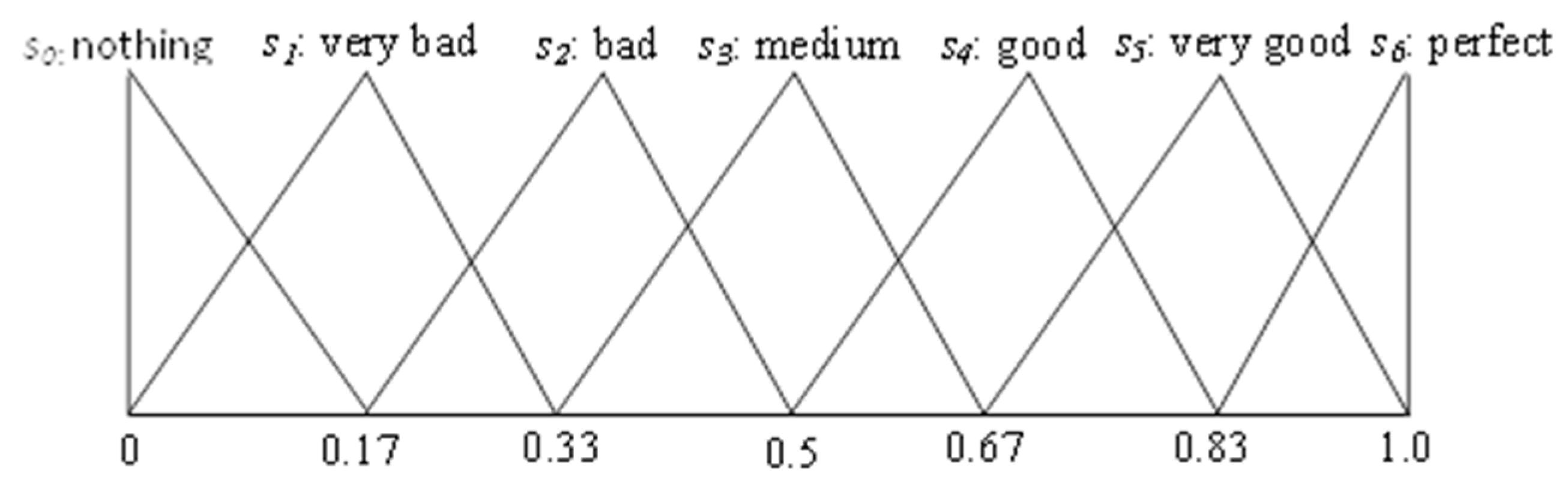
| Linguistic Expressions for the Criteria | Linguistic Expressions for the Alternatives | Triangular Fuzzy Numbers |
|---|---|---|
| Definitely low (DL) | Nothing (N) | (0, 0, 0.17) |
| Very low (VL) | Very bad (VB) | (0, 0.17, 0.33) |
| Low (L) | Bad (B) | (0.17, 0.33, 0.5) |
| Middle (M) | Medium (M) | (0.33, 0.5, 0.67) |
| High (H) | Good (G) | (0.5, 0.67, 0.83) |
| Very high (VH) | Very Good (VG) | (0.67, 0.83, 1) |
| Definitely high (DH) | Perfect (P) | (0.83, 1, 1) |
| The Aggregated Evaluations of the Criteria | |||||||||||
| Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 |
| CLEs | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH |
| The Aggregated Evaluations of the Alternatives with Respect to the Criteria | |||||||||||
| Alternatives\Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 |
| A1 | M | at least VG | at least M | at least G | between M and G | at least G | at most M | at least G | between M and VG | M | at least G |
| A2 | M | at least G | between M and VG | M | between B and M | at least G | between VB and M | at least G | between M and G | between M and G | at least G |
| A3 | between M and VG | at least G | M | M | between B and M | between M and VG | between B and G | between G and VG | between M and G | between M and VG | at least G |
| A4 | between M and VG | between G and VG | G | at least G | M | between M and VG | between B and G | at least VG | between G and VG | between M and VG | between G and VG |
| A5 | between M and VG | at least VG | M | between M and VG | between M and G | between M and VG | between VB and G | at least G | between M and VG | M | between M and G |
| A6 | M | between B and G | between M and VG | between M and VG | between M and G | between M and VG | between VB and G | between M and G | between B and M | between VB and M | between VB and M |
| Criteria | HFLTS | Fuzzy Envelopes | The Defuzzified Weight | The Normalized Weight | Rank |
|---|---|---|---|---|---|
| C1 | {L, M, H} | (0.17, 0.47, 0.53, 0.83) | 0.500 | 0.068 | 9 |
| C2 | {DH} | (0.83, 1.00, 1.00, 1.00) | 0.943 | 0.128 | 1 |
| C3 | {L, M, H, VH, DH} | (0.17, 0.18, 1.00, 1.00) | 0.587 | 0.080 | 7 |
| C4 | {M, H, VH} | (0.33, 0.64, 0.70, 1.00) | 0.667 | 0.091 | 6 |
| C5 | {DL, VL, L, M, H, VH} | (0.00, 0.00, 0.80, 1.00) | 0.452 | 0.061 | 10 |
| C6 | {M, H, VH, DH} | (0.33, 0.65, 1.00, 1.00) | 0.737 | 0.100 | 5 |
| C7 | {L, M} | (0.17, 0.33, 0.50, 0.67) | 0.418 | 0.057 | 11 |
| C8 | {H, VH} | (0.50, 0.67, 0.83, 1.00) | 0.750 | 0.102 | 4 |
| C9 | {H, VH, DH} | (0.50, 0.85, 1.00, 1.00) | 0.822 | 0.112 | 3 |
| C10 | {B, VH} | (0.17, 0.43, 0.73, 1.00) | 0.583 | 0.079 | 8 |
| C11 | {VH, DH} | (0.67, 0.97, 1.00, 1.00) | 0.889 | 0.121 | 2 |
| Alternatives\Criteria | The HFLTSs Generated from the CLEs for the Alternatives | ||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | |
| A1 | {M} | {G, VG} | {M, G, VG, P} | {G, VG, P} | {M, G} | {G, VG, P} | {N, VB, B, M} | {G, VG, P} | {M, G, VG} | {M} | {G, VG, P} |
| A2 | {M} | {G, VG, P} | {M, G, VG} | {M} | {B, M} | {G, VG, P} | {VB, B, M} | {G, VG, P} | {M, G} | {M, G} | {G, VG, P} |
| A3 | {M, G, VG} | {G, VG, P} | {M, G} | {M} | {B, M} | {M, G, VG} | {B, M, G} | {VG, P} | {M, G, VG} | {M, G, VG} | {G, VG, P} |
| A4 | {M, G, VG} | {G, VG} | {G} | {G, VG, P} | {M} | {M, G, VG} | {B, M, G} | {G, VG, P} | {G, VG} | {M, G, VG} | {G, VG} |
| A5 | {M, G, VG} | {VG, P} | {M, G} | {M, G, VG} | {M, G} | {M, G, VG} | {VB, B, M, G} | {G, VG, P} | {M, G, VG} | {B, M, G} | {M, G} |
| A6 | {M} | {B, M, G} | {M, G, VG} | {M, G, VG} | {M, G} | {M, G, VG} | {VB, B, M, G} | {M, G} | {B, M} | {VB, B, M} | {VB, B, M} |
| Alternatives\Criteria | The Fuzzy Decision Matrix Formed by the Fuzzy Envelopes of the HFLTSs | ||||||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | |
| A1 | (0.33, 0.50, 0.50, 0.67) | (0.67, 0.97, 1.00,100) | (0.33, 0.65, 1.00, 1.00) | (0.50, 0.85, 1.00, 1.00) | (0.33, 0.50, 0.67, 0.83) | (0.50, 0.85, 1.00, 1.00) | (0.00, 0.00, 0.35, 0.67) | (0.50, 0.85, 1.00, 1.00) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.50, 0.50, 0.67) | (0.50, 0.67, 0.83, 1.00) |
| A2 | (0.33, 0.50, 0.50, 0.67) | (0.50, 0.85, 1.00,1.00) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.50, 0.50, 0.67) | (0.17, 0.33, 0.50, 0.67) | (0.50, 0.85, 1.00,1.00) | (0.00, 0.30, 0.36, 0.67) | (0.50, 0.85, 1.00, 1.00) | (0.33, 0.50, 0.67, 0.83) | (0.33, 0.50, 0.67, 0.83) | (0.50, 0.67, 0.83, 1.00) |
| A3 | (0.33, 0.64, 0.70, 1.00) | (0.50, 0.85, 1.00,1.00) | (0.33, 0.50, 0.50, 0.67) | (0.33, 0.50, 0.50, 0.67) | (0.17, 0.33, 0.50, 0.67) | (0.33, 0.64, 0.70, 1.00) | (0.17, 0.47, 0.53, 0.83) | (0.50, 0.67, 0.83, 1.00) | (0.33, 0.50, 0.67, 0.83) | (0.33, 0.64, 0.70, 1.00) | (0.50, 0.67, 0.83, 1.00) |
| A4 | (0.33, 0.64, 0.70, 1.00) | (0.50, 0.67, 0.83, 1.00) | (0.50, 0.67, 0.67, 0.83) | (0.50, 0.85, 1.00,1.00) | (0.33, 0.50, 0.50, 0.67) | (0.33, 0.64, 0.70, 1.00) | (0.17, 0.47, 0.53, 0.83) | (0.67, 0.97, 1.00, 1.00) | (0.50, 0.67, 0.83, 1.00) | (0.33, 0.64, 0.70, 1.00) | (0.50, 0.85, 1.00, 1.00) |
| A5 | (0.33, 0.64, 0.70, 1.00) | (0.67, 0.97, 1.00, 1.00) | (0.33, 0.50, 0.50, 0.67) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.50, 0.67, 0.83) | (0.33, 0.64, 0.70, 1.00) | (0.00, 0.17, 0.66, 0.83) | (0.50, 0.85, 1.00, 1.00) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.50, 0.50, 0.67) | (0.50, 0.67, 0.83, 1.00) |
| A6 | (0.33, 0.50, 0.50, 0.67) | (0.17, 0.47, 0.53, 0.83) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.64, 0.70, 1.00) | (0.33, 0.50, 0.67, 0.83) | (0.33, 0.64, 0.70, 1.00) | (0.00, 0.17, 0.66, 0.83) | (0.33, 0.50, 0.67, 0.83) | (0.17, 0.33, 0.50, 0.67) | (0.00, 0.30, 0.36, 0.67) | (0.00, 0.30, 0.36, 0.67) |
| Alternatives\Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | EDi | HDi |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A1 | (0.08, 0.35, 0.40, 0.83) | (0.61, 1.07, 1.10, 1.10) | (0.08, 0.16, 1.36, 1.36) | (0.20, 0.66, 0.85, 1.22) | (0.00, 0.00, −0.12, −0.43) | (0.20, 0.67, 1.22, 1.22) | (0.00, 0.00, 0.35, 0.90) | (0.28, 0.64, 0.93, 1.12) | (0.22, 0.73, 0.93, 1.33) | (0.08, 0.32, 0.55, 1.00) | (0.41, 0.79, 1.01, 1.22) | 2.643 | 2.390 |
| A2 | (0.08, 0.35, 0.40, 0.83) | (0.46, 0.93, 1.10, 1.10) | (0.08, 0.16, 0.95, 1.36) | (0.13, 0.39, 0.43, 0.82) | (0.00, 0.00, 0.11, −0.15) | (0.20, 0.67, 1.22, 1.22) | (0.00, 0.20, 0.36, 0.90) | (0.28, 0.64, 0.93, 1.12) | (0.22, 0.57, 0.89, 1.11) | (0.08, 0.32, 0.73, 1.24) | (0.41, 0.79, 1.01, 1.22) | 2.331 | 2.062 |
| A3 | (0.08, 0.45, 0.56, 1.24) | (0.46, 0.93, 1.10, 1.10) | (0.08, 0.12, 0.68, 0.91) | (0.13, 0.39, 0.43, 0.82) | (0.00, 0.00, 0.11, −0.15) | (0.13, 0.51, 0.85, 1.22) | (0.06, 0.31, 0.53, 1.11) | (0.28, 0.50, 0.77, 1.12) | (0.22, 0.57, 0.89, 1.11) | (0.08, 0.41, 0.77, 1.50) | (0.41, 0.79, 1.01, 1.22) | 2.149 | 1.976 |
| A4 | (0.08, 0.45, 0.56, 1.24) | (0.46, 0.74, 0.91, 1.10) | (0.12, 0.16, 0.91, 1.13) | (0.20, 0.66, 0.85, 1.22) | (0.00, 0.00, 0.11, −0.15) | (0.13, 0.51, 0.85, 1.22) | (0.06, 0.31, 0.53, 1.11) | (0.38, 0.73, 0.93, 1.12) | (0.33, 0.76, 1.11, 1.33) | (0.08, 0.41, 0.77, 1.50) | (0.41, 1.00, 1.22, 1.22) | 3.006 | 2.769 |
| A5 | (0.08, 0.45, 0.56, 1.24) | (0.61, 1.07, 1.10, 1.10) | (0.08, 0.12, 0.68, 0.91) | (0.13, 0.50, 0.60, 1.22) | (0.00, 0.00, −0.12, −0.43) | (0.13, 0.51, 0.85, 1.22) | (0.00, 0.11, 0.66, 1.11) | (0.28, 0.64, 0.93, 1.12) | (0.22, 0.73, 0.93, 1.33) | (0.08, 0.32, 0.55, 1.00) | (0.41, 0.79, 1.01, 1.22) | 2.249 | 2.066 |
| A6 | (0.08, 0.35, 0.40, 0.83) | (0.16, 0.51, 0.59, 0.91) | (0.08, 0.16, 0.95, 1.36) | (0.13, 0.50, 0.60, 1.22) | (0.00, 0.00, −0.12, −0.43) | (0.13, 0.51, 0.85, 1.22) | (0.00, 0.11, 0.66, 1.11) | (0.19, 0.38, 0.63, 0.93) | (0.11, 0.37, 0.67, 0.89) | (0.00, 0.19, 0.40, 1.00) | (0.00, 0.35, 0.44, 0.82) | 0.651 | 0.512 |
| (0.08, 0.35, 0.40, 0.83) | (0.16, 0.51, 0.59, 0.91) | (0.08, 0.12, 0.68, 0.91) | (0.13, 0.40, 0.43, 0.82) | (0.00, 0.00, −0.12, −0.43) | (0.13, 0.51, 0.85, 1.22) | (0.00, 0.00, 0.35, 0.90) | (0.19, 0.38, 0.63, 0.93) | (0.11, 0.37, 0.67, 0.89) | (0.00, 0.19, 0.40, 1.00) | (0.00, 0.35, 0.44, 0.82) |
| Alternatives | RA | ASi | Ranking | |||||
|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A5 | A6 | |||
| A1 | 0 | 0.640 | 0.908 | −0.743 | 0.717 | 3.870 | 5.393 | 2 |
| A2 | −0.640 | 0 | 0.268 | −1.383 | 0.077 | 3.230 | 1.552 | 3 |
| A3 | −0.908 | −0.268 | 0 | −1.650 | −0.191 | 2.962 | −0.054 | 5 |
| A4 | 0.743 | 1.383 | 1.650 | 0 | 1.460 | 4.613 | 9.848 | 1 |
| A5 | −0.717 | −0.077 | 0.191 | −1.460 | 0 | 3.153 | 1.089 | 4 |
| A6 | −3.870 | −3.230 | −2.962 | −4.613 | −3.153 | 0 | −17.828 | 6 |
| Criteria | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | Ranking of the Alternatives |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Original CLEs | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 1 | M | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 2 | between L and H | between L and H | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 3 | between L and H | DH | between M and VH | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 4 | between L and H | DH | at least L | at least VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A5 > A2 > A3 > A6 |
| Case 5 | between L and H | DH | at least L | between M and VH | at most M | at least M | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A5 > A2 > A3 > A6 |
| Case 6 | between L and H | DH | at least L | between M and VH | at most VH | at least L | between L and M | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 7 | between L and H | DH | at least L | between M and VH | at most VH | at least M | at least H | between H and VH | at least H | between L and VH | at least VH | A4 > A1 > A5 > A3 > A2 > A6 |
| Case 8 | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between VL and M | at least H | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 9 | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at most VH | between L and VH | at least VH | A4 > A1 > A2 > A3 > A5 > A6 |
| Case 10 | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | VL | at least VH | A4 > A1 > A5 > A2 > A3 > A6 |
| Case 11 | between L and H | DH | at least L | between M and VH | at most VH | at least M | between L and M | between H and VH | at least H | between L and VH | between L and H | A4 > A1 > A2 > A3 > A5 > A6 |
| Alternatives | Fuzzy MCDM Methods | Performance Scores | |||||
|---|---|---|---|---|---|---|---|
| Fuzzy CODAS | Fuzzy EDAS | Fuzzy TOPSIS | Fuzzy WASPAS | Fuzzy ARAS | Fuzzy COPRAS | ||
| A1 | 2 | 3 | 2 | 2 | 2 | 3 | 2 |
| A2 | 3 | 5 | 3 | 5 | 4 | 5 | 5 |
| A3 | 5 | 4 | 5 | 4 | 5 | 4 | 4 |
| A4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| A5 | 4 | 2 | 4 | 3 | 3 | 2 | 3 |
| A6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| Fuzzy MCDM Methods | Fuzzy CODAS | Fuzzy EDAS | Fuzzy TOPSIS | Fuzzy WASPAS | Fuzzy ARAS | Fuzzy COPRAS | Performance Scores |
|---|---|---|---|---|---|---|---|
| Fuzzy CODAS | 1 | 0.714 | 1.000 | 0.829 | 0.943 | 0.714 | 0.829 |
| Fuzzy EDAS | – | 1 | 0.714 | 0.943 | 0.886 | 1.000 | 0.943 |
| Fuzzy TOPSIS | – | – | 1 | 0.829 | 0.943 | 0.714 | 0.829 |
| Fuzzy WASPAS | – | – | – | 1 | 0.943 | 0.943 | 1.000 |
| Fuzzy ARAS | – | – | – | – | 1 | 0.886 | 0.943 |
| Fuzzy COPRAS | – | – | – | – | – | 1 | 0.943 |
| Performance Scores | – | – | – | – | – | – | 1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yalçın, N.; Yapıcı Pehlivan, N. Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem. Symmetry 2019, 11, 493. https://doi.org/10.3390/sym11040493
Yalçın N, Yapıcı Pehlivan N. Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem. Symmetry. 2019; 11(4):493. https://doi.org/10.3390/sym11040493
Chicago/Turabian StyleYalçın, Neşe, and Nimet Yapıcı Pehlivan. 2019. "Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem" Symmetry 11, no. 4: 493. https://doi.org/10.3390/sym11040493
APA StyleYalçın, N., & Yapıcı Pehlivan, N. (2019). Application of the Fuzzy CODAS Method Based on Fuzzy Envelopes for Hesitant Fuzzy Linguistic Term Sets: A Case Study on a Personnel Selection Problem. Symmetry, 11(4), 493. https://doi.org/10.3390/sym11040493





