Abstract
The objective of this research is to examine growth and convergence processes in the provinces of Ecuador, considering sectoral productivity as an analysis variable. To do so, evidence of the productivity of the agricultural, secondary and service sectors is presented, and by applying the non-parametric method of density functions of the kernel, the complete distribution of the data is analyzed. The results obtained indicate that territorial inequality in Ecuador has very different behavior depending on the sectors of the economy. It is noted that inequality in terms of productivity is very high in the agricultural sector, it is at an average level in the secondary sector, and is less intense in the service sector. In the long-term, the overall balance is that sectoral inequality decreased among Ecuadorian provinces. However, there are two processes differentiated in time; in the first phase, inequality decreases more rapidly and in the second phase, it even increases in some sectors, as in the case of secondary sector returns.
1. Introduction
The discussion on inequality, specifically in relation to the growing disparity of incomes, has acquired new relevance at the global level, because the gaps between the rich and poor regions of the countries have been widening [1]. In this work, inequality is studied by focusing on individuals who are at the highest income distribution level, and their differences with the minority. Although its central thesis on the inequality spiral caused by return on capital levels above the growth rate is interesting, its perspective of analysis lacks a regional and sectoral dimension.
Nations and their regions grow unevenly, and others tend to equal or approximate to an average rate. Precisely, these asymmetries in growth levels have been the starting point for the analysis and discussion of the behavior of the main variables of economic activity among countries or regions, giving rise to the study of economic convergence and its derivations. In this area, the study of economic growth and regional inequality, as well as convergence, are necessary to “try to identify and explain the existing differences in well-being and wealth levels between countries and/or regions, as well as the determinants of their growth” ([2], p.62). The two traditional units of analysis for these studies were the comparison between countries or regions of the same country, and the two fundamental variables are income and productivity [3].
Traditionally, studies on economic growth that are carried out internationally [4,5,6,7,8,9,10,11,12,13,14] address the issue through the economic convergence hypothesis. The conditional convergence hypothesis “refers to the inverse relationship between the growth rate of per capita income and its initial level, for a set of regions or countries with similar structural characteristics and a specific period of time” [15]. This postulates in general terms the existence of a tendency to reduce economic disparities between countries or regions over time, reaching absolute economic convergence. In this field, according to Carrillo et al. [16], the poorest countries (or regions) tend to grow faster than those countries (or zones), which, by definition, are richer.
Despite the existence of what was called the “growth regression industry”, in which there are a considerable amount of studies on the subject and a great variety of theories and indicators [17], the empirical evidence continues to be inconclusive [18,19,20] and although there are studies that relate the economic structure with productivity [21,22], there are few studies that link this productive structure with the processes of beta-convergence in productivity [23]. Criticisms of convergence studies have also indicated that the convergence found in econometric models could even be present when regional dispersion was not decreasing [24,25]. Consequently, it is suggested that the distribution dynamics of the data should be analyzed [26].
In this context, this research aims to analyze the processes of the sub-national growth of Ecuador and its convergence, considering sectoral productivity as an analysis variable. The productive structure, broken down into three sectors, is considered: the primary, secondary and tertiary sectors. The complete distribution of the data is described and analyzed by using non-parametric methods, which enable the distributive dynamics of productivity in Ecuadorian provinces to be observed. The variables of 23 of the 24 Ecuadorian provinces are taken into account (Figure 1). Galápagos was excluded because it is an insular region, outside the continent, which does not allow for its involvement in the spatial methods (effect of neighborhood and contiguity) used in this study.
Figure 1.
Map of the provinces of Ecuador (Galápagos excluded). Source: Own elaboration.
The relevance of this study lies in the use of the Kernel method (non-parametric estimation of density functions). Contrary to parametric methods that incorporate rigid assumptions to the data, by means of this method, we have the advantage of developing models to predict the spatial behavior of the dependent variable as a function of the independent ones. Thus, by the means of a “weighted local regression”, it is possible that the closest neighboring regions outweigh the remote regions within a set of data. It must also be mentioned that in economic convergence analyses, per capita income has traditionally been used, while in this study, the structure and productivity of provinces are used.
The work is structured into five sections. In the introduction, the subject under study is contextualized and the objective is stated. In the theoretical framework section, the conceptual aspects of economic growth and convergence are discussed, as well as the existing models to measure convergence, and the empirical evidence is briefly discussed. The third section includes the methodology, and describes the calculation formulas for the indicators, the equations, and the regressions that will allow for the study of productivity in the sectoral structure of Ecuador, while the fourth section discusses an analysis of the variables and the results. Finally, the conclusions are presented in the last section.
2. A Previous Note on Convergence Analysis
The theoretical bases on economic growth were developed within the discipline of the economy between the mid-1950s and early 1990s [15]. In that period, two approaches were imposed: models of exogenous and endogenous growth. The former establishes the economic convergence hypothesis, and on the contrary, in the endogenous growth model proposed by Romer [8] and Lucas [11], we talk about divergence; this model predicts a gap between the different economies.
In the first model, of exogenous growth, the precursors were Solow [4] and Swan [5], who considered that economic growth depends on the intensity of the use of production, and their model predicted what is known as the absolute convergence of economies. Solow [4] developed the basic equation of economic growth based on the production function, and considered that when regions or countries reach a minimum level of development, this leads to growth convergence, and therefore, in their per capita income levels [16]. This is corroborated by Barro and Sala-i-Martin [27], who observe that the poorest countries or regions tend to grow in per capita terms more quickly than the most developed (richer) countries, and therefore, they tend to equalize.
At this point, it is necessary to define what is meant by convergence. According to Rabanal ([15], p.16), “it is a proposition according to which there is an inverse relationship between the growth rate of per capita income and its initial level, for a set of regions or countries and for a given period of time”. Convergence can be absolute or conditional; absolute convergence, as already mentioned, indicates that poor economies tend to grow faster than rich ones. According to Esquivel [28], convergence is absolute when the per capita income of an economy converges with that of other economies, regardless of the degree of similarity between economies, and this is dependent on the initial conditions.
The second approach, of endogenous growth, refers to the hypothesis that “there is an inverse relationship between the per capita growth rate and its initial level, for a set of regions or countries with similar structural characteristics and for a certain period of time” (Rabanal, [15], p. 119). This means, according to Mankiw, Romer and Weill [29] that the convergence process is verified in groups of countries that have certain common characteristics. This concept is applied when the growth rate of an economy is related to the gap between the product level of that economy and its own steady state [30].
The discussion on economic convergence has focused on obtaining empirical evidence mainly through two methodologies, sigma convergence (σ) and beta convergence (β), which are concepts created by Barro and Sala-i-Martin [12], whose background was based on the studies by Abramovitz [6], Baumol [7], Romer [8], and Lucas [11]. The first one is limited to measuring the dispersion of the cross-sectional data of the logarithm of per capita income, and whether this value decreases with time. It is concluded that there is sigma convergence. The second one is seen as a necessary condition, although not sufficient, of the first one, and it is limited to the evaluation of the beta sign in an econometric model; a negative and significant sign is evidence of beta convergence; this methodology was used in the studies by Barro and Sala-i-Martín [12,31].
The study of economic convergence has traditionally focused on the analysis of per capita Gross Domestic Product (GDP) growth. However, this does not allow for observations of the efficiency with which this process occurs to be made with greater clarity, because it obscures the role that is played by the sectoral productivity of the economy. Per capita GDP (GDPpc) can be disaggregated as the product of per capita occupation (Npc) and labor productivity (Ꙥ) as follows [32]: GDPpc = Npc* Ꙥ and in logarithms, it is expressed as ln(GDPpc) = ln(Npc) + ln(Ꙥ).
Consequently, the traditional convergence studies, by taking GDPpc as a central variable, link two processes that could have different trajectories, that of employment and that of labor productivity. In order to evaluate the efficiency with which the convergence processes occur, in this paper, we focus on the sectoral productivity of the Ecuadorian regions.
Quah [24,33] criticizes the methods that are traditionally used in the study of convergence, because when focusing on the manner in which an economy performs with respect to another one (convergence mechanism), it does not identify how an economy performs regarding its history (growth mechanism). When the two mechanisms are identified, it is possible to identify the processes of polarization, persistence, and stratification, that is, of convergence clubs.
The convergence mechanism can be compatible with highly polarized regional economies, since by observing only the mean and standard deviation, the data distribution from one moment of time to another is not observed; its intra-distributive dynamics are unknown. For this reason, in this research, the non-parametric proposal inspired by Quah’s work is taken up, in order to analyze the distribution dynamics of sectoral productivity data in Ecuadorian provinces.
In general, as Cuervo [34] points out, in Latin America, there are several studies on territorial economic convergence and divergence in its interior. These are partly due to the academic and political interests aroused by the work of Barro and Sala-I-Martin, as well as by some comparative research promoted by institutions, such as the Inter-American Development Bank (IDB) and the World Bank [35].
Mexico is undoubtedly the country with the most contributions on this subject (although they are not thorough), both in works that use parametric methods [28,36,37,38,39,40,41,42,43,44] and those that use non-parametric tools [35,45,46,47]. In all of them, there are different results in terms of convergence, depending on the period of analysis.
The work by Cárdenas, Potón and Trujillo [48] was the starting point in Colombia for research that uses income or proxy variables of wages [49,50,51,52,53,54]. Some of these investigations obtain ambiguous results, while in others, the conclusions of the different authors are complemented and explained ([34], p.49).
Subsequently, empirical studies of convergence and divergence were performed by using panel techniques, and with variables of human capital, physical capital, departmental taxes, and spatial models [55,56,57,58]. More recently, Royuela and García [59] studied convergence dynamics by applying parametric and non-parametric techniques. They considered social aspects such as life expectancy, child mortality, education, and crime. These authors verify the existence of convergence in Colombia in social variables, but not in the GDP per capita.
In the case of Brazil, several authors [60,61,62,63,64,65,66,67] found different findings and asymmetries in regional growth processes when studying the convergence phenomenon by means of traditional methods and then applying spatial econometric techniques. In Argentina, the convergence hypothesis in Argentine provinces is the main driving force of research [68,69,70,71].
In Ecuador, economic convergence and regional asymmetries have not been widely studied, due to lack of information (data restrictions) and the weak tradition of performing spatial analyses by Ecuadorian researchers [72]. Ramón-Mendieta et al. [73], and Ramón-Mendieta and Quintana-Romero [74], when studying growth, clusters and convergence in the 1993–2011 period, pointed out that Ecuador registered stable growth from 2000. However, this growth is not reflected in the interior of its provinces, due to the spatial concentration of per capita income. They also find that there is no significant spatial reconfiguration, since most of the traditional economic clusters did not move or contract. As a result, the emergence of new regions with considerable economic dynamism was limited.
Regarding Szeles and Muñoz [75], they study the economic convergence process for Ecuadorian provinces in the 2007–2014 period, using parametric and non-parametric methods. Their findings show that in heterogeneous territories, the regional distribution of GVA (Gross Value Added) has been polarized and it persists over time; and that the group of rich provinces advances faster than the less rich provinces. This makes the achievement of regional convergence even more difficult in the coming years.
The presence of territorial disparities and the contiguity effect were investigated by Arias [76]. By using the analysis of spatial econometrics as a methodology, they observed that the provincial specialization level is very diverse, while sigma convergence shows a descending path with the presence of convergence clubs. On the other hand, they verify the presence of absolute and conditional beta convergence, especially in labor productivity. Finally, they conclude that the contiguity effect benefits regional convergence.
The impact of public expenditure on convergence in Ecuador was addressed in the study by Flores-Chamba et al. [77]. The authors observed the existence of a “slight” process of per capita and productivity convergence, although with a significant level of territorial “segregation”. They also point out that the public investment made in the 2001–2015 period did not significantly increase the productivity of small and medium-sized provinces, severely conditioning the sustainability of the process of reducing disparities at the regional level.
At cantonal level, Mendieta-Muñoz [78] verifies the conditional convergence hypothesis through factors such as the illiteracy rate, the percentage of households with electric infrastructure, the average number of children, agricultural production, manufacturing production, and remittances as a percentage of the cantonal gross value added. The convergence speed is reduced to 1.12% per year, and indicates that differences in these variables would largely explain the slow territorial convergence in Ecuador. The convergence process of Ecuadorian cantons is also analyzed by Mendieta Muñoz and Pontarollo [79], who through spatial econometrics, identify groups of cantons that are determined by similar spatial patterns that can be interpreted as convergence clubs. They also warn of the presence of a convergence process that involves the most developed group of cantons, which leads to unbalanced spatial development.
3. Methodology
In this section, the calculation formulas of the indicators and the equations that are used to calculate the different types of convergence for the provinces of Ecuador are present, as well as the measures of dispersion and inequality that enable them to be compared with convergence levels. Finally, the Kernel estimator of conditional distribution that enable the study of productivity in the sectoral structure of Ecuador is presented.
Traditionally, regional economic convergence is used, that is, the tendency over time for per capita production levels in regions to equalize, to identify territorial economic disparities. As mentioned above, two convergence concepts have generally been used: i) sigma-convergence, establishes the relationship between the dispersion of per capita income and time; and ii) beta-convergence, which establishes the relationship between the growth rate of per capita income and its initial level.
3.1. Sigma Convergence
The way in which sigma convergence is measured has been questioned, because it does not take into account the existing size differences of the regions for which the standard deviation is calculated. In sigma convergence, the same weight is given to all geographic units [80]. In this research, the sigma convergence is explored by using the alternative indicators proposed by Ezcurra and Rodríguez-Pose [80], in which region participation is incorporated to the total population , to capture the heterogeneity of the regions.
(a) Coefficient of variation (C):
where:
= population participation of region i in a given year
= per capita income
(b) Standard deviation of the logarithms (v)
where:
As an alternative to the dispersion indicators, the distribution indicators are used:
(c) Gini Index (G):
(d) Generalized measures of entropy (GE):
(e) Atkinson Indexes (A):
Dispersion and distribution measures must be complemented with polarization indicators, since income dispersion and distribution may improve due to greater polarization. For example, if two groups of regions, one rich and one poor, reduce inequality, convergence will occur, but with two highly polarized regions [81].
(f) Generalized Polarization Index of Esteban (PEGR)
where:
is the average income of group j
pj is the population share of group j
α is the social sensitivity to polarization
is the number of groups in the partition obtained by minimizing the Gini index within each group.
is the grouping error
is the sensitivity to error
3.2. Convergence Models
The most abundant studies on the convergence hypothesis were made from the perspective of beta convergence. In the specific case of beta convergence, the econometric model to perform this estimation was proposed by Barro and Sala-i-Martin [27,82] and Barro [83]:
As the convergence speed is obtained by solving for lambda:
This model was also estimated, including other explanatory variables, in order to consider the differences in the steady states of regions. This is known in the literature as conditional convergence [84]. There is no consensus on the variables that must be included to condition the model. Durlauf et al. [17] identified around 145 different variables in the papers that they reviewed.
The variety of estimated models resulted in a number of measurements of the convergence coefficient, and its speed. The most influential result in the literature is the conventional rate, found in many studies, which is 2% per year [17]. However, this behavior that is so consistent could not be due to an equilibrium effect between the economies resulting from mobility and participation in the income of the factors depending on their marginal productivity, but to the characteristics of the statistical series and the methods used in the estimation.
As we pointed out in Section 2, Quah criticized the beta convergence model because it does not allow for the observation of polarization, stratification, and convergence clubs processes, and consequently, this makes an alternative proposal based on the distribution of the data. Ezcurra and Rodríguez-Pose [80] collect the contributions of Quah’s work on intra-distributive mobility, and point out that the distribution of the per capita income of a set of regions in a given period t has a measure of probability associated, , so that the task is to find the rule that, with time, describes the process . In simple terms, the probability of a region passing from one income group to another with time is sought. The simplest way to express this is through a first-order dependence process, so that:
where:
M is a transition probability matrix of a first-order Markov process.
and if for every s ≥1, you have that:
The criticism of this type of analysis proposed by Quah is that the temporal process depends only on the previous period of time, which is not consistent with studies on the subject, which show that per capita income in the long term does not follow a first-order stationary Markov process [85].
The alternative then consists of conditioning the income distribution to a given initial level, and finding an estimator of this conditional distribution [86]. One of the proposals in this regard was made by Hyndman [87] and Hyndman et al. [88], which suggested that use of a Kernel estimator of conditional distribution:
is the kernel estimator of conditional density;
K the kernel function
‖.‖ is a metric distance
b controls the softening of each conditional density in the direction of y
is estimated from:
where controls the softening of each conditional density in the x direction.
In this research work, Hyndman’s proposal for the study of the distribution of productivity in the sectoral structure of Ecuador is considered. In Arbia et.al. [89], and in Borrayo and Castañeda [46], it is possible to extensively review the practical advantages of performing this type of analysis, compared with conventional parametric methods. In particular, these authors point out that the beta-convergence, estimated from parametric regressions, does not allow for differentiatons between convergence, divergence, and stationarity of the growth differentials, because it only provides information on a representative economy, but not on the intra-distributive dynamics of the regions and sectors that operate in these processes [86]. As an alternative, these processes were studied through kernels, which allow for the description of the movement dynamics of the data distributions in the cross-sections of regions and sectors. Among the different analysis alternatives with kernels, Basile [90] shows that those proposed by Hyndman have the advantage of solving the bias problems that are presented by other methods, and they have better statistical properties.
4. Analysis of Data and Results
The analysis variable used was productivity, defined as the relationship between production and the work that is used. For the current study, production was estimated, based on the Provincial Gross Value Added (GVA) proxy variables available in the Regional Accounts prepared by the Central Bank of Ecuador (CBE), while the occupation of the population in the different sectors was taken from the Employment, Unemployment and Underemployment Surveys (ENEMDU) prepared by the National Institute of Statistics and Censuses (INEC).
Table 1 shows the main descriptive indicators of productivity at the beginning and end of the study period. In general, a different behavior was observed; maximum productivity was reached in 2014 in the primary sector, while for the secondary sector, the highest performance occurred in the year of 2007. If the average productivity was addressed, it was higher, both in 2007 and 2014 in the primary sector, and well above the results of the secondary and service sectors. On the other hand, in absolute terms (standard deviation) and in relative terms (coefficient of variation), the differences were significant. A higher standard deviation (34.6 in 2007 and 61.2 in 2014) in the primary sector with respect to their respective averages suggests that there was a greater dispersion in the productivity of this sector, in relation to the productivities of the secondary activities (11.5 in 2007 and 7.1 in 2014), and the tertiaries (2.4 in 2007 and 2014). This question was also fulfilled when observing the coefficients of variation that determine that it is in the primary sector, where there was a greater relative dispersion than in the other two sectors of the economy, both at the beginning and at the end of the series.

Table 1.
Descriptive measures at the beginning and end of the period.
4.1. Sectoral Productivity Evolution
The sectoral productivity evolution of Ecuador was very heterogeneous. The data that was available is shown in Figure 2 at the quantile level (variable values, arranged from the lowest to the highest, which divide the distribution into four parts, each with the same number of frequencies) for the primary sector, and it was observed that the highest levels of productivity occurred in the northeastern region in 2007, and there was a shift towards the coastal provinces of the north of the country. On the other hand, in the secondary sector, persistence in the productivity levels could be observed, since the provinces with the highest productivity were maintained over time, and they corresponded to the regions of the center of the coast and Morona-Santiago in the eastern sector of the country. Finally, in the tertiary sector, the greatest grouping of high productivity levels occurred in the provinces of the northern Amazon region.
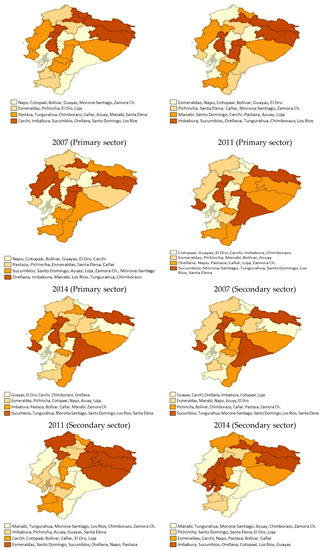
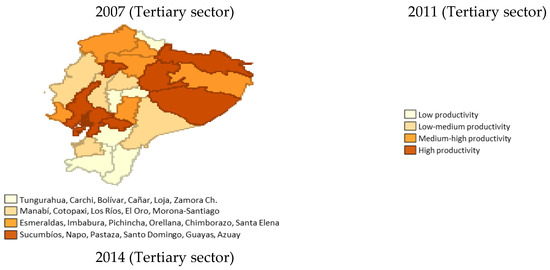
Figure 2.
Quantiles of provincial productivity for 2007, 2011, and 2014. Source: Own elaboration, based on Regional Accounts of the CBE [92], and ENEMDU Surveys of the INEC [92] (several years).
When contrasting the productivity levels with their growth dynamics, in Figure 3, it was observed that the most dynamic provinces, in general, were not those that had the highest productivity levels, which could imply the existence of a productivity convergence process.
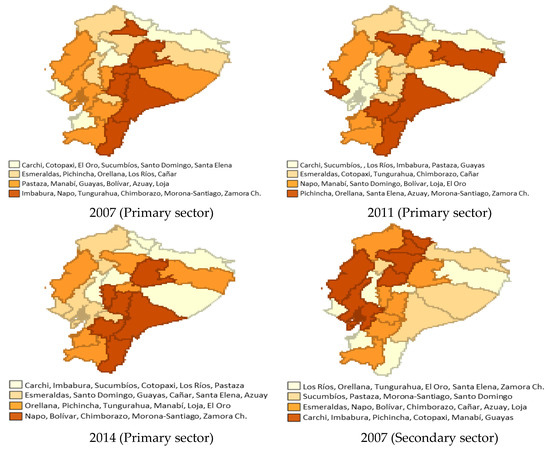
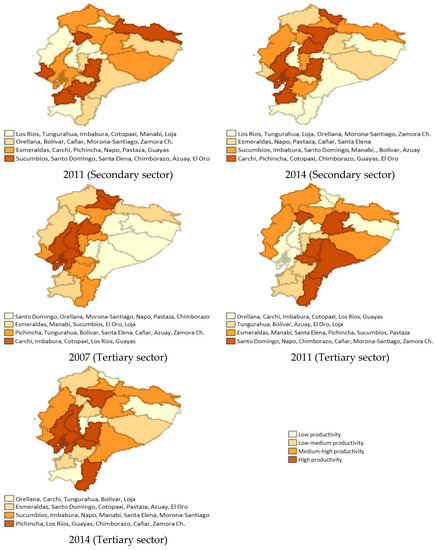
Figure 3.
Quantiles of the sectoral growth rates for 2007, 2011, and 2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], and ENEMDU Surveys of the INEC [92] (several years).
4.2. Gini Index and Sigma Convergence
In order to quantify the the territorial inequality of productivity in Ecuador, Figure 4 shows the results of the estimation of the Gini index and the sigma convergence, as measured by the standard deviation of the logarithm of productivity.
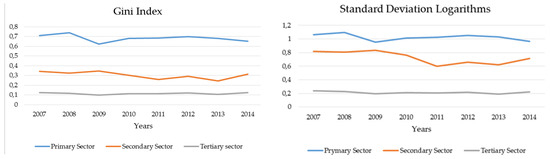
Figure 4.
Gini index and standard deviation of provincial productivity in Ecuador, 2007–2014. Source: Own elaboration, based on regional accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and Distributive Analysis Stata Package (DASP).
The trends in the data show that in fact, territorial productivity inequality decreased in the three sectors, with a decrease in the secondary sector being particularly faster, although inequality tended to increase, as of 2011. Regarding the tertiary sector, it had lower inequality levels, and its trend was more static over time. The Gini index shows that of the three sectors, the primary one was the one with the most heterogeneity among the regions, with the tertiary sector being the most uniform. In general, in the three sectors, that indicator and the coefficient of variation were lower than those that prevailed in 2007, which indicates that regional productivity inequality tends to decrease.
The previous results are also confirmed with the rest of the inequality indicators shown in Figure 5. Although the graphs indicate the existence of a tendency for dispersion to decrease, this is more evident in the primary sector if the results of the coefficient of variation are taken into account, which indicates a consistent decrease in that sector. On the other hand, in the secondary sector, there was less dispersion until 2011, and then an increase. Finally, in the services sector, there was also evidence of a decrease in inequality, although it was very small.
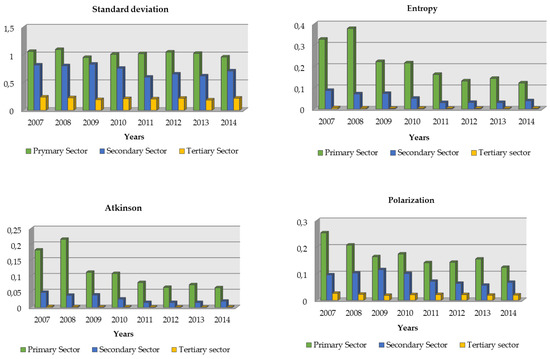
Figure 5.
Indices of inequality and polarization in the provincial sectoral productivity of Ecuador, 2007–2014. Source: Own elaboration, based on regional accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and Distributive Analysis Stata Package (DASP).
Regarding the polarization index, it was generally consistent with inequality behavior; when it increases, so does polarization. However, in the case of the secondary sector, the increase in inequality found as of 2011 did not immediately correspond to greater polarization, which was a reflection of the persistence of the territorial structure of productivity in Ecuadorian provinces.
4.3. Beta Convergence and Analysis of Sector Intra-Distributive Dynamics in Ecuadorian Provinces
In order to analyze the characteristics of the processes of production inequality reduction, estimates with the routines of Hyndman [87] were made, as already described in the methodology section.
Hyndman’s routines provide two types of graphs. The first is known as the Stacked Conditional Density Plot (SCD), and it shows the different side-by-side densities of the data, which makes it possible to distinguish the changes in the distribution throughout the conditioning variable with greater clarity, which in Convergence models, is the initial year (condition of beta convergence). The second graph shows the high-density regions (highest density regions, HDR), and each bar in the graph represents the conditional density for a given value; the dark shaded area is 50% HDR and the lighter area is 99% HDR; the mode is represented by a black dot [88].
Figure 6, Figure 7, Figure 8 show the results for the primary sector over three periods of time, with the first period being from 2007 to 2014, and the other two from 2007 to 2011 and from 2011 to 2014, respectively.
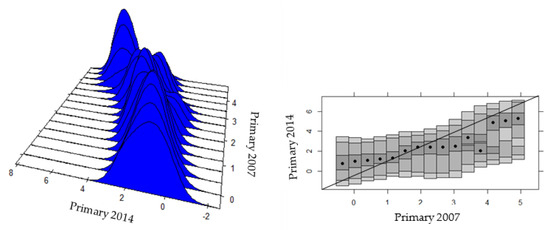
Figure 6.
Intra-distributive dynamics of provincial productivity in the primary sector of Ecuador, 2007–2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years) and a stacked conditional density plot (SCD) in R.
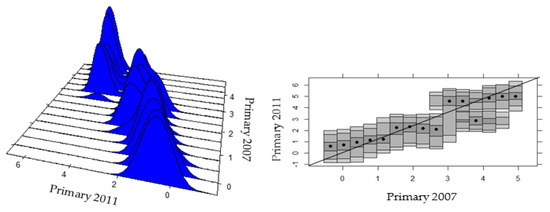
Figure 7.
Intra-distributive dynamics of provincial productivity in the primary sector of Ecuador, 2007-2011. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
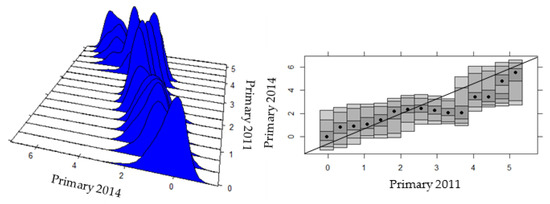
Figure 8.
Intra-distributive dynamics of provincial productivity in the primary sector of Ecuador, 2011-2014. Source: Own elaboration, based on Regional Accounts of the CBE [91]; ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
In the long term, it can be seen that inequality reduction was explained by the improvement in the productivity levels of the most backward regions, as can be seen by observing the HDR graph, in which those regions are above the 45° straight line, together with a decline in the richest ones, and in the average productivity regions that go below the line. The convergence process is slow to the extent that the average regions have bimodal processes, as shown in the graphs, so that some provinces of average productivity grow and others decrease, thus affecting the convergence speed.
By separating the data into two periods, two different processes can be highlighted; from 2007 to 2011, the most backward regions improve, and those with higher productivity are lagging behind, although some high-productivity regions have improved (Figure 7), while from 2011 to 2014, only the most backward regions are improving (Figure 8).
For the secondary sector, the SCD graph shows that in the long term, the process of reducing territorial inequality operates by improving the provinces with the lowest productivity and improving the deterioration of the other regions, in addition to observing the bimodal processes in the average-productivity regions (see Figure 9).
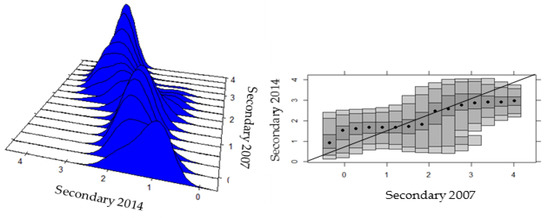
Figure 9.
Intra-distributive dynamics of provincial productivity in the secondary sector of Ecuador, 2007–2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
In the sub-periods, it is possible to identify the reasons for why the convergence process is reverted in the sector; from 2007 to 2011, the most lagged provinces improve and all of the other provinces worsen (Figure 10). However, from 2011 to 2014, practically all of the regions deteriorated, and only a small segment of long-lagging provinces experienced some improvement, but bimodal processes were in operation, which affected the growth rate (Figure 11).
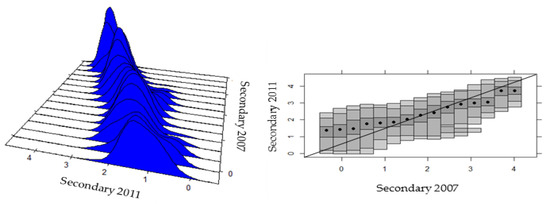
Figure 10.
Intra-distributive dynamics of provincial productivity in the secondary sector of Ecuador, 2007-2011. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
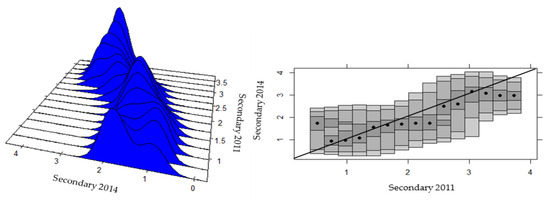
Figure 11.
Intra-distributive dynamics of provincial productivity in the secondary sector of Ecuador, 2011–2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
Finally, in the tertiary sector, there is a strong degree of heterogeneity that previously could not be observed with the dispersion indicators reported at the beginning of this section. The SCD graph shows processes with even three modes at high income levels and bimodal at the lowest levels (Figure 12). According to the HDR graph, the process of reducing regional productive inequality is very limited, because there are improvements in the productivity of lagged regions, but also in some more advanced ones.
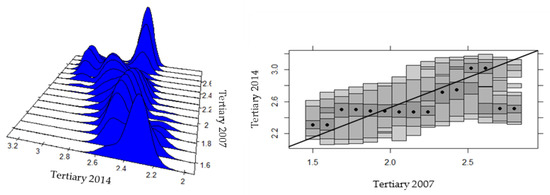
Figure 12.
Intra-distributive dynamics of provincial productivity in the tertiary sector of Ecuador, 2007–2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
In the sub-periods, we find evidence that between 2007 and 2011, the provinces of lower productivity and average productivity improve (Figure 13), while from 2011 to 2014, there were only improvements in the low-productivity provinces, while the average and most advanced provinces regressed strongly in relation to the previous period (Figure 14).
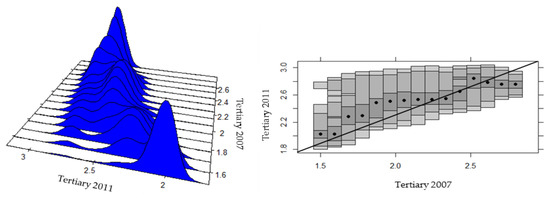
Figure 13.
Intra-distributive dynamics of provincial productivity in the tertiary sector of Ecuador, 2007–2011. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
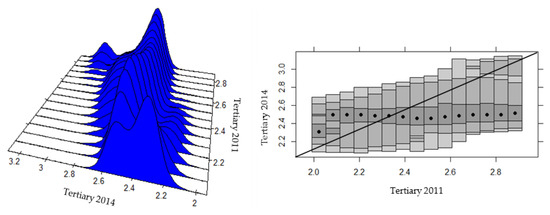
Figure 14.
Intra-distributive dynamics of provincial productivity in the primary sector of Ecuador, 2011–2014. Source: Own elaboration, based on Regional Accounts of the CBE [91], ENEMDU Surveys of the INEC [92] (several years), and a stacked conditional density plot (SCD) in R.
The convergence in labor productivity could have two implications. First, within each region, resources are being transferred from the least productive to the most dynamic sectors, and this occurs with greater intensity in the most backward regions [93]; second, there is a transfer of resources from the primary sector to the rest of the sectors that in theory, are more productive. In this sense, the convergence in productivity can be explained as a productive restructuring, under which the economy becomes more efficient. However, when the convergence in productivity works as a process in which the productivity of the most backward regions improve, and the most advanced deteriorate. The result in the aggregate would indicate a type of regressive convergence, in which efficiency is being lost in the most advanced sectors, and this seems to be the case for the Ecuadorian economy.
5. Conclusions
The present study represents a contribution to the few studies on convergence in Ecuador. Provincial sectoral productivity was used as an analysis variable, a factor that was not considered in previous studies, which is a novelty. In addition to this, the use of non-parametric methods complements the results of preliminary investigations, thus achieving a better understanding of the phenomenon of regional asymmetries and convergence processes.
In Ecuador, according to the data and variables used in this research, the presence of a productivity convergence process is observed. When correlating the productivity levels with growth dynamics, it was found that the most dynamic provinces, in general, are not those that have the highest productivity levels.
The results reveal a sectoral evolution of very heterogeneous productivity in the Ecuadorian territory; the highest yields of the primary sector are present in the northeastern region at the beginning of the analysis period (2007–2014). However, these shift to the provinces of the northern coast at the end of the period. In the provinces of the center of the Coast and in Morona Santiago (East), the highest productivity levels of the secondary sector persist; while with regard to the tertiary sector, the highest grouping of high productivity levels occurs in the provinces of the northern Amazon region.
In general, the analysis shows that territorial inequality in Ecuador has very different behaviors, depending on the sectors of the economy. It is noted that inequality in terms of productivity is very high in the agricultural sector; it is at an average level in the secondary sector, and is less intense in the service sector. In the long term, the overall balance from 2007 to 2014 is that sectoral inequality tended to decrease among Ecuadorian provinces. However, there are two processes that are differentiated over time; from 2007 to 2011, inequality decreases more rapidly, and from 2011 to 2014, it even increases in some sectors, as in the case of the secondary sector.
Convergence processes are caused by productivity growth in the most backward regions, and deterioration in average and wealthy regions. This means that Ecuador shows a type of regressive convergence, which is not based on improvements in productivity but in the deterioration of the most advanced regions, and an improvement in the most backward ones. One of the measures to reverse this situation should be the implementation of regional public policies that should consider productivity inequalities in the sectors of the economy in certain areas; this should be a criterion for the allocation of government investment and the application of policy instruments and incentives, in order to promote inter-regional equity.
Author Contributions
L.Q.-R, R.C.-Q, M.G.R.-M, J.Á.-G all authors contributed equally to this work. All authors wrote, reviewed and commented on the manuscript. All authors have read and approved the final manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- OECD. Regions at a Glance, Organisation for Economic Co-operation and Development. 2016. Available online: http://www.oecd.org/regional/oecd-regions-at-a-glance-19990057.htm (accessed on 25 March 2019).
- León, G. Crecimiento y convergencia económica: Una revisión para Colombia. Dimens. Empres. 2013, 11, 61–76. [Google Scholar] [CrossRef]
- Islam, N. What have we learnt from the convergence debate? J. Econ. Surv. 2005, 17, 309–354. [Google Scholar] [CrossRef]
- Solow, R.A. Contribution to the Theory of Economic Growth. Q. J. Econ. 1956, 70, 65–94. [Google Scholar] [CrossRef]
- Swan, T.W. Economic growth and capital accumulation. Econ. Rec. 1956, 32, 334–361. [Google Scholar] [CrossRef]
- Abramovitz, M. Catching up, forging ahead, and falling behind. J. Econ. Hist. 1986, 46, 385–406. [Google Scholar] [CrossRef]
- Baumol, W. Productivity Growth, Convergence and Welfare: What the Long-Run Data Show. Am. Econ. Rev. 1986, 76, 1072–1085. [Google Scholar]
- Romer, P.M. Increasing returns and long-run growth. J. Polit. Econ. 1986, 94, 1002–1037. [Google Scholar] [CrossRef]
- Baumol, W.J.; Wolff, E.N. Productivity growth, convergence, and welfare: Reply. Am. Econ. Rev. 1988, 78, 1155–1159. [Google Scholar]
- De Long, J.B. Productivity growth, convergence, and welfare: Comment. Am. Econ. Rev. 1988, 78, 1138–1154. [Google Scholar]
- Lucas, R.E., Jr. On the mechanics of economic development. J. Monetary Econ. 1988, 22, 3–42. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X.; Blanchard, O.J.; Hall, R.E. Convergence across states and regions. Brookings Papers Econ. Activity 1991, 22, 107–182. [Google Scholar]
- Quah, D. Galton’s Fallacy and Tests of the Convergence Hypothesis; Working Paper; LSE Economics Department: London, UK, 1993. [Google Scholar]
- Quah, D.T. Twin peaks: Growth and convergence in models of distribution dynamics. Econ. J. 1996, 16, 1045–1055. [Google Scholar] [CrossRef]
- Rabanal, C. Hipótesis sobre la convergencia económica: Una revisión de los enfoques utilizados. Economía y Administración 2017, 7, 113–132. [Google Scholar] [CrossRef]
- Carrillo Huerta, M.M.; Ceron Vargas, J.A.; Reyes Hernández, M.S. Análisis del Crecimiento Económico; e-libro Corp.: Madrid, Spain, 2007. [Google Scholar]
- Durlauf, S.; Johnson, P.A.; Jonathan, R.W.T. Growth Econometrics; Working Paper Series 61; Vassar College Department of Economics: New York, NY, USA, 2004. [Google Scholar]
- Young, A.; Higgins, M.; Levy, D. Sigma Convergence versus Beta Convergence: Evidence from U.S. County-Level Data. J. Money Credit Bank. 2008, 40, 1083–1093. [Google Scholar] [CrossRef]
- Fischer, M.; Stumpner, P. Income distribution dynamics and cross-region convergence in Europe. J. Geogr. Syst. 2008, 10, 109–139. [Google Scholar] [CrossRef]
- Górna, J.; Górna, K.; Szulc, E. Analysis of β-Convergence. From Traditional Cross-Section Model to Dynamic Panel Model. Dyn. Econom. Models 2013, 13, 127–143. [Google Scholar] [CrossRef]
- Fagerberg, J. Technological progress, structural change and productivity growth: A comparative study. Struct. Chang. Econ. Dyn. 2000, 11, 393–411. [Google Scholar] [CrossRef]
- Erbetta, F.; Petraglia, C. Drivers of Regional Efficiency Differentials in Italy: Technical Inefficiency or Allocative Distortions? Growth Chang. 2011, 42, 351–375. [Google Scholar] [CrossRef]
- Cuadrado, J.R.; Maroto, A. Convergencia Regional en Productividad y Cambios en la Estructura Productiva; Working Papers 12/08; Instituto Universitario de Análisis Económico y Social: Región de Valparaíso, Chile, 2008. [Google Scholar]
- Quah, D.T. Empirics for economic growth and convergence. Eur. Econ. Rev. 1996, 40, 1353–1375. [Google Scholar] [CrossRef]
- Quah, D. Growth and Distribution: Stratification, Polarization, and Convergence Clubs. J. Econ. Growth 1997, 2, 27–59. [Google Scholar] [CrossRef]
- Hyndman, R. Computing and Graphing Highest Density Regions. Am. Stat. 1996, 50, 120–126. [Google Scholar]
- Barro, R.J.; Sala-i-Martin, X. Economic Growth; McGraw-Hill: Mexico City, Mexico, 1995. [Google Scholar]
- Esquivel, G. Convergencia regional en México, 1940-1995. El Trimestre Económico 1999, XVI, 725–761. [Google Scholar]
- Mankiw, N.G.; Romer, D.; Weil, D.N. A contribution to the empirics of economic growth. Q. J. Econ. 1992, 107, 407–437. [Google Scholar] [CrossRef]
- Barro, R.J.; Sala-i-Martin, X.; Robinson, R.A.; de Espinoza, J.R. Crecimiento Económico; Reverté: Mexico City, Mexico, 2009. [Google Scholar]
- Barro, R.J.; Sala-i-Martin, X. Convergence. J. Polit. Econ. 1992, 100, 223–251. [Google Scholar] [CrossRef]
- García-Greciano, B.; Raymond, J.L.; Villaverde, J. Convergencia de las provincias españolas. Papeles de Economía Española 1995, 64, 38–53. [Google Scholar]
- Quah, D. Galton’s fallacy and tests of the convergence hypothesis. Scand. J. Econ. 1993, 820, 427–443. [Google Scholar] [CrossRef]
- Cuervo, L.M. Estudios de convergencia y divergencia regional en América Latina: Balance y perspectivas. J. Reg. Res. 2004, 5, 29–66. [Google Scholar]
- Aroca, P.; Bosch, M.; Maloney, W. Spatial Dimensions of Trade Liberalization and Economic Convergence: Mexico 1985–2002. World Bank Econ. Rev. 2005, 19, 345–378. [Google Scholar] [CrossRef]
- Juan-Ramón, V.H.; Rivera-Batiz, L.A. Regional growth in Mexico: 1970 93. Regional growth in Mexico: 1970–1993; IMF Working Papers, núm. WP/96/92; International Monetary Fund: Washington, DC, USA, 1996. [Google Scholar]
- Cermeño, R. Decrecimiento y convergencia de los estados mexicanos. Un análisis de panel. El Trimestre Económico 2001, LXVIII, 603–629. [Google Scholar]
- Carrillo, M. La teoría neoclásica de la convergencia y la realidad del desarrollo regional en México. Problemas del Desarrollo 2001, 127, 107–134. [Google Scholar] [CrossRef]
- Díaz-Bautista, A. Apertura comercial y crecimiento regional. Comercio Exterior 2003, 53, 995–1000. [Google Scholar]
- Mendoza-González, M.Á. La dinámica económica regional en México, 1940–2002. Territorio y Economía 2004, 7, 12–22. [Google Scholar]
- Chiquiar, D. Why Mexico’s Regional Income Convergence Broke Down. J. Dev. Econ. 2005, 77, 257–275. [Google Scholar] [CrossRef]
- Diáz-Pedroza, J.; Vargas, A.S.; González, M.Á.M. Convergencia hacia la economía regional líder en México: Un análisis de cointegración en panel. El Trimestre Económico 2009, LXXVI, 407–431. [Google Scholar]
- Asuad Sanén, N.; Quintana Romero, L. Crecimiento económico, convergencia y concentración económica espacial en las entidades federativas de México 1970-2008. Investig. Reg. 2010, 18, 83–106. [Google Scholar]
- Rodríguez-Benavides, D.; Mendoza-González, M.Á.; Venegas-Martínez, F. ¿Realmente existe convergencia regional en México? Un modelo de datos-panel TAR no lineal. Economía Sociedad y Territorio 2016, 16, 197–227. [Google Scholar] [CrossRef]
- García-Verdú, R. Income, Mortality, and Literacy Distribution Dynamics Across States in México: 1940–2000. Cuadernos de Economía 2005, 42, 165–192. [Google Scholar] [CrossRef]
- Borrayo López, R.; Castañeda Arriaga, J.M. Análisis de transición dinámica: Un enfoque no paramétrico aplicado a la región centro de México (1988–2003). Problemas del Desarrollo 2011, 42, 7–44. [Google Scholar] [CrossRef]
- Quintana, L.; Asuad, N. Growth, Concentration, Inequality and Regional Policy in Mexico. In Regional Problems and Policies in Latin America; Springer: Cham, Switzerland, 2013; pp. 165–195. [Google Scholar]
- Cárdenas, M.; Pontón, A.; Trujillo, J. Convergencia y migraciones interdepartamentales en Colombia: 1950–1983. Coyuntura Económica 1993, 23, 111–137. [Google Scholar] [PubMed]
- Cárdenas, M.; Pontón, A. Growth and convergence in Colombia 1950–1990. J. Dev. Econ. 1995, 47, 5–37. [Google Scholar] [CrossRef]
- Birchenall Jiménez, J.A.; Murcia Guzmán, G.E. Convergencia regional: Una revisión del caso colombiano. Desarrollo y Sociedad 1997, 40, 273–308. [Google Scholar]
- Sánchez, T.F.; Núñez, M.J. La geografia y el desarrollo económico en Colombia: Una aproximación municipal. Desarrollo y Sociedad 2000, 46, 43–108. [Google Scholar]
- Acevedo, S. Convergencia y crecimiento económico en Colombia 1980–2000. Ecos Economía 2003, 7, 51–78. [Google Scholar]
- Bonet Morón, J.; Meisel Roca, A. La Convergencia Regional en Colombia: Una Visión de Largo Plazo, 1926–1995; Documentos de Trabajo sobre Economía Regional, No. 8; Centro de Estudios Económicos Regionales, Banco de la República: Cartagena, Colombia, 1999.
- Bonet, J.; Meisel, A. Polarización del Ingreso Per Cápita Departamental en Colombia, 1975–2000; Documentos de Trabajo sobre Economía Regional, No. 76; Centro de Estudios Económicos Regionales, Banco de la República: Cartagena, Colombia, 2006.
- Gómez, C. Convergencia regional en Colombia: Un enfoque en los Agregados Monetarios y en el Sector Exportador. Ensayos Sobre Economía Regional 2006, 45, 1–50. [Google Scholar]
- Branisa, B.; Cardozo, A. Regional Growth Convergence in Colombia Using Social Indicators; Discussion Papers; Ibero America Institute for Economic Research: Torrance, CA, USA, 2009. [Google Scholar]
- Franco, L.; Raymond, J. Convergencia económica regional: El caso de los Departamentos colombianos. Ecos de Economía 2009, 28, 167–197. [Google Scholar]
- Galvis Aponte, L.A.; Hahn-de-Castro, L.W. Crecimiento municipal en Colombia: El papel de las externalidades espaciales, el capital humano y el capital físico. Documentos de Trabajo Sobre Economía Regional 2015, 216, 1–60. [Google Scholar]
- Royuela, V.; Garcia, C.G. Economic and social convergence in Colombia. Reg. Stud. 2015, 49, 219–239. [Google Scholar] [CrossRef]
- Diniz, C.C. A Dinamica Regional Recente da Economia Brasileira e suas Perspectivas; Instituto de Pesquisa Economica Aplicada: Brasília, Brazil, 1995. [Google Scholar]
- Azzoni, C.R.; Ferreira, D.A. Competitividad regional y reconcentración industrial: El futuro de las desigualdades regionales en Brasil. EURE Revista Latinoamericana de Estudios Urbano Regionales 1998, XXIV, 81–111. [Google Scholar] [CrossRef]
- Pitella, R. Migracoes e Convergencia no Brazil: 1960–1991. Revista Brasileira 1999, 53, 211–236. [Google Scholar]
- Azzoni, C.R.; Menezes Filho, N.; Menezes, T.; Silveira-Neto, R. Geography and Income Convergence Among Brazilian States (May 2000). IDB Working Paper No. 122. Available online: https://ssrn.com/abstract=1814668 or http://dx.doi.org/10.2139/ssrn.1814668 (accessed on 12 January 2019).
- Magalhães, A.; Hewings, G.; Azzoni, C.R. Spatial dependence and regional convergence in Brazil. Investigaciones Regionales 2005, 6, 5–20. [Google Scholar]
- Gondim, J.L.B.; Barreto, F.A.; Carvalho, J.R. Condicionantes de clubes de convergência no Brasil. Estudos Econômicos 2007, 37, 71–100. [Google Scholar] [CrossRef]
- Resende, G.M.; de Carvalho, A.X.; Sakowski, P.A.M.; Cravo, T.A. Evaluating multiple spatial dimensions of economic growth in Brazil using spatial panel data models. Ann. Reg. Sci. 2006, 56, 1–31. [Google Scholar] [CrossRef]
- Díaz Dapena, A.; Rubiera Morollón, F.; Pires, M.D.M.; Gomes, A.D.S. Convergence in Brazil: New evidence using a multilevel approach. Appl. Econ. 2017, 49, 5050–5062. [Google Scholar]
- Willington, M. Un análisis empírico del crecimiento económico regional en Argentina. Estudios 1998, 21, 1–47. [Google Scholar]
- Marina, A.; Garrido, N.; Sotelsek, D. Dinámica de la Distribución del Producto a Través de las Provincias Argentinas, 1970–1995; Anales de la XXV Reunión anual de la Asociación Argentina de Economía Política: Santa Cruz de la Sierra, Bolivia, 2000. [Google Scholar]
- Russo, J.L.; Ceña Delgado, F. Evolución de la convergencia y disparidades provinciales en Argentina. Revista de Estudios Regionales 2000, 57, 151–173. [Google Scholar]
- Garrido, N.; Marina, A.; Salem, D.S. Convergencia económica en las provincias argentinas (1970–1995). Estudios de Economía Aplicada 2002, 20, 403–421. [Google Scholar]
- Quintana-Romero, L.; Mendoza, M.A.; Correa-Quezada, R. Las Regiones Ecuatorianas en el Contexto Latinoamericano; Crecimiento, Industria, Migración y Empleo: Quito, Ecuador, 2014; pp. 13–27. [Google Scholar]
- Ramón-Mendieta, M.G.; Ochoa-Moreno, W.S.; Ochoa-Jiménez, D.A. Growth, Clusters, and Convergence in Ecuador: 1993–2011. In Regional Problems and Policies in Latin America; Springer: Berlin/Heidelberg, Germany, 2013; pp. 323–337. [Google Scholar]
- Ramón-Mendieta, M.; Quintana-Romero, L. Convergencia y Divergencia Regional en Ecuador; Crecimiento, Industria, Migración y Empleo: Quito, Ecuador, 2014; pp. 85–105. [Google Scholar]
- Szeles, M.R.; Muñoz, R.M. Analyzing the regional economic convergence in Ecuador. Insights from parametric and nonparametric models. Rom. J. Econ. Forecast. 2016, 19, 43–65. [Google Scholar]
- Arias, T.D.C.T. El Cambio Estructural y las Desigualdades Regionales en el Ecuador: 1993–2014. Ph.D. Thesis, Universidad de Alcalá, Alcalá de Henares, Spain, 2017. [Google Scholar]
- Flores-Chamba, J.; Correa-Quezada, R.; Álvarez-García, J.; del Río-Rama, M.C. Spatial Economic Convergence and Public Expenditure in Ecuador. Symmetry 2019, 11, 130. [Google Scholar] [CrossRef]
- Mendieta-Muñoz, R.M. La hipótesis de la convergencia condicional en Ecuador: Un análisis a nivel cantonal. Retos 2015, 5, 13–25. [Google Scholar] [CrossRef]
- Mendieta Muñoz, R.; Pontarollo, N. Cantonal Convergence in Ecuador: A Spatial Econometric Perspective. J. Appl. Econ. Sci. 2016, 1, 107–126. [Google Scholar]
- Ezcurra, R.; Rodríguez-Pose, A. Measuring the regional divide. In Handbook of Regional Growth and Development Theories; Edward Elgar Publishing: Cheltenham, UK, 2009; pp. 329–353. [Google Scholar]
- Ezcurra, R.; Rodríguez-Pose, A. Can the Economic Impact of Political Decentralisation Be Measured? Working Paper series in Economics and Social Sciences 2011/02; IMDEA: Madrid, Spain, 2011. [Google Scholar]
- Barro, R.J. Xavier Sala-i-Martin. Economic Growth and Convergence Across the United States; Working Paper no. 3419; National Bureau of Economic Research: Cambridge, MA USA, 1990. [Google Scholar]
- Barro, R.J. Economic Growth in a Cross Section of Countries. Q. J. Econ. 1991, 106, 407–443. [Google Scholar] [CrossRef]
- Sala-i-Martin, X. The classical approach to convergence analysis. Econ. J. 1996, 734, 1019–1036. [Google Scholar] [CrossRef]
- Bickenbach, F.; Eckhardt, B. Evaluating the Markov Property in Studies of Economic Convergence. Int. Reg. Sci. Rev. 2003, 26, 363–392. [Google Scholar] [CrossRef]
- Magrini, S. Analysing Convergence Through the Distribution Dynamics Approach: Why and How? Working paper Department of Economics, num. 13 /wp/2007; Ca’ Foscari University of Venice: Venice, Italy, 2007. [Google Scholar]
- Hyndman, R. Package Highest Density Regions and Conditional Density Estimation ‘Hdrcde’. 2015. Available online: http://www.robjhyndman.com/software/hdrcde (accessed on 14 November 2018).
- Hyndman, R.; Bashtannyk, D.; Grunwald, G. Estimating and visualizing conditional densities. J. Comput. Graph. Stat. 1996, 5, 315–336. [Google Scholar]
- Arbia, G.; Basile, R.; Piras, G. Analyzing Intra-Distribution Dynamics: A Reappraisal; Working Paper, Regional Economics Applications Laboratory at UIUC 2006; European Regional Science Association: Louvain-la-Neuve, Belgium, 2006. [Google Scholar]
- Basile, R. Intra-Distribution Dynamics of Regional Per-Capita Income in Europe: Evidence from Alternative Conditional Density Estimators. STATISTICA, LXX, n. 1. 2010. Available online: www.researchgate.net/publication/307715550 (accessed on 14 November 2018).
- Central Bank of Ecuador (CBE). Cuentas Nacionales Regionales. Available online: https://www.bce.fin.ec/index.php/component/k2/item/293-cuentas-provinciales/ (accessed on 12 November 2018).
- Instituto Nacional de Estadísticas y Censos (INEC). Encuestas de Empleo, Desempleo y Subempleo (ENEMDU). Available online: http://www.ecuadorencifras.gob.ec/informacion-historica-de-empleo/ (accessed on 14 November 2018).
- Maroto, A.; Cuadrado, J.R. New Regional Convergence in Productivity and Productive Structure, Application to European Southern Countries. IAES, Work Documents. 2008. Available online: https://www.researchgate.net/publication/237727809 (accessed on 25 March 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).