1. Introduction
Complex large-scale network structures arise in a variety of natural and technological settings [
1,
2], and they pose numerous challenges to computer scientists and applied mathematicians. Many interesting ideas in this area come from the analysis of social networks [
3], where each vertex (
actor) is associated with a set of properties (
attributes), and pairs of sets with nonempty intersections correspond to edges in the network. Complex and social networks represented by such
intersection graphs are copious in the real world. Well-known examples include the film actor network [
4], where actors are linked by an edge if they performed in the same movie, the academic co-authorship network [
5], where two researchers are linked by an edge if they have a joint publication, the circle of friends in online social networks (e.g., Google+), where two users are declared adjacent if they share a common interest, and the Eschenauer–Gligor key predistribution scheme [
6] in secure wireless sensor networks, where two sensors establish secure communication over a link if they have at least one common key. Remarkably, it was shown in Reference [
7] that all graphs are indeed intersection graphs.
To understand statistical properties of intersection graphs, a probability model was introduced in References [
8,
9] as a generalization of the classical model
of Erdős and Rényi [
10]. Formally, let
be positive integers and let
. We start with a random bipartite graph
with independent vertex sets
and
and edges between
V and
W existing independently with probability
p. In terms of social networks,
V is interpreted as a set of actors and
W a set of attributes. We then define the
random intersection graph with vertex set
V and vertices
adjacent if and only if there exists some
such that both
and
are adjacent to
w in
. Several variant models of random intersection graphs have been proposed, and many graph-theoretic properties of
, such as degree distribution, connected components, fixed subgraphs, independence number, clique number, diameter, Hamiltonicity and clustering, have been extensively studied [
8,
9,
11,
12,
13,
14]. We refer the reader to References [
15,
16] for an updated review of recent results in this prolific field.
In light of the above list of properties studied, it is, perhaps, surprising that there has been little work regarding
isoperimetric numbers of random intersection graphs. The isoperimetric numbers, which measure the expansion properties of a graph (see
Section 2 below for precise definitions), have a long history in random graph theory [
17,
18,
19] and are strongly related to the graph spectrum and expanders [
20]. They have found a wide range of applications in theoretical computer science, including algorithm design, data compression, rapid mixing, error correcting codes, and robust computer networks [
21]. Social networks such as co-authorship networks are commonly believed to have poor expansion properties (i.e., small isoperimetric numbers), which indicate the existence of bottlenecks (e.g., cuts with small size) inside the networks, because of their modular and community organization [
22,
23]. In this paper, we hope to show that it is possible to increase the isoperimetric numbers by a gentle perturbation of the original bipartite graph structure underlying the intersection graphs.
In recent times, there has been an effort to study the effect of random perturbation on graphs. The most mathematically famous example is perhaps the Newman–Watts small-world network [
1,
24], which is a random instance obtained by adding random edges to a cycle, exhibiting short average distance and high clustering coefficient, namely, the so-called small-world phenomenon. A random graph model
[
25] with general connected base graph
G on
n vertices and
R being a sparse Erdos-Rényi random graph
where
is some small constant has been introduced in [
26], and its further properties, such as connectivity, fixed subgraphs, Hamiltonicity, diameter, mixing time, vertex and edge expansion, have been intensively examined; see, e.g., [
27,
28,
29,
30,
31,
32,
33,
34] and references therein. For instance, in Reference [
29], a necessary condition for the base graph is given under which the perturbed graph
is an expander a.a.s. (asymptomatically almost surely); for a connected base graph
G, it is shown in Reference [
30] that, a.a.s. the perturbed graph has an edge–isoperimetric number
, diameter
, and vertex–isoperimetric number
, where for the last property
G is assumed to have bounded maximum degree. Here, we say that
possesses a graph property
asymptotically almost surely, or a.a.s. for brevity, if the probability that
possesses
tends to 1 as
n goes to infinity. In this paper, to go a step further in this line of research, we investigate the bipartite graph type perturbation, where random edges are only added to the base (bipartite) graph between the two independent sets. We provide lower bounds for the isoperimetric numbers of random intersection graphs induced by such perturbations.
The rest of the paper is organized as follows. In
Section 2, we state and discuss the main results, with proofs relegated to
Section 4. In
Section 3, we give numerical examples based upon real network data, complementing our theoretical results in small network sizes.
Section 5 contains some concluding remarks.
2. Results
Let
be a graph with vertex set
V and edge set
E. If
is a set of vertices, then
denotes the set of edges of
G having one end in
S and the other end in
. Given
, write
for the subgraph of
G induced by
S. We use
to denote the collection of vertices of
which are adjacent to some vertex of
S. For a vertex
,
is the neighborhood of
v, and we denote by
the second neighborhood of
v. The above subscript
G will be omitted when no ambiguity may arise. For a graph
G, its edge–isoperimetric number,
(also called its Cheeger constant), is given by:
The vertex–isoperimetric number of
G,
, can be defined similarly as:
It is well-known that
[
35], where
is the maximum degree of
G.
We will consider the following model of randomly perturbed intersection graphs. Given a fixed bipartite graph with two independent vertex sets V () and W (), the intersection graph derived from B is denoted by . That is, is a graph on the vertex set V with two vertices adjacent if they have a common neighbor in B. For each pair of vertices and , we add the edge to B independently with probability p. The resulting bipartite graph, denoted , can be viewed as the union of B and a bipartite graph , meaning that R is a random graph distributed according to . We write , the intersection graph derived from . Clearly, if the base graph is taken to be the empty bipartite graph, our model reduces to the random intersection graph .
Throughout the paper, the standard Landau asymptotic notations will be utilized (see, e.g., [
10]). Let
be the round-down operator. As customary in the theory of random intersection graphs, we take
for a fixed real
, which allows for a natural progression from sparse to dense graphs. Recall that we say that
possesses a graph property
a.a.s. if the probability that
possesses
tends to 1 as
n goes to infinity.
We are now ready to formulate the main results of this paper.
Theorem 1. Let be a bipartite graph with and such that any two vertices in V are connected by a path and is a constant (i.e., independent of n). For any , let with if and if . Then there exists some constant satisfying a.a.s.
A couple of remarks are in order.
Remark 1. The local effects of the perturbation are quite mild, as a small ε is of interest. Nonetheless, the global influence on the vertex–isoperimetric number can be prominent. To see this, note that any connected (intersection) graph G has . In particular, if G is a tree, we have (see e.g., [36]). Remark 2. It is easy to check that the maximum degree of is Δ. In fact, and are adjacent in if and only if they have a common neighbor , namely, and . Hence, the degree of v is . The assumption that Δ is a constant cannot be removed in general. Indeed, when , consider the bipartite graph with , , and the edge set . It is clear that is a star with center over the vertex set V. There are no more than edges over in the graph , which covers at most vertices. In , there will be an independent set S (meaning that is empty) of order at least:and . Therefore, . When , consider the bipartite graph with the edge set , . Then can be thought of as the joining of a star having center and a complete graph by identifying with any vertex of . After adding edges to B, in , there will be an independent set S of order at least and . Therefore, . Recall that the inequality holds for any graph G. Therefore, a direct corollary of Theorem 1 reads a.a.s. for some . The following theorem shows that this lower bound for edge–isoperimetric number actually holds without any assumption on .
Theorem 2. Let be a bipartite graph with and such that any two vertices in V are connected by a path. For any , let with . Then there exists some constant satisfying a.a.s.
Theorems 1 and 2 hold in the sense of large n limit. In the next section, we shall demonstrate that the isoperimetric numbers can be improved as well for small randomly perturbed intersection graphs based upon real network data.
3. Illustration on Small Networks
To find the exact isoperimetric numbers, one needs to calculate the minimum fraction of neighboring vertices or edges over the nodes inside the subset for all possible subsets of vertices with order at most
. Since this is an NP-hard problem, it is intractable to compute the exact values for general graphs [
21,
35]. It is well known that Cheeger’s inequality, also known as the Alon–Milman inequality, provides bounds for the isoperimetric numbers using graph Laplacian eigenvalues. On the other hand, standard algorithms in linear algebra can be used to efficiently compute the spectrum of a given large graph. Here, instead of evaluating “approximate” values involving other parameters such as eigenvalues, we are interested in obtaining exact values of
and
for small networks.
Two intersection-based social networks are considered here: (i) The Norwegian interlocking directorate network Nor-Boards [
37], where two directors are adjacent if they are sitting on the board of the same company based on the Norwegian Business Register on 5 August 2009. The underlying bipartite graph
contains
directors,
companies, and
edges indicating the affiliation relations; (ii) the co-authorship network ca-CondMat [
5] based on preprints posted to the Condensed Matter Section of arXiv E-Print Archive between 1995 and 1999. The underlying bipartite graph
contains
16,726 authors,
22,016 papers, and
58,596 edges indicating authorship.
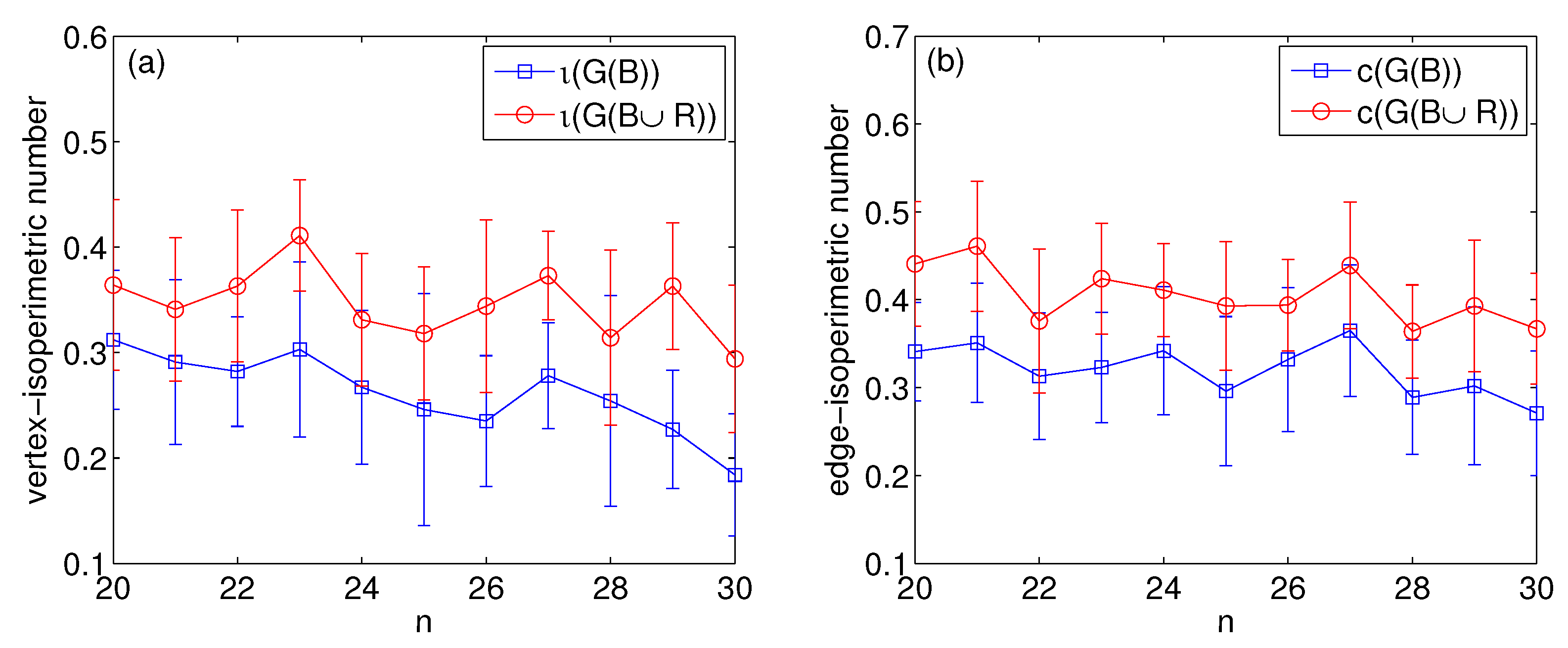
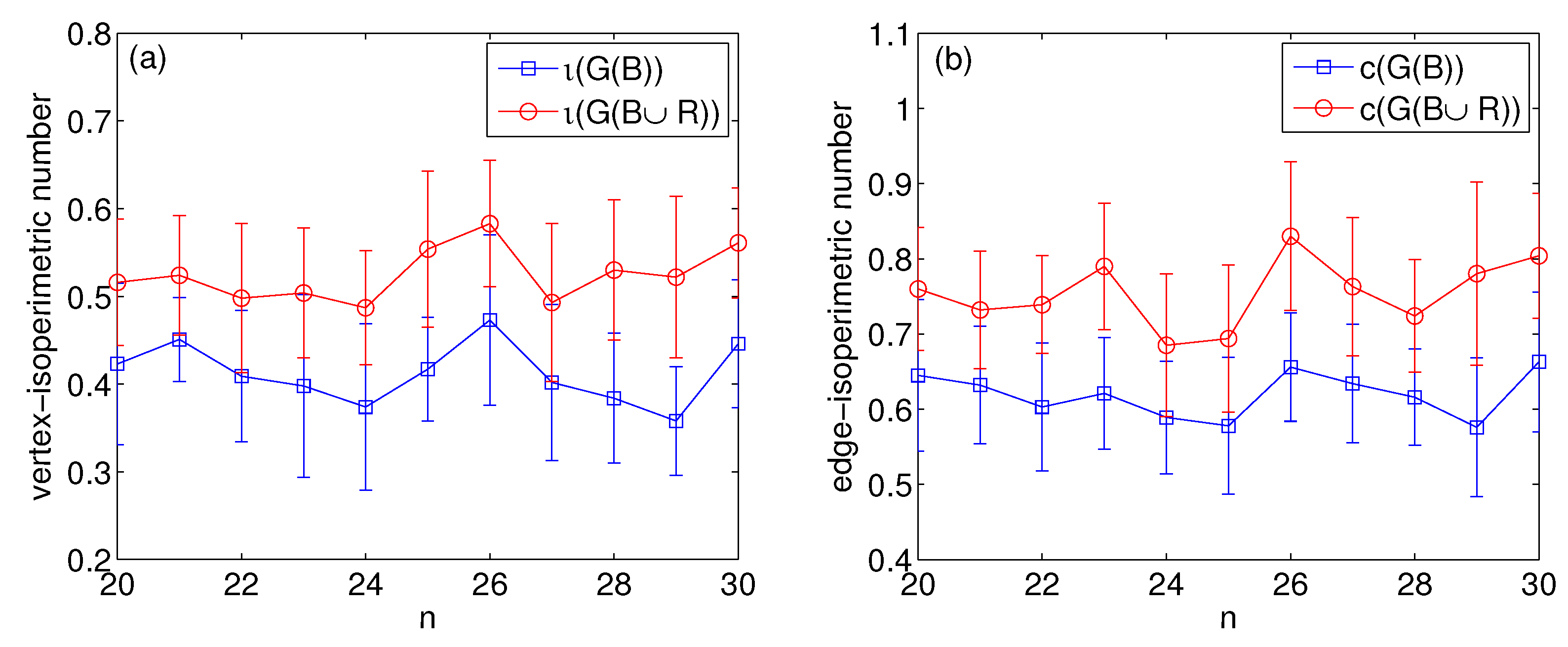
Figure 1 and
Figure 2 report the vertex–isoperimetric numbers and edge–isoperimetric numbers for subsets of Nor-Boards and ca-CondMat, respectively. For a given
, we first take a subgraph
from
with
so that
is connected and calculate its vertex–isoperimetric and edge–isoperimetric numbers. Each data point (blue square) in
Figure 1 and
Figure 2 is obtained by means of an ensemble averaging of 30 independently taken graphs. For each chosen bipartite graph
B, we then perturb it following the rules specified in Theorems 1 and 2 with
to get the perturbed intersection graph
. Each data point (red circle) in
Figure 1 and
Figure 2 is obtained by means of a mixed ensemble averaging of 50 independently-implemented perturbations for 30 graphs. From a statistics viewpoint, it is clear that our random perturbation scheme increases both the vertex–isoperimetric and the edge–isoperimetric number for both cases. This, together with the theoretical results, suggests that the quantitative effect of random perturbations is independent of the order of the network.
Remark 3. It is worth stressing that the theoretical results (Theorems 1 and 2) are in the large limit of the network size n. In other words, the form only makes sense as . The simulation results presented in Figure 1 and Figure 2 are for very small networks. Therefore, these results have no bearing on the dependence (although a slight decline tendency for can be seen in Figure 1a). The main phenomenon we observe from Figure 1 and Figure 2 is that the random perturbation increases both vertex– and edge–isoperimetric numbers for all the cases considered. The numerical results (for small finite graphs) are a nice complement to the theoretical results (for infinite graphs). However, our numerical observations neither prove the dependence would hold for small graphs nor show that such an increase of isoperimetric numbers would be universal in any sense. (A practical issue stems from graph sampling. To establish a proper model fit to the data, Akaike information criteria and Bayesian information criteria need to be applied.) The establishment of correlation between isoperimetric numbers and graph size n for finite intersection graphs is an interesting future work. 4. Proofs
In this section, we prove Theorems 1 and 2. Our idea behind this is somewhat simple: If the network can be carefully decomposed into some subnetworks so that the resulting super-network (with these subnetworks being super-vertices) is sparse and highly connected, then its isoperimetric numbers are expected to be high. Similar approaches have been applied in, e.g., References [
29,
30,
31].
Proof of Theorem 1. Set
for some constant
to be determined. By assumption,
is connected. Following Reference [
38] (Proposition 4.5), we can divide the vertex set
V into disjoint sets
satisfying
and
connected for each
i. Clearly,
. Let
. For a graph
, we say two sets
have common neighbors in
G if there exist
,
, and
such that
and
hold.
We will first show the following property for the random bipartite graph R holds a.a.s.: For every with , there exist at least many of () which have common neighbors with in R.
Indeed, the probability that two sets
and
have no common neighbors in
R can be computed as
. Hence, the probability that there exists a set
with
such that no more than
many of
(
) have common neighbors with
in
R is upper bounded by:
where
counts the choice of
(with
) and the corresponding sets
described above, the estimate
for all
is utilized in the multiplicative probabilities (i.e., there are at least
sets in the union
), and the upper bound comes from a direct application of inequalities ([
10], p. 386). The above probability is further upper bounded by
when
, and is upper bounded by
when
for a sufficiently large
C. Therefore, the above property for the random bipartite graph
R holds a.a.s. In the following, we will condition on such an
R.
Fix a set
with
. Define three sets of indices:
,
, and
. Note that
and
are deterministic, but
is a random set. If
,
a.a.s. by the above assumed property of
R. Similarly, if
, we have
a.a.s., where
. Hence,
a.a.s. Recall that
. We derive that
, and thus,
. Therefore, we have a.a.s.:
By definition, we have
. Thus,
. Since
for
is connected,
. Now we consider two cases. If
, then
. If
, then
a.a.s. Therefore:
Recall the definition of s at the beginning of the proof, and we complete the proof by taking . □
We have made no attempt to optimize the constants in the proof. It is easy to check that the condition that is connected in Theorem 1 can be weakened. For example, the above proof holds if each connected component of is of order at least .
Let be a graph of order n. For integers a, b, and c, define as a collection of all sets such that and there exists a partition , where each is connected, there are no edges in E connecting different , and . The next lemma gives an upper bound of the size of .
Proof of Theorem 2. Consider the family
of sets defined in graph
. Since
is connected, we have for each
,
. Note that
holds. It suffices to show that the following property for the random bipartite graph
R holds a.a.s.: There are constants
such that for any
, we have:
for each
with
. Indeed, when
, we can choose a small
such that
. Thus,
.
It follows from Lemma 1 and
that:
for some constant
, where the first inequality holds since
is increasing on
and the second inequality holds since
is increasing on
.
Note that
and
. For a fixed
S with
, we obtain:
provided
, where the first inequality relies on Reference [
9] (Theorem 2.2) and the last line uses a standard Chernoff’s bound (e.g., [
10]). Hence:
By taking and , the last line above is upper bounded by as . The proof is complete. □