Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction
Abstract
1. Introduction
2. Mathematical Modeling and Formulation
- Oldroyd-B nanofluid when .
- Maxwell nanofluid when .
- Jeffrey nanofluid when .
3. Solution by Homtopy Analysis Method (HAM)
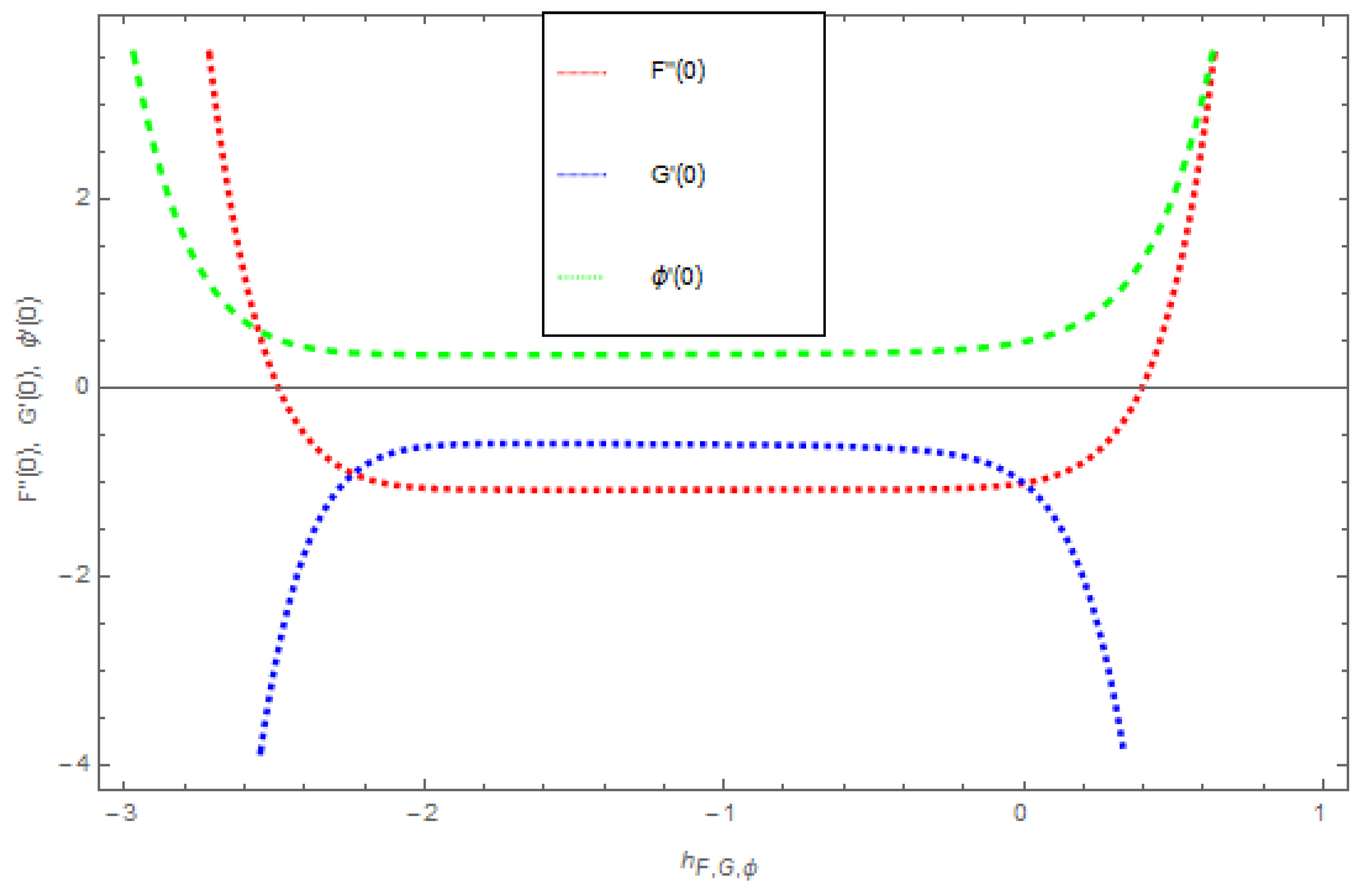
4. HAM Solution Convergences
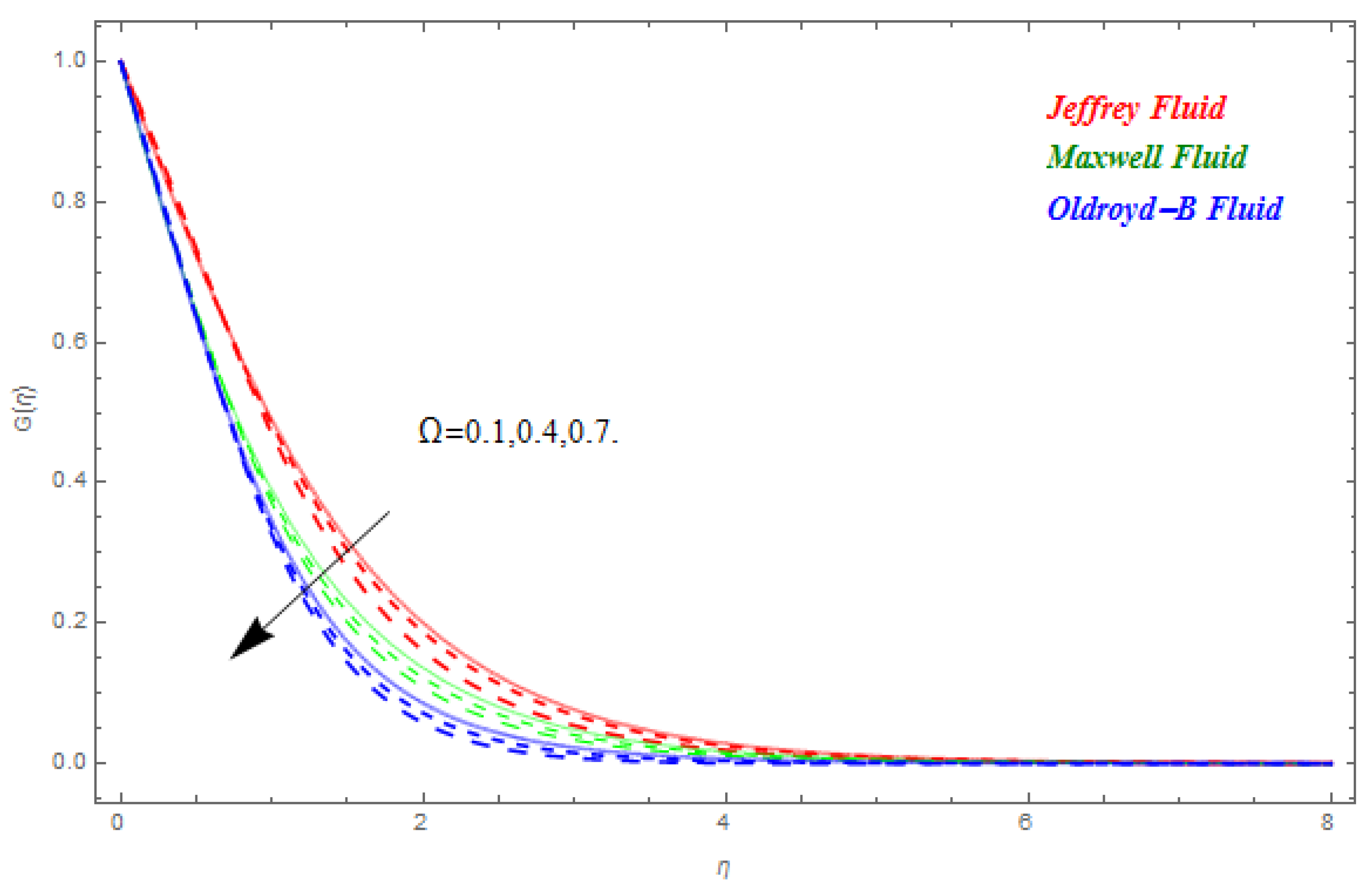
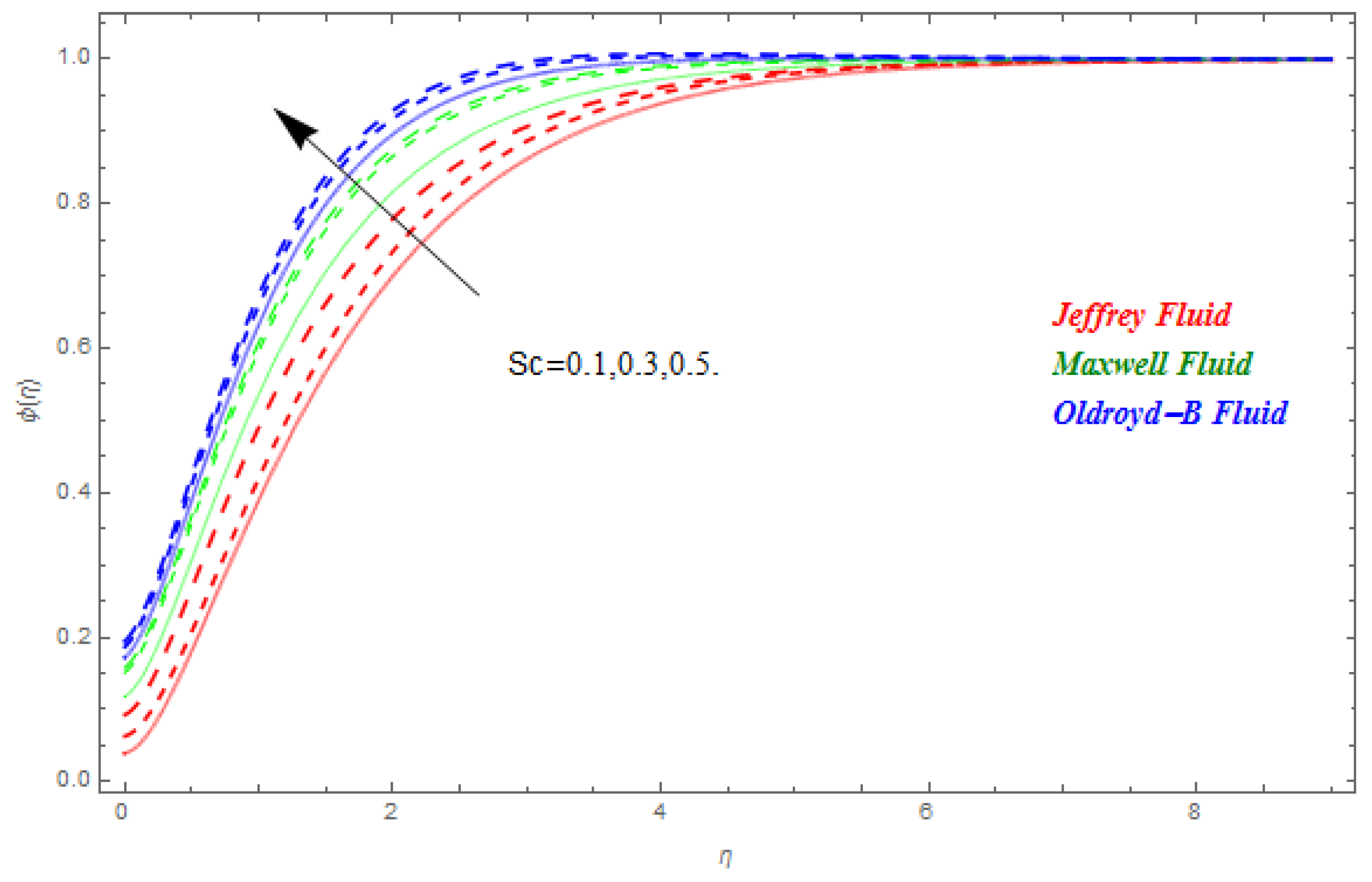
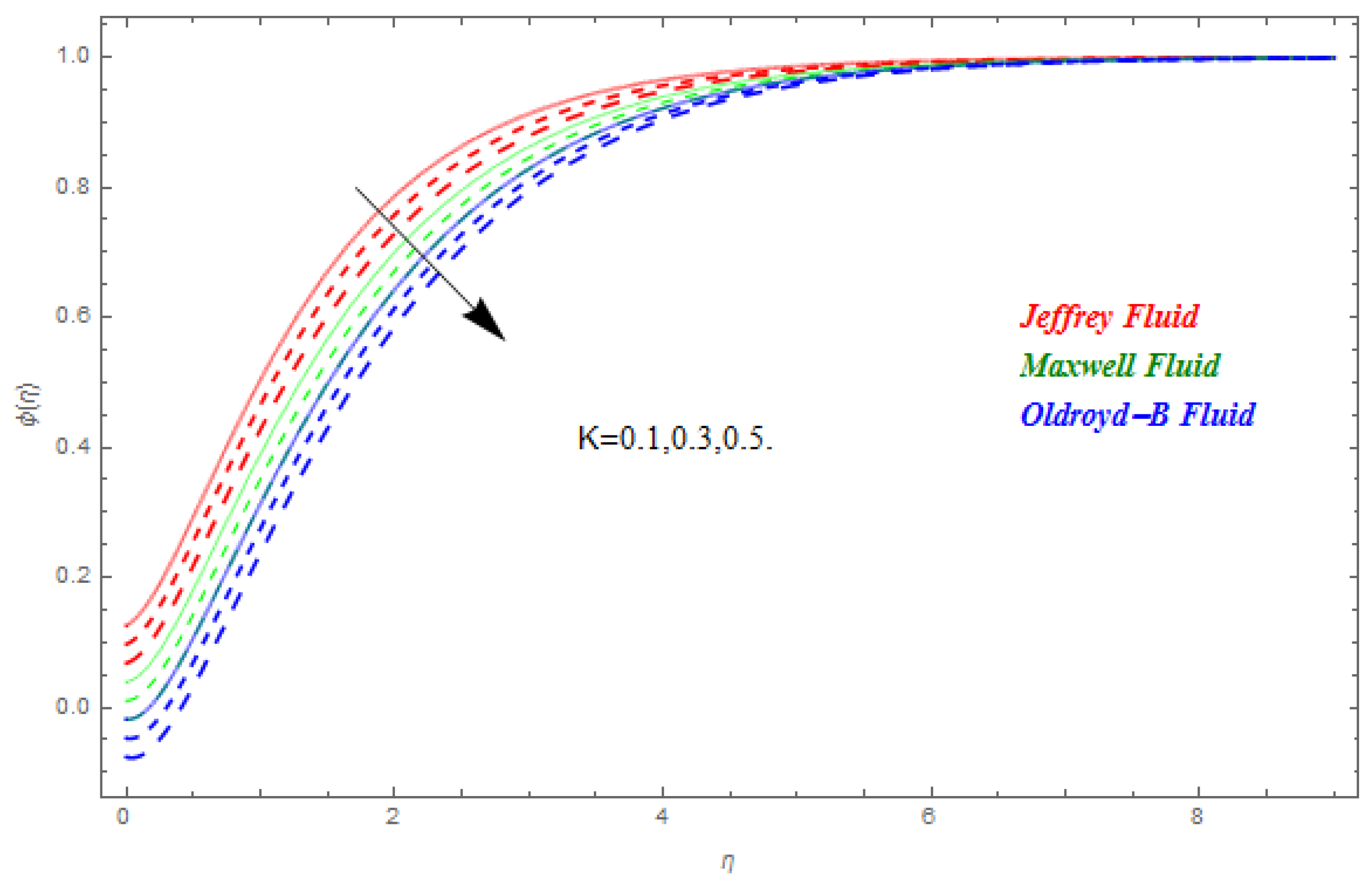
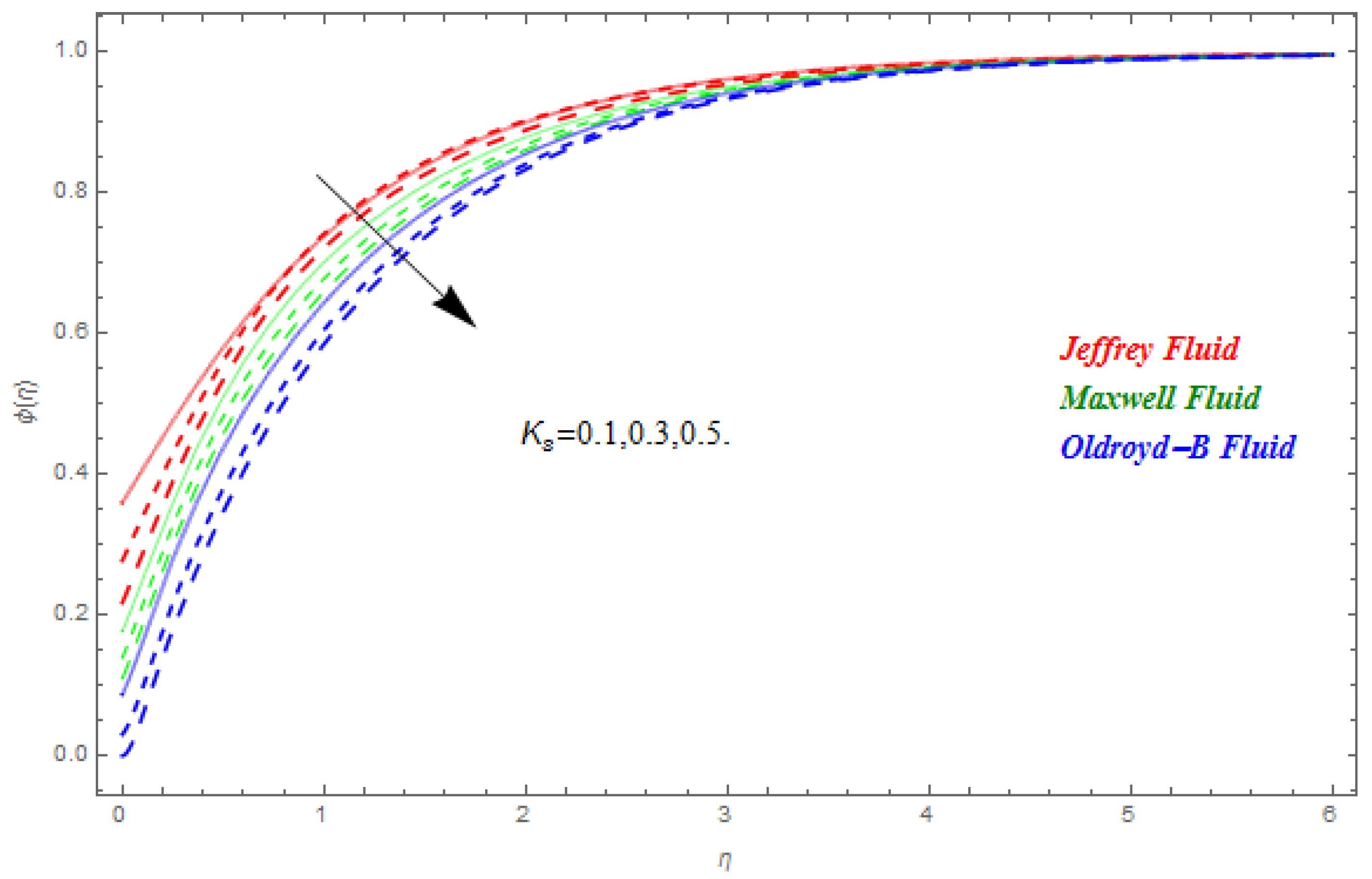
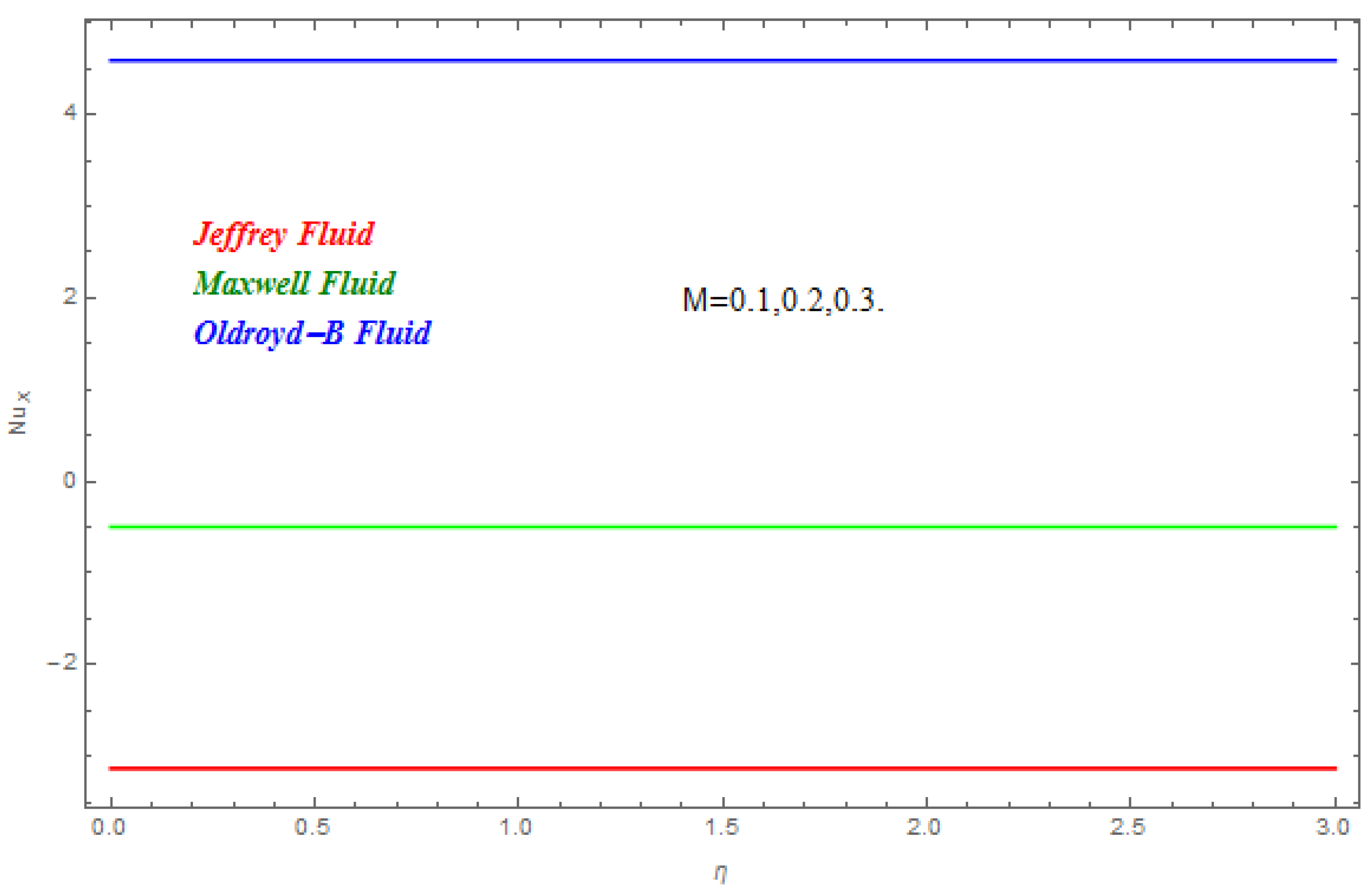
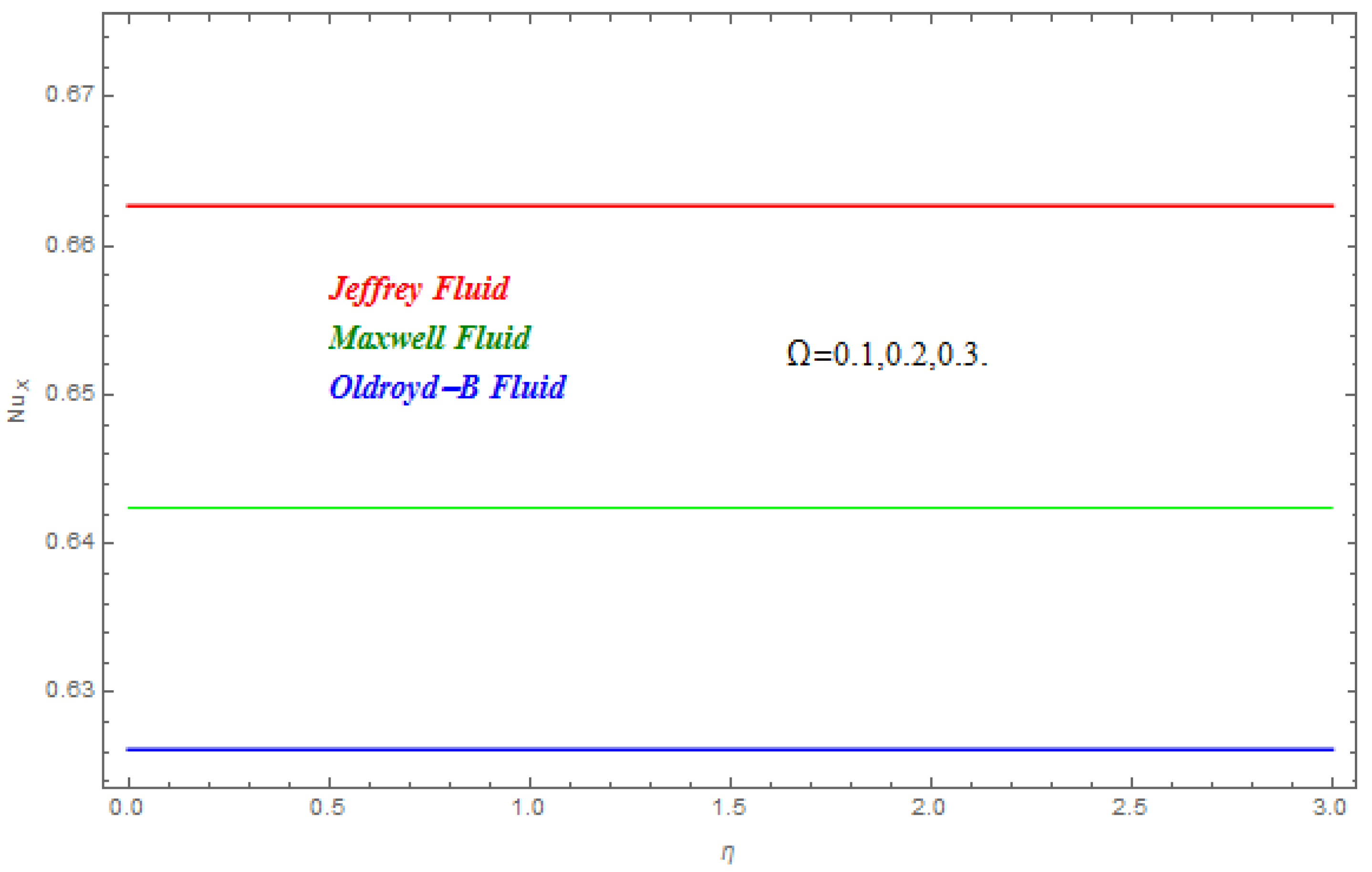
5. Results and Discussion
Tables Discussion
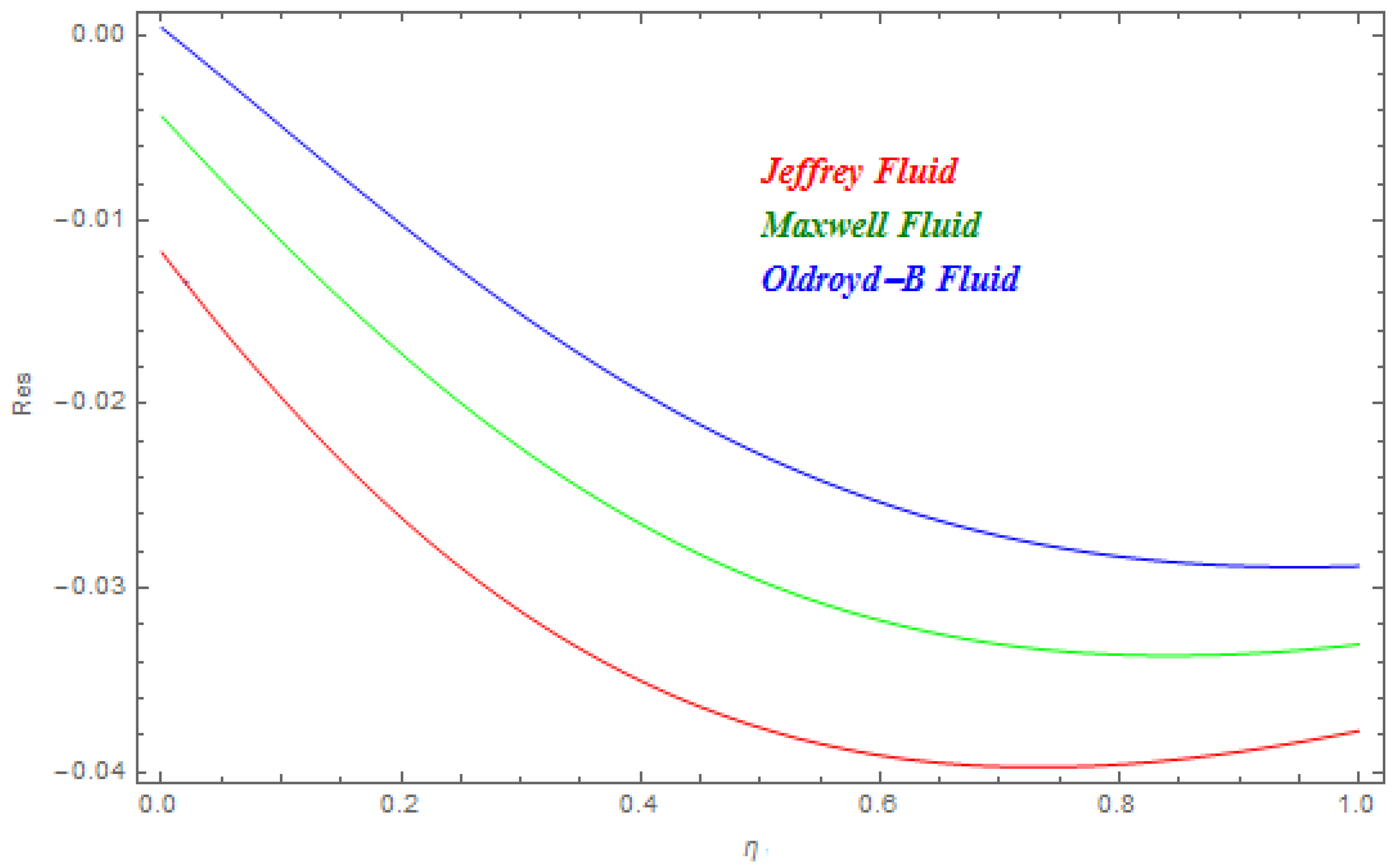
6. Comparison of Analytical Solutions and Numerical Solutions
7. Conclusions
- ➢
- The upsurges in magnetic field diminishes the velocity field.
- ➢
- The upsurges in Prandtl number and thermal relaxation parameters diminish the temperature field.
- ➢
- The upsurges in Schmidt number upsurges the concentration field.
- ➢
- The larger homogeneous reaction and heterogeneous reaction strengths falloff from the concentration field.
Author Contributions
Conflicts of Interest
Nomenclature
| Magnetic field strength (NmA−1) | |
| Skin friction coefficient | |
| , | Diffusion coefficients |
| Velocity profile | |
| Temperature profile | |
| , | Chemical species |
| i, j | Concentration |
| Strength of homogenous reaction | |
| Strength of heterogeneous reaction | |
| Thermal conductivity (Wm−1K−1) | |
| Magnetic parameter | |
| Nusselt number | |
| Prandtl number | |
| Heat flux (Wm−2) | |
| Local Reynolds number | |
| Schmidt number | |
| Sherwood number | |
| Fluid temperature (K) | |
| Surface temperature (K) | |
| Temperature at infinity (K) | |
| , | Velocity components (ms−1) |
| Coordinates | |
| Thermal diffusivity (m2s−1) | |
| Similarity variable | |
| Dynamic viscosity (mPa) | |
| Kinematic viscosity (mPa) | |
| Density (Kgm−3) | |
| Relaxation time | |
| Relaxation to retardation time | |
| Retardation time | |
| Stretching rate | |
| Deborah number | |
| Thermal relaxation parameter | |
| Electrical conductivity (Sm−1) | |
| Dimensional concentration profile |
References
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. Int. Mech. Eng. Congr. Expo. 1995, 66, 99–105. [Google Scholar]
- Fourier, J.B.J. TheÂorie Analytique De La Chaleur; Chez Firmin Didot, père et fils: Paris, France, 1822. [Google Scholar]
- Cattaneo, C. Sulla conduzione delcalore. Atti Semin Mat Fis Univ Modena Reggio Emilia 1948, 3, 83–101. [Google Scholar]
- Christov, C.I. On frame indifferent formulation of the Maxwell-Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Mustafa, M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. 2015, 5, 047109. [Google Scholar] [CrossRef]
- Chen, C.H. Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. J. Non-Newton. Fluid Mech. 2005, 135, 128–135. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafi, A.; Khan, I.; Itili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019, 9, 1196. [Google Scholar] [CrossRef] [PubMed]
- Sheikholeslami, M.; Shah, Z.; Tassaddiq, A.; Shafee, A.; Khan, I. Application of Electric Field for Augmentation of Ferrofluid Heat Transfer in an Enclosure Including Double Moving Walls. IEEE Access 2019, 7, 21048–21056. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.L.; Shafee, A.; Zhixiong, L. Heat transfer behavior of Nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int. J. Heat Mass Transf. 2019, 130, 1322–1342. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gerdroodbary, M.B.; Moradi, R.; Shafee, A.; Zhixiong, L. Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel. Comput. Methods Appl. Mech. Eng. 2019, 344, 1–12. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Numerical study of heat transfer enhancement in a pipe filled with porous media by axisymmetric TLB model based on GPU. Int. J. Heat Mass. Trans. 2014, 70, 1040–1049. [Google Scholar]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Altaf Khan, M. The Elcerical MHD And Hall Current Impact on Micropolar Nanofluid Flow Between Rotating Parallel Plates. Results Phys. 2018. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Gul, T. Impact of thermal radiation on electrical mhd rotating flow of carbon nanotubes over a stretching sheet. AIP Adv. 2019, 9, 015115. [Google Scholar] [CrossRef]
- Shah, Z.; Tassaddiq, A.; Islam, S.; Alklaibi, A.; Khan, I. Cattaneo–Christov Heat Flux Model for Three-Dimensional Rotating Flow of SWCNT and MWCNT Nanofluid with Darcy–Forchheimer Porous Medium Induced by a Linearly Stretchable Surface. Symmetry 2019, 11, 331. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq., M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef] [PubMed]
- Dawar, A.; Shah, Z.; Khan, W.; Islam, S.; Idrees, M. An optimal analysis for Darcy-Forchheimer 3-D Williamson Nanofluid Flow over a stretching surface with convective conditions. Adv. Mech. Eng. 2019, 11, 1–15. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative Heat and Mass Transfer Analysis of Micropolar Nanofluid Flow of Casson Fluid between Two Rotating Parallel Plates with Effects of Hall Current. ASME J. Heat Transf. 2019. [Google Scholar] [CrossRef]
- Maleki, H.; Safaei, M.R.; Alrashed, A.A.A.A.; Kasaeian, A. Flow and heat transfer in non-Newtonian nanofluids over porous surfaces. J. Anal. Calorim. 2019, 135, 1655. [Google Scholar] [CrossRef]
- Nasiri, H.; Abdollahzadeh Jamalabadi, M.Y.; Sadeghi, R.; Safaei, M.R.; Nguyen, T.K.; Shadloo, M.S. A smoothed particle hydrodynamics approach for numerical simulation of nano-fluid flows. J. Anal. Calorim. 2019, 135, 1733. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nasiri, M.; Shadloo, M.S.; Yang, Z. Entropy Generation in a Circular Tube Heat Exchanger Using Nanofluids: Effects of Different Modeling Approaches. Heat Transf. Eng. 2017, 38, 853–866. [Google Scholar] [CrossRef]
- Safaei, M.R.; Shadloo, M.S.; Goodarzi, M.S.; Hadjadj, A.; Goshayeshi, H.R.; Afrand, M.; Kazi, S.N. A survey on experimental and numerical studies of convection heat transfer of nanofluids inside closed conduits. Adv. Mech. Eng. 2016. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Siavashi, M.; Taylor, R.A.; Niazmand, H.; et al. Recent advances in modeling and simulation of nanofluid flows-Part I: Fundamentals and theory. Phys. Rep. 2019, 790, 1–48. [Google Scholar] [CrossRef]
- Mahian, O.; Kolsi, L.; Amani, M.; Estelle, P.; Ahmadi, G.; Kleinstreuer, C.; Marshall, J.S.; Taylor, R.A.; Abu-Nada, E.; Rashidi, S.; et al. Recent advances in modeling and simulation of nanofluid flows-Part II: Applications. Phys. Rep. 2019, 791, 1–59. [Google Scholar] [CrossRef]
- Kartini, A.; Zahir, H.; Anuar, I. Mixed convection Jeffrey fluid flow over an exponentially stretching sheet with magnetohydrodynamic effect. AIP Adv. 2016, 6, 035024. [Google Scholar]
- Kartini, A.; Anuar, I. Magnetohydrodynamic Jeffrey fluid over a stretching vertical surface in a porous medium. Propuls. Power Res. 2017, 6, 269–276. [Google Scholar]
- Hayat, T.; Hussain, T.; Shehzad, S.A.; Alsaedi, A. Flow of Oldroyd-B fluid with nano particles and thermal radiation. Appl. Math. Mech. Engl. Ed. 2015, 36, 69–80. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Gnaneswar, R.M. Effect of nonlinear thermal radiation on 3D Jeffrey fluid flow in the presence of homogeneous–heterogeneous reactions. Int. J. Eng. Res. Afr. 2016, 21, 52–68. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate withcross diffusion. J. Mol. Liq. 2016, 215, 115–126. [Google Scholar] [CrossRef]
- Alla, A.M.A.; Dahab, S.M.A. Magnetic field and rotation effects on peristaltic transport on Jeffrey fluid in an asymmetric channel. J. Mag. Magn. Mater. 2015, 374, 680–689. [Google Scholar] [CrossRef]
- Khan, A.A.; Ellahi, R.; Usman, M. Effects of variable viscosity on the flow of non-Newtonian fluid through a porous medium in an inclined channel with slip conditions. J. Porous Media 2013, 16, 59–67. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Riaz, A.; Sheikholeslami, M. Effects of magnetohydrodynamics on peristaltic flow of Jeffrey fluid in a rectangular duct through a porous medium. J. Porous Media 2014, 17, 143–147. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, N. A mathematical description of peristaltic hydromagnetic flow in a tube. Appl. Math. Comput. 2007, 188, 1491–1502. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. Series solution for the upper convected Maxwell fluid over a porous stretching plate. Phys. Lett. A 2006, 358, 396–403. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N. Heat and mass transfer in 3D non-Newtonian nano and Ferro fluids over a bidirectional stretching surface. Int. J. Eng. Res. Afr. 2016, 21, 33–51. [Google Scholar] [CrossRef]
- Sandeep, N.; Sulochana, C. Dual solutions for unsteady mixed convection flow of MHD micropolar fluid over a stretching/ shrinking sheet with non-uniform heat source/sink. Eng. Sci. Technol. Int. J. 2015, 18, 738–745. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Sandeep, N.; Sulochana, C.; Sugunamma, V.; Jayachandra, B.M. Radiation, inclined magnetic field and cross diffusion effects on flow over a stretching surface. J. Niger. Math. Soc. 2015, 34, 169–180. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Influence of haet and mass transfer on a peristaltic motion of a Jeffrey-six constant fluid in an annulus. Heat Mass Transf. 2010, 46, 485–493. [Google Scholar] [CrossRef]
- Makinde, O.D.; Chinyoka, T.; Rundora, L. Unsteady flow of a reactive variable viscosity non-Newtonian fluid through a porous saturated medium with asymmetric convective boundary conditions. Comput. Math. Appl. 2011, 62, 3343–3352. [Google Scholar] [CrossRef]
- Sheikholeslami, M. KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel. Phys. Lett. A 2014, 378, 3331–3339. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer Flow of Radiative Carbon Nanotubes with Microstructure and Inertial Characteristics in the Rotating Frame. Case Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Chai, L.R.; Shaukat, L.; Wang, H.; Wang, S. A review on heat transfer and hydrodynamic characteristics of nano/microencapsulated phase change slurry (N/MPCS) in mini/microchannel heat sinks. Appl. Therm. Eng. 2018. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C.; Khan, A.Z. Cattaneo-Christov model for Electrical Magnetite Micropoler Casson Ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. Case Stud. Therm. Eng. 2018. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Islam, S.; Idress, M.; Khan, W. Magnetohydrodynamic CNTs Casson Nanofluid and Radiative heat transfer in a Rotating Channels. J. Phys. Res. Appl. 2018, 1, 017–032. [Google Scholar]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Imtiaz, M.; Hayat, T.; Alsaedi, A.; Hobiny, A. Homogeneous-heterogeneous reactions in MHD flow due to an unsteady curved stretching surface. J. Mol. Liq. 2016, 221, 245–253. [Google Scholar] [CrossRef]
- Hayat, T.; Hussain, Z.; Muhammad, T.; Alsaedi, A. Effects of homogeneous and heterogeneous reactions in flow of nanofluids over a nonlinear stretching surface with variable surface thickness. J. Mol. Liq. 2016, 221, 1121–1127. [Google Scholar] [CrossRef]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Khan, S.N. Radiative flow of magneto hydrodynamics single-walled carbon nanotube over a convectively heated stretchable rotating disk with velocity slip effect. Adv. Mech. Eng. 2019, 11, 1–11. [Google Scholar]
- Nasir, S.; Shah, Z.; Islam, S.; Khan, W.; Bonyah, E.; Ayaz, M.; Khan, A. Three dimensional Darcy-Forchheimer radiated flow of single and multiwall carbon nanotubes over a rotating stretchable disk with convective heat generation and absorption. AIP Adv. 2019, 9, 035031. [Google Scholar] [CrossRef]
- Hammed, K.; Haneef, M.; Shah, Z.; Islam, I.; Khan, W.; Asif, S.M. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Ullah, A.; Alzahrani, E.O.; Shah, Z.; Ayaz, M.; Islam, S. Nanofluids Thin Film Flow of Reiner-Philippoff Fluid over an Unstable Stretching Surface with Brownian Motion and Thermophoresis Effects. Coatings 2019, 9, 21. [Google Scholar] [CrossRef]





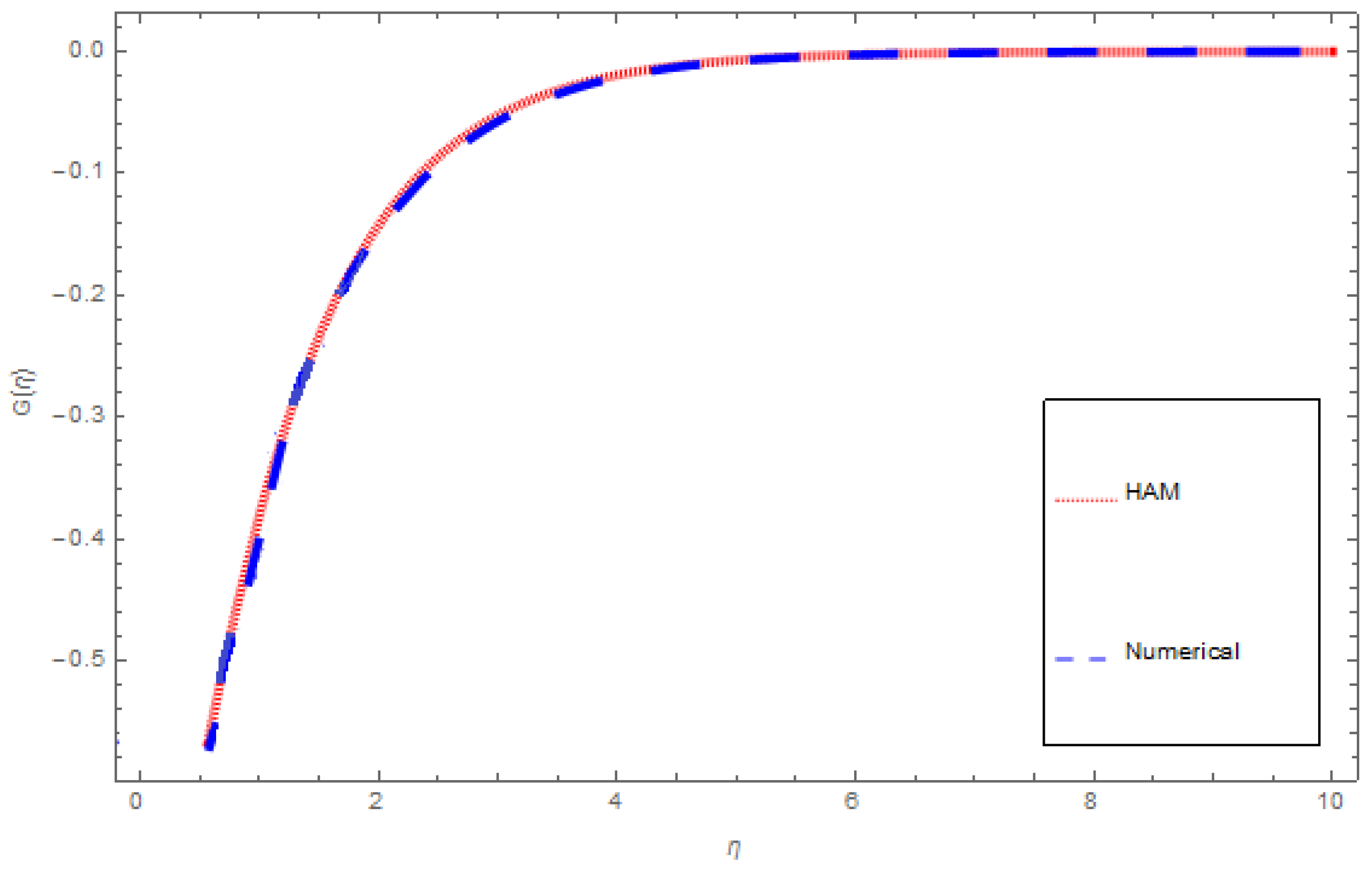
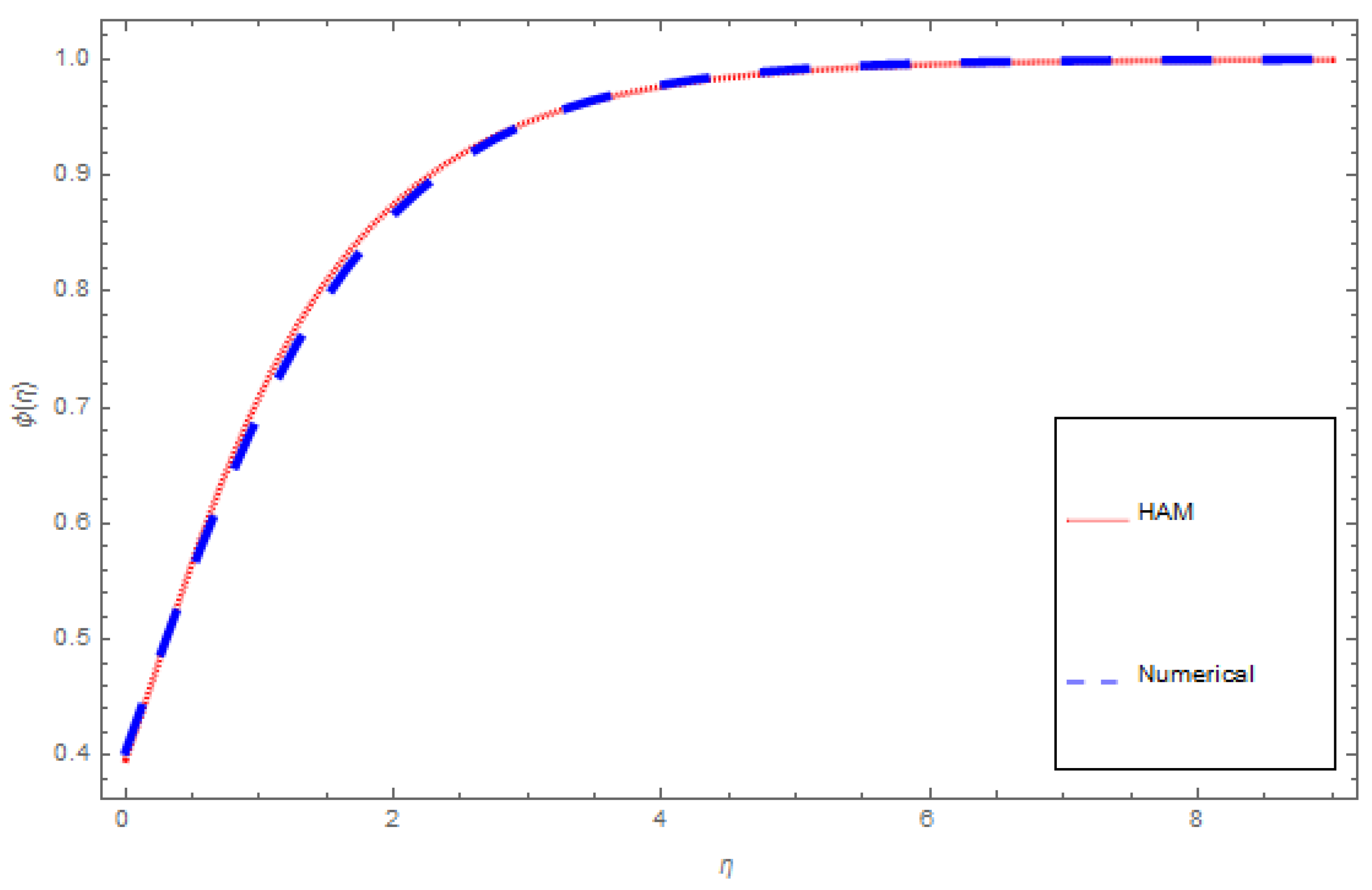
| M | Ref. [47] | Present Results for Jeffrey Nanofluid | Ref. [47] | Present Results for Maxwell Nanofluid | Ref. [47] | Present Results for Oldroyd-B Nanofluid |
|---|---|---|---|---|---|---|
| 1.0 | 1.210458 | 0.210462 | 1.504151 | 1.504153 | 1.071019 | 1.071022 |
| 2.0 | 1.431584 | 1.431587 | 1.804788 | 1.804791 | 1.248081 | 1.248084 |
| Ω | Pr | Ref. [47] | Jeffrey Nanofluid | Ref. [47] | Maxwell Nanofluid | Ref. [47] | Oldroyd-B Nanofluid |
|---|---|---|---|---|---|---|---|
| 1.0 | ---------- | 0.610394 | ---------- | 0.595298 | ---------- | 0.610846 | |
| 1.2 | ---------- | 0.607503 | ---------- | 0.593311 | ---------- | 0.607993 | |
| 6.0 | 0.418081 | 0.513786 | 0.421167 | 0.511247 | 0.426476 | 0.5154367 | |
| 7.0 | 0.439695 | 0.626865 | 0.441919 | 0.548966 | 0.447670 | 0.5477974 |
| Sc | K | Ks | Jeffrey | Maxwell | Oldroyd-B |
|---|---|---|---|---|---|
| 1.2 | −0.096477 | −0.095593 | −0.096771 | ||
| 1.5 | −0.096782 | −0.095890 | −0.097081 | ||
| 1.5 | −0.058030 | −0.047238 | −0.049135 | ||
| 1.7 | −0.056699 | −0.037230 | −0.039262 | ||
| 0.5 | −0.018933 | −0.037233 | 0.012399 | ||
| 0.8 | −0.160028 | 0.046603 | −0.125205 |
| HAM | Numerical | Absolute Error AE | |
|---|---|---|---|
| 0.0 | 3.33067 × 10−16 | 0.000000 | 3.33067 × 10−16 |
| 0.1 | 0.0950433 | 0.093334 | 0.002876 |
| 0.2 | 0.180827 | 0.173972 | 0.009647 |
| 0.3 | 0.258260 | 0.242791 | 0.016488 |
| 0.4 | 0.328165 | 0.300578 | 0.020276 |
| 0.5 | 0.391281 | 0.348033 | 0.019089 |
| 0.6 | 0.448277 | 0.385777 | 0.011828 |
| 0.7 | 0.499753 | 0.414357 | 0.085396 |
| 0.8 | 0.546251 | 0.434262 | 0.111989 |
| 0.9 | 0.588258 | 0.445923 | 0.142335 |
| 1.0 | 0.626213 | 0.449730 | 0.176483 |
| HAM | Numerical | Absolute Error AE | |
|---|---|---|---|
| 0.0 | 1.000000 | 1.00000 | 0.000000 |
| 0.1 | 0.915165 | 0.887477 | 0.002876 |
| 0.2 | 0.835725 | 0.775917 | 0.009647 |
| 0.3 | 0.761845 | 0.666195 | 0.016488 |
| 0.4 | 0.693506 | 0.559077 | 0.020276 |
| 0.5 | 0.630563 | 0.45522 | 0.019089 |
| 0.6 | 0.572791 | 0.355165 | 0.011828 |
| 0.7 | 0.519912 | 0.259342 | 0.250570 |
| 0.8 | 0.471618 | 0.168073 | 0.303545 |
| 0.9 | 0.427594 | 0.0815811 | 0.346013 |
| 1.0 | 0.387518 | 5.60459 × 10−9 | 0.387517 |
| HAM | Numerical | Absolute Error AE | |
|---|---|---|---|
| 0.0 | 0.396762 | 0.404080 | 0.007318 |
| 0.1 | 0.429884 | 0.436425 | 0.006841 |
| 0.2 | 0.464667 | 0.468606 | 0.003939 |
| 0.3 | 0.499830 | 0.500349 | 0.000519 |
| 0.4 | 0.534490 | 0.531418 | 0.003072 |
| 0.5 | 0.568056 | 0.561618 | 0.006438 |
| 0.6 | 0.600146 | 0.590789 | 0.009357 |
| 0.7 | 0.630533 | 0.618810 | 0.011723 |
| 0.8 | 0.659102 | 0.645589 | 0.013513 |
| 0.9 | 0.685811 | 0.671065 | 0.014746 |
| 1.0 | 0.710675 | 0.695202 | 0.015473 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saeed, A.; Islam, S.; Dawar, A.; Shah, Z.; Kumam, P.; Khan, W. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry 2019, 11, 439. https://doi.org/10.3390/sym11030439
Saeed A, Islam S, Dawar A, Shah Z, Kumam P, Khan W. Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry. 2019; 11(3):439. https://doi.org/10.3390/sym11030439
Chicago/Turabian StyleSaeed, Anwar, Saeed Islam, Abdullah Dawar, Zahir Shah, Poom Kumam, and Waris Khan. 2019. "Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction" Symmetry 11, no. 3: 439. https://doi.org/10.3390/sym11030439
APA StyleSaeed, A., Islam, S., Dawar, A., Shah, Z., Kumam, P., & Khan, W. (2019). Influence of Cattaneo–Christov Heat Flux on MHD Jeffrey, Maxwell, and Oldroyd-B Nanofluids with Homogeneous-Heterogeneous Reaction. Symmetry, 11(3), 439. https://doi.org/10.3390/sym11030439







