A New Ranking Methodology for Pythagorean Trapezoidal Uncertain Linguistic Fuzzy Sets Based on Einstein Operations

Abstract

In this article, we proposed new Pythagorean trapezoidal uncertain linguistic fuzzy aggregation information—namely, the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein weighted averaging (PTULFEWA) operator, the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein ordered weighted averaging (PTULFEOWA) operator, and the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein hybrid weighted averaging (PTULFEHWA) operator—using the Einstein operational laws. We studied some important properties of the suggested aggregation operators and showed that the PTULFEHWA is more general than the other proposed operators, which simplifies these aggregation operators. Furthermore, we presented a multiple attribute group decision making (MADM) process for the proposed aggregation operators under the Pythagorean trapezoidal uncertain linguistic fuzzy (PTULF) environment. A numerical example was constructed to determine the effectiveness and practicality of the proposed approach. Lastly, a comparative analysis was performed of the presented approach with existing approaches to show that the proposed method is consistent and provides more information that may be useful for complex problems in the decision-making process.

1. Introduction

The communication of the decision-making process is a very complex problem when we are receiving information about attributes. One the most powerful theories is that of the multi attribute decision making (MADM), which handles problems that extensively impact the human real-life problems. The basic methodology is that a decision maker is presented with his evaluation in a set of many attributes and alternatives to find the best ranking order alternative in MADM approaches. Zadeh [1] introduced a fuzzy set with the generalization of a classical set to solve ambiguous and vague information. Fuzzy set is used in many practical situations and has grown as an independent theory that interests researchers in many fields. After the success, fuzzy set was generalized to intuitionistic fuzzy set (IFS) by Atanassov [2] under the restriction that the membership and non-membership function sum was less than or equal to one. In [2] proposed a different mathematical operation under the IFS environment and studied the important properties. Uncertainty in human real problems is one of the continuous research areas and produces many new theories. Fuzzy decision-making (FDM) problems and their extension are presented in different ways to solve real life problems and have more attractive research to obtain the best results. Many decision making (DM) techniques have been proposed to explain the multi attribute decision-making process. Ramon et al. [3] presented the 2-tuple model and customer segmentation and their algorithms, k-means, which are more effective methods in the calculation of frequency and monetary exploitation.

Revanasiddappa and Harish [4] presented a new feature selection technique based on intuitionistic fuzzy entropy (IFE) for text classification. Firstly, intuitionistic fuzzy C-means (IFCM) clustering technique is employed to compute the intuitionistic membership values. The computed intuitionistic membership values are then used to estimate intuitionistic fuzzy entropy via match degree. Additionally, features with lower entropy values are selected to categorize the text documents. Juan Antonio Morente-Molinera et al. [5] focused on solving the problem by carrying out multi-criteria group decision making approaches using different new methods. Concretely, fuzzy ontologies reasoning procedures are used in order to reduce, at the very least, the experts needed to participate in the preference providing step. In this new advanced technique, the logic of alternative comparison relies on the ontology reasoning process, allowing experts to focus on how important the criteria are to them. Albadan et al. [6] proposed the procedures of selection of personnel delimited only to the making of non-programmed decisions through the implementation of game mechanics. In order to model this selection, the purpose of the following study is to carry out the formulation of inference rules based on fuzzy logic in order to capture the tacit transfer of certain types of information in personnel selection processes and to determine the aspects that allow the shaping of aspirants. In [7], the author defined generalized operation for intuitionistic fuzzy numbers.

Morente-Molinera proposed the technique of fuzzy ontologies in order to allow the experts to focus on determining the importance that should be given to different criteria. Thus, they deal directly with a high number of alternatives. Experts decide the importance of each criterion, and the alternatives ranking is calculated automatically using the fuzzy ontology. Liang et al. [8] presented the partial estimations, which determined that the introduced estimator is more capable and trusted to evaluate, consequently improving the overall results. There are many methodologies that evaluate the overall information that converges in different suppositions. If an ordinary collection of information is not considered in this environment, there is other information that can be considered by linguistic variables (LV) related to FNs, which are related to the membership function to one and the non-membership function to zero—more precisely, “good” and “bad”. Wang et al. [9] proposed ILS, and their MADM approach of using the IL aggregation information achieved some great consideration. Liu et al. [10] presented a new power aggregation operator, while Su et al. [11] generalized the concept to ordered weighted averaging (OWA) and intuitionistic linguistic ordered weighted averaging (ILOWA) operator. Xiao et al. [12] studied the ILOWA operator and applied it in the financial DM process. Liu and Jin [13] extended the intuitionistic uncertain linguistic values (IULVs) by using LV in intuitionistic linguistic variables (ILV) and studying their important properties. We observed that LVs are special facets of IULVs, which are more general and have more information. Liu et al. [14] presented and extended the linguistic (LF) aggregation operators. Yager [15] introduced a new Pythagorean fuzzy (PFS) set that is a generalization of IFS by membership and non-membership functions under the condition that the square sum of these functions is less than or equal to one. To motivate this idea, Yager [16] explained this shortcoming with an example—a decision maker makes a decision in the form of MD as $\left(\frac{\sqrt{3}}{2}\right)$, a N-MD is $\frac{1}{2}$. Under IFS, the value does not satisfy the condition of a sum greater than 1, while in PFS, it satisfies the condition that the square sum is less than or equal to 1. After the successful implementation, Peng and Yang [17] presented the different aggregation operators, namely, the Pythagorean fuzzy weighted averaging (PFWA), the Pythagorean fuzzy weighted power averaging (PFWPA), and the Pythagorean fuzzy weighted power geometric (PFWPG) operator. Garg [18] introduced a new generalized Pythagorean fuzzy aggregation operator using Einstein operational laws and used them in the decision- making process.

Shakeel et al. [19] presented some aggregation operators to use the decision information represented by PTFNS, including the Pythagorean trapezoidal fuzzy weighted averaging (PTFWA) operator, the Pythagorean trapezoidal fuzzy ordered weighted averaging (PTFOWA) operator, and the Pythagorean trapezoidal fuzzy hybrid averaging (PTFHA) operator. Shakeel et al. [20] extended the work of aggregation operators into the interval-valued Pythagorean trapezoidal fuzzy weighted averaging (IVPTFWA) operator, the ordered weighted (IVPTFOWA), and the hybrid averaging (IVPTFHA) operators. Shakeel et al. [20] used Einstein operational laws and proposed a new concept of the Pythagorean trapezoidal fuzzy Einstein ordered weighted geometric (I-IVPTFEOWG) operator, the induced interval-valued Pythagorean trapezoidal fuzzy Einstein hybrid geometric (I-IVPTFEHG) operator, and their applications in decision making problems. Shakeel et al. [21] further extended the work to interval-valued Pythagorean trapezoidal fuzzy aggregation operators, the interval-valued Pythagorean trapezoidal fuzzy Einstein weighted geometric, (IVPTFEWG) operator, the interval-valued Pythagorean trapezoidal fuzzy Einstein ordered weighted geometric (IVPTFEOWG) operator, the interval-valued Pythagorean trapezoidal fuzzy Einstein hybrid geometric (IVPTFEHG), and their applications in decision making. The detail literature survey of aggregation operators and their applications in decision making problems discussed in [22,23,24,25,26,27,28,29,30,31,32].

In this paper, we introduce a new aggregation operator using Einstein operations under trapezoidal uncertain linguistic fuzzy sets and their applications in decision making. The motivations for the study are listed below.

(1)

Our anticipated aggregation information is more general and precise compared to the existing information.

(2)

The objectives of the study include proposing a PTULF Einstein aggregation operator and its operational laws, score, and accuracy function, establishing the MADM program approach based on the PTULF Einstein aggregation operators, and providing illustrative examples of the MADM program.

(3)

The comparative analysis is a strong testament to the new approach, as it shows that the proposed study is consistent.

To solve a MADM process, the weight of the attributes plays an important role in making decisions under the aggregation approaches.

The rest of the paper is arranged is follows. Section 2 consists of the background materials. Section 3 presents a new PTULF aggregation operator under Einstein operations, the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein weighted averaging (PTULFEWA) operator, the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein ordered weighted averaging (PTULFEOWA), and the Pythagorean trapezoidal uncertain linguistic fuzzy Einstein hybrid averaging (PTULFEHA) operator. Section 4 describes the MADM technique under the PTFL environment. In Section 5, a numerical example is given to demonstrate the importance of the methodologies. Section 6 shows a comparative study of the proposed and existing approaches. The conclusion is given in Section 7.

2. Preliminaries

Definition 1.

[10]. Let $[s_{\theta \left(p\right)},s_{t\left(p\right)}]\in \overline{s}$, and $P$ is a given domain as follows:

$$U=\{[s_{\theta \left(p\right)},s_{t\left(p\right)}],({\mathrm{\Psi }}_u(p),{\mathsf{\Upsilon }}_u(p))]:p\in P\},$$

(1)

is called an intuitionistic uncertain linguistic set (IULS), where $s_{\theta \left(p\right)},s_{t\left(p\right)}\in \overline{s}$. Where ${\mathrm{\Psi }}_u(p)$ and ${\mathsf{\Upsilon }}_u(p)$ represent the MD and N-MD, respectively, with the condition $0\le {\mathrm{\Psi }}_u(p)+{\mathsf{\Upsilon }}_u(p)\le 1,$ $\forall p\in P$. The MD and N-MD of the element $p$ to the ULV $[s_{\theta \left(p\right)},s_{t\left(p\right)}].$ For each $ILS,$ $U$ in $p,$ if ${\pi }_U(p)=1-{\mathrm{\Psi }}_U(p)-{\mathsf{\Upsilon }}_U(p),$ for all $p\in P,$ then ${\pi }_u(p)$ is called the degree of indeterminacy degree of $p$ to the ULV $[s_{\theta \left(p\right)},s_{t\left(p\right)}].$ It is obvious that $0\le {\pi }_u(p)\le 1,$ $\forall p\in P.$

Definition 2.

[10]. Let $U=\{[s_{\theta \left(p\right)},s_{t\left(p\right)}],({\mathrm{\Psi }}_u(p),{\mathsf{\Upsilon }}_u(p))]\}:p\in P\},$ be (IULS), the quaternion $⟨[s_{\theta \left(p\right)},s_{t\left(p\right)}],({\gamma }_u(p),{\mathsf{\varsigma }}_u(p))]⟩$ is called an $IULV,$ and $U$ can also be viewed as a collection of the $IULV$. Thus, it can also be expressed as follows:

$$U=\{[s_{\theta \left(p\right)},s_{t\left(p\right)}],({\mathrm{\Psi }}_u(p),{\mathsf{\Upsilon }}_u(p))]\}:p\in P\}.$$

(2)

Definition 3.

[24] Let ${\tilde{\alpha }}_1=(\left[p_1,q_1,r_1,s_1\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_1},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}),$ and ${\tilde{\alpha }}_2=(\left[p_2,q_2,r_2,s_2\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_2},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})$ be two ITF numbers and $\delta \ge 0.$ Then,

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left(\begin{array}{c}\left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ ({\mathrm{\Psi }}_{{\tilde{\alpha }}_1})+({\mathrm{\Psi }}_{{\tilde{\alpha }}_2})-({\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}),{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}\end{array}\right)$

(2) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2=\left(\begin{array}{c}\left[p_1{p}_2,q_1{q}_2,r_1{r}_2,s_1{s}_2\right];\\ {\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2},({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})+({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})-({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})\end{array}\right)$

(3) 

$\delta \tilde{\alpha }=(\left[\delta p,\delta q,\delta r,\delta s\right];1-{\left(1-{\mathrm{\Psi }}_{\tilde{\alpha }}\right)}^{\delta };{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^{\delta })$

(4) 

${\tilde{\alpha }}^{\delta }=(\left[p^{\delta },q^{\delta },r^{\delta },s^{\delta }\right];{\mathrm{\Psi }}_{\tilde{\alpha }}^{\delta },1-{\left(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}\right)}^{\delta }).$

Example 1.

Let $=\left(\left[0.2,0.3,0.4,0.5\right];\left(0.5,0.3\right)\right)$ ${\alpha }_1=\left(\left[0.1,0.3,0.3,0.2\right];\left(0.3,0.6\right)\right)$, ${\alpha }_2=\left(\left[0.8,0.2,0.6,0.1\right];\left(0.4,0.2\right)\right)$ be any three ITFNs, and $\delta =0.2.$ Then, we verify the above results such that,

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left(\begin{array}{c}[0.9,0.5,0.9,0.3];\\ (0.3)+(0.4)-\left(0.3\right)\left(0.4\right),\left(0.6\right)\left(0.2\right)\end{array}\right)=\left([0.9,0.5,0.9,0.3];0.58,0.12\right).$

(2) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2=\left(\begin{array}{c}[0.08,0.06,0.18,0.02];\\ \left(0.3\right)\left(0.4\right),\left(0.6\right)+\left(0.2\right)-\left(0.6\right)\left(0.2\right)\end{array}\right)=([0.08,0.06,0.18,0.02];(0.12,0.68).$

(3) 

$\delta \tilde{\alpha }=\left(\begin{array}{c}[0.2(0.2),0.2(0.3),0.2(0.4),0.2(0.5)];\\ 1-{\left(1-0.5\right)}^{0.2},{\left(0.3\right)}^{0.2}\end{array}\right)=[0.04,0.06,0.08,0.1];(0.25,0.78).$

(4) 

${\tilde{\alpha }}^{\delta }=\left(\begin{array}{c}[{(0.2)}^{0.2},{(0.3)}^{0.2},{(0.4)}^{0.2},{(0.5)}^{0.2}];\\ {\left(0.5\right)}^{0.2},1-{\left(1-0.3\right)}^{0.2}\end{array}\right)=\left(\begin{array}{c}[(0.72),(0.78),(0.83),(0.87)];\\ \left(0.87\right),0.06\end{array}\right).$

Definition 4.

[15]. Let $L$ be a fixed set. The $PFS,$ $U$ in $L$ is an object having the form;

$$A=\left\{⟨l,{\mathrm{\Psi }}_U(l),{\mathsf{\Upsilon }}_U(l)⟩\right|l\in L\}$$

(3)

Definition 5.

[16]. Let $\tilde{\alpha }=\left({\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}\right),$ ${\tilde{\alpha }}_1=\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_1},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}\right)$ and ${\tilde{\alpha }}_2=\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_2},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}\right)$ be three $PFNs$ and $\delta >0.$ Then,

(1) 

${\tilde{\alpha }}^c=\left({\mathsf{\Upsilon }}_{\tilde{\alpha }},{\mathrm{\Psi }}_{\tilde{\alpha }}\right)$

(2) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left(\sqrt{{({\mathrm{\Psi }}_{{\tilde{\alpha }}_1})}^2+{({\mathrm{\Psi }}_{{\tilde{\alpha }}_2})}^2-({\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}\right)$

(3) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2=\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2},\sqrt{{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})}^2+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})}^2-({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}\right)$

(4) 

$\delta \tilde{\alpha }=\sqrt{1-{\left(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^{\delta }};{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^{\delta })$

(5) 

${\tilde{\alpha }}^{\delta }=({\mathrm{\Psi }}_{\tilde{\alpha }}^{\delta },\sqrt{1-{\left(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^{\delta }}).$

Example 2.

Let $\tilde{\alpha }=(0.8,0.3),$ ${\tilde{\alpha }}_1=(0.5,0.6)$, ${\tilde{\alpha }}_2=(0.4,0.7)$ be any three PFNs, and $\delta =0.3.$ Then, we verify the above results such that,

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left(\begin{array}{c}\sqrt{{(0.5)}^2+{(0.4)}^2-({0.5}^2)({0.4}^2)},\\ \left(0.6\right)\left(0.7\right)\end{array}\right)=\left(\sqrt{0.37},0.42\right)=(0.85,0.17).$

(2) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2=\left(\begin{array}{c}\left(0.5\right)\left(0.4\right),\\ \sqrt{{(0.6)}^2+{(0.7)}^2-{(0.6)}^2({0.7}^2)}\end{array}\right)=\left(\left(0.5\right)\left(0.4\right),\sqrt{0.6736}\right)=(0.20,0.82).$

(3) 

$\delta \tilde{\alpha }=(\sqrt{1-{\left(1-{0.8}^2\right)}^{0.3}};{(0.3)}^{0.3})=(0.50,0.69).$

(4) 

${\tilde{\alpha }}^{\delta }=({(0.8)}^{0.3},\sqrt{1-{\left(1-{0.3}^2\right)}^{0.3}})=(0.93,0.16).$

Definition 6.

[19] Let $\tilde{\alpha }=(\left[p,q,r,s\right];[{\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}])$ be a PTFN, the score function $s$ is;

$$s(\tilde{\alpha })=\left(\frac{p+q+r+s}{4}\cdot \left({\mathrm{\Psi }}_{\tilde{\alpha }}^2-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)\right)s(\tilde{\alpha })\in [-1,1].$$

(4)

Example 3.

Let ${\tilde{p}}_1=\left\{\left[0.4,0.3,0.5,0.6\right];\left(0.6,0.5\right)\right\}$, ${\tilde{p}}_2=\left\{\left[0.1,0.4,0.3,0.2\right];\left(0.7,0.4\right)\right\}$ and ${\tilde{p}}_3=\left\{\left[0.2,0.1,0.6,0.5\right];\left(0.8,0.5\right)\right\}$ be PTFNs, a score new example function $S$ of PTFNs can be represented as follows:

$$\begin{array}{l}S({\tilde{p}}_1)=\frac{0.4+0.3+0.5+0.6}{4}({0.6}^2-{0.5}^2)=0.0495,\\ S({\tilde{p}}_2)=\frac{0.1+0.4+0.3+0.2}{4}({0.7}^2-{0.4}^2)=0.060,\\ S({\tilde{p}}_3)=\frac{0.2+0.1+0.6+0.5}{4}({0.8}^2-{0.5}^2)=0.1365.\end{array}$$

Definition 7.

[19]. Let $\tilde{\alpha }=(\left[p,q,r,s\right];[\mathrm{\Psi },\mathsf{\Upsilon }])$ be PTFN, an accuracy function $h$ is:

$$h(\tilde{\alpha })=\left(\frac{p+q+r+s}{4}\cdot \left({\mathrm{\Psi }}_{\tilde{\alpha }}^2+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)\right)h(\tilde{\alpha })\in [0,1].$$

(5)

Example 4.

Let ${\tilde{p}}_1=\left\{\left[0.4,0.3,0.5,0.6\right];\left(0.6,0.5\right)\right\}$, ${\tilde{p}}_2=\left\{\left[0.1,0.4,0.3,0.2\right];\left(0.7,0.4\right)\right\}$ and ${\tilde{p}}_3=\left\{\left[0.2,0.1,0.6,0.5\right];\left(0.8,0.5\right)\right\}$ be PTFNs, an accuracy new example function $h$ of PTFNs can be represented as follows:

$$\begin{array}{l}h({\tilde{p}}_1)=\frac{0.4+0.3+0.5+0.6}{4}({0.6}^2+{0.5}^2)=0.2745,\\ S({\tilde{p}}_2)=\frac{0.1+0.4+0.3+0.2}{4}({0.7}^2+{0.4}^2)=0.1625,\\ S({\tilde{p}}_3)=\frac{0.2+0.1+0.6+0.5}{4}({0.8}^2+{0.5}^2)=0.3115.\end{array}$$

Einstein Operations with Pythagorean Trapezoidal Fuzzy Numbers

The main Einstein operational laws are defined as follows:

$$a{\otimes }_{\epsilon }b=\frac{a.b}{\sqrt{1+\left(1-a^2\right)\cdot \left(1-b^2\right)}},a{\otimes }_{\epsilon }b=\frac{\sqrt{\left(a^2+b^2\right)}}{\sqrt{\left(1+a^2\cdot b^2\right)}},\mathrm{for}\mathrm{all}\left(a,b\right)\in {\left[0,1\right]}^2$$

(6)

Definition 8.

[20]. Let $\tilde{\alpha }=\left\{\begin{array}{c}\left[p,q,r,s\right];\\ ({\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }})\end{array}\right\}$, ${\tilde{\alpha }}_1=\left\{\begin{array}{c}\left[p_1,q_1,r_1,s_1\right];\\ ({\mathrm{\Psi }}_{{\tilde{\alpha }}_1},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})\end{array}\right\}$ and ${\tilde{\alpha }}_2=\left\{\begin{array}{c}\left[p_2,q_2,r_2,s_2\right];\\ ({\mathrm{\Psi }}_{{\tilde{\alpha }}_2},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})\end{array}\right\}$ be any three $PTF$, numbers and $\delta \ge 0.$ Then,

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left\{\begin{array}{l}\left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \sqrt{{({\mathrm{\Psi }}_{{\tilde{\alpha }}_1})}^2+{({\mathrm{\Psi }}_{{\tilde{\alpha }}_2})}^2-{({\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2})}^2},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}\end{array}\right\}$

(2) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2=\left\{\begin{array}{c}\left[p_1{p}_2,q_1{q}_2,r_1{r}_2,s_1{s}_2\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2},\\ \sqrt{{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})}^2+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})}^2-{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})}^2}\end{array}\right\}$

(3) 

$\delta \tilde{\alpha }=\left\{(\left[\delta p,\delta q,\delta r,\delta s\right];\sqrt{1-{\left(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^{\delta }};{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^{\delta })\right\}$

(4) 

${\tilde{\alpha }}^{\delta }=\left\{(\left[p^{\delta },q^{\delta },r^{\delta },s^{\delta }\right];{\mathrm{\Psi }}_{\tilde{\alpha }}^{\delta },\sqrt{1-{\left(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^{\delta }})\right\}.$

Example 5.

Let $\tilde{\alpha }=\left\{\begin{array}{c}\left(s_2,s_3\right)\\ \left[0.3,0.4,0.5,0.6\right]\\ \left(0.7,0.4\right)\end{array}\right\},{\tilde{\alpha }}_1=\left\{\begin{array}{c}\left(s_3,s_6\right)\\ \left[0.3,0.4,0.5,0.6\right]\\ \left(0.8,0.5\right)\end{array}\right\}$ and ${\tilde{\alpha }}_2=\left\{\begin{array}{c}\left(s_4,s_3\right)\\ \left[0.5,0.3,0.4,0.4\right]\\ \left(0.8,0.3\right)\end{array}\right\}$ be any three $PTULFNS$ and $\delta =0.4.$ Then, we verify the results as follows:

(1) 

$\begin{array}{cc}\hfill {\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2& =\left(\begin{array}{c}[0.3+0.5,0.4+0.3,0.5+0.4,0.6+0.4];\\ \sqrt{{(0.8)}^2+{(0.8)}^2-{(0.8)}^2{(0.8)}^2},(0.5)(0.3)\end{array}\right)=\left(\begin{array}{c}[0.8,0.7,0.9,0.6+1.0];\\ \sqrt{(0.64)+(0.64)-(0.64)(0.64},(0.5)(0.3)\end{array}\right)\hfill \\ & =\left([0.8,0.7,0.9,0.6+1.0];\left(0.93,0.15\right)\right)\hfill \end{array}$

(2) 

$\begin{array}{cc}\hfill {\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2& =\left(\begin{array}{c}[\left(0.8\right)\left(0.5\right),\left(0.4\right)\left(0.3\right),\left(0.5\right)\left(0.4\right),\left(0.6\right)\left(0.4\right);\\ \left(0.8\right)\left(0.8\right),\sqrt{{0.5}^2+{0.3}^2-({\left(0.5\right)}^2{(0.3)}^2},\end{array}\right)=\left(\begin{array}{c}[0.4,0.12,0.20,0.24];\\ (0.64),\sqrt{0.25+0.09-0.0225},\end{array}\right)\hfill \\ & =\left([0.4,0.12,0.20,0.24;(0.64,0.5634\right)\hfill \end{array}$

(3) 

$\begin{array}{cc}\hfill \delta \tilde{\alpha }& =\left(\begin{array}{c}\left[\left(0.4\right)\left(0.3\right),\left(0.4\right)\left(0.4\right),\left(0.4\right)\left(0.5\right),\left(0.4\right)\left(0.6\right)\right];\\ \left[\sqrt{1-{\left(1-{0.7}^2\right)}^{0.4}},{(0.4)}^{0.4}\right],\end{array}\right)=\left(\begin{array}{c}\left[0.12,0.16,0.20,0.16\right];\\ \sqrt{1-{\left(1-{0.7}^2\right)}^{0.4}},{(0.4)}^{0.4},\end{array}\right)\hfill \\ & =\left(\begin{array}{c}\left[0.12,0.16,0.20,0.16\right];\\ \left(0.4859,0.6901\right)\end{array}\right)\hfill \end{array}$

(4) 

$\begin{array}{cc}\hfill {\tilde{\alpha }}^{\delta }& =\left(\begin{array}{c}\left[{0.3}^{0.4},{0.4}^{0.4},{0.5}^{0.4},{0.6}^{0.4}\right];,\\ \left[{0.4}^{0.4},\sqrt{1-{\left(1-{0.7}^2\right)}^{0.4}}\right]\end{array}\right)=\left(\begin{array}{c}\left[0.61,0.69,0.75,0.85\right];,\\ \left[{0.4}^{0.4},\sqrt{1-{\left(1-{0.7}^2\right)}^{0.4}}\right]\end{array}\right)\hfill \\ & =\left(\left[0.61,0.69,0.75,0.85\right];,(0.69,0.48)\right).\hfill \end{array}$

Definition 9.

Consider $\tilde{\alpha }=\left\{\begin{array}{c}\left(s_{\theta \left(p\right)},s_{t\left(p\right)}\right)\\ \left[p,q,r,s\right]\\ \left({\mathsf{\Psi }}_{\alpha },{\mathsf{{\rm Y}}}_{\alpha }\right)\end{array}\right\},{\tilde{\alpha }}_1=\left\{\begin{array}{c}\left(s_{\theta \left(p\right)},s_{t\left(p\right)}\right)\\ \left[p_1,q_1,r_1,s_1\right]\\ \left({\mathsf{\Psi }}_{{\alpha }_1},{\mathsf{{\rm Y}}}_{{\alpha }_1}\right)\end{array}\right\}$ and ${\tilde{\alpha }}_2=\left\{\begin{array}{c}\left(s_{\theta \left(p_2\right)},s_{t\left(p_2\right)}\right)\\ \left[p_2,q_2,r_2,s_2\right]\\ \left({\mathsf{\Psi }}_{{\alpha }_2},{\mathsf{{\rm Y}}}_{{\alpha }_2}\right)\end{array}\right\}$ be a PTULNs and $\delta \ge 0.$ Then

(1) 

${\tilde{\alpha }}_1{\oplus }_{\epsilon }{\tilde{\alpha }}_2=\left\{\begin{array}{c}(s_{\theta \left(p_1\right)}+s_{\theta \left(p_2\right)},s_{t\left(p_1\right)}+s_{t\left(p_2\right)}),\\ \left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \frac{\sqrt{{({\mathrm{\Psi }}_{{\tilde{\alpha }}_1})}^2+{({\mathrm{\Psi }}_{{\tilde{\alpha }}_2})}^2}}{\sqrt{1+{({\mathrm{\Psi }}_{{\tilde{\alpha }}_1})}^2{({\mathrm{\Psi }}_{{\tilde{\alpha }}_2})}^2}},\frac{{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}}{\sqrt{1+(1-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)(1-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}}\end{array}\right\}$

(2) 

${\tilde{\alpha }}_1{\otimes }_{\epsilon }{\tilde{\alpha }}_2=\left\{\begin{array}{c}(s_{\theta \left(p_1\right)}{s}_{\theta \left(p_2\right)},s_{t\left(p_1\right)}{s}_{t\left(p_2\right)}),\\ \left[p_1{p}_2,q_1{q}_2,r_1{r}_2,s_1{s}_2\right];\\ \frac{{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}}{\sqrt{1+(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}},\frac{\sqrt{{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})}^2+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})}^2}}{\sqrt{1+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1})}^2{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2})}^2}},\end{array}\right\}$

(3) 

${\delta }_{\stackrel{.}{\epsilon }}\tilde{\alpha }=\left\{\begin{array}{c}(s_{\delta \theta \left(p\right)},s_{\delta t\left(p\right)})\left[\delta p,\delta q,\delta r,\delta s\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{\delta }-{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{\delta }}}{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{\delta }+{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{\delta }}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }+{({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }}},\end{array}\right\}$

(4) 

${\tilde{\alpha }}^{{\wedge }_{\epsilon }\delta }=\left\{\begin{array}{c}(s_{\theta {\left(p\right)}^{\delta }},s_{t{\left(p\right)}^{\delta }}),\left[p^{\delta },q^{\delta },r^{\delta },s^{\delta }\right];\\ \frac{\sqrt{2{\left({\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathrm{\Psi }}_{\tilde{\alpha }})}^{\delta }+{({\mathrm{\Psi }}_{\tilde{\alpha }})}^{\delta }}},\frac{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }-{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }}}{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }+{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{\delta }}}\end{array}\right\}.$

Example 6.

Let $\tilde{\alpha }=\left\{\begin{array}{c}\left(s_2,s_3\right)\\ \left[0.3,0.4,0.5,0.6\right]\\ \left(0.7,0.4\right)\end{array}\right\},{\tilde{\alpha }}_1=\left\{\begin{array}{c}\left(s_1,s_2\right)\\ \left[0.3,0.4,0.5,0.6\right]\\ \left(0.8,0.5\right)\end{array}\right\}$ and ${\tilde{\alpha }}_2=\left\{\begin{array}{c}\left(s_3,s_3\right)\\ \left[0.5,0.3,0.4,0.4\right]\\ \left(0.8,0.3\right)\end{array}\right\}$ be any three PTULFNs and $\delta =0.4.$ Then, we verify the above laws as follows:

(1) 

$\begin{array}{cc}{\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2& =\left\{\begin{array}{c}(s_1+s_3,s_2+s_2)\\ [0.3+0.5,0.4+0.3,0.5+0.4,0.6+0.4];\\ \frac{\sqrt{{0.8}^2+{0.8}^2}}{\sqrt{1+{(0.8)}^2{(0.8)}^2}},\frac{(0.5)(0.3)}{\sqrt{1+(1-{0.5}^2)(1-{0.3}^2)}}\end{array}\right\}=\left\{\begin{array}{c}(s_4,s_4)\\ [0.8,0.7,0.9,0.6+1.0];\\ \frac{\sqrt{{0.8}^2+{0.8}^2}}{\sqrt{1+{(0.8)}^2{(0.8)}^2}},\frac{(0.5)(0.3)}{\sqrt{1+(1-{0.5}^2)(1-{0.3}^2)}}\end{array}\right\}\hfill \\ & =\left\{\begin{array}{c}(s_4,s_4)\\ [0.8,0.7,0.9,0.6+1.0];(\frac{1.1313}{1.5099},\frac{0.15}{1.2884})\end{array}\right\}=\left\{(s_4,s_4)[0.8,0.7,0.9,0.6+1.0];\left(0.7492,0.1164\right)\right\}\hfill \end{array}$

(2) 

$\begin{array}{cc}\hfill {\tilde{\alpha }}_1{\otimes }_{\epsilon }{\tilde{\alpha }}_2& =\left\{\begin{array}{c}(s_1{s}_3,s_2{s}_2)\\ [(0.3)(0.5),(0.4)(0.3),\\ (0.5)(0.4),(0.6)(0.4)];\\ \frac{(0.8)(0.8)}{\sqrt{1+(1-{0.8}^2)(1-{0.8}^2)}},\frac{\sqrt{{0.5}^2+{0.3}^2}}{\sqrt{1+{(0.5)}^2{(0.3)}^2}}\end{array}\right\}=\left\{\begin{array}{c}(s_3,s_4)\\ [0.15,0.12,0.20),0.24];\frac{(0.64)}{\sqrt{1.1296}},\frac{\sqrt{0.34}}{\sqrt{1.0225}}\end{array}\right\}\hfill \\ & =\left\{\begin{array}{c}(s_3,s_4)\\ [0.15,0.12,0.20),0.24];\frac{0.64}{1.0628},\frac{0.5830}{1.0111}\end{array}\right\}=\left\{\begin{array}{c}(s_3,s_4)\\ [0.15,0.12,0.20),0.24];\\ (0.6021,0.5765)\end{array}\right\}\hfill \end{array}$

(3) 

$\begin{array}{cc}\hfill {\delta }_{\stackrel{.}{\epsilon }}\tilde{\alpha }& =\left\{\begin{array}{c}(s_{0.4(2)},s_{0.4(3)})\left[\begin{array}{c}0.4(0.3),0.4(0.4),\\ 0.4(0.5),0.4(0.6)\end{array}\right];\\ \frac{\sqrt{{(1+{0.7}^2)}^{0.4}-{(1-{0.7}^2)}^{0.4}}}{\sqrt{{(1+{0.7}^2)}^{0.4}+{(1-{0.7}^2)}^{0.4}}},\frac{\sqrt{2{\left({0.4}^2\right)}^{0.4}}}{\sqrt{{(2-{0.4}^2)}^{0.4}+{({0.4}^2)}^{0.4}}},\end{array}\right\}=\left\{\begin{array}{c}(s_{0.8},s_{0.9})\left[0.12,0.16,0.20,0.24\right];\\ \frac{\sqrt{1.1729-0.76}0}{\sqrt{1.1729+0.76}0},\frac{\sqrt{0.9600}}{\sqrt{(1.2762+(0.9609)}},\end{array}\right\}\hfill \\ & =\left\{\begin{array}{c}(s_{0.8},s_{0.9})\left[0.12,0.16,0.20,0.24\right];\\ \frac{0.6425}{0.9658},\frac{0.9797}{1.4973},\end{array}\right\}=\left\{(s_{0.8},s_{0.9})\left[\begin{array}{c}0.12,0.16,\\ 0.20,0.24\end{array}\right];0.6652,0.6543,\right\}\hfill \end{array}$

(4) 

$\begin{array}{cc}\hfill {\tilde{\alpha }}^{{\wedge }_{\epsilon }\delta }& =\left\{\begin{array}{c}(s_{2^{0.4}},s_{3^{0.4}}),\left[{0.3}^{0.4},{0.4}^{0.4},{0.5}^{0.4},{0.6}^{0.4}\right];\\ \frac{\sqrt{2{\left({0.7}^2\right)}^{0.4}}}{\sqrt{{(2-0.7)}^{0.4}+{(0.7)}^{0.4}}},\frac{\sqrt{{(1+{0.4}^2)}^{0.4}-{(1-{0.4}^2)}^{0.4}}}{\sqrt{{(1+{0.4}^2)}^{0.4}+{(1-{0.4}^2)}^{0.4}}}\end{array}\right\}=\left\{\begin{array}{c}(s_{1.13},s_{1.55}),\left[0.61,0.69,0.75,0.81\right];\\ \frac{\sqrt{1.50}}{\sqrt{(1.17+(0.67)}},\frac{\sqrt{1.0611-0.9326}}{\sqrt{1.0611+0.9326}}\end{array}\right\}\hfill \\ & =\left\{\begin{array}{c}(s_{1.13},s_{1.55}),\left[0.61,0.69,0.75,0.81\right];\\ \frac{1.2247}{1.3564},\frac{0.3589}{1.4119}\end{array}\right\}=\left\{\begin{array}{c}(s_{1.13},s_{1.55}),\left[\begin{array}{c}0.61,0.69,\\ 0.75,0.81\end{array}\right];\\ 0.9029,0.2548\end{array}\right\}\hfill \end{array}$

Definition 10.

Consider $\tilde{\alpha }=(s_{\theta \left(p\right)},s_{t(p)}),\left[p,q,r,s\right];[{\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}])$ be PTULFNs, a score function $s$ is;

$$s(\tilde{\alpha })=\left\{\begin{array}{c}\frac{(s_{\theta \left(p\right)},s_{t(p)}),[p+q+r+s]}{8}\\ \left({\mathrm{\Psi }}_{\tilde{\alpha }}^2-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)\end{array}\right\}s(\tilde{\alpha })\in [-1,1].$$

(7)

Definition 11.

Suppose $\tilde{\alpha }=(s_{\theta \left(p\right)},s_{t(p)}),\left[p,q,r,s\right];[{\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}])$ be PTULNs, an accuracy function $h$ is;

$$h(\tilde{\alpha })=\left\{\begin{array}{c}\frac{(s_{\theta \left(p\right)},s_{t(p)}),[p+q+r+s]}{8}\\ \left({\mathrm{\Psi }}_{\tilde{\alpha }}^2+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)\end{array}\right\}s(\tilde{\alpha })\in [-1,1].$$

(8)

Theorem 1.

Let ${\tilde{\alpha }}_1,{\tilde{\alpha }}_2$ and $\tilde{\alpha }$ be three Pythagorean trapezoidal uncertain linguistic fuzzy Einstein fuzzy (PTULFENs) and $n,m\in R^{+}$,

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2$

(2) 

${\tilde{\alpha }}_1\otimes {\tilde{\alpha }}_2$

(3) 

${\delta }_{\stackrel{.}{\epsilon }}\tilde{\alpha }$

(4) 

${\tilde{\alpha }}^{{\wedge }_{\epsilon }\delta }$are also PTULFENs.

Proof. 

(1), (2) Easy to proof.

(3). Let $n$ be a positive integer and $\tilde{\alpha }$ is PTULFE. Then,

$$n_{\stackrel{.}{\epsilon }}\tilde{\alpha }=\stackrel{n}{\overbrace{\tilde{\alpha }{\oplus }_{\epsilon }\tilde{\alpha }{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }\tilde{\alpha }}}.$$

(9)

To prove the above theorem, we use mathematical induction. First, Equation $\left(9\right)$ holds for $n=2.$

Since

$$\begin{array}{cc}\hfill \tilde{\alpha }+\tilde{\alpha }& =\left(\begin{array}{c}(s_{{\theta }_{\left(p\right)}}+s_{{\theta }_{\left(p\right)}},s_{t_{\left(p\right)}}+s_{t_{\left(p\right)}}),\\ \left[p+p,q+q,r+r,s+s\right];\\ \frac{\sqrt{{({\mathrm{\Psi }}_{\tilde{\alpha }})}^2+{({\mathrm{\Psi }}_{\tilde{\alpha }})}^2}}{\sqrt{1+{({\mathrm{\Psi }}_{\tilde{\alpha }})}^2{({\mathrm{\Psi }}_{\tilde{\alpha }})}^2}},\frac{{\mathsf{\Upsilon }}_{\tilde{\alpha }}{\mathsf{\Upsilon }}_{\tilde{\alpha }}}{\sqrt{1+(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}(2s_{{\theta }_{\left(p\right)}},2s_{t_{\left(p\right)}}),\left[2p,2q,2r,2s\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^2-{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^2}}{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^2+{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^2}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^2}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2+{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2}}\end{array}\right)=2_{\stackrel{.}{\epsilon }}\tilde{\alpha }.\hfill \end{array}$$

Therefore, Equation (9) holds for $n=2$. If Equation (9) holds for $n=k.$ Then, $n_{\stackrel{.}{\epsilon }}\tilde{\alpha }=\stackrel{n}{\overbrace{\tilde{\alpha }{\oplus }_{\epsilon }\tilde{\alpha }{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }\tilde{\alpha }}.}$ When $n=k+1,$ we have

$$\begin{array}{cc}\hfill \stackrel{n+1}{\overbrace{\tilde{\alpha }{\oplus }_{\epsilon }\tilde{\alpha }{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }\tilde{\alpha }}}& =\stackrel{n}{\overbrace{\tilde{\alpha }{\oplus }_{\epsilon }\tilde{\alpha }{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }\tilde{\alpha }}{\oplus }_{\epsilon }\tilde{\alpha }=}{n}_{\stackrel{.}{\epsilon }}\tilde{\alpha }{\oplus }_{\epsilon }\tilde{\alpha }\hfill \\ & =\left(\begin{array}{c}n{s}_{{\theta }_{\left(p\right)}},n{s}_{t_{\left(p\right)}}\left[np,nq,nr,ns\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^n-{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^n}}{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^n+{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^n}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^n}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^n+{({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^n}}\end{array}\right)\hfill \\ & {\oplus }_{\epsilon }\left(s_{{\theta }_{\left(p\right)}},s_{t_{\left(p\right)}}),\left[p,q,r,s\right];{\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}\right),\hfill \\ & =\left(\begin{array}{c}(n+1)s_{{\theta }_{\left(p\right)}},(n+1)s_{t_{\left(p\right)}}),\\ \left[(n+1)p,(n+1)q,(n+1)r,(n+1)s\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{n+1}-{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{n+1}}}{\sqrt{{(1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{n+1}+{(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{n+1}}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2\right)}^{n+1}}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{n+1}+{({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{n+1}}}\end{array}\right),\hfill \\ & ={\left(n+1\right)}_{\stackrel{.}{\epsilon }}\tilde{\alpha }.\hfill \end{array}$$

Hence Equation (9) holds for $n=k+1$, therefore Equation (9) holds for all $n$.

(4). Let $m$ be any positive integer and $\tilde{\alpha }$ is Pythagorean trapezoidal fuzzy number. Then,

$${\tilde{\alpha }}^{{\wedge }_{\epsilon }m}=\stackrel{m}{\overbrace{\tilde{\alpha }{\otimes }_{\epsilon }\tilde{\alpha }{\otimes }_{\epsilon }\dots {\otimes }_{\epsilon }\tilde{\alpha }}.}$$

First, we show that Equation (9) holds for $m=2.$ Since

$$\begin{array}{cc}\hfill \tilde{\alpha }{\otimes }_{\epsilon }\tilde{\alpha }& =\left(\begin{array}{c}(s_{{\theta }_{\left(p\right)}}.s_{{\theta }_{\left(p\right)}},s_{t_{\left(p\right)}}.s_{t_{\left(p\right)}}),\left[p.p,q.q,r.r,s.s\right];\\ \frac{{\mathrm{\Psi }}_{\tilde{\alpha }}{\mathrm{\Psi }}_{\tilde{\alpha }}}{\sqrt{1+(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)(1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}}\frac{\sqrt{{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2+{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2}}{\sqrt{1+{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2{({\mathsf{\Upsilon }}_{\tilde{\alpha }})}^2}}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}(s_{{\theta }_{\left(p\right)}^2},s_{t_{\left(p\right)}^2}),\left[p^2,q^2,r^2,s^2\right];\\ \frac{\sqrt{2{\left({\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^2}}{\sqrt{{(2-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^2+{({\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^2}}\frac{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^2-{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^2}}{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^2+{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^2}}\end{array}\right)={\tilde{\alpha }}^{{\wedge }_{\epsilon }2}.\hfill \end{array}$$

Therefore, Equation (9) holds for $m=2.$ If Equation (9) holds for $m=k,$ such that

$${\tilde{\alpha }}_1^{{\wedge }_{\epsilon }m}=\stackrel{m}{\overbrace{{\tilde{\alpha }}_1{\otimes }_{\epsilon }{\tilde{\alpha }}_1{\otimes }_{\epsilon }\dots {\otimes }_{\epsilon }{\tilde{\alpha }}_1}}.$$

Then, we have

$$\begin{array}{cc}\hfill \stackrel{m+1}{\overbrace{\tilde{\alpha }{\otimes }_{\epsilon }\tilde{\alpha }{\otimes }_{\epsilon }\dots {\otimes }_{\epsilon }\tilde{\alpha }}}& =\stackrel{m}{\overbrace{\tilde{\alpha }{\otimes }_{\epsilon }\tilde{\alpha }{\otimes }_{\epsilon }\dots {\otimes }_{\epsilon }\tilde{\alpha }}{\otimes }_{\epsilon }\tilde{\alpha }=}{\tilde{\alpha }}^{{\wedge }_{\epsilon }m}{\otimes }_{\epsilon }\tilde{\alpha }\hfill \\ & =\left(\begin{array}{c}(s_{{\theta }_{\left(p\right)}^m},s_{t_{\left(p\right)}^m}),\left[p^m,q^m,r^m,s^m\right];\\ \frac{\sqrt{2{\left({\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^m}}{\sqrt{{(2-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^m+{({\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^m}}\frac{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^m-{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^m}}{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^m+{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^m}},\end{array}\right)\hfill \\ & {\otimes }_{\epsilon }\left(s_{{\theta }_{\left(p\right)}},s_{t_{\left(p\right)}}),\left[p,q,r,s\right];{\mathrm{\Psi }}_{\tilde{\alpha }},{\mathsf{\Upsilon }}_{\tilde{\alpha }}\right)\hfill \\ & =\left(\begin{array}{c}(s_{{\theta }_{\left(p\right)}^{m+1}},s_{t_{\left(p\right)}^{m+1}})\left[p^{(m+1)},q^{(m+1)},r^{(m+1)},s^{(m+1)}\right];\\ \frac{\sqrt{2{\left({\mathrm{\Psi }}_{\tilde{\alpha }}^2\right)}^{m+1}}}{\sqrt{{(2-{\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{m+1}+{({\mathrm{\Psi }}_{\tilde{\alpha }}^2)}^{m+1}}}.\frac{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{m+1}-{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{m+1}}}{\sqrt{{(1+{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{m+1}+{(1-{\mathsf{\Upsilon }}_{\tilde{\alpha }}^2)}^{m+1}}}\end{array}\right)={\tilde{\alpha }}_1^{{\wedge }_{\epsilon }m+1}.\hfill \end{array}$$

□

Hence Equation (9) holds for $m=k+1$. Therefore, Equation (9) holds for all $m$. The Einstein operational laws of PTF numbers satisfy the following properties:

Theorem 2.

${\tilde{\alpha }}_1=\left\{\begin{array}{c}(s_{{\theta }_{\left(p_1\right)}},s_{t_{\left(p_1\right)}}),\\ \left[p_1,q_1,r_1,s_1\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_1},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}\end{array}\right\}$ and ${\tilde{\alpha }}_2=\left\{\begin{array}{c}(s_{{\theta }_{\left(p_2\right)}},s_{t_{\left(p_2\right)}}),\\ \left[p_2,q_2,r_2,s_2\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_2},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}\end{array}\right\}$ be any two PTULFNs. Then, the operational laws between ${\tilde{\alpha }}_1$ and ${\tilde{\alpha }}_2$ are shown as follows:

(1) 

${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2={\tilde{\alpha }}_2\oplus \tilde{\alpha }$;

(2) 

$\delta \left({\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2\right)=\delta {\tilde{\alpha }}_1\oplus \delta {\tilde{\alpha }}_2$$\delta \ge 0;$

(3) 

${\delta }_1{\tilde{\alpha }}_1\oplus {\delta }_2{\tilde{\alpha }}_1=\left({\delta }_1+{\delta }_2\right){\tilde{\alpha }}_1$${\delta }_1,{\delta }_2\ge 0.$

Proof. 

(1) Result is obvious.

(2) By Einstein operational laws (1) in Definition 9 we have

$${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left\{\begin{array}{l}(s_{{\theta }_{\left(p_1\right)}}+s_{{\theta }_{\left(p_1\right)}},s_{t_{\left(p_1\right)}}+s_{t_{\left(p_2\right)}}),\left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \frac{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)-(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}}{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)+(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}},\frac{\sqrt{2\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}{\sqrt{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)+\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}\end{array}\right\},$$

$${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left\{\begin{array}{l}(s_{{\theta }_{\left(p_1\right)}}+s_{{\theta }_{\left(p_1\right)}},s_{t_{\left(p_1\right)}}+s_{t_{\left(p_2\right)}}),\left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \frac{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)-(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}}{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)+(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}},\frac{\sqrt{2\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}{\sqrt{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)+\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}\end{array}\right\}.$$

We can write the above equation into the following form:

$${\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2=\left[\begin{array}{l}(s_{{\theta }_{\left(p_1\right)}}+s_{{\theta }_{\left(p_1\right)}},s_{t_{\left(p_1\right)}}+s_{t_{\left(p_2\right)}}),\left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \frac{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)-(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}}{\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)+(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}},\frac{\sqrt{2\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}{\sqrt{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)+\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}}\end{array}\right]$$

Let $x=\sqrt{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2),}y=\sqrt{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)},z=\sqrt{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)},g=\sqrt{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}.$

Then,

$${\tilde{\alpha }}_1+{\tilde{\alpha }}_2=\left\{\begin{array}{c}(s_{{\theta }_{\left(p_1\right)}}+s_{{\theta }_{\left(p_1\right)}},s_{t_{\left(p_1\right)}}+s_{t_{\left(p_2\right)}}),\\ \left[p_1+p_2,q_1+q_2,r_1+r_2,s_1+s_2\right];\\ \frac{x-y}{x+y},\frac{\sqrt{2}z}{g+z}\end{array}\right\}.$$

We have

$$\begin{array}{cc}\hfill \delta ({\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2)& =\left(\begin{array}{c}(s_{\delta (\theta \left(p_1\right)+\theta \left(p_2\right))},s_{\delta (t\left(p_1\right)+t\left(p_2\right)}),\\ \left[\delta \left(p_1+p_2\right),\delta \left(q_1+q_2\right),\delta \left(r_1+r_2\right),\delta \left(s_1+s_2\right)\right];\\ \frac{{\left(1+\frac{x-y}{x-y}\right)}^{\delta }-{\left(1-\frac{x-y}{x-y}\right)}^{\delta }}{{\left(1+\frac{x-y}{x-y}\right)}^{\delta }+{\left(1-\frac{x-y}{x-y}\right)}^{\delta }},\\ \frac{\sqrt{2}{\left(\frac{\sqrt{2}z}{g+z}\right)}^{\delta }}{{\left(2-\frac{\sqrt{2}z}{g+z}\right)}^{\delta }+{\left(\frac{\sqrt{2}z}{g+z}\right)}^{\delta }}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}(s_{\delta (\theta \left(p_1\right)+\theta \left(p_2\right))},s_{\delta (t\left(p_1\right)+t\left(p_2\right)}),\\ \left[\delta \left(p_1+p_2\right),\delta \left(q_1+q_2\right),\delta \left(r_1+r_2\right),\delta \left(s_1+s_2\right)\right];\\ \frac{{(x)}^{\delta }-{(y)}^{\delta }}{{(x)}^{\delta }+{(y)}^{\delta }},\frac{\sqrt{2}{\left(z\right)}^{\delta }}{{\left(g\right)}^{\delta }+{\left(z\right)}^{\delta }}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}(s_{\delta (\theta \left(p_1\right)+\theta \left(p_2\right))},s_{\delta (t\left(p_1\right)+t\left(p_2\right)}),\\ \left[\delta \left(p_1+p_2\right),\delta \left(q_1+q_2\right),\delta \left(r_1+r_2\right),\delta \left(s_1+s_2\right)\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}}\end{array}\right)\hfill \end{array}$$

Let $\delta {\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_1\right)}},s_{t_{\delta \left(p_1\right)}}),\\ \left[\delta p_1,\delta q_1,\delta r_1,\delta s_1\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }}},\end{array}\right)$, $\delta {\tilde{\alpha }}_2=\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_2\right)}},s_{t_{\delta \left(p_2\right)}}),\\ \left[\delta p_2,\delta q_2,\delta r_2,\delta s_2\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}},\end{array}\right)$.

We consider

$$\begin{array}{c}{x}_1=\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }},y_1=\sqrt{{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }},z_1=\sqrt{{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{\delta }}\\ x_2=\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }},g_2=\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }},z_2=\sqrt{{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{\delta }}.\end{array}$$

Then

$$\begin{array}{c}\delta {\tilde{\alpha }}_1=\left((s_{{\theta }_{\delta \left(p_1\right)}},s_{t_{\delta \left(p_1\right)}}),\left[\delta p_1,\delta q_1,\delta r_1,\delta s_1\right];\frac{x_1-y_1}{x_1+y_1},\frac{\sqrt{2}{z}_1}{g_1+z_1}\right)\\ \delta {\tilde{\alpha }}_2=\left((s_{{\theta }_{\delta \left(p_2\right)}},s_{t_{\delta \left(p_2\right)}}),\left[\delta p_2,\delta q_2,\delta r_2,\delta s_2\right];\frac{x_2-y_2}{x_2+y_2},\frac{\sqrt{2}{z}_2}{g_2+z_2}\right).\end{array}$$

By property (1) and (3), and Definition 9,

$$\begin{array}{cc}\hfill \delta {\tilde{\alpha }}_1\oplus \delta {\tilde{\alpha }}_2& =\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_1\right)}},s_{t_{\delta \left(p_1\right)}}),\left[\delta p_1,\delta q_1,\delta r_1,\delta s_1\right];\\ \frac{x_1-y_1}{x_1+y_1},\frac{\sqrt{2}{z}_1}{g_1+z_1}\end{array}\right)\hfill \\ & \oplus \left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_2\right)}},s_{t_{\delta \left(p_2\right)}}),\left[\delta p_2,\delta q_2,\delta r_2,\delta s_2\right];\\ \frac{x_2-y_2}{x_2+y_2},\frac{\sqrt{2}{z}_2}{g_2+z_2}\end{array}\right)\hfill \\ & =\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_1\right)}}+s_{{\theta }_{\delta \left(p_2\right)}},s_{t_{\delta \left(p_1\right)}}+s_{t_{\delta \left(p_2\right)}}),\\ \left[\begin{array}{c}\delta p_1+\delta p_2,\delta q_1+\delta q_2,\\ \delta r_1+\delta r_2,\delta s_1+\delta s_2\end{array}\right];\\ \frac{\frac{x_1-y_1}{x_1+y_1}-\frac{x_2-y_2}{x_2+y_2}}{1+\frac{x_1-y_1}{x_1+y_1}.\frac{x_2-y_2}{x_2+y_2}},\frac{\frac{\sqrt{2}{z}_1}{g_1+z_1}.\frac{\sqrt{2}{z}_2}{g_2+z_2}}{1+\left(1-\frac{\sqrt{2}{z}_1}{g_1+z_1}\right).\left(1-\frac{\sqrt{2}{z}_2}{g_2+z_2}\right)}\end{array}\right),\hfill \end{array}$$

$$\begin{array}{l}=\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_1+p_2\right)}},s_{t_{\delta \left(p_1+p_2\right)}}),\\ \left[\begin{array}{c}\delta (p_1+p_2),\delta (q_1+q_2),\\ \delta (r_1+r_2),\delta (s_1+s_2)\end{array}\right];\\ \frac{x_1{x}_2-y_1{y}_2}{x_1{x}_2+y_1{y}_2},\frac{\sqrt{2}{z}_1{z}_2}{g_1{g}_2+z_1{z}_2}\end{array}\right)\\ =\left(\begin{array}{c}(s_{{\theta }_{\delta \left(p_1+p_2\right)}},s_{t_{\delta \left(p_1+p_2\right)}}),\\ \left[\begin{array}{c}\delta \left(p_1+p_2\right),\delta \left(q_1+q_2\right),\\ \delta \left(r_1+r_2\right),\delta \left(s_1+s_2\right)\end{array}\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{\delta }}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{\delta }{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2)}^{\delta }}}\end{array}\right).\end{array}$$

Therefore, it is proved that $\delta \left({\tilde{\alpha }}_1\oplus {\tilde{\alpha }}_2\right)=\delta {\tilde{\alpha }}_1\oplus \delta {\tilde{\alpha }}_2.$

(3) Since

$$\begin{array}{l}{\delta }_1{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{{\theta }_{{\delta }_1\left(p_1\right)}},s_{t_{{\delta }_1\left(p_1\right)}}),\\ \left[{\delta }_1{p}_1,{\delta }_1{q}_1,{\delta }_1{r}_1,{\delta }_1{s}_1\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_1}}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}}},\end{array}\right)\\ {\delta }_2{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{{\theta }_{{\delta }_2\left(p_1\right)}},s_{t_{{\delta }_2\left(p_1\right)}}),\\ \left[{\delta }_2{p}_1,{\delta }_2{q}_1,{\delta }_2{r}_1,{\delta }_2{s}_1\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}}},\frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_2}}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}+{({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}}},\end{array}\right)\end{array}$$

where ${\delta }_1,{\delta }_1\ge 0.$

Let

$$\begin{array}{l}{x}_1=\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}},y_1=\sqrt{{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}},z_1=\sqrt{{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_1}},g_1=\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1}}\\ x_2=\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}},y_2=\sqrt{{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}},z_2=\sqrt{{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_2}},g_2=\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_2}}.\end{array}$$

Then, we have

$$\begin{array}{l}{\delta }_1{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{{\theta }_{{\delta }_1\left(p_1\right)}},s_{t_{{\delta }_1\left(p_1\right)}}),\left[{\delta }_1{p}_1,{\delta }_1{q}_1,{\delta }_1{r}_1,{\delta }_1{s}_1\right];\\ \frac{x_1-y_1}{x_1+y_1},\frac{\sqrt{2}{z}_1}{g_1+z_1}\end{array}\right)\\ {\delta }_2{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{{\theta }_{{\delta }_2\left(p_1\right)}},s_{t_{{\delta }_2\left(p_1\right)}}),\left[{\delta }_2{p}_1,{\delta }_2{q}_1,{\delta }_2{r}_1,{\delta }_2{s}_1\right];\\ \frac{x_2-y_2}{x_2+y_2},\frac{\sqrt{2}{z}_2}{g_2+z_2}\end{array}\right).\end{array}$$

Using (1) and (3) with Definition 9, we have

$$\begin{array}{cc}\hfill {\delta }_1{\tilde{\alpha }}_1\oplus {\delta }_2{\tilde{\alpha }}_1& =\left(\begin{array}{c}(s_{{\theta }_{{\delta }_1\left(p_1\right)}},s_{t_{{\delta }_1\left(p_1\right)}}),\left[{\delta }_1{p}_1,{\delta }_1{q}_1,{\delta }_1{r}_1,{\delta }_1{s}_1\right];\\ \frac{x_1-y_1}{x_1+y_1},\frac{\sqrt{2}{z}_1}{g_1+z_1}\end{array}\right)\hfill \\ & \oplus \left(\begin{array}{c}(s_{{\theta }_{{\delta }_2\left(p_1\right)}},s_{t_{{\delta }_2\left(p_1\right)}}),\left[{\delta }_2{p}_1,{\delta }_2{q}_1,{\delta }_2{r}_1,{\delta }_2{s}_1\right];\\ \frac{x_2-y_2}{x_2+y_2},\frac{\sqrt{2}{z}_2}{g_2+z_2}\end{array}\right)\end{array}$$

$$\begin{array}{l}=\left(\begin{array}{c}(s_{{\theta }_{{\delta }_1\left(p_1\right)}}+s_{{\theta }_{{\delta }_2\left(p_1\right)}},s_{t_{{\delta }_1\left(p_1\right)}}+s_{t_{{\delta }_2\left(p_1\right)}}),\\ \left[\begin{array}{c}{\delta }_1{p}_1+{\delta }_2{p}_1,{\delta }_1{q}_1+{\delta }_2{q}_1,\\ {\delta }_1{r}_1+{\delta }_2{r}_1,{\delta }_1{s}_1+{\delta }_2{s}_1\end{array}\right];\\ \frac{\frac{x_1-y_1}{x_1+y_1}-\frac{x_2-y_2}{x_2+y_2}}{1+\frac{x_1-y_1}{x_1+y_1}.\frac{x_2-y_2}{x_2+y_2}},\frac{\frac{\sqrt{2}{z}_1}{g_1+z_1}.\frac{\sqrt{2}{z}_2}{g_2+z_2}}{1+\left(1-\frac{\sqrt{2}{z}_1}{g_1+z_1}\right).\left(1-\frac{\sqrt{2}{z}_2}{g_2+z_2}\right)}\end{array}\right)\\ =\left(\begin{array}{c}(s_{{\theta }_{\left({\delta }_{1+}{\delta }_2)p_1\right)}},s_{t_{\left({\delta }_{1+}{\delta }_2)p_1\right)}}),\\ \left[\begin{array}{c}{p}_1({\delta }_1+{\delta }_2),q_1({\delta }_1+{\delta }_2),\\ r_1({\delta }_1+{\delta }_2),s_1({\delta }_1+{\delta }_2)\end{array}\right];\\ \frac{x_1{x}_2-y_1{y}_2}{x_1{x}_2+y_1{y}_2},\frac{\sqrt{2}{z}_1{z}_2}{g_1{g}_2+z_1{z}_2}\end{array}\right)\end{array}$$

$$=\left(\begin{array}{c}(s_{{\theta }_{\left({\delta }_{1+}{\delta }_2)p_1\right)}},s_{t_{\left({\delta }_{1+}{\delta }_2)p_1\right)}}),\\ \left[\begin{array}{c}\left({\delta }_1+{\delta }_2\right)p_1,\left({\delta }_1+{\delta }_2\right)q_1,\\ \left({\delta }_1+{\delta }_2\right)r_1,\left({\delta }_1+{\delta }_2\right)s_1\end{array}\right];\\ \frac{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1+{\delta }_2}-{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1+{\delta }_2}}}{\sqrt{{(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1+{\delta }_2}+{(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1+{\delta }_2}}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_1+{\delta }_2}}}{\sqrt{{(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2)}^{{\delta }_1+{\delta }_2}+{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{{\delta }_1+{\delta }_2}}}\end{array}\right)=\left({\delta }_1+{\delta }_2\right){\tilde{\alpha }}_1.$$

□

3. Pythagorean Trapezoidal Uncertain Linguistic Fuzzy Einstein Aggregation Operators

In this section, we suggested some new aggregation information using Einstein operation laws and studied their important properties.

Pythagorean Trapezoidal Uncertain Linguistic Fuzzy Einstein Averaging Aggregation Operators

Definition 12.

Consider ${\tilde{\alpha }}_j=\left\{(s_{\theta \left(p_j\right)},s_{t\left(p_j\right)}),\left[p_j,q_j,r_j,s_j\right];{\mathrm{\Psi }}_{{\tilde{\alpha }}_j},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}\right\}$ a group of PTLUFNs. Then $(PTULFEWA)$ operator is $n$ dimension mapping $PTULFEWA:{\mathrm{\Omega }}^n->\mathrm{\Omega }$, defined is

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_j\right),$$

(10)

where $w={\left(w_1,w_2,\dots w_n\right)}^T$ is the weight vector of ${\tilde{\alpha }}_j\left(j=1,2\dots ,n\right)$ with $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

Theorem 3.

Let ${\tilde{\alpha }}_j\left(j=1,2,\dots ,n\right)$ be a collection of PTULFNs, then the value aggregated by using $PTULFEWA$ operator is also a PTULFNs;

$$\begin{array}{cc}& PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_j\right)\hfill \\ \hfill =& \left(\begin{array}{c}({\displaystyle \sum _{j=1}^n}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^n}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^n}{w}_j{p}_j,{\displaystyle \sum _{j=1}^n}{w}_j{q}_j,{\displaystyle \sum _{j=1}^n}{w}_j{r}_j,{\displaystyle \sum _{j=1}^n}{w}_j{s}_j\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}\end{array}\right)\hfill \end{array}$$

(11)

where $w={\left(w_1,w_2,\dots w_n\right)}^T$ is the weight vector of ${\tilde{\alpha }}_j\left(j=1,2\dots ,n\right)$, with $w_j\in [0,1]$ and ${\displaystyle {\displaystyle \sum _{j=1}^n}}{w}_j=1.$

Proof. 

In the following, we prove the second result by using mathematical induction on $n.$

(1) We first prove that Equation (11) holds for $n=2.$ Since

$$w_1{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{w_1\theta \left(p_1\right)},s_{w_{1}t\left(p_1\right)}),\left[w_1{p}_1,w_1{q}_1,w_1{r}_1,w_1{s}_1\right];\\ \frac{\sqrt{{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}-{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}}}{\sqrt{{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}+{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}}}{\sqrt{{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}+{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1}}}\end{array}\right)$$

And

$$w_2{\tilde{\alpha }}_2=\left(\begin{array}{c}(s_{w_2\theta \left(p_2\right)},s_{w_{2}t\left(p_2\right)}),\left[w_2{p}_2,w_2{q}_2,w_2{r}_2,w_2{s}_2\right];\\ \frac{\sqrt{{\left(2+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}-{\left(2-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}}}{\sqrt{{\left(2+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}+{\left(2-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}}}{\sqrt{{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}+{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}}}\end{array}\right)$$

Let

$$\begin{array}{c}{x}_1={\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1},y_1={\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1},z_1={\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1},g_1={\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_1}^2\right)}^{w_1},\\ x_2={\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2},y_2={\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2},z_2={\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2},g_2={\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_2}^2\right)}^{w_2}.\end{array}$$

Then, $w_1{\tilde{\alpha }}_1=\left(\begin{array}{c}(s_{w_1\theta \left(p_1\right)},s_{w_{1}t\left(p_1\right)}),\\ \left[w_1{p}_1,w_1{q}_1,w_1{r}_1,w_1{s}_1\right];\frac{\sqrt{x_1-y_1}}{\sqrt{x_1+y_1}},\frac{\sqrt{2z_1}}{\sqrt{g_1+z_1}}\end{array}\right)$.

And

$$w_2{\tilde{\alpha }}_2=\left(\begin{array}{c}{s}_{w_2\theta \left(p_2\right)},s_{w_{2}t\left(p_2\right)}),\\ \left[w_2{p}_2,w_2{q}_2,w_2{r}_2,w_2{s}_2\right];\frac{\sqrt{x_2-y_2}}{\sqrt{x_2+y_2}},\frac{\sqrt{2z_2}}{\sqrt{g_2+z_2}}\end{array}\right).$$

Thus, by $\left(3\right)$ and Definition 9,

$$\begin{array}{cc}& PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2\right)=w_1{\tilde{\alpha }}_1{\oplus }_{\epsilon }{w}_2{\tilde{\alpha }}_2=\left(\begin{array}{c}(s_{w_1\theta \left(p_1\right)}+s_{w_2\theta \left(p_2\right)},s_{w_{1}t\left(p_1\right)}+s_{w_{2}t\left(p_2\right)}),\\ [w_1{p}_1+w_2{p}_2,w_1{q}_1+w_2{q}_2,\\ w_1{r}_1+w_2{r}_2,w_1{s}_1+w_2{s}_2];\\ \frac{\sqrt{x_1{x}_2-y_1{y}_2}}{\sqrt{x_1{x}_2+y_1{y}_2}},\frac{\sqrt{2z_1{z}_2}}{\sqrt{g_1{g}_2+z_1{z}_2}}\end{array}\right)\hfill \\ \hfill =& \left(\begin{array}{c}({\displaystyle \sum _{j=1}^2}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^2}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^2}{w}_j{p}_j,{\displaystyle \sum _{j=1}^2}{w}_j{q}_j,{\displaystyle \sum _{j=1}^2}{w}_j{r}_j,{\displaystyle \sum _{j=1}^2}{w}_j{s}_j\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^2}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^2}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^2}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^2}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^2}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^2}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^2}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}\end{array}\right).\hfill \end{array}$$

(2) If Equation (11) holds for $n=k,$ that is

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_k\right)\stackrel{k}{=\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_j\right)=\left(\begin{array}{c}({\displaystyle \sum _{j=1}^k}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^k}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^k}{w}_j{p}_j,{\displaystyle \sum _{j=1}^k}{w}_j{q}_j,{\displaystyle \sum _{j=1}^k}{w}_j{r}_j,{\displaystyle \sum _{j=1}^k}{w}_j{s}_j\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^k}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^k}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^k}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^k}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^k}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^k}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^k}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}\end{array}\right)$$

when, $n=k+1,$ we have

$$\begin{array}{l}PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_{k+1}\right)=PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_k\right){\oplus }_{\epsilon }\left(w_{k+1}{\tilde{\alpha }}_{k+1}\right)\\ =PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_k\right){\oplus }_{\epsilon }=\left(\begin{array}{c}(s_{w_{k+1}\theta \left(p_{k+1}\right)},s_{w_{k+1}t\left(p_{k+1}\right)}),\\ \left[\begin{array}{c}{w}_{k+1}{p}_{k+1},w_{k+1}{q}_{k+1},\\ w_{k+1}{r}_{k+1},w_{k+1}{s}_{k+1},\end{array}\right];\\ \frac{\sqrt{{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}-{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}}}{\sqrt{{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}+{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}}},\\ \frac{\sqrt{2{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}}}{\sqrt{{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}+{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_{k+1}}}}\end{array}\right).\end{array}$$

Let

$$\begin{array}{l}{x}_1={\displaystyle \prod _{j=1}^k}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j},y_1={\displaystyle \prod _{j=1}^k}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}\right)}^{w_j},z_1={\displaystyle \prod _{j=1}^k}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j},g_1={\displaystyle \prod _{j=1}^k}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j},\\ x_2={\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_j},y_2={\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_j},z_2={\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_j},g_2={\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{k+1}}^2\right)}^{w_j}.\end{array}$$

Then, by $\left(3\right)$ and Definition 9,

$$\begin{array}{cc}& PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_{k+1}\right)\hfill \\ \hfill =& PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_k\right){\oplus }_{\epsilon }\left(w_{k+1}{\tilde{\alpha }}_{k+1}\right),\hfill \\ \hfill =& \left(\begin{array}{c}({\displaystyle \sum _{j=1}^k}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^k}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^k}{w}_j{p}_j,{\displaystyle \sum _{j=1}^k}{w}_j{q}_j,{\displaystyle \sum _{j=1}^k}{w}_j{r}_j,{\displaystyle \sum _{j=1}^k}{w}_j{s}_j\right];\\ \frac{\sqrt{x_1-y_1}}{\sqrt{x_1+y_1}},\frac{\sqrt{2z_1}}{\sqrt{g_1+z_1}},\end{array}\right){\oplus }_{\epsilon }\left(\begin{array}{c}(s_{w_{k+1}\theta \left(p_{k+1}\right)},s_{w_{k+1}t\left(p_{k+1}\right)}),\\ \left[\begin{array}{c}{w}_{k+1}{p}_{k+1},w_{k+1}{q}_{k+1},\\ w_{k+1}{r}_{k+1},w_{k+1}{s}_{k+1},\end{array}\right];\\ \frac{\sqrt{x_2-y_2}}{\sqrt{x_2+y_2}},\frac{\sqrt{2z_2}}{\sqrt{g_2+z_2}}\end{array}\right),\hfill \end{array}$$

$$\begin{array}{l}=\left(\begin{array}{c}({\displaystyle \sum _{j=1}^{k+1}}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^{k+1}}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^{k+1}}{w}_j{p}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{q}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{r}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{s}_j\right];\\ \frac{\sqrt{x_1{x}_2-y_1{y}_2}}{\sqrt{x_1{x}_2+y_1{y}_2}},\frac{\sqrt{2z_1{z}_2}}{\sqrt{g_1{g}_2+z_1{z}_2}},\end{array}\right)\\ =\left(\begin{array}{c}({\displaystyle \sum _{j=1}^{k+1}}{s}_{w_j\theta \left(p_j\right)},{\displaystyle \sum _{j=1}^{k+1}}{s}_{w_{j}t\left(p_j\right)}),\\ \left[{\displaystyle \sum _{j=1}^{k+1}}{w}_j{p}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{q}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{r}_j,{\displaystyle \sum _{j=1}^{k+1}}{w}_j{s}_j\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^{k+1}}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^{k+1}}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^{k+1}}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^{k+1}}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^{k+1}}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^{k+1}}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^{k+1}}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}},\end{array}\right).\end{array}$$

□

Theorem 4.

Let ${\tilde{\alpha }}_j\left(j=1,2,\dots ,n\right)$ be a collection of $PTULFENs$, where $w={\left(w_1,w_2,\dots ,w_n,\right)}^T$ is the weighting vector of ${\tilde{\alpha }}_j\left(j=1,2,\dots ,n\right)$, with $w_j\in \left[0,1\right]$ and ${\sum }_{j=1}^n{w}_j=1.$ Then, the $PTULFEWA$ operator satisfies the following properties:

Proof. 

(1) $\left(\mathrm{Idempotency}\right)$ If all ${\tilde{\alpha }}_j\left(j=1,2,\dots ,n\right)$ are equal, i.e., ${\tilde{\alpha }}_j=\tilde{\alpha }$ for all $j,$ then

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\tilde{\alpha }.$$

(12)

By Definition 11, we have

$$\begin{array}{cc}\hfill PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)& =w_1{\tilde{\alpha }}_1{\oplus }_{\epsilon }{w}_2{\tilde{\alpha }}_2{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }{w}_n{\tilde{\alpha }}_n,\hfill \\ & =w_1\tilde{\alpha }{\oplus }_{\epsilon }{w}_2\tilde{\alpha }{\oplus }_{\epsilon }\dots {\oplus }_{\epsilon }{w}_n\tilde{\alpha },\hfill \\ & ={\displaystyle {\displaystyle \sum }_{j=i}^n}{w}_j\tilde{\alpha }=\tilde{\alpha }.\hfill \end{array}$$

(2) $\left(\mathrm{Boundray}\right)$ Let ${\tilde{\alpha }}_{\min }=\min \{{\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\}$ and ${\tilde{\alpha }}_{\max }=\max \{{\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\},$ then

$${\tilde{\alpha }}_{\min }\le PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)\le {\tilde{\alpha }}_{\max }.$$

(13)

Let

$$f\left(x\right)=\sqrt{\frac{1-x^2}{1+x^2}},x\in \left[0,1\right];\mathrm{then}{f}^{/}\left(x\right)=\frac{-2x}{{\left(1+x^2\right)}^2}\sqrt{\frac{1+x^2}{1-x^2}}<0.$$

Since $f\left(x\right)$ is decreasing function ${\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_j}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}$ for all $j,$

Then

$$f\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}\right)\le f\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_j}\right)\le f\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}\right);$$

$$\begin{array}{c}\sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)}\le \sqrt{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}\le \sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)},\\ \sqrt{{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)}^{w_j}}\le \sqrt{{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}}\le \sqrt{{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)}^{w_j}},\\ \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)}^{w_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)}^{w_j}},\\ \sqrt{{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)}^{{\displaystyle \sum _{j=1}^n}{w}_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}}\le \sqrt{{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)}^{{\displaystyle \sum _{j=1}^n}{w}_j}},\end{array}$$

$$\begin{array}{c}\sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}}\le \sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)},\\ \sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\right)+1}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}+1}\le \sqrt{\left(\frac{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}\right)+1},\\ \left(\frac{\sqrt{2}}{\sqrt{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}}\right)\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}+1}\le \left(\frac{\sqrt{2}}{\sqrt{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}}\right),\\ \left(\frac{\sqrt{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}}{\sqrt{2}}\right)\le \frac{1}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}+1}}\le \left(\frac{\sqrt{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2}}{\sqrt{2}}\right),\\ \sqrt{1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2}\le \frac{\sqrt{2}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{1-{\mathrm{\Psi }}_{\tilde{\alpha }}^2}{1+{\mathrm{\Psi }}_{\tilde{\alpha }}^2}\right)}^{w_j}+1}}\le \sqrt{1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}^2},\\ {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}\le \frac{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}.\end{array}$$

Again suppose $g\left(y\right)=\sqrt{\frac{2-y^2}{y^2}},y\in (0,1],$ then $g^{/}\left(y\right)=\frac{-2}{y^3}\sqrt{\frac{y^2}{2-y^2}}<0.$ Thus $g\left(y\right)$ is a decreasing function. Since ${\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}\le {\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}\le {\mathsf{\Upsilon }}_{\tilde{\alpha }\min }$ for all $j,$ where ${\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}>0,$ then $g\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\right)\le {\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}\le g\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}\right),$ therefore

$$\begin{array}{c}\sqrt{\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}}\le \sqrt{\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}}\le \sqrt{\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}},\\ \sqrt{{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}\right)}^{w_j}}\le \sqrt{{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}}\le \sqrt{{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}\right)}^{w_j}},\\ \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2\right)}{\left({\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}^2\right)}\right)}^{w_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}\right)}^{w_j}},\\ \sqrt{{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}\right)}^{{\displaystyle \sum _{i=1}^n}{w}_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}\right)}^{{\displaystyle \sum _{i=1}^n}{w}_j}},\\ \sqrt{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}\right)+1}\le \sqrt{{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}+1}\le \sqrt{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}\right)+1},\end{array}$$

$$\begin{array}{c}\left(\frac{\sqrt{2}}{\sqrt{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}}\right)\le \sqrt{1+{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}}\le \left(\frac{\sqrt{2}}{\sqrt{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}}\right),\\ \left(\frac{\sqrt{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}^2\right)}}{\sqrt{2}}\right)\le \frac{1}{\sqrt{1+{\displaystyle \prod _{j=1}^n}{\left(\frac{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}\right)}^{w_j}}}\le \left(\frac{\sqrt{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}^2\right)}}{\sqrt{2}}\right),\\ \left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}\right)\le \frac{\sqrt{2{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^2\right)}^{w_j}}}\le \left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\right).\end{array}$$

Since

$$\begin{array}{c}{p}_{\min }\le p_j\le p_{\max },q_{\min }\le q_j\le q_{\max },r_{\min }\le r_j\le r_{\max },s_{\min }\le s_j\le s_{\max },\\ w_j{p}_{\min }\le w_j{p}_j\le w_j{p}_{\max },w_j{q}_{\min }\le w_j{q}_j\le w_j{q}_{\max },\\ w_j{r}_{\min }\le w_j{r}_j\le w_j{r}_{\max },w_j{s}_{\min }\le w_j{s}_j\le w_j{s}_{\max },\\ {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{p}_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{p}_j\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{p}_{\max },{\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{q}_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{q}_j\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{q}_{\max },\\ {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{r}_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{r}_j\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{r}_{\max },{\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j,s_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{s}_j\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_j{s}_{\max }.\end{array}$$

Then,

$$\begin{array}{c}{p}_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_{j}p\le p_{\max },q_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_{j}q\le q_{\max },\\ r_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_{j}r\le r_{\max },s_{\min }\le {\displaystyle {\displaystyle \sum }_{j=1}^n}{w}_{j}s\le s_{\max }.\end{array}$$

Let,

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\tilde{\alpha }=\left((s_{\theta },s_t),\left[p,q,r,s\right];{\mathrm{\Psi }}_{\alpha },{\mathsf{\Upsilon }}_{\alpha }\right)$$

then, we have

$$\begin{gathered} p_{\min }\le p\le p_{\max },q_{\min }\le q\le q_{\max },r_{\min }\le r\le r_{\max }, \\ {s}_{\min }\le s\le s_{\max },{\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}\le {\mathrm{\Psi }}_{\tilde{\alpha }}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\le {\mathsf{\Upsilon }}_{\tilde{\alpha }}\le {\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}. \end{gathered}$$

we get

$$\begin{gathered} p_{\min }+q_{\min }+r_{\min }+s_{\min }\le p+q+r+s\le p_{\max }+q_{\max }+r_{\max }+s_{\max }, \\ {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\le {\mathrm{\Psi }}_{\tilde{\alpha }}-{\mathsf{\Upsilon }}_{\tilde{\alpha }}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}. \end{gathered}$$

Similarly,

$$\begin{gathered} s_{(\theta )\min }\le s_{\left(\theta \right)}\le s_{\left(\theta \right)\max ,}{s}_{(t)\min }\le s_{\left(t\right)}\le s_{\left(t\right)\max }, \\ {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}\le {\mathrm{\Psi }}_{\tilde{\alpha }}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\le {\mathsf{\Upsilon }}_{\tilde{\alpha }}\le {\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}, \\ {s}_{(\theta )\min }+s_{(t)\min }\le s_{\left(\theta \right)}+s_{\left(t\right)}\le s_{(t)\min }+s_{\left(t\right)\max }, \\ {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\min }}-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\min }}\le {\mathrm{\Psi }}_{\tilde{\alpha }}-{\mathsf{\Upsilon }}_{\tilde{\alpha }}\le {\mathrm{\Psi }}_{{\tilde{\alpha }}_{\max }}-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{\max }}. \end{gathered}$$

Therefore ${\tilde{\alpha }}_{\min }\le PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)\le {\tilde{\alpha }}_{\max }.$

(3) $\left(\mathrm{Monotonicity}\right)$ Let ${\tilde{\alpha }}_j^{\ast }=\left((s_{\theta \left(p_j\right)}^{\ast },s_{t\left(p_j\right)}^{\ast }),\left[p_j^{\ast },q_j^{\ast },r_j^{\ast },s_j^{\ast }\right],{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^{\ast },{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^{\ast }\right)$ $\left(j=1,2\dots ,n\right)$ be a collection of Pythagorean trapezoidal fuzzy numbers. If ${\tilde{\alpha }}_j\le {\tilde{\alpha }}_j^{\ast },$ for all $j$, then

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)\le PTFEWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right).$$

(14)

Let

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)={\displaystyle \sum _{j=1}^n}{w}_j{\tilde{\alpha }}_j,PTULFEWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right)={\displaystyle \sum _{j=1}^n}{w}_j{\tilde{\alpha }}_j^{\ast }.$$

Since ${\tilde{\alpha }}_j\le {\tilde{\alpha }}_j^{\ast }$ for all j, then we have $w_j{\tilde{\alpha }}_j\le w_j{\tilde{\alpha }}_j^{\ast }.$ Therefore, we have

$$PTULFEWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)\le PTUlFEWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right).$$

□

Definition 13.

Let ${\tilde{\alpha }}_j=\left((s_{\theta \left(p_j\right)},s_{t\left(p_j\right)}),\left[p_j,q_j,r_j,s_j\right],{\mathrm{\Psi }}_{{\tilde{\alpha }}_j},{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}\right)$ where $j=\left(1,2\dots ,n\right)$ be a collection of PTULFNs. The $(PTULFEOWA)$ operator of dimension $n$ is mapping $PTULFEOWA:{\mathrm{\Omega }}^n->\mathrm{\Omega }$, and $w={\left(w_1,w_2,\dots w_n\right)}^T$ is the weight vector of ${\tilde{\alpha }}_j\left(j=1,2\dots ,n\right)$, with $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1$.

$$PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\right)$$

(15)

where $\left(\sigma \left(1\right),\sigma \left(2\right),\dots ,\sigma \left(n\right)\right)$ is a permutation of $\left(1,2\dots ,n\right)$, such that, ${\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\le$ ${\tilde{\alpha }}_{{\sigma }_{\left(j-1\right)}}$ for all $j=1,2,\dots ,n.$

Theorem 5.

Let ${\tilde{\alpha }}_i\left(i=1,2,\dots ,n\right)$ be a collection of PTULFNs, then their aggregated value by using the $PTULFEOWA$ operator is also and PTULFNs,

$$\begin{array}{cc}\hfill PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)& =\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\right)\hfill \\ & =\left(\begin{array}{c}(s_{\theta \left(p_{{\sigma }_{\left(j\right)}}\right)},s_{t\left(p_{{\sigma }_{\left(j\right)}}\right)}),\\ \left[{\displaystyle \sum _{j=1}^n}{w}_j{p}_{{\sigma }_{\left(j\right)}},{\displaystyle \sum _{j=1}^n}{w}_j{q}_{{\sigma }_{\left(j\right)}},{\displaystyle \sum _{j=1}^n}{w}_j{r}_{{\sigma }_{\left(j\right)}},{\displaystyle \sum _{j=1}^n}{w}_j{s}_{{\sigma }_{\left(j\right)}}\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\mathrm{\Psi }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left(1-{\mathrm{\Psi }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(2-{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left({\mathsf{\Upsilon }}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}\end{array}\right)\hfill \end{array}$$

(16)

where $\left(\sigma \left(1\right),\sigma \left(2\right),\dots ,\sigma \left(n\right)\right)$ is a permutation of $\left(1,2\dots ,n\right)$, such that, ${\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\le$${\tilde{\alpha }}_{{\sigma }_{\left(j-1\right)}}$ for all $j=1,2,\dots ,n.$ $w={\left(w_1,w_2,\dots w_n\right)}^T$ is weight vector of $PTULFEOWA$ operator, with $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1$.

Proof. 

Similar to Theorem 3. □

Theorem 6.

Let ${\tilde{\alpha }}_i\left(i=1,2,\dots ,n\right)$ $\left(j=1,2\dots ,n\right)$ be a collection of $PTULFENs,$ and $w={\left(w_1,w_2,\dots w_n\right)}^T$ is the weighting vector of $PTULFEOWA$ with $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1$, which satisfies the following properties;

(1) 

(Idmpotency) If for all ${\tilde{\alpha }}_j\left(j=1,2\dots ,n\right)$ are equal, i.e., ${\tilde{\alpha }}_j=\tilde{\alpha },$ for all $j,$ then

$$PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\tilde{\alpha }.$$

(17)

(2) 

(Boundray) Let ${\tilde{\alpha }}_{\min }=\min \{{\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\}$ and ${\tilde{\alpha }}_{\max }=\max \{{\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\},$ then

$${\tilde{\alpha }}_{\min }\le PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)\le {\tilde{\alpha }}_{\max }.$$

(18)

(3) 

(Monotonicity) Let

$${\tilde{\alpha }}_j^{\ast }=\left((s_{\theta \left(p_j\right)}^{\ast },s_{t\left(p_j\right)}^{\ast }),\left[p_j^{\ast },q_j^{\ast },r_j^{\ast },s_j^{\ast }\right],{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^{\ast },{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^{\ast }\right)$$

(19)

$\left(j=1,2\dots ,n\right)$ be a collection of PTULFNs. If ${\tilde{\alpha }}_j\le {\tilde{\alpha }}_j^{\ast },$ for all $j,$ then

(4) 

(Commutativity) Let ${\tilde{\alpha }}_j^{\ast }=\left((s_{\theta \left(p_j\right)}^{\ast },s_{t\left(p_j\right)}^{\ast }),\left[p_j^{\ast },q_j^{\ast },r_j^{\ast },s_j^{\ast }\right],{\mathrm{\Psi }}_{{\tilde{\alpha }}_j}^{\ast },{\mathsf{\Upsilon }}_{{\tilde{\alpha }}_j}^{\ast }\right)$ $\left(j=1,2\dots ,n\right)$ be a collection of PTULFNs, then

$$PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=PTULFEOWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right).$$

(20)

where $\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right)$ is any permutation of $\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right).$

Proof. 

Let

$$\begin{array}{c}PTULFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\right),\\ PTULFEOWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}^{\ast }\right).\end{array}$$

Since $\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)$ is any permutation of $\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right)$, we have ${\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\le {\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}^{\ast }$, then

$$PTFEOWA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=PTFEOWA\left({\tilde{\alpha }}_1^{\ast },{\tilde{\alpha }}_2^{\ast },\dots ,{\tilde{\alpha }}_n^{\ast }\right).$$

□

Definition 14.

Let ${\tilde{\alpha }}_j$ $\left(j=1,2\dots ,n\right)$ be a collection of Pythagorean trapezoidal uncertain linguistic fuzzy numbers. Pythagorean trapezoidal uncertain linguistic fuzzy Einstein hybrid averaging $(PTULFEHA)$ operator of dimension n is mapping $PTULFEHA:$ ${\mathrm{\Omega }}^n->\mathrm{\Omega }$ having weight $w={\left(w_1,w_2,\dots w_n\right)}^T$ such that $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1.$

$$PTULFEHA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)=\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}\right)$$

(21)

where ${\tilde{\beta }}_{{\sigma }_{\left(j\right)}}$ is the $jth$ largest of the weighted Pythagorean trapezoidal uncertain linguistic fuzzy numbers ${\tilde{\beta }}_j\left({\tilde{\beta }}_j=n{w}_j{\tilde{\alpha }}_j,j=1,2,\dots ,n\right),$ and $w={\left(w_1,w_2,\dots w_n\right)}^T$ such that $w_j\in [0,1]$ and ${\displaystyle \sum _{j=1}^n}{w}_j=1,$

$$\begin{array}{cc}\hfill PTULFEHA({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n)& =\stackrel{n}{\underset{j=1}{{\oplus }_{\epsilon }}}\left(w_j{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}^{.}\right)\hfill \\ & =\left(\begin{array}{c}({\displaystyle \sum _{j=1}^n}{s}_{w_{j\theta \left({\sigma }_{\left(j\right)}\right)}}^{.},{\displaystyle \sum _{j=1}^n}{s}_{w_{jt\left({\sigma }_{\left(j\right)}\right)}}^{.}),\left[\begin{array}{c}{\displaystyle \sum _{j=1}^n}{w}_j{\stackrel{.}{p}}_{{\sigma }_{\left(j\right)}},{\displaystyle \sum _{j=1}^n}{w}_j{\stackrel{.}{q}}_{{\sigma }_{\left(j\right)}},\\ {\displaystyle \sum _{j=1}^n}{w}_j{\stackrel{.}{r}}_{{\sigma }_{\left(j\right)}},{\displaystyle \sum _{j=1}^n}{w}_j{\stackrel{.}{s}}_{{\sigma }_{\left(j\right)}}\end{array}\right];\\ \frac{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\stackrel{.}{\mathrm{\Psi }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}-{\displaystyle \prod _{j=1}^n}{\left(1-{\stackrel{.}{\mathrm{\Psi }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(1+{\stackrel{.}{\mathrm{\Psi }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left(1-{\stackrel{.}{\mathrm{\Psi }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}},\\ \frac{\sqrt{2{\displaystyle \prod _{j=1}^n}{\left({\stackrel{.}{\mathsf{\Upsilon }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}{\sqrt{{\displaystyle \prod _{j=1}^n}{\left(2-{\stackrel{.}{\mathsf{\Upsilon }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}+{\displaystyle \prod _{j=1}^n}{\left({\stackrel{.}{\mathsf{\Upsilon }}}_{{\tilde{\alpha }}_{{\sigma }_{\left(j\right)}}}^2\right)}^{w_j}}}\end{array}\right)\hfill \end{array}$$

(22)

Proof. 

Similar to Theorem 3. □

Theorem 7.

The $PTULFEWA$ operator is a special case of the $PTULFEHA$ operator.

Proof. 

Let $w=\left(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n},\right)$, Then

$$\begin{array}{ll}PTULFEHA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)& =w_1{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\oplus w_2{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\dots \oplus w_n{\tilde{\alpha }}_{{\sigma }_{\left(n\right)}}\\ & =\frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\oplus \frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\dots \oplus \frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(n\right)}}\\ & =w_1{\tilde{\alpha }}_1\oplus w_2{\tilde{\alpha }}_2\dots \oplus w_n{\tilde{\alpha }}_n\\ & =PTULFEHA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right).\end{array}$$

□

Theorem 8.

The $PTULFEOWA$ operator is a special case of the $PTFEHA$ operator.

Proof. 

Let $w=\left(\frac{1}{n},\frac{1}{n},\dots ,\frac{1}{n},\right)$, Then

$$\begin{array}{cc}\hfill PTULFEHA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right)& =w_1{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\oplus w_2{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\dots \oplus w_n{\tilde{\alpha }}_{{\sigma }_{\left(n\right)}}\hfill \\ & =\frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\oplus \frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(1\right)}}\dots \oplus \frac{1}{n}{\tilde{\alpha }}_{{\sigma }_{\left(n\right)}}\hfill \\ & =PTULFEHA\left({\tilde{\alpha }}_1,{\tilde{\alpha }}_2,\dots ,{\tilde{\alpha }}_n\right).\hfill \end{array}$$

□

4. A Novel Method for MAGDM Based on the Proposed PTULFEWA and PTULFEHA Operators

This section introduces the MADM process under the suggested aggregation information to propose a technique based on the PTULFSs. The detail description of the algorithm given in Figure 1.

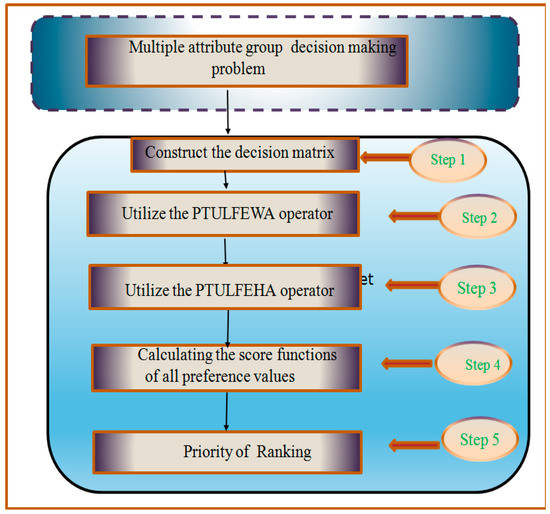
Figure 1. Flow chart of proposed algorithm.

Algorithm: 

To present the method of the MADM process, suppose $A=\{A_1,A_2,\dots ,A_m\}$ is a collection of alternatives, $C=\{C_1,C_2,\dots ,C_n\}$ is a collection of attributes, and $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ is the weight vector such that $w_j\in \left[0,1\right]$ and ${\sum }_{j=1}^n{w}_j=1.$ Consider $M=\{m_1,m_2,\dots ,m_p\}$ the set of decision-makers and $\lambda ={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)}^T$ is the weight vector of decision-makers ${\lambda }_k\in \left[0,1\right]$ and ${\sum }_{k=1}^p{\lambda }_k=1.$ Let $R^{\left(k\right)}={\left(r_{ij}^{\left(k\right)}\right)}_{m\times n}\left(k=1,2,\dots p\right)$ be PTULF decision matrix, where $h_{ij}^{\left(k\right)}=\left((s_{{\theta }_{ij}}^{\left(k\right)},s_{t_{ij}}^{\left(k\right)}),\left[h_{1ij}^{\left(k\right)},h_{2ij}^{\left(k\right)},h_{3ij}^{\left(k\right)},h_{4ij}^{\left(k\right)}\right];{\mathrm{\Psi }}_{ij}^{\left(k\right)},{\mathsf{\Upsilon }}_{ij}^{\left(k\right)}\right)$ is PTULFN given by the decision-makers $m_k\in M,$

$$0\le {\mathrm{\Psi }}_{ij}^{\left(k\right)}\le 1,0\le {\mathsf{\Upsilon }}_{ij}^{\left(k\right)}\le 1,0\le {\mathrm{\Psi }}_{ij}^{2\left(k\right)}+{\mathsf{\Upsilon }}_{ij}^{2\left(k\right)}\le 1,i=1,2,\dots ,m,j=1,2,\dots ,n.$$

We use the $PTULFEWA$ and $PTULFEHA$ operators to present a method in the MADM process using the following steps.

• Step 1. Construct PTULF matrix $R^{\left(k\right)}={\left(r_{ij}^{\left(k\right)}\right)}_{m\times n}$, from the decision of DM.
• Step 2. Use the information of PTULF matrix $R^{\left(k\right)}={\left(r_{ij}^{\left(k\right)}\right)}_{m\times n},$ and apply the $PTULFEWA$ operator to collect the separate overall preference values $r_i^{\left(k\right)}$ of the alternative $A_i,$ by using the weight vector.

  $$r_i^{\left(k\right)}=PTULFEWA\left(r_{i1}^{\left(k\right)},r_{i2}^{\left(k\right)},\dots ,r_{in}^{\left(k\right)}\right),i=1,2,\dots ,m,k=1,2,\dots ,p.$$

  (23)
• Step 3. Utilizing the $PTULFEHA$ operator to collect all the information from the separated set to PTULF values $r_i^{\left(k\right)}\left(k=1,2,\dots p\right)$ $r_i,$ where $w={\left(w_1,w_2,\dots ,w_n\right)}^T$ is the corresponding vector and $\lambda ={\left({\lambda }_1,{\lambda }_2,\dots ,{\lambda }_p\right)}^T$ is the weight vector of decision-makers.

  $$r_i=PTULFEHA\left(r_i^{\left(1\right)},r_i^{\left(2\right)},\dots ,r_i^{\left(p\right)}\right),i=1,2,\dots ,m,k=1,2,\dots ,p.$$

  (24)
• Step 4. Use Equation (7) to find the scores values. If some of the score values are equal, use Equation (8) to find the accuracy.
• Step 5. Rank the scores values.

5. Illustrative Example Surface Irrigation Problem

An illustrative example was considered to demonstrate the suggested technique in DM. The ratio of upper respiratory tract infection (URTI) was increasing day-by-day in Pakistan; consequently, we wanted to control the ratio of this disease. For this, we considered four possible alternatives, $A_i$ $\left(i=1,2,3,4\right)$ such as,

• A₁: Augmentin,
• A₂: Moxiflaxacin,
• A₃: Levofloxacin,
• A₄: Clathromycin.

A group of decision makers was invited to assess the best one under the following four attributes, C_j (j = 1, 2, 3, 4). Suppose w = (0.40, 0.30, 0.20, 0.10) is a weight vector of C_j

• C₁: Spending of the Medicine,
• C₂: Potentials of the Medicine,
• C₃: Less side effects of the Medicine,
• C₄: Accessibility in the market.

The detail description of criteria and alternative are given in Figure 2a,b, respectively.

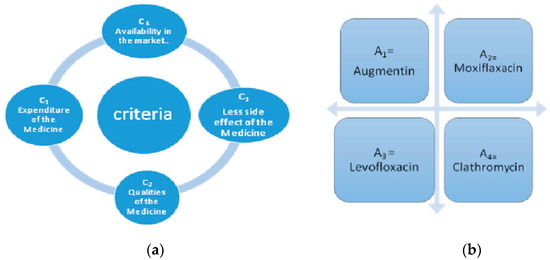
Figure 2. (a) Four alternatives; (b) Four attributes.

The decision makers gave their decisions and considered the weights λ = (0.10, 0.20, 0.30, 0.40).

Table 1, Table 2, Table 3 and Table 4 show the decisions of the exports under the PTLUF, $R^{\left(k\right)}={\left(r_{ij}^{\left(k\right)}\right)}_{4\times 4}\left(k=1,2,3,4\right).$

Table 1. Decision Matrix Z⁽¹⁾.

Ai	C1	C2
A1	{(s6,s2),[0.4,0.5,0.6,0.5];(0.7,0.5)}	{(s5,s2),[0.3,0.4,0.5,0.4];(0.6,0.5)}
A2	{(s3,s2),[0.9,0.6,0.3,0.4];(0.8,0.3)}	{(s2,s3),[0.4,0.5,0.4,0.1];(0.6,0.4)}
A3	{(s2,s4),[0.4,0.5,0.1,0.2];(0.6,0.5)}	{(s4,s2),[0.7,0.6,0.3,0.2];(0.5,0.5)}
A4	{(s3,s4),[0.3,0.4,0.3,0.5];(0.6,0.5)}	{(s6,s2),[0.8,0.4,0.3,0.4];(0.8,0.2)}
Ai	C3	C4
A1	{(s2,s3),[0.6,0.2,0.3,0.4];(0.7,0.3)}	{(s6,s2),[0.4,0.5,0.6,0.9];(0.8,0.4)}
A2	{(s3,s4),[0.4,0.5,0.6,0.7];(0.7,0.5)}	{(s4,s3),[0.3,0.4,0.5,0.9];(0.5,0.5)}
A3	{(s6,s3),[0.4,0.6,0.2,0.3];(0.7,0.4)}	{(s5,s2),[0.6,0.7,0.8,0.6];(0.8,0.5)}
A4	{(s4,s5),[0.4,0.6,0.3,0.4];(0.9,0.3)}	{(s2,s3),[0.4,0.5,0.6,0.5];(0.9,0.2)}

Table 2. Decision Matrix Z⁽²⁾.

Ai	C1	C2
A1	{(s2,s3),[0.9,0.3,0.1,0.2];(0.8,0.3)}	{(s5,s4),[0.3,0.4,0.5,0.6];(0.6,0.4)}
A2	{(s3,s2),[0.4,0.2,0.2,0.5];(0.7,0.5)}	{(s2,s3),[0.4,0.5,0.6,0.4];(0.6,0.5)}
A3	{(s6,s5),[0.3,0.4,0.5,0.7];(0.6,0.5)}	{(s3,s2),[0.4,0.6,0.3,0.5];(0.5,0.5)}
A4	{(s6,s2),[0.4,0.9,0.6,0.3];(0.8,0.2)}	{(s2,s2),[0.6,0.3,0.1,0.4];(0.6,0.4)}
Ai	C3	C4
A1	{(s4,s3),[0.1,0.4,0.5,0.3];(0.7,0.5)}	{(s2,s4),[0.6,0.2,0.5,0.1];(0.5,0.5)}
A2	{(s3,s2),[0.4,0.7,0.8,0.9];(0.7,0.3)}	{(s6,s3),[0.4,0.6,0.3,0.2];(0.8,0.4)}
A3	{(s2,s3),[0.6,0.8,0.3,0.2];(0.7,0.4)}	{(s3,s4),[0.5,0.8,0.7,0.3];(0.8,0.5)}
A4	{(s5,s4),[0.3,0.4,0.7,0.2];(0.6,0.5)}	{(s4,s3),[0.3,0.5,0.6,0.9];(0.9,0.1)}

Table 3. Decision Matrix Z⁽³⁾.

Ai	C1	C2
A1	{(s4,s3),[0.3,0.4,0.4,0.3];(0.8,0.2)}	{(s2,s2),[0.7,0.5,0.6,0.3];(0.6,0.4)}
A2	{(s2,s4),[0.4,0.3,0.6,0.3];(0.6,0.5)}	{(s3,s4),[0.3,0.1,0.2,0.4];(0.5,0.5)}
A3	{(s6,s3),[0.5,0.3,0.6,0.4];(0.8,0.3)}	{(s5,s2),[0.2,0.1,0.3,0.5];(0.6,0.4)}
A4	{(s3,s4),[0.9,0.6,0.4,0.1];(0.7,0.5)}	{(s3,s3),[0.4,0.3,0.4,0.2];(0.6,0.5)}
Ai	C3	C4
A1	{(s3,s2),[0.3,0.5,0.6,0.6];(0.6,0.5)}	{(s3,s4),[0.4,0.5,0.2,0.3];(0.9,0.1)}
A2	{(s5,s3),[0.4,0.5,0.7,0.2];(0.7,0.4)}	{(s4,s2),[0.4,0.3,0.2,0.1];(0.8,0.5)}
A3	{(s3,s4),[0.3,0.1,0.2,0.3];(0.7,0.5)}	{(s5,s2),[0.6,0.8,0.9,0.2];(0.5,0.5)}
A4	{(s6,s5),[0.4,0.3,0.4,0.6];(0.7,0.3)}	{(s2,s3),[0.4,0.5,0.4,0.3];(0.8,0.4)}

Table 4. Decision Matrix Z⁽⁴⁾.

Ai	C1	C2
A1	{(s3,s5),[0.4,0.5,0.7,0.5];(0.7,0.5)}	{(s2,s2),[0.4,0.3,0.6,0.7];(0.6,0.5)}
A2	{(s2,s3),[0.3,0.4,0.4,0.6];(0.6,0.5)}	{(s4,s4),[0.3,0.4,0.5,0.6];(0.5,0.5)}
A3	{(s4,s2),[0.5,0.4,0.2,0.3];(0.8,0.3)}	{(s6,s3),[0.4,0.5,0.7,0.8];(0.6,0.4)}
A4	{(s3,s4),[0.4,0.6,0.3,0.4];(0.8,0.2)}	{(s2,s2),[0.3,0.4,0.5,0.7];(0.6,0.4)}
Ai	C3	C4
A1	{(s2,s3),[0.8,0.2,0.3,0.4];(0.7,0.3)}	{(s3,s4),[0.8,0.2,0.3,0.4];(0.7,0.3)}
A2	{(s3,s2),[0.4,0.3,0.2,0.1];(0.7,0.4)}	{(s2,s4),[0.4,0.5,0.3,0.1];(0.8,0.5)}
A3	{(s4,s4),[0.4,0.5,0.7,0.8];(0.6,0.4)}	{(s4,s2),[0.4,0.5,0.3,0.1];(0.8,0.5)}
A4	{(s5,s2),[0.4,0.5,0.6,0.7];(0.6,0.5)}	{(s2,s3),[0.4,0.3,0.1,0.3];(0.9,0.1)}

• Step 1. The decision makers’ decisions are presented in the following Tables.
• Step 2. Use the PTULF matrix, $R^{\left(k\right)}\left(k=1,2,3,4\right)$, and the $PTULFEWA$ operator to collect the different overall preference PTL values $r_i^{\left(k\right)}\left(i=1,2,3,4\right)$ of the alternative $A_i$ (in Table 5)
  Table 5. Collective aggregation information using $PTULFEWA$.

  ${\mathit{r}}_{\mathit{i}}^{\left(\mathit{k}\right)}$	Aggregated Values	${\mathit{r}}_{\mathit{i}}^{\left(\mathit{k}\right)}$	Aggregated Values
  $r_1^{(1)}$	{(s4.9,s2.2),[0.41,0.41,0.51,0.49];(0.68,0.44)}	$r_2^{(1)}$	{(s3.3,s3.4),[0.53,0.34,0.34,0.33];(0.71,0.38)}
  $r_1^{(2)}$	{(s2.8,s2.9),[0.62,0.53,0.41,0.42];(0.71,0.38)}	$r_2^{(2)}$	{(s3.0,s2.4.),[0.40,0.43,0.45,0.52];(0.68,0.44)}
  $r_1^{(3)}$	{(s3.7,s3.0),[0.48,0.45,0.33,0.45];(0.80,0.31)}	$r_2^{(3)}$	{(s3.2,s3.6),[0.41,0.57,0.42,0.50];(0.65,0.47)}
  $r_1^{(4)}$	{(s4.0,s3.5),[0.48,0.45,0.33,0.45];(0.80,0.31)}	$r_2^{(4)}$	{(s4.4,s2.5),[0.43,0.58,0.47,0.37];(0.37,0.27)}
  $r_3^{(1)}$	{(s2.9,s2.6),[0.43,0.44,0.46,0.36];(0.73,0.27)}	$r_4^{(1)}$	{(s2.5,s3.6),[0.47,0.37,0.57,0.55];(0.68,0.44)}
  $r_3^{(2)}$	{(s3.3,s3.2),[0.37,0.31,0.46,0.29];(0.65,0.47)}	$r_4^{(2)}$	{(s2.8,s3.2),[0.33,0.39,0.38,0.45];(0.65,0.47)}
  $r_3^{(3)}$	{(s5.1,s2.8),[0.38,0.25,0.46,0.39];(0.71,0.38)}	$r_4^{(3)}$	{(s4.6,s2.7),[0.43,0.44,0.43,0.54];(0.71,0.38)}
  $r_3^{(4)}$	{(s3.5,s2.9),[0.96,0.44,0.40,0.25];(0.68,0.44)}	$r_4^{(4)}$	{(s3.1,s2.9),[0.37,0.49,0.40,0.54];(0.73,0.27}

• Step 3. Apply the $PTULFEHA$ operator to collect the overall values see in Table 6.
  Table 6. Collective aggregation information using $PTULFEHA$.

  r(k)	Aggregated Values
  r(1)	{(s3.76,s3.10),[0.49,0.59,0.51,0.40];(0.76,0.28)}
  r(2)	{(s3.65,s2.00),[0.66,0.52,0.57,0.53];(0.73,0.32)}
  r(3)	{(s3.88,s2.90),[0.30,0.31,0.33,0.34];(0.59,0.56)}
  r(4)	{(s3.47,s2.97),[0.18,0.15,0.18,0.17];(0.47,0.71)}

• Step 4. Find the scores and ranking of $A_i$ are given in Figure 3.

  $$S\left({\tilde{r}}_1\right)=0.8517,S\left({\tilde{r}}_2\right)=0.6930,S\left({\tilde{r}}_3\right)=0.3730,S\left(r_4\right)=-0.1546.$$
  

  Figure 3. Score representation.
• Step 5. Arrange the scores, $A_1>A_2>A_3>A_4.$ The best one is $A_1.$

6. Comparison Analysis with Existing Methods

To demonstrate the effectiveness of the suggested technique, a systematic comparison analysis was presented with the existing methods from [17,18], and [6].

6.1. A Comparison Analysis with Existing MADM Pythagorean Trapezoidal Fuzzy Sets

• Step 1. According to the decision information given in the PTFNs decision matrix $Z^{\left(k\right)}=\left(z_{ij}^k\right)$ in Table 7.
  Table 7. Decision Matrix Z^k.

  Ai	C1	C2
  A1	{(s6,s2),[0.4,0.5,0.6,0.5];(0.8,0.5)}	{(s3,s4),[0.9,0.6,0.3,0.4];(0.7,0.4)}
  A2	{(s5,s3),[0.3,0.4,0.5,0.4];(0.4,0.8)}	{(s2,s2),[0.4,0.5,0.4,0.1];(0.5,0.6)}
  A3	{(s4,s2),[0.6,0.2,0.3,0.4];(0.5,0.7)}	{(s6,s3),[0.4,0.5,0.6,0.7];(0.4,0.7)}
  A4	{(s2,s4),[0.4,0.5,0.6,0.9];(0.4,0.8)}	{(s3,s2),[0.3,0.4,0.5,0.9];(0.3,0.5)}
  Ai	C1	C2
  A1	{(s5,s2),[0.4,0.5,0.1,0.2];(0.5,0.5)}	{(s4,s3),[0.3,0.4,0.3,0.5];(0.6,0.5)}
  A2	{(s6,s3),[0.6,0.7,0.3,0.2];(0.4,0.7)}	{(s1,s2),[0.8,0.4,0.3,0.4];(0.3,0.8)}
  A3	{(s3,s4),[0.4,0.6,0.2,0.3];(0.3,0.8)}	{(s4,s3),[0.4,0.5,0.3,0.4];(0.7,0.7)}
  A4	{(s4,s3),[0.6,07,0.8,0.6];(0.5,0.6)}	{(s3,s5),[0.4,0.5,0.6,0.5];(0.7,0.4)}

• Step 2. Utilize the $PTFWA$ operator to aggregate the decision matrices into a single collective decision matrix $r_i^k$ of the alternative $B_i$ see in Table 8. Suppose that the weighted vectors of the alternative are $(0.3,0.4,0.1,0.2)$ such that,
  Table 8. r^(k).

  r(k)	Aggregated Values
  r(1)	{[0.58,0.52,0.37,0.43];(0.85,0.49)}
  r(2)	{[0.48,0.46,0.40,0.26];(0.70,0.44)}
  r(3)	{[0.51,0.55,0.32,0.40];(0.56,0.32)}
  r(4)	{[0.18,0.41,0.44,0.65];(0.60,0.31)}

• Step 3. Calculate the scores $S\left({\tilde{r}}_i\right)$ of all the overall Pythagorean trapezoidal fuzzy values, shown in Figure 4.

  $$S\left({\tilde{r}}_1\right)=0.2291,S\left({\tilde{r}}_2\right)=0.1185,S\left({\tilde{r}}_3\right)=0.0939,S\left(r_4\right)=0.1108.$$
  

  Figure 4. Score representation.
• Step 4. Arrange all the scores, $A_1>A_2>A_4>A_3.$ The best alternative is $A_1.$

6.2. A Comparison Analysis with Existing MADM Linguistic Pythagorean Fuzzy Sets

• Step 1. The matrix given by PTULF is $Z^{\left(k\right)}=\left(z_{ij}^k\right)$ given in Table 9.
  Table 9. Z^(k).

  Ai	C1	C2	C3	C4
  A1	(s2,0.8,0.5)	(s4,0.7,0.4)	(s5,0.5,0.5)	(s6,0.6,0.5)
  A2	(s1,0.8,0.4)	(s2,0.5,0.6)	(s3,0.7,0.4)	(s5,0.8,0.3)
  A3	(s2,0.5,0.7)	(s3,0.4,0.7)	(s5,0.8,0.3)	(s6,0.7,0.7)
  A4	(s4,0.4,0.8)	(s5,0.3,0.5)	(s8,0.5,0.6)	(s7,0.7,0.4)

• Step 2. Utilize the $LPFWA$ operator to aggregate all the decision matrix into a single collective decision matrix $r_i^k$ of the alternative $B_i$ in Table 10. Suppose that the weighted vectors of the alternative are $(0.3,0.4,0.1,0.2)$ such that,
  Table 10. r^(k).

  r(k)	Aggregated Values
  r(1)	{(0.6989,0.4781)}
  r(2)	{(0.7607,0.3866)}
  r(3)	{(0.7742,0.6431)}
  r(4)	{(0.5663,0.5362)}

• Step 3. Calculate the scores $S\left({\tilde{r}}_i\right)$ of all the overall linguistic Pythagorean fuzzy values such that,

  $$\begin{array}{c}S\left({\tilde{r}}_1\right)=\sqrt[s]{6.6099}=2.5709,S\left({\tilde{r}}_2\right)=\sqrt[s]{2.3590},=1.5359,\\ S\left({\tilde{r}}_3\right)=\sqrt[s]{14.7350},=3.8386,S\left(r_4\right)=\sqrt[s]{11.5361}=3.3964.\end{array}$$
• Step 4. We arrange the score value in descending order such that $A_3>A_4>A_1>A_2.$ Thus, the most desirable alternative is $A_3.$

6.3. A Comparison Analysis with Existing MADM Pythagorean Fuzzy Sets

• Step 1. According to the decision information given in the Pythagorean fuzzy number decision matrix $Z^{\left(k\right)}=\left(z_{ij}^k\right)$ in Table 11.
  Table 11. Z^(k).

  Ai	C1	C2	C3	C4
  A1	(0.8,0.5)	(0.7,0.4)	(0.5,0.5)	(0.6,0.5)
  A2	(0.8,0.4)	(0.5,0.6)	(0.7,0.4)	(0.8,0.3)
  A3	(0.5,0.7)	(0.4,0.7)	(0.8,0.3)	(0.7,0.7)
  A4	(0.4,0.8)	(0.3,0.5)	(0.5,0.6)	(0.7,0.4)

• Step 2. Utilize the $PFWA$ operator to aggregate all the decision matrix into single collective decision matrix $r_i^k$ of the alternative $B_i$ in Table 12. Suppose that the weighted vectors of the alternative are $(0.3,0.4,0.1,0.2)$ such that,
  Table 12. Collective aggregation information.

  r(k)	Aggregated Values
  r(1)	{s3.6,0.6980,0.4781}
  r(2)	{s2.3,0.7607,0.3866}
  r(3)	{s3.3,0.7742,0.6431}
  r(4)	{s4.8,0.5663,0.5362}

• Step 3. Calculate the scores $S\left({\tilde{r}}_i\right)$ of all the overall intuitionistic trapezoidal fuzzy values in see in Figure 5.

  $$S\left({\tilde{r}}_1\right)=0.2598,S\left({\tilde{r}}_2\right)=0.4292,S\left({\tilde{r}}_3\right)=0.1858,S\left(r_4\right)=0.0331.$$
  

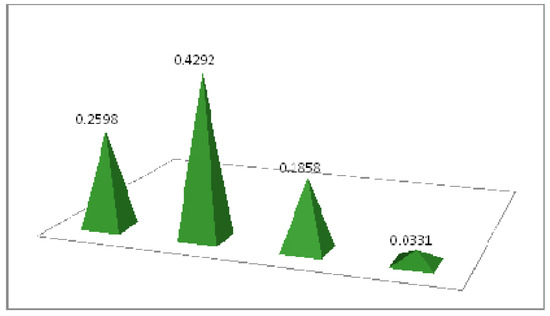  Figure 5. Score representation.
• Step 4. We arrange the score value in descending order such that $A_2>A_1>A_3>A_4$. The sensitive analysis of comparison of different aggregation operators with the proposed aggregation operators is given in Table 13 and Figure 6.
  Table 13. Comparison of existing methods.

  Method Ranking Results
  PTULFE	information	A1 > A2 > A3 > A4
  PTF	information	A1 > A2 > A4 > A3
  LPF	information	A3 > A4 > A1 > A2
  PF	information	A2 > A1 > A3 > A4

  

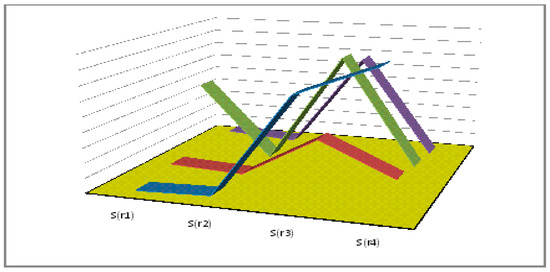  Figure 6. Score representation.

7. Conclusions

We proposed a new PTULF operator using Einstein operations and studied some important properties. We defined different types of aggregation operators—PTULFEWA, PTULFEOWA, and PTULFEHA—using the Einstein operations. A MADM approach was presented for the proposed aggregation operators based on the PTULF environment. An illustrative example was given to show that the presented MADM approach was more accurate, general, and effective. Moreover, our presented method is different from the existing methods for MADM due to the use of PTULF numbers, which did not produce any loss of information in the process. A systematic comparison analysis was given to verify the results. In future research work, we will try to extend the work in various directions, such as confidence level, picture fuzzy set, symmetric aggregation operators, logarithmic aggregation operators, power aggregation operators, Dombi aggregation operators, and their applications in decision making.