Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata
Abstract
1. Introduction
2. Related Work
2.1. Transit Media as a Form of Outdoor Advertising
2.2. Information Spreading in Offline and Online Environments
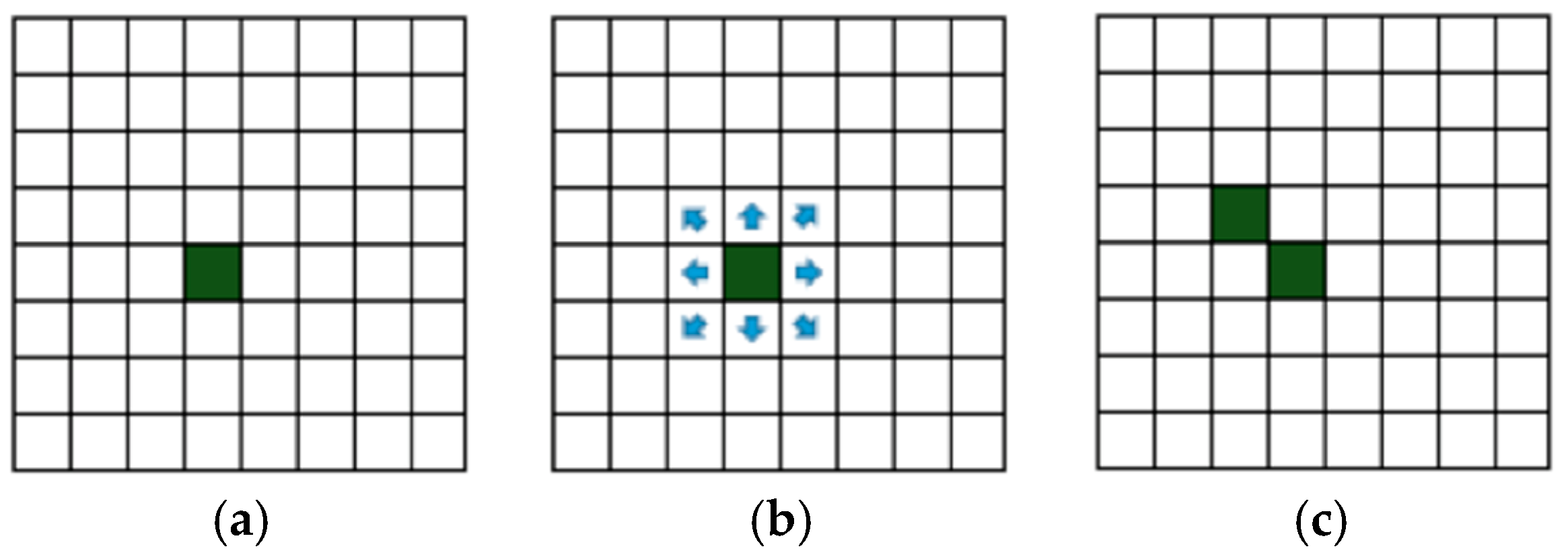
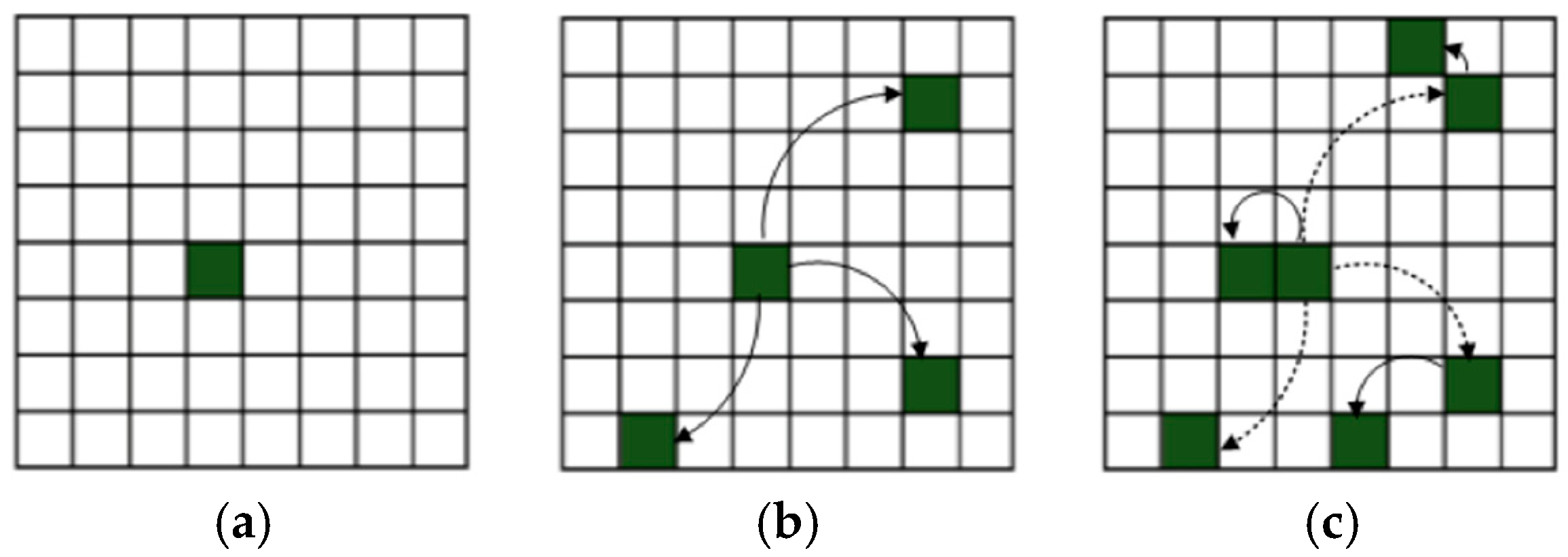
2.3. Information-Spreading Modelling with Cellular Automata and Graph-Based Cellular Automata
2.4. The Motivation for the Presented Study
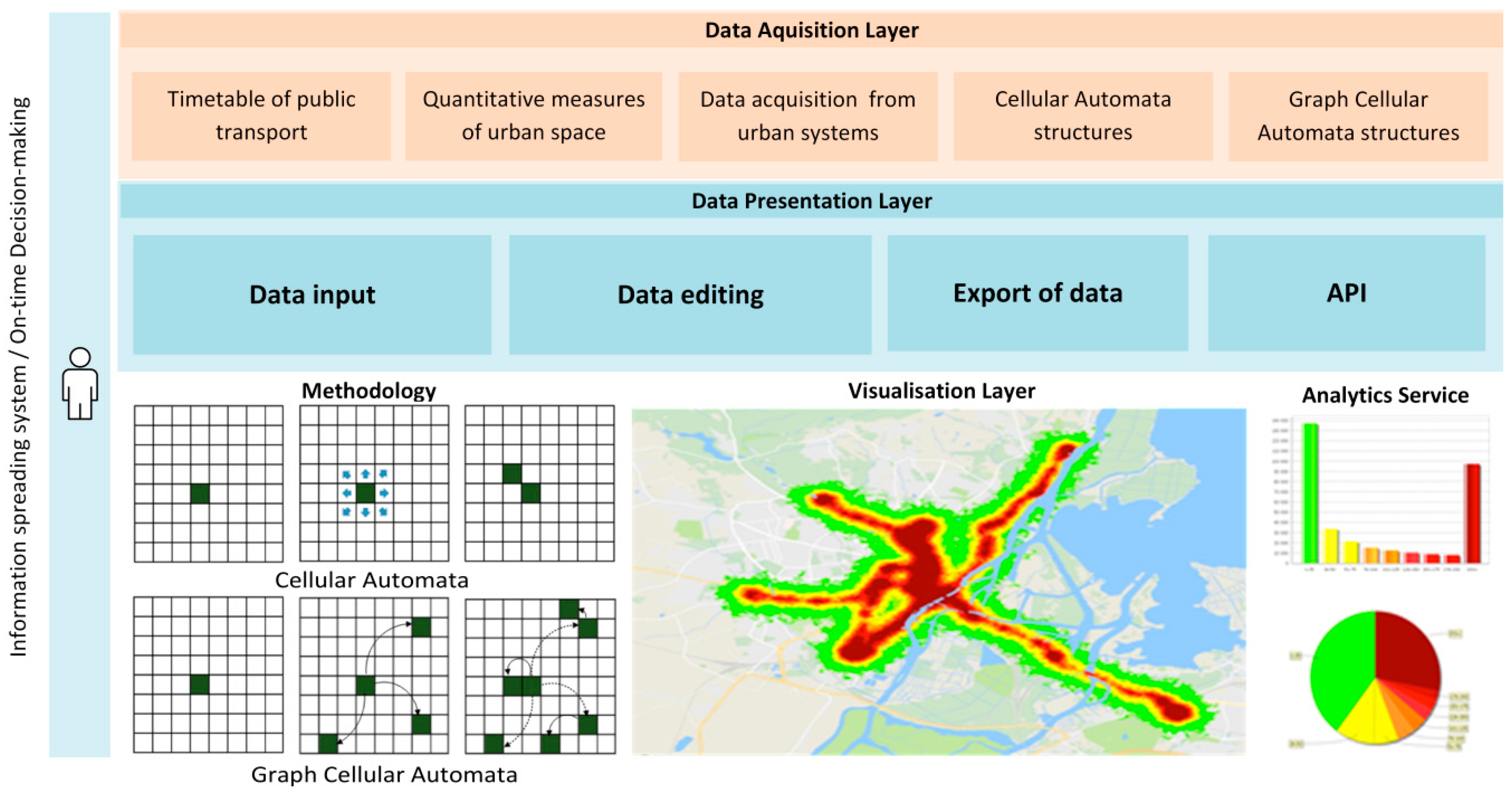
3. Proposed Approach
- automaton state , which depends on sets of states of individual cells;
- cell grid in (dimensional space ();
- rule defining the state of cell at time , which depends on the state of this cell and its neighbourhood at time . If is dependent on a random variable, then it is a probabilistic CA.
- dimension in a (dimensional space ()) that represents a cell grid;
- : activity state of an automaton, which depends on the set of activity states of individual cells;
- : state of the automaton, which depends on the set of states of individual cells;
- : directed weighted graph , which is defined by a set of nodes (hereinafter, vertices) , set of edges , set of weights and edge weight function . Function (the weight function) defines the weights of the edges of graph :where or, more generally, . Weights are values that indicate the significance of the connections between the vertices. In systems where there are many vertices that are connected to each other, not all connections have the same priority. For example, in the real world, crossing the road from one city to another may require a specific amount of time or energy; in the virtual world (in social networks), a user has various “friends” but does not have the same relationship with each of them.
- is a function that defines the state of automaton cell at time and depends on the state of this cell and its neighbourhood at time ;
- is a global rule that defines the conditions of activation or deactivation of CA cells and the rules of graph reconfiguration (defines sets of added and removed vertices and edges of graph by ), and depends on the automaton state (which represents the states of all cells); and
- is a function that reconfigures the graph and activates/deactivates cells based on conditions that are set by .
- physical: corresponding to the neighbourhood of the CA cells in the d-dimensional space within urban space, and
- logical: a set of relational neighbourhoods within social networks that are described by a -graph (which is reconfigurable in time), which enables the modelling of a system with a variable number of objects in time.
- any relation between the objects represented by the vertices of the graph (e.g., the relationship between people in an urban space or the relationship between people who are registered on the social network); or
- the distance between objects represented by the vertices of the graph.
- if the person is up to 20 m from the vehicle with the advertisement, then ;
- if the distance is between 21 and 30 m, then ;
- if the distance is between 31 and 40 m, then ;
- if the distance is between 41 and 50 m, then ;
- if the distance is between 51 and 60 m, then ;
- if the distance is between 61 and 80 m, then ;
- if the distance exceeds 80 m, .
- activating inactive cells of the CA (which corresponds to the addition of related vertices to the graph);
- deactivating cells of the CA (which corresponds to the removal of the corresponding vertices in the graph and the edges that are associated with them); and
- adding or removing edges in a graph, which results in the establishment or breaking of a neighbourhood relationship.
4. Results of Simulation
- timetables, which were acquired from the public transport company;
- a city map with a resolution of 640 × 640;
- the probability of stopping the person who is propagating information;
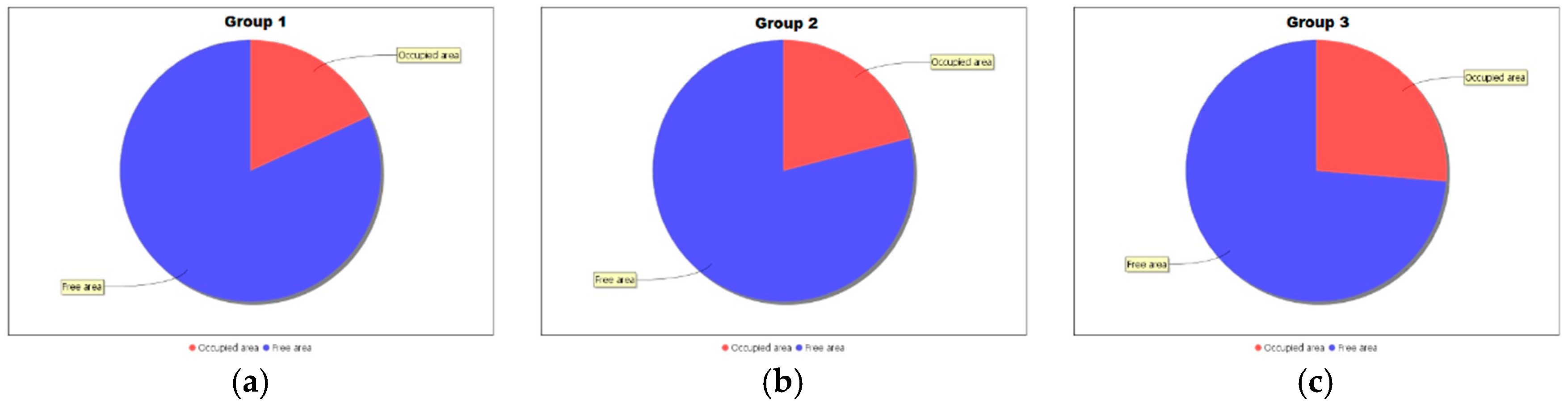
- tramway line numbers, followed by vehicles with the same advertisement, to increase the reminding effect: three tram lines: 1, 7, and 11 (Group 1); five tram lines: 2, 3, 6, 8, and 12 (Group 2); and all ten tram lines (Group 3): 1, 2, 3, 5, 6, 7, 8, 10, 11, and 12.
4.1. Modelling Results Based on Classic Cellular Automata
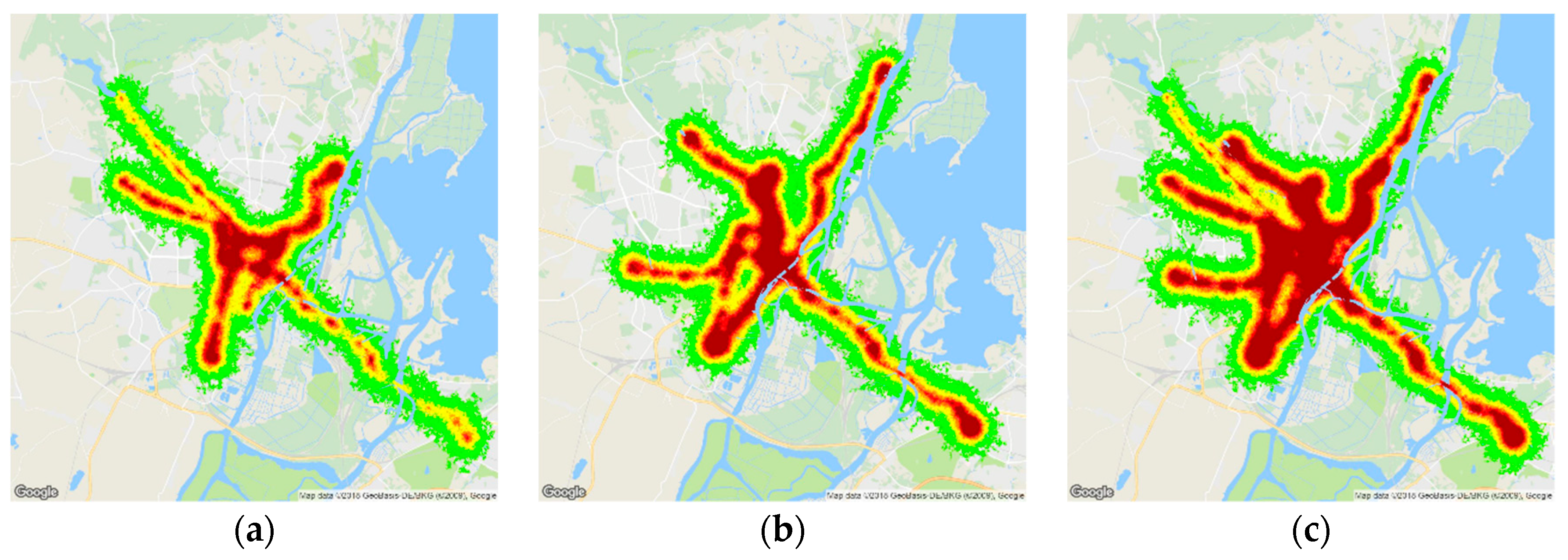
4.2. Modelling Results Based on Graph Cellular Automata
4.3. Symmetry Aspects
4.4. Limitations of the Study
5. Conclusions
- development of a model that is based on classical and cellular graph automata for the representation of information propagation within an urban space that is initiated by transit advertising;
- development of a new method for measuring the effectiveness of transit advertising within an urban space; and
- implementation of a practical framework for simulation research and verification of the presented methods.
Author Contributions
Funding
Conflicts of Interest
References
- Broderick, F. The Biggest Data Trends for Outdoor Advertising in 2017—CARTO Blog. Available online: https://carto.com/blog/biggest-data-trends-outdoor-advertising-2017/ (accessed on 25 May 2018).
- Stillman, L.; Letang, V. Global Advertising Forecast. Available online: https://www.magnaglobal.com/wp-content/uploads/2016/12/MAGNA-December-Global-Forecast-Update-Press-Release-1.pdf (accessed on 25 May 2018).
- Fortenberry, J.L.; McGoldrick, P.J. Receptiveness of Black Americans to outdoor advertising. J. Bus. Res. 2011, 64, 586–593. [Google Scholar] [CrossRef]
- Veloutsou, C.; O’Donnell, C. Exploring the effectiveness of taxis as an advertising medium. Int. J. Advert. 2005, 24, 217–239. [Google Scholar] [CrossRef]
- Gray, J. How to move into moving media: Transit media. J. Mark. 2008, 4, 40–41. [Google Scholar]
- Pavel, C.; Cătoiu, I. Unconventional advertising for unconventional media. Rev. Econ. 2009, 2, 142–145. [Google Scholar]
- Belch, G.E.; Belch, M.A. Advertising and Promotion: An Integrated Marketing Communications Perspective; McGraw-Hill: New York, NY, USA, 2004. [Google Scholar]
- Hampp, A. Advertising Boosts Transit Budgets. Available online: http://adage.com/article/media/advertising-boosts-transit-budgets/132024/ (accessed on 13 Jun 2018).
- Hoffman, D.L.; Novak, T.P. Marketing in Hypermedia Environment Foundations: Conceptual Foundations. J. Mark. 1996, 60, 50–68. [Google Scholar] [CrossRef]
- Lamberton, C.; Stephen, A.T. A Thematic Exploration of Digital, Social Media, and Mobile Marketing: Research Evolution from 2000 to 2015 and an Agenda for Future Inquiry. J. Mark. 2016, 80, 146–172. [Google Scholar] [CrossRef]
- Chaffey, D.; Ellis-Chadwick, F.; Mayer, R.; Johnston, K. Internet Marketing:Strategy, Implementation and Practice; Pearson Education: London, UK, 2009; ISBN 9780273694052. [Google Scholar]
- Roux, T.; van der Waldt, D.L.R.; Ehlers, L. A classification framework for out-of-home advertising media in South Africa. Communicatio 2013, 39, 383–401. [Google Scholar] [CrossRef]
- Lee, S.E.; McElheny, M.J.; Gibbons, R. Driving Performance and Digital Billboards; Research report, Virginia Tech Transportation Institute: Blacksburg, VA, USA, 2007. [Google Scholar]
- Liu, X.; Krahnstoever, N.; Yu, T.; Tu, P. What are customers looking at? In Proceedings of the 2007 IEEE Conference on Advanced Video and Signal Based Surveillance, London, UK, 5–7 September 2007; pp. 405–410. [Google Scholar]
- Want, R.; Schilit, B.N. Interactive digital signage. Comput. (Long Beach Calif.) 2012, 45, 21–24. [Google Scholar] [CrossRef]
- Roux, T. The Effectiveness of Car Advertising Media: Perceptions of Generation-Y Consumers. Mediterr. J. Soc. Sci. 2014, 5, 1877. [Google Scholar] [CrossRef]
- Bhargava, M.; Donthu, N. Sales response to outdoor advertising. J. Advert. Res. 1999, 39, 7–18. [Google Scholar]
- Bhargava, M.; Donthu, N.; Caron, R. Improving the Effectiveness of Outdoor Advertising: Lessons from a Study of 282 Campaigns. J. Advert. Res. 1994, 34, 46–55. [Google Scholar]
- Woodside, A.G. Outdoor advertising as experiments. J. Acad. Mark. Sci. 1990, 18, 229–237. [Google Scholar] [CrossRef]
- Osborne, A.C.; Coleman, R. Outdoor advertising recall: A comparison of newer technology and traditional billboards. J. Curr. Issues Res. Advert. 2008, 30, 13–30. [Google Scholar] [CrossRef]
- Taylor, C.R.; Franke, G.R.; Bang, H.-K. Use and Effectiveness of Billboards: Perspectives from Selective-Perception Theory and Retail-Gravity Models. J. Advert. 2006, 35, 21–34. [Google Scholar] [CrossRef]
- Wilson, R.T.; Till, B.D. Effects of outdoor advertising: Does location matter? Psychol. Mark. 2011, 28, 909–933. [Google Scholar] [CrossRef]
- Jurca, M.A. The Forms of Unconventional Advertising—A Theoretical Approach. Manag. Mark. J. 2010, 8, 323–333. [Google Scholar]
- Kobliski, K.J. The Advantages of Transit Advertising. Available online: https://www.entrepreneur.com/article/76826 (accessed on 18 March 2018).
- Chan, K.; Fung, M. Effectiveness of subway advertising in Hong Kong. J. Mass Commun. 2013, 3, 486–501. [Google Scholar]
- Hall, E. London bus ads change as locations do. Advert. Age 2006, 77, 12. [Google Scholar]
- Donthu, N.; Cherian, J.; Bhargava, M. Factors influencing recall of outdoor advertising. J. Advert. Res. 1993, 33, 64–72. [Google Scholar]
- King, K.W.; Tinkham, S.F. The learning and retention of outdoor advertising. J. Advert. Res. 1989, 29, 47–56. [Google Scholar] [CrossRef]
- Gambetti, R.C. Ambient Communication: How to Engage Consumers in Urban Touch-Points. Calif. Manag. Rev. 2010, 52, 34–51. [Google Scholar] [CrossRef]
- Keller, E.; Keller, E.; Berry, J.; Berry, J. Word-of-mouth: The real action is offline. Advert. Age 2006, 77, 20. [Google Scholar]
- Fay, K.; Thomson, S. WOM is More Offline Than Online around Brands. Available online: https://www.warc.com/content/paywall/article/admap/wom_is_more_offline_than_online/97996 (accessed on 13 May 2018).
- Katz, E.; Lazarsfeld, P.F. Personal Influence, the Part Played by People in the Flow of Mass Communications; Transaction Publishers: Piscataway, NJ, USA, 1966. [Google Scholar]
- Brown, J.J.; Reingen, P.H. Social Ties and Word-of-Mouth Referral Behavior. J. Consum. Res. 1987, 14, 350–362. [Google Scholar] [CrossRef]
- Bone, P.F. Word-of-mouth effects on short-term and long-term product judgments. J. Bus. Res. 1995, 32, 213–223. [Google Scholar] [CrossRef]
- Sundaram, D.S.; Mitra, K.; Webster, C. Word-of-Mouth Communications: A Motivational Analysis. Available online: http://w.acrwebsite.org/search/view-conference-proceedings.aspx?Id=8208 (accessed on 13 May 2018).
- Helm, S. Viral Marketing—Establishing Customer Relationships by “Word-of-mouse”. Electron. Mark. 2000, 10, 158–161. [Google Scholar] [CrossRef]
- Chen, W.; Wang, C.; Wang, Y. Scalable influence maximization for prevalent viral marketing in large-scale social networks. In Proceedings of the 16th ACM SIGKDD international conference on Knowledge discovery and data mining—KDD ’10, Washington, DC, USA, 25–28 July 2010; p. 1029. [Google Scholar]
- Trusov, M.; Bucklin, R.E.; Pauwels, K. Effects of Word-of-Mouth Versus Traditional Marketing: Findings from an Internet Social Networking Site. J. Mark. 2009, 73, 90–102. [Google Scholar] [CrossRef]
- Kandhway, K.; Kuri, J. How to run a campaign: Optimal control of SIS and SIR information epidemics. Appl. Math. Comput. 2014, 231, 79–92. [Google Scholar] [CrossRef]
- Kempe, D.; Kleinberg, J.; Tardos, É. Maximizing the spread of influence through a social network. In Proceedings of the ninth ACM SIGKDD international conference on Knowledge discovery and data mining—KDD ’03, Washington, DC, USA, 24–27 August 2003; p. 137. [Google Scholar]
- Rosnow, R.L.; Esposito, J.L.; Gibney, L. Factors influencing rumor spreading: Replication and extension. Lang. Commun. 1988, 8, 29–42. [Google Scholar] [CrossRef]
- Pittel, B. On Spreading a Rumor. SIAM J. Appl. Math. 1987, 47, 213–223. [Google Scholar] [CrossRef]
- Kesten, H.; Sidoravicius, V. The spread of a rumor or infection in a moving population. Annu. Probab. 2005, 33, 2402–2462. [Google Scholar] [CrossRef]
- Fu, L.; Song, W.; Lv, W.; Lo, S. Simulation of emotional contagion using modified SIR model: A cellular automaton approach. Phys. A 2014, 405, 380–391. [Google Scholar] [CrossRef]
- Huang, L.; Park, K.; Lai, Y.C. Information propagation on modular networks. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2006, 73, 035103. [Google Scholar] [CrossRef] [PubMed]
- Bampo, M.; Ewing, M.T.; Mather, D.R.; Stewart, D.; Wallace, M. The effects of the social structure of digital networks on viral marketing performance. Inf. Syst. Res. 2008, 19, 273–290. [Google Scholar] [CrossRef]
- Aral, S.; Muchnik, L.; Sundararajan, A. Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc. Natl. Acad. Sci. USA 2009, 106, 21544–21549. [Google Scholar] [CrossRef] [PubMed]
- Sahneh, F.D.; Scoglio, C.; Van Mieghem, P. Generalized epidemic mean-field model for spreading processes over multilayer complex networks. IEEE/ACM Trans. Netw. 2013, 21, 1609–1620. [Google Scholar] [CrossRef]
- Stonedahl, F.; Rand, W.; Wilensky, U. Evolving viral marketing strategies. In Proceedings of the 12th annual conference on Genetic and evolutionary computation—GECCO ’10, Portland, OR, USA, 7–11 July 2010; ACM Press: New York, NY, USA, 2010; p. 1195. [Google Scholar]
- Toffoli, T. Cellular Automata As an Alternative To Differential Equations in Modeling Physics. Phys. D 1984, 10, 117–127. [Google Scholar] [CrossRef]
- Toffoli, T.; Margolus, N. Cellular Automata Machines: A New Environment for Modeling; MIT Press: Cambridge, MA, USA, 1988. [Google Scholar]
- White, R.; Engelen, G. Cellular Automata and Fractal Urban Form: A Cellular Modelling Approach to the Evolution of Urban Land-Use Patterns. Environ. Plan. A 1993, 25, 1175–1199. [Google Scholar] [CrossRef]
- Batty, M.; Xie, Y. From Cells to Cities. Environ. Plan. B Plan. Des. 1994, 21, S31–S48. [Google Scholar] [CrossRef]
- Wagner, D.F. Cellular automata and geographic information systems. Environ. Plan. B Plan. Des. 1997, 24, 219–234. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G. Calibration of cellular automata by using neural networks for the simulation of complex urban systems. Environ. Plan. A 2001, 33, 1445–1462. [Google Scholar] [CrossRef]
- Dietzel, C.; Clarke, K. The effect of disaggregating land use categories in cellular automata during model calibration and forecasting. Comput. Environ. Urban Syst. 2006, 30, 78–101. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.O. Principal component analysis of stacked multi-temporal images for the monitoring of rapid urban expansion in the Pearl River Delta. Int. J. Remote Sens. 1998, 19, 1501–1518. [Google Scholar] [CrossRef]
- Lo, C.P.; Yang, X. Drivers of Land-Use/Land-Cover Changes and Dynamic Modeling for the Atlanta, Georgia Metropolitan Area. Photogramm. Eng. Remote Sens. 2002, 68, 1073–1082. [Google Scholar]
- Ward, D.P.; Murray, A.T.; Phinn, S.R. A stochastically constrained cellular model of urban growth. Comput. Environ. Urban Syst. 2000, 24, 539–558. [Google Scholar] [CrossRef]
- Li, X.; Yeh, A.G.-O. Neural-network-based cellular automata for simulating multiple land use changes using GIS. Int. J. Geogr. Inf. Sci. 2002, 16, 323–343. [Google Scholar] [CrossRef]
- Arai, K. Cell Based GIS as Cellular Automata for Disaster Spreading Predictions and Required Data Systems. Data Sci. J. 2013, 12, WDS154–WDS158. [Google Scholar] [CrossRef]
- Alexandridis, A.; Vakalis, D.; Siettos, C.I.; Bafas, G.V. A cellular automata model for forest fire spread prediction: The case of the wildfire that swept through Spetses Island in 1990. Appl. Math. Comput. 2008, 204, 191–201. [Google Scholar] [CrossRef]
- Gao, N.; Weng, W.; Ma, W.; Ni, S.; Huang, Q.; Yuan, H. Fire Spread Model for Old Towns Based on Cellular Automaton. Tsinghua Sci. Technol. 2008, 13, 736–740. [Google Scholar] [CrossRef]
- Progias, P.; Sirakoulis, G.C. An FPGA processor for modelling wildfire spreading. Math. Comput. Model. 2013, 57, 1436–1452. [Google Scholar] [CrossRef]
- Shyue, S.; Sung, H.; Chiu, Y. Oil Spill Modeling Using 3D Cellular Automata For Coastal Waters. In Proceedings of the The Seventeenth International Offshore and Polar Engineering Conference, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Gług, M.; Wąs, J. Modeling of oil spill spreading disasters using combination of Langrangian discrete particle algorithm with Cellular Automata approach. Ocean Eng. 2018, 156, 396–405. [Google Scholar] [CrossRef]
- Holko, A.; Mędrek, M.; Pastuszak, Z.; Phusavat, K. Epidemiological modeling with a population density map-based cellular automata simulation system. Expert Syst. Appl. 2016, 48, 1–8. [Google Scholar] [CrossRef]
- Ion, S.; Marinoschi, G. A Self-Organizing Criticality Mathematical Model for Contamination and Epidemic Spreading. Discret. Contin. Dyn. Syst. B 2017, 22, 383–405. [Google Scholar] [CrossRef]
- Pereira, F.M.M.; Schimit, P.H.T. Dengue fever spreading based on probabilistic cellular automata with two lattices. Phys. A Stat. Mech. Appl. 2018, 499, 75–87. [Google Scholar] [CrossRef]
- Burkhead, E.G.; Hawkins, J.M. Nondeterministic and stochastic cellular automata and virus dynamics. J. Cell. Autom. 2018, 13, 103–119. [Google Scholar]
- Daliri Khomami, M.M.; Rezvanian, A.; Bagherpour, N.; Meybodi, M.R. Irregular cellular automata based diffusion model for influence maximization. In Proceedings of the 2017 5th Iranian Joint Congress on Fuzzy and Intelligent Systems (CFIS), Qazvin, Iran, 7–9 March 2017; pp. 69–74. [Google Scholar]
- Hu, Y.; Yu, J.; Zong, F. Cellular Automata Model to Simulate the Spreading of Mobile Phone Messages Virus. J. Inf. Comput. Sci. 2013, 10, 3579–3586. [Google Scholar] [CrossRef]
- Schimit, P.H.T.; Barros Junior, D.F.; Araújo, S.A. On estimating the impact of information spreading in a consumer market modeled by probabilistic cellular automata and ordinary differential equations. Simulation 2017, 93, 1063–1072. [Google Scholar] [CrossRef]
- Wu, A.; Control, A.R.-I. Cellular graph automata. I. Basic concepts, graph property measurement, closure properties. Inf. Control 1979, 42, 305–329. [Google Scholar] [CrossRef]
- Marr, C.; Hütt, M.T. Topology regulates pattern formation capacity of binary cellular automata on graphs. Phys. A Stat. Mech. Appl. 2005, 354, 641–662. [Google Scholar] [CrossRef]
- Marr, C.; Hütt, M.T. Cellular automata on graphs: Topological properties of er graphs evolved towards low-entropy dynamics. Entropy 2012, 14, 993–1010. [Google Scholar] [CrossRef]
- O’Sullivan, D. Graph-cellular automata: A generalised discrete urban and regional model. Environ. Plan. B Plan. Des. 2001, 28, 687–705. [Google Scholar] [CrossRef]
- Małecki, K.; Jankowski, J.; Rokita, M. Application of graph cellular automata in social network based recommender system. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2013; Volume 8083, pp. 21–29. ISBN 9783642404948. [Google Scholar]
- Małecki, K.; Watróbski, J. The Classification of Internet Shop Customers based on the Cluster Analysis and Graph Cellular Automata. Procedia Comput. Sci. 2017, 112, 2280–2289. [Google Scholar] [CrossRef]
- Pendleton, S.C. Rumor research revisited and expanded. Lang. Commun. 1998, 18, 69–86. [Google Scholar] [CrossRef]
- Daley, D.J.; Kendall, D.G. Epidemics and Rumours. Nature 1964, 204, 1118. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology: I. An Introduction; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Narayanam, R.; Nanavati, A.A. Viral marketing for product cross-sell through social networks. In Lecture Notes in Computer Science (including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Berlin/Heidelberg, Germany, 2012; Volume 7524, pp. 581–596. ISBN 9783642334856. [Google Scholar]
- Aldrees, M.; Ykhlef, M. A Seeding Cellular Learning Automata Approach for Viral Marketing In Social Network. In Proceedings of the 16th International Conference on Information Integration and Web-based Applications & Services—iiWAS ’14, Hanoi, Viet Nam, 4–6 December 2014; pp. 59–63. [Google Scholar] [CrossRef]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002; ISBN 1579550088. [Google Scholar]
- Hoffmann, R.; Völkmann, K.P.; Waldschmidt, S.; Heenes, W. GCA: Global Cellular Automata. A Flexible Parallel Model. In Parallel Computing Technologies; Springer: Berlin/Heidelberg, Germany, 2001; pp. 66–73. ISBN 9783540425229. [Google Scholar]
- Barredo, J.; Kasanko, M. Modelling dynamic spatial processes: Simulation of urban future scenarios through cellular automata. Landsc. Urban Plan. 2003, 64, 145–160. [Google Scholar] [CrossRef]
- Stevens, D.; Dragićević, S. A GIS-based irregular cellular automata model of land-use change. Environ. Plan. B Plan. Des. 2007, 34, 708–724. [Google Scholar] [CrossRef]
- Santé, I.; García, A.M.; Miranda, D.; Crecente, R. Cellular automata models for the simulation of real-world urban processes: A review and analysis. Landsc. Urban Plan. 2010, 96, 108–122. [Google Scholar] [CrossRef]
- Barreira-González, P.; Barros, J. Configuring the neighbourhood effect in irregular cellular automata based models. Int. J. Geogr. Inf. Sci. 2017, 31, 617–636. [Google Scholar] [CrossRef]
- Dahal, K.R.; Chow, T.E. Characterization of neighborhood sensitivity of an irregular cellular automata model of urban growth. Int. J. Geogr. Inf. Sci. 2015, 29, 475–497. [Google Scholar] [CrossRef]
- Mamei, M.; Roli, A.; Zambonelli, F. Emergence and control of macro-spatial structures in perturbed cellular automata, and implications for pervasive computing systems. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2005, 35, 337–348. [Google Scholar] [CrossRef]
- Missoum, S.; Gürdal, Z.; Setoodeh, S. Study of a new local update scheme for cellular automata in structural design. Struct. Multidiscip. Optim. 2005, 29, 103–112. [Google Scholar] [CrossRef]
- Wąs, J.; Sirakoulis, G.C. Cellular Automata Applications for Research and Industry. J. Comput. Sci. 2015, 11. [Google Scholar] [CrossRef]
- Weimar, J.R. Cellular automata for reaction-diffusion systems. Parallel Comput. 1997, 23, 1699–1715. [Google Scholar] [CrossRef]
- Wixted, J.T.; Ebbesen, E.B. Genuine power curves in forgetting: A quantitative analysis of individual subject forgetting functions. Mem. Cogn. 1997, 25, 731–739. [Google Scholar] [CrossRef]
- Małecki, K. Graph cellular automata with relation-based neighbourhoods of cells for complex systems modelling: A case of traffic simulation. Symmetry (Basel) 2017, 9, 322. [Google Scholar] [CrossRef]
- Weidmann, U. Transporttechnik der Fußgänger—Transporttechnische Eigenschaften des Fußgängerverkehrs (Literaturauswertung). In Schriftenreihe des IVT (90); ETH Zürich: Zürich, Switzerland, 1992. [Google Scholar]
- Tanaka, I. Effects of initial symmetry on the global symmetry of one-dimensional legal cellular automata. Symmetry (Basel) 2015, 7, 1768–1779. [Google Scholar] [CrossRef]
- Evsutin, O.; Shelupanov, A.; Meshcheryakov, R.; Bondarenko, D.; Rashchupkina, A. The algorithm of continuous optimization based on the modified cellular automaton. Symmetry (Basel) 2016, 8, 84. [Google Scholar] [CrossRef]
- Vellarayil Mohandas, N.; Jeganathan, L. Classification of Two Dimensional Cellular Automata Rules for Symmetric Pattern Generation. Symmetry (Basel) 2018, 10, 772. [Google Scholar] [CrossRef]
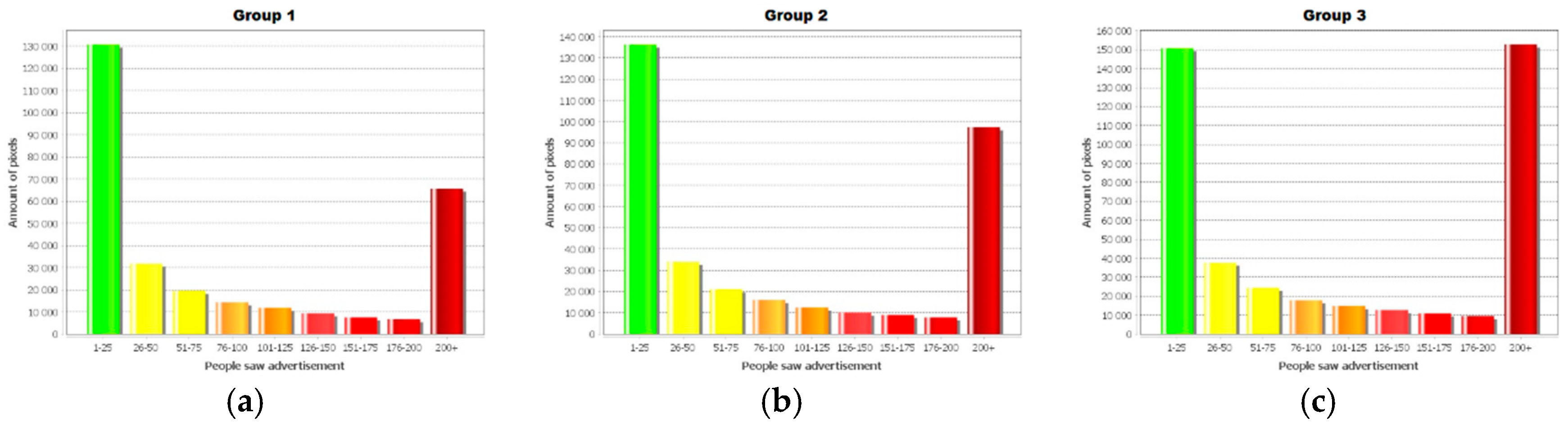
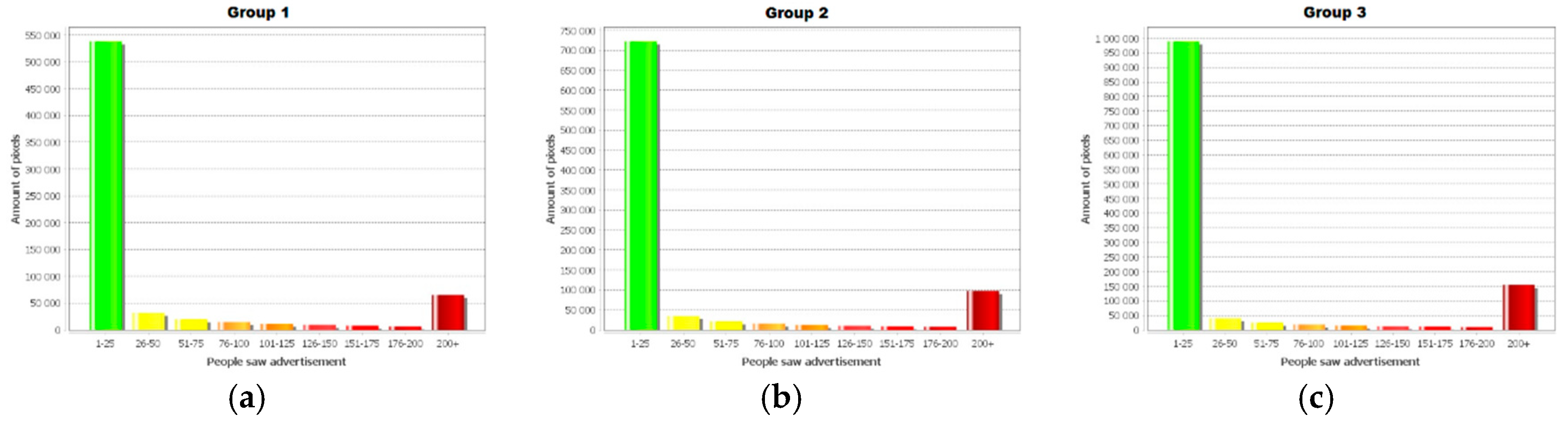

| Contacts | Three Lines | Five Lines | Ten Lines | |||
|---|---|---|---|---|---|---|
| Cells | Coverage | Cells | Coverage | Cells | Coverage | |
| 201+ | 65,694 | 22.08% | 97,311 | 28.29% | 152,742 | 35.45% |
| 176–200 | 6726 | 2.26% | 7832 | 2.28% | 9420 | 2.19% |
| 151–175 | 7515 | 2.53% | 8979 | 2.61% | 10,848 | 2.52% |
| 126–150 | 9355 | 3.14% | 10,074 | 2.93% | 12,598 | 2.92% |
| 101–125 | 11,819 | 3.97% | 12,474 | 3.63% | 14,712 | 3.41% |
| 76–100 | 14,326 | 4.81% | 16,002 | 4.65% | 17,778 | 4.13% |
| 51–75 | 19,476 | 6.54% | 20,988 | 6.10% | 24,278 | 5.64% |
| 26–50 | 31,846 | 10.70% | 34,059 | 9.90% | 37,634 | 8.74% |
| 1–25 | 130,816 | 43.96% | 136,318 | 39.62% | 150,804 | 35.00% |
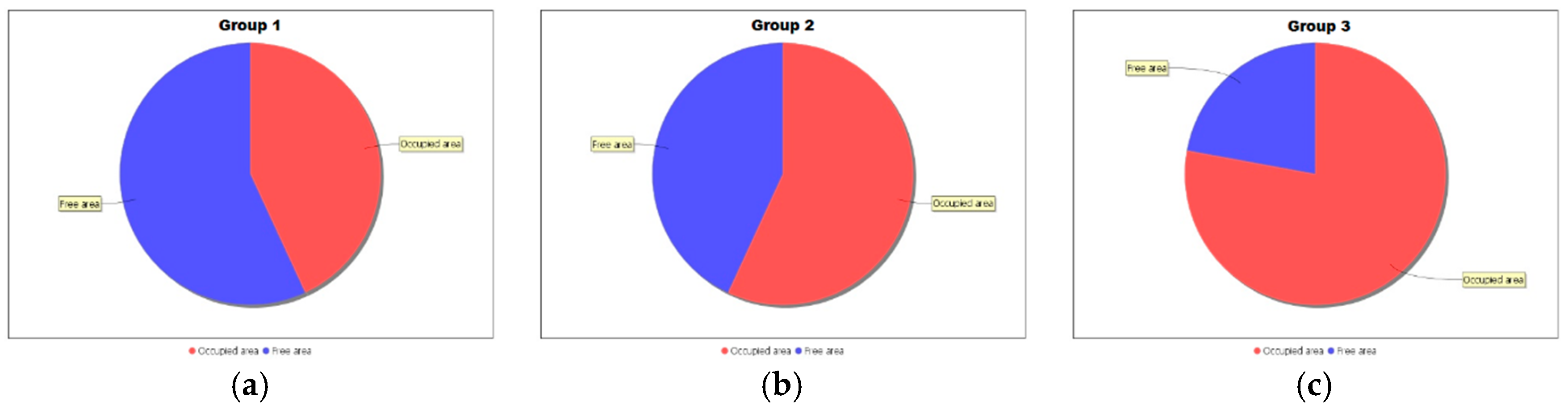
| Reached | 297,573 | 18.16% | 344,037 | 21.00% | 430,814 | 26.29% |
| Not reached | 1,340,827 | 81.84% | 1,294,363 | 79.00% | 1,207,586 | 73.71% |
| Contacts | Three Lines | Five Lines | Ten Lines | |||
|---|---|---|---|---|---|---|
| Cells | Coverage | Cells | Coverage | Cells | Coverage | |
| 201+ | 65,283 | 9.25% | 97,550 | 10.46% | 154,055 | 12.08% |
| 176–200 | 6562 | 0.93% | 7834 | 0.84% | 9694 | 0.76% |
| 151–175 | 7908 | 1.12% | 8946 | 0.96% | 11,463 | 0.90% |
| 126–150 | 9420 | 1.33% | 10,532 | 1.13% | 12,717 | 1.00% |
| 101–125 | 11,524 | 1.63% | 12,461 | 1.34% | 15,023 | 1.18% |
| 76–100 | 14,769 | 2.09% | 16,059 | 1.72% | 18,472 | 1.45% |
| 51–75 | 19,843 | 2.81% | 21,344 | 2.29% | 24,884 | 1.95% |
| 26–50 | 32,058 | 4.54% | 34,946 | 3.75% | 40,357 | 3.16% |
| 1–25 | 538,339 | 76.28% | 722,761 | 77.51% | 989,143 | 77.53% |
| Reached | 705,706 | 43.07% | 932,433 | 56.91% | 1,275,808 | 77.87% |
| Not reached | 932,694 | 56.93% | 705,967 | 43.09% | 362,592 | 22.13% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Małecki, K.; Jankowski, J.; Szkwarkowski, M. Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata. Symmetry 2019, 11, 428. https://doi.org/10.3390/sym11030428
Małecki K, Jankowski J, Szkwarkowski M. Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata. Symmetry. 2019; 11(3):428. https://doi.org/10.3390/sym11030428
Chicago/Turabian StyleMałecki, Krzysztof, Jarosław Jankowski, and Mateusz Szkwarkowski. 2019. "Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata" Symmetry 11, no. 3: 428. https://doi.org/10.3390/sym11030428
APA StyleMałecki, K., Jankowski, J., & Szkwarkowski, M. (2019). Modelling the Impact of Transit Media on Information Spreading in an Urban Space Using Cellular Automata. Symmetry, 11(3), 428. https://doi.org/10.3390/sym11030428






