Abstract
The 2-tuple linguistic information model (2TLIM) is a useful tool to avoid the loss of information, which has been widely adapted in the study of the multiple attribute decision making (MADM) problem. However, there is a limitation, the limitation is that the difference between the neighboring 2-tuple linguistic information is fixed regardless of the decision-makers’ attitude. In this paper, we define the utility transformation functions based on the 2-tuple linguistic utility to overcome the drawback. Firstly, by introducing the economic utility theory, the 2-tuple linguistic utility is defined, the 2-tuple linguistic utility parameter (2TLUP) and the 2-tuple linguistic marginal utility (2TLMU) are constructed to achieve the measurement of the decision-makers’ attitude. The utility transformation functions are developed on the decision-makers’ attitude. Secondly, the 2-tuple linguistic operational laws are presented with the extended Hamacher T-norm (TN) and T-conorm (TC). Subsequently, we propose the 2-tuple linguistic utility weighted average (2TLUWA) operator and the method of MADM. Lastly, the application and the comparison with the existing methods are summarized to verify the practicality and advantages of the proposed method of MADM.
1. Introduction
There are many multiple attribute decision making (MADM) problems with imprecise information in the actual world, Zadeh [1] presented the fuzzy sets (FSs) to express the evaluation value by fuzzy information, which have been widely used to certify the practicality. Subsequently, the extended fuzzy sets have been proposed to express the evaluation value in detail. The hesitant fuzzy sets [2] could indicate the evaluation value with the membership function, which could show the subjective membership value of the evaluation value; the intuitionistic fuzzy sets [3] produced by Atanassov could express the evaluation value with the membership functions and non-membership functions, which could show the subjective membership value and non-membership value of the evaluation value. In view of the difficulty in giving the numerical evaluation value, the definition of linguistic term sets (LTSs) [4] has been proposed to overcome the issue, then the evaluation value could be expressed qualitatively. In order to indicate the linguistic information specifically, the extended linguistic term sets have been defined, such as the hesitant fuzzy linguistic term sets [5], the linguistic intuistionstic fuzzy sets [6], and the probabilistic linguistic term sets [7], to enrich the study of MADM. The study of multi-criteria decision aid (MCDA) has attracted many experts: Morente-Molinera [8] proposed the fuzzy ontologies and multi-granular linguistic modeling methods to solve the MADM problem; W. Sałabun [9] settled the MADM problem without the rank reversal phenomenon; S. Faizi [10] presented the characteristic objects method to handle the group decision-making problem; Garca-Daz [11] introduced the probabilistic classifiers into the study of MADM problem.
In the operational aggregation of linguistic term information, the result may exceed the range of LTSs. So as to prevent the information distortion, the 2-tuple linguistic information model (2TLIM) [4] has been developed with the transformation functions. By adding the symbolic translation value with the linguistic term, the 2TLIM achieves the transformation between the aggregation result value and the 2-tuple linguistic information. The 2TLIM constructs a continuous representation without loss of information, which is an effective tool for the MADM problem.
Considering the practicality of the 2TLIM, the extended 2TLIMs have been proposed, such as the intuitionistic 2-tuple linguistic set [12], the interval valued 2-tuple linguistic model [13]. Additionally, the methods for MADM with the extended 2TLIM have been extensively studied. Just as the TOPSIS methods [14,15], the grey relational analysis methods [16,17], the VIKOR methods [18,19]. The key step of the methods is the aggregation of evaluation value. So some operators have been used to achieve the aggregation, such as the Bonferroni operators [20], the power weighted average operators [21], the Choquet integral operators [22,23]. Additionally, the core of the aggregation operator is the 2-tuple linguistic information operational laws. The operational laws with 2-tuple linguistic information have been widely studied, Herrera and Martinez [4] defined the transformation functions which could convert the 2-tuple linguistic information into the aggregation value. Wan [24] defined the 2-tuple linguistic operational laws, but the aggregation results may exceed the range. Then the T-norm (TN) and the T-conorm (TC)are introduced to the study of 2TLIM, Tao [25] proposed the novel 2-tuple linguistic operational laws to overcome this issue. Additionally, Liu [26] presented the extended 2-tuple linguistic operational laws based on the extended TN and TC, which enriched the aggregation methods of the 2-tuple linguistic information. Not only the operational laws of 2TLIM, but also the study of MADM with 2TLIM is constructed on the 2-tuple linguistic information transformation functions.
Let S be a LTS, by imposing the numerical value , the 2TLIM is developed as . Based on the existing transformation functions, the difference of the linguistic information is fixed as 1, namely, the range of the . However, in the real MADM, the difference may be not fixed with the different decision-makers’ attitude, the existing transformation functions couldn’t address this issue. Then we construct the utility transformation function based on the 2-tuple linguistic utility. When giving the 2-tuple linguistic evaluation value, there must be a satisfying value for the decision maker, and the same 2-tuple linguistic information may cause the different satisfying value for the different decision makers. Based on the existing transformation functions, the 2-tuple linguistic satisfying value is decided by the 2-tuple linguistic evaluation value, so the 2-tuple linguistic satisfying value difference between the neighboring 2-tuple linguistic information is fixed. It is easy to find the 2-tuple linguistic satisfying value is not only decided by the 2-tuple linguistic information, but also by the decision-makers’ attitude. Referring to the economic utility theory, the measurement of the satisfying value is based on the utility value. Hence, we define the 2-tuple linguistic utility and 2-tuple linguistic utility parameter (2TLUP). With the 2TLUP, the difference could be measured with the decision-makers’ attitude, the 2TLUP is more suitable for the decision-making environment and the utility transformation function are constructed with the decision-makers’ attitude. The main attributions of this paper are summarized below:
- (1)
- By introducing the economic utility theory, the definition of utility and the 2TLIM are combined to be the 2-tuple linguistic utility. Obviously, the 2-tuple linguistic utility is decided by the decision-makers’ attitude, the specific value can be indicated by the change of 2-tuple linguistic marginal utility (2TLMU). Then the 2TLUP is developed to measure the decision-makers’ attitude.
- (2)
- The utility transformation function are presented on the 2-tuple linguistic utility, the decision-makers’ attitude can be controlled by the value of 2TLUP, then the difference between the linguistic information can be changed with the decision-makers’ attitude.
- (3)
- Because the operational laws based on the TN and TC are closed, the 2-tuple linguistic operational laws are constructed with the utility transformation function and the extended Hamacher TN and TC. Ultimately, the 2-tuple linguistic utility weighted average (2TLUWA)operators are produced to realize the aggregation of the 2-tuple linguistic information.
- (4)
- The method of MADM with the 2-tuple linguistic information is presented with the specific step, and an application example is given to certify the availability of the utility transformation function.
The rest of this article is organized as follows. In Section 2, we review some concepts of LTSs, 2TLIM, and the economic utility theory. In Section 3, we define the 2-tuple linguistic utility, the 2TLMU, the 2TLUP and the 2-tuple linguistic utility transformation functions. In Section 4, we propose the 2-tuple linguistic Algebraic operational laws, the 2-tuple linguistic Einstein operational laws, the 2-tuple linguistic Hamacher operational laws and discuss their properties. In Section 5, we develop the 2TLUWA operator based on the novel operational laws and we present the new method for MADM based on the utility transformation function. In Section 6, we compare the presented method with the existing one to show the advantages and practicality. In Section 7, we give the conclusions.
2. Preliminaries
In this section, we briefly recall some basic concepts and properties of LTSs, the 2TLIM and the economic utility theory.
2.1. LTSs
Compared with the quantitative expression, the qualitative expression is more suitable for the MADM, in order to better solve the MADM problem, the concept of LTS is presented:
Definition 1.
[4] Let be a LTS. The LTS satisfies the properties: (1) for , the linguistic term is an qualitative expression, and is ranked in order; (2) the cardinal number of the LTSs is an odd number.
For example, if the cardinal number of the LTS is 7, we can get very bad, bad, slightly bad, fair, slightly good, good, very good}. The linguistic term is a kind of the qualitative evaluation value, which keeps with the decision making habits better. For convenience, then, we simplify the LTSs as .
2.2. 2-Tuple Linguistic Information Model
Because the operational results of LTSs may exceed the range of LTSs, then Herrera and Martinez [4] defined the 2TLIM to avoid the issue, the definition of 2TLIM and the transformation functions , are described as follows.
Definition 2.
[4] Let be a LTS, , and β represents the symbolic aggregation operation result, the equivalent information of β could be expressed by the 2-tuple linguistic information:
where , , and is the round operation.
Definition 3.
[4] Let be a LTS and be a 2-tuple linguistic information, , the equivalent information of 2-tuple could be expressed by the β:
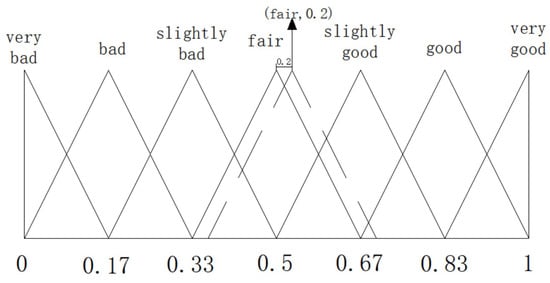
Let be a LTS, then is the 2TLIM, where the represents the linguistic term, the symbolic translation value α is the translation value from the aggregation value β to the index of the closest linguistic term . By the transformation functions Δ and , it is easy to convert the 2-tuple linguistic information into the real number , and the LTS is the special case of the 2TLIM, if , we can obtain . For convenience, the 2-tuple linguistic information is called 2-tuples. Suppose is the aggregation result value, and very bad, bad, slightly bad, fair, slightly good, good, very good}, the 2-tuple indicates the same information of β is (fair, 0.2) (see Figure 1).

Figure 1.
A 2-tuple linguistic information model.
Definition 4.
[4] For the 2-tuple , the negation operator of this 2-tuple is defined as follows [4].
where the cardinality of S is , and .
And the property of the comparison between 2-tuples is described as listed.
Theorem 1.
[4] Let and be two 2-tuples, and the property of comparison is given:
- (1)
- if , then ;
- (2)
- if ,
- when , then ;
- when , then ;
- when , then .
2.3. The Extended TN and TC
The TN and TC families are the effective methods to achieve the information aggregation, TN could achieve the intersections of the information, TC could achieve the unions of the information, then some basic operational laws are constructed on the basis of TN and TC. So as to adapt the TN and TC into the 2TLIM, Liu [26] extended the normal TN and TC of range into the range , which could work better in 2TLIM.
Definition 5.
[26] The function is called the extended TN, and a monotonically decreasing function is defined for the generator of the extended TN, for any , the extended TN is generated as ; the function is called the extended TC, and a monotonically increasing function is defined for the generator of the extended TC, for any , the extended TC is generated as , where .
The extended TN and TC families such as the extended Algebraic TN and TC, the extended Einstein TN and TC, the extended Hamacher TN and TC are constructed.
Theorem 2.
[26] Let be a LTS and the be the 2TLIM, so the range of the 2TLIM is . By extending the domain of the TN and TC, the extended one is more suitable for the 2TLIM. For any real number , the special cases of the extended TN and TC are listed.
Proof.
The extended Algebraic TN and TC are described by:
The extended Einstein TN and TC are described by:
The extended Hamacher TN and TC with the parameter are described by:
□
In summary, the extended TN and TC are shown in Table 1.

Table 1.
The extended TN and TC.
2.4. The Economic Utility Theory
The economic utility is defined to describe the satisfying value when in consumption activity, which is decided by the consumption quantity and the consumer attitude. And the utility theory is widely applied in the commodity selection.
When buying the commodity in quantity i, the consumer will obtain the utility value of . And the marginal utility(MU) can indicate the utility change from the continuous increase in each unit of consumption, as consumers increase the consumption of a certain commodity, which is described as follows:
When , it is called the increasing marginal utility;
when , it is called the fixed marginal utility;
when , it is called the decreasing marginal utility.
The utility is a subjective feeling of the consumer, the exact value of utility is decided by the consumption quantity i and the attitude of the consumer, so the change of the marginal utility can indicate the attitude of the consumer, which has been widely applied in the study of consumption habits. Bigger the utility value is, the more likely consumer are to consume.
3. The Utility Transformation Function Based on 2-Tuple Linguistic Utility
According the Definition 2, the 2TLIM is composed of the LTSs and the symbolic translation value . The is added to measure the difference between the linguistic information and avoid the loss of aggregation result. However, there is a drawback, the translation value is added to measure the difference of the aggregation value and the closest linguistic term , which indicates the difference of linguistic information is fixed as . It is easy to find the difference may be not fixed, for example: let be a LTS, and is the 2TLIM, then the difference between very good and good may be not same to the difference between good and slightly good. Additionally, for different decision-makers’ attitude, the difference maybe various.
When giving the 2-tuple linguistic evaluation value, there will be an utility value for the decision maker, the mentioned difference can be regarded as the difference of the 2-tuple linguistic utility value. Similar to the economic utility theory, we define the 2-tuple linguistic utility theory to not ignore the satisfying value of the 2-tuple linguistic information with different decision-makers’ attitude.
Definition 6.
When giving the 2-tuple linguistic information, there will be a satisfying value for the decision makers, the satisfying value is called the 2-tuple linguistic utility, which is determined by the decision-makers’ attitude. The 2-tuple linguistic utility function is defined, when giving the 2-tuple linguistic information evaluation value , there will be the 2-tuple linguistic utility for the decision maker, and the 2TLMU is produced as follows:
When , it is called the increasing 2-tuple linguistic marginal utility;
when , it is called the fixed 2-tuple linguistic marginal utility;
when , it is called the decreasing 2-tuple linguistic marginal utility.
It is not hard to find the 2-tuple linguistic utility is decided by the 2-tuple linguistic evaluation value and the 2-tuple linguistic utility attitude of decision maker, then the change of 2TLMU, can indicate the 2-tuple linguistic utility attitude of decision maker.
Obviously, the difference of linguistic information may be not fixed, and the difference value is not only decided by the 2-tuple linguistic information, but also by the decision-makers’ attitude. In the process of the MADM, there will be an utility value for the people with the 2-tuple linguistic evaluation value, the mentioned difference can be viewed as the difference of the 2-tuple linguistic utility. Let be a LTS, the 2TLIM is constructed as , the existing transformation functions convert the 2-tuple linguistic information to the real number by the addition of the index of and , which causes the difference is fixed. The existing transformation functions of 2TLIM is not enough to handle the issue, it is not easy to change the range of directly, so we incorporate the existing transformation functions with the 2-tuple linguistic utility to develop the utility transformation function, and the 2TLUP is proposed to measure the decision-makers’ attitude.
Definition 7.
Let be a LTS and be a 2-tuple linguistic information, when giving the 2-tuple , the decision maker will obtain the utility value as :
Definition 8.
Let be a LTS, the 2TLIM is constructed as . For the aggregated utility result , with the 2TLUP , then the 2-tuple linguistic information that express the utility information is obtained by the utility transformation function:
where and is the round operation.
The study of MADM can be regarded as the study on the utility value of alternatives. By the utility transformation function, it is easy to achieve the translation between the 2-tuple linguistic information and the aggregation utility result. The 2TLUP is decided by the 2-tuple linguistic utility attitude of the decision makers, the utility transformation functions are as realistic as possible to not ignore the decision-makers’ attitude.
Similar to the economic utility theory, the properties of the 2-tuple linguistic utility are given as follows:
Definition 9.
Let be a LTS, the 2TLIM is constructed as . When giving the 2-tuple linguistic information , the 2TLMU is the derivative of the 2-tuple linguistic utility function.
The 2TLUP is developed to measure the decision-makers’ attitude, same to the economic utility theory, the changes of 2TLMU are shown as follows:
When the 2TLUP , then , which indicates the increasing 2TLMU, as the 2-tuple linguistic information increases, the 2TLMU increases, and it reveals the high 2-tuple linguistic utility attitude of the decision makers;
when the 2TLUP , then , which indicates the fixed 2TLMU, as the 2-tuple linguistic information increases, the 2TLMU keeps fixed, and it reveals the fixed 2-tuple linguistic utility attitude of the decision makers, which is the existing transformation function , ;
when the 2TLUP , then , which indicates the decreasing 2TLMU, as the 2-tuple linguistic information increases, the 2TLMU decreases, and it reveals the low 2-tuple linguistic utility attitude of the decision makers.
By the above-mentioned study, each decision maker will match a 2TLUP in the MADM, and the different value of the 2TLUP will reveal the different 2-tuple linguistic utility attitude. With the fixed 2-tuple linguistic utility attitude, , the existing 2-tuple linguistic transformation function [4] is the special case of the utility transformation function. The utility transformation function achieve the translation between the 2-tuples and the aggregated result with the decision-makers’ attitude.
Example 1.
Let be a LTS, the 2TLIM is constructed as , by the utility transformation function, the aggregated utility result and the 2-tuple linguistic information could be translated with the 2-tuple linguistic utility attitude.
Case 1.
As for the decision maker with the high 2-tuple linguistic utility attitude, the corresponding 2TLUP , the specific value is decided by the decision maker.
If , then the corresponding utility transformation functions are given as follows:
For the aggregated utility result , the translated 2-tuple linguistic information is obtained as , , then ;
for the 2-tuple linguistic information , , , the utility values are obtained as , , ;
as for the difference of the linguistic information, it is obvious to get , with the 2-tuples increasing, the 2-tuple linguistic utility increases, and the 2TLMU increases.
Case 2.
As for the decision maker with the fixed 2-tuple linguistic utility attitude, the corresponding 2TLUP , the specific value is decided by the decision maker.
If , then the corresponding utility transformation functions are given as follows:
For the aggregated utility result , the translated 2-tuple linguistic information is obtained as , , then ;
for the 2-tuple linguistic information , , , the utility values are obtained as , , ;
as for the difference of the linguistic information, it is obvious to get , with the 2-tuples increasing, the 2-tuple linguistic utility increases, and the 2TLMU is fixed.
Case 3.
As for the decision maker with the low 2-tuple linguistic utility attitude, the corresponding 2TLUP , the specific value is decided by the decision maker.
If , then the corresponding utility transformation functions are given as follows:
For the aggregated utility result , the translated 2-tuple linguistic information is obtained as , , then ;
for the 2-tuple linguistic information , , , the utility values are obtained as , , ;
as for the difference of the linguistic information, it is obvious to get , with the 2-tuples increasing, the 2-tuple linguistic utility increases, and the 2TLMU is fixed.
Above all, the utility transformation function can achieve the measurement of the decision makers utility attitude, then it can calculate the difference between the linguistic information changes with the decision makers utility attitude. The different difference corresponds to the different decision-makers’ attitude. By changing the value of 2TLUP, the measurement of the different decision makers utility attitude and the difference between the linguistic information can be realized. To better understand the utility transformation function, with the different decision-makers’ attitude and the corresponding 2TLUP, the representational figures are given (see Figure 2, Figure 3 and Figure 4).
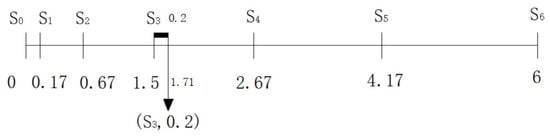
Figure 2.
The utility transformation function with .
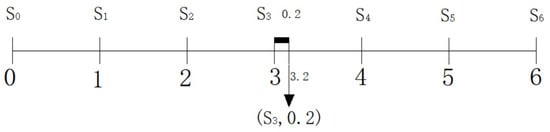
Figure 3.
The utility transformation function with .
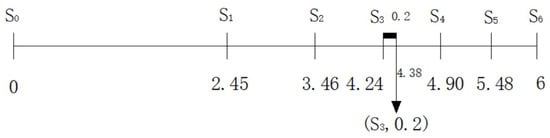
Figure 4.
The utility transformation function with .
By combining the existing transformation functions with the 2-tuple linguistic utility, the utility transformation function are constructed. There is an important parameter 2TLUP decided by the decision-makers’ attitude, then the functions achieve the measurement of the 2-tuple linguistic utility, the 2TLMU and the difference of the linguistic information, and the difference can be changed with the decision-makers’ attitude. By the change of 2TLUP, we realize the match of the 2-tuple linguistic utility and the utility attitude of the decision makers, which is more in line with the actual MADM problem.
4. The 2-Tuple Linguistic Operational Laws Based on the Utility Transformation Function
The researchers have done a lot in the aggregation of 2-tuples, and both the methods are based on the transformation functions and . Now, we develop the utility transformation function with the decision makers utility attitude, then the corresponding 2-tuple linguistic operational laws are constructed on the utility transformation function u and .
Definition 10.
Let be a LTS and be the 2TLIM, for 2-tuples , , with , based on the utility transformation function and the extended TN and TC families, the basic 2-tuple linguistic operational laws are described as follows:
For 2-tuples , , the results of the basic 2-tuple linguistic operational laws are still in the 2TLIM.
Proof.
Obviously, the utility transformation function and are the monotonically increasing functions and and are the monotonically increasing functions. It is easy to get , , with , then , and ; with , then ; with , it easy to get . Similarly, we can prove the aggregation results of the other operational laws are still in the 2TLIM. □
Meanwhile, the TN and TC families are too abundant to be researched, the special cases of the TN and TC families are picked up, just as the Algebraic TN and TC, the Einstein TN and TC and the Hamacher TN and TC. Then, based on the extended Algebraic TN and TC, the extended Einstein TN and TC and the extended Hamacher TN and TC [26], the 2-tuple linguistic operational laws based on the utility transformation function are developed.
Definition 11.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , based on the utility transformation function and the extended Algebraic TN and TC families, the extended Algebraic 2-tuple linguistic operational laws are constructed as follows:
Example 2.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , with the different value of 2TLUP , , , then we have:
For the decision maker with the high decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Algebraic operational laws with the high decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the fixed utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Algebraic operational laws with the fixed decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the low utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Algebraic operational laws with the low decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; .
Definition 12.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , based on the utility transformation function and the extended Einstein TN and TC families, the extended Einstein 2-tuple linguistic operational laws are constructed as follows:
Example 3.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , with the different value of 2TLUP , , , then we have:
For the decision maker with the high utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Einstein operational laws with the high decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the fixed utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Einstein operational laws with the fixed decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the low utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Einstein operational laws with the low decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; .
Definition 13.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , based on the utility transformation function and the extended Hamacher TN and TC families, the extended Hamacher 2-tuple linguistic operational laws with the parameter γ are constructed as follows:
Example 4.
Let be a LTS and be the 2TLIM, for 2-tuples , , for , the , with the different value of 2TLUP , , , then we have:
For the decision maker with the high utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Hamacher operational laws with the high decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the fixed utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Hamacher operational laws with the fixed decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; ;
for the decision maker with the high utility decision-makers’ attitude, and . By the utility transformation function, it is easy to get:
The aggregation results of the 2-tuple linguistic Hamacher operational laws with the low decision-makers’ attitude are shown as follows:
Analogously, it is easy to get ; ; .
5. The 2TLUWA Operator and the MADM Method
Based on the utility transformation function, the novel 2-tuple linguistic operational laws are developed, so we construct the 2TLUWA operator to achieve the aggregation of 2-tuples.
5.1. The 2TLUWA Operator
Definition 14.
Let be a LTS and be the corresponding 2TLIM, let be a group of 2-tuples, and , let be the weighting vector of the group Ω, where , . According to the novel transformation function, the corresponding 2-tuple linguistic operational laws are constructed. Combined with the 2-tuple linguistic utility, the 2TLUWA operator is developed as follows:
And the aggregation result of the 2TLUWA operator is still a 2-tuple.
Proof.
By the basic operational laws, we can obtain:
Further, we can obtain:
For the 2-tuples , it is easy to obtain
further, we can obtain:
finally, it obviously:
Above all, the the aggregation result of the 2TLUWA operator is still a 2-tuple. □
The properties of the 2TLUWA operator are investigated.
Theorem 3.
Let be a LTS and be the corresponding 2TLIM, let be a group of 2-tuples, and , let be the weighting vector of the group Ω, where , . When , then
Proof.
Then we can obtain . □
Theorem 4.
Let and be two groups of 2-tuples. When for , then
Proof.
Because the utility transformation function u, are both monotonically increasing functions, the functions , are both monotonically increasing functions, we can get , , , further, we can obtain.
Then, we have , , ⋯, . □
Theorem 5.
Let be a group of 2-tuples, let , , then
Proof.
Because . According to Theorem 3, we can obtain , and by the Theorem 3, we can obtain and .
Then, we can obtain . □
Based on the extended TN and TC, the 2TLUWA operator is shown in Equation (15), then the special cases of the extended TN and TC are listed.
Theorem 6.
The special 2TLUWA operators of the extended TN and TC are shown as follows:
By the extended Algebraic TN and TC, the 2-tuple linguistic utility Algebraic weighted averaging(2TLUAWA) operator is described as follows:
By the extended Einstein TN and TC, the 2-tuple linguistic utility Einstein weighted averaging(2TLUEWA) operator is described as follows:
By the extended Hamacher TN and TC, the 2-tuple linguistic utility Hamacher weighted averaging(2TLUHWA) operator is described as follows:
5.2. The MADM Method Based on the Utility Transformation Function
Let be the group of alternatives and is the group of attributes with the weighting vector , where , and is the group the decision makers with the weighting vector , where . Additionally, 2TLUP is picked for the decision maker . The decision maker give the evaluation value by 2TLIM, let be the evaluation value matrix of decision maker , and describes the 2-tuple linguistic evaluation value of alternative and attribute given by decision maker . Based on the 2TLUWA operator, the steps of the MADM method are given as follows:
Step 1: Normalize the evaluation value. Convert the cost type into the benefit type, the specific conversation method is listed:
Step 2: For each decision maker , the corresponding 2TLUP is matched. The novel 2-tuple linguistic transformation functions are constructed for decision maker as follows:
By the novel 2-tuple linguistic transformation functions, the 2-tuple linguistic information is converted into the utility value with the 2-tuple linguistic utility attitude of the decision maker .
Step 3: According to the 2TLUWA operator, it is easy to aggregate the attributes of the alternative, then is obtained:
Step 4: According to the 2TLUWA operator, the aggregation value of alternative is obtained:
where the is presented to aggregate the 2TLUP , and the final aggregation is obtained by the 2TLUWA operator.
Step 5: Rank the aggregation value of alternative , then the best alternative is picked by the biggest .
6. An Application Example
An application example of personnel selection is adopted to illustrate the presented MADM method. Suppose the school plans to recruit a statistic teacher, there are four people , , and who apply for the position, the expert panel consists of three experts , and with the weighted vector , and the corresponding 2TLUPs are picked as , both the experts give the 2-tuple linguistic evaluation value under the four attributes : academic ability, : education background, : age, : excepted salary, with the weighted vector . Let , , , , , , , and the experts give the evaluation value under the 2TLIM , and the evaluation matrices of the expert are shown in Table 2, Table 3 and Table 4.

Table 2.
Evaluation matrix given by .

Table 3.
Evaluation matrix given by .

Table 4.
Evaluation matrix given by .
Step 1: Normalize the evaluation matrices, the attributes are both benefit type, so we skip the step.
Step 2: For the decision maker with the 2TLUP , then the corresponding utility transformation functions could be constructed by the Equation (21).
Step 3: Aggregate the attributes of the alternative by the 2TLUAWA operator, then we can obtain , which is shown in Table 5.

Table 5.
The aggregated matrix .
Step 4: Adopt the Equation (19) to get the aggregated and apply the 2TLUAWA operator to obtain the final aggregation value , it is easy to get:
Step 5: Rank the final aggregation value, we can get the best alternative.
Above all, the alternative is the best alternative.
The Discussion about the 2TLUP
In the research on the MADM with 2TLIM, the existing methods with transformation functions may ignore the difference between the linguistic information. It is obvious that the difference depends on the decision-makers’ attitude. Analogous to the economic utility theory, the 2-tuple linguistic utility is defined to overcome this issue. By the change of the 2TLUP, the different decision-makers’ attitude will be measured, and the difference will be measured with different attitude. In the actual MADM problem, the different decision makers may have different attitude, which match the different 2TLUP, but it may be hard to enumerate all these situations. So as to indicate the influence of decision-makers’ attitude and the utility transformation function specifically, based on the application example of Section 6, the special cases where the decision makers both have the same decision-makers’ attitude with the same 2TLUP are picked up; the specific value of 2TLUP is shown in Table 6. With different 2TLUP, the aggregation results and the rank results are shown in Table 6.

Table 6.
The results of the picked cases.
The different value of 2TLUP can indicate the different attitude of the decision makers, by changing the value of , the different attitude can be measured. By the results of the picked cases, it is easy to find the results may be different with different attitude.
For 2TLUP , the high decision-makers’ attitude is matched, the rank result is , then the alternative is the best alternative; for 2TLUP , the fixed decision-makers’ attitude is matched, the rank result is , then the alternative is the best alternative; for 2TLUP , the low decision-makers’ attitude is matched, the rank result is , then the alternative is the best alternative. With the different decision-makers’ attitude, the rank result maybe different, the existing transformation function is the special case of the utility transformation function with the fixed decision-makers’ attitude and . So as to show the impact of the utility transformation function, the results of the existing transformation function and the utility transformation function are shown in the Table 7.

Table 7.
The result of the comparison.
Obviously, just with the fixed decision-makers’ attitude, the existing method is not enough to deal with the real MADM, then the proposed method with novel transformation function may be much in line with the actual MADM, the results of Table 7 can certify it clearly. Remark by the existing MADM method, the difference between the linguistic information is fixed as the range of , which is just a fixed value. We introduce the economic utility theory into the study of the method for MADM with 2-tuple linguistic information, the drawback can be solved with the utility transformation function, the difference can be expressed by the utility, and the 2TLUP can measure the decision-makers’ attitude, which makes it much practical. Not just the 2-tuple linguistic utility transformation functions can measure the difference between linguistic information, but also it can control the 2-tuple linguistic utility under the decision-makers’ attitude. Further, the method based on the utility transformation function is realistic and useful.
7. Conclusions
In this paper, in order to avoid the difference between the linguistic information is fixed with various decision-makers’ attitude, we have defined the 2-tuple linguistic utility and the 2TLUP. The core of the MADM is the aggregation of the alternatives utility with decision-makers’ attitude, the expression form of the evaluation value is the medium. As the existing MADM method of 2-tuple linguistic information just take into account the fact that the difference is fixed and all decision makers have the same attitude, then we have developed the utility transformation function with the 2-tuple linguistic utility, where the 2TLUP can indicate the decision-makers’ attitude of the decision maker. The utility transformation function of 2TLIM can achieve the conversion between the 2-tuples and the aggregated result with the decision-makers’ attitude. Moreover, based on the utility transformation function, the 2-tuple linguistic operational laws have been presented, and the 2TLUWA operators have been produced to rich the MADM methods of 2TLIM. Finally, an application example is constructed to indicate the practicality and advantages of the proposed MADM method, and the value of 2TLUP has been discussed to show the influence of the decision-makers’ attitude. The main contributions of this article are as follows: (1) the definition of 2-tuple linguistic utility and 2TLUP has been developed; (2) the novel 2-tuple linguistic transformation functions have been produced with the decision-makers’ attitude; (3) the 2-tuple linguistic operational laws have been constructed on the novel 2-tuple linguistic transformation functions, and three special cases have been developed; (4) the 2TLUWA operators have been proposed, such as the 2TLUAWA operators, 2TLUEWA operators and 2TLUHWA operators; and (5) the new MADM method based on the utility transformation function has been proposed. In the following study, the new MADM method and the utility transformation function will be adopted into the other research of the 2TLIM, such as the hesitant 2-tuple linguistic set, the intuitionistic 2-tuple linguistic set and so on.
Author Contributions
All authors contributed equally.
Funding
This work was supported by National Natural Science Foundation of China (Grant No. 11661053, 11771198) and the Provincial Natural Science Foundation of Jiangxi, China (Grant No. 20181BAB201003).
Acknowledgments
The authors would like to thank the editors and anonymous reviewers for their insightful and constructive commendations that have lead to an improved version of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Torra, V. Hesitant fuzzy sets. Int. J. Intell. Syst. 2010, 25, 529–539. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Herrera, F.; Martnez, L. A 2-tuple fuzzy linguistic representation model for computing with words. IEEE Trans. Fuzzy Syst. 2000, 8, 746–752. [Google Scholar]
- Rodrguez, R.M.; Martnez, L.; Herrera, F. Hesitant fuzzy linguistic term sets. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, P.; Pei, Z. An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers. Int. J. Comput. Intell. Syst. 2015, 8, 747–760. [Google Scholar] [CrossRef]
- Pang, Q.; Wang, H.; Xu, Z. Probabilistic linguistic term sets in multi-attribute group decision making. Inf. Sci. 2016, 369, 128–143. [Google Scholar] [CrossRef]
- Morente-Molinera, J.A.; Kou, G.; Gonzlez-Crespo, R.; Corchado, J.M.; Herrera-Viedma, E. Solving multi-criteria group decision making problems under environments with a high number of alternatives using fuzzy ontologies and multi-granular linguistic modelling methods. Knowl.-Based Syst. 2017, 137, 54–63. [Google Scholar] [CrossRef]
- Sałabun, W.; Karczmarczyk, A.; Wątrbski, J.; Jankowski, J. Handling Data Uncertainty in Decision Making with COMET. In Proceedings of the IEEE Symposium Series on Computational Intelligence, Bangalore, India, 11 October 2017; pp. 1478–1484. [Google Scholar]
- Faizi, S.; Sałabun, W.; Rashid, T.; Wątrbski, J.; Zafar, S. Group decision-making for hesitant fuzzy sets based on characteristic objects method. Symmetry 2017, 9, 136. [Google Scholar] [CrossRef]
- Garca-Daz, V.; Espada, J.P.; Crespo, R.G.; G-Bustelo, B.C.P.; Lovelle, J.M.C. An approach to improve the accuracy of probabilistic classifiers for decision support systems in sentiment analysis. Appl. Soft Comp. 2018, 67, 822–833. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. An intuitionistic 2-tuple linguistic information model and aggregation operators. Int. J. Intell. Syst. 2015, 31, 569–592. [Google Scholar] [CrossRef]
- Zhang, H. The multiattribute group decision making method based on aggregation operators with interval-valued 2-tuple linguistic information. Math. Comput. Model. 2012, 56, 27–35. [Google Scholar] [CrossRef]
- Wei, G.W. Extension of topsis method for 2-tuple linguistic multiple attribute group decision making with incomplete weight information. Knowl. Inf. Syst. 2010, 25, 623–634. [Google Scholar] [CrossRef]
- Geng, X.; Gong, X.; Chu, X. Component oriented remanufacturing decision-making for complex product using dea and interval 2-tuple linguistic topsis. Int. J. Comput. Intell. Syst. 2016, 9, 984–1000. [Google Scholar] [CrossRef]
- Wei, G.W. Grey relational analysis method for 2-tuple linguistic multiple attribute group decision making with incomplete weight information. Expert Syst. Appl. 2011, 38, 4824–4828. [Google Scholar] [CrossRef]
- Liu, H.; Li, P.; You, J.; Chen, Y. A novel approach for fmea: Combination of interval 2-tuple linguistic variables and gray relational analysis. Qual. Reliab. Eng. Int. 2015, 31, 761–772. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Wu, J. Material selection using an interval 2-tuple linguistic vikor method considering subjective and objective weights. Mater. Des. 2013, 52, 158–167. [Google Scholar] [CrossRef]
- You, X.Y.; You, J.X.; Liu, H.C.; Zhen, L. Group multi-criteria supplier selection using an extended vikor method with interval 2-tuple linguistic information. Expert Syst. Appl. Int. J. 2015, 42, 1906–1916. [Google Scholar] [CrossRef]
- Dutta, B.; Guha, D.; Mesiar, R. A model based on linguistic 2-tuples for dealing with heterogeneous relationship among attributes in multi-expert decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1817–1831. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, H. Approaches based on 2-tuple linguistic power aggregation operators for multiple attribute group decision making under linguistic environment. Appl. Soft Comput. 2011, 11, 3988–3997. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Z. New aggregation operators based on the choquet integral and 2-tuple linguistic information. Expert Syst. Appl. 2012, 39, 2662–2668. [Google Scholar] [CrossRef]
- Wang, J.Q.; Wang, D.D.; Zhang, H.Y.; Chen, X.H. Multi-criteria group decision making method based on interval 2-tuple linguistic information and choquet integral aggregation operators. Soft Comput. 2015, 19, 389–405. [Google Scholar] [CrossRef]
- Wan, S.P. 2-tuple linguistic hybrid arithmetic aggregation operators and application to multi-attribute group decision making. Knowl.-Based Syst. 2013, 45, 31–40. [Google Scholar] [CrossRef]
- Tao, Z.; Chen, H.; Zhou, L.; Liu, J. On new operational laws of 2-tuple linguistic information using archimedean t-norm and s-norm. Knowl.-Based Syst. 2014, 66, 156–165. [Google Scholar] [CrossRef]
- Liu, P.; Chen, S.M. Multiattribute group decision making based on intuitionistic 2-tuple linguistic information. Inf. Sci. 2018, 430–431, 599–619. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).