1. Introduction
As early as in 1927 [
1], Paul A. M. Dirac considered the problem of extending Heisenberg’s uncertainty relations to the Lorentz-covariant world. In 1945 [
2], he attempted to construct the Lorentz group using the Gaussian wave function. In 1949 [
3], Dirac pointed out that the task of constructing relativistic dynamics is to construct a representation of the inhomogeneous Lorentz group. He then wrote down the ten generators of this group and their closed set of commutation relations. This set is known as the Lie algebra of the Poincaré group.
In 1963 [
4], Dirac considered two coupled harmonic oscillators and constructed an algebra leading to the Lie algebra for the
de Sitter group, which is the Lorentz group applicable to three space dimensions and two time-like variables.
From the mathematical point of view, it is straightforward to contract one of those two time-like dimensions to construct or the Poincaré group. This is what we present in this paper. However, from the physical point of view, we are deriving the Poincaré symmetry for the Lorentz-covariant quantum world purely from the symmetries of Heisenberg’s uncertainty relations.
In
Section 2, it is noted that a one-dimensional uncertainty relation contains the symmetry of the
group in the two-dimensional phase space. It is pointed out that this group, with three generators, is isomorphic to the Lorentz group applicable to two space dimensions and one time variable. We can next consider another set with three additional generators.
In
Section 3, we write those Heisenberg uncertainty relations in term of step-up and step-down operators in the oscillator system. It is then possible to consider the two coupled oscillator system with the ten generators constructed by Dirac in 1963 [
4]. It is gratifying to note that this oscillator system can serve as the basic language for the two-photon system of current interest [
5,
6].
In
Section 4, we contract one of the time-like variables in
to arrive at the inhomogeneous Lorentz group
or the Poincaré group. In
Section 5, we give some concluding remarks.
2. Sp(2) Symmetry for the Single-Variable Uncertainty Relation
It is known that the symmetry of quantum mechanics and quantum field theory is governed by the Poincaré group [
3,
7]. The Poincaré group means the inhomogeneous Lorentz group which includes the Lorentz group applicable to the four-dimensional Minkowskian space-time, plus space-time translations [
8].
The question is whether this Poincaré symmetry is derivable from Heisenberg’s uncertainty relation, which takes the familiar form
There are three commutation relations in this equation. Let us choose one of them, and write it as
This commutation relation possesses the symmetry of the Poisson bracket in classical mechanics [
9,
10]. The best way to address this property is to use the Gaussian form for the Wigner function defined in the phase space, which takes the form [
11,
12,
13]
This distribution is concentrated in the circular region around the origin. Let us define the circle as
We can use the area of this circle in the phase space of
x and
p as the minimum uncertainty. This uncertainty is preserved under rotations in the phase space:
as well as the squeeze of the form
The rotation and the squeeze are generated by
respectively. If we take the commutation relation with these two operators, the result is
with
Indeed, these three generators form a closed set of commutation relations:
This closed set is called the Lie algebra of the group, isomorphic to the Lorentz group applicable to two space dimensions and one time dimension.
Let us consider the Minkowskian space of
. It is possible to write three four-by-four matrices satisfying the Lie algebra of Equation (
10). The three four-by-four matrices satisfying this set of commutation relations are:
However, these matrices have null second rows and null second columns. Thus, they can generate Lorentz transformations applicable only to the three-dimensional space of , while the y variable remains invariant.
3. Two-Oscillator System
To generate Lorentz transformations applicable to the full Minkowskian space, along with
, and
we need two more Heisenberg commutation relations. Indeed, Paul A. M. Dirac started this program in 1963 [
4]. It is possible to write the two uncertainty relations using two harmonic oscillators as
with
and
where
i and
j could be 1 or 2.
More recently in 1986, this two-oscillator system was considered by Yurke et al. [
6] in their study of two-mode interferometers. They considered first
which leads to the generation of the two-mode coherent state or the squeezed state [
5].
Yurke et al. then considered possible interferometers requiring the following two additional operators.
The three Hermitian operators from Equations (
15) and (
16) satisfy the commutation relations
These relations are like those given in Equation (
10) for the Lorentz group applicable to two space-like and one time-like dimensions.
In addition, in the same paper [
6], Yurke et al. discussed the possibility of constructing interferometers exhibiting the symmetry generated by
These generators satisfy the closed set of commutation relations
and therefore define a Lie algebra which is the same as that for
or the three-dimensional rotation group.
We are then led to ask whether it is possible to construct a closed set of commutation relations with the six Hermitian operators from Equations (
15), (
16) and (
18). It is not possible. We must add four additional operators, namely
There are now ten operators from Equations (
15), (
16), (
18) and (
20). Indeed, these ten operators satisfy the following closed set of commutation relations.
As Dirac noted in 1963 [
4], this set is the same as the Lie algebra for the
de Sitter group, with ten generators. This is the Lorentz group applicable to the three-dimensional space with two time variables. This group plays a very important role in space-time symmetries.
In the same paper, Dirac pointed out that this set of commutation relations serves as the Lie algebra for the four-dimensional symplectic group commonly called , applicable to the systems of two one-dimensional particles, each with a two-dimensional phase space.
For a dynamical system consisting of two pairs of canonical variables
and
, we can use the four-dimensional space with the coordinate variables defined as [
14]
Then the four-by-four transformation matrix
M applicable to this four-component vector is canonical if [
15,
16]
where
is the transpose of the
M matrix, with
According to this form of the J matrix, the area of the phase space for the and variables remains invariant, and the story is the same for the phase space of and
We can then write the generators of the
group as
and
where
I is the two-by-two identity matrix, while
, and
are the two-by-two Pauli matrices. The four matrices given in Equation (
25) generate rotations, while those of Equation (
26) lead to squeezes in the four-dimensional phase space.
As for the difference in methods used in
Section 2 and
Section 3, let us look at the ten four-by-four matrices given in Equations (
25) and (
26). Among these ten matrices, six of them are diagonal. They are
and
. In the language of two harmonic oscillators, these generators do not mix up the first and second oscillators. There are six of them because each operator has three generators for its own
symmetry. Let us consider the three generators,
, and
. For each oscillator, the generators consist of
These separable generators thus constitute the Lie algebra of Sp(2) group for the one-oscillator system, which we discussed in
Section 2. Hence, the one-oscillator system constitutes a subgroup of the two-oscillator system.
The off-diagonal matrix
couples the first and second oscillators without changing the overall volume of the four-dimensional phase space. However, to construct the closed set of commutation relations, we need the three additional generators:
and
The commutation relations given in Equation (
21) are clearly consequences of Heisenberg’s uncertainty relations.
4. Contraction of SO(3, 2) to ISO(3, 1)
Let us next go back to the
contents of this two-oscillator system [
4]. There are three space-like coordinates
and two time-like coordinates
s and
t. It is thus possible to construct the five-dimensional space of
, and to consider four-dimensional Minkowskian subspaces consisting of
and
.
As for the
s variable, we can make it longer or shorter, according to procedure of group contractions introduced first by Inönü and Wigner [
17]. In this five-dimensional space, the boosts along the
x direction with respect to the
t and
s variables are generated by
respectively. The boost generators along the
y and
z directions take similar forms.
Let us then introduce the five-by-five contraction matrix [
18,
19]
This matrix leaves the first four columns and rows invariant, and the four-dimensional Minkowskian sub-space of stays invariant.
As for the boost with respect to the
s variable, according to the procedure spelled out in Refs. [
18,
19], the contracted boost generator becomes
Likewise,
and
become
respectively.
As for the
t direction, the transformation applicable to the
s and
t variables is a rotation, generated by
This matrix also becomes contracted to
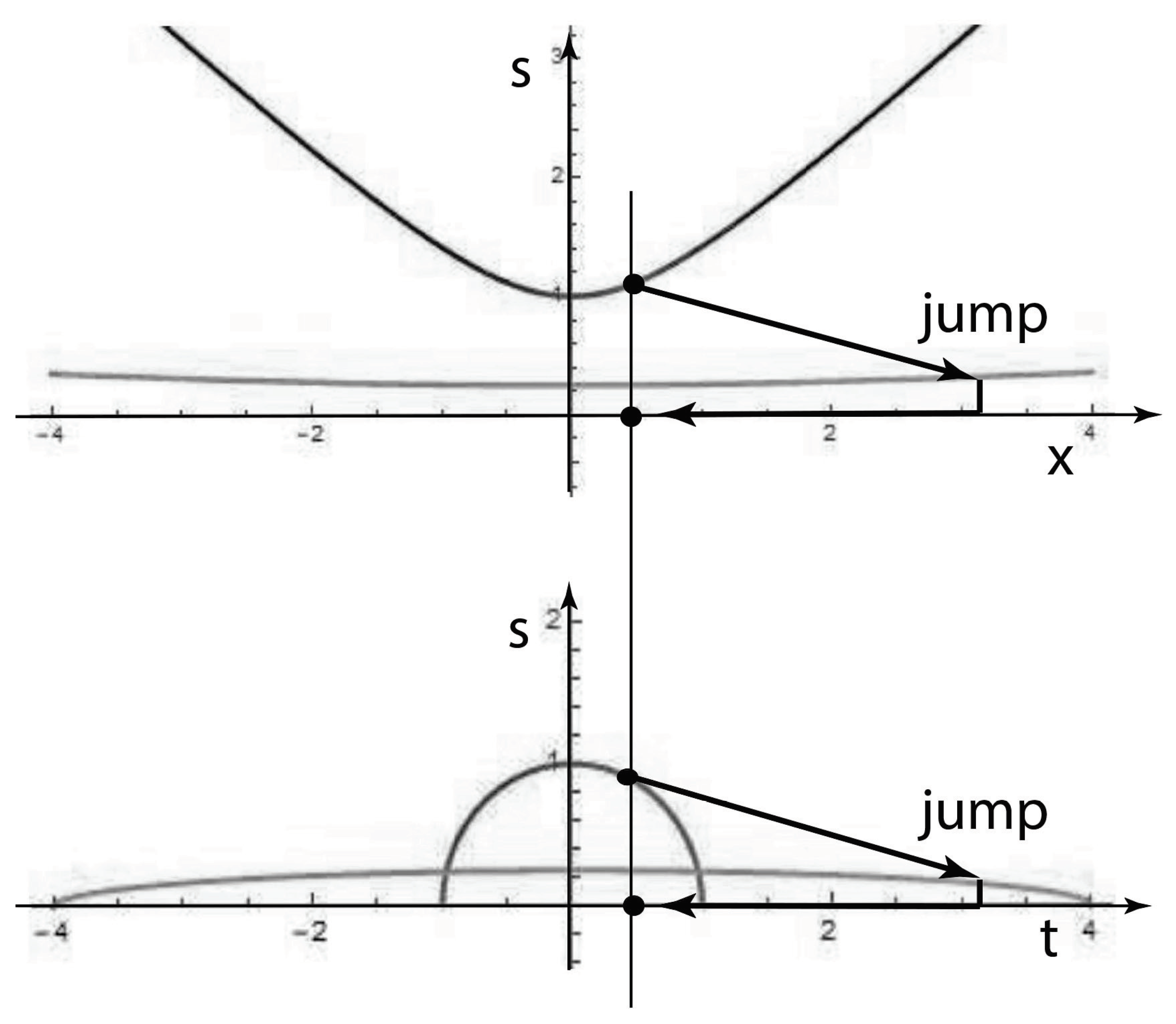
These contraction procedures are illustrated in
Figure 1.
These four contracted generators lead to the five-by-five transformation matrix
performing translations:
This matrix leaves the first four rows and columns invariant. They are for the Lorentz transformation applicable to the Minkowskian space of .
In this way, the boosts along the
s direction become contracted to the translation. This means the group
derivable from the Heisenberg’s uncertainty relations, becomes the inhomogeneous Lorentz group governing the Poincaré symmetry for quantum mechanics and quantum field theory in the Lorentz-covariant world [
4,
7].
The group contraction has a long history in physics, starting from the 1953 paper by Inönü and Wigner [
17]. It starts with a geometrical concept. Our earth is a sphere, but is convenient to consider a flat surface tangent to a given point on the spherical surface of the earth. This approximation is called the contraction of
to
or the two-dimensional Euclidean group with one rotational and two translational degrees of freedom.
This mathematical method was extended to the contraction of the
Lorentz group to the three-dimensional Euclidean group. More recently, Kim and Wigner considered a cylindrical surface tangent to the sphere [
18,
19] at its equatorial belt. This cylinder has one rotational degree of freedom and one up-down translational degree of freedom. It was shown that the rotation and translation correspond to the helicity and gauge degrees of freedom for massless particles.
Since the Lorentz is isomorphic to the group of two-by-two matrices, we can ask whether it is possible to perform the same contraction procedure in the regime of two-by-two matrices. It does not appear possible to represent the (inhomogeneous Euclidean group) with two-by-two matrices. Likewise, there seem to be difficulties in addressing the question of contracting to within the frame work of the four-by-four matrices of .