Abstract
We discuss the calculation of one-loop effective actions in Lorentzian spacetimes, based on a very simple application of the method of steepest descent to the integral over the field. We show that for static spacetimes this procedure agrees with the analytic continuation of Euclidean calculations. We also discuss how to calculate the effective action by integrating a renormalization group equation. We show that the result is independent of arbitrary choices in the definition of the coarse-graining and we see again that the Lorentzian and Euclidean calculations agree. When applied to quantum gravity on static backgrounds, our procedure is equivalent to analytically continuing time and the integral over the conformal factor.
1. Introduction
The path integral of a Lorentzian Quantum Field Theory (QFT) is
where g may denote external parameters or background fields. It is often said that this expression is badly defined because of the oscillating character of the exponential. This is then fixed by turning time to Euclidean time. One defines a Euclidean action by
and thereby converts the functional integral (1) to the Euclidean functional integral
Since the Euclidean action is typically positive definite, this is now a better-defined object. More precisely, the integral over each field mode is now convergent. The functional integral still needs regularization and renormalization, because of the infinite number of field modes. In the end the results can be analytically continued back to real time, which means that the Lorentzian and Euclidean Effective Actions (EA) are related in the same way as the classical actions
This procedure is much less clear when the background metric is curved. In a gravitational context, one would like to preserve invariance under coordinate transformations. Since time is now merely a coordinate, one must make a choice of which time should be analytically continued. The problematic nature of this choice has been emphasized by Visser [1].
The procedure is even more problematic when gravity itself is treated as a quantum field. In a one-loop calculation, where the graviton field can be seen as a free quantum field propagating on a curved background, the LaGrangian of the spin-zero degree of freedom of the metric has opposite sign relative to the spin-two degree of freedom. The sign of the Hilbert action is chosen so that the latter has the correct sign (so that free gravitons in flat space carry positive energy) and therefore the spin-zero field has negative energy. This in itself is not problematic, because the spin-zero field does not propagate, but it means that while the Euclidean integral over the spin-two degrees of freedom is exponentially damped, the integral over the spin-zero degrees of freedom is exponentially divergent.
This can be seen also at non-perturbative level: the spin-zero field is related to the conformal part of the metric, and the Hilbert action can be made arbitrarily negative by performing a highly oscillating conformal transformation [2]. Insofar as the conformal factor is a gauge degree of freedom, one may doubt that this is significant. In fact, the conformal factor is absent in unimodular gravity. However, in that case another scalar component of the graviton has wrong-sign action. The existence of a scalar with wrong-sign action is a gauge-independent statement. The standard way out, that we shall refer to as the “Cambridge prescription”, is to rotate the integration over the conformal factor in the complex plane, to make the integral over the conformal factor convergent.
Returning to general QFT in curved spacetime, there is an alternative to analytically continuing time, that is analytically continuing the metric. In an ADM decomposition, this can be thought of as analytically continuing the lapse. Even more generally, one can think of a one-parameter family of metrics
where is a Lorentzian metric and is a unit time-like vector field in the metric .
For one has the original Lorentzian metric while for one has a Euclidean metric. This procedure has been used in [3] and its advantages extolled in [1]. One of the advantages is that all the metrics are defined on the same underlying manifold. This puts strong restrictions on the class of manifolds that one may have to sum over, and this in turn is known to greatly improve the definition of the path integral [4,5,6].
On the other hand, this definition is also not free of ambiguity: there is no preferred choice of vector field . One may try to restrict this freedom by imposing some additional conditions, such as mapping Einstein manifolds to Einstein manifolds, or preserving the number of Killing vectors of the metric. However, it can be seen that in some cases these requirements clash with the requirement of preserving the manifold structure [7].
For this reason, in the present paper we shall explore an alternative procedure, where no Wick rotation is performed. By this we mean that neither time nor the metric are changed. Instead, an analytic continuation is performed on the quantum field itself. More precisely, one can choose a contour in the integral over the field such as to make the integral over each mode convergent. This procedure is inspired by recent work on quantum cosmology [8], where the integral over the lapse is made convergent by using Picard–Lefschetz theory. Here we shall discuss only the case of quadratic actions, where it is enough to use the steepest-descent definition of the Fresnel integrals, which is actually the simplest application of Picard–Lefschetz theory and, as we shall mention in Section 6, is all that one needs in perturbative QFT. The main point we would like to make is that the functional integral is not ill-defined because of the oscillatory character of the integrand, but because of the presence of infinitely many degrees of freedom. This issue is exactly the same in the Euclideanized theory and in the Lorentzian theory treated by the steepest-descent method.
Instead of giving a general proof, we will show by explicit calculations that this is true on static spacetimes, where the notion of Euclidean continuation is unambiguous. In all cases, the spatial section is a d-dimensional manifold with suitable boundary conditions that allow integrations by parts to be performed without boundary remnants. We give general formulas for the dependence of the EA on the metric in , in any dimension, but the main point is already clear when is a flat torus of side L, in which case the dependence on the metric reduces simply to the dependence on the total volume .
We begin in Section 2, by defining directly the Lorentzian functional integral by the steepest-descent method. We then consider in Section 3 the EA of a massive theory where time is non-compact. We prove that the results of the Euclidean and Lorentzian calculations are indeed related as in Equation (4). In Section 4 we consider the case where time is periodic with period T, which is somewhat pathological in the Lorentzian case, but is useful to illustrate the behavior of massless fields. Again, we prove that results of the Euclidean and Lorentzian calculations are related as in Equation (4), both in the massive and massless case. We also discuss the limit . In Section 5 we show how the EA can be calculated by integrating a Renormalization Group (RG) equation. This is useful for applications of the RG to gravity. As a side result we show that the EA calculated in this way is independent of the choice of the cutoff that enters the definition of the coarse-graining. Section 6 contains some final remarks.
2. Lorentzian Functional Integral
Consider a massive scalar field on a d-dimensional static spacetime M, with action
Here is the covariant d’Alembertian, whose eigenfunctions will be denoted , where n is a composite index comprising an energy eigenvalue for the Fourier modes in time and another set of labels for the eigenvalue of the spatial Laplacian . They are orthonormal with respect to the inner product on
where is a constant with dimension of mass. Please note that this has nothing to do with the Klein-Gordon inner product that is used in canonical quantization, which is only defined for the solutions of the classical equations of motion. The eigenfunctions form a basis in the space of functions on M, so we can decompose the field as: . (Please note that the coefficients are dimensionless.) Using the eigenvalue equation
the action becomes
where is the set that labels the eigenvalues. The path integral measure can be written formally
where N is an infinite, field-independent, dimensionless normalization factor, which we define by the following Gaussian normalization condition
Using the spectral decomposition of , the r.h.s. becomes a product of integrals of the form
The integrals over the on the real axis are not well-defined, but one can deform the integration contour in the complex plane to follow the steepest-descent path at the origin, which is shown in Figure 1. The two eighths of a circle that are needed for this deformation give no contribution when their radius tends to infinity, so that each integral is equal to . Thus, we get
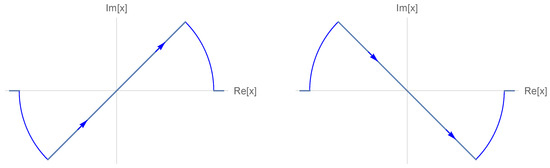
Figure 1.
Steepest-descent paths for the integrals with (left) and (right).
Let us split the spectrum into , where , , corresponds to , , , respectively. In general, there will be no zero eigenvalues. If there is any, the mass must be given a small imaginary part , which implies that : in this way the contribution of the zero eigenvalues becomes a product of standard Gaussian integrals.
Now let us choose for each integral the path of steepest descent, shown in Figure 1. For each positive eigenvalue we get a factor and for each negative eigenvalue a factor . Altogether, using the steepest-descent method and Equation (8), the functional integral becomes
In the absence of zero eigenvalues, which is the normal situation, we can drop the and we are led to the standard formula
We note that the previous calculation was mathematically well-defined. What is ill-defined is only the trace in this last expression, which is a sum over infinitely many, growing, terms. This requires regularization and renormalization. We will discuss this in the next sections, showing that the results of the direct Lorentzian calculation agree with the analytic continuation of the results of the Euclidean calculation.
3. Non-Compact Time
In this section, we discuss the case when spacetime has topology where is a compact -dimensional manifold. The line element is . The time dependence of the field can be expanded in Fourier integrals with normal modes where is a continuous index. The trace of the heat kernel of the one-dimensional Laplacian is
where is (infrared) divergent. This is unavoidable for a static physical system existing for an infinite time. It could be regulated by putting the system in a large “time box” of finite duration T. In this section we will implicitly assume that this has been done. In the next section we will discuss the case when time is periodic with a finite period T.
The eigenvalues of the spatial Laplacian will be denoted , where is a discrete label, and the trace of its heat kernel has the small-s expansion
The first expansion coefficients are
where V is the volume of and the curvatures are those of the metric .
3.1. Euclidean, Non-Compact Time
The Euclidean EA can be expressed as
where is the heat kernel of the (positive) Euclidean kinetic operator , whose eigenvalues are are
Since the time and space parts of the Laplacian commute, the trace of the heat kernel factors into
The integral in the first line is convergent and gives the result in the second line when . Elsewhere, it can be defined by analytic continuation. It has poles for that can be isolated by sending . For example, for [9],
Alternatively, one can put an UV cutoff on the theory by integrating s from to infinity. This gives an incomplete Gamma function
In the case the expansion of the incomplete Gamma function gives
From here we see that the leading divergences are powers and logs, multiplied by the heat kernel coefficients, and we also see that the log divergences exactly reproduce the dimensional poles in (21).
3.2. Lorentzian, Non-Compact Time
In the Lorentzian case the eigenvalues of the kinetic operator are
where we have again added the term in case that there are zero modes. The Lorentzian EA is given by the general formula (17), where we replace the Euclidean kinetic operator by the Lorentzian one, and s by
This formula can also be obtained from Schwinger’s action principle; see e.g., [10]. For the existence of a Lorentzian “heat” kernel see also [11]. Note that because of the different sign of the temporal part in the eigenvalues the temporal contribution to the Heat Kernel is simply , while the spatial contribution is . From here we obtain
This expression has the same divergences that we encountered in the Euclidean calculation, and can be regularized and renormalized in the same way.
For our purposes, we can already compare the Euclidean and the Lorentzian result. Recalling that in the standard definition of Wick rotation , we clearly must have . Indeed, we see that the two EAs are related as in (4), namely
Thus, the direct Lorentzian calculation correctly reproduces the analytic continuation of the Euclidean calculation.
3.3. Zeta Function Regularization
In this section, we investigate further the nature of the relation (26). We recall that the determinant of an operator can be calculated using a generalized zeta function [12,13,14]. In the non-compact time Euclidean case, it is given by
Then the recipe for the determinant is [15]
Putting
We see that the divergences exactly reproduce the dimensional poles in (21).
Similarly, in the Lorentzian case
We see that
The formula (26) can now be seen as a consequence of this relation, since the effective action are proportional to the derivative evaluated for of the zeta function associated with the Hessian of the action.
4. Compact Time
In this section, we discuss a scalar field in the case when spacetime has topology where is a circle of period T and is, as before, a compact -dimensional manifold. In this case, we will consider both the massive and the massless case. The time dependence of the field can be expanded in Fourier series with normal modes where
and . The eigenvalues of the one-dimensional Laplacian are and the trace of the heat kernel is
Please note that is finite here, in fact this calculation can be seen as an infrared regularization of the one performed in the previous section. We shall discuss the limit in Section 4.4.
The usual physical interpretation of the Euclidean EA in d dimensions with a periodic coordinate is as thermal partition function of a system in dimensions at temperature . Here, however, we shall also consider the partition function of a real system in d dimensions with periodic time. This example is unphysical, but it serves as an illustration of the fact that partition functions of massless fields can be calculated directly in Lorentzian signature.
4.1. Euclidean Compact Time
The spectrum of the kinetic operator for a massive scalar is
where and are the eigenvalues of the Laplace-Beltrami operator on . The quantum action is given by (17). The heat kernel can now be written
Now using (17) and separating the mode from the others
We can thus write
where, compared to (20),
is equal to the Euclidean effective action of a massive scalar field in the dimensional manifold and
If we use dimensional regularization to isolate the poles in this expression, we find that for a given dimension d there is only one divergent term in the sum: in particular for even d there is a dimensional pole when , coming from the zeta functions, while for odd d there is a pole for coming from the gamma function.
For example, in dimensions (note that to have dimensionless it is necessary to send ) we obtain
In the MS scheme, the finite part of the EA is obtained by simply dropping the term. The first term correctly reproduces the free energy of a relativistic gas in a box of volume V at temperature . Please note that in the case when is flat, there are still infinitely many contributions coming from the higher that give the dependence on the mass.
4.2. Lorentzian Compact Time
The spectrum of □ is
where . Using this in (24) and proceeding as before and keeping track of the additional factors of i, we find
As before, we can thus write
where, compared to (20),
is equal to i times the Euclidean effective action of a massive scalar field in the dimensional manifold and
For example, in dimensions we obtain
4.3. Even vs. Odd Dimensions
The overall coefficient in (37) is real or imaginary, depending on the dimension. For example, for a massless scalar field on a flat torus,
so we see that is real if d is even and imaginary if d is odd. This is related to the fact that the Euclidean action is real and contains , so that the Wick rotation produces a factor . This contrasts with the case when time is non-compact, where there is always just one power of T in the EA.
The physical origin of this behavior may be related to the different propagation properties of fields in even and odd dimensions. Consider a massless scalar field in , satisfying the wave equation
If d is even the value of at a point is determined by its value on the past light cone of the point . By contrast, if d is odd, then the value of at is determined by its value in the interior of the past light cone [16,17].
Now let us compactify the time to by identifying and , where . There are now closed time-like curves, which lead to causality violation. However, for a generic point (which means that its coordinates are irrational multiples of the periods), the past light cone never passes through the point itself. Thus, generically there are no closed light rays and therefore in even dimensions there is no violation of causality for massless fields. If d is odd the value of the field is affected by its whole causal past and the presence of closed time-like curves leads to violation of causality.
4.4. The Limit .
In the infinite volume limit the EA of a massless theory has infrared divergences. Therefore, there are two possible ways of taking the limit : either by separating the mass term from the heat kernel expansion of the spatial part, or by introducing an explicit IR regulator in the integral over s.
Let us first consider the Euclidean case. Using the identity
we can write
In the limit only the first term in the square bracket survives and we arrive at
which agrees with (20). Using the same trick as above, the Lorentzian EA reads
Before taking the limit, we must remember the prescription and , which is equivalent to . If we keep fixed, the second term in the square bracket becomes . As before, in the limit , only the first term in the square bracket survives and then taking we arrive at (25).
5. Deriving the EA from an RG Equation
The Effective Average Action (EAA) is the EA for a theory where the action has been modified by the addition of a “cutoff term” that suppresses the contribution of low-momentum modes. It depends on the “IR cutoff” k and reduces to the ordinary EA when . The cutoff term has the general form
where z is a suitable second order differential operator and the function tends to for and goes rapidly to zero for . The “cutoff kinetic operator” is then
The choice of the regulator function is largely arbitrary and is somewhat analogous to choosing a renormalization scheme in perturbation theory. At one loop the EAA is then given by
Please note that the one-loop EAA is ill-defined and needs UV regularization and renormalization. However, if we take a derivative with respect to k, the resulting expression is UV finite. It can be interpreted as an RG equation [18,19,20]
The EA can be calculated by integrating the flow from some UV scale to . For some concrete examples see [21]. The usual divergences of QFT are hidden in the choice of the initial condition for the EAA at the UV scale and reappear when we try to send .
Normally, in a Euclidean setting, one chooses z to be a Laplace-type operator. This preserves rotational invariance and guarantees that the cutoff represents physically a coarse-graining of the degrees of freedom of the system. The RG Equation (42) is much less used in a Lorentzian setting. One may try to introduce a cutoff preserving Lorentz invariance by choosing z to be a d’Alembertian operator, but in this way there would be no restriction on the modulus of the spatial momenta. In other words, one would not be really coarse-graining in the usual sense. Alternatively, one could impose separate cutoffs on the space and time components of the momentum, so that only low wave numbers and low frequencies are suppressed. In this way one would lose Lorentz covariance. For a general discussion see [22,23].
5.1. Compact Time with Optimized Regulator
For the calculations of the EA in periodic time, where Euclidean/Lorentz invariance is broken anyway by the static metric, it will be adequate to cut off only the space momenta [24,25]. In this section, we will treat the Euclidean and Lorentzian calculations together. The kinetic operator is , where , are both positive operators, and in the Euclidean case while in the Lorentzian case. We choose a cutoff of the form , so that the cutoff kinetic operator is , where . Thus, the RG Equation (42) becomes
where the prefactor accounts for the i in (11) in the Lorentzian case. As we have seen in the preceding examples, the trace factors as a product of two traces, over the time and space quantum numbers. Even though we have not put a cutoff on the time quantum numbers, both traces are now finite, as we shall see below.
With our choice of cutoff and with the eigenvalues of Equations (30) and (35), the Euclidean RG equation reads
Let us first see what this gives for . The sum over then becomes an integral over space momenta p. This leads to the formula
where
Defining and where , the relevant Q-functionals can be rewritten as
where . In general, these functionals depend on the shape of the function , but in the case (corresponding to ) they do not [26].
In general, the Q-functional can be calculated explicitly for the optimized cutoff
Then using
we arrive at
Let us specialize to the case . Integrating the LHS of (49) we obtain , where is an arbitrary UV scale
For , expanding the last four terms in the square bracket around gives
In the limit we thus obtain
To extract the EA , we need to specify the initial condition . For it must reproduce the classical action, which in the case of vanishing field that we are considering here is simply zero. This means that must be chosen to be equal to the divergent term on the r.h.s., and the final result is
in accordance with (34). For , we have to remember that there is a prescription which is equivalent to : as a consequence the exponential factor in the polylogs function becomes . So, we have the same expansion as before and we obtain
in accordance with (38).
5.2. Compact Time with General Regulator
The sums in (44) can be treated also for general using the general formula for the trace of a function of a Laplacian, given in Appendix A of [26]. One obtains
whose first term indeed agrees with (45).
In the preceding calculation we had to choose a special regulator to be able to perform all the integrals and sums in closed form. However, it is possible to show that the final result for the EA is actually independent of the choice of cutoff function .
Since the integral over s and the sum over n cannot be performed for a general cutoff, to show cutoff-independence we must perform the integration over k before the integral over y and the sum over n. This inversion is legitimate because the sums and integrals are convergent.
Let us go back to Equation (54) and integrate both sides. In the r.h.s. we encounter the integrals
The k-integral can be performed exactly, yielding a hypergeometric function. For large it diverges, leaving a finite part
With this, the y-integral is seen to become the integral of a total y-derivative, and therefore becomes independent of the shape of the cutoff function. The final result is
5.3. Non-Compact Time with General Regulator
To pass from the compact case to the non-compact one we just do the following substitution
The integral in E gives
6. Discussion
We have discussed the definition of functional integrals directly in Lorentzian signature, by means of the steepest descent procedure. We conclude with two remarks. We have considered here only Gaussian functional integrals. For an interacting theory, the perturbative expansion can be derived from the expression
where is the Laplacian for and the d’Alembertian for . The only path integral that one has evaluated is a Gaussian one. Thus, the steepest-descent procedure is enough to define the Lorentzian theory perturbatively. It is only when one wants to go beyond the perturbative treatment that more complicated contours will have to be chosen, such as in [8,27].
In the case of quantum gravity, as noted in the introduction, there is the issue that the free action of gravitons has opposite sign for the spin-two and for the spin-zero components. We note that the steepest-descent prescription implies different integration contours for these fields, each leading to a determinant. Thus, we arrive at the same result as the analytic continuation of the Euclidean integral, treated with the Cambridge prescription.
Author Contributions
Conceptualization, A.B., R.P. and V.S.; formal analysis, A.B., R.P. and V.S.; writing–original draft preparation, A.B. and R.P.; writing–review and editing, A.B. and R.P.; supervision, R.P.
Acknowledgments
R.P. wishes to thank the organizers of the conference “The path integral for gravity”, which was held at Perimeter Institute, 13–17 November 2017, and provided the motivation for this work. This research was supported in part by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through Industry Canada and by the Province of Ontario through the Ministry of Economic Development and Innovation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Visser, M. How to Wick rotate generic curved spacetime. arXiv, 2017; arXiv:1702.05572. [Google Scholar]
- Gibbons, G.W.; Hawking, S.W.; Perry, M.J. Path Integrals and the Indefiniteness of the Gravitational Action. Nucl. Phys. B 1978, 138, 141. [Google Scholar] [CrossRef]
- Candelas, P.; Raine, D.J. Feynman Propagator in Curved Space-Time. Phys. Rev. D 1977, 15, 1494. [Google Scholar] [CrossRef]
- Ambjorn, J.; Loll, R. Nonperturbative Lorentzian quantum gravity, causality and topology change. Nucl. Phys. B 1998, 536, 407. [Google Scholar] [CrossRef]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Emergence of a 4-D world from causal quantum gravity. Phys. Rev. Lett. 2004, 93, 131301. [Google Scholar] [CrossRef] [PubMed]
- Ambjorn, J.; Jurkiewicz, J.; Loll, R. Reconstructing the universe. Phys. Rev. D 2005, 72, 064014. [Google Scholar] [CrossRef]
- Baldazzi, A.; Percacci, R.; Skrinjar, V. Wicked metrics. arXiv, 2018; arXiv:1811.03369. [Google Scholar]
- Feldbrugge, J.; Lehners, J.L.; Turok, N. Lorentzian Quantum Cosmology. Phys. Rev. D 2017, 95, 103508. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Parker, L.; Toms, D. Quantum Field Theory in Curved Spacetime; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Vassilevich, D.V. Heat kernel expansion: User’s manual. Phys. Rep. 2003, 388, 279. [Google Scholar] [CrossRef]
- Hawking, S.W. Zeta Function Regularization of Path Integrals in Curved Space-Time. Commun. Math. Phys. 1977, 55, 133. [Google Scholar] [CrossRef]
- Elizalde, E. Zeta Function Methods and Quantum Fluctuations. J. Phys. A 2008, 41, 304040. [Google Scholar] [CrossRef]
- Elizalde, E. Ten Physical Applications of Spectral Zeta Functions, 2nd ed.; Springer: Berlin, Germany, 2012. [Google Scholar]
- Bytsenko, A.A.; Cognola, G.; Elizalde, E.; Moretti, V.; Zerbini, S. Analytic Aspects of Quantum Fields; World Scientific: River Edge, NJ, USA, 2003; 350p. [Google Scholar]
- Balazs, N.L. Wave propagation in even and odd dimensional spaces. Proc. Phys. Soc. 1955, A68, 521. [Google Scholar] [CrossRef]
- Dai, D.C.; Stojkovic, D. Origin of the tail in Green’s functions in odd-dimensional space-times. Eur. Phys. J. Plus 2013, 128, 122. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the average Potential. Phys. Lett. 1993, B301, 90. [Google Scholar] [CrossRef]
- Morris, T.R. Derivative expansion of the exact renormalization group. Phys. Lett. 1994, B329, 241–248. [Google Scholar] [CrossRef]
- Floreanini, R.; Percacci, R. The Heat kernel and the average effective potential. Phys. Lett. B 1995, 356, 205. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R.; Rachwał, L.; Tonero, A. Computing the Effective Action with the Functional Renormalization Group. Eur. Phys. J. C 2016, 76, 226. [Google Scholar] [CrossRef]
- Floerchinger, S. Analytic Continuation of Functional Renormalization Group Equations. JHEP 2012, 1205, 021. [Google Scholar] [CrossRef]
- Pawlowski, J.M.; Strodthoff, N. Real time correlation functions and the functional renormalization group. Phys. Rev. D 2015, 92, 094009. [Google Scholar] [CrossRef]
- Manrique, E.; Rechenberger, S.; Saueressig, F. Asymptotically Safe Lorentzian Gravity. Phys. Rev. Lett. 2011, 106, 251302. [Google Scholar] [CrossRef]
- Rechenberger, S.; Saueressig, F. A functional renormalization group equation for foliated spacetimes. JHEP 2013, 1303, 10. [Google Scholar] [CrossRef]
- Codello, A.; Percacci, R.; Rahmede, C. Investigating the Ultraviolet Properties of Gravity with a Wilsonian Renormalization Group Equation. Ann. Phys. 2009, 324, 414. [Google Scholar] [CrossRef]
- Basar, G.; Dunne, G.V.; Unsal, M. Resurgence theory, ghost-instantons, and analytic continuation of path integrals. JHEP 2013, 1310, 041. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).