Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics
Abstract
1. Introduction
2. The Model
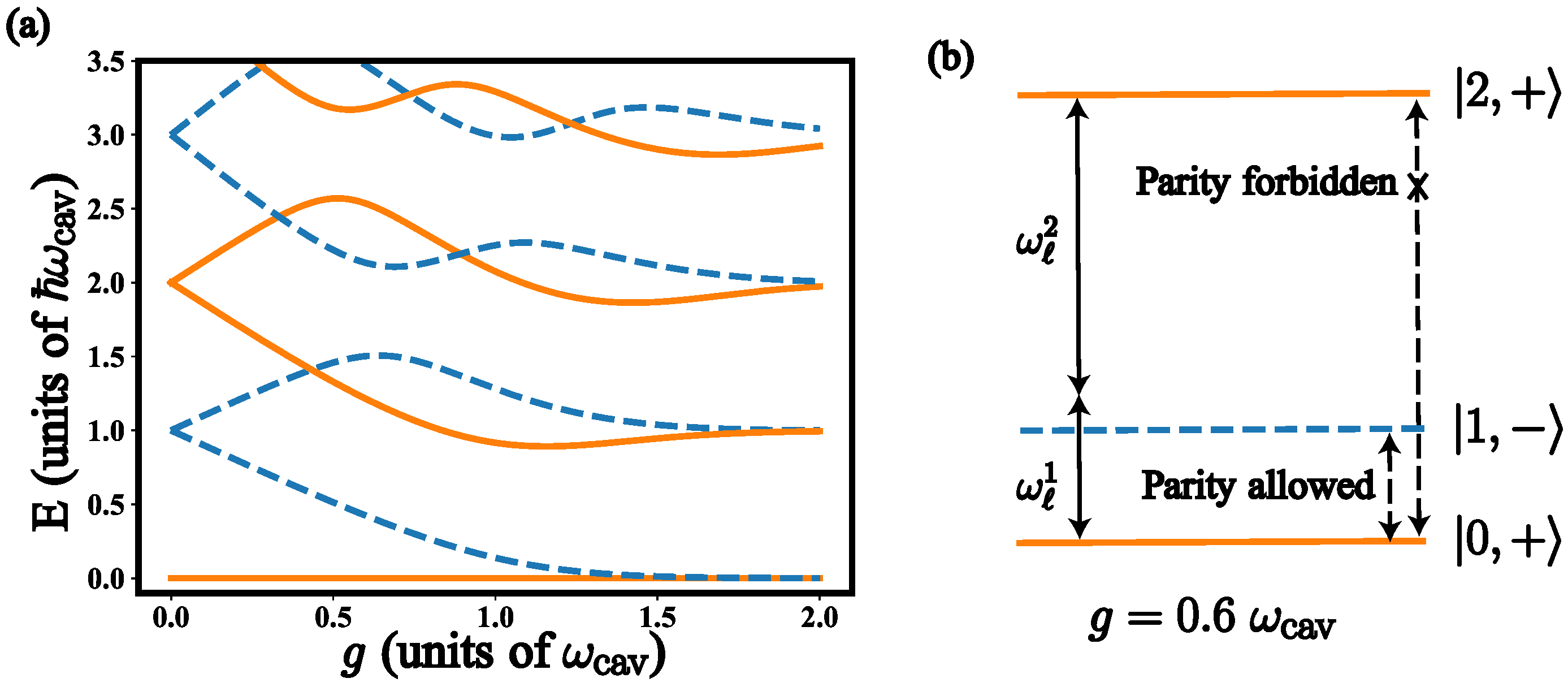
3. Parity Symmetry and Selection Rules
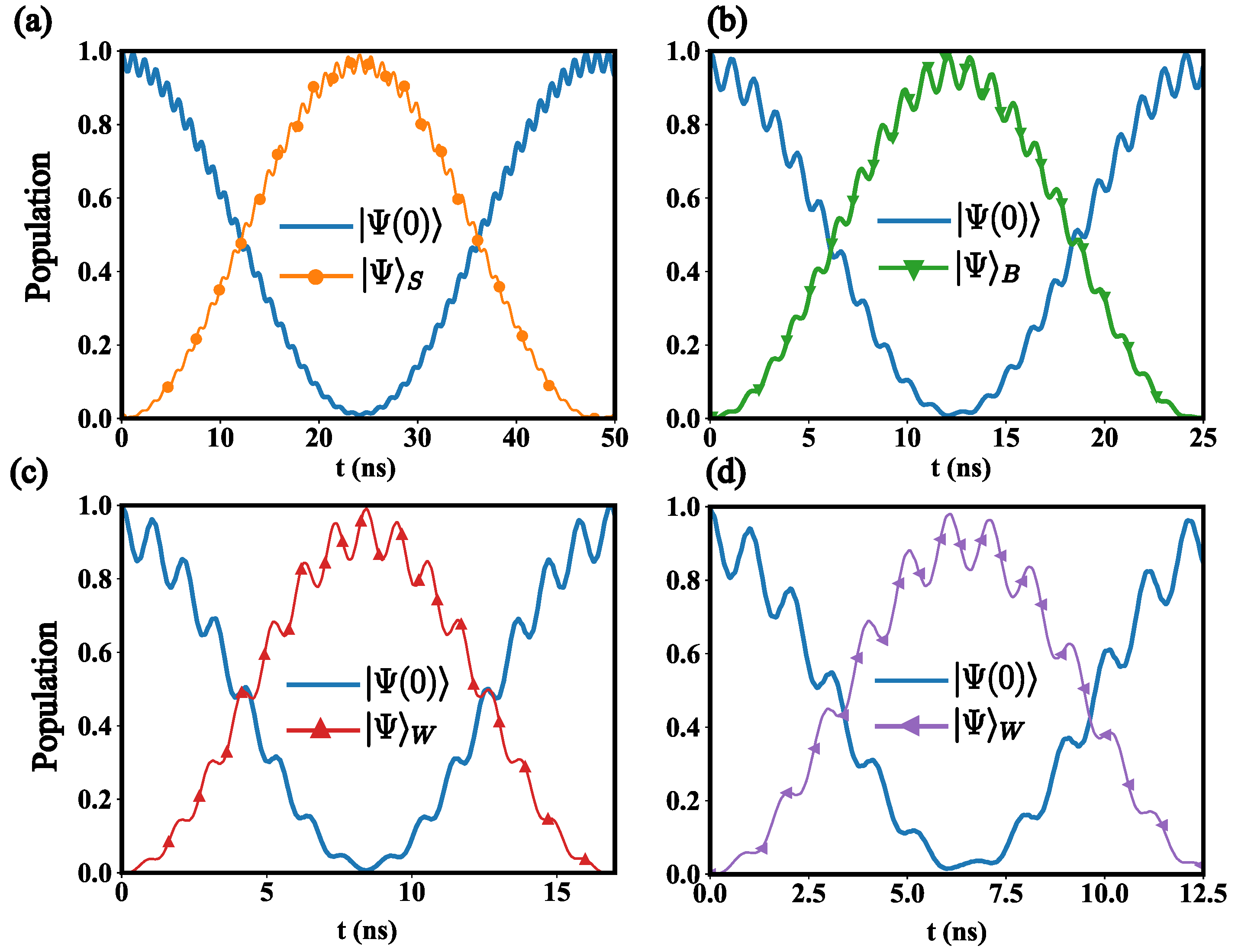
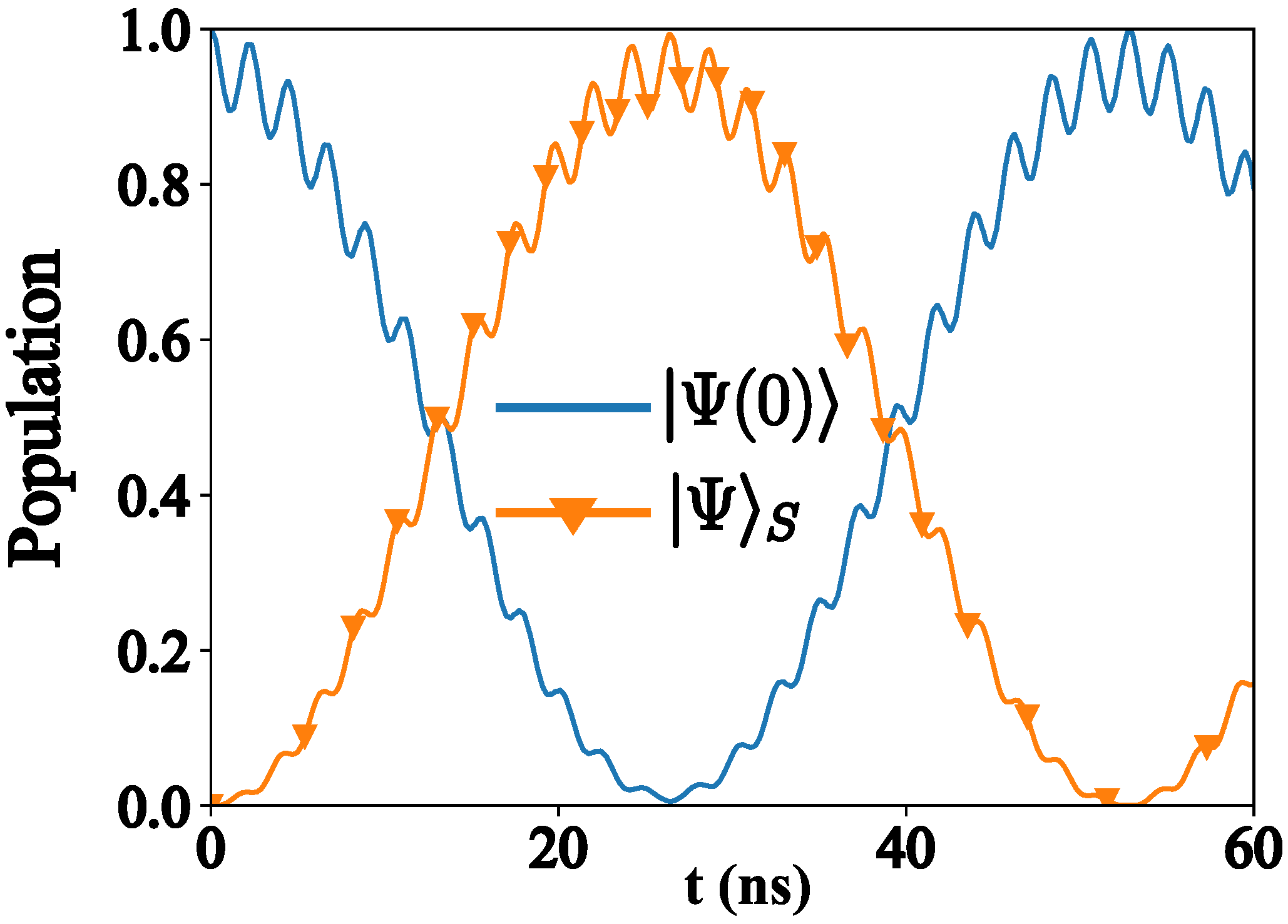
4. Two Photon Process Mediated by a Quantum Rabi System
5. Copies of Density Matrices
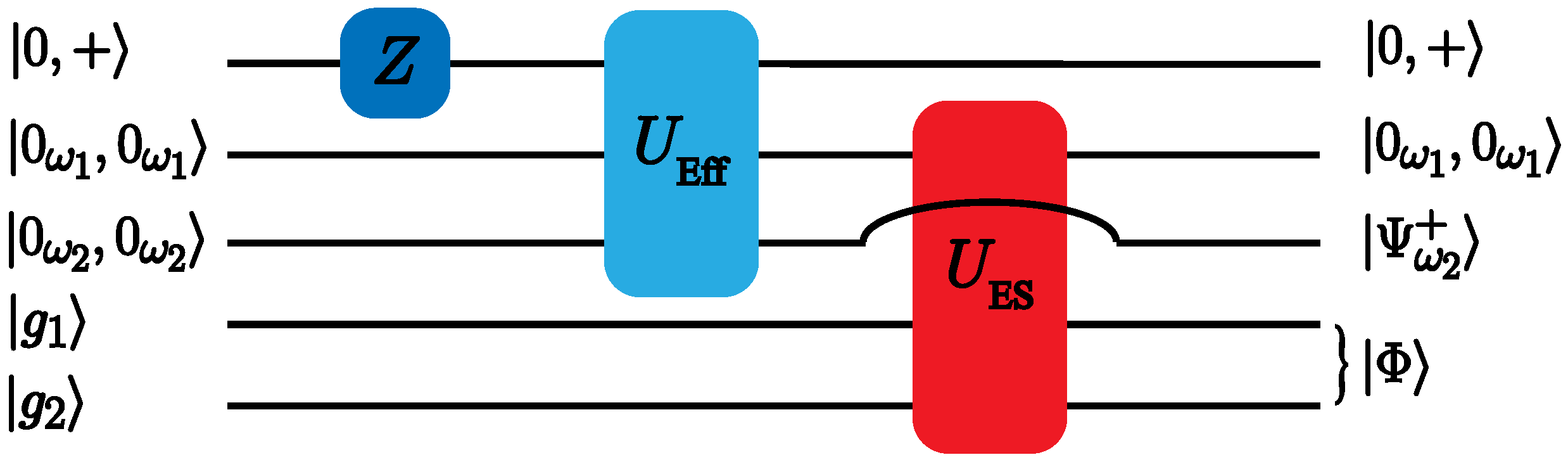
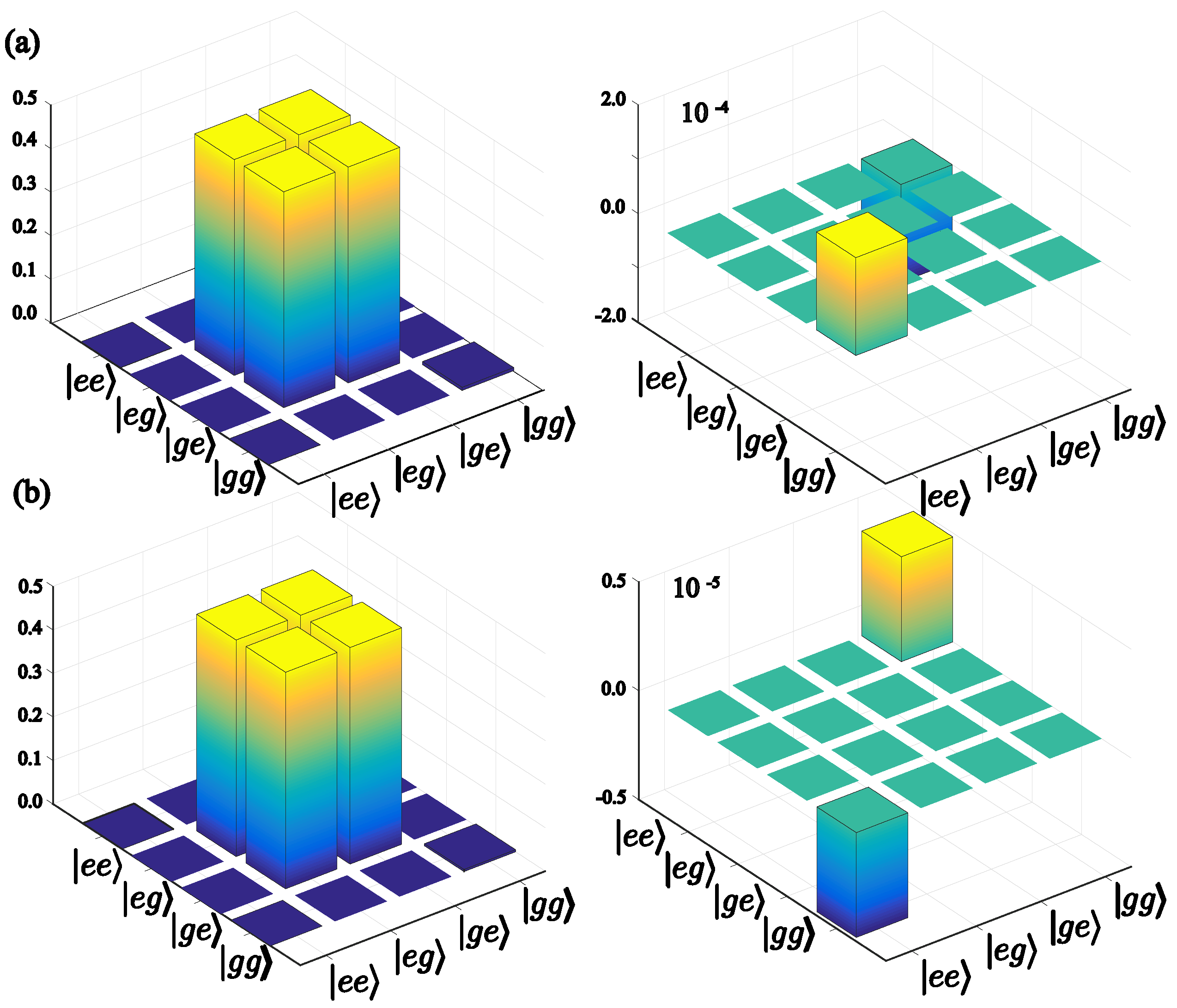
6. Entanglement Swapping between Distant Superconducting Qubits
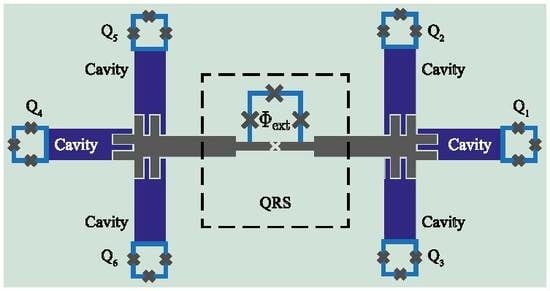
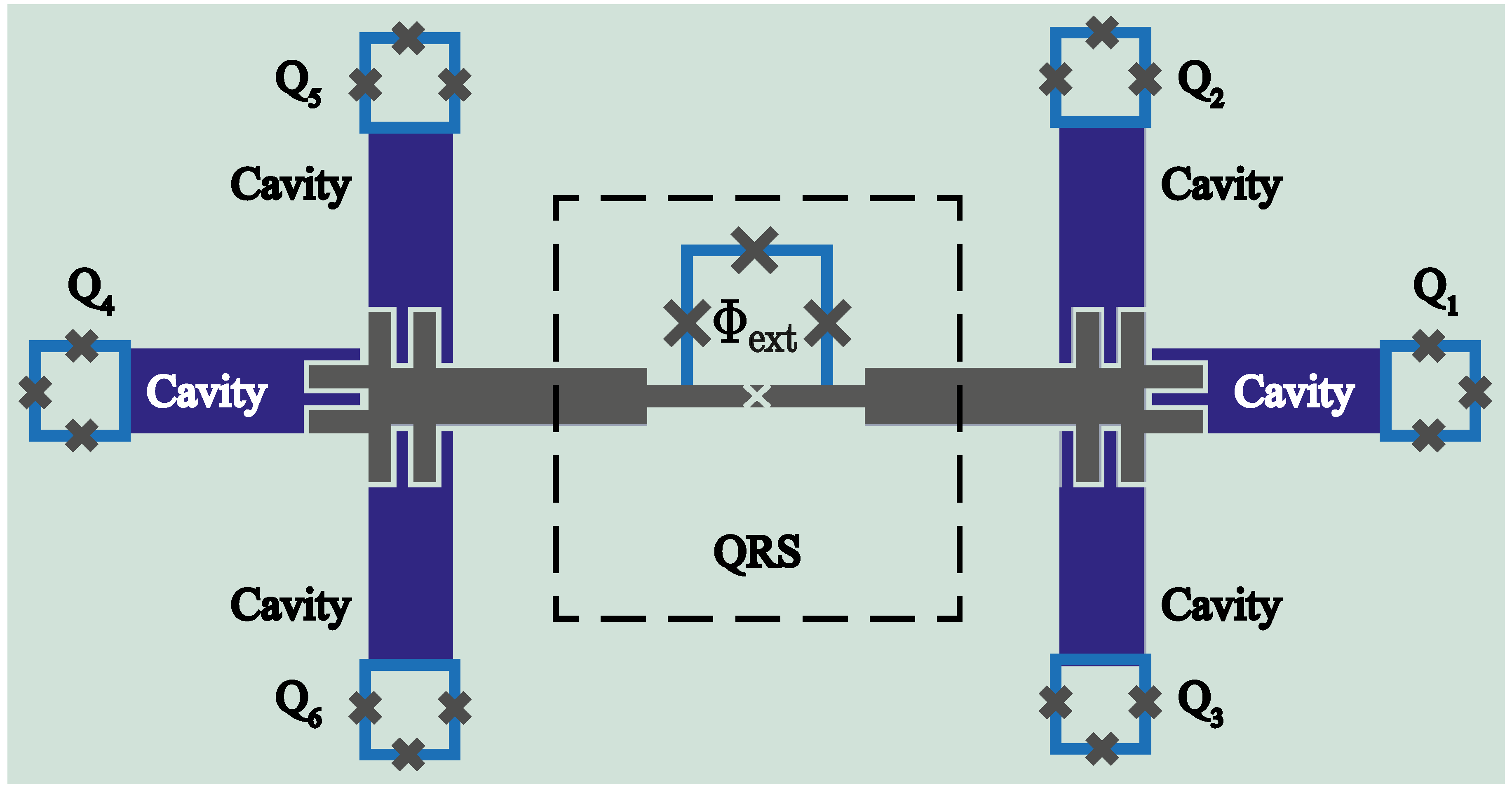
7. Implementation in Circuit QED
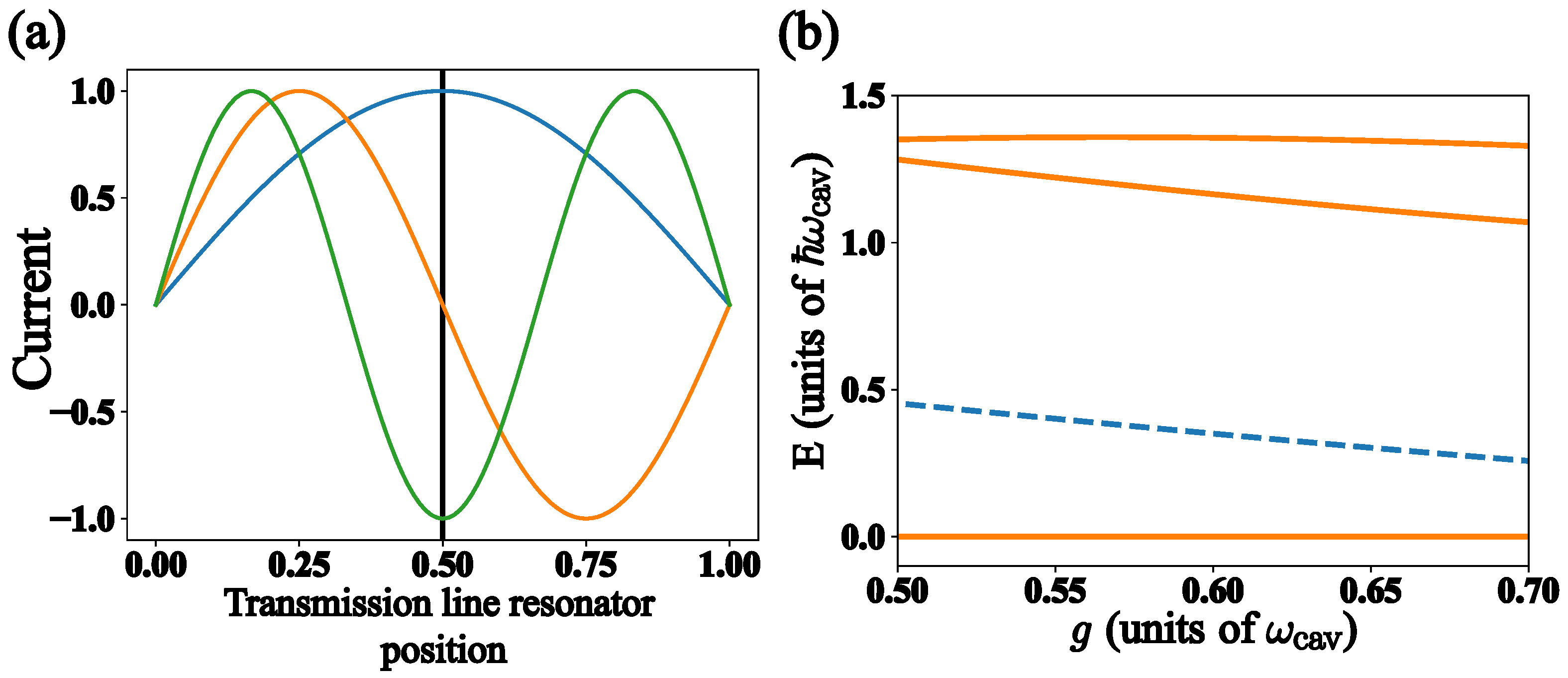
7.1. Rabi System Hamiltonian
7.2. Multimode Cavity Hamiltonian
7.3. Complete Model
7.4. Driving the Superconducting Qubit
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- You, J.Q.; Nori, F. Atomic physics and quantum optics using superconducting circuits. Nature 2011, 474, 589–597. [Google Scholar] [CrossRef] [PubMed]
- Houck, A.A.; Türeci, H.E.; Koch, J. On-chip quantum simulation with superconducting circuits. Nat. Phys. 2012, 8, 292–299. [Google Scholar] [CrossRef]
- Devoret, M.H.; Schoelkopf, R.J. Superconducting circuits for quantum information: An outlook. Science 2013, 339, 1169–1174. [Google Scholar] [CrossRef]
- Wallraff, A.; Schuster, D.I.; Blais, A.; Frunzio, L.; Huang, R.S.; Majer, J.; Kumar, S.; Girvin, S.M.; Schoelkopf, R.J. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 2004, 431, 162–167. [Google Scholar] [CrossRef] [PubMed]
- Blais, A.; Huang, R.S.; Wallraff, A.; Girvin, S.M.; Schoelkopf, R.J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 2004, 69, 062320. [Google Scholar] [CrossRef]
- Nakamura, Y. Microwave quantum photonics in superconducting circuits. In Proceedings of the IEEE Photonics Conference 2012, Burlingame, CA, USA, 23–27 September 2012; pp. 544–545. [Google Scholar]
- Gu, X.; Kockum, A.F.; Miranowicz, A.; Liu, Y.X.; Nori, F. Microwave photonics with superconducting quantum circuits. Phys. Rep. 2017, 718–719, 1–102. [Google Scholar] [CrossRef]
- Orlando, T.P.; Mooij, J.E.; Tian, L.; van der Wal, C.H.; Levitov, L.S.; Lloyd, S.; Mazo, J.J. Superconducting persistent-current qubit. Phys. Rev. B 1999, 60, 15398–15413. [Google Scholar] [CrossRef]
- Koch, J.; Terri, M.Y.; Gambetta, J.; Houck, A.A.; Schuster, D.I.; Majer, J.; Blais, A.; Devoret, M.H.; Girvin, S.M.; Schoelkopf, R.J. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 2007, 76, 042319. [Google Scholar] [CrossRef]
- Göppl, M.; Fragner, A.; Baur, M.; Bianchetti, R.; Filipp, S.; Leek, J.M.F.P.J.; Puebla, G.; Steffen, L.; Wallraff, A. Coplanar waveguide resonators for circuit quantum electrodynamics. J. Appl. Phys. 2008, 104, 113904. [Google Scholar] [CrossRef]
- Abdumalikov, A.A.; Astafiev, O.; Zagoskin, A.M.; Pashkin, Y.A.; Nakamura, Y.; Tsai, J.S. Electromagnetically induced transparency on a single artificial atom. Phys. Rev. Lett. 2010, 104, 193601. [Google Scholar] [CrossRef]
- Lang, C.; Bozyigit, D.; Eichler, C.; Steffen, L.; Fink, J.M.; Abdumalikov, A.A., Jr.; Baur, M.; Filipp, S.; Da Silva, M.P.; Blais, A.; et al. Observation of resonant photon blockade at microwave frequencies using correlation function measurements. Phys. Rev. Lett. 2011, 106, 243601. [Google Scholar] [CrossRef]
- Goetz, J.; Deppe, F.; Fedorov, K.G.; Eder, P.; Fischer, M.; Pogorzalek, S.; Xie, E.; Marx, A.; Gross, R. Parity-Engineered Light-Matter Interaction. Phys. Rev. Lett. 2018, 121, 060503. [Google Scholar] [CrossRef]
- Bergeal, N.; Vijay, R.; Manucharyan, V.E.; Siddiqi, I.; Schoelkopf, R.J.; Girvin, S.M.; Devoret, M.H. Analog information processing at the quantum limit with a Josephson ring modulator. Nat. Phys. 2010, 6, 296–302. [Google Scholar] [CrossRef]
- Boissonneault, M.; Gambetta, J.M.; Blais, A. Improved superconducting qubit readout by qubit-induced nonlinearities. Phys. Rev. Lett. 2010, 105, 100504. [Google Scholar] [CrossRef] [PubMed]
- Bourassa, J.; Beaudoin, F.; Gambetta, J.M.; Blais, A. Josephson-junction-embedded transmission-line resonators: From Kerr medium to in-line transmon. Phys. Rev. A 2012, 86, 013814. [Google Scholar] [CrossRef]
- Leib, M.; Deppe, F.; Marx, A.; Gross, R.; Hartmann, M.J. Networks of nonlinear superconducting transmission line resonators. New J. Phys. 2012, 14, 075024. [Google Scholar] [CrossRef]
- Hoi, I.-C.; Kockum, A.F.; Palomaki, T.; Stace, T.M.; Fan, B.; Tornberg, L.; Sathyamoorthy, S.R.; Johansson, G.; Delsing, P.; Wilson, C.M. Giant Cross–Kerr Effect for Propagating Microwaves Induced by an Artificial Atom. Phys. Rev. Lett. 2013, 111, 053601. [Google Scholar] [CrossRef] [PubMed]
- Marquardt, F. Efficient on-chip source of microwave photon pairs in superconducting circuit QED. Phys. Rev. B 2007, 76, 205416. [Google Scholar] [CrossRef]
- Koshino, K. Down-conversion of a single photon with unit efficiency. Phys. Rev. A 2009, 79, 013804. [Google Scholar] [CrossRef]
- Liu, Y.X.; Sun, H.C.; Peng, Z.H.; Miranowicz, A.; Tsai, J.S.; Nori, F. Controllable microwave three-wave mixing via a single three-level superconducting quantum circuit. Sci. Rep. 2014, 4, 7289. [Google Scholar] [CrossRef]
- Sánchez-Burillo, E.; Martín-Moreno, L.; García-Ripoll, J.J.; Zueco, D. Full two-photon down-conversion of a single photon. Phys. Rev. A 2016, 94, 053814. [Google Scholar] [CrossRef]
- Yurke, B.; Corruccini, L.R.; Kaminsky, P.G.; Rupp, L.W.; Smith, A.D.; Silver, A.H.; Simon, R.W.; Whittaker, E.A. Observation of parametric amplification and deamplification in a Josephson parametric amplifier. Phys. Rev. A 1989, 39, 2519–2533. [Google Scholar] [CrossRef]
- Everitt, M.J.; Clark, T.D.; Stiffell, P.B.; Vourdas, A.; Ralph, J.F.; Prance, R.J.; Prance, H. Superconducting analogs of quantum optical phenomena: Macroscopic quantum superpositions and squeezing in a superconducting quantum-interference device ring. Phys. Rev. A 2004, 69, 043804. [Google Scholar] [CrossRef]
- Zagoskin, A.M.; Il’chev, E.; McCutcheon, M.W.; Young, J.F.; Nori, F. Controlled generation of squeezed states of microwave radiation in a superconducting resonant circuit. Phys. Rev. Lett. 2008, 101, 253602. [Google Scholar] [CrossRef]
- Moon, K.; Girvin, S.M. Theory of microwave parametric down-conversion and squeezing using circuit QED. Phys. Rev. Lett. 2005, 95, 140504. [Google Scholar] [CrossRef]
- Didier, N.; Qassemi, F.; Blais, A. Perfect squeezing by damping modulation in circuit quantum electrodynamics. Phys. Rev. A 2014, 89, 013820. [Google Scholar] [CrossRef]
- Strauch, F.W. All-resonant control of superconducting resonators. Phys. Rev. Lett. 2012, 109, 210501. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.-J.; Wang, C.; Zhu, X.; Liu, Y.-X. Engineering entangled microwave photon states through multiphoton interactions between two cavity fields and a superconducting qubit. Sci. Rep. 2016, 6, 23646. [Google Scholar] [CrossRef]
- Merkel, S.T.; Wilhelm, F.K. Generation and detection of NOON states in superconducting circuits. New J. Phys. 2010, 12, 093036. [Google Scholar] [CrossRef]
- Strauch, F.W.; Jacobs, K.; Simmonds, R.W. Arbitrary Control of Entanglement between two Superconducting Resonators. Phys. Rev. Lett. 2010, 105, 050501. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Mariantoni, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; O’Connell, A.D.; Sank, D.; Weides, M.; Wenner, J.; et al. Deterministic Entanglement of Photons in Two Superconducting Microwave Resonators. Phys. Rev. Lett. 2011, 106, 060401. [Google Scholar] [CrossRef]
- Gasparinetti, S.; Pechal, M.; Besse, J.C.; Mondal, M.; Eichler, C.; Wallraff, A. Correlations and entanglement of microwave photons emitted in a cascade decay. Phys. Rev. Lett. 2017, 119, 140504. [Google Scholar] [CrossRef] [PubMed]
- Campagne-Ibarcq, P.; Zalys-Geller, E.; Narla, A.; Shankar, S.; Reinhold, P.; Burkhart, L.D.; Axline, C.J.; Pfaff, W.; Frunzio, L.; Schoelkopf, R.J.; et al. Deterministic remote entanglement of superconducting circuits through microwave two-photon transitions. Phys. Rev. Lett. 2018, 120, 200501. [Google Scholar] [CrossRef] [PubMed]
- Rosenblum, S.; Gao, Y.Y.; Reinhold, P.; Wang, C.; Axline, C.J.; Frunzio, L.; Girvin, S.M.; Jiang, L.; Mirrahimi, M.; Devoret, M.H.; et al. A CNOT gate between multiphoton qubits encoded in two cavities. Nat. Commun. 2018, 9, 652. [Google Scholar] [CrossRef] [PubMed]
- Narla, A.; Shankar, S.; Hatridge, M.; Leghtas, Z.; Sliwa, K.M.; Zalys-Geller, E.; Mundhada, S.O.; Pfaff, W.; Frunzio, L.; Shoelkopf, R.J.; et al. Robust concurrent remote entanglement between two superconducting qubits. Phys. Rev. X 2016, 6, 031036. [Google Scholar] [CrossRef]
- Kurpiers, P.; Magnard, P.; Walter, T.; Royer, B.; Pechal, M.; Heinsoo, J.; Salathé, Y.; Akin, A.; Storz, S.; Besse, J.C.; et al. Deterministic Quantum State Transfer and Generation of Remote Entanglement using Microwave Photons. Nature 2018, 558, 264–267. [Google Scholar] [CrossRef]
- Bourassa, J.; Gambetta, J.M.; Abdumalikov, A.A.; Astafiev, O.; Nakamura, Y.; Blais, A. Ultrastrong coupling regime of cavity QED with phase-biased flux qubits. Phys. Rev. A 2009, 80, 032109. [Google Scholar] [CrossRef]
- Niemczyk, T.; Deppe, F.; Huebl, H.; Menzel, E.P.; Hocke, F.; Schwarz, M.J.; García-Ripoll, J.J.; Zueco, D.; Hümmer, T.; Solano, E.; et al. Circuit quantum electrodynamics in the ultrastrong-coupling regime. Nat. Phys. 2010, 6, 772–776. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lisenfeld, J.; Marcos, D.; García-Ripoll, J.J.; Solano, E.; Harmans, C.J.P.M.; Mooij, J.E. Observation of the Bloch-Siegert shift in a qubit-oscillator system in the ultrastrong coupling regime. Phys. Rev. Lett. 2010, 105, 237001. [Google Scholar] [CrossRef]
- Andersen, C.K.; Blais, A. Ultrastrong coupling dynamics with a transmon qubit. New J. Phys. 2017, 19, 023022. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; García-Ripoll, J.J.; Peropadre, B.; Orgiazzi, J.L.; Yurtalan, M.A.; Belyansky, R.; Wilson, C.M.; Lupascu, A. Ultrastrong coupling of a single artificial atom to an electromagnetic continuum in the nonperturbative regime. Nat. Phys. 2017, 13, 39–43. [Google Scholar] [CrossRef]
- Martínez, J.P.; Léger, S.; Gheeraert, N.; Dassonneville, R.; Planat, L.; Foroughi, F.; Krupko, Y.; Buisson, O.; Naud, C.; Hasch-Guichard, W.; et al. A tunable Josephson platform to explore many-body quantum optics in circuit-QED. arXiv, 2018; arXiv:1802.00633. [Google Scholar]
- Casanova, J.; Romero, G.; Lizuain, I.; García-Ripoll, J.J.; Solano, E. Deep Strong Coupling Regime of the Jaynes-Cummings Model. Phys. Rev. Lett. 2010, 105, 263603. [Google Scholar] [CrossRef]
- Yoshihara, F.; Fuse, T.; Ashhab, S.; Kakuyanagi, K.; Saito, S.; Semba, K. Superconducting qubit-oscillator circuit beyond the ultrastrong-coupling regime. Nat. Phys. 2017, 13, 44–47. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Lamata, L.; Rico, E.; Kono, J.; Solano, E. Ultrastrong coupling regimes of light–matter interaction. arXiv, 2018; arXiv:1804.09275. [Google Scholar]
- Kockum, A.F.; Miranowicz, A.; de Liberato, S.; Savasta, S.; Nori, F. Ultrastrong coupling between light and matter. Nat. Rev. Phys. 2019, 1, 19–40. [Google Scholar] [CrossRef]
- Rabi, I.I. On the Process of Space Quantization. Phys. Rev. 1936, 49, 324–328. [Google Scholar] [CrossRef]
- Braak, D. Integrability of the Rabi Model. Phys. Rev. Lett. 2011, 107, 100401. [Google Scholar] [CrossRef] [PubMed]
- Nataf, P.; Ciuti, C. Protected Quantum Computation with Multiple Resonators in Ultrastrong Coupling Circuit QED. Phys. Rev. Lett. 2011, 107, 190402. [Google Scholar] [CrossRef] [PubMed]
- Romero, G.; Ballester, D.; Wang, Y.M.; Scarani, V.; Solano, E. Ultrafast Quantum Gates in Circuit QED. Phys. Rev. Lett. 2012, 108, 120501. [Google Scholar] [CrossRef] [PubMed]
- Kyaw, T.H.; Felicetti, S.; Romero, G.; Solano, E.; Kwek, L.-C. Scalable quantum memory in the ultrastrong coupling regime. Sci. Rep. 2015, 5, 8621. [Google Scholar] [CrossRef] [PubMed]
- Felicetti, S.; Douce, T.; Romero, G.; Milman, P.; Solano, E. Parity-dependent state engineering and tomography in the ultrastrong coupling regime. Sci. Rep. 2015, 5, 11818. [Google Scholar] [CrossRef] [PubMed]
- Kyaw, T.H.; Herrera-Martí, D.A.; Solano, E.; Romero, G.; Kwek, L.-C. Creation of quantum error correcting codes in the ultrastrong coupling regime. Phys. Rev. B 2015, 91, 064503. [Google Scholar] [CrossRef]
- Wang, Y.M.; Zhang, J.; Wu, C.; You, J.Q.; Romero, G. Holonomic quantum computation in the ultrastrong-coupling regime of circuit QED. Phys. Rev. A 2016, 94, 012328. [Google Scholar] [CrossRef]
- Albarrán-Arriagada, F.; Lamata, L.; Solano, E.; Romero, G.; Retamal, J.C. Spin-1 models in the ultrastrong-coupling regime of circuit QED. Phys. Rev. A 2018, 97, 022306. [Google Scholar] [CrossRef]
- Garziano, L.; Stassi, R.; Macrì, V.; Kockum, A.F.; Savasta, S.; Nori, F. Multiphoton quantum Rabi oscillations in ultrastrong cavity QED. Phys. Rev. A 2015, 92, 063830. [Google Scholar] [CrossRef]
- Kockum, A.F.; Miranowicz, A.; Macrì, V.; Savasta, S.; Nori, F. Deterministic quantum nonlinear optics with single atoms and virtual photons. Phys. Rev. A 2017, 95, 063849. [Google Scholar] [CrossRef]
- Kockum, A.F.; Macrì, V.; Garziano, L.; Savasta, S.; Nori, F. Frequency conversion in ultrastrong cavity QED. Sci. Rep. 2017, 7, 5313. [Google Scholar] [CrossRef]
- Stassi, R.; Macrì, V.; Kockum, A.F.; di Stefano, O.; Miranowicz, A.; Savasta, S.; Nori, F. Quantum nonlinear optics without photons. Phys. Rev. A 2017, 96, 023818. [Google Scholar] [CrossRef]
- Mlynek, J.A.; Abdumalikov, A.A., Jr.; Fink, J.M.; Steffen, L.; Baur, M.; Lang, C.; van Loo, A.F.; Wallraff, A. Demonstrating W-type entanglement of Dicke states in resonant cavity quantum electrodynamics. Phys. Rev. A 2012, 86, 053838. [Google Scholar] [CrossRef]
- Wei, X.; Chen, M.-F. Preparation of multi-qubit W states in multiple resonators coupled by a superconducting qubit via adiabatic passage. Quantum Inf. Process. 2013, 14, 2419–2433. [Google Scholar] [CrossRef]
- Liu, X.; Liao, Q.; Xu, X.; Fang, G.; Liu, S. One-step schemes for multiqubit GHZ states and W-class states in circuit QED. Opt. Commun. 2016, 359, 359–363. [Google Scholar] [CrossRef]
- Çakmak, B.; Campbell, S.; Vacchini, B.; Müstecaplıoǧlu, Ė.; Paternostro, M. Robust multipartite entanglement generation via a collision model. Phys. Rev. A 2019, 99, 012319. [Google Scholar] [CrossRef]
- Wei, X.; Chen, M.-F. Generation of N-Qubit W State in N Separated Resonators via Resonant Interaction. Int. J. Theor. Phys. 2014, 54, 812–820. [Google Scholar] [CrossRef]
- Egger, D.J.; Wilhelm, F.K. Multimode Circuit Quantum Electrodynamics with Hybrid Metamaterial Transmission Lines. Phys. Rev. Lett. 2013, 111, 163601. [Google Scholar] [CrossRef] [PubMed]
- Underwood, D.L.; Shanks, W.E.; Koch, J.; Houck, A.A. Low-disorder microwave cavity lattices for quantum simulation with photons. Phys. Rev. A 2012, 86, 023837. [Google Scholar] [CrossRef]
- Wu, Y.; Yang, X. Strong-coupling theory of periodically driven two-level systems. Phys. Rev. Lett. 2007, 98, 013601. [Google Scholar] [CrossRef]
- Brune, M.; Raimond, J.M.; Haroche, S. Theory of the Rydberg-atom two-photon micromaser. Phys. Rev. A 1987, 35, 154. [Google Scholar] [CrossRef]
- Brune, M.; Raimond, J.M.; Goy, P.; Davidovich, L.; Haroche, S. Realization of a two-photon maser oscillator. Phys. Rev. Lett. 1987, 59, 1899–1902. [Google Scholar] [CrossRef] [PubMed]
- Dür, W.; Vidal, G.; Cirac, J.I. Three qubits can be entangled in two inequivalent ways. Phys. Rev. A 2000, 62, 062314. [Google Scholar] [CrossRef]
- Macri, V.; Nori, F.; Kockum, A.F. Simple preparation of Bell and GHZ states using ultrastrong-coupling circuit QED. Phys. Rev. A 2018, 98, 062327. [Google Scholar] [CrossRef]
- Beaudoin, F.; Gambetta, J.M.; Blais, A. Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 2011, 84, 043832. [Google Scholar] [CrossRef]
- Ridolfo, A.; Leib, M.; Savasta, S.; Hartmann, M.J. Photon Blockade in the Ultrastrong Coupling Regime. Phys. Rev. Lett. 2012, 109, 193602. [Google Scholar] [CrossRef]
- Settineri, A.; Macri, V.; Ridolfo, A.; di Stefano, O.; Kockum, A.F.; Nori, F.; Savasta, S. Dissipation and Thermal Noise in Hybrid Quantum Systems in the Ultrastrong Coupling Regime. Phys. Rev. A 2019, 98, 053834. [Google Scholar] [CrossRef]
- Reuther, G.M.; Zueco, D.; Deppe, F.; Hoffmann, E.; Menzel, E.P.; Weißl, T.; Mariantoni, M.; Kohler, S.; Marx, A.; Solano, E.; et al. Two-resonator circuit quantum electrodynamics: Dissipative theory. Phys. Rev. B 2010, 81, 144510. [Google Scholar] [CrossRef]
- Forn-Díaz, P.; Romero, G.; Harmans, C.J.P.M.; Solano, E.; Mooij, J.E. Broken selection rule in the quantum Rabi model. Sci. Rep. 2016, 6, 26720. [Google Scholar] [CrossRef]
- Boissonneault, M.; Gambetta, J.M.; Blais, A. Dispersive regime of circuit QED: Photon-dependent qubit dephasing and relaxation rates. Phys. Rev. A 2009, 79, 013819. [Google Scholar] [CrossRef]
- Masluk, N.A. Reducing the Losses of the Fluxonium Artificial Atom. Ph.D. Thesis, Yale University, New Haven, CT, USA, 2013. [Google Scholar]
- Yurke, B.; Denker, J.S. Quantum network theory. Phys. Rev. A 1984, 29, 1419–1437. [Google Scholar] [CrossRef]
- Devoret, M.H. Quantum Fluctuations in electrical circuits. In Les Houches Session LXIII; Reynaud, S., Giacobino, E., Zinn-Justin, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 351–386. [Google Scholar]
- Ashhab, S.; Johansson, J.R.; Zagoskin, A.M.; Nori, F. Two-level systems driven by large-amplitude fields. Phys. Rev. A 2007, 75, 063414. [Google Scholar] [CrossRef]
| 0.9898 | 0.9818 | 0.9832 | |
| 0.9892 | - | - | |
| - | 0.9945 | - | |
| - | - | 0.9904 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cárdenas-López, F.A.; Romero, G.; Lamata, L.; Solano, E.; Retamal, J.C. Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics. Symmetry 2019, 11, 372. https://doi.org/10.3390/sym11030372
Cárdenas-López FA, Romero G, Lamata L, Solano E, Retamal JC. Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics. Symmetry. 2019; 11(3):372. https://doi.org/10.3390/sym11030372
Chicago/Turabian StyleCárdenas-López, Francisco A., Guillermo Romero, Lucas Lamata, Enrique Solano, and Juan Carlos Retamal. 2019. "Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics" Symmetry 11, no. 3: 372. https://doi.org/10.3390/sym11030372
APA StyleCárdenas-López, F. A., Romero, G., Lamata, L., Solano, E., & Retamal, J. C. (2019). Parity-Assisted Generation of Nonclassical States of Light in Circuit Quantum Electrodynamics. Symmetry, 11(3), 372. https://doi.org/10.3390/sym11030372