A Nonparametric HEWMA-p Control Chart for Variance in Monitoring Processes

Abstract

Control charts are considered as powerful tools in detecting any shift in a process. Usually, the Shewhart control chart is used when data follows the symmetrical property of a normal distribution. In practice, the data from the industry may follow a non-symmetrical distribution or an unknown distribution. The average run length (ARL) is a significant measure to assess the performance of the control chart. The ARL may mislead when the statistic is computed from an asymmetric distribution. To handle this issue, in this paper, an ARL-unbiased hybrid exponentially weighted moving average proportion (HEWMA-p) chart is proposed for monitoring the process variance for a non-normal distribution or an unknown distribution. The efficiency of the proposed chart is compared with the existing chart in terms of ARLs. The proposed chart is more efficient than the existing chart in terms of ARLs. A real example is given for the illustration of the proposed chart in the industry.

1. Introduction

The aim of quality refers to the quality of those product characteristics that will appeal to potential customers. It takes into account what it would cost to produce the product and what the customers are willing to pay for the product. It can be thought of as the perspective for accomplishing manufactured quality. Once the manufacturing process has started, the process does not always produce a unit in conformity with what was proposed. This may be due to causes of defects arising in materials, parts, subassemblies, assemblies, and in the final product. Due to defective or nonconforming resources, parts, assemblies, and finished products that are discarded or reworked during the manufacturing process result in increased cost and customer dissatisfaction. The waste of time and effort in manufacturing the defective or nonconforming product, the delays in delivery, and other associated costs attributable to a poorly manufactured product are the consequence of manufactured quality. If a company wishes to produce higher quality products, it usually needs higher costs for manufactured products. However, the aim should always be to offer customers good quality at a low cost. Therefore, quality is also part of the corporate approach. Understanding quality concepts leads to correct implementation and management of product quality, which adds benefits to the entire production endeavor. If an industry understands and applies quality control principles in their manufactured products, it will produce well finished products, and reduction of the costs of the products may be possible.

The control charts are effectively used for the monitoring of the process. The Shewhart control chart is designed under the assumption that the data coming from the industry follows a normal distribution. This chart is more effective in detecting a relatively large shift in a process. The Shewhart control chart cannot be applied for a monitoring process when the industrial data follow the non-normal distribution or unknown distribution. Several authors focused on designing control charts for monitoring process mean, including for example [1,2,3]. Some authors designed control charts for monitoring the process variance; see for example [4,5]. More details on control charts can be seen in [6,7,8,9,10,11,12,13].

As mentioned by [14] practitioners are often not statisticians and may have problems in implementing control charts based on non-parametric approaches. Keeping in mind this issue, several authors, including for example, references [15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41] focused on designing control charts for monitoring the process mean that were easier to apply as compared to existing charts. Later on, Yang et al. [42] worked on the extension of the chart designed in [43] to monitor the process variance using a simple arcsin transformed symmetric exponentially weighted moving average (EWMA) statistic. Yang et al. [42] further extended the work of [5] by mixing the arcsin transformed EWMA and simple EWMA statistic. Yang et al. [5] designed the arcsin transformed EWMA to monitor process variance. The average run length (ARL) is used to assess the performance of a control chart. Smaller ARL means more efficient and faster detection of a shift in the process. According to [5] “For a monitoring statistic with an asymmetrical distribution, the control chart leads to a biased ARL. That is, the in-control ARL may be smaller than any out-of-control ARL, thus taking longer to detect shifts in the parameter than to trigger a false alarm”. Lowry et al. [44] proposed a chart to tackle this issue.

Haq [45] proposed a control chart using two EWMA statistics and called it a hybrid EWMA (HEWMA) chart. He claimed that their proposed chart performed better than the usual EWMA chart. The HEWMA statistic consists of two EWMA statistics and two smoothing constants. The control chart based on HEWMA statistic has the ability to detect the shift in the process earlier than the EWMA-based control chart. The operational process of the HEWMA based control chart is the same as the EWMA control chart. Several authors worked on these statistics in the literature. There are various variable charts for joint monitoring; see for example, Nyau et al. [11], who designed the multivariate EWMA chart for the median run-length. Riaz et al. [12] proposed a mixed Tukey EWMA–CUSUM (cumulative sum) control chart and Osei-Aning et al. [13] worked on the mixed EWMA–CUSUM and mixed CUSUM–EWMA. Haq [46] presented a discussion on the HEWMA control chart. Noor-ul-Amin et al. [47] worked on the HEWMA chart for the regression estimator. Several authors proposed the attribute control chart using EWMA and HEWMA statistics. Aslam et al. [48] designed the mixed EWMA control chart. Haq [49] worked on the nonparametric EWMA chart. Riaz et al. [50] designed the nonparametric double EWMA control chart. Aslam et al. [51] worked on the HEWMA–CUSUM chart for the Weibull distribution. Aslam et al. [52] worked on the HEWMA chart for the COM–Poisson distribution.

Yang et al. [14] designed an ARL unbiased EWMA-p chart. According to the best of our knowledge, there is no work on designing a EWMA-p chart using a hybrid EWMA. The proposed methodology presents an approach to evaluate the performance using the combination of a hybrid EWMA control chart with weighted moving average proportion (EWMA-p) control chart. The hybrid EWMA and EWMA-p charts are chosen since it has been shown that these charts are efficient in detecting small but possibly detrimental shifts in the process. Aslam et al. [52] also pointed out that in a general manufacturing process, an exponentially weighted moving average EWMA control chart is more efficient in detecting small process shifts. The control chart based on the EWMA method consists of an exponential weight factor applied to the data, which gives current or recent past observations more weight than older data values. The combination of a hybrid EWMA chart and EWMA-p charts will be explored to determine the best conditions, i.e., the appropriate values of control variables for monitoring concrete strength. In this paper, we will present the enhanced hybrid exponential weighted moving average proportion (enhanced HEWMA-p) chart. The structure of the proposed chart will be presented and its efficacy will be compared with [14].

2. Design of the Enhanced HEWMA-p Chart

In this section, we will present some equations taken from [14] and present the operational procedure of the proposed control chart.

Let a random sample of size $n$ be drawn from process $X$ whose distribution is unknown with a variance ${\sigma }^2$ to practitioners. Yang et al. [14] suggested to select an even sample size $n$ for convenience. Assuming that these samples are independently distributed with known variance, let

$$Y_{i/2}^{*}={\left(X_i-X_{i-1}\right)}^2/2,i=2,4,\dots ,n.$$

(1)

Then,

$$E(Y_j^{*})={\sigma }^2, j=1,2,\dots ,0.5n.$$

(2)

Define

$$V={\displaystyle \sum }_{j=1}^{0.5n}{I}_j,$$

(3)

where

$$I_j=\{\begin{array}{ll}1,& if Y_j^{*}>{\sigma }^2\\ 0,& otherwise\end{array}\mathrm{for} j=1,2,\dots ,0.5n.$$

Therefore, when the process is in control, $V$ is distributed as a binomial with parameters $0.5n$ and $p_{v0}$, where the value of $p_{v0}$ depends on the distribution of $X_i$. Let us define $p_{v0}=P(Y_j^{*}>{\sigma }^2)$. The null hypothesis is that the process is in control state at $p_{v0}$. The alternative hypothesis is that the process has been shifted at $p_{v1}$. According to [14], the statistic of $V_t/0.5n$ has the mean of $p_{v0}$ and the variance of $p_{v0}\left(1-p_{v0}\right)/0.5n$.

We define the following two EWMA statistics:

$$EWM{A}_{p_t}={\lambda }_2{V}_t/0.5n+\left(1-{\lambda }_2\right)EWM{A}_{p_{t-1}}$$

(4)

$$HEWM{A}_{p_t}={\lambda }_{1}EWM{A}_{p_t}+\left(1-{\lambda }_1\right)HEWM{A}_{p_{t-1}}$$

(5)

where ${\lambda }_1\in \left[0,1\right]$ and ${\lambda }_2\in \left[0,1\right]$ are smoothing constants, and $HEWM{A}_{p_t}$ is the statistic of enhanced HEWMA-p at t.

The proposed control chart is stated as follows:

• Step 1: Select a random sample of size $n$($X_1,\dots , X_n$) from the process at time t. Compute $V_t$ using (3) and $HEWM{A}_{p_t}$ using (5).
• Step 2: The process is declared to be as out-of-control if $HEWM{A}_{p_t}\ge UCL$ or $HEWM{A}_{p_t}\le LCL$ and to be in-control if $LCL<HEWM{A}_{p_t}<UCL$, here LCL and UCL show the lower control limit and upper control limit.

The proposed control chart is the extension of the chart proposed by [14]. The proposed chart reduces to [14] chart when ${\lambda }_1={\lambda }_2=\lambda$ or ${\lambda }_1$ = 1 or ${\lambda }_2$ = 1. The proposed chart becomes the Shewhart chart when ${\lambda }_1$ = 1 and ${\lambda }_2$ = 1. It is assumed that the starting value of ${HEWMA}_{p_t}$ is the mean of $p_{v0}$, i.e., $HEWM{A}_{p_t}=p_{v0}$ for an in control process. By following [45], the mean and variance of statistic $HEWM{A}_{p_t}$ is given by

$$E\left(HEWM{A}_{p_t}\right)=p_{v0}$$

(6)

and

$$V\left(HEWM{A}_{p_t}\right)=\frac{{\lambda }_1^2{\lambda }_2{p}_{v0}\left(1-p_{v0}\right)}{\left(2-{\lambda }_2\right)0.5n}\left[\frac{1-{\left(1-{\lambda }_1\right)}^{2t}}{{\lambda }_1\left(2-{\lambda }_1\right)}-\frac{{\left(1-{\lambda }_2\right)}^2\left\{{\left(1-{\lambda }_2\right)}^{2t}-{\left(1-{\lambda }_1\right)}^{2t}\right\}}{{\left(1-{\lambda }_2\right)}^2-{\left(1-{\lambda }_1\right)}^2}\right]$$

(7)

Thus, the asymptotic variance of $HEWM{A}_{p_t}$ is given as

$$V\left(HEWM{A}_{p_t}\right)=\frac{{\lambda }_1{\lambda }_2{p}_{v0}\left(1-p_{v0}\right)}{\left(2-{\lambda }_2\right)\left(2-{\lambda }_1\right)0.5n}$$

(8)

As suggested by [14] “the new variance chart may be constructed based on the distribution of the monitoring statistic $V_t/0.5n$, which is an asymmetric distribution having similar defects to those of the corresponding Shewhart $p$ chart”. Therefore, monitoring the process variance is the same as the monitoring process proportion $p_{v0}$, as the proportion $p_{v0}$ of statistic $V_t/0.5n$ may not be same. The control limits of the proposed control chart are given as

$$UCL=p_{v0}+k_1\sqrt{\frac{{\lambda }_1{\lambda }_2{p}_{v0}\left(1-p_{v0}\right)}{\left(2-{\lambda }_2\right)\left(2-{\lambda }_1\right)0.5n}}$$

(9)

$$LCL=p_{v0}-k_2\sqrt{\frac{{\lambda }_1{\lambda }_2{p}_{v0}\left(1-p_{v0}\right)}{\left(2-{\lambda }_2\right)\left(2-{\lambda }_1\right)0.5n}}$$

(10)

$$CL=p_{v0}$$

where $k_1>k_2$ are control limit coefficients.

3. The Average Run Length of Enhanced HEWMA-p Control Chart

The proposed enhanced hybrid exponential weighted moving average proportion (enhanced HEWMA-p) control chart performance measure can be used as the average run length (ARL). In this paper, we have limited our study to non-normal distributions with finite variance. The control limits of the enhanced HEWMA-p control chart are determined by setting the in-control ARL (ARL_v0) to be a specified value, usually 370. The ARL represents the expected number of samples until a control chart signals. The proposed control chart comprises of two control coefficients, $k_1$ and $k_2$, which are obtained by considering the desired in-control ARL. Once the coefficients $k_1$ and $k_2$ are determined, the control limits of the enhanced HEWMA-p control chart are obtained and the out-of-control ARLs (ARL_v1) can be obtained according to various values of shift in proportion, p_v1 = c p_v0, c ≠ 1, and 0 < p_v1 ≤ 1. We use the following Monte Carlo simulation procedure to compute control coefficients $k_1$ and $k_2$, and to calculate the out-of-control ARL (ARL_v1) under a specified n, p_v0, ${\lambda }_1,{\lambda }_2$ and ARL_v0 values.

• Step 1. Setting specified values of n, p_v0, ${\lambda }_1, {\lambda }_2,$ and ARL_v0.
• Step 2. Evaluation of proposed control chart coefficients $k_1$ and $k_2$ for in-control process
• 2.1. Generate 10,000 possible values of control chart coefficients $k_1$ and $k_2$.
• 2.2. When the process is in-control, from a binomial distribution with the in-control parameters $0.5n\mathrm{and}{p}_{v0}.$ a random sample of size 2000 is generated, i.e., $V_t~binomial\left(0.5n,p_{v0}\right)$ at time t.
• 2.3. The enhanced HEWMA-p statistic HEWMA-p is computed for each subgroup of size 2000.
• 2.4. The proposed statistic HEWMA-p is plotted and in-control if $LCL\le HEWM{A}_p\le UCL;$ go to step 2.5 and the run length for out of control process is noted.
• 2.5. Repeat 10,000 times steps 2.2 through 2.3, to compute run lengths. If the average of these run lengths (ARLs) is equal to the specified ARL_v0 note the corresponding values of $k_1$ and $k_2$, and move to step 3, otherwise select other possible values of $k_1$ and $k_2$, and repeat the procedure from steps 2.2.
• Step 3 Evaluation of ARL_v1 for proposed control chart when the process is shifted
• 3.1. Let the out-of-control proportion, p_v1, be a proportion of the in-control proportion, p_v0. That is, p_v1 = c p_v0, c ≠ 1, and 0 < p_v1 ≤ 1, where c is the amount of shift in the process proportion, p_v0.
• 3.2. From binomial distribution, with the in-control parameters, $0.5n\mathrm{and}{p}_{v1}$, a random sample of size 2000 is generated, i.e., $V_t~binomial \left(0.5n,p_{v1}\right)$ at time t.
• 3.3. The Enhanced HEWMA-p Statistic HEWMA-p is Computed for Each Subgroup of Size 2000.
• 3.4. Using the Values of $k_1$ and $k_2$, the proposed statistic HEWMA-p is plotted and in-control if $LCL<HEWM{A}_{p_t}<UCL;$ go to step 3.5 and the run length for out of control process is noted.
• 3.5. Repeat 10,000 times steps 3.2 through 3.3, to compute run lengths. The average of run length (ARL_v1) and standard error of run length (SERL_v1) for each specified amount of shift is computed.

In Table 1, we present control chart coefficients $k_1$ and $k_2$, and corresponding upper and lower control limits of the enhanced HEWMA-p control chart for n = 8 (1) 30, p_v0 = 0.1, ${\lambda }_1=0.2,\mathrm{and}{\lambda }_2$ = 0.2 with ARL_v0 ≈ 370. Table 2 presents ARL_v1 and SERL_v1 values (in second row corresponding to each n value) for p_v1 = 0.025 (0.025) 0.200 at n = 8 (1) 30, p_v0 = 0.1, ${\lambda }_1=0.2,\mathrm{and} {\lambda }_2$ = 0.2 with ARL_v0 ≈ 370. In Table 3, we present control chart coefficients $k_1$ and $k_2$, and corresponding upper and lower control limits of the enhanced HEWMA-p control chart for n = 8 (1) 30, p_v0 = 0.3, ${\lambda }_1=0.2,\mathrm{and}{\lambda }_2$ = 0.2 with ARL_v0 ≈ 370. Table 4 presents ARL_v1 and SERL_v1 values (in second row corresponding to each n value) for p_v1 = 0.200 (0.025) 0.400 at n = 8 (1) 30, p_v0 = 0.3, ${\lambda }_1=0.2,\mathrm{and}{\lambda }_2$ = 0.2 with ARL_v0 ≈ 370.

Table 1. The control limits for enhanced HEWMA-p control chart with ARL₀ = 370 when ${\lambda }_1$ = 0.2, ${\lambda }_2$ = 0.2, and p_v0 = 0.1. HEWMA-p is hybrid exponentially weighted moving average proportion, ARL is average run length, UCL is upper control limit, LCL is lower control limit.

n	0.5n	UCL	LCL	${\mathit{k}}_1$	${\mathit{k}}_2$
8	4	0.1892	0.0126	5.3509	5.2421
10	5	0.1823	0.0252	5.5211	5.0203
12	6	0.1751	0.0314	5.5216	5.0416
14	7	0.1699	0.0364	5.5459	5.0498
16	8	0.1689	0.0430	5.8435	4.8326
18	9	0.1612	0.0431	5.5045	5.1243
20	10	0.1573	0.0448	5.4378	5.2352
22	11	0.1618	0.0525	6.1448	4.7231
24	12	0.1553	0.0524	5.7484	4.9475
26	13	0.1566	0.0561	6.1275	4.7436
28	14	0.1492	0.0541	5.5185	5.1495
30	15	0.1477	0.0558	5.5422	5.1406

Table 2. The ARLs of the enhanced HEWMA-p control chart for ${\lambda }_1$ = 0.2, ${\lambda }_2$ = 0.2, and p_v0 = 0.1.

n	0.5n	pv1 = 0.025	pv1 = 0.050	pv1 = 0.075	pv0 = 0.100	pv1 = 0.125	pv1 = 0.150	pv1 = 0.175	pv1 = 0.200
8	4	35.29	107.03	227.89	370.30	108.55	47.74	27.62	18.52
		0.2125	0.8830	4.1031	3.7450	1.0118	0.4055	0.2032	0.1169
10	5	22.51	55.24	204.00	370.36	107.43	45.55	25.30	16.80
		0.1067	0.4342	1.9517	3.7060	0.9798	0.3844	0.1749	0.0992
12	6	19.22	44.42	168.19	370.36	101.22	40.28	22.00	14.99
		0.0794	0.3273	1.5208	3.5468	0.9420	0.3305	0.1508	0.0837
14	7	16.81	37.03	141.92	370.09	98.87	36.21	19.87	13.64
		0.0630	0.2572	1.3294	3.7582	0.9133	0.2828	0.1276	0.0716
16	8	14.15	28.21	100.20	370.12	106.17	37.22	18.71	12.36
		0.0473	0.1753	0.8503	3.5983	0.9782	0.2861	0.1260	0.0680
18	9	14.17	29.27	116.90	370.35	82.10	29.98	16.52	11.66
		0.0443	0.1870	1.0169	3.6899	0.7268	0.2192	0.0986	0.0549
20	10	13.41	27.90	114.63	370.35	74.67	26.99	15.20	9.83
		0.0411	0.1772	1.0130	3.7271	0.6372	0.1921	0.0860	0.0478
22	11	11.07	20.20	65.97	370.20	101.72	31.72	15.01	9.60
		0.0285	0.1097	0.5498	3.5711	0.9293	0.2351	0.0942	0.0491
24	12	10.12	19.51	71.04	370.29	78.48	24.22	12.61	8.29
		0.0270	0.1122	0.5978	3.6796	0.7026	0.1885	0.0756	0.0420
26	13	9.21	17.79	57.10	370.28	90.92	24.92	11.07	7.55
		0.0219	0.0912	0.4547	3.6574	0.7930	0.1952	0.0787	0.0420
28	14	9.69	19.33	70.98	370.34	62.21	21.78	11.49	7.28
		0.0231	0.1001	0.5895	3.8081	0.5213	0.1400	0.0600	0.0339
30	15	9.28	18.12	65.59	370.11	60.42	20.57	11.07	7.07
		0.0213	0.0921	0.5349	3.8897	0.5151	0.1291	0.0566	0.0326

First row ARL and second row SERL (standard error of run length).

Table 3. The control constants with ARL₀ = 370 for enhanced HEWMA-p control chart. when ${\lambda }_1$ = 0.2, ${\lambda }_2$ = 0.2, and p_v0 = 0.3.

n	0.5n	UCL	LCL	${\mathit{k}}_1$	${\mathit{k}}_2$
8	4	0.4404	0.1691	5.5158	5.1435
10	5	0.4342	0.1873	5.8915	4.9485
12	6	0.4137	0.1911	5.4695	5.2405
14	7	0.4049	0.1990	5.4499	5.2481
16	8	0.4040	0.2094	5.7765	5.0350
18	9	0.3931	0.2111	5.4839	5.2395
20	10	0.3924	0.2186	5.7395	5.0565
22	11	0.3883	0.2225	5.7495	5.0485
24	12	0.3803	0.2230	5.4635	5.2414
26	13	0.3815	0.2287	5.7725	5.0515
28	14	0.3925	0.2352	6.7985	4.7655
30	15	0.3887	0.2376	6.7485	4.7465

Table 4. The ARL_v1 of the enhanced HEWMA-p control chart for ${\lambda }_1$ = 0.2, ${\lambda }_2$ = 0.2, and p_v0 = 0.3.

n	0.5n	pv1 = 0.20	pv1 = 0.225	pv1 = 0.250	pv1 = 0.275	pv0 = 0.300	pv1 = 0.325	pv1 = 0.350	pv1 = 0.375	pv1 = 0.400
8	4	35.28	60.05	118.01	245.61	370.90	226.17	107.71	61.38	38.35
		0.2524	0.4932	1.0515	2.3753	3.8363	2.2024	0.9818	0.5119	0.3029
10	5	26.68	43.27	84.94	188.98	370.31	280.15	124.92	63.86	38.04
		0.1754	0.3237	0.7445	1.7778	3.5587	2.7424	1.1877	0.5410	0.2896
12	6	25.94	43.63	88.21	218.61	370.36	193.66	82.10	44.11	27.30
		0.1651	0.3323	0.7546	2.1131	3.7020	1.8944	0.7278	0.3442	0.1879
14	7	22.86	38.41	77.95	203.34	370.12	180.32	72.49	38.13	23.90
		0.1408	0.2824	0.6669	1.9692	3.6434	1.7636	0.6397	0.2950	0.1580
16	8	19.08	30.41	59.02	155.32	370.12	213.84	80.71	40.05	23.99
		0.1092	0.2102	0.4795	1.4364	3.6315	2.0796	0.7144	0.3078	0.1549
18	9	18.64	29.35	61.47	169.83	370.12	161.54	62.54	31.54	19.87
		0.0991	0.1991	0.5082	1.6226	3.5624	1.5162	0.5296	0.2273	0.1222
20	10	16.21	25.20	49.94	139.81	370.11	185.81	65.54	29.22	19.90
		0.0827	0.1632	0.3935	1.3342	3.6760	1.8122	0.5570	0.2378	0.1183
22	11	15.02	23.56	45.65	128.87	370.29	176.40	61.05	27.67	16.29
		0.0716	0.1513	0.3694	1.1736	3.5888	1.6707	0.5079	0.2084	0.1034
24	12	14.60	23.50	46.43	141.41	370.11	132.92	49.45	22.94	16.06
		0.0683	0.1484	0.3717	1.2653	3.5991	1.3040	0.4106	0.1661	0.0836
26	13	13.54	20.49	39.45	115.26	370.11	161.59	52.72	26.01	15.38
		0.0593	0.1236	0.3016	1.0572	3.6564	1.5568	0.4251	0.1730	0.0858
28	14	12.08	17.50	32.06	88.77	370.20	356.82	88.25	29.94	13.28
		0.0489	0.0966	0.2331	0.7514	3.6537	3.4724	0.7457	0.2628	0.1168
30	15	11.49	16.59	30.72	83.96	370.08	326.41	79.90	27.51	13.22
		0.0457	0.0902	0.2163	0.7208	3.6923	3.1849	0.6792	0.2246	0.1001

First row ARL and second row SERL (standard error of run length).

From Table 2 and Table 4 we observe the following trend in ARL_v1

• 1. If n is increased, there is a decrease in ARL_v1 and SERL_v1 values, as we expected. For example, for 0.5n = 4 and p_v1 = 0.05 from Table 2 we have ARL_v1 = 107.03 and SERL_v1 = 0.8830, whereas if 0.5n = 15, we have ARL_v1 = 18.12 and SERL_v1 = 0.0921. We also observed a similar trend from Table 4.
• 2. The ARL_v1 and SERL_v1 values decrease when p_v1 is far away from p_v0.
• 3. The ARL_v1 and SERL_v1 values decrease more rapidly as c increases rather than it decreases. For example, for 0.5n = 4 and p_v1 = 0.05 (c = 0.5) from Table 2 we have ARL_v1 = 107.03 and SERL_v1 = 0.8830, whereas if p_v1 = 0.15 (c = 1.5), we have ARL_v1 = 47.74 and SERL_v1 = 0.4055. We also observed a similar trend from Table 4.

The R codes for this study are given in the Appendix A.

4. Comparative Study

Now, we discuss the performance of the proposed control chart with the existing control charts proposed by [4,14] for $\lambda$ = 0.2. The proposed chart reduces to [14] chart when ${\lambda }_1={\lambda }_2=\lambda$ = 0.2 (for example). We present the values of ARL_v1 for the proposed control chart as well as control charts given by [4,14] in Table 5 when in-control ARL_v0 ≈ 370.

Table 5. The comparison of the proposed chart with existing charts.

n	0.5n	pv0 = 0.1			pv0 = 0.3
		Yang and Arnold [4]	Yang and Arnold [14]	Enhanced	Yang and Arnold [4]	Yang and Arnold [14]	Enhanced	Yang and Arnold [4]	Yang and Arnold [14]	Enhanced
		pv1 = 0.2	pv1 = 0.2	pv1 = 0.2	pv1 = 0.2	pv1 = 0.2	pv1 = 0.2	pv1 = 0.4	pv1 = 0.4	pv1 = 0.4
8	4	28.2	25.50	18.52	41.90	43.59	35.28	50.50	47.55	38.35
10	5	22.7	19.02	16.80	33.70	34.06	26.68	40.80	40.29	38.04
12	6	19	17.43	14.99	28.20	31.24	25.94	34.20	31.36	27.30
14	7	16.4	14.54	13.64	24.20	25.69	22.86	29.40	28.23	23.90
16	8	16.4	12.55	12.36	21.30	22.42	19.08	25.80	24.58	23.99
18	9	13	11.85	11.66	19.00	19.96	18.64	23.00	22.13	19.87
20	10	11.8	10.67	9.83	17.20	17.27	16.21	20.70	20.96	19.90
22	11	10.9	9.67	9.60	15.70	17.92	15.02	18.90	17.03	16.29
24	12	10.1	7.47	8.29	14.50	14.77	14.90	17.40	17.25	15.96
26	13	9.4	7.95	7.55	13.40	14.07	13.54	16.10	15.62	15.38
28	14	8.9	7.87	7.28	12.60	13.45	12.08	15.10	14.26	13.28
30	15	8.4	7.51	7.07	11.80	11.98	11.59	14.10	14.23	13.22

From Table 5, we observe that the proposed control chart has smaller values of ARL_v1 as compared to the existing two control charts. For example, when 0.5n = 6, ${\lambda }_1={\lambda }_2=\lambda$ = 0.2, p_v0 = 0.3, p_v1 = 0.4 the proposed control chart gives ARL_v1 is 27.30, the ARL_v1 from the two existing control charts are 31.36 and 34.20, respectively. Thus, the proposed control chart performs better than the existing control charts.

Table 5ARL_v1s comparison between the chart proposed by [4,14] for $\lambda$ = 0.2 and enhanced HEWMA-p control chart for ${\lambda }_1$ = 0.2, ${\lambda }_2$ = 0.2. Figure 1 depicts the ARL_v1 profile comparison at p_v0 = 0.1 and p_v1 = 0.2 for different values of n under HEWMA-p chart and two existing charts. From Figure 1, we noticed that ARL_v1 values of enhanced HEWMA-p control chart are smaller than in the two existing control charts. Hence, our proposed enhanced HEWMA-p control chart performed well as compared with existing charts.

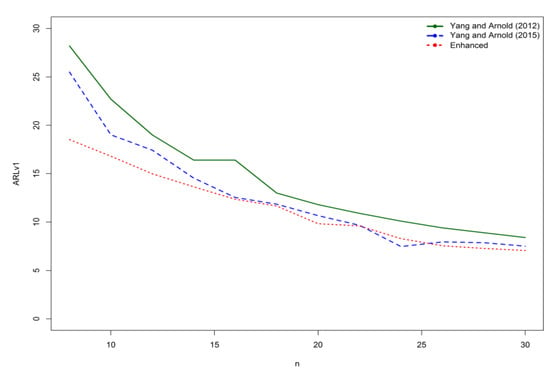
Figure 1. The ARL_v1 profile comparison at p_v0 = 0.1 and p_v1 = 0.2 for different values of n under HEWMA-p chart and Yang and Arnold [4,14].

5. Example

In this section, we present an example given by [14]. The service time of a bank branch in Taiwan is used to illustrate the application of the proposed enhanced HEWMA-p control chart to monitor the variability of service time. According to [14] “From the historical data, the in-control data of service times (unit: minutes) is a non-normal/unknown distribution with variance 27.805. Reference [14] illustrated that the resulting in-control probability that the service time is larger than the in-control variance is $p_{v0}=P(Y_j^{*}>27.805)$ = 0.31”. To construct the enhanced HEWMA-p control chart, we also use the same value of $p_{v0}$. The upper and lower control limits of the enhanced HEWMA-p control chart with ${\lambda }_1=0.2,{\lambda }_2=0.2$ when in-control ARL_v0 ≈ 370 are UCL = 0.4454 and LCL = 0.1963.

Ten new samples of size 10 each from new automatic service system of the bank branch under study were considered [14] and listed in Table 6. To illustrate the out-of-control detection ability, for each sample in Table 6, the statistic, V_t and the monitoring statistic $HEWM{A}_{p_t}={\lambda }_{1}EWM{A}_{p_t}+\left(1-{\lambda }_1\right) HEWM{A}_{p_{t-1}}$ where ${EWMA}_{p_t}={\lambda }_2{V}_t/0.5n+\left(1-{\lambda }_2\right)EWM{A}_{p_{t-1}}$ at time t, t = 1, 2, …, 10, were computed. The corresponding enhanced HEWMA-p control chart detected out-of-control variance signals from the third sample onward (samples 3–10 on the enhanced HEWMA-p control chart) (Figure 2). By comparing Figure 2 with the chart in [14], it can be seen that the existing chart indicated a shift at the 4th sample. Therefore, the proposed chart was more efficient in detecting a shift in the process as compared to existing chart of Yang and Arnold [14]. The same performance was also shown by the results in Table 2 and Table 4. For this study, we can conclude that the proposed chart shows better performance than the existing two charts.

Table 6. The new service times from 10 counters in a bank branch. EWMA is exponentially weighted moving average.

t	X1	X2	X3	X4	X5	X6	X7	X8	X9	X10	Vt	EWMApt	HEWMApt
1	3.54	0.01	1.33	7.27	5.52	0.09	1.84	1.04	2.91	0.63	0	0.2480	0.2976
2	0.86	1.61	1.15	0.96	0.54	3.05	4.11	0.63	2.37	0.05	0	0.1984	0.2381
3	1.45	0.19	4.18	0.18	0.02	0.70	0.80	0.97	3.60	2.94	0	0.1587	0.1905
4	1.37	0.14	1.54	1.58	0.45	6.01	4.59	1.74	3.92	4.82	0	0.1270	0.1524
5	3.00	2.46	0.06	1.80	3.25	2.13	2.22	1.37	2.13	0.25	0	0.1016	0.1219
6	1.59	3.88	0.39	0.54	1.58	1.70	0.68	1.25	6.83	0.31	0	0.0813	0.0975
7	5.01	1.85	3.10	1.00	0.09	1.16	2.69	2.79	1.84	2.62	0	0.0650	0.0780
8	4.96	0.55	1.43	4.12	4.06	1.42	1.43	0.86	0.67	0.13	0	0.0520	0.0624
9	1.08	0.65	0.91	0.88	2.02	2.88	1.76	2.87	1.97	0.62	0	0.0416	0.0499
10	4.56	0.44	5.61	2.79	1.73	2.46	0.53	1.73	7.02	2.13	0	0.0333	0.0399

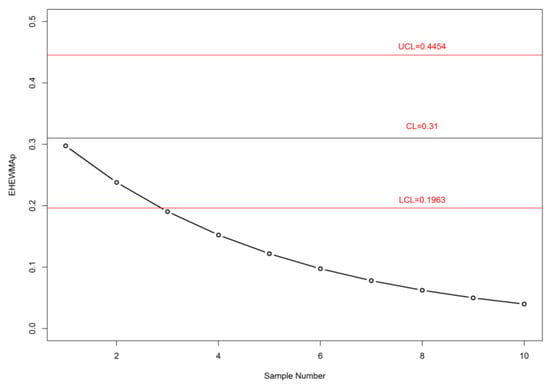
Figure 2. The enhanced HEWMA-p chart for the example.

6. Concluding Remarks

In this paper, an enhanced hybrid EWMA-p chart is proposed for monitoring the process variance. A simulation procedure is presented for calculating its average run lengths (ARLs). Some tables are presented for practical use. The simulation study supports that the proposed chart is more efficient in detecting a shift in the process. A real example is presented for illustration purposes. The proposed control chart can be used in the industry for the monitoring of processes when the distribution is unknown in practice. The limitation of the proposed chart is that it can be used for only a fixed sample size. The variable sample size enhanced hybrid EWMA-p chart will be considered as our future research. In addition, the proposed control chart for a variable sample size can be considered as future research. The proposed chart using autocorrelation can be considered as future research.