1. Introduction
In today’s competitive world, the selection of suppliers has become a complicated problem that involves a large number of academics and professionals [
1]. The selection of the provider depends on a variety of criteria such as characteristics of markets, demands from customers, delivery times, quality, price and service excellence [
2,
3]. Therefore, choosing the best suppliers can be conflicting in nature. According to Kang et al. [
4], a supplier’s selection can be modeled as a typical multi-criteria decision making problem.
Moreover, various supplier selection methods such as Analytical Hierarchy Process (AHP), Analytic Network Process (ANP), Artificial Neural Network (ANN), Technique for Order Preference by Similarity to Idal Solution (TOPSIS), Data Envelopment Analysis (DEA), Integer programming, Genetic Algorithms and combinations of any of these tools are observed in the literature [
1]. However, in decision making, most of these methods only consider quantitative criteria, and other type of factors—such as incomplete information, qualitative criteria and imprecision preferences—are not included [
5].
In this context, the Fuzzy Set method has recently been applied for supplier selection [
5]. As per a proposal from Jafarnejad and Aghasi [
6], the integration of fuzzy Preference Ranking Organization Methods for Enrichment Evaluations (PROMETHEE) and linear programs for supplier selection under uncertainty. This is applicable in business to allow for the building of road maps for profit maximization. Mavi, Goh and Mavi [
7] proposed a Shannon entropy and fuzzy TOPSIS, the first for weighing criteria and the second for ranking suppliers. Their findings show that demand risk is the most important factor. On other hand, Bolturk [
8] developed the Pythagorean fuzzy extension of the COmbinative Distance-based Assessment (CODAS) method, which is applicable in supplier selection problems that are vague and imprecise. Additionally, the literature shows [
5,
6,
9,
10] that most of these methods such as AHP, TOPSIS—including fuzzy versions—and others have the following limitations:
Do not take into account the interrelationship among three or more arguments.
Limited qualitative criteria.
Imprecise preferences of decision makers.
Dimensional Analysis (DA) is able to capture the interrelationship between multiple arguments (or criteria) into single dimensionless indexes [
11], making it convenient in multi-criteria decision making (MCDM) problems with different measurement scales [
11,
12,
13]. The main advantage of DA is that is can integrate the opinions of a group of decision makers (DM) on diverse information, such as alternatives, criteria and the importance of each criteria [
11]. Nevertheless, DA is weak using quantitative (crisp) and qualitative (fuzzy) information, which is commonly present in MCDM problems.
On the other hand, Pythagorean Fuzzy Sets (PFS) have become a new generalization of fuzzy sets (FS) and can handle and model uncertain information in a more “flexible” way in the DM process than can Intuitionistic Fuzzy Sets (IFS). The main advantage of PFS is the condition that the square sum of their degree of membership and the degree of non-membership is equal to or less than
[
14,
15,
16,
17,
18,
19,
20,
21]. For example, when a decision maker provides the evaluation information whose membership grade is 0.4 and the degree of non-membership is 0.9, an IFS cannot address this problem because 0.4 + 0.9 > 1. However,
+
< 1. That is, a PFS is able to represent this evaluation information [
15].
Based on the aforementioned considerations, this research could have industrial application in medium and small enterprises, and may be directed to management, engineers and buyers that tackle the issue of supplier appraisal. Using an integrated tool: an extension of DA with PFS: the qualitative criteria, imprecision preferences of the DMs and interrelationship among the multi-input arguments can be overcame for multi-input arguments. The rest of the paper is organized as follows: In
Section 2, the preliminaries of Pythagorean Fuzzy Sets (PFS) and Dimensional Analysis (DA) are given. In
Section 3, the methodology of the integration of PFS and DA is given, and an algorithm is proposed in eight steps. In
Section 4, two illustrated examples for supplier selection problems are presented, applying the proposed method. This approach is as follows: (1) A sensitivity analysis, (2) a comparative analysis with other fuzzy methods; in addition a Spearman correlation and Cronbach’s alpha in order to validate our method; (3) results. Finally, in
Section 5, the conclusion is given and suggestions for further research are presented.
3. Methodology
In this section, we introduced the Pythagorean Fuzzy Dimensional Analysis (PFDA) approach for MCDM problems.
Based on Equation (18), the definition of PFDA is given as follows.
Definition 7. Pythagorean Fuzzy Set Dimensional Analysis method. Letandbe a collection of P,
ifthenis named “Pythagorean Fuzzy Index of Similarity” for alternative. Here,is the Pythagorean fuzzy evaluation of criterionfor alternative,is the Pythagorean fuzzy value of the “ideal alternative” for criterion, andis the corresponding crisp weight for criterionsatisfyingand Based on Equations (3)–(7) of the PFS described in
Section 2, the next results can be derived.
Theorem 1. Letbe a collection of PFS. Therefore, the aggregated value, by usingis the following: Proof. Based on Equation (15) described in
Section 2, we can obtained Equation (23):
Also, according to Equation (17):
This completes the proof of Theorem 1. □
When the MCDM problem contains both types of criteria, benefit criteria (
BN) and cost criteria (
C), the following has to be considered. If
; then:
Otherwise, if
; then,
Following the next conditions,
where
If
is a Pythagorean fuzzy number, the weight of DM [
27] is represented by:
where
.
Preferences of the DM need to be gathered in a Pythagorean fuzzy matrix [
27]:
The algorithm for proposed PF-DA below.
In accordance with above analysis, PF-DA is defined in the following steps:
Step 1: Define the Pythagorean decision matrix.
Step 2: Select the ideal solution in accordance with BN or C criteria values.
Step 3: Establish criteria weights, use Equations (30) and (31).
Step 4: Standardized matrix—use Equation (25) for BN criteria, Equation (26) for C criteria.
Step 5: Standardized matrix elevated in accordance with criteria weights, use Equation (16).
Step 6: Generate PFIS index, use Equation (21).
Step 7: Establish the highest index of the index of similarity (IS), use Equation (4).
Step 8: Establish the ranking, with highest values to lowest values.
4. Numerical Illustration
In this section, we consider a decision making problem that a manufacturing company is facing at Ciudad Juárez, Mexico. Mainly the problem is focused on supplier selection to achieve cost reductions at the finished goods manufacturing phase. The company is considering five suppliers for electronics items. Suppliers are defined by . Four criteria involved are defined as:
Price : the most minimum values are selected.
Facility : great assessments are selected.
Lead time : high assessments are selected.
Quality : great assessments are selected.
Step 1: In accordance with DM evaluations, the Pythagorean fuzzy decision matrix is defined as follows:
Step 2: Establish the ideal solution in accordance with criteria values:
Step 3: Establish the criteria weights, use Equations (30) and (31):
Step 4: In order to standardize the matrix, use Equations (25) and (26) in accordance with
BN or
C:
Step 5: Then, each criteria column in the standardized matrix is elevated with criteria weights; use Equation (16):
Step 6: Then, to generate an index of similarity,
, use Equation (21):
Step 7: To obtain the highest index of similarity, use Equation (4):
Step 8: Establish the ranking; the results reveal that:
Therefore is selected as the best supplier, and the highest index of similarity is chosen as the best alternative.
Illustration Example 2
In this example taken from the literature [
8], an entrepreneur wants to select a supplier. Suppliers are defined by
, and the evaluation criteria are defined as:
Product Quality : BN criteria.
Delivery Compliance : BN criteria.
Price : high assessment C criteria.
Production Capability : C criteria.
Technological Capability : C criteria.
Step 1: A linguistic evaluation process is preferred since expert’s opinions, and then the Pythagorean fuzzy decision matrix is defined by DMs:
Step 2: Establish the ideal solution in accordance with criteria values:
Step 3: Weights are assigned to each criterion by the experts:
Step 4: In order to standardize the matrix, use Equations (26) and (27) in accordance with
BN or
C:
Step 5: Then, each criteria column in the standardized matrix is elevated with criteria weights; use Equation (18):
Step 6: Then, to generate an index of similarity,
, use Equation (22):
Step 7: To obtain the highest index of similarity, use Equation (4):
Step 8: Establish the ranking; the results reveal that:
Therefore is selected as the best supplier; the highest index of similarity is chosen as the best alternative.
4.1. Sensitivity Analysis
Different weights are assigned by changing the criteria weights to those obtained by PF-DA in order to observe how much it would influence the final rankings of alternatives. In the first example, we changed the weights of criteria as is shown in
Table 1.
In the second example, we changed the weights of criteria as is shown in
Table 2.
4.2. Comparative Analysis
In accordance with example 1, using the PF-Multi-O bjective Optimization based on Ratio Analysis (MOORA) method, the results were the following:
Furthermore, applying the PF-Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) method [
15], we obtained the following results in
Table 3.
The Spearman correlation coefficient is based on the ranked values for each variable rather than the raw data. Spearman correlation is often used to evaluate relationships involving ordinal variables [
28].
Table 4 shows the rankings to calculate the Spearman correlation coefficient [
28,
29] is given by:
When
n = 5, and
, then we have the following:
On other hand, Cronbach’s alpha [
30,
31,
32] is calculated using SPSS as is shown in
Table 5.
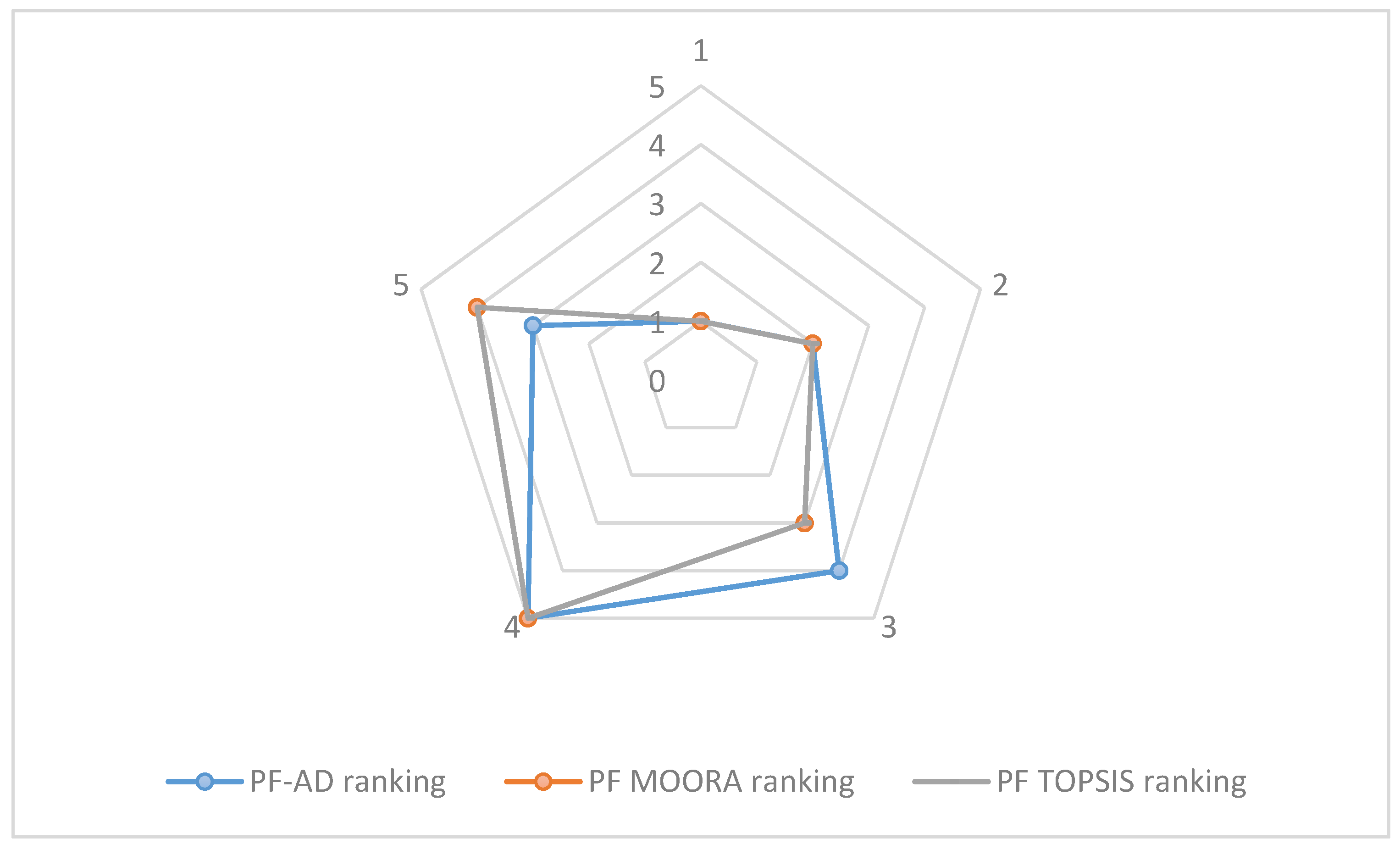
The
Figure 1 is a graphic with the ranking comparison for PF-DA, PF MOORA and PF-TOPSIS.
In accordance with example 2, using the PF-CODAS method, the results show the following:
Table 6 shows the rankings to calculate the Spearman correlation coefficient [
28,
29], for illustration example 2:
When
n = 4, and
, then we have the following:
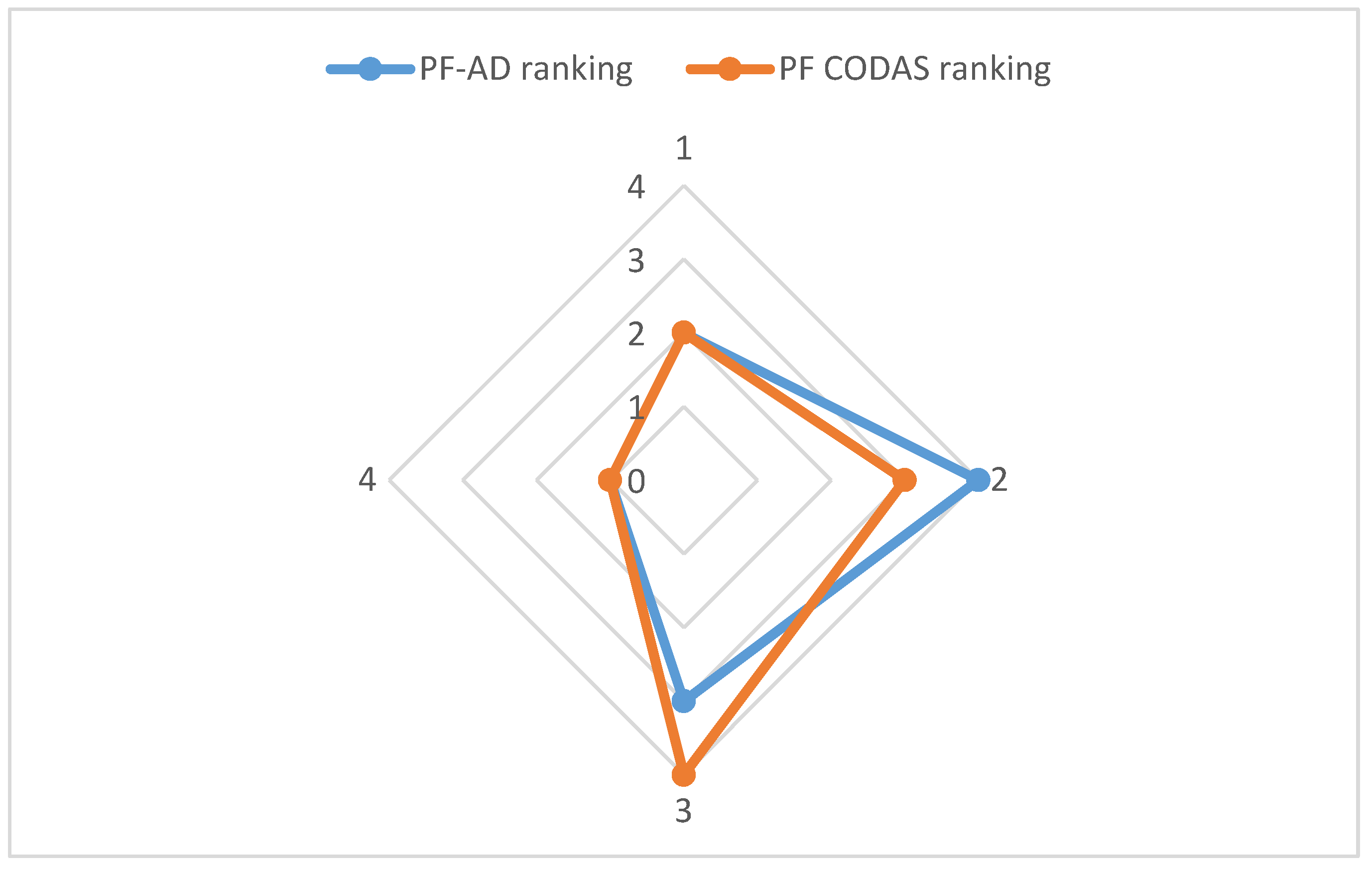
The
Figure 2 is a graphic with the ranking comparison for PF-DA and PF-CODAS.
On other hand, Cronbach’s alpha [
30,
31,
32] is calculated using SPSS as is shown in
Table 7.
4.3. Results
Due the PFS satisfies the condition that the square sum of their degree of membership and the degree of non-membership was equal to or less than 1 [
14,
16,
17,
18,
19,
20,
21], the PFS is able to represent the evaluation information [
15]; then we presented two illustrated examples using PFS.
In illustration example 1, for PF-DA, PF-MOORA and PF-TOPSIS, where
was selected as the best supplier, the highest index of similarity was chosen as the optimal alternative. The result shows that the Spearman correlation was 0.9, which proved that there is a substantial correspondence between our approach, PF-DA, and the two MCDM approaches stated in the literature, namely PF-MOORA and PF-TOPSIS. On other hand, the Cronbach’s alpha was 0.977, which is a high value and indicates strong consistency [
33]. This means that PF-DA is suitable for dealing with MCDM problems. Moreover, the integration of PF-DA provides advantages over PF-MOORA and PF-TOPSIS as DA attempts to integrate the opinions of a group of decision makers (DM) on diverse information, including alternatives, criteria and the importance of such criteria [
11], whereas MOORA and TOPSIS do not.
On other hand, in illustration example 2, for PF-DA and PF-CODAS,
was selected as the best supplier as it presented the highest index of similarity, indicating the optimal alternative. However, in CODAS the negative ideal solution is considered [
8], while in DA the positive ideal solution is considered [
11,
12]. The Spearman correlation was 0.8, which means that there is substantial similarity between the PF-DA and PF-CODAS approaches. The Cronbach’s alpha was 0.889, which is a high value and indicates strong consistency [
33].