Residual Stress Analysis of an Orthotropic Composite Cylinder under Thermal Loading and Unloading
Abstract
1. Introduction
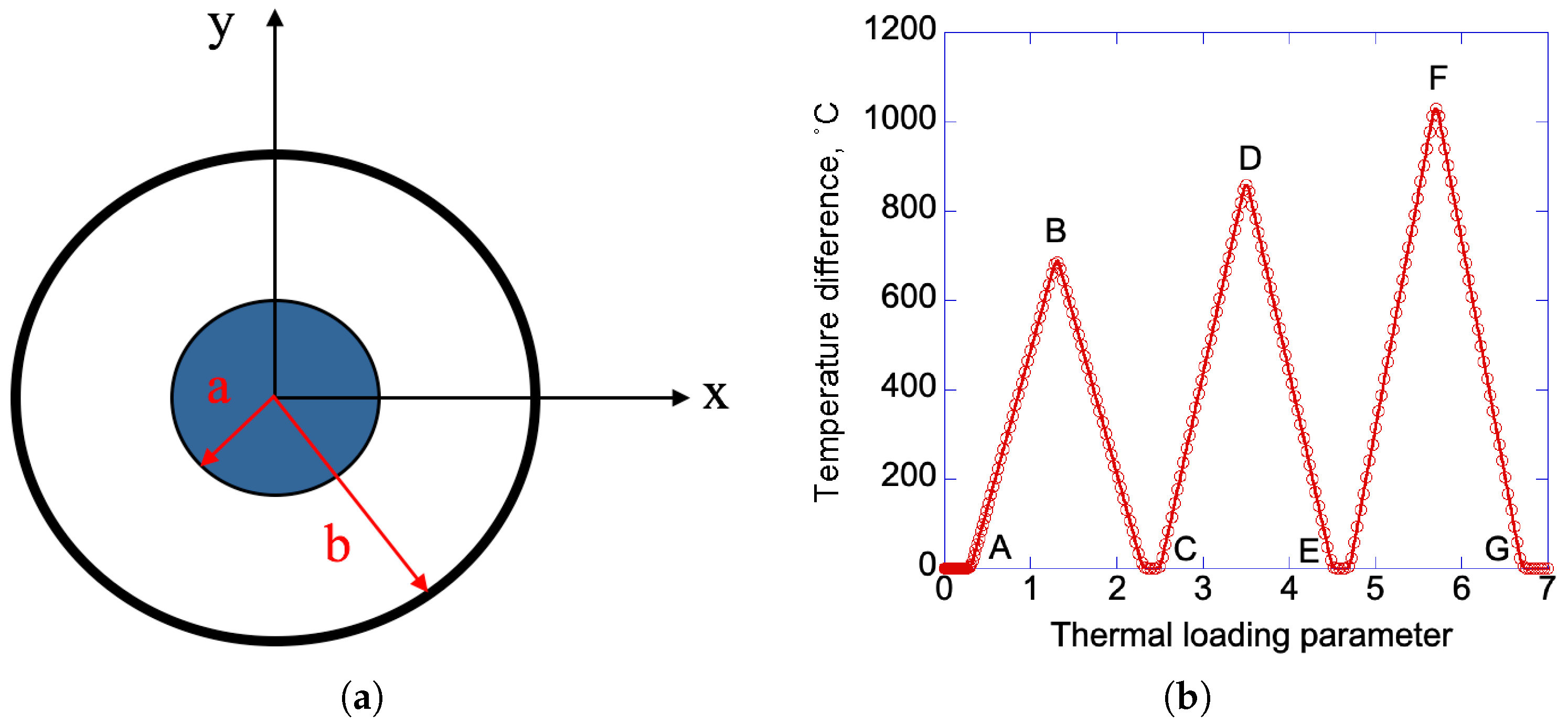
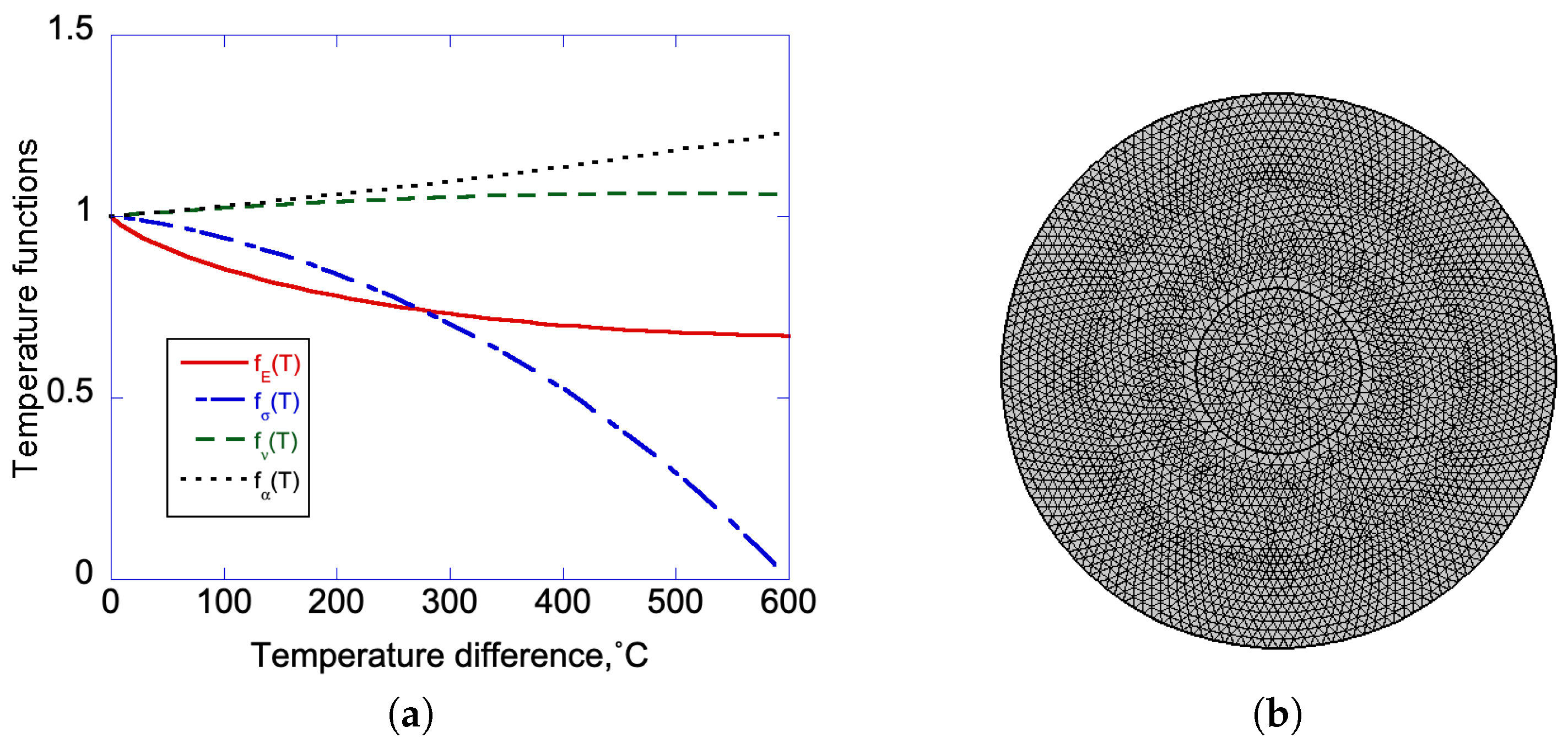
2. Theoretical and Numerical Considerations
3. Results and Discussion
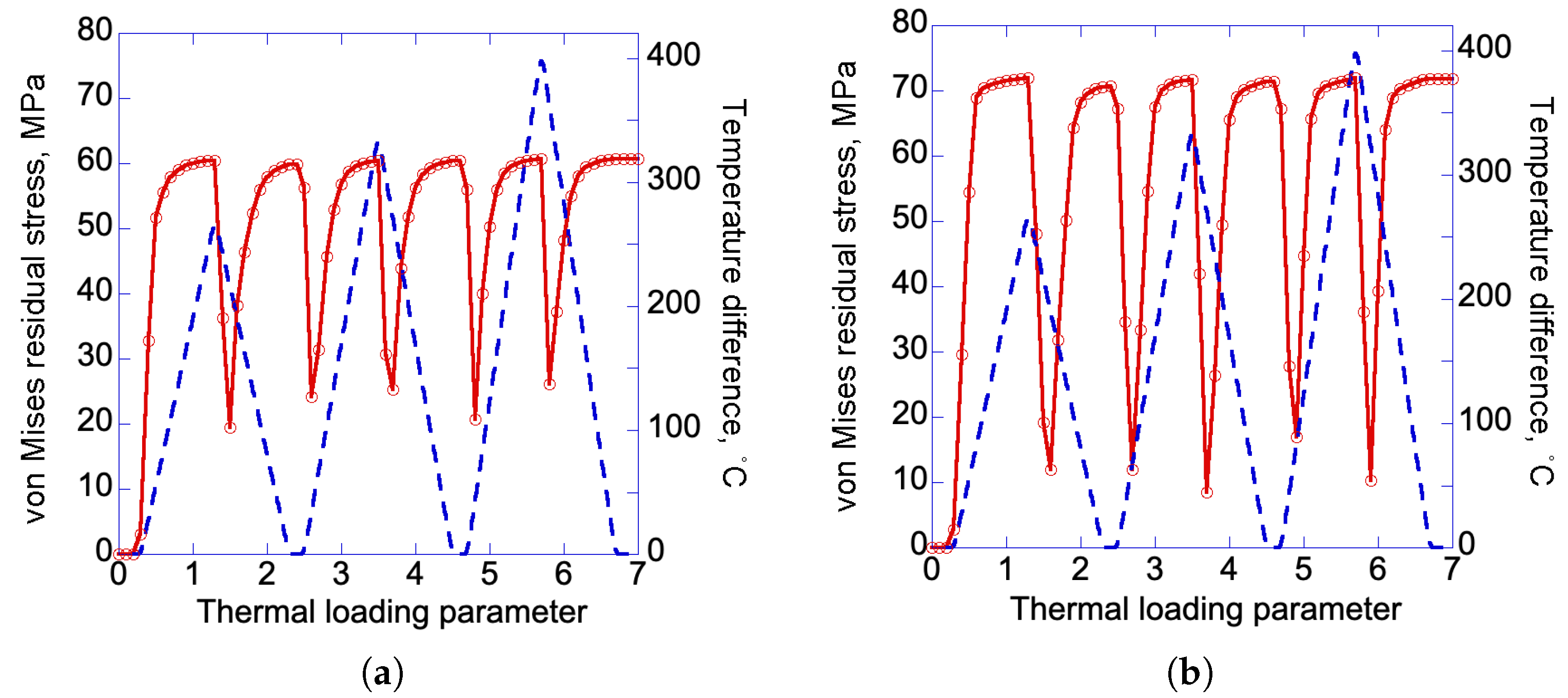
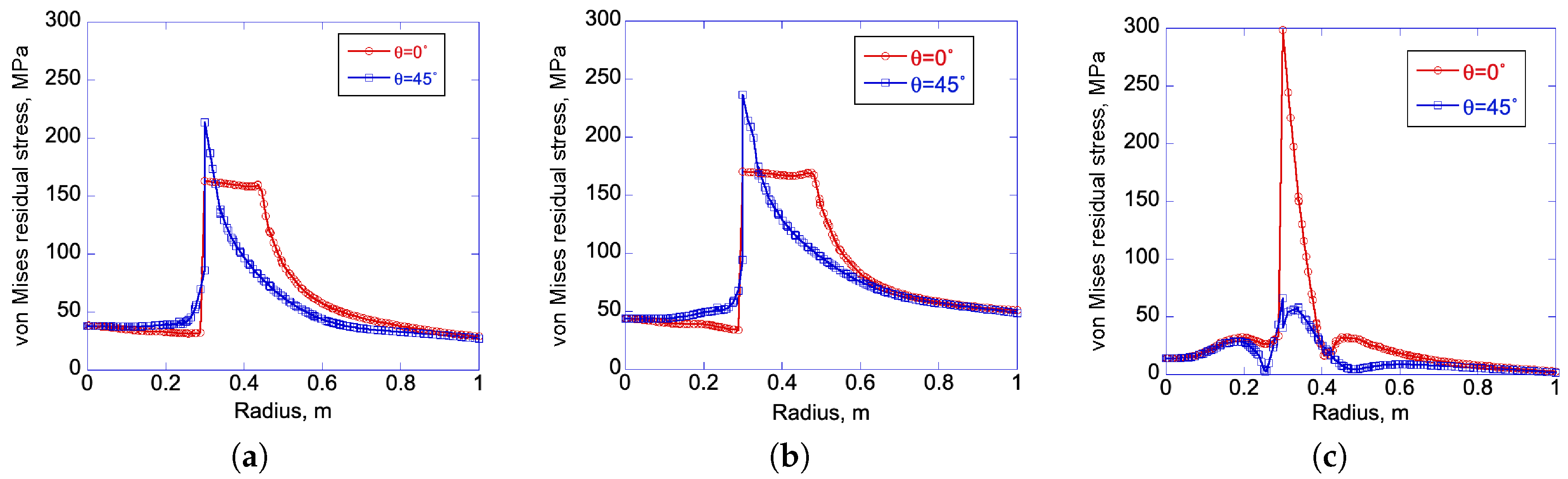
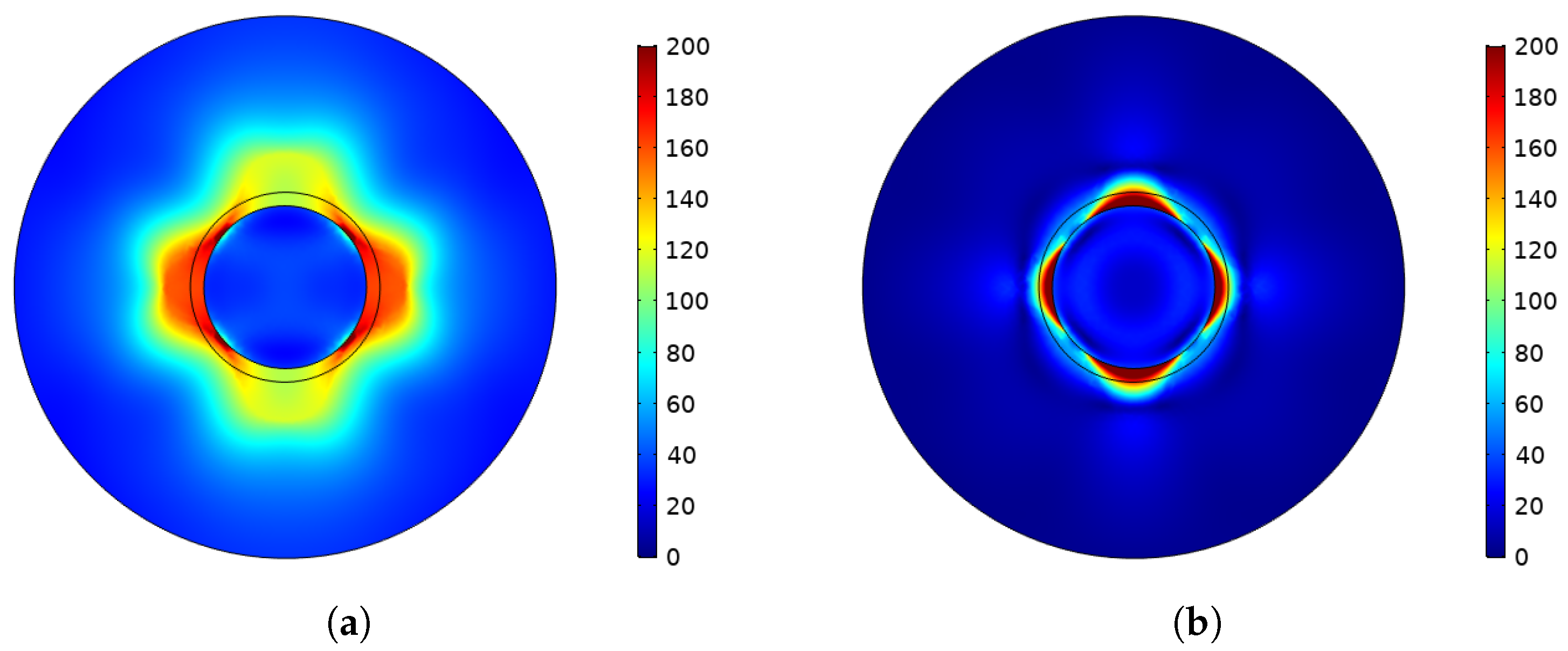
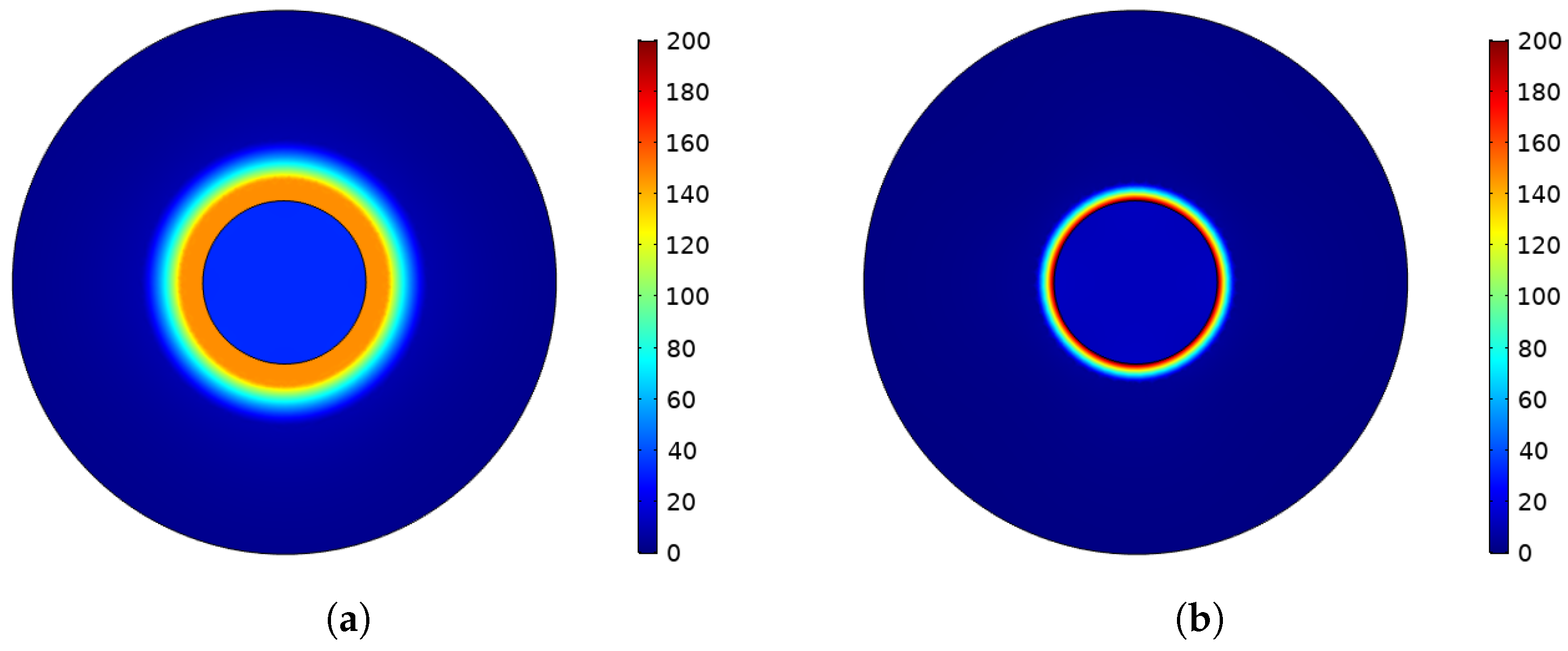
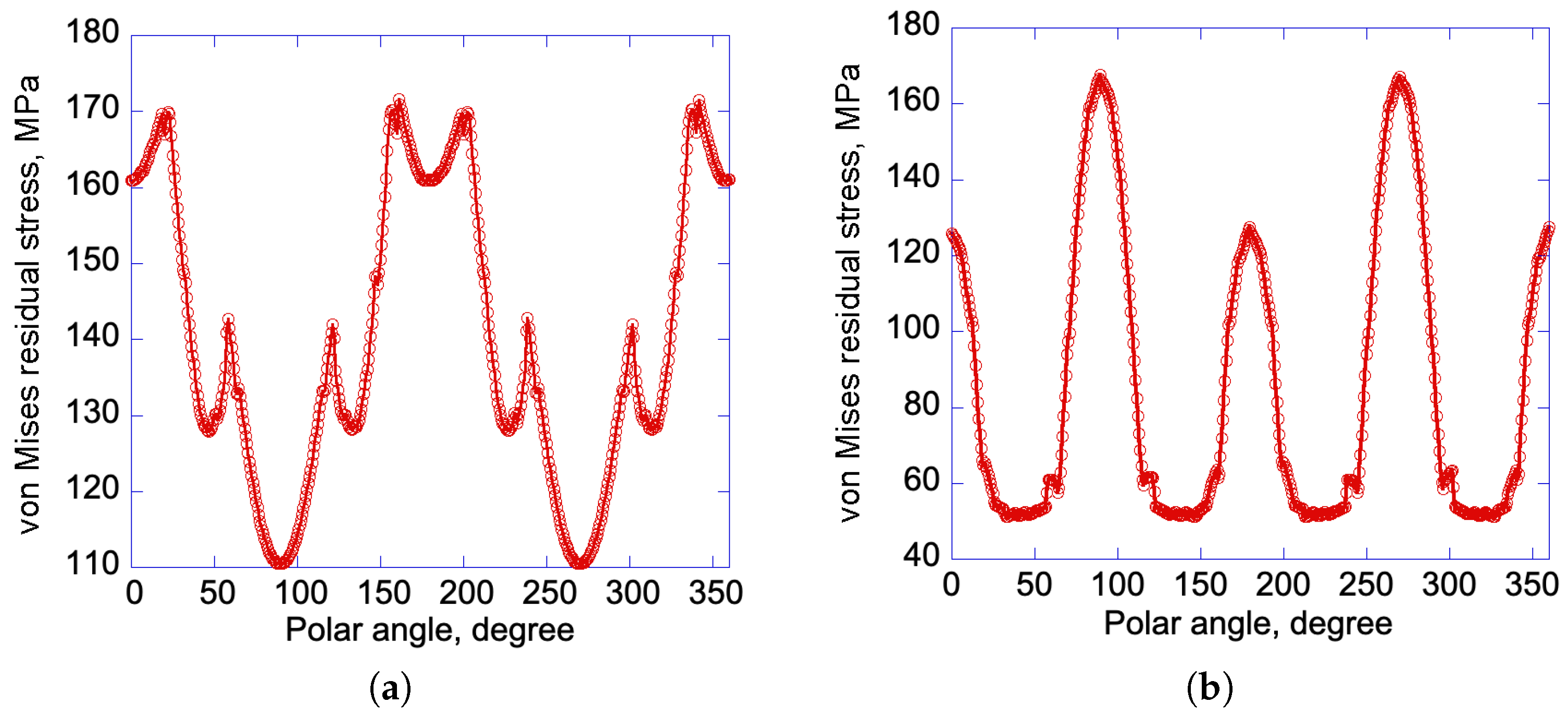
3.1. Residual Stress Analysis Under Elastic-Perfectly Plastic Assumption
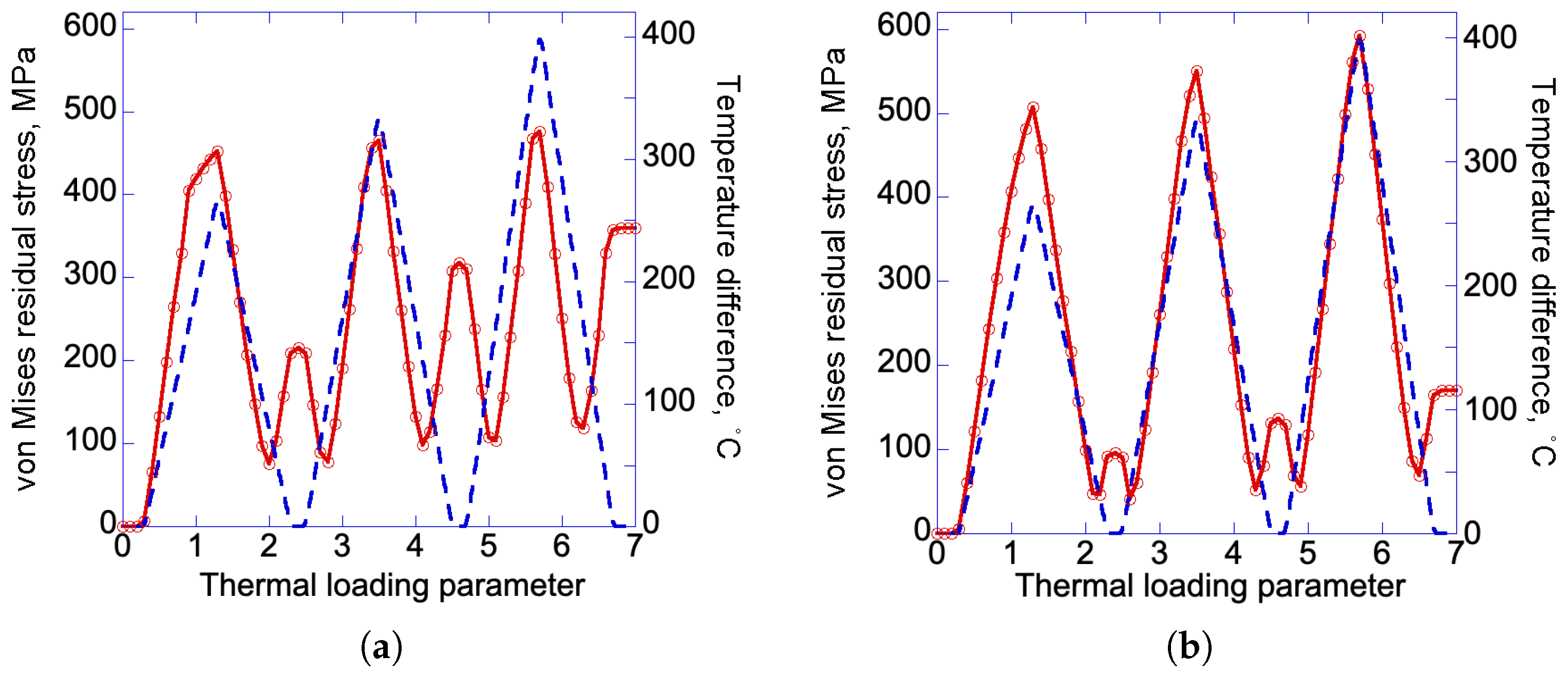
3.2. Effects of Selective Temperature Dependent Material Properties on Residual Stress
3.3. Residual Stress Analysis with Linear Hardening
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alexandrov, S.; Chikanova, N. Elastic-plastic stress-strain state of a plate with a pressed-in inclusion in thermal field. Mech. Solids 2000, 35, 125–132. [Google Scholar]
- Alexandrov, S.; Alexandrova, N. Thermal effects on the development of plastic zones in thin axisymmetric plates. J. Strain Anal. Eng. Des. 2001, 36, 169–175. [Google Scholar] [CrossRef]
- Sayman, O.; Arman, Y. Thermal stresses in a thermoplastic composite disc under a steady state temperature distribution. J. Rein. Plas. Comp. 2006, 25, 1709–1722. [Google Scholar] [CrossRef]
- Topcu, M.; Altan, G.; Callioglu, H.; Altan, B.D. Thermal elastic-plastic analysis of an aluminium composite disc under linearly decreasing thermal loading. Adv. Comp. Lett. 2008, 17, 87–96. [Google Scholar] [CrossRef]
- Lubliner, J. Plasticity Theory; Macmillan: New York, NY, USA, 1990. [Google Scholar]
- Hill, R. A theory of the yielding and plastic flow of anisotropic metals. Soc. Lond. Ser. A 1948, 193, 281–297. [Google Scholar]
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hill, R. A user-friendly theory of orthotropic plasticity in sheet metals. Int. J. Mech. Sci. 1993, 35, 19–25. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Cazacu, O.; Yoon, J.W.; Dick, R.E. Earing predictions for strongly textured aluminum sheets. Intl. J. Mech. Sci. 2010, 52, 1563–1578. [Google Scholar] [CrossRef]
- Zhang, S.; Leotoing, L.; Guines, D.; Thuillier, S.; Zang, S.-L. Calibration of anisotropic yield criterion with conventional tests or biaxial test. Intl. J. Mech. Sci. 2014, 85, 142–151. [Google Scholar] [CrossRef]
- Callioglu, H.; Topcu, M.; Tarakcilar, A.R. Elastic–plastic stress analysis of an orthotropic rotating disc. Intl. J. Mech. Sci. 2006, 48, 985–990. [Google Scholar] [CrossRef]
- Noda, N. Thermal stresses in materials with temperature-dependent properties. Appl. Mech. Rev. 1991, 44, 383–397. [Google Scholar] [CrossRef]
- Argeso, H.; Eraslan, A.N. On the use of temperature-dependent physical properties in thermomechanical calculations for solid and hollow cylinders. Int. J. Thermal Sci. 2008, 47, 136–146. [Google Scholar] [CrossRef]
- Seif, M.; Main, J.; Weigand, J.; Sadek, F.; Choe, L.; Xhang, C.; Gross, J.; Luecke, W.; McColskey, D. Temperature-Dependent Material Modeling for Structural Steels: Formulation and Application. NIST Technical Note 1907 2016. [Google Scholar] [CrossRef]
- Alexandrov, S.; Wang, Y.C.; Aizikovich, S. Effect of temperature-dependent mechanical properties on plastic collapse of thin discs. J. Mech. Eng. Sci. Part C 2014, 228, 2483–2487. [Google Scholar] [CrossRef]
- Alexandrov, S.; Wang, Y.C.; Jeng, Y.R. Elastic-plastic stresses and strains in thin discs with temperature-dependent properties subject to thermal loading. J. Therm. Stresses 2014, 37, 488–505. [Google Scholar] [CrossRef]
- Wang, Y.C.; Alexandrov, S.; Jeng, Y.R. Effects of thickness variations on the thermal elastoplastic behavior of annular discs. Struct. Eng. Mech. 2013, 47, 839–856. [Google Scholar] [CrossRef]
- Zarandi, S.B.; Wang, Y.C.; Novozhilova, O.V. Plastic behavior of circular discs with temperature-dependent properties containing an elastic inclusion. Str. Eng. Mech. 2016, 58, 731–743. [Google Scholar] [CrossRef]
- Alexandrov, S.; Wang, Y.C.; Lang, L. A theory of elastic/plastic plane strain pure bending of FGM sheets at large strain. Materials 2019, 12, 456. [Google Scholar] [CrossRef] [PubMed]
- Simo, J.C. Numerical analysis and simulation of plasticity. In Handbook of Numerical Analysis VI; Ciarlet, P.G., Lions, J.L., Eds.; Elsevier Science: Amsterdam, The Netherlands, 1998; pp. 183–499. [Google Scholar]
- Simo, J.C.; Hughes, T.J.R. Computational Inelasticity; Springer: New York, NY, USA, 1998. [Google Scholar]
- COMSOL Website (2019). Available online: www.comsol.com (accessed on 27 February 2019).
- Young, W.B. Residual Stress in Design, Process and Materials Selections; ASM Intl.: Materials Park, OH, USA, 1989. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zarandi, S.B.; Lai, H.-W.; Wang, Y.-C.; Aizikovich, S. Residual Stress Analysis of an Orthotropic Composite Cylinder under Thermal Loading and Unloading. Symmetry 2019, 11, 320. https://doi.org/10.3390/sym11030320
Zarandi SB, Lai H-W, Wang Y-C, Aizikovich S. Residual Stress Analysis of an Orthotropic Composite Cylinder under Thermal Loading and Unloading. Symmetry. 2019; 11(3):320. https://doi.org/10.3390/sym11030320
Chicago/Turabian StyleZarandi, Somayeh Bagherinejad, Hsiang-Wei Lai, Yun-Che Wang, and Sergey Aizikovich. 2019. "Residual Stress Analysis of an Orthotropic Composite Cylinder under Thermal Loading and Unloading" Symmetry 11, no. 3: 320. https://doi.org/10.3390/sym11030320
APA StyleZarandi, S. B., Lai, H.-W., Wang, Y.-C., & Aizikovich, S. (2019). Residual Stress Analysis of an Orthotropic Composite Cylinder under Thermal Loading and Unloading. Symmetry, 11(3), 320. https://doi.org/10.3390/sym11030320





