A Generalized Approach towards Soft Expert Sets via Neutrosophic Cubic Sets with Applications in Games

Abstract

Games are considered to be the most attractive and healthy event between nations and peoples. Soft expert sets are helpful for capturing uncertain and vague information. By contrast, neutrosophic set is a tri-component logic set, thus it can deal with uncertain, indeterminate, and incompatible information where the indeterminacy is quantified explicitly and truth membership, indeterminacy membership, and falsity membership independent of each other. Subsequently, we develop a combined approach and extend this concept further to introduce the notion of the neutrosophic cubic soft expert sets (NCSESs) by using the concept of neutrosophic cubic soft sets, which is a powerful tool for handling uncertain information in many problems and especially in games. Then we define and analyze the properties of internal neutrosophic cubic soft expert sets (INCSESs) and external neutrosophic cubic soft expert sets (ENCSESs), P-order, P-union, P-intersection, P-AND, P-OR and R-order, R-union, R-intersection, R-AND, and R-OR of NCSESs. The NCSESs satisfy the laws of commutativity, associativity, De Morgan, distributivity, idempotentency, and absorption. We derive some conditions for P-union and P-intersection of two INCSESs to be an INCSES. It is shown that P-union and P-intersection of ENCSESs need not be an ENCSES. The R-union and R-intersection of the INCSESs (resp., ENCSESs) need not be an INCSES (resp. ENCSES). Necessary conditions for the P-union, R-union and R-intersection of two ENCSESs to be an ENCSES are obtained. We also study the conditions for R-intersection and P-intersection of two NCSESs to be an INCSES and ENCSES. Finally, for its applications in games, we use the developed procedure to analyze the cricket series between Pakistan and India. It is shown that the proposed method is suitable to be used for decision-making, and as good as or better when compared to existing models.

1. Introduction

Researchers always try to discover methods to handle imprecise and vague information, which is not possible using classical set theory. In this regard, Zadeh gave the concept of fuzzy set [1], to cope with uncertainty. However, fuzzy sets were considered imperfect since it is not always easy to give an exact degree of membership to any element. To overcome this problem, the interval-valued fuzzy set was proposed by Turksen [2]. Atanassov [3] extended the notion of fuzzy sets to intuitionistic fuzzy sets by introducing the non-membership of an element with its membership in a set X, which were proven to be a better tool than fuzzy sets. Furthermore, the intuitionistic fuzzy sets are used in many directions [4]. Smarandache gave the notion of neutrosophic sets as a generalization of intuitionistic fuzzy sets and fuzzy sets [5]. The idea of neutrosophic sets are further expanded to different directions [6,7,8,9] by various researchers. Jun et al. [10] gave the idea of cubic set and it was characterized by interval-valued fuzzy set and fuzzy set, which is a more general tool to capture uncertainty and vagueness, since fuzzy set deals with single-value membership while interval-valued fuzzy set ranges the membership in the form of intervals. The hybrid platform provided by cubic set has the main advantage since it contains more information than a fuzzy set and interval-valued fuzzy set. By using this concept, different problems arising in several areas can be solved by choosing the finest choice by means of cubic sets as in the works of Abughazalah and Yaqoob [11], Rashid et al. [12], Gulistan et al. [13], Ma et al. [14], Naveed at al. [15], Gulistan et al. [16], Khan et al. [17,18], Yaqoob et al. [19], and Aslam et al. [20].

More recently, Jun et al. [21] gave the idea of neutrosophic cubic set and it was subsequently used in many areas by Khan et al. [22] and Gulistan et al. [23,24].

On the other hand, Molodtsov [25] introduced the concept of soft sets that can be seen as a new mathematical theory for dealing with uncertainty. It was applied to many different fields by Maji et al. [26] who later defined fuzzy soft set theory and some properties of fuzzy soft sets [27]. Hybrids of soft sets were further developed [28,29,30,31,32].

Alkhazaleh and Salleh in 2011 defined the concept of soft expert set in which the user could know the opinion of all the experts in one model and gave an application of this concept in the decision-making problem [33]. Arokia et al. [34] studied fuzzy parameterizations for decision-making in risk management systems via soft expert set. Arokia and Arockiarani [35] provided a fusion of soft expert set and matrix models. Alkhazaleh and Salleh [36] extended the concept of soft expert set in terms of fuzzy set and provided its application. Bashir and Salleh [37] provided the concept of fuzzy parameterized soft expert set. Bashir et al. [38] discussed possibility fuzzy soft expert set. Alhazaymeh et al. [39] provided the application of generalized vague soft expert set in decision-making. Broumi and Smarandache [40] extended the soft expert sets in terms of intuitionistic fuzzy sets. Abu Qamar and Hassan [41,42] presented the idea of Q-neutrosophic soft relation and its entropy measures of distance and similarity. Sahin et al. [43] gave the idea of neutrosophic soft expert sets while Uluçay et al. [44], introduced the concept of generalized neutrosophic soft expert set for multiple-criteria decision-making. Neutrosophic vague soft expert set theory was put forward by Al-Quran and Hassan [45] and developed it further to complex neutrosophic soft expert set [46,47]. Qayyum et al. [48] gave the idea of cubic soft expert sets for a more general approach. Ziemba and Becker [49] presented analysis of the digital divide using fuzzy forecasting, which is a new approach in decision-making.

Hence it is natural to extend the concept of expert sets to neutrosophic cubic soft expert sets for a more generalized approach. The major contribution of this paper is the development of neutrosophic cubic soft expert sets(NCSESs) by using the concept of neutrosophic cubic soft sets which generalizes the concept of fuzzy soft expert sets, intuitionistic soft expert sets, and cubic soft expert sets. We define and analyze the properties of internal neutrosophic cubic soft expert sets (INCSESs) and external neutrosophic cubic soft expert sets (ENCSESs), P-order, P-union, P-intersection, P-AND, P-OR, and R-order, R-union, R-intersection, R-AND, and R-OR of NCSESs. The NCSESs satisfy the laws of commutativity, associativity, De Morgan, distributivity, idempotentency, and absorption. We derive some conditions for P-union and P-intersection of two INCSESs to be an INCSES. It is shown that P-union and P-intersection of ENCSESs need not be an ENCSES. The R-union and R-intersection of the INCSESs (resp., ENCSESs) need not be an INCSES (resp. ENCSES). Necessary conditions for the P-union, R-union, and R-intersection of two ENCSESs to be an ENCSES are obtained. We also study the conditions for R-intersection and P-intersection of two NCSESs to be an INCSES and ENCSES. This paper is organized as follows. Section 2 will be on preliminaries, while Section 3 develops an approach to neutrosophic cubic soft expert set. We focus on the basic operations, namely P-order, R-order, P-containment, R-containment, P-union, P-intersection, R-union, R-intersection, complement, P-AND, P-OR, R-AND, and R-OR of NCSESs. Section 4 will present more results on NCSESs, followed by Section 5 on application in analyzing a cricket series. A comparison analysis will be discussed in Section 6 and a conclusion is drawn in Section 7.

2. Preliminaries

Here we recall some of the basic material from the literature to develop the new theory. For simplicity, the symbol $(F_S^E,A)$ stands for the soft expert set, N stands for the neutrosophic set, $I^N$ stands for the interval neutrosophic set and $\left(NC\right)$ for the neutrosophic cubic sets.

In psychology, decision-making (also spelled decision-making) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several alternative possibilities. Every decision-making process produces a final choice, which may or may not prompt action. Decision-making is the process of identifying and choosing alternatives based on the values, preferences, and beliefs of the decision-maker. Experts set is a technique used in decision-making problems, which is further extended to generalized forms, such as fuzzy experts set, intuitionistic fuzzy expert set, cubic expert sets, neutrosophic expert set and other hybrids. We begin by stating the definition of expert set.

Definition 1.

[33] Let U be a universe, E be a set of parameters, and X be a set of experts. Let $O=\{0=$ disagree, $1=$ agree} be a set of two valued opinion, $Z=E\times X\times O$ and $A\subseteq Z$. A pair $\left(F_S^E,A\right)$ is called a soft expert set over U, where $F_S^E$ is a mapping given by $F_S^E:A⟶P\left(U\right)$ where $P\left(U\right)$ denotes the power set of U.

Definition 2.

[33] Two soft expert sets $\left(F_S^E,A\right)$ and $\left(G_S^E,B\right)$ over U, $\left(F_S^E,A\right)\subseteq \left(G_S^E,B\right)$ if

$$H_S^E\left(a\right)=\left\{\begin{array}{c}A\subseteq B\\ F_S^E\left(a\right)\subseteq G_S^E\left(a\right)\mathrm{for}\mathrm{all}a\in A\end{array}\right.$$

and $\left(F_S^E,A\right)=\left(G_S^E,B\right)$ if and only if $\left(F_S^E,A\right)\subseteq \left(G_S^E,B\right)$ as well as $\left(G_S^E,B\right)\subseteq \left(F_S^E,A\right).$

Definition 3.

[33] Let E be a set of parameters and X be a set of experts. The NOT set $\acute{I}Z$ of $Z=E\times X\times O$ is defined by

$$\acute{I}Z=\{(\acute{I}{e}_i,x_i,o_k).\acute{I}{e}_i\notin E,x_j\in Xand{o}_k\in O\forall i,j,k\}$$

Definition 4.

[33] The complement of a soft expert set $\left(F_S^E,A\right)$ is denoted by ${\left(F_S^E,A\right)}^c=(F_S^{Ec},\acute{I}A)$ where $F_S^{Ec}:\acute{I}A⟶P\left(U\right)$ is a mapping given by $F_S^{Ec}\left(a\right)=U-F_S^E(\acute{I}a)$, for all $a\in \acute{I}A.$

Definition 5.

[33] If $Z=E\times X\times \left\{1\right\}$ in Definition 1 then $\left(F_S^E,A\right)$ is called agree soft expert set over U and it is denoted by ${\left(F_S^E,A\right)}_1.$

Definition 6.

[33] If $Z=E\times X\times \left\{0\right\}$ in Definition 1 then $\left(F_S^E,A\right)$ is called disagree soft expert set over U and it is denoted by ${\left(F_S^E,A\right)}_0$

Definition 7.

[33] The union of two soft expert sets $\left(F_S^E,A\right)$ and $\left(G_S^E,B\right)$ over U denoted by $\left(F_S^E,A\right)\cup \left(G_S^E,B\right)$, is the soft expert set $(H_S^E,C)$ where $C=A\cup B$, and for all $a\in C,$

$$H_S^E\left(a\right)=\left\{\begin{array}{c}{F}_S^E\left(a\right)ifa\in A-B\\ G_S^E\left(a\right)ifa\in B-A\\ F_S^E\left(a\right)\cup G_S^E\left(a\right)ifa\in A\cap B.\end{array}\right.$$

Definition 8.

[33] The intersection of two soft expert sets $\left(F_S^E,A\right)$ and $\left(G_S^E,B\right)$ over U denoted by $\left(F_S^E,A\right)\cap \left(G_S^E,B\right)$, is the soft expert set $(H_S^E,C)$ where $C=A\cap B$, and for all $a\in C,$

$$H_S^E\left(a\right)=\left\{\begin{array}{c}{F}_S^E\left(a\right)ifa\in A-B\\ G_S^E\left(a\right)ifa\in B-A\\ F_S^E\left(a\right)\cap G_S^E\left(a\right)ifa\in A\cap B.\end{array}\right.$$

Definition 9.

[33] If $\left(F_S^E,A\right)$ and $\left(G_S^E,B\right)$ are two soft expert sets over U then $\left(F_S^E,A\right)$ AND $\left(G_S^E,B\right)$ denoted by $\left(F_S^E,A\right)\wedge (G_S^E,B)$, is defined by

$$\left(F_S^E,A\right)\wedge (G_S^E,B)=(H_S^E,A\times B)$$

where $H_S^E(a,b)=F_S^E\left(a\right)\cap G_S^E\left(b\right)$, for all $(a,b)\in A\times B$.

Definition 10.

[33] If $\left(F_S^E,A\right)$ and $\left(G_S^E,B\right)$ are two soft expert sets then $\left(F_S^E,A\right)$ OR $(G_S^E,B)$ denoted by $\left(F_S^E,A\right)\vee (G_S^E,B)$ is defined by

$$\left(F_S^E,A\right)\vee (G_S^E,B)=(H_S^E,A\times B)$$

where $H_S^E(a,b)=F_S^E\left(a\right)\cup G_S^E\left(b\right)$, for all $(a,b)\in A\times B$.

Definition 11.

[5] A neutrosophic set in X is the structure of the form

$$N:=\left\{⟨x,T_N\left(x\right),I_N\left(x\right),F_N\left(x\right)⟩:x\in X\right\}$$

where $T_N,I_N,F_N:X\to [0,1]$ such that $0\le T_N\left(x\right)+I_N\left(x\right)+F_N\left(x\right)\le 3.$

Definition 12.

[8] An interval neutrosophic set in X is the structure of the form

$$I^N:=\left\{⟨x,T_{{}^{I^N}}\left(x\right),I_{{}^{I^N}}\left(x\right),F_{I^N}\left(x\right)⟩:x\in X\right\}$$

where $T_N,I_N,F_N:X\to D[0,1]$ such that $[0,0]⪯T_N\left(x\right)+I_N\left(x\right)+F_N\left(x\right)⪯[3,3].$

Definition 13.

[21] A neutrosophic cubic set in X is a pair $\left(NC\right)=(I^N,N)$ where

$$I^N:=\left\{⟨x,T_{I^N}\left(x\right),I_{I^N}\left(x\right),F_{I^N}\left(x\right)⟩:x\in X\right\}$$

is an interval neutrosophic set in X where $T_{I^N},I_{I^N},F_{I^N}:X\to D[0,1]$ and

$$N:=\left\{⟨x,T_N\left(x\right),I_N\left(x\right),F_N\left(x\right)⟩:x\in X\right\}$$

is a neutrosophic set in X where $T_N,I_N,F_N:X\to [0,1].$

3. Neutrosophic Cubic Soft Expert Set

In this section, we develop an approach to neutrosophic cubic soft expert set which is a more general approach for soft expert set theory. We focus on the basic operations namely, P-order, R-order, P-containment, R-containment, P-union, P-intersection, R-union, R-intersection, complement, P-AND, P-OR, R-AND, and R-OR of neutrosophic cubic soft expert sets. The symbol $({\left(NC\right)}_S^E,E,X)$ stands for the neutrosophic cubic soft expert set.

Definition 14.

Let U be a finite set containing n alternatives, E be a set of criteria, X be a set of experts. A triplet $({\left(NC\right)}_S^E,E,X)$ is called neutrosophic cubic soft expert set over U, if and only if ${\left(NC\right)}_S^E:E\times X\to NCP\left(U\right)$ is a mapping into the set of all neutrosophic cubic set in U and defined as

$$({\left(NC\right)}_S^E,E,X)=\left\{{\left(NC\right)}_S^E(e,x)=\{⟨u,I_{(e,x)}^N\left(u\right),N_{(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E\times X\right\},$$

where

$$I_{(e,x)}^N\left(u\right)=\{(u,{\tilde{T}}_{I^N}\left(u\right),{\tilde{I}}_{I^N}\left(u\right),{\tilde{F}}_{I^N}\left(u\right))\},N_{(e,x)}\left(x\right)=\{(u,T_N\left(u\right),I_N\left(u\right),F_N\left(u\right)\},$$

such that

$$[0,0]⪯{\tilde{T}}_{I^N}\left(u\right)+{\tilde{I}}_{I^N}\left(u\right)+{\tilde{F}}_{I^N}\left(u\right)⪯[3,3],0\le T_N\left(u\right)+I_N\left(u\right)+F_N\left(u\right)\le 3.$$

Example 1.

Let $U=\left\{u_1=India,u_2=Pakistan\right\}$ be the set of countries playing a cricket series, $E=\{e_1=$ playing conditions, $e_2=$ historic record} be the set of factors affecting the series, $X=\left\{x_1,x_2,x_3\right\}$ be the set of experts giving their expert opinion. Let $E\times X=\{(e_1,x_1),(e_1,x_2),(e_2,x_1),(e_2,x_2)\}.$ Then the neutrosophic cubic soft expert set $({\left(NC\right)}_S^E,E,X)$ is given by

$$\begin{array}{cc}\hfill {\left(NC\right)}_S^E(e_1,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.6\right],\left[0.2,0.3\right],\left[0.1,0.2\right],0.1,0.4,0.5\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.6\right],\left[0.2,0.3\right],\left[0.1,0.2\right],0.1,0.4,0.5\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,x_3)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.6\right],\left[0.2,0.3\right],\left[0.1,0.2\right],0.4,0.3,0.5\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_3)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.6,0.9\right],\left[0.6,0.9\right],0.9,0.7,0.6\right),\end{array}\right\}\hfill \end{array}$$

The function of the form $({\tilde{T}}_{I^N}\left(u\right),T_N\left(u\right))$ denotes the range of values where the experts are sure to give certain membership to a certain element, $({\tilde{I}}_{I^N}\left(u\right),I_N\left(u\right))$ denotes the range of values where the experts are hesitant and $({\tilde{F}}_{I^N}\left(u\right),F_N\left(u\right))$ denotes the range of values where the experts are sure to give negative points to a certain element as a non-membership. Thus, experts have a wide range of scale to make their conclusion as compared to the previous defined versions of fuzzy sets. More specific in the current example is the function of the form $({\tilde{T}}_{I^N}\left(u\right),T_N\left(u\right))$ which gives the expert opinion for the past performance of these two countries, $({\tilde{I}}_{I^N}\left(u\right),I_N\left(u\right))$ gives the expert opinion for running series between these two countries and $({\tilde{F}}_{I^N}\left(u\right),F_N\left(u\right))$ gives the expert opinion for the upcoming series between these two countries which is not to be held in the near future.

Definition 15.

A neutrosophic cubic soft expert set

$$({\left(NC\right)}_S^E,E,X)=\left\{{\left(NC\right)}_S^E(e,x)=\{⟨u,I_{(e,x)}^N\left(u\right),N_{(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E\times X\right\}$$

over U is said to be:

(i) 

Internal truth neutrosophic cubic soft experts set (briefly, $ITNCSESs$) if for all $u\in U,$ so that

$$T_{I^N}^{-}\left(u\right)\le T_N\left(u\right)\le T_{I^N}^{+}\left(u\right),\forall u\in U.$$

(ii) 

Internal indeterminacy neutrosophic cubic soft experts set (briefly, $IINCSESs$) if for all $u\in U,$ so that

$$I_{I^N}^{-}\left(u\right)\le I_N\left(u\right)\le I_{I^N}^{+}\left(u\right),\forall u\in U.$$

(iii) 

Internal falsity neutrosophic cubic soft experts set (briefly, $IFNCSESs$) if for all $u\in U,$ so that

$$F_{I^N}^{-}\left(u\right)\le F_N\left(u\right)\le F_{I^N}^{+}\left(u\right),\forall u\in U.$$

If a neutrosophic cubic soft expert set $({\left(NC\right)}_S^E,E,X)$ in $X,$ satisfies (i), (ii), (iii), then it is known as internal neutrosophic cubic soft expert set in $X,$ abbreviated as ($INCSESs$).

Example 2.

Consider the Example 1. Then the internal neutrosophic cubic soft expert set is given by

$$\begin{array}{cc}\hfill {\left(NC\right)}_S^E(e_1,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.5,0.4,0.3\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.5,0.9\right],\left[0.6,0.8\right],0.7,0.6,0.7\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.7\right],\left[0.2,0.4\right],\left[0.1,0.4\right],0.6,0.3,0.2\right),\\ \left(u_{2,}\left[0.6,0.9\right],\left[0.7,0.9\right],\left[0.6,0.8\right],0.7,0.8,0.7\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.7,0.2,0.3\right),\\ \left(u_{2,}\left[0.5,0.9\right],\left[0.6,0.8\right],\left[0.4,0.9\right],0.6,0.7,0.6\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.8\right],\left[0.3,0.9\right],\left[0.6,0.9\right],0.7,0.7,0.8\right),\\ \left(u_{2,}\left[0.3,0.9\right],\left[0.7,0.9\right],\left[0.6,0.8\right],0.6,0.8,0.7\right)\end{array}\right\}\hfill \end{array}$$

Remark 1.

We can draw the following conclusion from Example 2;

(i) If the value of $N_{(e,x)}\left(u\right)$ lies in the interval $I_{(e,x)}^N\left(u\right),$ then it means that the respective team is going to maintain its progress in different time frames.

(ii) If the panel of experts consists of the internal panel (meaning that the experts are from the same country or same cricket board), then it is known as INCSESs.

Definition 16.

A neutrosophic cubic soft expert set

$$({\left(NC\right)}_S^E,E,X)=\left\{{\left(NC\right)}_S^E(e,x)=\{⟨u,I_{(e,x)}^N\left(u\right),N_{(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E\times X\right\}$$

over U is said to be:

(i) 

External truth neutrosophic cubic soft expert set (briefly, $ETNCSESs$) if for all $u\in U,$ we have

$$T_N\left(u\right)\notin (T_{I^N}^{-}\left(u\right),T_{I^N}^{+}\left(u\right)),\forall u\in U$$

(ii) 

External indeterminacy neutrosophic cubic soft expert set (briefly, $EINCSESs$) if for all $u\in U,$ we have

$$I_N\left(x\right)\notin (I_{I^N}^{-}\left(x\right),I_{I^N}^{+}\left(x\right)),\forall u\in U$$

(iii) 

External falsity neutrosophic cubic soft expert set (briefly, $EFNCSESs$) if for all $u\in U,$ we have

$$F_N\left(x\right)\notin (F_{I^N}^{-}\left(x\right),F_{I^N}^{+}\left(x\right)),\forall u\in U$$

If a neutrosophic cubic soft expert set $({\left(NC\right)}_S^E,E,X)$ over $U,$ satisfies (i), (ii), (iii), then it is known as external neutrosophic cubic soft expert set in $X,$ abbreviated as ($ENCSESs$).

Example 3.

Let U be the set of countries playing a one-day international (ODI) triangular series provided in Example 1, then the external neutrosophic cubic soft expert set is given by;

$$\begin{array}{cc}\hfill {\left(NC\right)}_S^E(e_1,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_1)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.7\right],\left[0.2,0.4\right],\left[0.1,0.4\right],0.8,0.5,0.6\right),\\ \left(u_{2,}\left[0.4,0.6\right],\left[0.3,0.5\right],\left[0.6,0.8\right],0.7,0.2,0.4\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.4,0.4,0.5\right),\\ \left(u_{2,}\left[0.1,0.3\right],\left[0.6,0.8\right],\left[0.4,0.6\right],0.6,0.5,0.3\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,x_2)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.7\right],\left[0.3,0.4\right],\left[0.6,0.8\right],0.8,0.7,0.5\right),\\ \left(u_{2,}\left[0.3,0.5\right],\left[0.7,0.8\right],\left[0.6,0.7\right],0.6,0.5,0.8\right),\end{array}\right\}\hfill \end{array}$$

Remark 2.

We can draw the following conclusion from Example 3;

(i) If the value of $N_{(e,x)}\left(u\right)$ does not lie in the interval $I_{(e,x)}^N\left(u\right),$ then it means the respective team is not maintaining its progress in different time frames.

(ii) If the panel of experts consists of the external panel (meaning that the experts are not from the same country or same cricket board), then it is known as ENCSESs.

Our next discussion is to define some basic operations on neutrosophic cubic soft expert sets to get more insight of neutrosophic cubic soft expert sets.

Definition 17.

A $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ over U is said to be P-order contained in another $NCSESs$ $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, denoted by $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2),$

if $\left(i\right)E_1\subseteq E_2,$

$\left(ii\right)X_1\subseteq X_2,$

$\left(iii\right){\left(NC\right)}_{S1}^E(e,x){\subseteq }_P{\left(NC\right)}_{S2}^E(e,x)\mathit{for}\mathit{all}e\in E_1,x\in X_1,$where condition $\left(iii\right)$ implies that

$$I_{1{\left(NC\right)}_S^E(e_1,x_1)}^N\left(x\right)⪯I_{2{\left(NC\right)}_S^E(e_2,x_2)}^N\left(x\right),N_{1{\left(NC\right)}_S^E(e_1,x_1)}\left(x\right)\le N_{2{\left(NC\right)}_S^E(e_2,x_2)}\left(x\right).$$

Definition 18.

A $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ over U is said to be R-order contained in another $NCSES$ $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, denoted by $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_R({\left(NC\right)}_{S2}^E,E_2,X_2),$

if $\left(i\right)E_1\subseteq E_2,$

$\left(ii\right)X_1\subseteq X_2,$

$\left(iii\right){\left(NC\right)}_{S1}^E(e,x){\subseteq }_R{\left(NC\right)}_{S2}^E(e,x)$$\mathrm{for}\mathrm{all}e\in E_1,x\in X_1,$

where condition $\left(iii\right)$ implies that

$$I_{1{\left(NC\right)}_S^E(e_1,x_1)}^N\left(x\right)⪯I_{2{\left(NC\right)}_S^E(e_2,x_2)}^N\left(x\right),N_{1{\left(NC\right)}_S^E(e_1,x_1)}\left(x\right)\ge N_{2{\left(NC\right)}_S^E(e_2,x_2)}\left(x\right).$$

Definition 19.

Two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U is said to be equal which is denoted by $({\left(NC\right)}_{S1}^E,E_1,X_1)=({\left(NC\right)}_{S2}^E,E_2,X_2),$

if $\left(i\right)A=B,$

$\left(ii\right)X_1=X_2,$

$\left(iii\right)$${\left(NC\right)}_{S1}^E\left(e\right)={\left(NC\right)}_{S2}^E\left(e\right)$$\mathrm{for}\mathrm{all}e\in E=A=B,x\in X=X_1=X_2,$

where condition $\left(iii\right)$ implies that

$$I_{1{\left(NC\right)}_S^E(e_1,x_1)}^N\left(x\right)=I_{2{\left(NC\right)}_S^E(e_2,x_2)}^N\left(x\right),N_{1{\left(NC\right)}_S^E(e_1,x_1)}\left(x\right)=N_{2{\left(NC\right)}_S^E(e_2,x_2)}\left(x\right).$$

Remark 3.

(a) We observe from Definitions 17–19, that for any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U;

(i) If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2){\subseteq }_P({\left(NC\right)}_{S1}^E,E_1,X_1),$

then $({\left(NC\right)}_{S1}^E,E_1,X_1)=({\left(NC\right)}_{S2}^E,E_2,X_2),$

(ii) If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2){\subseteq }_R({\left(NC\right)}_{S1}^E,E_1,X_1),$

then $({\left(NC\right)}_{S1}^E,E_1,X_1)=({\left(NC\right)}_{S2}^E,E_2,X_2).$

(b) Using Definitions 17–19, one can easily compare the performance of two cricket teams in different time frames.

Definition 20.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $NCSESs$ in $U.$

Then we define (i) $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cup E_2,X_3=X_1\cup X_2$

$${\left(NC\right)}_{S3}^E\left(e_i\right)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E\left(e_i\right)if{e}_i\in E_1-E_2\\ {\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_2-E_1\\ {\left(NC\right)}_{S1}^E\left(e_i\right){\vee }_P{\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_1\cap E_2\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e_i\right){\vee }_P{\left(NC\right)}_{S2}^E\left(e_i\right)& =\left\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\vee I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N,N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\vee N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),{\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right)\\ ,{\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right)\end{array}\right),\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee T_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),I_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee I_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge F_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right)\end{array}\right)\end{array}⟩\}\end{array}$$

(ii) $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cap E_2,X_3=X_1\cap X_2$

$${\left(NC\right)}_{S3}^E\left(e_i\right)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E\left(e_i\right){\wedge }_P{\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_1\cap E_2\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e_i\right){\wedge }_P{\left(NC\right)}_{S2}^E\left(e_i\right)& =\left\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\wedge I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N,N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),{\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),\\ {\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right)\end{array}\right)\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge T_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),I_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge I_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee F_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right)\end{array}\right)\end{array}⟩\}\end{array}$$

(iii) $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cup E_2,X_3=X_1\cup X_2,$

$${\left(NC\right)}_{S3}^E\left(e_i\right)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E\left(e_i\right)if{e}_i\in E_1-E_2\\ {\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_2-E_1\\ {\left(NC\right)}_{S1}^E\left(e_i\right){\vee }_R{\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_1\cap E_2\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e_i\right){\vee }_R{\left(NC\right)}_{S2}^E\left(e_i\right)& =\left\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\vee I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N,N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),{\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),\\ {\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right)\end{array}\right)\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge T_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),I_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge I_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee F_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right)\end{array}\right)\end{array}⟩\end{array}$$

(iv) $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cap E_2,X_3=X_1\cap X_2,$

$${\left(NC\right)}_{S3}^E\left(e_i\right)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E\left(e_i\right){\wedge }_R{\left(NC\right)}_{S2}^E\left(e_i\right)if{e}_i\in E_1\cap E_2\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e_i\right){\wedge }_R{\left(NC\right)}_{S2}^E\left(e_i\right)& =\left\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\wedge I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N,N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\vee N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),{\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\wedge {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right),\\ {\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N}\left(u\right)\end{array}\right)\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee T_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),I_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\vee I_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}}\left(u\right)\wedge F_{N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\left(u\right)\end{array}\right)\end{array}⟩\}\end{array}$$

(v) The complement of a neutrosophic cubic soft expert set $({\left(NC\right)}_S^E,E,X)$ denoted by

$${({\left(NC\right)}_S^E,E,X)}^c=\{{\left(NC\right)}_S^{Ec}\left(e_i\right)=\{⟨u,\tilde{1}-I_{{\left(NC\right)}_S^E\left(e_i\right)}^N\left(u\right),1-N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)⟩,u\in U\},e_i\in A\}.$$

Proposition 1.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$, $({\left(NC\right)}_{S2}^E,E_2,X_2),$ $({\left(NC\right)}_{S3}^E,E_3,X_3),$ $({\left(NC\right)}_{S4}^E,E_4,X_4)$ be $NCSESs$ in $U.$ Then

(i) 

If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S4}^E,E_4,X_4)$

then $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S4}^E,E_4,X_4).$

(ii) 

If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$

then ${({\left(NC\right)}_{S2}^E,E_2,X_2)}^c{\subseteq }_P{({\left(NC\right)}_{S1}^E,E_1,X_1)}^c.$

(iii) 

If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S4}^E,E_4,X_4)$

then $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2){\cap }_P({\left(NC\right)}_{S4}^E,E_4,X_4).$

(iv) 

If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$

then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2).$

(v) 

If $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ and $({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S4}^E,E_4,X_4)$

then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2){\cup }_P({\left(NC\right)}_{S4}^E,E_4,X_4)$,$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S3}^E,E_3,X_3){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2){\cap }_P({\left(NC\right)}_{S4}^E,E_4,X_4).$

Proof. 

The proof is straightforward.  □

Theorem 1.

For any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U the following properties hold:

(i) 

Idempotent law: $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S1}^E,E_1,X_1)=({\left(NC\right)}_{S1}^E,E_1,X_1),$$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S1}^E,E_1,X_1)=({\left(NC\right)}_{S1}^E,E_1,X_1).$

(ii) 

Commutative law: $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S2}^E,E_2,X_2){\cup }_P({\left(NC\right)}_{S1}^E,E_1,X_1),$$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S2}^E,E_2,X_2){\cap }_P({\left(NC\right)}_{S1}^E,E_1,X_1).$

(iii) 

Associative law: $(({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2)){\cup }_P({\left(NC\right)}_{S3}^E,E_3,X_3)=({\left(NC\right)}_{S1}^E,E_1,X_1)$ ${\cup }_P(({\left(NC\right)}_{S2}^E,E_2,X_2){\cup }_P({\left(NC\right)}_{S3}^E,E_3,X_3)),$ $(({(NC)}_{S1}^E,E_1,X_1){\cap }_P({(NC)}_{S2}^E,E_2,X_2)){\cap }_P({(NC)}_{S3}^E,E_3,X_3)=({(NC)}_{S1}^E,E_1,X_1){\cap }_P(({(NC)}_{S2}^E,E_2,X_2)$ ${\cap }_P({(NC)}_{S3}^E,E_3,X_3)).$

(iv) 

Distributive and De Morgan’s laws also true.

(v) 

Involution law: ${({({\left(NC\right)}_{S1}^E,E_1,X_1)}^c)}^c=({\left(NC\right)}_{S1}^E,E_1,X_1).$

Proposition 2.

For any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U the following properties are equivalent:

(i) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2),$

(ii) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S1}^E,E_1,X_1),$

(iii) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S2}^E,E_2,X_2).$

Proof. 

$\left(i\right)\Rightarrow \left(ii\right)$ By Definition 20, we have

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\cap }_P\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=({\left(NC\right)}_{S1}^E{\cap }_P{\left(NC\right)}_{S2}^E,A\cap B)=({\left(NC\right)}_{S1}^E{\cap }_P{\left(NC\right)}_{S2}^E,A)$$

as $A\subseteq B$ by hypothesis. Now for any $e\in E_1,$ since ${\left(NC\right)}_{S1}^E\left(e\right){\subseteq }_P{\left(NC\right)}_{S2}^E\left(e\right),$ using Definition 17, implies that $I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right)⪯I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)$ and $N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\le N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)$ for any $u\in U,$ where ${\left(NC\right)}_{S1}^E\left(e_i\right)=\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)⟩u\in U\}$. Since $I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)$ and $I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right).$ Thus

$$\begin{array}{cc}\hfill inf\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\}& =[inf\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\hfill \\ \hfill inf\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}]& =[I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)]\hfill \end{array}$$

and $inf\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\}=N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right).$ So It is ok.

$$\begin{array}{cc}\hfill {\left(NC\right)}_{S1}^E\left(e\right){\cap }_P{\left(NC\right)}_{S2}^E\left(e\right)& =\{⟨u,inf\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\},\hfill \\ \hfill inf\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)⟩:u\in U\}& =\{⟨u,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)⟩:u\in U\}\hfill \\ \hfill & ={\left(NC\right)}_{S1}^E\left(e\right)\hfill \end{array}$$

Hence ${\left(NC\right)}_{S1}^E\left(e\right){\cap }_P{\left(NC\right)}_{S2}^E\left(e\right)={\left(NC\right)}_S^E\left(e\right).$  □

(ii)⇒(iii) By Definition 20, we have

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\cup }_P\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=({\left(NC\right)}_{S1}^E{\cup }_P{\left(NC\right)}_{S2}^E,A\cup B)=({\left(NC\right)}_{S1}^E{\cup }_P{\left(NC\right)}_{S2}^E,A)$$

as $A\cap A=A$ and ${\left(NC\right)}_{S2}^E\cap {\left(NC\right)}_{S2}^E={(NC)}_{S2}^E$, by hypothesis. Now for any $e\in E_1,$ since ${\left(NC\right)}_{S1}^E\left(e\right){\cap }_P{\left(NC\right)}_{S2}^E\left(e\right)={\left(NC\right)}_{S1}^E\left(e\right),$ by Definition 20, we have

$$\begin{array}{cc}\hfill inf\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\}& =I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right)\hfill \\ \hfill \mathrm{and}inf\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\}& =N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\hfill \end{array}$$

this implies that

$$\begin{array}{cc}\hfill sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\}& =I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\hfill \\ \hfill \mathrm{and}sup\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_{i1}\right)}\left(u\right)\}& =N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\hfill \end{array}$$

Thus, we have

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e\right){\cup }_P{\left(NC\right)}_{S2}^E\left(e\right)& =\{⟨\begin{array}{c}u,sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\},\\ sup\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\end{array}⟩:u\in U\}\\ & =\{⟨u,I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)⟩:u\in U\}={\left(NC\right)}_{S2}^E\left(e\right).\end{array}$$

Hence ${\left(NC\right)}_{S1}^E\left(e\right){\cap }_P{\left(NC\right)}_{S2}^E\left(e\right)={\left(NC\right)}_{S2}^E\left(e\right).$

(iii)⇒(i) By hypothesis we have

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\cup }_P\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=({\left(NC\right)}_{S1}^E{\cup }_P{\left(NC\right)}_{S2}^E,A\cup B)=({\left(NC\right)}_{S1}^E{\cup }_P{\left(NC\right)}_{S2}^E,A)$$

as $A\cup A=A$ and ${\left(NC\right)}_{S2}^E\cup {\left(NC\right)}_{S2}^E={\left(NC\right)}_{S2}^E\Rightarrow A\subseteq A$ and ${\left(NC\right)}_{S2}^E\subseteq {\left(NC\right)}_{S2}^E.$ Also

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E\left(e\right){\cup }_P{\left(NC\right)}_{S2}^E\left(e\right)& =\{⟨\begin{array}{c}u,sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)\},\\ sup\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\end{array}⟩:u\in U\}\\ & =\{⟨u,I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)⟩:u\in U\}={\left(NC\right)}_{S2}^E\left(e\right)\end{array}$$

this implies that $I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(u\right)⪯I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N\left(u\right)$ and $N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\le N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)$ for any $u\in U$.

Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X_2).$

Corollary 1.

If we take $X_1=X_2=X$ in the Proposition 2, then the following are equivalent:

(i) 

$({\left(NC\right)}_{S1}^E,E_1,X){\subseteq }_P({\left(NC\right)}_{S2}^E,E_2,X),$

(ii) 

$({\left(NC\right)}_{S1}^E,E_1,X){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X)=({\left(NC\right)}_{S1}^E,E_1,X),$

(iii) 

$({\left(NC\right)}_{S1}^E,E_1,X){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X)=({\left(NC\right)}_{S2}^E,E_2,X).$

Proof. 

The proof is straightforward.  □

4. More on NCSESs

In this section, we discuss different types of union and intersection of the NCSESs and their related conditions.

1. The following example shows thatR-Union of two$INCSESs$inUneed not be$INCSESs$in$U.$

Example 4.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $INCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.1,0.2],[0.4,0.5],[0.5,0.6]),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}=(0.2,0.3,0.4)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.3,0.4],[0.3,0.5],[0.5,0.7]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.4,0.6,0.3)\}.$$

Now by Definition 20, we have $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3)$

$$\left({\left(NC\right)}_{S3}^E,E_3,X_3\right)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.3,0.4],[0.4,0.5],[0.5,0.7],N_{{\left(NC\right)}_{S3}^E\left(e_i\right)}=(0.2,0.3,0.4)\}$$

As $0.2\notin [0.4,0.5],0.3\notin [0.4,0.5]$ and $0.4\notin [0.5,0.7].$

Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is not a $INCSES$ in U.

The following theorem gives the condition under which R-union of two $INCSESs$ in U is also a $INCSES$ in U.

Theorem 2.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $INCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$

and $({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$

such that

$$sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\}\le \left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}$$

for all $u\in U$ and $(g,z)\in (E_1\cap E_2\times X_1\cap X_2).$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is $INCSESs$ in U.

Proof. 

By Definition 20, we know $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cup E_2,X_3=X_1\cup X_2,$

$${\left(NC\right)}_{S3}^E(e_3,x_3)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_1\times X_1\right)-\left(E_2\times X_2\right)\\ {\left(NC\right)}_{S2}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_2\times X_2\right)-\left(E_1\times X_1\right)\\ {\left(NC\right)}_{S1}^E(e_3,x_3){\vee }_R{\left(NC\right)}_{S2}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_1\times E_2\right)\cap \left(X_1\times X_2\right)\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E(e_3,x_3){\vee }_R{\left(NC\right)}_{S2}^E(e_3,x_3)& =\left\{⟨u,I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N\vee I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N,N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}\wedge N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right),\\ {\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\vee {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right),\\ {\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right)\end{array}\right)\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\wedge T_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right),\\ I_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\wedge I_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\vee F_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right)\end{array}\right)\end{array}⟩\end{array}$$

If $(e_3,x_3)\in \left(E_1\times X_1\right)-\left(E_2\times X_2\right)$ or if $(e_3,x_3)\in \left(E_2\times X_2\right)-\left(E_1\times X_1\right)$ then the result is trivial. If $(e_3,x_3)\in \left(E_1\cap E_2\times X_1\cap X_2\right),$ then ${\left(NC\right)}_{S3}^E\left(e_3,x_3\right)=\left\{⟨u,I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N\vee I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N,N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}\wedge N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}⟩:u\in U\right\}.$  □

Since $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ are $INCSESs$ in U. So $I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^{N-}\left(u\right)\le N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^{N+}\left(u\right)$ and $I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^{N-}\left(u\right)\le N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^{N+}\left(u\right).$ Also

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^{N-}\left(u\right)\vee I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^{N-}\left(u\right)& \le N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}\left(u\right)\\ & \le I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^{N+}\left(u\right)\vee I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^{N+}\left(u\right)\end{array}$$

for all $u\in U$ and $(e_3,x_3)\in \left(E_2\cap E_2,X_1\cap X_2\right).$ Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is $INCSESs$ in U.

2. The following example yields thatR-intersection of two$INCSESs$ need not be a$INCSESs$.

Example 5.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $INCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.1,0.2],[0.3,0.5],[0.3,0.6]),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}=(0.2,0.3,0.4)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.2,0.6],[0.3,0.6],[0.5,0.7]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.4,0.6,0.5)\}.$$

Now by Definition 20, we have $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3)$

$$({\left(NC\right)}_{S2}^E,E_2,X_2)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.1,0.2],[0.3,0.5],[0.5,0.7],N_{{\left(NC\right)}_S^E\mathcal{3}\left(ei\right)}=(0.4,0.6,0.4)\}.$$

As $0.4\notin [0.1,0.2],$ $0.6\notin [0.3,0.5]$ and $0.4\notin [0.5,0.7].$

Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is not a $INCSES$ in U.

The following theorem gives the condition that R-intersection of two $INCSESs$ is to be a $INCSES.$

Theorem 3.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $INCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$inf\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(x\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\ge \left\{N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)\vee N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}$$

for all $u\in U$ and $(g,z)\in (E_1\cap E_2\times X_1\cap X_2).$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is a $INCSES$ in U.

Proof. 

Similar to the proof of the Theorem 2.  □

3. The following example yields thatR-union of two$ENCSESs$need not be an$ENCSESs$.

Example 6.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.3,0.4],[0.4,0.7],[0.3,0.6]),N_{{\left(NC\right)}_S^E\left(e_i\right)}=(0.5,0.3,0.7)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.2,0.6],[0.3,0.5],[0.5,0.6]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.1,0.2,0.4)\}.$$

Now by Definition 20, we have $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3)$

$$\left({\left(NC\right)}_{S3}^E,E_3,X_3\right)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.3,0.6],[0.4,0.7],[0.5,0.6],N_{{\left(NC\right)}_{S3}^E\left(ei\right)}=(0.1,0.2,0.7)\}.$$

As $0.1\notin [0.3,0.6],0.2\notin [0.4,0.7]$ and $0.7\notin [0.5,0.6].$

Hence R-union is not a $ENCSESs$ in U.

The following theorem gives the condition that R-union of two $ENCSESs$ to be a $ENCSESs$.

Theorem 4.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$ and$({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$\begin{array}{c}\{inf\{sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \\ <\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\hfill \\ \le \{sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\},\hfill \end{array}$$

for all $u\in U$ and $(g,z)\in (E_1\cap E_2\times X_1\cap X_2).$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is a $ENCSES$ in U.

Proof. 

By Definition 20, we know $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3),$ where $E_3=E_1\cup E_2,X_3=X_1\cup X_2,$

$${\left(NC\right)}_{S3}^E(e_3,x_3)=\left\{\begin{array}{c}{\left(NC\right)}_{S1}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_1\times X_1\right)-\left(E_2\times X_2\right)\\ {\left(NC\right)}_{S2}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_2\times X_2\right)-\left(E_1\times X_1\right)\\ {\left(NC\right)}_{S1}^E(e_3,x_3){\vee }_R{\left(NC\right)}_{S2}^E(e_3,x_3)\mathrm{if}(e_3,x_3)\in \left(E_1\times E_2\right)\cap \left(X_1\times X_2\right)\end{array}\right.$$

where

$$\begin{array}{ll}{\left(NC\right)}_{S1}^E(e_3,x_3){\vee }_R{\left(NC\right)}_{S2}^E(e_3,x_3)& =\left\{⟨\begin{array}{c}u,I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N\vee I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N,\\ N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}\wedge N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}\end{array}⟩:u\in U\right\}\\ & =\{⟨\begin{array}{c}u,\left(\begin{array}{c}{\tilde{T}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\vee {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right),\\ {\tilde{I}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\vee {\tilde{I}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right),\\ {\tilde{F}}_{I_{{\left(NC\right)}_{S1}^E(e_3,x_3)}^N}\left(u\right)\wedge {\tilde{T}}_{I_{{\left(NC\right)}_{S2}^E(e_3,x_3)}^N}\left(u\right)\end{array}\right)\\ \left(\begin{array}{c}{T}_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\wedge T_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right),\\ I_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\wedge I_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right),\\ F_{N_{{\left(NC\right)}_{S1}^E(e_3,x_3)}}\left(u\right)\vee F_{N_{{\left(NC\right)}_{S2}^E(e_3,x_3)}}\left(u\right)\end{array}\right)\end{array}⟩\end{array}$$

If $(e_3,x_3)\in \left(E_1\cap E_2\times X_1\cap X_2\right),$ take

$$h=\left(\begin{array}{c}\{inf\{sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\\ sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\end{array}\right)$$

and

$$k=\left(\begin{array}{c}\{sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\\ sup{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\end{array}\right)$$

Then h is one of

$$\left(I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\right).$$

If we choose $h=I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)$ or $I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right),$ then

$$I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)$$

and so $k=I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right).$ Thus

$$\left(\begin{array}{c}sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\}=I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\\ =h>\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}.\end{array}\right).$$

Hence

$$\left(\begin{array}{c}\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ \notin (sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\\ sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}).\end{array}\right).$$

Now if $h=I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)$ then $I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)$ and so $sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\}.$ Assume $k=I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),$ then we have

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)& \le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)<\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ & <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right).\end{array}$$

So, we can write

$$\left(\begin{array}{c}{I}_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)<\\ \left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ =I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}\right).$$

For the case

$$\left(\begin{array}{c}{I}_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)\\ <\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ =I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}\right)$$

which contradicted the fact that $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in U. For the case

$$\left(\begin{array}{c}{I}_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)=\\ \left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}\right)$$

we have

$$\left(\begin{array}{c}\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ \notin (sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\})\\ =I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)=\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\end{array}\right).$$

Again, assume that $k=I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right),$ then we have

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)& \le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)<\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ & <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}$$

or

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)& \le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)=\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ & <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right).\end{array}$$

For the case

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)& \le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)<\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ & <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}$$

which contradict $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in U. For the case

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)& \le I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)=\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\\ & <I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\end{array}$$

we have

$$\begin{array}{ll}\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}& \notin \{((sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\}),\\ & (sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\})\}\end{array}$$

because

$$((sup\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\})=,I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)=\left\{N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}.$$

If $e_i=(e_3,x_3)\in \left(E_1\times X_1\right)-\left(E_2\times X_2\right)$ or if $e_i=(e_3,x_3)\in \left(E_2\times X_2\right)-\left(E_1\times X_1\right)$ then the result is trivial. Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is a $ENCSES$ in $U.$

4. The following example shows thatR-intersection of two$ENCSESs$need not be$ENCSESs$.

Example 7.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.3,0.4],[0.4,0.7],[0.5,0.6]),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}=(0.2,0.3,0.4)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.2,0.3],[0.3,0.5],[0.6,0.7]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.4,0.6,0.5)\}.$$

Now by Definition 20, we have $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)=({\left(NC\right)}_{S3}^E,E_3,X_3)$

$$({\left(NC\right)}_{S3}^E,E_3,X_3)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.2,0.3],[0.3,0.5],[0.6,0.7],N_{{\left(NC\right)}_{S3}^E\left(ei\right)}=(0.4,0.6,0.4)\}.$$

As $0.4\notin [0.2,0.3],0.6\notin [0.3,0.5]$ and $0.4\notin [0.6,0.7].$ Hence $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is not a $ENCSES$ in U.

The following theorem gives the condition that R-intersection of two $ENCSESs$ is also a $ENCSES$.

Theorem 5.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$ and$({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$\begin{array}{c}\{inf\{sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \\ <\left\{N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)\vee N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\hfill \\ \le \{sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \end{array}$$

for all $u\in U$ and $(g,z)\in (E_1\cap E_2\times X_1\cap X_2).$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is $ENCSESs$ in U.

Proof. 

Similar to the proof of Theorem 4.  □

5. The following example shows thatP-union of two$ENCSESs$need not to be a$ENCSES$.

Example 8.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.3,0.5],[0.4,0.7],[0.5,0.6]),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}=(0.6,0.8,0.4)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.2,0.3],[0.3,0.5],[0.6,0.7]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.4,0.6,0.5)\}.$$

Now by Definition 20, we have

$$({\left(NC\right)}_{S3}^E,E_3,X_3)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.3,0.5],[0.4,0.7],[0.5,0.6],N_{{\left(NC\right)}_{S3}^E\left(ei\right)}=(0.6,0.8,0.4)\}.$$

As $0.6\notin [0.3,0.5],0.8\notin [0.4,0.7]$ and $0.4\notin [0.5,0.6].$

Hence P-union of $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ is not $ENCSES$ in $U.$

The following theorem gives the condition under which P-union of two $ENCSESs$ is a $ENCSESs$.

Theorem 6.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1(=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$ and$({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$\begin{array}{c}sup\{inf\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \\ <\left\{N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)\vee N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\hfill \\ \le inf\{sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \end{array}$$

for all $e\in (A\cap A\times B\cap B)$ and $u\in U.$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ is a $ENCSES$ over $U.$

Proof. 

Similar to the proof of Theorems 2 and 4.  □

6. The following example shows thatP-intersection of two$ENCSESs$need not be a$ENCSES$.

Example 9.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$ where

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right)=\{I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N=([0.3,0.5],[0.4,0.7],[0.5,0.6]),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}=(0.6,0.8,0.4)\}$$

and

$$\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\{I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^N=([0.2,0.3],[0.3,0.5],[0.6,0.7]),N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}=(0.4,0.6,0.5)\}.$$

Now by Definition 20, we have

$$({\left(NC\right)}_{S3}^E,E_3,X_3)=\{I_{{\left(NC\right)}_{S3}^E\left(e_i\right)}^N=([0.2,0.3],[0.3,0.5],[0.6,0.7],N_{{\left(NC\right)}_{S3}^E\left(ei\right)}=(0.4,0.6,0.5)\}.$$

As $0.4\notin [0.2,0.3],0.6\notin [0.3,0.5]$ and $0.5\notin [0.6,0.7].$

Hence P-intersection of $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ is not $ENCSES$ in $U.$

Theorem 7.

Let ${\{{\left(NC\right)}_{Si}^E\}}_{i\in I}={\{({\left(NC\right)}_{Si}^E,E_i,X_i)\}}_{{}_{i\in I}}$ be a family of internal cubic soft expert set ($INCSESs$) sets over $U,$ $u\in U$ for any $e_i\in E_i,$ $x\in X_i\}$. Then ${\cup }_{P_{i\in I}}\{{\left(NC\right)}_{Si}^E\}$ and ${\cap }_{P_{i\in I}}\{{\left(NC\right)}_{Si}^E\}$ are internal cubic soft expert set ($INCSESs$) sets over $U.$

Proof. 

As ${\{{\left(NC\right)}_{Si}^E\}}_{i\in I}$ be a family of internal generalized cubic soft expert set ($INCSESs$) over U so we have $I_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right)\le N_{{\left(NC\right)}_{Si}^E(e,x)}\left(u\right)\le I_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right)$ for each $i\in I$ this implies that

$${\cup }_{P_{i\in I}}{I}_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right)\le {\cup }_{P_{i\in I}}{N}_{{\left(NC\right)}_{Si}^E(e,x)}\left(u\right)\le {\cup }_{P_{i\in I}}{I}_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right)$$

and

$${\cap }_{P_{i\in I}}{I}_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right)\le {\cap }_{P_{i\in I}}{N}_{{\left(NC\right)}_{Si}^E(e,x)}\left(u\right)\le {\cap }_{P_{i\in I}}{I}_{{\left(NC\right)}_{Si}^E(e,x)}^{N-}\left(u\right).$$

Hence $\underset{i\in I}{{\cup }_p}\{{\left(NC\right)}_{Si}^E\}$ and $\underset{i\in I}{{\cap }_p}\{{\left(NC\right)}_{Si}^E\}$ are ($INCSESs$) over U.  □

Theorem 8.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$

and $({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$\begin{array}{c}sup\{inf\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \\ <\left\{N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)\wedge N_{{\left(NC\right)}_{S2}^E\left(e_i\right)}\left(u\right)\right\}\hfill \\ \le inf\{sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup{I}_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\hfill \end{array}$$

for all $e\in (A\cap A\times B\cap B)$ and $u\in U.$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X_2)$ is also an $ENCSESs$ and $INCSESs$ over $U.$

Proof. 

Similar to the proof of Theorems 2 and 4.  □

Theorem 9.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ be two $ENCSESs$ in $U,$

where $({\left(NC\right)}_{S1}^E,E_1,X_1)=\left\{{\left(NC\right)}_{S1}^E(e,x)=\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\right\}$ and

$({\left(NC\right)}_{S2}^E,E_2,X_2)=\left\{{\left(NC\right)}_{S2}^E(f,y)=\{⟨u,I_{2(f,y)}^N\left(u\right),N_{2(f,y)}\left(u\right)⟩,u\in U\},(f,y)\in E_2\times X_2\right\}$ such that

$$\left(N_{{\left(NC\right)}_S^E\left(e_{i}x\right)}\vee N_{{}_{{\left(NC\right)}_{S2}^E\left(e_i\right)}}\right)\left(u\right)\in \left\{\begin{array}{c}inf\{sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},sup\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\},\\ \{inf\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N-}\left(u\right)\},inf\{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S2}^E\left(e_i\right)}^{N+}\left(u\right)\}\}\end{array}\right.$$

for all $e\in (A\cap A\times B\cap B)$ and $u\in U.$ Then $({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2)$ is a $ENCSES$ and $INCSES$ over $U.$

Proof. 

Similar to the proof of Theorems 2 and 4.  □

Theorem 10.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$, and $({\left(NC\right)}_{S2}^E,E_2,X_2),$ be any two NCSESs in $U.$ Then

(i) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_P(({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P({\left(NC\right)}_{S2}^E,E_2,X_2))=({\left(NC\right)}_{S1}^E,E_1,X_1)$,

(ii) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_P(({\left(NC\right)}_{S2}^E,E_2,X_2){\cup }_P({\left(NC\right)}_{S2}^E,E_2,X_2))=({\left(NC\right)}_{S1}^E,E_1,X_1),$

(iii) 

$(({\left(NC\right)}_{S1}^E,E_1,X_1){\cup }_R(({\left(NC\right)}_{S2}^E,E_2,X_2)){\cap }_R({\left(NC\right)}_{S2}^E,E_2,X_2))=({\left(NC\right)}_{S1}^E,E_1,X_1)$,

(iv) 

$({\left(NC\right)}_{S1}^E,E_1,X_1){\cap }_R(({\left(NC\right)}_{S2}^E,E_2,X_2){\cup }_R({\left(NC\right)}_{S2}^E,E_2,X_2))=({\left(NC\right)}_{S1}^E,E_1,X_1).$

Proof. 

The proof is straightforward.  □

Next we define some more operations on NCSESs.

Definition 21.

For two neutrosophic cubic soft expert sets ($NCSESs$) $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, P-AND is denoted as

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\displaystyle \underset{P}{\bigwedge }}\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right),$$

where

$$\begin{array}{ll}\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right)& ={\left(NC\right)}_{S3}^E((e,f),(x,y))\\ & ={\left(NC\right)}_{S1}^E(e,x){\cap }_P{\left(NC\right)}_{S2}^E(f,y)\\ & =\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\}\\ and\{⟨u,I_{2(e,x)}^N\left(u\right),N_{2(e,x)}\left(u\right)⟩,u& \in U\},(e,x)\in E_1\times X_1\}.\end{array}$$

Definition 22.

For any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, R-AND is denoted as

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\displaystyle \underset{R}{\bigwedge }}\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right),$$

where

$$\begin{array}{ll}\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right)& ={\left(NC\right)}_{S3}^E((e,f),(x,y))={\left(NC\right)}_{S1}^E(e,x){\cap }_R{\left(NC\right)}_{S2}^E(f,y)\\ & =\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\}\\ and\{⟨u,I_{2(e,x)}^N\left(u\right),N_{2(e,x)}\left(u\right)⟩,u& \in U\},(e,x)\in E_1\times X_1\}.\end{array}$$

Definition 23.

For any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, P-OR is denoted as

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\displaystyle \underset{P}{\bigvee }}\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right),$$

where

$$\begin{array}{ll}\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right)& ={\left(NC\right)}_{S3}^E((e,f),(x,y))={\left(NC\right)}_{S1}^E(e,x){\cap }_R{\left(NC\right)}_{S2}^E(f,y)\\ & =\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\}\\ and\{⟨u,I_{2(e,x)}^N\left(u\right),N_{2(e,x)}\left(u\right)⟩,u& \in U\},(e,x)\in E_1\times X_1\}.\end{array}$$

Definition 24.

For any two $NCSESs$ $({\left(NC\right)}_{S1}^E,E_1,X_1)$ and $({\left(NC\right)}_{S2}^E,E_2,X_2)$ over U, R-OR is denoted as

$$\left({\left(NC\right)}_{S1}^E,E_1,X_1\right){\displaystyle \underset{R}{\bigvee }}\left({\left(NC\right)}_{S2}^E,E_2,X_2\right)=\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right),$$

where

$$\begin{array}{ll}\left({\left(NC\right)}_{S3}^E,(E_1\times E_2),(X_1\times X_2)\right)& ={\left(NC\right)}_{S3}^E((e,f),(x,y))={\left(NC\right)}_{S1}^E(e,x){\cap }_R{\left(NC\right)}_{S2}^E(f,y)\\ & =\{⟨u,I_{1(e,x)}^N\left(u\right),N_{1(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E_1\times X_1\}\\ and\{⟨u,I_{2(e,x)}^N\left(u\right),N_{2(e,x)}\left(u\right)⟩,u& \in U\},(e,x)\in E_1\times X_1\}.\end{array}$$

Theorem 11.

Let $({\left(NC\right)}_{S1}^E,E_1,X_1)$, be a neutrosophic cubic soft expert sets in $U.$ If $({\left(NC\right)}_{S1}^E,E_1,X_1)$, is an $INCSESs$ (resp., $ENCSESs$). Then ${({\left(NC\right)}_{S1}^E,E_1,X_1)}^C$ is $INCSESs$ (resp., $ENCSESs$) respectively.

Proof. 

Since $({\left(NC\right)}_{S1}^E,E_1,X_1)$, is an $INCSESs$ (resp., $ENCSESs$) in $U,$ so for any $e\in E_1$ we have ${\left(NC\right)}_{S1}^E\left(e\right)=\{⟨x,I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^N\left(x\right),N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)⟩:u\in U\}.$ As

$$\begin{array}{ll}{I}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right)& \le N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\le I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\\ & \Rightarrow 1-I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right)\le 1-N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\le 1-I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right).\end{array}$$

Hence ${({\left(NC\right)}_{S1}^E,E_1,X_1)}^C$ is an $INCSES$. Also

$$\begin{array}{ll}{N}_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)& \notin (I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right))\forall u\in U\\ & \Rightarrow (1-N_{{\left(NC\right)}_{S1}^E\left(e_i\right)}\left(u\right)\notin (1-I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N+}\left(u\right),1-I_{{\left(NC\right)}_{S1}^E\left(e_i\right)}^{N-}\left(u\right))\end{array}$$

Hence ${({\left(NC\right)}_{S1}^E,E_1,X_1)}^C$ is an $ENCSES$.  □

5. Applications

In this section, we use NCSESs to construct an algorithm and applied it to a decision-making problem. The series between Pakistan and India remains a hot cake for cricket lovers and this cricket rivalry existed between them at the start of partition. The first series between the two teams took place in 1951–52, when Pakistan made a tour of India. India made a tour of Pakistan for the first time in 1954–55. Between 1962 and 1977, no cricket was played between the two countries owing to two major wars in 1965 and 1971. The 1999 Kargil War and the 2008 Mumbai terrorist attacks have also interrupted the game of cricket between the two nations. The growth of large expatriate populations from India and Pakistan across the world led to neutral venues such as the United Arab Emirates and Canada hosting several bilateral and multilateral ODI series involving the two teams. Tickets for The India-Pakistan match in the 2015 World Cup in Australia sold out in 12 min at the ticket counters.

We try to use NCSESs in India–Pakistan cricket rivalry to conclude which country is suffering more from the above mentioned conflicts.

For this we first define the neutrosophic cubic soft expert weight average operator ($NCSEWAO$) and score function.

Definition 25.

Let $({\left(NC\right)}_S^E,E,X)=\left\{{\left(NC\right)}_S^E(e,x)=\{⟨u,I_{(e,x)}^N\left(u\right),N_{(e,x)}\left(u\right)⟩,u\in U\},(e,x)\in E\times X\right\}$ be a $NCSESs$. Then neutrosophic cubic soft expert weight average operator ($NCSEWAO$) is denoted and define as

$$\begin{array}{c}{\mathbb{Q}}_{w_i}(I_{{\left(NC\right)}_S^E\left(e_i\right)}^N\left(x\right),N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(x\right))\hfill \\ =\left(\begin{array}{c}\left[\begin{array}{c}\frac{{\displaystyle \prod _{i=1}^n}\left(1+I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}{\left(u\right)}^{w_i}\right)-{\displaystyle \prod _{i=1}^n}\left(1-I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}{\left(u\right)}^{w_i}\right)}{{\displaystyle \prod _{i=1}^n}\left(1+I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}{\left(u\right)}^{w_i}\right)+{\displaystyle \prod _{i=1}^n}\left(1-I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}{\left(u\right)}^{w_i}\right)},\\ \frac{{\displaystyle \prod _{i=1}^n}\left(1+I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}{\left(u\right)}^{w_i}\right)-{\displaystyle \prod _{i=1}^n}\left(1-I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}{\left(u\right)}^{w_i}\right)}{{\displaystyle \prod _{i=1}^n}\left(1+I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}{\left(u\right)}^{w_i}\right)+{\displaystyle \prod _{i=1}^n}\left(1-I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}{\left(u\right)}^{w_i}\right)}\end{array}\right],\\ {\displaystyle \prod _{i=1}^n}\{N_{{\left(NC\right)}_S^E\left(e_i\right)}{\left(u\right)}^{w_i}\}\end{array}\right)\hfill \end{array}$$

where $w_i$ is the weight of expert opinion, $w_i\in [0,1]$ and ${\displaystyle \sum _{i=1}^n}{w}_i=1.$

Definition 26.

Let ${\left(NC\right)}_S^E=⟨\left[I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right),I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right)\right],N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)⟩$ be neutrosophic cubic soft expert value. A score function Q of ${\left(NC\right)}_S^E$ is defined as $Q({\left(NC\right)}_S^E)=\frac{I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N-}\left(u\right)+I_{{\left(NC\right)}_S^E\left(e_i\right)}^{N+}\left(u\right)-N_{{\left(NC\right)}_S^E\left(e_i\right)}\left(u\right)}{9}$, where $Q({\left(NC\right)}_S^E)\in [-3,3].$

Decision-making problems have been studied using fuzzy soft sets. Now, we are going to present multicriteria neutrosophic cubic soft set in decision-making along with weights and score function. For this we propose the following algorithmic steps as pictured in Figure 1.

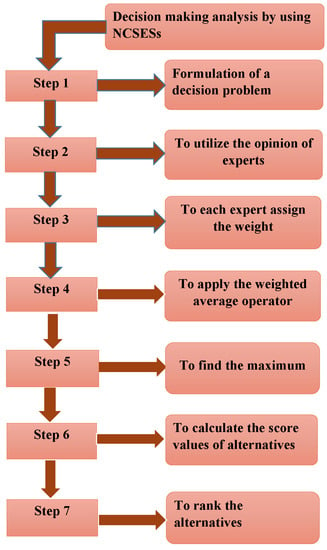
Figure 1. Flow chart of NCSESs based on MADM Problem.

Step 1: Define a decision problem by inputting the neutrosophic cubic soft expert set ${\left(NC\right)}_S^E(e_i,x_i).$

Step 2: Use the opinions of experts in the form of $NCSESs$ to determine the opinions regarding given criteria. Make a separate table for the opinion of each expert.

Step 3: Assign weight to each expert according to their expertise.

Step 4: Apply neutrosophic cubic soft expert weighted average operator to each above table and find the neutrosophic cubic soft expert weighted average corresponding to each attribute.

Step 5: Calculate the ${\displaystyle \underset{P}{\bigvee }}$ of $U_j.$

Step 6: Calculate the score of each $U_j.$

Step 7: Generate the non-increasing order of all the alternatives according to their scores.

Example 10.

Let $U=\left\{u_1=India,u_2=Pakistan\right\}$ be the set of countries playing a cricket series, $E=\{e_1=$ Pakistan Cricket Board (PCB), $e_2=$ The Board of Control for Cricket in India (BCCI), $e_3=$ Bilateral relations between Pakistan and India} be the set of factors affecting the series, $X=\left\{p,q,r\right\}$ be the set of experts giving their expert opinion. The expert may consider the most burning parameter as “ICC’s Future Tours Programme (FTP)” when they are giving their opinion by considering three times of frames as past, present, and future.

Step 1: After a serious discussion, the committee constructed the following neutrosophic cubic soft expert set.

$$\begin{array}{cc}\hfill {\left(NC\right)}_S^E(e_1,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.7\right],\left[0.2,0.4\right],\left[0.1,0.4\right],0.8,0.5,0.6\right),\\ \left(u_{2,}\left[0.4,0.6\right],\left[0.3,0.5\right],\left[0.6,0.8\right],0.7,0.2,0.4\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_3,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.4,0.4,0.5\right),\\ \left(u_{2,}\left[0.1,0.3\right],\left[0.6,0.8\right],\left[0.4,0.6\right],0.6,0.5,0.3\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.4,0.4,0.5\right),\\ \left(u_{2,}\left[0.1,0.3\right],\left[0.6,0.8\right],\left[0.4,0.6\right],0.6,0.5,0.3\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.7\right],\left[0.3,0.4\right],\left[0.6,0.8\right],0.8,0.7,0.5\right),\\ \left(u_{2,}\left[0.3,0.5\right],\left[0.7,0.8\right],\left[0.6,0.7\right],0.6,0.5,0.8\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_3,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_1,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.7\right],\left[0.3,0.4\right],\left[0.6,0.8\right],0.8,0.7,0.5\right),\\ \left(u_{2,}\left[0.3,0.5\right],\left[0.7,0.8\right],\left[0.6,0.7\right],0.6,0.5,0.8\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_2,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill {\left(NC\right)}_S^E(e_3,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \end{array}$$

Step 2: Opinion of expert p

$$\begin{array}{cc}\hfill (e_1,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill (e_2,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.7\right],\left[0.2,0.4\right],\left[0.1,0.4\right],0.8,0.5,0.6\right),\\ \left(u_{2,}\left[0.4,0.6\right],\left[0.3,0.5\right],\left[0.6,0.8\right],0.7,0.2,0.4\right),\end{array}\right\}\hfill \\ \hfill (e_3,p)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.4,0.4,0.5\right),\\ \left(u_{2,}\left[0.1,0.3\right],\left[0.6,0.8\right],\left[0.4,0.6\right],0.6,0.5,0.3\right),\end{array}\right\}\hfill \end{array}$$

Opinion of expert q

$$\begin{array}{cc}\hfill (e_1,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.5,0.8\right],\left[0.1,0.3\right],\left[0.1,0.4\right],0.4,0.4,0.5\right),\\ \left(u_{2,}\left[0.1,0.3\right],\left[0.6,0.8\right],\left[0.4,0.6\right],0.6,0.5,0.3\right),\end{array}\right\}\hfill \\ \hfill (e_2,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.7\right],\left[0.3,0.4\right],\left[0.6,0.8\right],0.8,0.7,0.5\right),\\ \left(u_{2,}\left[0.3,0.5\right],\left[0.7,0.8\right],\left[0.6,0.7\right],0.6,0.5,0.8\right),\end{array}\right\}\hfill \\ \hfill (e_3,q)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \end{array}$$

Opinion of expert r

$$\begin{array}{cc}\hfill (e_1,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.6,0.7\right],\left[0.3,0.4\right],\left[0.6,0.8\right],0.8,0.7,0.5\right),\\ \left(u_{2,}\left[0.3,0.5\right],\left[0.7,0.8\right],\left[0.6,0.7\right],0.6,0.5,0.8\right),\end{array}\right\}\hfill \\ \hfill (e_2,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \\ \hfill (e_3,r)& =\left\{\begin{array}{c}\left(u_{1,}\left[0.4,0.6\right],\left[0.2,0.5\right],\left[0.1,0.5\right],0.3,0.1,0.7\right),\\ \left(u_{2,}\left[0.6,0.7\right],\left[0.5,0.6\right],\left[0.6,0.8\right],0.8,0.7,0.9\right),\end{array}\right\}\hfill \end{array}$$

Step 3: Let $w=(0.5,0.25,0.25)$ be the weight vector assigned to the experts $p,q$ and r respectively.

Step 4: The neutrosophic cubic soft expert weighted average (NCSEWA) of each attribute is displayed in Table 1.

Table 1. NCSEWA of each attribute.

	${\mathit{u}}_1$	${\mathit{u}}_2$
$e_1$	$\left(\begin{array}{c}(\left[0.009,0.051\right],[0.77,0.87],\\ [0.61,0.90]),\\ (0.41,0.15,0.58)\end{array}\right)$	$\left(\begin{array}{c}(\left[0.97,0.98\right],[0.98,0.99],\\ [0.98,0.99]),\\ (0.52,0.14,0.19)\end{array}\right)$
$e_2$	$\left(\begin{array}{c}\left(\right[0.66,0.75],[0.40,0.49],\\ [0.54,0.80]),\\ (0.46,0.028,0.048)\end{array}\right)$	$\left(\begin{array}{c}\left(\begin{array}{c}[0.78,0.99],[0.57,0.86],\end{array}\right),\\ [0.80,0.99]\\ \left(0.68,0.47,0.34\right)\end{array}\right)$
$e_3$	$\left(\begin{array}{c}\left(\right[0.34,0.671],[0.80,0.99],\\ [0.23,0.71]),\\ (0.95,0.92,0.91)\end{array}\right)$	$\left(\begin{array}{c}\left(\right[0.43,0.67],[0.76,0.98],\\ [0.34,0.61]),\\ (0.25,0.32,0.51)\end{array}\right)$

Step 5: Calculate the ${\displaystyle \underset{P}{\bigvee }}$ of the first and second columns of Table 1 by using Definition 23. Thus we have

$$\begin{array}{cc}\hfill U_1& ={\displaystyle \underset{j=1}{\overset{3}{\bigvee }}}=\left([0.66,0.75],[0.80,0.99],[0.61,0.90],(0.95,0.92,0.91)\right)\hfill \\ \hfill U_2& ={\displaystyle \underset{j=1}{\overset{3}{\bigvee }}}=\left(\left[0.97,0.99\right],[0.98,0.99],[0.98,0.99],(0.68,0.47,0.51)\right)\hfill \end{array}$$

Step 6: Using Definition 26, we have $Q\left(u_1\right)=0.2244,$$Q\left(u_2\right)=0.4711$.

Step 7: The score of the $NCSESs$ values corresponding to ${\displaystyle \underset{P}{\bigvee }}$ of $U_j$ implies the following order $u_2>u_1$.

Thus, we can conclude that the country $u_2=$ Pakistan is affected more by the factors, $e_1=$ PCB, $e_2=$ BCCI, $e_3=$ Bilateral relations between Pakistan and India.

6. Comparison Analysis

In this paper, we extend the concept of soft expert sets to neutrosophic cubic soft expert sets. This new idea generalizes the different types of expert sets presented by Alkhazaleh and Salleh [33,36], Broumi and Smarandache [40], Qayyum et al. [48] and Sahin et al. [43].

1. If we consider only truth part or indeterminacy part or falsity part, then our model and the model presented by Qayyum et al. [48] coincides with each other.

2. Since NCSESs consists of interval neutrosophic soft expert soft sets and neutrosophic soft expert sets and if we consider only the part containing the neutrosophic soft expert sets then our model reduces to the model presented by Sahin et al. [43].

3. If we consider the part containing the interval neutrosophic soft expert soft sets, we get a special class of soft expert sets.

4. Similarly imposing some extra conditions to our model it will reduce it to those models presented by Alkhazaleh and Salleh [33,36], Broumi and Smarandache [40].

7. Conclusions

The model of NCSESs can be used in many decision-making problems and it will produce more reliable results as compared to the previously defined versions of soft expert sets. This paper is of introductory nature where we establish this new generalized theory of soft expert sets with its basic properties and provide an application. In future we shall apply this model to other areas to illustrate its novelty. We have defined different operations of NCSESs including different versions of NCSESs. We have designed aggregation operators and score functions of neutrosophic cubic soft expert value. We have also constructed an algorithm based on this new concept and applied the developed approach to a numerical example.

The substantial impact of our outcome for the research field is that we gave a generalized form of soft expert system which certainly improves the decision-making theory due to its wide range of values in the form of truth, indeterminacy, and falsity. We have not used any software for the decision-making, since the preliminary research is on a small scale. We intend to expand the research to a larger scale on an applied problem so that we can develop a software and related interface. We also intend to apply the developed approach to a variety of games, signature theory and others, since the nature of NCSESs enables us to deal with vague and inconsistent data. In decision-making theory, we often deal with data which are inconsistent and vague. Thus, ex-ante decision-making problems can also be handled easily through NCSESs. In future, arguments and modern theories linked to behavioral patterns could strengthen the idea of NCSESs, especially using aggregation operators and methods that effectively deal with the uncertainty and inaccuracy of the input data [49].