Toward Self-Driving Bicycles Using State-of-the-Art Deep Reinforcement Learning Algorithms
Abstract
1. Introduction
2. Background
2.1. Reinforcement Learning and Policy Gradient Based Method
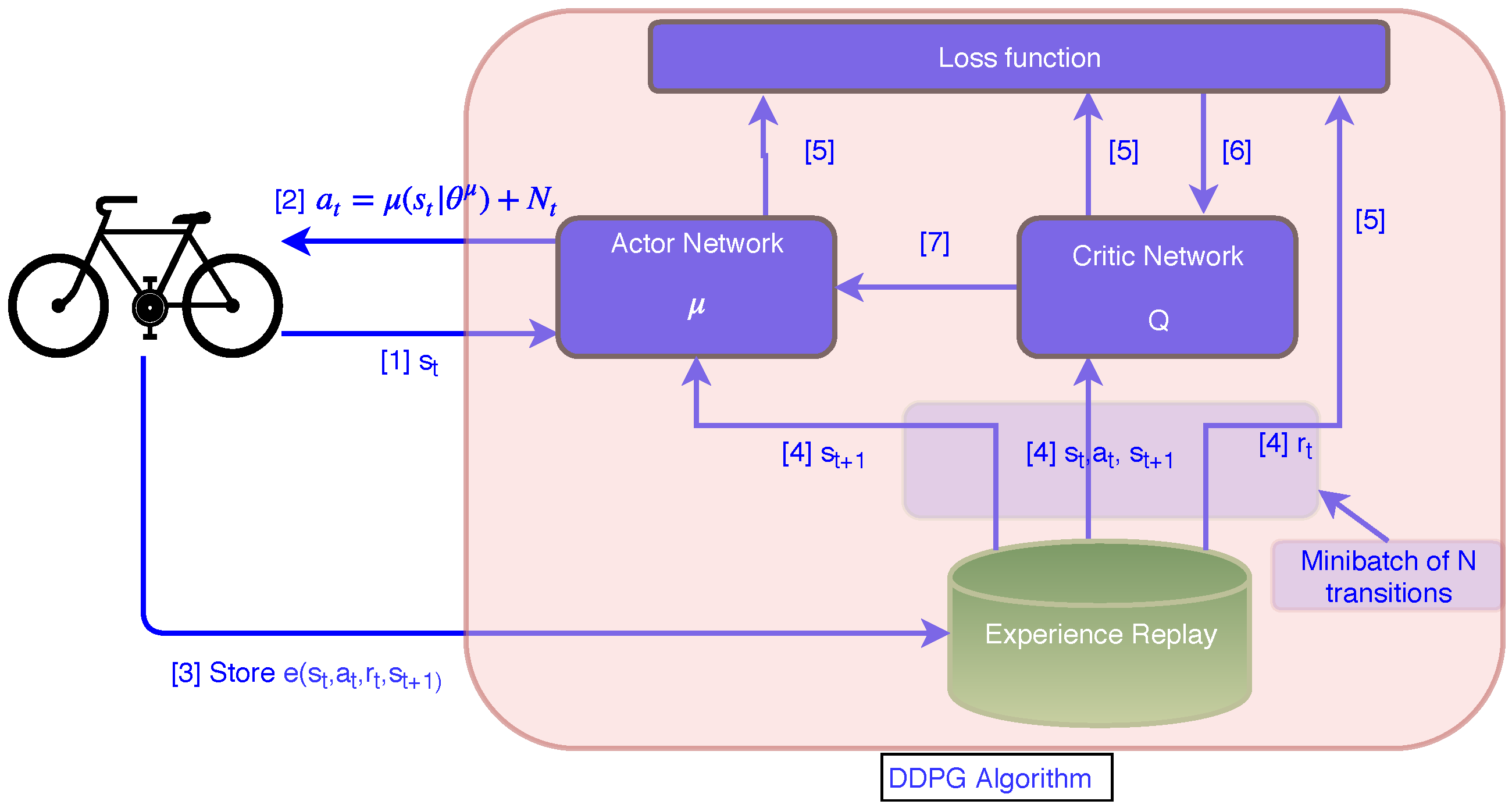
2.2. Deep Deterministic Policy Gradient Algorithm
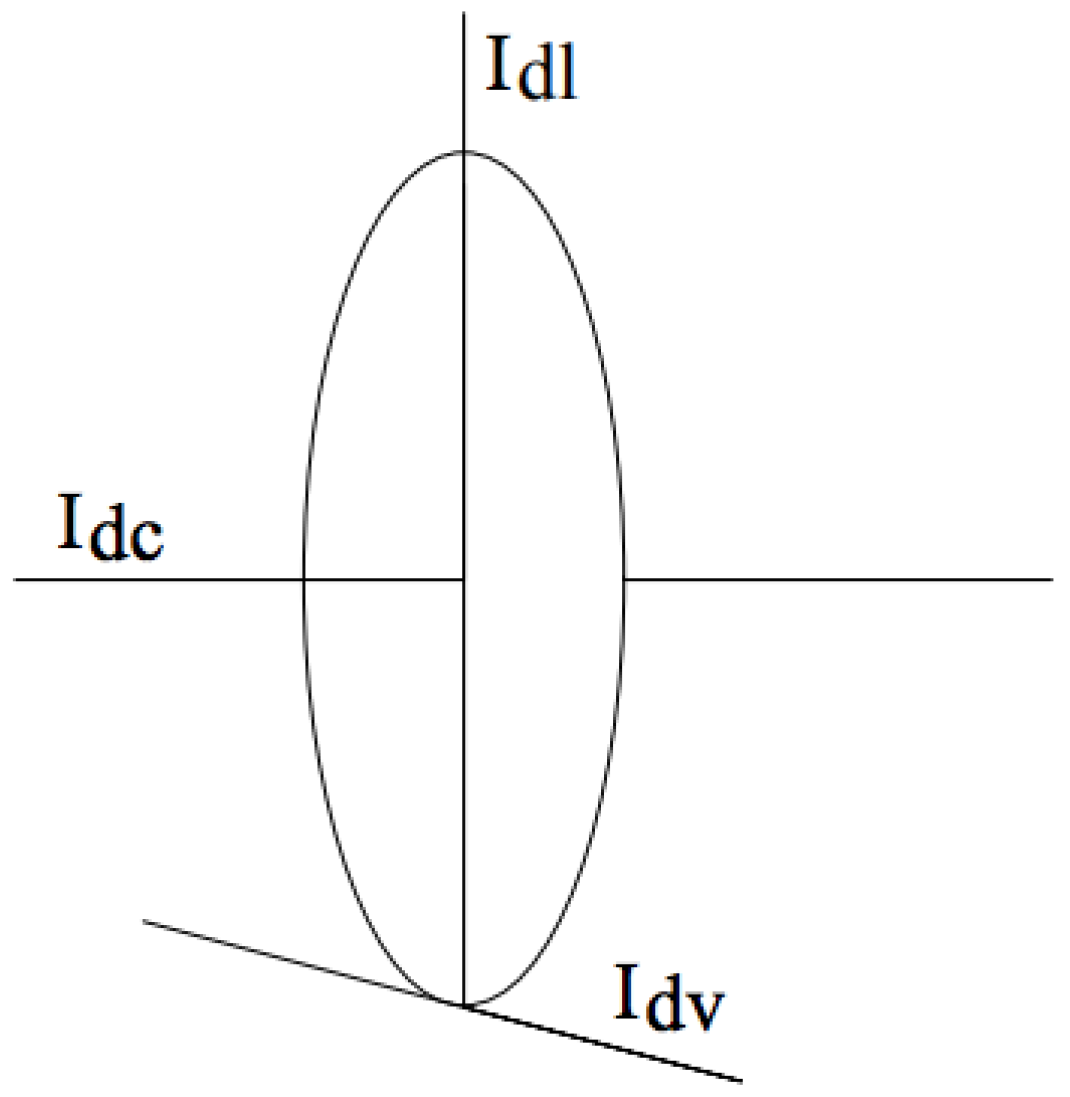
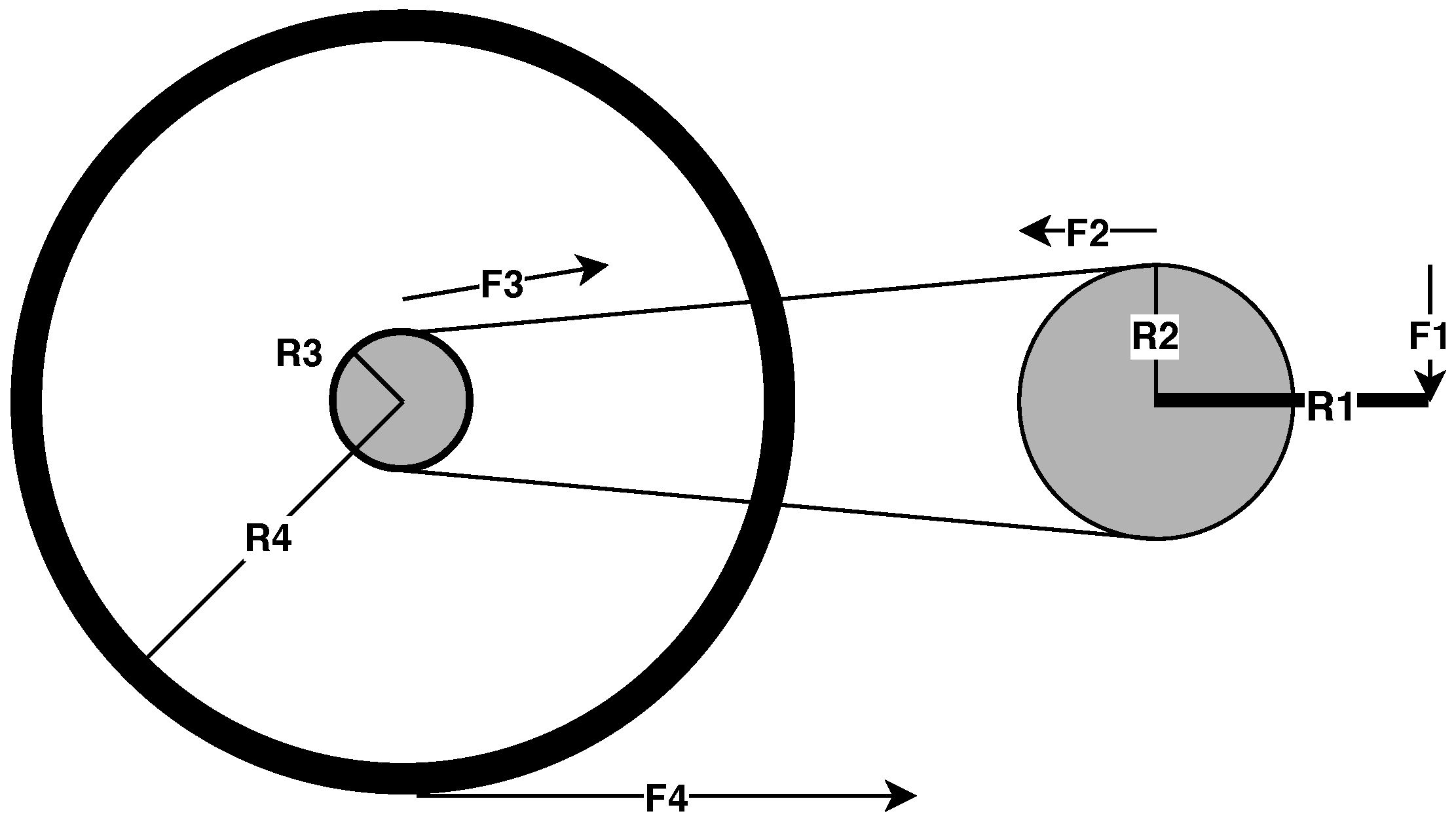
3. Extended Bicycle Dynamics
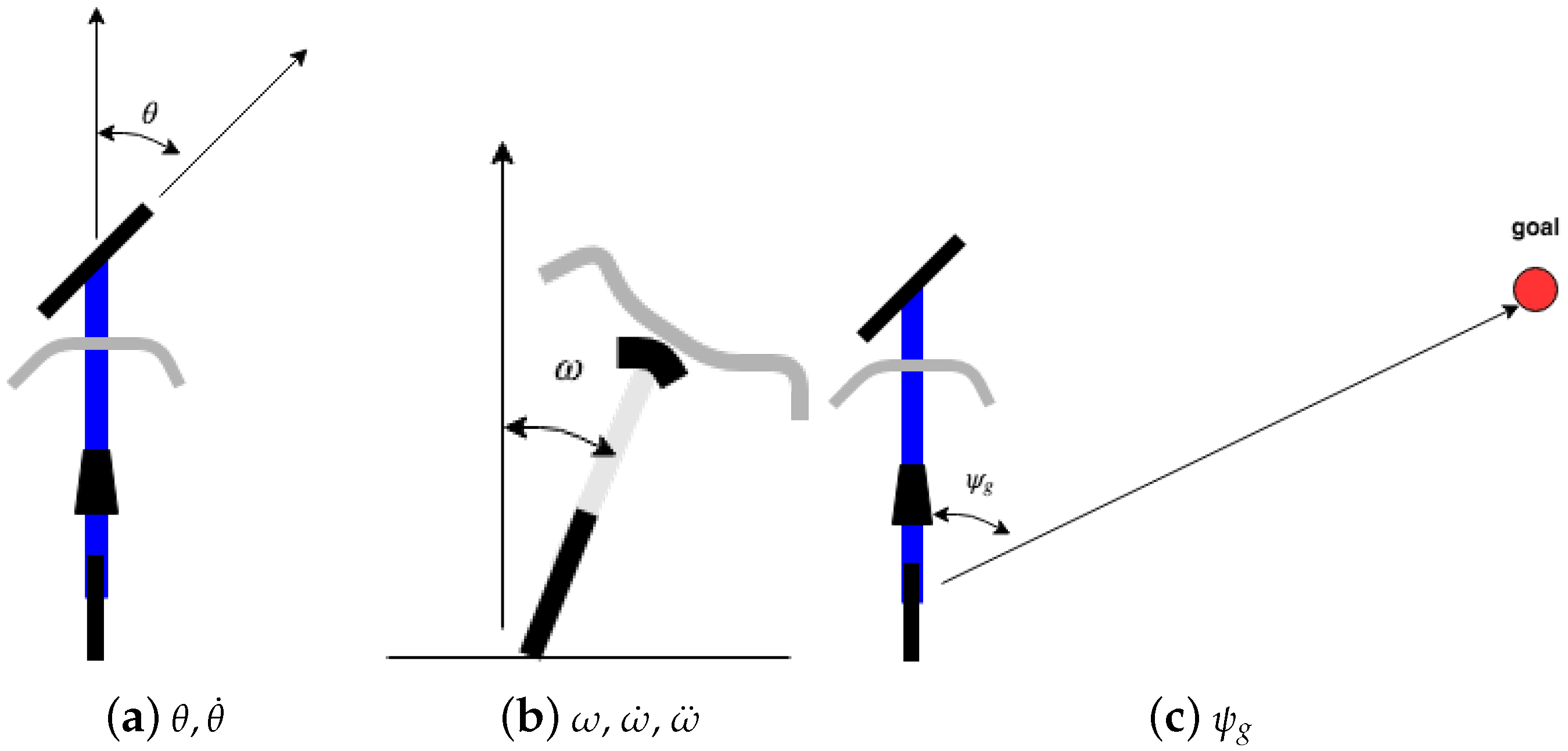
4. Method to Control Bicycle
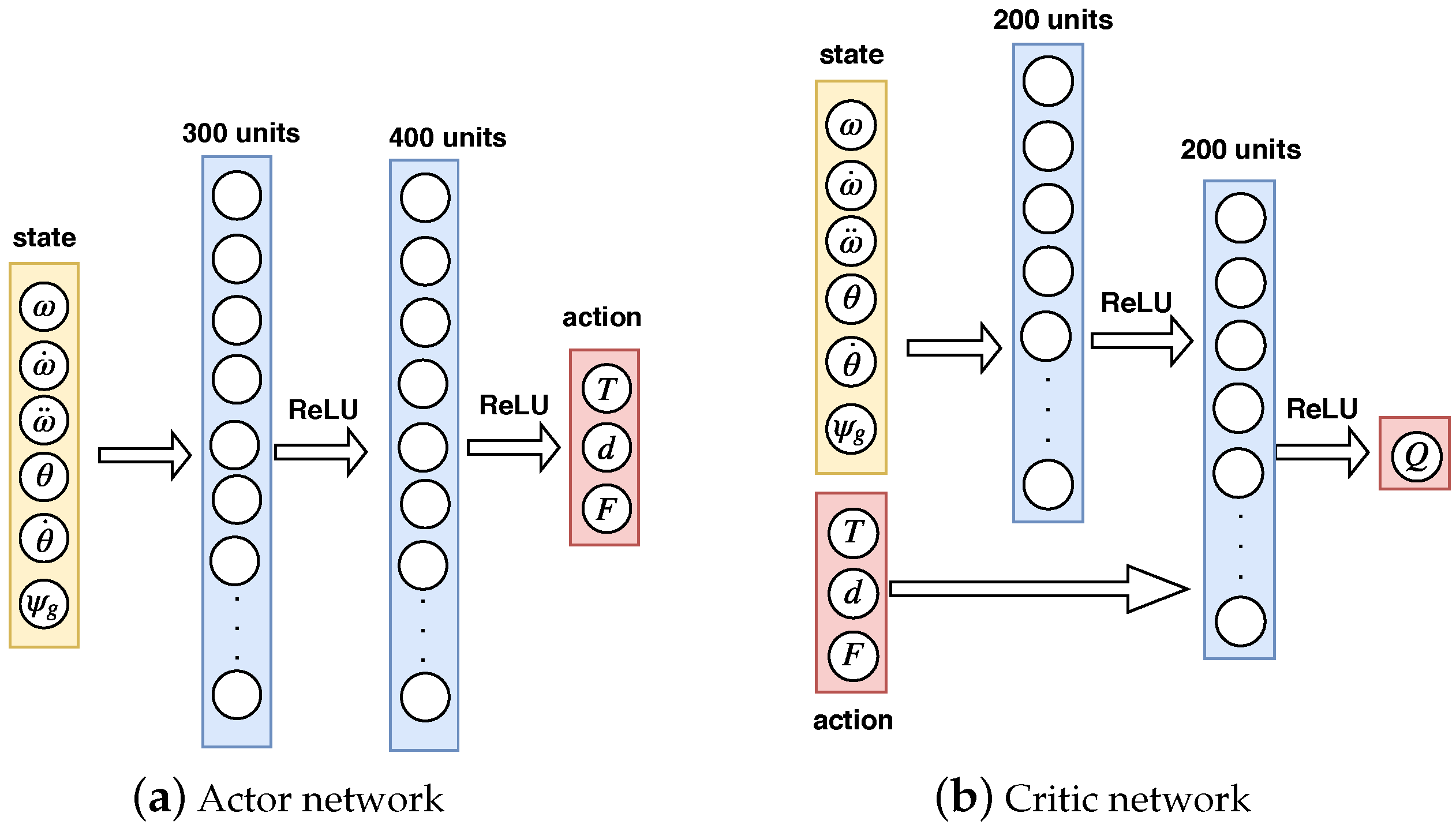
4.1. Network Structure
4.2. Network Training
4.3. Learning Process
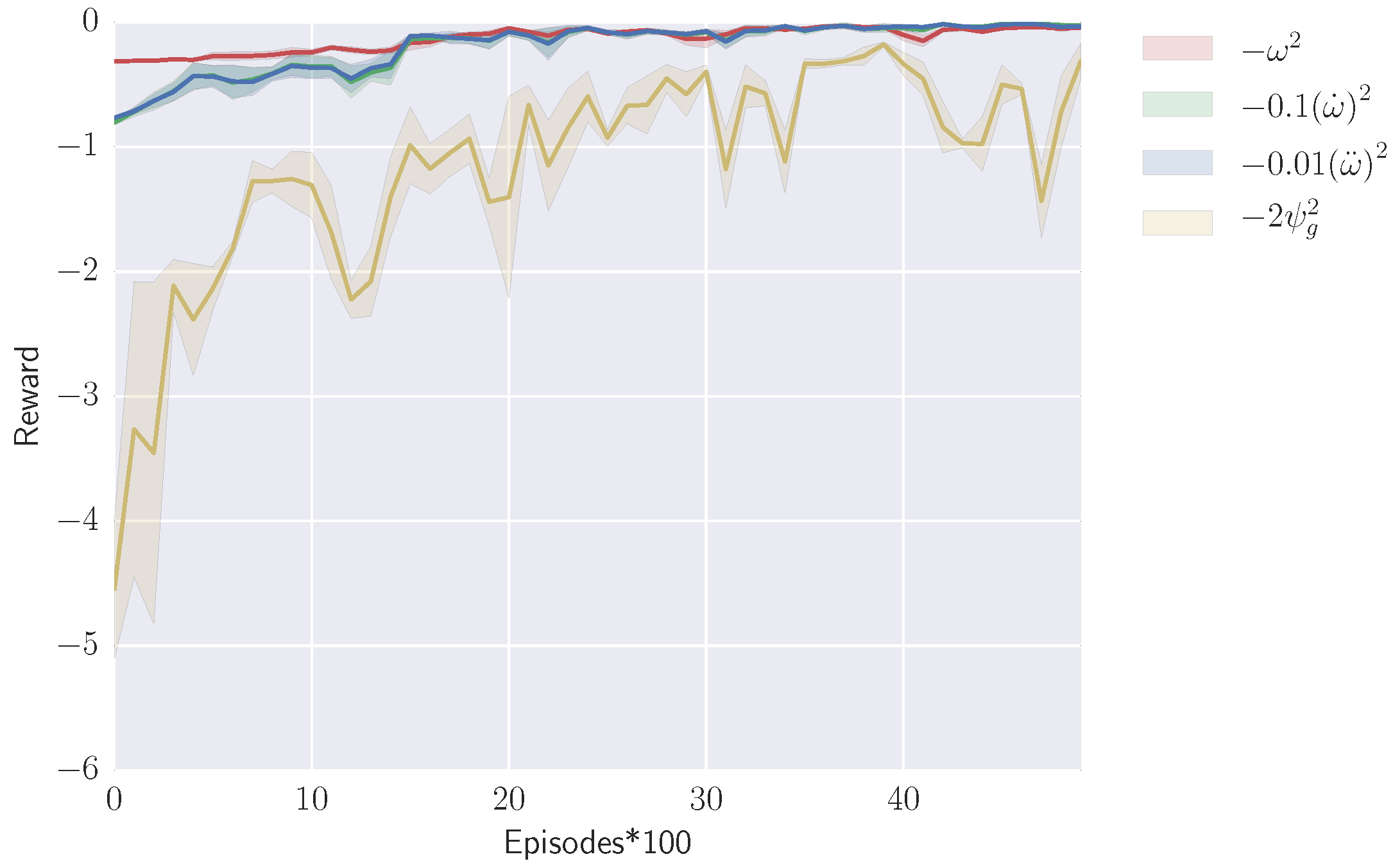
4.4. Reward Function
5. Experiments
5.1. Settings
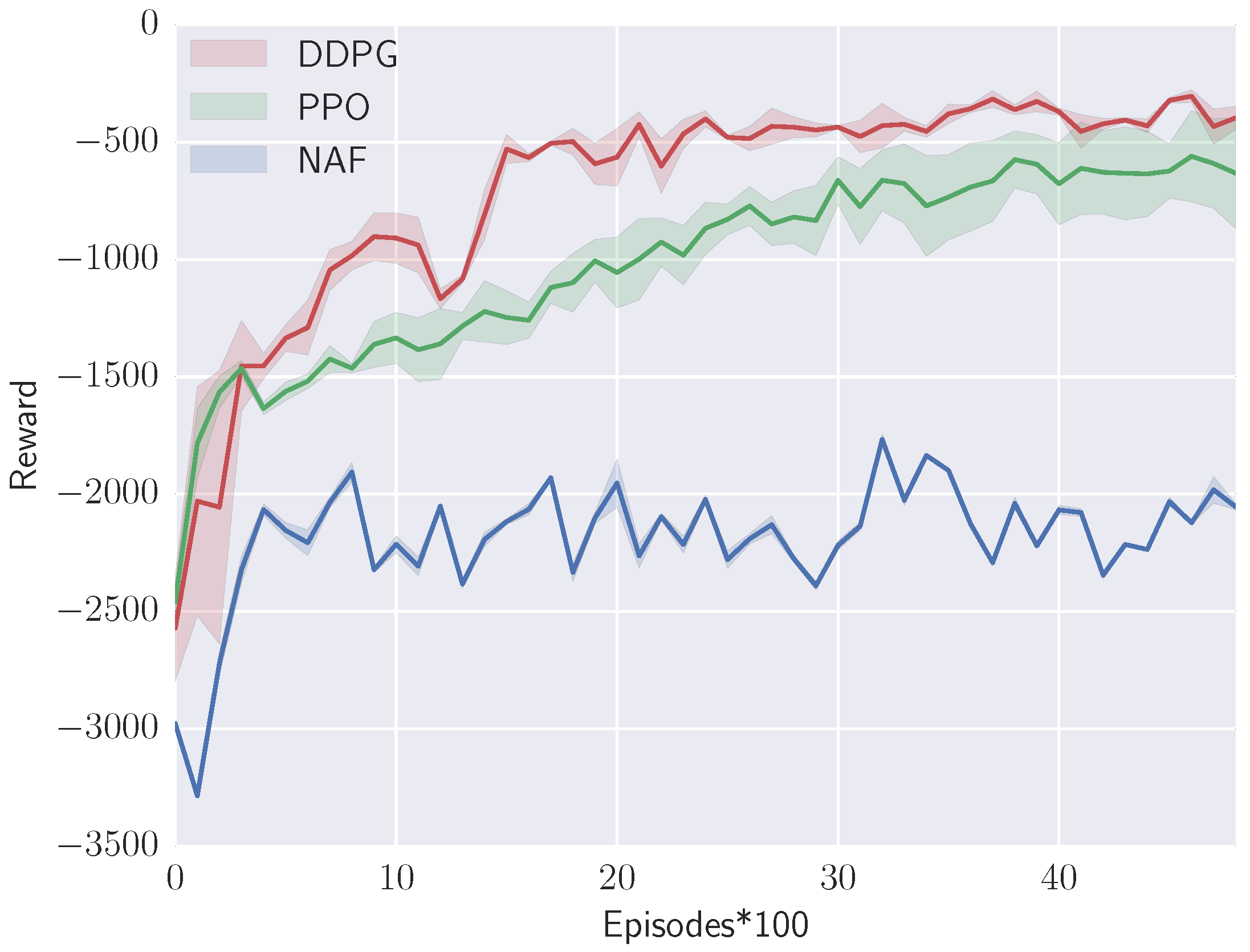
5.2. Baselines
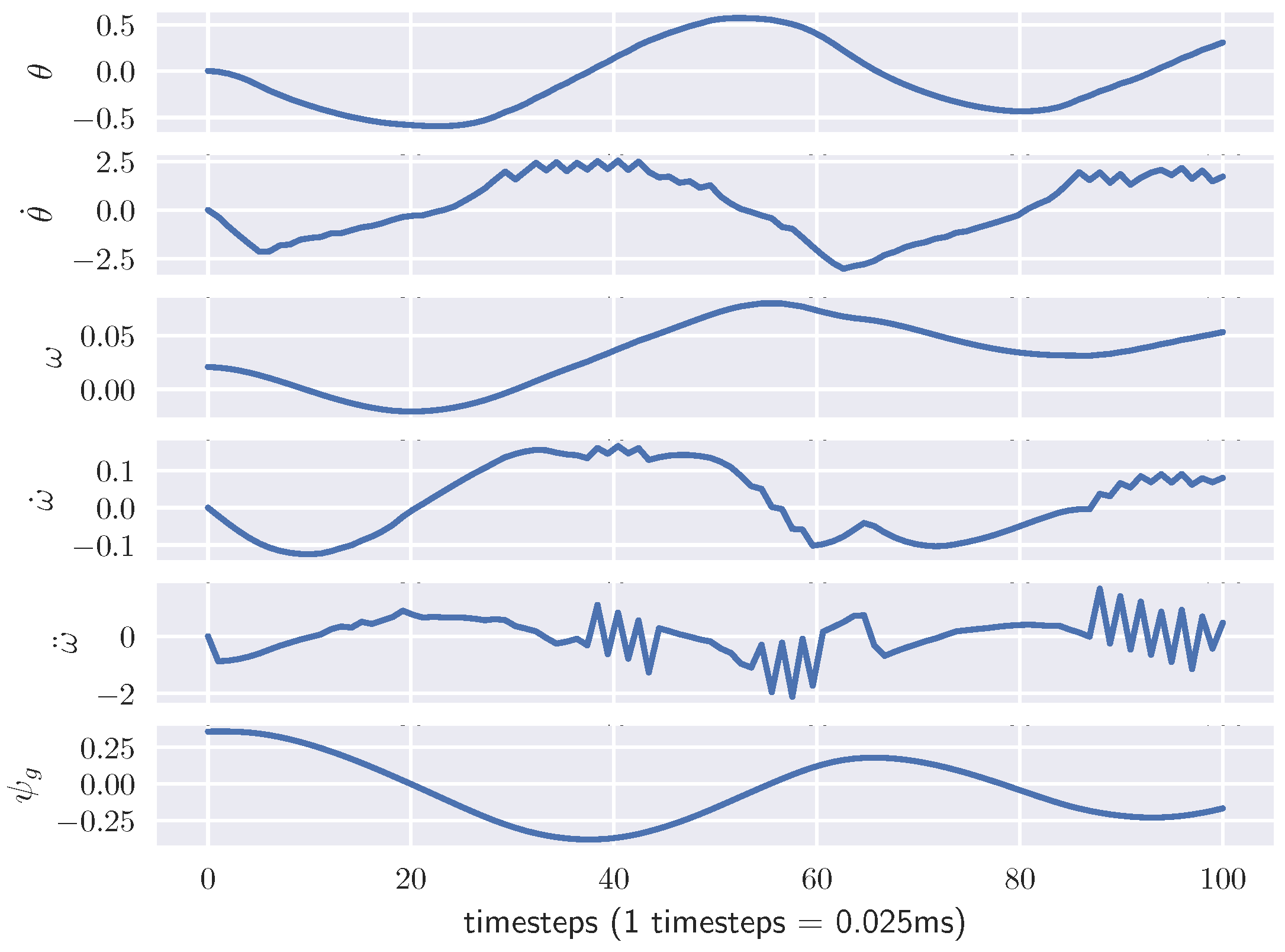
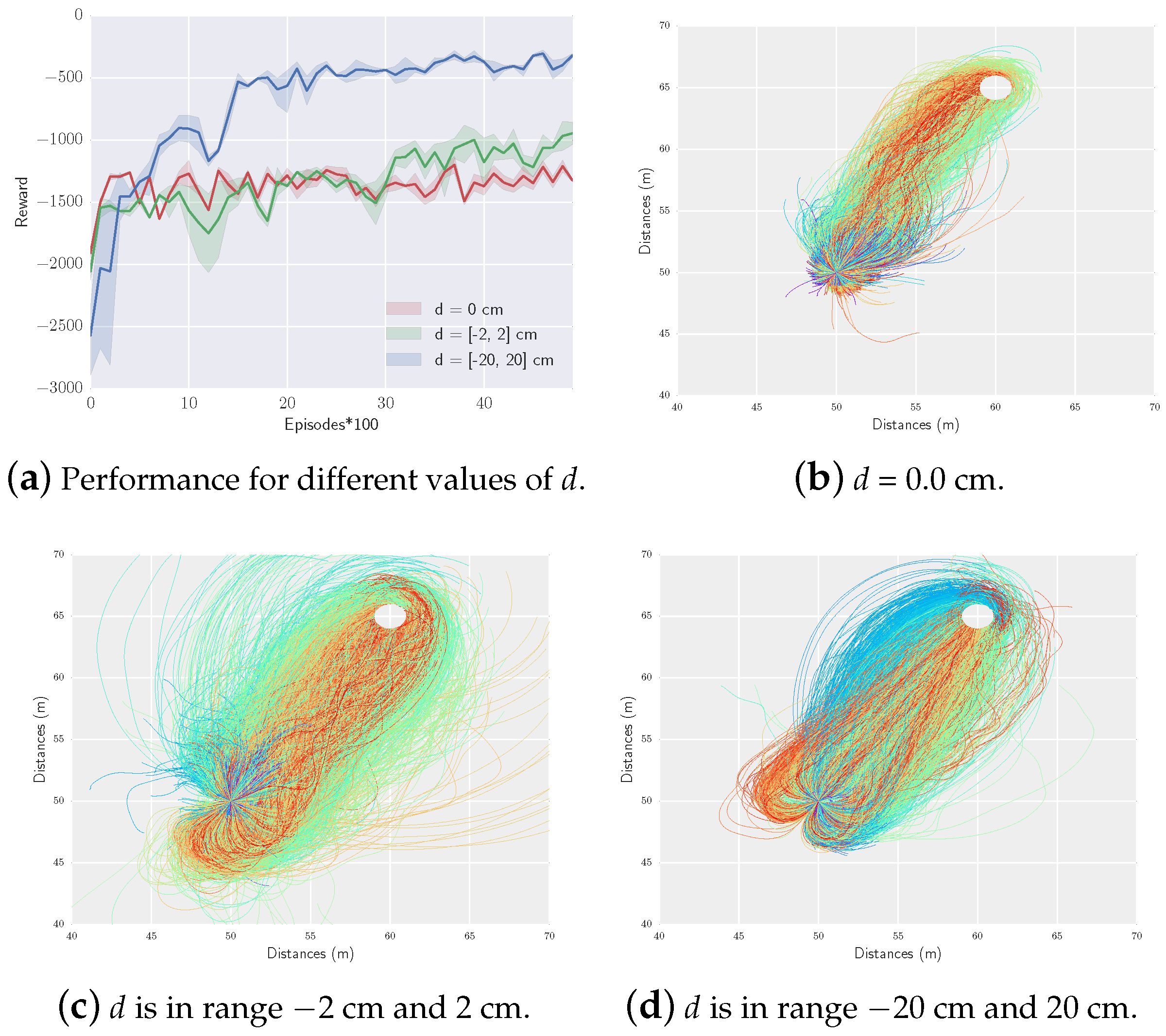
5.3. Results and Discussion
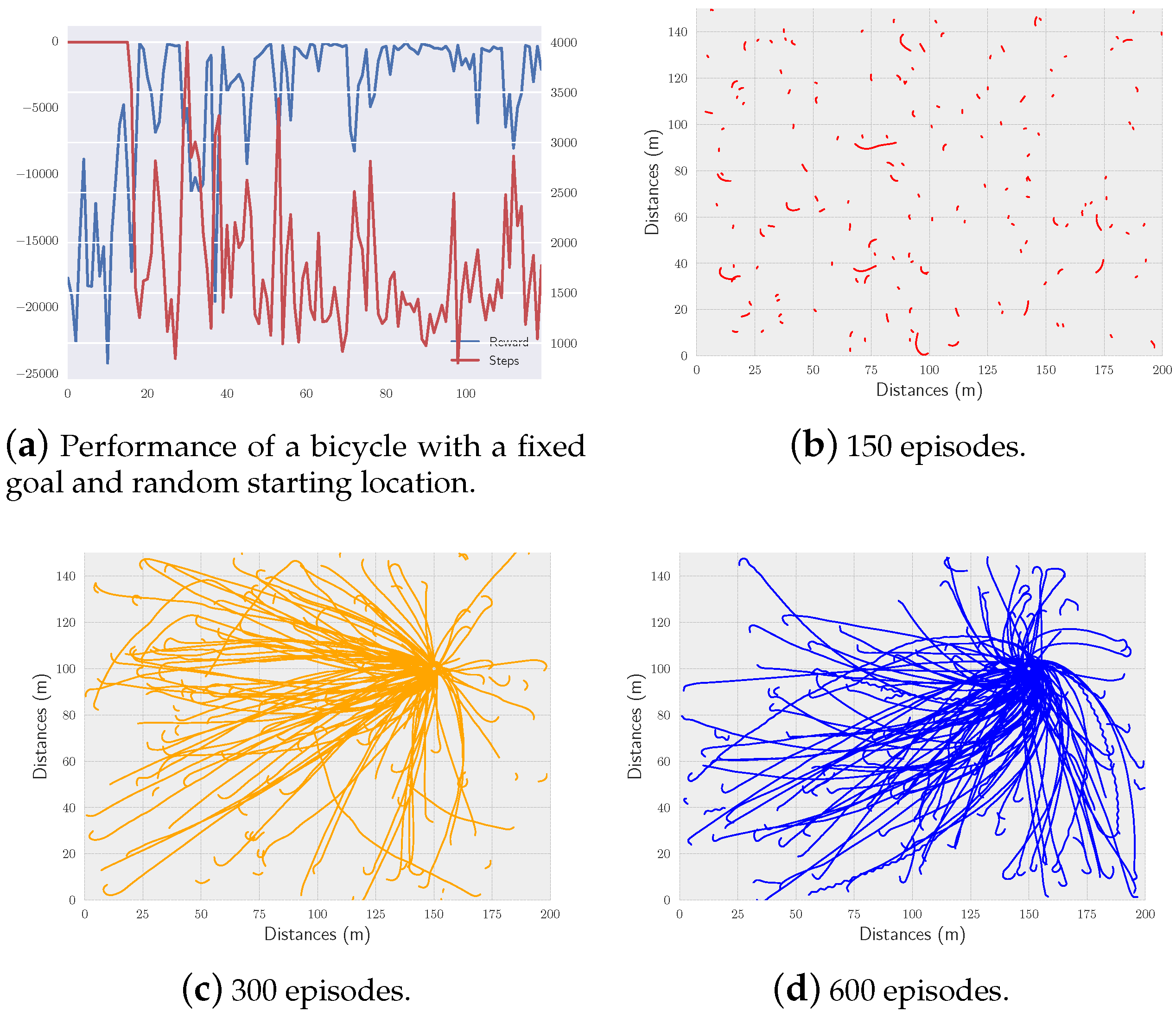
5.3.1. Simulation without Controlling the Velocity
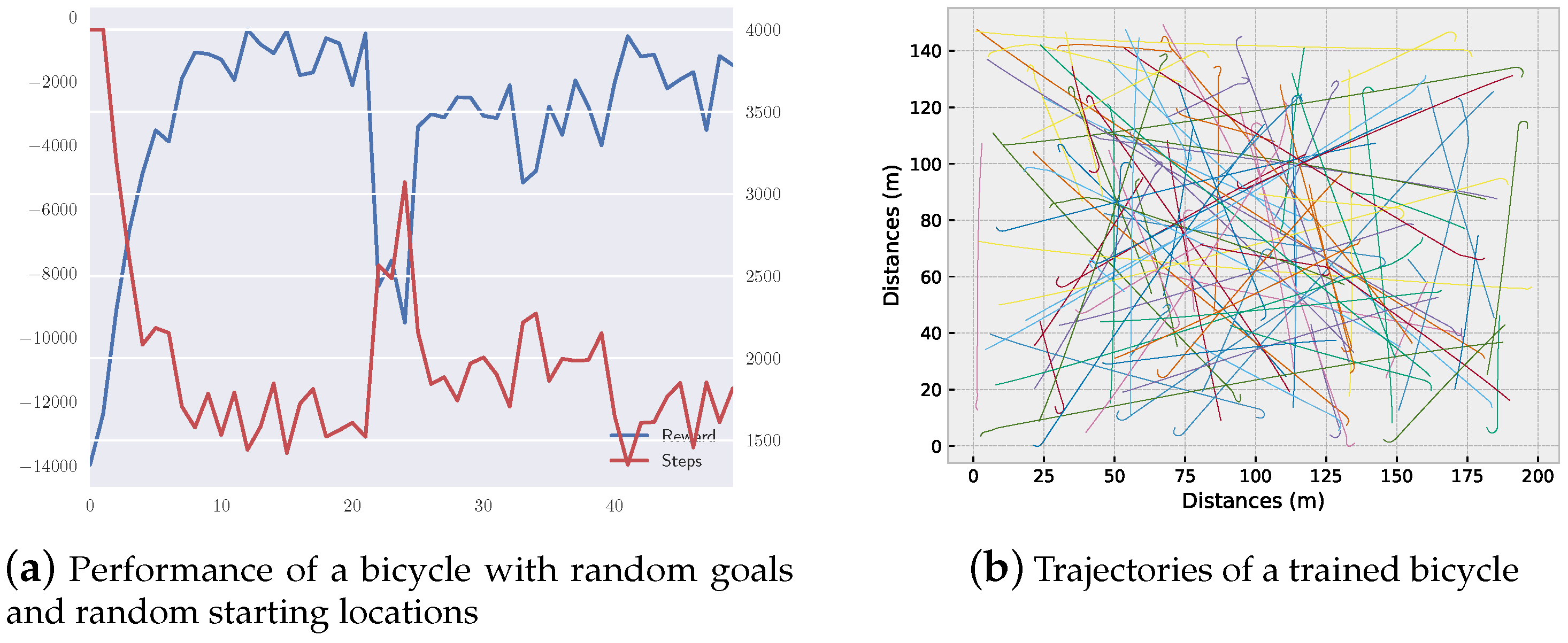
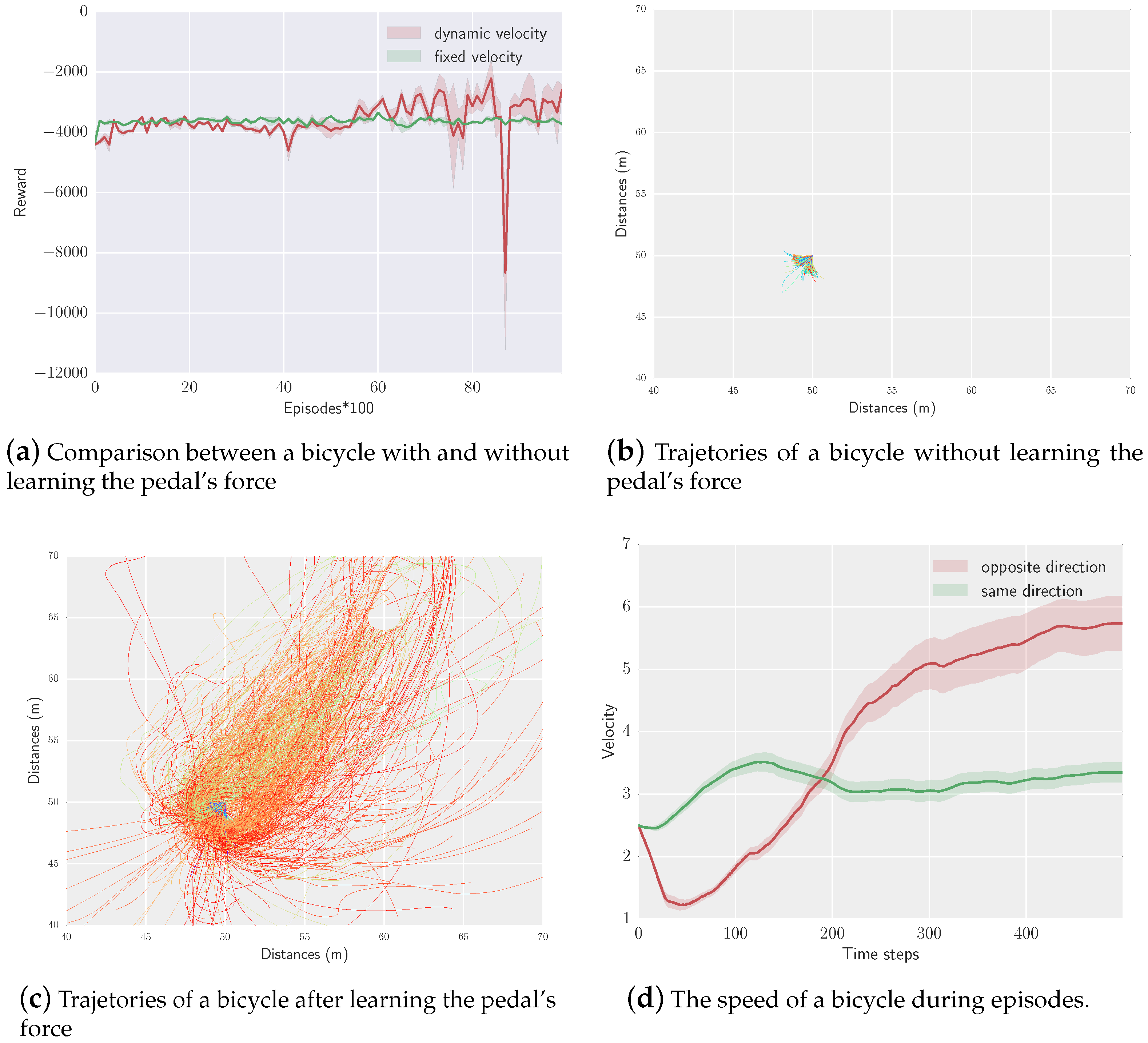
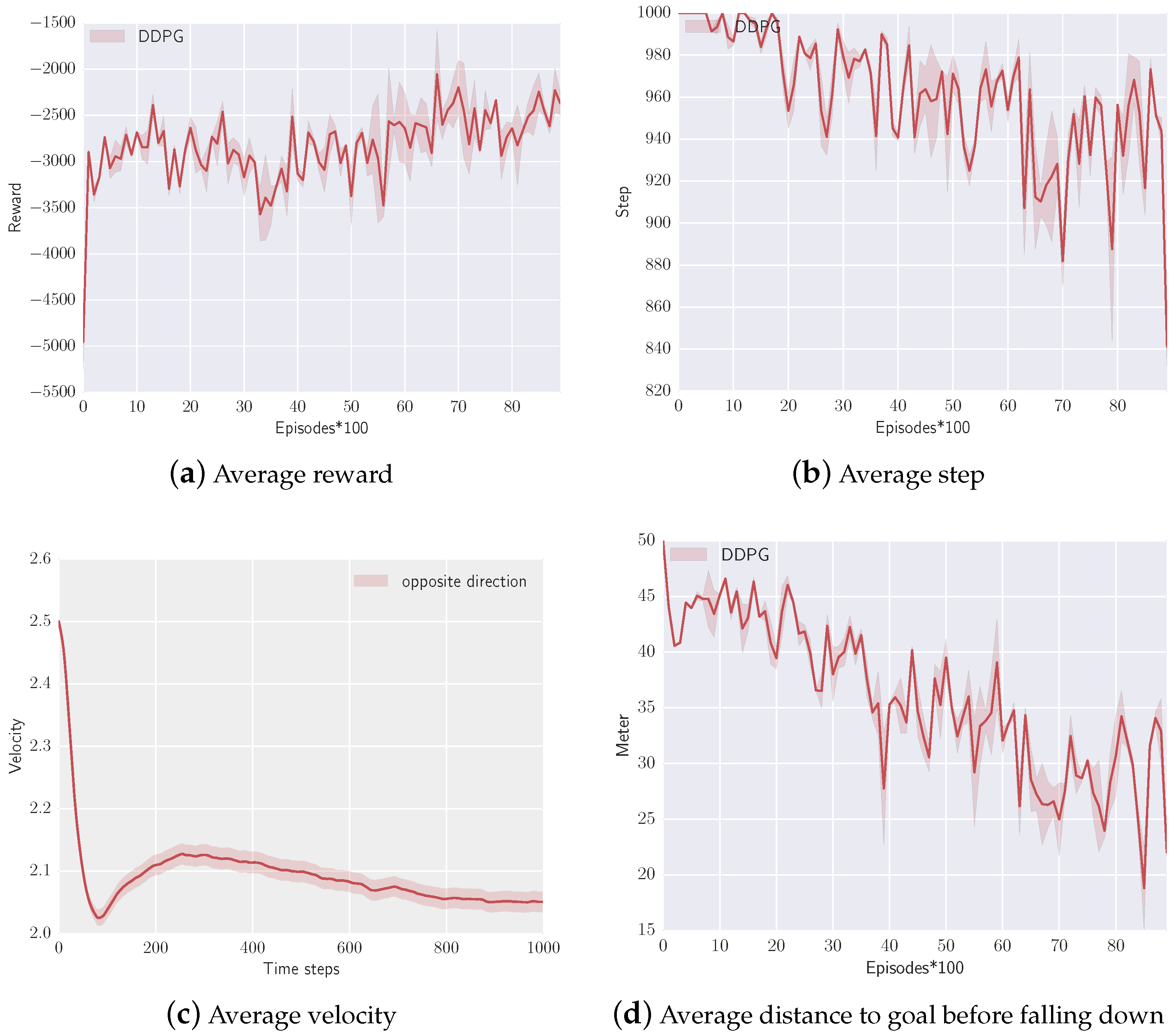
5.3.2. Simulation with Controlling the Velocity
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Nederland, G. Introducing the self-driving bicycle in The Netherlands. Available online: https://www.youtube.com/watch?v=LSZPNwZex9s (accessed on 10 December 2018).
- Keo, L.; Yamakita, M. Controlling balancer and steering for bicycle stabilization. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, 10–15 October 2009; pp. 4541–4546. [Google Scholar]
- Meijaard, J.P.; Papadopoulos, J.M.; Ruina, A.; Schwab, A.L. Linearized dynamics equations for the balance and steer of a bicycle: a benchmark and review. In Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences; The Royal Society: London, UK, 2007; Volume 463, pp. 1955–1982. [Google Scholar]
- Schwab, A.; Meijaard, J.; Kooijman, J. Some recent developments in bicycle dynamics. In Proceedings of the 12th World Congress in Mechanism and Machine Science; Russian Academy of Sciences: Moscow, Russia, 2007. [Google Scholar]
- Tan, J.; Gu, Y.; Liu, C.K.; Turk, G. Learning bicycle stunts. ACM Trans. Gr. (TOG) 2014, 33, 50. [Google Scholar] [CrossRef]
- Lu, M.; Li, X. Deep reinforcement learning policy in Hex game system. In Proceedings of the IEEE Chinese Control And Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 6623–6626. [Google Scholar]
- Bejar, E.; Moran, A. Deep reinforcement learning based neuro-control for a two-dimensional magnetic positioning system. In Proceedings of the IEEE 4th International Conference on Control, Automation and Robotics (ICCAR), Auckland, New Zealand, 20–23 April 2018; pp. 268–273. [Google Scholar]
- Yasuda, T.; Ohkura, K. Collective behavior acquisition of real robotic swarms using deep reinforcement learning. In Proceedings of the Second IEEE International Conference on Robotic Computing (IRC), Laguna Hills, CA, USA, 31 January–2 February 2018; pp. 179–180. [Google Scholar]
- Randløv, J.; Alstrøm, P. Learning to drive a bicycle using reinforcement learning and shaping. ICML 1998, 98, 463–471. [Google Scholar]
- Le, T.P.; Chung, T.C. Controlling bicycle using deep deterministic policy gradient algorithm. In Proceedings of the 14th International Conference on Ubiquitous Robots and Ambient Intelligence (URAI), Jeju, Korea, 28 June–1 July 2017; pp. 413–417. [Google Scholar]
- Sutton, R.; Barto, A. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef] [PubMed]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv, 2015; arXiv:1509.02971. [Google Scholar]
- Le, T.P.; Quang, N.D.; Choi, S.; Chung, T. Learning a self-driving bicycle using deep deterministic policy Gradient. In Proceedings of the 18th International Conference on Control, Automation and Systems (ICCAS), Pyeongchang, Korea, 17–20 October 2018; pp. 231–236. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.L.; Wu, H.M.; Shih, C.L. Fuzzy sliding-mode underactuated control for autonomous dynamic balance of an electrical bicycle. IEEE Trans. Control Syst. Technol. 2009, 17, 658–670. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv, 2014; arXiv:1412.6980. [Google Scholar]
- Uhlenbeck, G.E.; Ornstein, L.S. On the theory of the Brownian motion. Phys. Rev. 1930, 36, 823. [Google Scholar] [CrossRef]
- Gu, S.; Lillicrap, T.; Sutskever, I.; Levine, S. Continuous deep q-learning with model-based acceleration. In Proceedings of the International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; pp. 2829–2838. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv, 2017; arXiv:1707.06347. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 1889–1897. [Google Scholar]
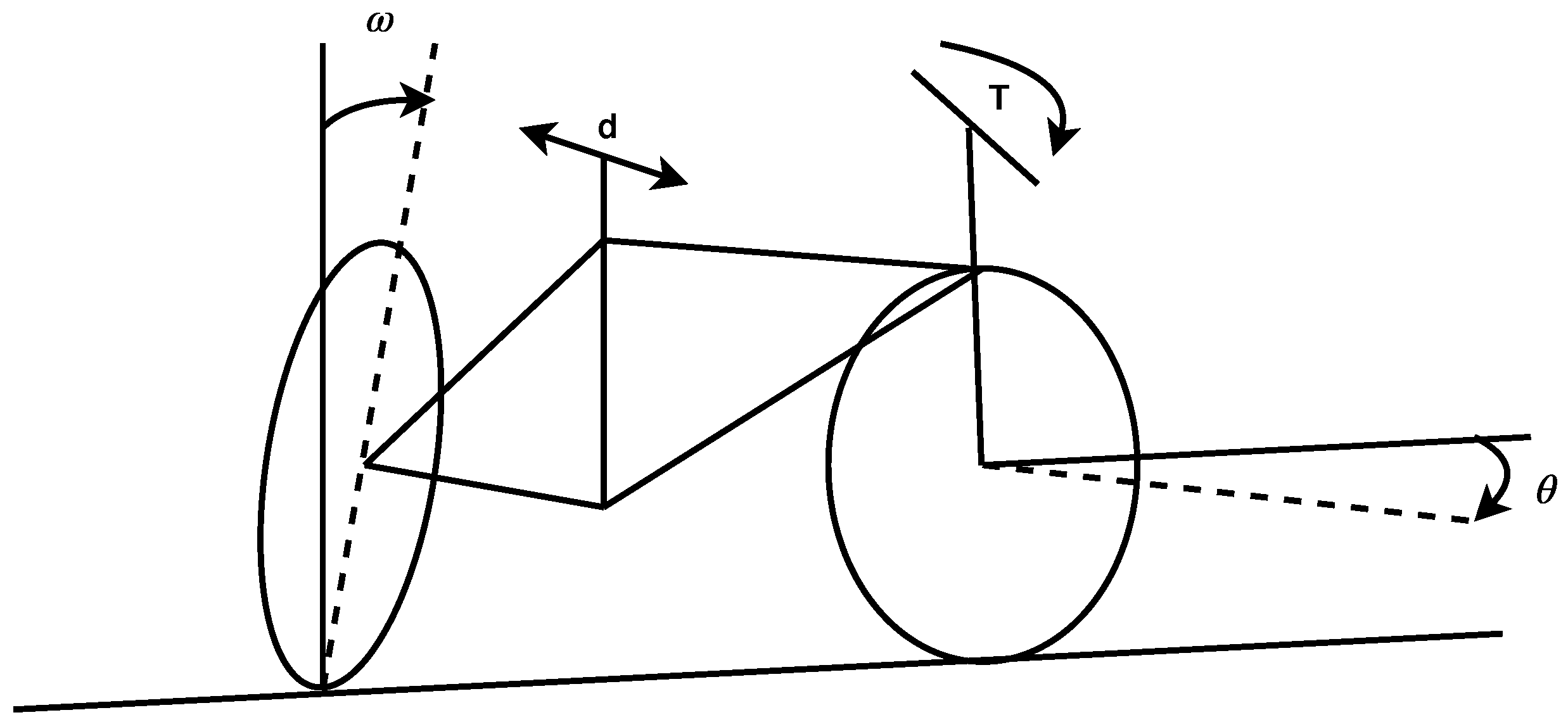
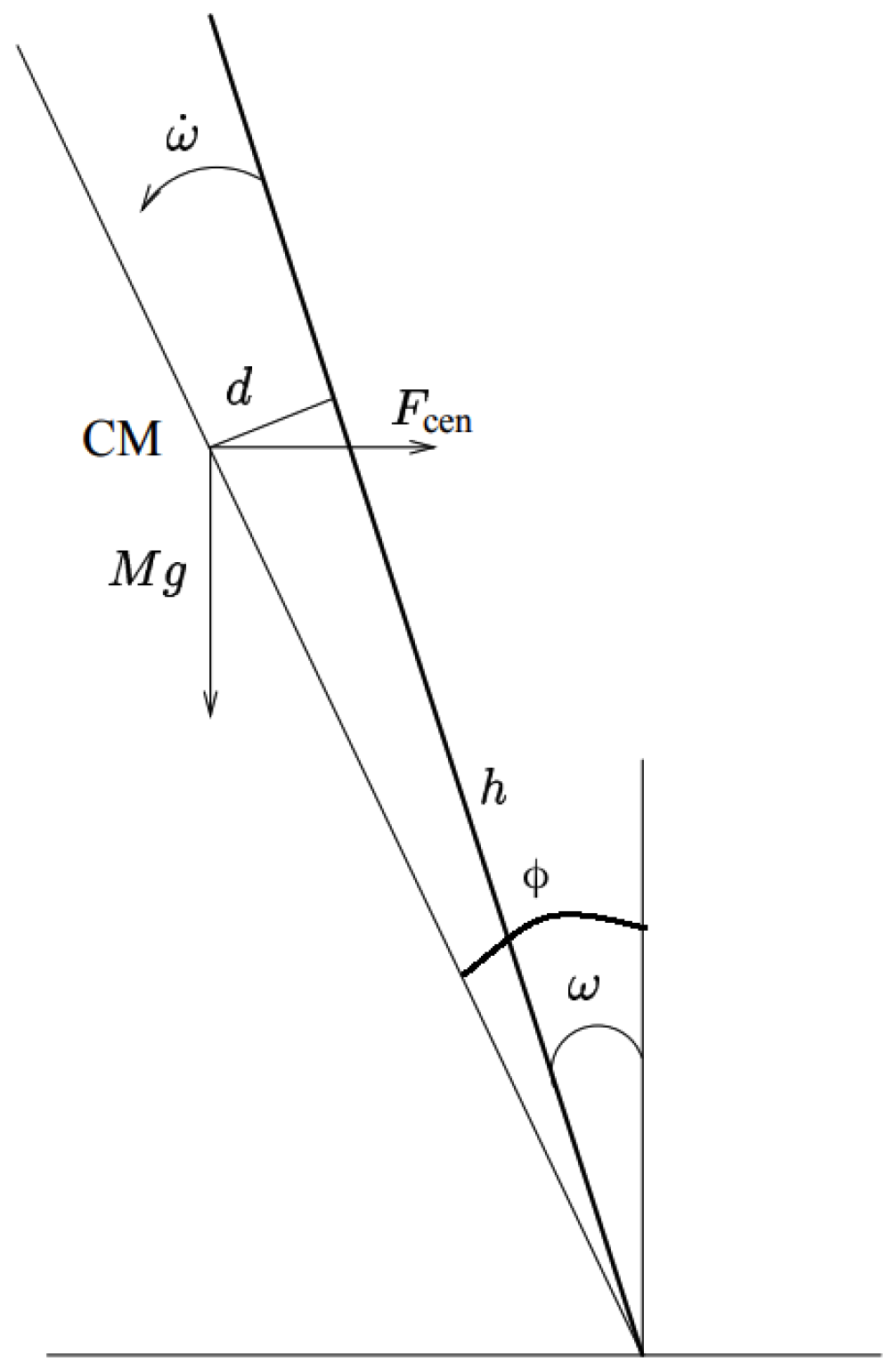
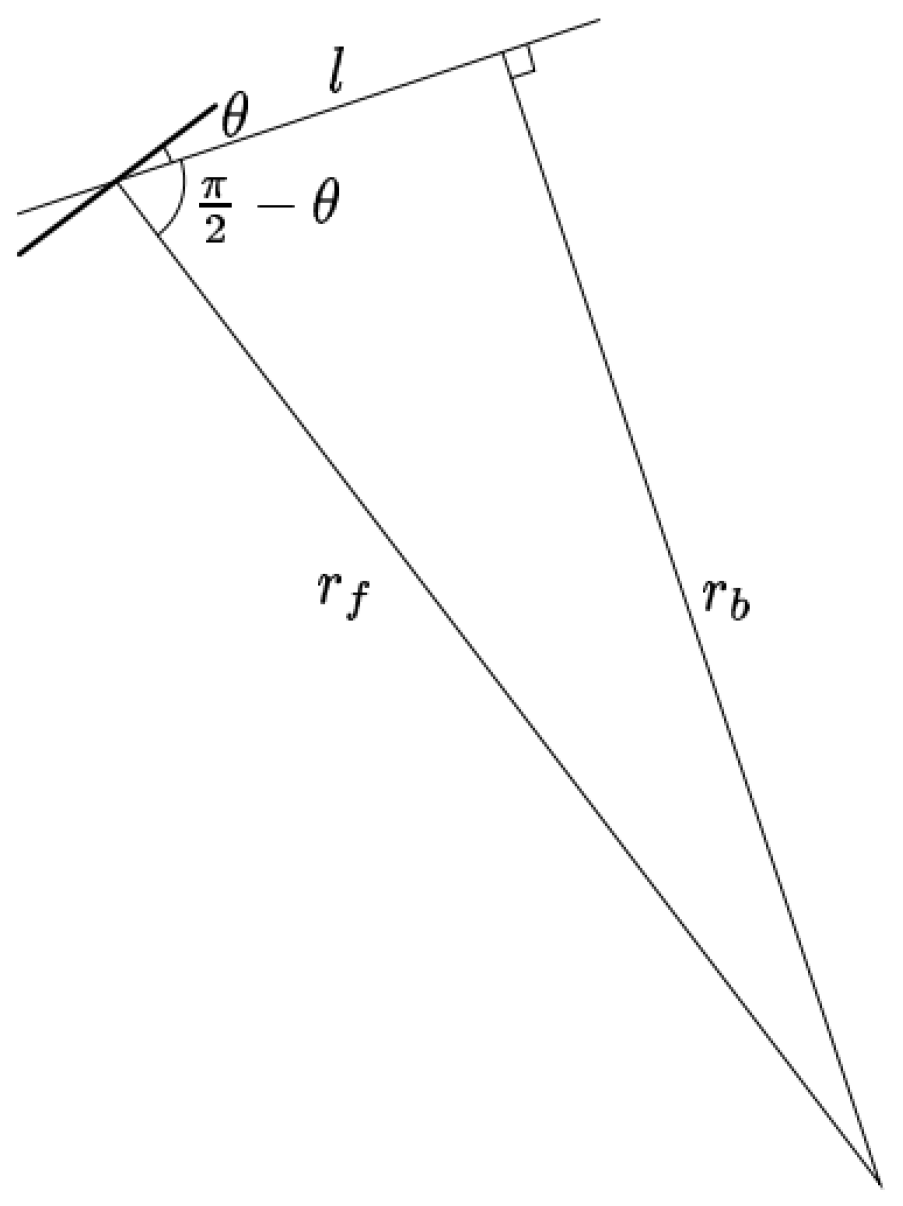
| Notation | Description | Value |
|---|---|---|
| c | Horizontal distance between the point, where the front wheel touches the ground and the CM | 66 cm |
| The Center of Mass of the bicycle and cyclist as a whole | ||
| d | The agent’s choice of the displacement of the CM perpendicular to the plane of the bicycle | |
| The vertical distance between the CM for the bicycle and for the cyclist | 30 cm | |
| h | Height of the CM over the ground | 94 cm |
| l | Distance between the front tire and the back tyre at the point where they touch the ground | 111 cm |
| Mass of the bicycle | 15 kg | |
| Mass of a tire | 1.7 kg | |
| Mass of the cyclist | 60 kg | |
| r | Radius of the tire | 34 cm |
| The angular velocity of a tire | ||
| T | The torque the agent applies to the handlebars | |
| Time step | 0.025 s |
| Name | Actor | Critic |
|---|---|---|
| Input layer | A state vector () | State vector and action vector () |
| 1st fully-connected layer | 400 units | 200 units |
| 2nd fully-connected layer | 300 units | 200 units |
| Output layer | An action vector () | Q-value |
| Initial parameters | Uniformly random between | Uniformly random between |
| Learning rate | 0.001 | 0.001 |
| Optimizer | ADAM [18] | ADAM [18] |
| Name | Value |
|---|---|
| Input dimension | 6 (states) |
| Output dimension | 3 (actions) |
| Discounted factor | 0.99 |
| Random noise | Ornstein-Uhlenbeck process [19] with and |
| Experience memory capacity | 500,000 |
| Batch size | 64 samples |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, S.; Le, T.P.; Nguyen, Q.D.; Layek, M.A.; Lee, S.; Chung, T. Toward Self-Driving Bicycles Using State-of-the-Art Deep Reinforcement Learning Algorithms. Symmetry 2019, 11, 290. https://doi.org/10.3390/sym11020290
Choi S, Le TP, Nguyen QD, Layek MA, Lee S, Chung T. Toward Self-Driving Bicycles Using State-of-the-Art Deep Reinforcement Learning Algorithms. Symmetry. 2019; 11(2):290. https://doi.org/10.3390/sym11020290
Chicago/Turabian StyleChoi, SeungYoon, Tuyen P. Le, Quang D. Nguyen, Md Abu Layek, SeungGwan Lee, and TaeChoong Chung. 2019. "Toward Self-Driving Bicycles Using State-of-the-Art Deep Reinforcement Learning Algorithms" Symmetry 11, no. 2: 290. https://doi.org/10.3390/sym11020290
APA StyleChoi, S., Le, T. P., Nguyen, Q. D., Layek, M. A., Lee, S., & Chung, T. (2019). Toward Self-Driving Bicycles Using State-of-the-Art Deep Reinforcement Learning Algorithms. Symmetry, 11(2), 290. https://doi.org/10.3390/sym11020290





