An Upgraded Version of the Binary Search Space-Structured VQ Search Algorithm for AMR-WB Codec

Abstract

Adaptive multi-rate wideband (AMR-WB) speech codecs have been widely used for high speech quality in modern mobile communication systems, e.g., handheld mobile devices. Nevertheless, a major handicap is that a remarkable computational load is required in the vector quantization (VQ) of immittance spectral frequency (ISF) coefficients of an AMR-WB coding. In view of this, a two-stage search algorithm is presented in this paper as an efficient way to reduce the computational complexity of ISF quantization in AMR-WB coding. At stage 1, an input vector is assigned to a search subspace in an efficient manner using the binary search space-structured VQ (BSS-VQ) algorithm, and a codebook search is performed over the subspace at stage 2 using the iterative triangular inequality elimination (ITIE) approach. Through the use of the codeword rejection mechanisms equipped in both stages, the computational load can be remarkably reduced. As compared with the original version of the BSS-VQ algorithm, the upgraded version provides a computational load reduction of up to 51%. Furthermore, this work is expected to satisfy the energy saving requirement when implemented on an AMR-WB codec of mobile devices.

1. Introduction

The development of the adaptive multi-rate wideband (AMR-WB) speech codec [1,2,3,4] aims to considerably improve the speech quality on handheld mobile devices. It is an algebraic code-excited linear-prediction (ACELP)-based coding technique [4,5], and is equipped with nine coding modes with bitrates between 6.6 and 23.85 kbps. Regardless of its excellent speech coding technique, the price paid is a high computational complexity during coding. In other words, the speech quality of a smartphone can be improved at the cost of high battery power consumption, using an AMR-WB codec.

It takes an AMR-WB encoder a tremendous amount of time to quantize immittance spectral frequency (ISF) coefficients in various coding modes [6,7,8,9]. The ISF coefficient in AMR-WB is quantized through the combined use of a split vector quantization (SVQ) and a multistage VQ technique, designated as split-multistage VQ (S-MSVQ) [1]. Traditionally, a full search is employed to obtain a codeword best matched with an arbitrary input vector, and an enormous computational load is required consequently. Accordingly, efforts have been made to reduce the search complexity of an encoding process in [10,11,12,13,14,15,16,17,18], among which the binary search space-structured VQ (BSS-VQ) search algorithm in [10], a piece of our previous studies, was presented as a simple but efficient way to quantize the ISF coefficient in AMR-WB. A remarkable computational load reduction is achieved therein with a well-maintained speech quality. The BSS-VQ search algorithm was also experimentally validated to outperform an equal-average equal-variance equal-norm nearest neighbor search (EEENNS) algorithm [11,12,13,14] and triangular inequality elimination (TIE)-based algorithms [15,16,17], e.g., the DI-TIE algorithm [15], short for a TIE with a dynamic and an intersection mechanism, and a multiple TIE (MTIE) approach [17].

A deeper investigation reveals that the search performance of the BSS-VQ algorithm is subject to the codeword distributions. As a way to boost the search performance, an upgraded version of the BSS-VQ algorithm is developed herein through a sequential use of the BSS-VQ algorithm and the iterative TIE (ITIE) approach [18]. To begin with, an input vector is assigned to a search subspace in an efficient manner using the BSS-VQ algorithm, and subsequently, a codebook search is performed over the subspace using the ITIE approach. Via the use of the codeword rejection mechanisms equipped in BBS-VQ and ITIE, the search load is reduced significantly as intended. The presented algorithm is ultimately validated to well outperform its counterparts, and is fit to meet the energy saving requirement when implemented on an AMR-WB codec of mobile devices. In addition, the Enhanced Voice Services (EVS) codec [19] is a new standard of audio codec optimized for operation with voice and music/mixed content signals. The EVS codec also provides interoperation with AMR-WB over all nine coding modes. That is to say the contribution of this study is also applicable to the speech coding in EVS codec.

The rest of this paper is organized as follows. The ISF coefficient quantization in AMR-WB is described in Section 2. Section 3 presents the proposed search algorithm for ISF quantization. Experimental results are demonstrated and discussed in Section 4, and finally Section 5 concludes this work.

2. ISF Quantization in AMR-WB

A linear prediction analysis in AMR-WB is illustrated as follows: To begin with, a frame is applied to evaluate linear predictive coefficients (LPCs), followed by a conversion into ISF coefficients. Subsequently, ISF coefficients are quantized by following a process, as will be seen below.

2.1. Linear Prediction Analysis

The 16th-order LPC, a_i, of a linear prediction filter is evaluated using a Levinson–Durbin algorithm, defined as

$$\frac{1}{A(z)}=\frac{1}{1+{\displaystyle \sum _{i=1}^{16}{a}_i{z}^{-i}}},$$

(1)

and the LPC parameters are then converted into the immittance spectral pair (ISP) coefficients for the purposes of parametric quantization and interpolation. The ISP coefficients are defined as the roots of the following two polynomials:

$$F_1^{\prime }(z)=A(z)+z^{-16}A(z^{-1}),$$

(2)

$$F_2^{\prime }(z)=A(z)-z^{-16}A(z^{-1}).$$

(3)

$F_1^{\prime }(z)$ and $F_2^{\prime }(z)$ are symmetric and antisymmetric polynomials, respectively. It can be proven that all the roots of $F_1^{\prime }(z)$ and $F_2^{\prime }(z)$ lie and alternate successively on a unit circle in the z-domain. Also, $F_2^{\prime }(z)$ has two roots at z = 1 (ω = 0) and z = −1 (ω = π), which can be eliminated by the introduction of the following polynomials, with 8 and 7 conjugate roots on the unit circle respectively, represented as

$$F_1(z)=F_1^{\prime }(z)=(1+a_{16}){\displaystyle \prod _{i=0,2,\dots ,14}(1-2q_i{z}^{-1}+z^{-2})},$$

(4)

$$F_2(z)=\frac{{F^{\prime }}_2(z)}{(1-z^{-2})}=(1-a_{16}){\displaystyle \prod _{i=1,3,\dots ,13}(1-2q_i{z}^{-1}+z^{-2})},$$

(5)

where the coefficients q_i are referred to as the ISPs in the cosine domain, and a₁₆ symbolizes the last predictor coefficient. Both Equations (4) and (5) can be solved using a Chebyshev polynomial. Subsequently, the 16th-order ISF coefficients ω_i, derived from the ISP coefficients, can be acquired via the transformation ω_i = arccos(q_i).

2.2. Quantization of ISF Coefficients

Ahead of a quantization process, a mean-removed and a first order moving average (MA) filtering are performed on the ISF coefficients to obtain a residual ISF vector, expressed as

$$r(n)=z(n)-p(n),$$

(6)

where z(n) and p(n) respectively represent the mean-removed ISF vector and the predicted ISF vector at frame n using a first order MA prediction. The latter expression is defined as

$$p(n)=\frac{1}{3}\widehat{r}(n-1),$$

(7)

where $\widehat{r}(n-1)$ denotes the quantized residual vector at the previous frame.

S-MSVQ is then performed on r(n).

Table 1. Structure of split-multistage vector quantization (S-MSVQ) in adaptive multi-rate wideband (AMR-WB) in the 8.85–23.85 kbps coding modes.

Structure of S-MSVQ
Stage 1	CB1: r1 (1–9 order of r) (8 bits)			CB2: r2 (10–16 order of r) (8 bits)
Stage 2	CB11: r(2)1,1–3 (6 bits)	CB12: r(2)1,4–6 (7 bits)	CB13: r(2)1,7–9 (7 bits)	CB21: r(2)2,1–3 (5 bits)	CB22: r(2)2,4–7 (5 bits)

gives the structure of S-MSVQ for AMR-WB in the 8.85–23.85 kbps coding modes. In stage 1, r(n) is split into two subvectors, that is, a nine-dimensional subvector r₁(n) and a seven-dimensional subvector r₂(n), associated with codebooks CB1 and CB2 respectively, for VQ encoding. In the beginning of stage 2, the quantization error vectors are split into five subvectors, symbolized as $r_i^{(2)}=r_i-{\widehat{r}}_i,i=1,2$, respectively. For example, r⁽²⁾_1,1–3 in Table 1 denotes the subvector split from the first to the third components of r₁, on which VQ encoding is then performed over codebook CB11. Similarly, r⁽²⁾_2,4–7 represents the subvector split from the 4th to the 7th components of r₂, on which VQ encoding is then performed over codebook CB22. Lastly, the Euclidean distance is used as a measure of the squared error ISF distortion in all the quantization processes.

3. Proposed Search Algorithm

In this paper, an upgraded version of the BSS-VQ search algorithm is presented as an efficient way to reduce the computational complexity when quantizing ISF coefficients in AMR-WB. This is done through a sequential use of BSS-VQ and ITIE, which are detailed by turns below.

3.1. The BSS-VQ Search Algorithm

As a prerequisite of a VQ codebook search in the BSS-VQ algorithm, an input vector is assigned in an efficient manner to a subspace, over which a small number of codeword searches is conducted through the combined use of lookup tables and a fast locating technique. As it turns out, the computational load can be reduced significantly.

To begin with, each dimension is dichotomized into two subspaces, and an input vector is then assigned to a subspace according to the entries of the input vector. This is illustrated as follows. For instance, given a 9-dimensional subvector r₁(n) associated with codebook CB1, there are up to 2⁹ = 512 subspaces, to one of which an input vector is then assigned by means of a dichotomy, according to each entry of the input vector.

As defined in [10], a dichotomy position refers to the mean of all the codewords contained in a codebook, expressed as

$$dp(j)=\frac{1}{CSize}{\displaystyle \sum _{i=1}^{CSize}{c}_i(j)},0\le j<Dim,$$

(8)

where c_i(j) denotes the jth component of the ith codeword c_i, and dp(j) the mean value of all the jth components. For example, CSize = 256, Dim = 9 in the codebook CB1, all the dp(j) values are saved, and then presented in

Table 2. Dichotomy position for each dimension in the codebook CB1.

jth-Order	Mean
0	15.3816
1	19.0062
2	15.4689
3	21.3921
4	26.8766
5	28.1561
6	28.0969
7	21.6403
8	16.3302

. That is, the values in Table 2 are obtained by way of using (8) to calculate the statistical mean of all the codewords in CB1.

A quantity ν_n(j) is then defined for vector quantization on the nth input vector x_n, expressed as

$$v_n(j)=\{\begin{array}{c}{2}^j,\hspace{1em}{x}_n(j)\ge dp(j)\\ 0,\hspace{1em}{x}_n(j)<dp(j)\end{array},0\le j<Dim,$$

(9)

where x_n(j) symbolizes the jth component of x_n. Subsequently, x_n is assigned to subspace k (bss_k), where k is the sum of ν_n(j) over all of the dimensions, expressed as

$$\mathit{Assigning}:x_n\in bs{s}_k|k={\displaystyle \sum _{j=0}^{Dim-1}{v}_n(j)}.$$

(10)

Since 0 ≤ k < BSize and BSize = 2⁹ = 512 in this article, there are a total of 512 subspaces. For example, given an input vector x_n = {16.0, 17.1, 18.2, 19.3, 20.4, 21.5, 22.6, 23.7, 24.8}, ν_n(j) = {2⁰, 0, 2², 0, 0, 0, 0, 2⁷, 2⁸} for each j, 0 ≤ j ≤ 8, and k = 389 are given by (9) and (10), respectively. Thus, the input vector x_n is assigned to the subspace bss_k with k = 389. In this manner, merely a small number of basic operations, i.e., comparison, shift, and addition, are required, meaning that an input vector is efficiently assigned to a subspace as requested.

As stated in Reference [10], a lookup table is prebuilt in each subspace by performing a training mechanism after the dichotomy position for each dimension is determined. The lookup tables give the probability that each codeword works as the best-matched codeword in each subspace, referred to as the hit probability of a codeword in a subspace for short, and symbolized as P_hit(c_i | bss_k), 1 ≤ i ≤ CSize, 0 ≤ k < BSize. Moreover, a quantity P_hit(m | bss_k), 1 ≤ m ≤ CSize, is defined as the m ranked probability that a codeword hits the best-matched codeword in subspace bss_k for sorting purposes. For example, $P_{hit}(m|bs{s}_k){|}_{m=1}=\underset{c_i}{\max }\{P_{hit}(c_i|bs{s}_k)\}$ denotes the highest hit probability in bss_k. As can be seen, the lookup table in each subspace gives the ranked hit probability in descending order and the corresponding codeword.

In the encoding procedure of BSS-VQ, the cumulative probability P_cum(M | bss_k) is firstly defined as the sum of the top M P_hit(m | bss_k) in bss_k, namely

$$P_{cum}(M|bs{s}_k)={\displaystyle \sum _{m=1}^M{P}_{hit}(m|bs{s}_k)},1\le M\le \mathit{CSize}.$$

(11)

Subsequently, given a threshold of quantization accuracy (TQA), a quantity M_k(TQA) refers to the minimum value of M that meets the condition P_cum(M | bss_k) ≥ TQA in bss_k, namely

$$M_k(TQA)=\arg \underset{M}{\min }\{M:P_{cum}(M|bs{s}_k)\ge TQA\},1\le M\le \mathit{CSize},0\le k<\mathit{BSize}.$$

(12)

Finally, a BSS-VQ encoding procedure is described below as Algorithm 1:

Algorithm1 Encoding procedure of BSS-VQ

Step 1. Given a TQA, Mk(TQA) satisfying (12) is found directly in the lookup table in bssk.

Step 2. Referencing Table 2 and by means of (9) and (10), an input vector is assigned to a subspace bssk in an efficient manner.

Step 3. A full search for the best-matched codeword is performed among the top Mk(TQA) sorted codewords in bssk, and then the index of the found codeword is output.

Step 4. Repeat Steps 2 and 3 until all the input vectors are encoded.

In short, Table 2, the first lookup table, is prebuilt by performing (8). Subsequently, the second lookup table regarding P_hit(m | bss_k) and the corresponding codeword is built for each subspace by following the training mechanism. Accordingly, the VQ encoding can be completed using Algorithm 1.

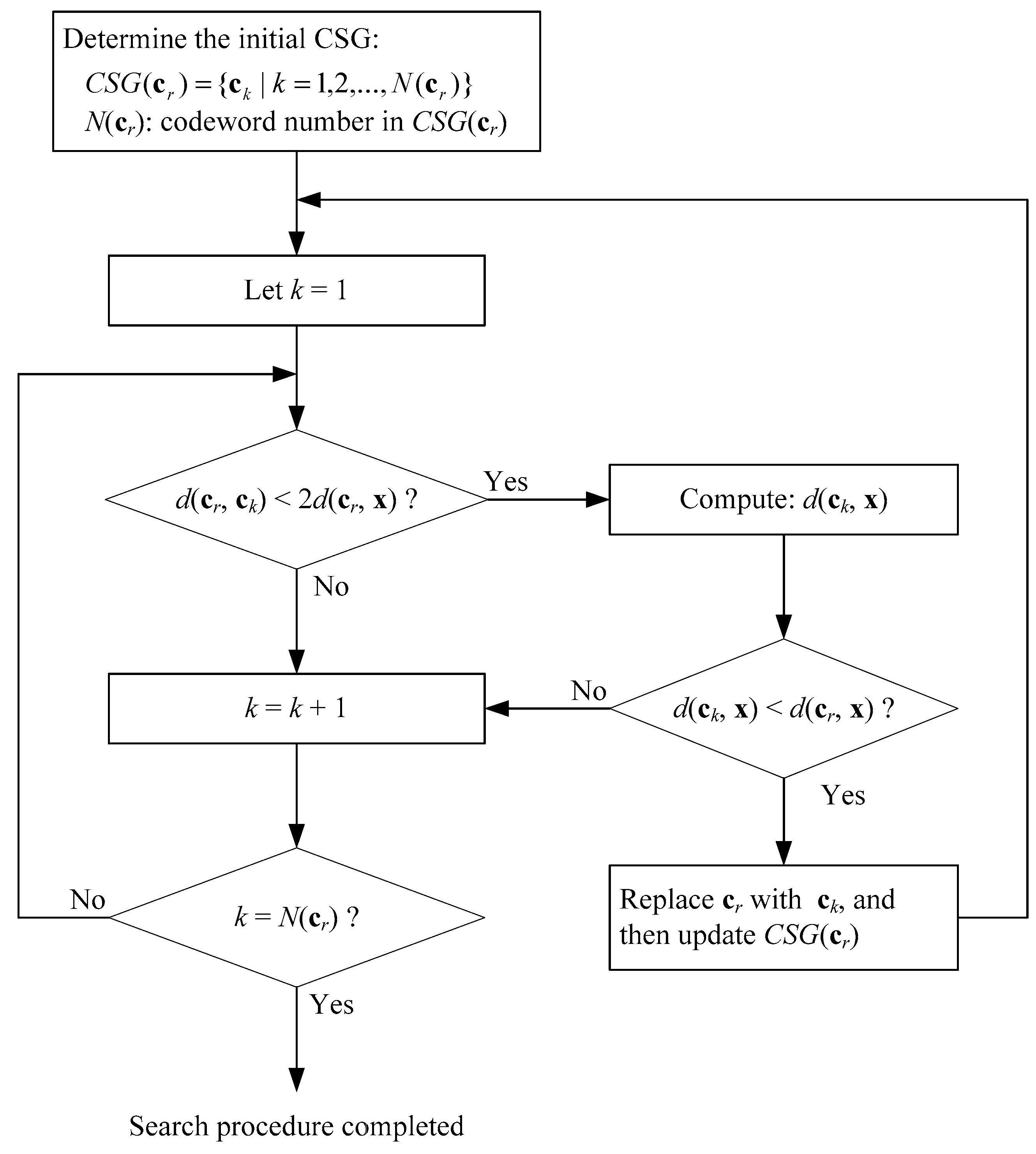
3.2. The ITIE Search Algorithm

As a preliminary to the ITIE algorithm, a TIE algorithm is briefly described below. First of all, a codeword captured from the preceding frame is viewed as a reference codeword c_r in the current frame, and the Euclidean distance between c_r and an input vector x, symbolized as d(c_r, x), is calculated [16]. A set, consisting of all the codewords c_i and meeting the condition d(c_r, c_i) < 2d(c_r, x), is referred to as a candidate search group (CSG), represented as

TIE: CSG(c_r) = {c_i | d(c_r, c_i) < 2d(c_r, x)}, 1 ≤ i ≤ CSize,

(13)

where CSize denotes the total number of the codewords. CSG(c_r) is the search space over which a current codebook search is conducted. Additionally, a lookup table, listing all the codewords sorted by the Euclidean distance, is constructed in advance for the TIE search algorithm.

Subsequently, the ITIE algorithm works as illustrated in Figure 1 and stated in Algorithm 2. Just as in the TIE case, a codeword captured from the preceding frame is viewed as a reference codeword c_r in the current frame, and then a codebook search is performed over CSG(c_r) using (13). As in the TIE case, the condition d(c_r, c_k) < 2d(c_r, x) is checked. If the condition is true, then d(c_k, x) is computed, and another condition d(c_k, x) < d(c_r, x) is checked. If the condition is true, then c_r is replaced with c_k, and the search scope CSG(c_r) is updated. CSG(c_r) updates and shrinks each time through the above-stated loop.

Algorithm2 Search procedure of ITIE

Step 1. Build a TIE lookup table.

Step 2. Given a cr, compute d(cr, x), and then CSG(cr) is found directly in the TIE lookup table, that is,

CSG(cr) = {ck | k = 1,2,...,N(cr)}, (14) where ck and N(cr) denote the codewords and the number thereof in CSG(cr), respectively.

Step 3. Starting at k = 1, obtain d(cr, ck) from the lookup table.

Step 4. If (d(cr, ck) < 2d(cr, x)), then compute d(ck, x), and perform Step 5.

Otherwise, let k = k + 1, and then repeat Step 4, until k = N(cr).

Step 5. If (d(ck, x) < d(cr, x)), then replace cr with ck, update new CSG(cr), let k = 1, and repeat Step 3.

Otherwise, let k = k + 1, and then repeat Step 4, until k = N(cr).

3.3. Upgraded Version of the BSS-VQ Search Algorithm

The search performance of the BSS-VQ algorithm is subject to codeword distributions. As a way to ease the distribution effect, an input vector is assigned to a search subspace in an efficient manner using BSS-VQ at stage 1 of this work, and a codebook search is conducted over the subspace using ITIE as an alternative to the full search algorithm. This is simply because a codeword of interest therein can be well located either by ITIE or by the full search counterpart. This paper presents a two-stage codebook search algorithm as an effective way to remarkably reduce the amount of codebook searches and the time complexity in the evaluation of Euclidean distances. This is done via a sequential use of codeword rejection mechanisms provided by BSS-VQ and ITIE, respectively. This codebook search mechanism is presented in Algorithm 3, stated as follows:

Algorithm3 Search mechanism of the upgraded version

Step 1. Initial setting: Given a TQA, Mk(TQA) satisfying (12) is found directly in the lookup table in bssk. A TIE lookup table is also built.

Step 2. Referencing Table 2 and through (9) and (10), an input vector is efficiently assigned to a subspace bssk. And then a set, composed of the top Mk(TQA)-sorted codewords in bssk, is denoted by CSG(bssk) and formulated as

CSG(bssk) = {ck | k = 1,2,...,Mk(TQA)}. (15)

Step 3. Starting at k = 1, set cr = ck | k = 1 in (15), then compute d(cr, x).

Step 4. Let k = k + 1, then obtain d(cr, ck) from the TIE lookup table.

Step 5. If (d(cr, ck) < 2d(cr, x)), then compute d(ck, x), and perform Step 6.

Otherwise, let k = k + 1, and then repeat Step 5, until k = Mk(TQA).

Step 6. If (d(ck, x) < d(cr, x)), then replace cr with ck, and repeat Step 4.

Otherwise, let k = k + 1, and then repeat Step 5, until k = Mk(TQA).

On the issue of speech quality, it was concluded in Reference [10] that a nearly lossless speech quality is provided in BSS-VQ at a TQA no less than 0.90. This fact definitely applies to the presented search algorithm, since the upgraded version of BSS-VQ offers exactly the same speech quality as the original version.

4. Experimental Results

In this work, a performance comparison is conducted among the EEENNS, DI-TIE, ITIE, and the original and upgraded versions of BSS-VQ. Since EEENNS, DI-TIE, and ITIE provide a 100% search accuracy in comparison with the full search approach, there is no degradation in the speech quality. Furthermore, as mentioned in the previous section, a nearly lossless speech quality is provided in both the original and the upgraded versions of BSS-VQ. For this reason, performance is compared in terms of the search load, i.e., the average number of searches. For testing purposes, a speech database, including one male and one female speaker, in total requires more than 221 MB of memory, takes up more than 120 min, and covers 363,281 speech frames as well.

Table 3. Average number of searches among various approaches in the 8.85–23.85 kbps modes.

Codebooks		Full Search	EEENNS	DI-TIE	ITIE
Stage 1	CB1	256	58.82	42.46	58.01
	CB2	256	63.87	42.79	62.03
Stage 2	CB11	64	14.17	12.31	13.10
	CB12	128	22.91	14.40	15.32
	CB13	128	21.01	13.50	14.40
	CB21	32	11.08	8.95	9.48
	CB22	32	17.44	12.42	13.21

gives a comparison on the average number of searches among the full search, EEENNS, DI-TIE, and ITIE, while

Table 4. Search load versus threshold of quantization accuracy (TQA) values in the 8.85–23.85 kbps modes for the original version of the binary search space-structured vector quantization (BSS-VQ) algorithm.

TQA	Average Number of Searches in Various Codebooks
	CB1	CB2	CB11	CB12	CB13	CB21	CB22
0.90	15.40	26.45	12.47	19.96	19.93	7.11	6.66
0.91	16.10	27.52	12.86	20.84	20.62	7.11	6.72
0.92	16.80	28.85	12.99	21.50	21.19	7.64	6.91
0.93	17.79	30.23	13.52	21.84	22.02	7.64	7.15
0.94	18.87	31.71	14.04	22.85	22.72	8.00	7.57
0.95	20.03	33.58	14.61	23.85	23.72	8.26	7.84
0.96	21.36	35.81	15.04	24.76	24.95	8.87	8.21
0.97	23.18	38.37	15.86	25.93	26.24	9.27	8.51
0.98	25.71	41.82	16.73	27.60	27.86	10.00	9.33
0.99	29.71	47.12	18.21	29.61	29.99	10.49	10.15

and

Table 5. Search load versus TQA values in the 8.85–23.85 kbps modes for the upgraded version of BSS-VQ.

TQA	Average Number of Searches in Various Codebooks
	CB1	CB2	CB11	CB12	CB13	CB21	CB22
0.90	10.56	15.82	6.55	8.48	8.21	4.06	4.69
0.91	10.99	16.26	6.62	8.56	8.30	4.06	4.72
0.92	11.40	16.79	6.63	8.65	8.38	4.22	4.82
0.93	11.86	17.36	6.73	8.70	8.49	4.22	4.90
0.94	12.40	17.89	6.80	8.76	8.54	4.28	5.10
0.95	13.00	18.57	6.89	8.84	8.60	4.34	5.19
0.96	13.67	19.44	6.95	8.91	8.68	4.41	5.32
0.97	14.53	20.27	7.10	8.98	8.73	4.50	5.43
0.98	15.71	21.50	7.16	9.09	8.85	4.68	5.74
0.99	17.46	23.28	7.33	9.22	8.97	4.75	6.04

list the search load versus the TQA values for the original and the upgraded versions of BSS-VQ, respectively. Furthermore, with the search load required in the full search approach as a benchmark,

Table 6. Load reduction comparison among various algorithms.

Method		LR in CB1 (%)	LR in CB2 (%)	Overall Search Load	Overall LR (%)
Full Search		Benchmark	Benchmark	5280	Benchmark
EEENNS		77.03	75.05	1253.76	76.26
DI-TIE		83.42	83.29	878.88	83.36
ITIE		77.34	75.77	1165.99	77.92
Original version of BSS-VQ (TQA)	0.90	93.98	89.67	528.78	89.99
	0.91	93.71	89.25	548.77	89.61
	0.92	93.44	88.73	570.76	89.19
	0.93	93.05	88.19	595.34	88.72
	0.94	92.63	87.61	624.92	88.16
	0.95	92.18	86.88	657.95	87.54
	0.96	91.66	86.01	696.62	86.81
	0.97	90.95	85.01	743.15	85.93
	0.98	89.96	83.66	808.06	84.70
	0.99	88.39	81.60	902.67	82.90
Upgraded version (TQA)	0.90	95.88	93.82	306.41	94.20
	0.91	95.71	93.65	314.19	94.05
	0.92	95.55	93.44	323.09	93.88
	0.93	95.37	93.22	332.32	93.71
	0.94	95.15	93.01	342.42	93.51
	0.95	94.92	92.75	353.80	93.30
	0.96	94.66	92.40	367.20	93.05
	0.97	94.32	92.08	382.26	92.76
	0.98	93.86	91.60	404.15	92.35
	0.99	93.18	90.91	435.10	91.76

compares the load reduction (LR) among various search algorithms listed in Table 3, Table 4 and Table 5. Obviously, a high search load reduction is indicated by a high value of LR. Moreover, columns 2 and 3 give LRs in codebooks CB1 and CB2, respectively. The overall LR refers to the total search load, defined as the sum of the average number of searches multiplied by the vector dimension in each codebook, and is employed to compare the total search load required during an entire VQ encoding procedure for an input vector, as presented in the rightmost two columns therein.

As can be found in Table 3, Table 4 and Table 5, the upgraded version of BSS-VQ outperforms its counterparts to a great extent with respect to the search load required in each codebook. Particularly, Table 6 gives a clear view of the LR comparisons. As tabulated therein, the codebook search, required in CB1 and CB2 at stage 1, occupies a high percentage of the search load in an entire VQ encoding procedure. For instance, the full search algorithm requires a search load of 4096 (= 256 × 9 + 256 × 7) at stage 1, accounting for 77% of a 5280 overall search load, as tabulated in Table 3 and Table 6.

A further observation in Table 6 reveals that the corresponding values of LR in CB1 and CB2 are close among various search algorithms, but exclusive of the original version of BSS-VQ, and this fact applies to the values of overall LR as well. This finding validates the argument that the search performance of BSS-VQ is affected by codeword distributions, and the adverse distribution effect can be eased using the presented search algorithm. Furthermore, the upgraded version of BBS-VQ provides an overall LR of up to 94.20% at TQA = 0.90, and is experimentally validated to outperform its counterparts.

With the original version of BSS-VQ as a benchmark,

Table 7. Overall search load comparison between BSS-VQ and proposed algorithms.

TQA	BSS-VQ (Benchmark)	Proposed	LR (%)
0.90	528.78	306.41	42.05
0.91	548.77	314.19	42.75
0.92	570.76	323.09	43.39
0.93	595.34	332.32	44.18
0.94	624.92	342.42	45.21
0.95	657.95	353.80	46.23
0.96	696.62	367.20	47.29
0.97	743.15	382.26	48.56
0.98	808.06	404.15	49.99
0.99	902.67	435.10	51.80

exclusively gives an overall search load reduction using the presented algorithm versus TQA. As tabulated therein, the values of LR range between 42.05 and 51.80%, a significant outperformance over the benchmark.

On the other hand,

Table 8. Memory required of lookup tables for presented algorithm.

Memory Size (Byte)	BSS Space	Dichotomy Position	TIE	Sum
CB1	524,288	36	326,400	850,724
CB2	131,072	28	326,400	457,500
CB11	2048	12	20,160	22,220
CB12	4096	12	81,280	85,388
CB13	4096	12	81,280	85,388
CB21	1024	12	4960	5996
CB22	2048	16	4960	7024
Sum	668,672	128	845,440	1,514,240

presents the memory required of lookup tables for the proposed algorithm. Table 8 is divided into three portions: Storage for BSS spaces, dichotomy positions, and TIE lookup tables. The memory size of each BSS space is equal to BSize x CSize x 4 (for FLOAT data type) bytes, each dichotomy position = Dim x 4 (FLOAT data type) bytes, and each TIE tables = CSize x (CSize – 1) x 5 (UINT8 + FLOAT data type). Accordingly, a total of 1.45 MB of memory is required for whole lookup tables in Table 8. The memory requirement is very small in this work. Finally, in our previous experiments, the linear prediction analysis and quantization occupied 8–13% of the total operation in an AMR-WB encoder, depending on the coding modes. In other words, this work could eliminate 7.5–12.2% of the total operation in the AMR-WB encoder.

5. Conclusions

A two-stage search algorithm is presented herein for the improvement of search performance in the ISF vector quantization of an AMR-WB speech codec. At stage 1, an input vector was assigned to a search subspace in an efficient manner using the BSS-VQ algorithm, and a codebook search was performed over the subspace using the ITIE approach at stage 2. Through the use of the codeword rejection mechanisms equipped in both stages, the search load was reduced remarkably as intended. Experimental results show that the upgraded version of BBS-VQ provided an overall LR of up to 94.20% at TQA = 0.90, and was validated to outperform its counterparts. As compared with the original version of the BSS-VQ algorithm, the upgraded version provided a computational load reduction of up to 51%, a significant outperformance over the benchmark. This work would be beneficial for reaching the energy saving requirement when implemented on an AMR-WB codec of mobile devices. On the other hand, the contribution of this work is also applicable to the speech coding in EVS codec, which is a new standard of audio codec and provides interoperation with AMR-WB. In future work, the authors will pay their efforts to make further improvements on the computational complexity of EVS codec.