Assessing the Human Resource in Science and Technology for Asian Countries: Application of Fuzzy AHP and Fuzzy TOPSIS
Abstract
:1. Introduction
2. Literature Review
2.1. HRST Competitiveness
2.2. Indicators of HRST Competitiveness
2.2.1. Infrastructure Indicators
2.2.2. Input Indicators
2.2.3. Output Indicators
3. Methods
3.1. Fuzzy AHP
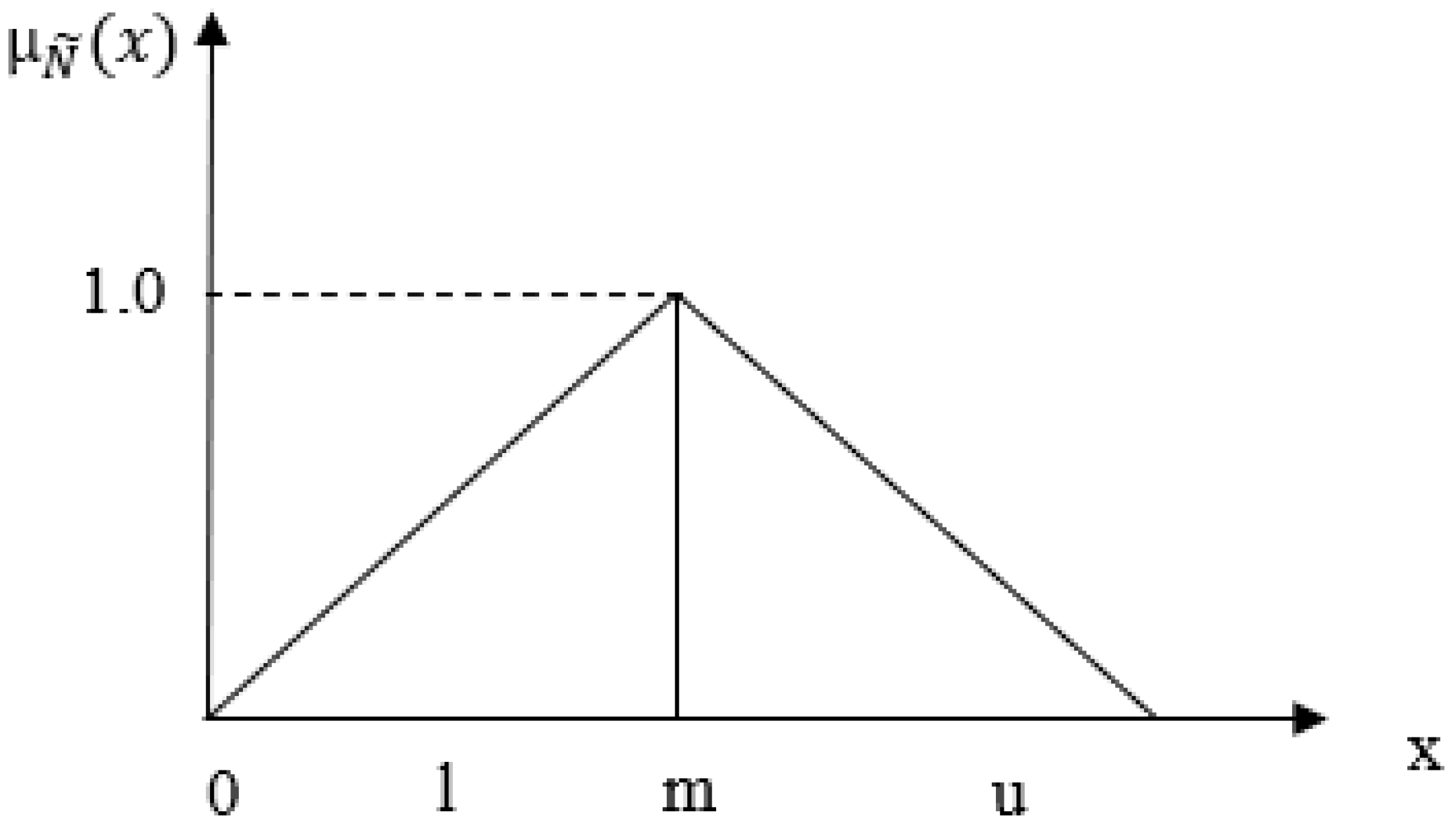
3.1.1. Establishing Fuzzy Numbers
3.1.2. Determining the Linguistic Variables
3.1.3. The Fuzzy AHP Method
- Step 1:
- Conduct pair-wise comparison matrices for all criteria in the dimensions of the hierarchy system. Equation (7) shows that represents the kth decision makers’ preference of the ith criterion over the jth criterion via TFNs.
- Step 2:
- If more than one decision maker is present, then the preferences for each decision maker are average as shown in the following equation:
- Step 3:
- Update the pair-wise comparison matrices for all criteria in the hierarchy system dimensions on the basis of the averaged preferences.
- Step 4:
- Use the geometrical mean technique to define the fuzzy geometrical mean and fuzzy weights of each criterion.
- Step 5:
- Determine the fuzzy weight of the criteria.
- Step 6:
- Calculate the average and normalized weight criteria.
3.2. Fuzzy TOPSIS
- Step 1:
- Determine the weights of the evaluation criteria.The present study applies fuzzy AHP to determine fuzzy preference weights.
- Step 2:
- Construct the fuzzy decision matrix and choose the appropriate linguistic variables as alternatives for the criteria.,where is the performance rating of the alternative with respect to criterion evaluated by the th expert and .
- Step 3:
- Normalize the fuzzy decision matrix.The normalized fuzzy decision matrix denoted by is depicted as follows:Thereafter, the normalization process can be performed as follows:where . Alternatively, we can set the best aspired level and is equal to 1; otherwise, the worst is 0.The normalized continues to be TFNs. For trapezoidal fuzzy numbers, the normalization process can be performed in the same manner. The weighted fuzzy normalized decision matrix is stated as the following matrix :where .
- Step 4:
- Determine the fuzzy positive-ideal solution (FPIS) and fuzzy negative-ideal solution (FNIS).The weighted normalized fuzzy decision matrix indicates that the elements are normalized positive and their ranges belong to the closed interval [0,1]. Thereafter, we can define the FPIS (aspiration levels) and FNIS (the worst levels) as follows:where and ,
- Step 5:
- Calculate the distance of each alternative from FPIS and FNIS.The distances ( and ) of each alternative from and can be calculated using the area compensation method:
- Step 6:
- Obtain the closeness coefficients (relative gaps–degree) and improve the alternatives to achieve the aspiration levels in each criterion.
4. Empirical Data Analysis and Results
- (1)
- In accordance with the committee of sixteen representatives, if the relative importance of the dimensions is followed, then the pair-wise comparison matrices of the dimensions will be obtained. We apply the fuzzy numbers provided in Table 1 and transfer the linguistic scales to the corresponding fuzzy numbers.
- (2)
- Buckley [15] suggested computing the elements of synthetic pair-wise comparison matrix by using the geometric mean method., for as the example:The results can be obtained from the other matrix elements via the same computational procedure. Therefore, the synthetic pair-wise comparison matrices of the five representatives will be constructed as follows for matrix :
- (3)
- To calculate the fuzzy weights of dimensions, the computational procedures are displayed as the following components:Similarly, we can obtain the remaining as follows:The weight of each dimension can be calculated as follows:We can also calculate the remaining as follows:
- (4)
- The COA method is used to compute the value of the fuzzy weights of each dimension. As an example, the following calculation process is used to obtain the value of the weight of (Infrastructure):
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Roessner, J.D.; Porter, A.L.; Newman, N.; Cauffiel, D. Anticipating the future High-Tech competitiveness of nations. Technol. Forecast. Soc. Chang. 1996, 1, 133–149. [Google Scholar] [CrossRef]
- Bejaković, P.; Lowther, J. The Competitiveness of Croatia’s Human Resources; Institute of Public Finance: Zagreb, Croatia, 2004. [Google Scholar]
- Gao, X.; Wu, B. Research on enterprise human resource competitiveness based on BP ANN. Presented at the 2010 3rd IEEE International Conference on Computer Science and Information Technology (ICCSIT), Chengdu, China, 9–11 July 2010. [Google Scholar]
- Carlson, B. Human Resources, Technological Capacity and Competition in Latin America. Presented at the ECLAC-IDB Seminario: “Camino a la Competitividad”, WA, USA; 2001. [Google Scholar]
- IMD. The World Competitiveness Yearbook 2010; International Institute for Management Development (IMD): Lausanne, Switzerland, 2010. [Google Scholar]
- Chou, Y.-C.; Sun, C.-C.; Yen, H.-Y. Evaluating the criteria for human resource for science and technology based on integrated fuzzy AHP and fuzzy DEMATEL approach. Appl. Soft Comput. 2012, 12, 64–71. [Google Scholar] [CrossRef]
- Pawan, S. Legal measures and tax incentives for encouraging science and technology development: The examples of Japan, Korea and India. Technol. Soc. 1998, 20, 45–60. [Google Scholar]
- Sallehuddin, I. The role of university in promoting and developing technology: A case study of Universiti Teknologi Malaysia. High. Educ. Policy 1997, 2, 121–126. [Google Scholar]
- Oyebisi, T.O.; Agboola, A.A. The impact of the environment on the growth of Nigeria. Int. J. Inf. Manag. 2003, 23, 313–321. [Google Scholar] [CrossRef]
- Madanmohan, T.R.; Kumar, U.; Kumar, V. Import-led technological capability: A comparative analysis of Indian and Indonesian manufacturing firms. Technovation 2004, 24, 979–993. [Google Scholar] [CrossRef]
- Geisler, E. An integrated cost-performance model of research and development evaluation. Omega 1995, 3, 281–294. [Google Scholar] [CrossRef]
- Nagesh, K. Determinants of location of overseas R&D activity of multinational enterprises: The case of US and Japanese corporations. Res. Policy 2001, 30, 159–174. [Google Scholar]
- Jyoti Banwet, D.K.; Deshmukh, S.G. Evaluating performance of national R&D organizations using integrated DEA-AHP technique. Int. J. Prod. Perform. Manag. 2008, 57, 370–388. [Google Scholar]
- Lee, S.K.; Mogi, G.; Lee, S.K.; Hui, K.S.; Kim, J.W. Econometric analysis of the R&D performance in the national hydrogen energy technology development for measuring relative efficiency: The fuzzy AHP/DEA integrated model approach. Int. J. Hydrogen Energy 2010, 35, 2236–2246. [Google Scholar]
- Buckley, J.J. Fuzzy hierarchical analysis. Fuzzy Sets Syst. 1985, 17, 233–247. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Liou, J.J.H.; Yen, L.; Tzeng, G.H. Building an effective safety management system for airlines. J. Air Transp. Manag. 2007, 14, 20–26. [Google Scholar] [CrossRef]
- Yang, C.C.; Chen, B.S. Key quality performance evaluation using fuzzy AHP. J. Chin. Inst. Ind. Eng. 2004, 21, 543–550. [Google Scholar] [CrossRef]
- Hsieh, T.Y.; Lu, S.T.; Tzeng, G.H. Fuzzy MCDM approach for planning and design tenders selection in public office buildings. Int. J. Proj. Manag. 2004, 22, 573–584. [Google Scholar] [CrossRef]
- Gumus, A.T. Evaluation of hazardous waste transportation firms by using a two step fuzzy-AHP and TOPSIS methodology. Expert Syst. Appl. 2009, 36, 4067–4074. [Google Scholar] [CrossRef]
- Hwang, C.L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications; Lecture Notes in Economics and Mathematical Systems; Chapman and Hall/CRC: New York, NY, USA, 1981. [Google Scholar]
- Wang, T.C.; Chang, T.H. Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst. Appl. 2007, 33, 870–880. [Google Scholar] [CrossRef]
- Shadbegian, R.J.; Gray, W.B. Assessing multi-dimensional performance: Environmental and economic outcomes. J. Prod. Anal. 2006, 26, 213–234. [Google Scholar] [CrossRef]
- Kuo, M.S.; Tzeng, G.H.; Huang, W.C. Group decision making based on concepts of ideal and anti-ideal points in fuzzy environment. Math. Comput. Model. 2007, 45, 324–339. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Nebol, E. Selection of the strategic alliance partner in logistics value chain. Int. J. Prod. Econ. 2007, 113, 148–158. [Google Scholar] [CrossRef]
- Opricovic, S.; Tzeng, G.H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
| Saaty Scale | Definition | Fuzzy Triangle Scale |
|---|---|---|
| 1 | Equally important | (1,1,1) |
| 3 | Weakly important | (2,3,4) |
| 5 | Fairly important | (4,5,6) |
| 7 | Strongly important | (6,7,8) |
| 9 | Absolutely important | (9,9,9) |
| 2 | Intermittent values between two adjacent scales | (1,2,3) |
| 4 | (3,4,5) | |
| 6 | (5,6,7) | |
| 8 | (7,8,9) |
| Dimensions | Criteria | Sub-Criteria | Weights | BNP | Rank | |
|---|---|---|---|---|---|---|
| Infrastructure | (0.141,0.171,0.209) | |||||
| Education | (0.144,0.207,0.299) | |||||
| Higher education achievement | (0.115,0.169,0.245) | (0.002,0.006,0.015) | 0.008 | 23 | ||
| Total public expenditure on education | (0.170,0.249,0.361) | (0.003,0.009,0.023) | 0.012 | 19 | ||
| Science degrees | (0.224,0.325,0.475) | (0.005,0.012,0.030) | 0.015 | 18 | ||
| Language skills | (0.177,0.257,0.377) | (0.004,0.009,0.024) | 0.012 | 19 | ||
| Value | (0.187,0.280,0.418) | |||||
| Value of society | (0.166,0.218,0.290) | (0.004,0.010,0.025) | 0.013 | 16 | ||
| Youth interest in science | (0.266,0.349,0.461) | (0.007,0.017,0.040) | 0.021 | 13 | ||
| Flexibility and adaptability | (0.320,0.433,0.579) | (0.008,0.021,0.051) | 0.027 | 9 | ||
| Cooperation | (0.154,0.223,0.325) | |||||
| Technological cooperation | (0.369,0.522,0.717) | (0.008,0.020,0.049) | 0.026 | 10 | ||
| Knowledge Transfer | (0.166,0.224,0.310) | (0.004,0.009,0.021) | 0.011 | 21 | ||
| Development an application of technology | (0.186,0.254,0.360) | (0.004,0.010,0.024) | 0.013 | 16 | ||
| Labor Market | (0.192,0.290,0.433) | |||||
| Overall productivity | (0.066,0.088,0.121) | (0.002,0.004,0.011) | 0.006 | |||
| Compensation levels | (0.225,0.315,0.468) | (0.006,0.016,0.042) | 0.021 | 13 | ||
| Working hours | (0.410,0.597,0.838) | (0.011,0.030,0.076) | 0.039 | 8 | ||
| Input | (0.331,0.405,0.501) | |||||
| R&D Expenses | (0.622,0.748,0.888) | |||||
| Total expenditure on R&D per capita | (0.342,0.457,0.604) | (0.070,0.138,0.269) | 0.159 | 3 | ||
| Business expenditure on R&D per capita | (0.410,0.543,0.725) | (0.084,0.165,0.322) | 0.191 | 1 | ||
| Human Capital | (0.215,0.252,0.307) | |||||
| Total R&D personnel nationwide per capita | (0.295,0.389,0.511) | (0.021,0.040,0.079) | 0.046 | 7 | ||
| Total R&D personnel in business per capita | (0.323,0.432,0.578) | (0.023,0.044,0.089) | 0.052 | 5 | ||
| Qualified engineers | (0.134,0.179,0.241) | (0.010,0.018,0.037) | 0.022 | 12 | ||
| Output | (0.335,0.424,0.529) | |||||
| Intermediate output | (0.502,0.647,0.816) | |||||
| High-tech exports | (0.439,0.567,0.721) | (0.074,0.155,0.311) | 0.180 | 2 | ||
| Basic research | (0.343,0.433,0.558) | (0.058,0.119,0.241) | 0.139 | 4 | ||
| Immediate output | (0.282,0.353,0.459) | |||||
| Scientific articles | (0.437,0.604,0.816) | (0.041,0.090,0.198) | 0.110 | 21 | ||
| Patents granted to residents | (0.190,0.253,0.346) | (0.018,0.038,0.084) | 0.047 | 6 | ||
| Securing patents abroad | (0.109,0.143,0.195) | (0.010,0.021,0.047) | 0.026 | 10 |
| Linguistic Variable | Corresponding Triangular Fuzzy Number |
|---|---|
| Very poor (VP) | (0, 1, 3) |
| Poor (P) | (1, 3, 5) |
| Fair (F) | (3, 5, 7) |
| Good (G) | (5, 7, 9) |
| Very good (VG) | (7, 9,10) |
| Higher education achievement | (6.09,8.09,9.45) | (5.18,7.18,8.91) | (5.36,7.36,8.91) | (5.00,7.00,8.73) | (3.00,5.00,6.91) | (2.82,4.64,6.64) | (1.55,3.18,5.18) | (1.45,3.18,5.18) | (2.45,4.27,6.27) | |
| Total public expenditure on education | (5.36,7.36,9.00) | (4.82,6.82,8.64) | (3.91,5.91,7.82) | (4.27,6.27,8.27) | (2.45,4.45,6.45) | (2.91,4.64,6.55) | (1.45,3.00,4.91) | (1.18,2.82,4.82) | (2.09,3.73,5.73) | |
| Science degrees | (4.27,6.27,8.09) | (4.64,6.64,8.45) | (4.64,6.64,8.36) | (4.27,6.27,8.00) | (2.82,4.82,6.82) | (3.18,5.18,7.09) | (1.45,3.00,4.91) | (0.82,2.27,4.27) | (3.00,4.82,6.82) | |
| Language skills | (6.27,8.27,9.64) | (2.64,4.64,6.64) | (3.18,5.18,7.09) | (5.36,7.36,9.00) | (3.73,5.73,7.55) | (2.45,4.45,6.45) | (0.91,2.45,4.45) | (2.45,4.27,6.27) | (3.91,5.91,7.82) | |
| Value of society | (4.82,6.82,8.64) | (3.09,5.00,6.91) | (3.18,5.18,7.09) | (4.64,6.64,8.55) | (3.00,5.00,7.00) | (2.18,4.09,6.00) | (2.82,4.64,6.64) | (1.91,3.73,5.73) | (2.55,4.45,6.45) | |
| Youth interest in science | (3.73,5.73,7.64) | (3.91,5.91,7.73) | (4.27,6.27,8.18) | (3.00,5.00,7.00) | (2.45,4.45,6.45) | (3.55,5.55,7.45) | (1.82,3.73,5.73) | (1.64,3.55,5.55) | (3.91,5.91,7.91) | |
| Flexibility and adaptability | (4.45,6.45,8.27) | (3.55,5.55,7.45) | (5.00,7.00,8.73) | (5.36,7.36,9.09) | (2.64,4.64,6.64) | (2.90,4.80,6.70) | (2.82,4.64,6.64) | (2.55,4.45,6.45) | (3.18,5.18,7.09) | |
| Technological cooperation | (4.82,6.82,8.55) | (4.82,6.82,8.73) | (4.27,6.27,8.09) | (4.82,6.82,8.55) | (2.45,4.45,6.45) | (2.36,4.27,6.27) | (1.36,3.18,5.18) | (1.36,3.36,5.36) | (3.00,5.00,7.00) | |
| Knowledge transfer | (5.18,7.18,8.82) | (4.82,6.82,8.64) | (4.60,6.60,8.40) | (4.45,6.45,8.18) | (2.45,4.45,6.45) | (2.55,4.45,6.45) | (1.20,3.00,5.00) | (1.36,3.36,5.36) | (3.00,5.00,7.00) | |
| Development an application of technology | (5.18,7.18,8.91) | (4.82,6.82,8.55) | (4.64,6.64,8.55) | (4.45,6.45,8.27) | (2.36,4.27,6.18) | (2.55,4.45,6.45) | (1.09,2.82,4.82) | (0.82,2.64,4.64) | (2.82,4.82,6.82) | |
| Overall productivity | (5.73,7.73,9.36) | (5.55,7.55,9.27) | (5.73,7.73,9.27) | (5.73,7.73,9.27) | (3.18,5.18,7.18) | (3.55,5.55,7.27) | (1.82,3.73,5.73) | (1.64,3.55,5.55) | (3.36,5.36,7.27) | |
| Compensation levels | (5.73,7.73,9.27) | (4.27,6.27,8.18) | (4.09,6.09,8.09) | (5.18,7.18,8.82) | (2.82,4.82,6.82) | (2.09,4.09,6.09) | (1.73,3.55,5.55 | (1.18,3.00,5.00) | (1.91,3.73,5.73) | |
| Working hours | (5.18,7.18,9.00) | (4.27,6.27,8.09) | (3.73,5.55,7.27) | (4.45,6.45,8.18) | (3.55,5.55,7.36) | (3.09,5.00,6.82) | (2.91,4.82,6.73) | (2.82,4.82,6.73) | (3.09,5.00,6.91) | |
| Total expenditure on R&D per capita | (4.45,6.45,8.36) | (5.55,7.55,9.18) | (4.09,6.09,8.00) | (4.09,6.09,8.09) | (2.27,4.27,6.27) | (4.09,6.09,7.91) | (2.00,3.91,5.91) | (1.45,3.36,5.36) | (2.45,4.27,6.27) | |
| Business expenditure on R&D per capita | (4.82,6.82,8.64) | (5.00,7.00,8.73) | (3.91,5.91,7.91) | (3.73,5.73,7.64) | (2.45,4.45,6.45) | (3.36,5.36,7.18) | (1.91,3.73,5.73) | (1.64,3.55,5.55) | (2.27,4.09,6.09) | |
| Total R&D personnel nationwide per capita | (4.45,6.45,8.36) | (4.45,6.45,8.36) | (4.82,6.82,8.55) | (3.18,5.18,7.09) | (2.36,4.27,6.27) | (2.27,4.09,6.00) | (1.73,3.55,5.55) | (1.45,3.36,5.36) | (2.27,3.91,5.91) | |
| Total R&D personnel in business per capita | (5.18,7.18,8.82) | (4.64,6.64,8.36) | (4.09,6.09,7.91) | (4.09,6.09,7.91) | (2.36,4.27,6.27) | (2.45,4.27,6.27) | (1.91,3.73,5.73) | (1.64,3.55,5.55) | (2.36,4.09,6.00) | |
| Qualified engineers | (6.27,8.27,9.45) | (5.73,7.73,9.00) | (5.36,7.36,8.73) | (6.27,8.27,9.45) | (3.91,5.91,7.55) | (3.18,5.18,7.00) | (1.64,3.36,5.36) | (1.18,3.00,5.00) | (4.45,6.45,8.00) | |
| High-tech exports | (5.00,7.00,8.45) | (5.73,7.73,9.00) | (4.27,6.27,7.91) | (4.18,6.09,7.64) | (2.82,4.82,6.64) | (3.55,5.55,7.27) | (0.82,2.45,4.45) | (0.73,2.45,4.45) | (3.00,4.82,6.55) | |
| Basic research | (5.18,7.18,8.64) | (5.36,7.36,8.73) | (5.36,7.36,8.73) | (5.00,7.00,8.45) | (2.82,4.82,6.73) | (4.82,6.82,8.27) | (1.00,2.64,4.64) | (0.64,2.27,4.27) | (3.00,4.82,6.55) | |
| Scientific articles | (5.73,7.73,9.09) | (5.36,7.36,8.73) | (5.55,7.55,8.91) | (5.36,7.36,8.73) | (2.09,3.91,5.82) | (4.09,6.09,7.73) | (0.73,2.27,4.27) | (0.36,1.73,3.73) | (3.55,5.36,7.00) | |
| Patents granted to residents | (4.45,6.45,8.00) | (6.09,8.09,9.27) | (5.55,7.55,8.91) | (4.00,5.91,7.45) | (2.09,3.91,5.82) | (3.55,5.55,7.27) | (1.00,2.64,4.64) | (0.55,2.09,4.09) | (3.18,5.00,6.73) | |
| Securing patents abroad | (4.73,6.64,8.09) | (6.09,8.09,9.27) | (5.55,7.55,8.91) | (3.91,5.91,7.55) | (2.27,4.09,5.91) | (3.00,5.00,6.82) | (0.73,2.27,4.27) | (0.55,2.09,4.09) | (2.30,4.00,5.90) |
| Higher education achievement | (0.63,0.84,0.98) | (0.56,0.77,0.96) | (0.58,0.79,0.96) | (0.53,0.74,0.92) | (0.40,0.66,0.92) | (0.34,0.56,0.80) | (0.23,0.47,0.77) | (0.22,0.47,0.77) | (0.31,0.53,0.78) | |
| Total public expenditure on education | (0.56,0.76,0.93) | (0.52,0.74,0.93) | (0.42,0.64,0.84) | (0.45,0.66,0.88) | (0.33,0.59,0.86) | (0.35,0.56,0.79) | (0.22,0.45,0.73) | (0.18,0.42,0.72) | (0.26,0.47,0.72) | |
| Science degrees | (0.44,0.65,0.84) | (0.50,0.72,0.91) | (0.50,0.72,0.90) | (0.45,0.66,0.85) | (0.37,0.64,0.90) | (0.38,0.63,0.86) | (0.22,0.45,0.73) | (0.12,0.34,0.64) | (0.38,0.60,0.85) | |
| Language skills | (0.65,0.86,1.00) | (0.28,0.50,0.72) | (0.34,0.56,0.76) | (0.57,0.78,0.95) | (0.49,0.76,1.00) | (0.30,0.54,0.78) | (0.14,0.36,0.66) | (0.36,0.64,0.93) | (0.49,0.74,0.98) | |
| Value of society | (0.50,0.71,0.90) | (0.33,0.54,0.75) | (0.34,0.56,0.76) | (0.49,0.70,0.90) | (0.40,0.66,0.93) | (0.26,0.49,0.73) | (0.42,0.69,0.99) | (0.28,0.55,0.85) | (0.32,0.56,0.81) | |
| Youth interest in science | (0.39,0.59,0.79) | (0.42,0.64,0.83) | (0.46,0.68,0.88) | (0.32,0.53,0.74) | (0.33,0.59,0.86) | (0.43,0.67,0.90) | (0.27,0.55,0.85) | (0.24,0.53,0.82) | (0.49,0.74,0.99) | |
| Flexibility and adaptability | (0.46,0.67,0.86) | (0.38,0.60,0.80) | (0.54,0.75,0.94) | (0.57,0.78,0.96) | (0.35,0.61,0.88) | (0.35,0.58,0.81) | (0.42,0.69,0.99) | (0.38,0.66,0.96) | (0.40,0.65,0.89) | |
| Technological cooperation | (0.50,0.71,0.89) | (0.52,0.74,0.94) | (0.46,0.68,0.87) | (0.51,0.72,0.90) | (0.33,0.59,0.86) | (0.29,0.52,0.76) | (0.20,0.47,0.77) | (0.20,0.50,0.80) | (0.38,0.63,0.88) | |
| Knowledge transfer | (0.54,0.75,0.92) | (0.52,0.74,0.93) | (0.50,0.71,0.91) | (0.47,0.68,0.87) | (0.33,0.59,0.86) | (0.31,0.54,0.78) | (0.18,0.45,0.74) | (0.20,0.50,0.80) | (0.38,0.63,0.88) | |
| Development an application of technology | (0.54,0.75,0.92) | (0.52,0.74,0.92) | (0.50,0.72,0.92) | (0.47,0.68,0.88) | (0.31,0.57,0.82) | (0.31,0.54,0.78) | (0.16,0.42,0.72) | (0.12,0.39,0.69) | (0.35,0.60,0.85) | |
| Overall productivity | (0.59,0.80,0.97) | (0.60,0.81,1.00) | (0.62,0.83,1.00) | (0.61,0.82,0.98) | (0.42,0.69,0.95) | (0.43,0.67,0.88) | (0.27,0.55,0.85) | (0.24,0.53,0.82) | (0.42,0.67,0.91) | |
| Compensation levels | (0.59,0.80,0.96) | (0.46,0.68,0.88) | (0.44,0.66,0.87) | (0.55,0.76,0.93) | (0.37,0.64,0.90) | (0.25,0.49,0.74) | (0.26,0.53,0.82) | (0.18,0.45,0.74) | (0.24,0.47,0.72) | |
| Working hours | (0.54,0.75,0.93) | (0.46,0.68,0.87) | (0.40,0.60,0.78) | (0.47,0.68,0.87) | (0.47,0.73,0.98) | (0.37,0.60,0.82) | (0.43,0.72,1.00) | (0.42,0.72,1.00) | (0.39,0.63,0.86) | |
| Total expenditure on R&D per capita | (0.46,0.67,0.87) | (0.60,0.81,0.99) | (0.44,0.66,0.86) | (0.43,0.64,0.86) | (0.30,0.57,0.83) | (0.49,0.74,0.96) | (0.30,0.58,0.88) | (0.22,0.50,0.80) | (0.31,0.53,0.78) | |
| Business expenditure on R&D per capita | (0.50,0.71,0.90) | (0.54,0.75,0.94) | (0.42,0.64,0.85) | (0.39,0.61,0.81) | (0.33,0.59,0.86) | (0.41,0.65,0.87) | (0.28,0.55,0.85) | (0.24,0.53,0.82) | (0.28,0.51,0.76) | |
| Total R&D personnel nationwide per capita | (0.46,0.67,0.87) | (0.48,0.70,0.90) | (0.52,0.74,0.92) | (0.34,0.55,0.75) | (0.31,0.57,0.83) | (0.27,0.49,0.73) | (0.26,0.53,0.82) | (0.22,0.50,0.80) | (0.28,0.49,0.74) | |
| Total R&D personnel in business per capita | (0.54,0.75,0.92) | (0.50,0.72,0.90) | (0.44,0.66,0.85) | (0.43,0.64,0.84) | (0.31,0.57,0.83) | (0.30,0.52,0.76) | (0.28,0.55,0.85) | (0.24,0.53,0.82) | (0.30,0.51,0.75) | |
| Qualified engineers | (0.65,0.86,0.98) | (0.62,0.83,0.97) | (0.58,0.79,0.94) | (0.66,0.88,1.00) | (0.52,0.78,1.00) | (0.38,0.63,0.85) | (0.24,0.50,0.80) | (0.18,0.45,0.74) | (0.56,0.81,1.00) | |
| High-tech exports | (0.52,0.73,0.88) | (0.62,0.83,0.97) | (0.46,0.68,0.85) | (0.44,0.64,0.81) | (0.37,0.64,0.88) | (0.43,0.67,0.88) | (0.12,0.36,0.66) | (0.11,0.36,0.66) | (0.38,0.60,0.82) | |
| Basic research | (0.54,0.75,0.90) | (0.58,0.79,0.94) | (0.58,0.79,0.94) | (0.53,0.74,0.89) | (0.37,0.64,0.89) | (0.58,0.82,1.00) | (0.15,0.39,0.69) | (0.09,0.34,0.64) | (0.38,0.60,0.82) | |
| Scientific articles | (0.59,0.80,0.94) | (0.58,0.79,0.94) | (0.60,0.81,0.96) | (0.57,0.78,0.92) | (0.28,0.52,0.77) | (0.49,0.74,0.93) | (0.11,0.34,0.64) | (0.05,0.26,0.55) | (0.44,0.67,0.88) | |
| Patents granted to residents | (0.46,0.67,0.83) | (0.66,0.87,1.00) | (0.60,0.81,0.96) | (0.42,0.63,0.79) | (0.28,0.52,0.77) | (0.43,0.67,0.88) | (0.15,0.39,0.69) | (0.08,0.31,0.61) | (0.40,0.63,0.84) | |
| Securing patents abroad | (0.49,0.69,0.84) | (0.66,0.87,1.00) | (0.60,0.81,0.96) | (0.41,0.63,0.80) | (0.30,0.54,0.78) | (0.36,0.60,0.82) | (0.11,0.34,0.64) | (0.08,0.31,0.61) | (0.29,0.50,0.74) |
| Higher education achievement | (0.001,0.005,0.015) | (0.001,0.005,0.015 | (0.001,0.005,0.015) | (0.001,0.004,0.014) | (0.001,0.004,0.014) | (0.001,0.003,0.012) | (0.001,0.003,0.012) | (0.001,0.003,0.012) | (0.001,0.003,0.012) | |
| Total public expenditure on education | (0.002,0.007,0.021) | (0.002,0.006,0.021) | (0.001,0.006,0.019) | (0.002,0.006,0.020) | (0.001,0.005,0.019) | (0.001,0.005,0.018) | (0.001,0.004,0.016) | (0.001,0.004,0.016) | (0.001,0.004,0.016) | |
| Science degrees | (0.002,0.008,0.025) | (0.002,0.008,0.027) | (0.002,0.008,0.027) | (0.002,0.008,0.025) | (0.002,0.007,0.027) | (0.002,0.007,0.025) | (0.001,0.005,0.022) | (0.001,0.004,0.019) | (0.002,0.007,0.025) | |
| Language skills | (0.002,0.008,0.024) | (0.001,0.005,0.017) | (0.001,0.005,0.018) | (0.002,0.007,0.022) | (0.002,0.007,0.024) | (0.001,0.005,0.018) | (0.000,0.003,0.016) | (0.001,0.006,0.022) | (0.002,0.007,0.023) | |
| Value of society | (0.002,0.007,0.023) | (0.001,0.006,0.019) | (0.002,0.006,0.019) | (0.002,0.007,0.023) | (0.002,0.007,0.024) | (0.001,0.005,0.018) | (0.002,0.007,0.025) | (0.001,0.006,0.022) | (0.001,0.006,0.020) | |
| Youth interest in science | (0.003,0.010,0.032) | (0.003,0.011,0.034) | (0.003,0.011,0.036) | (0.002,0.009,0.030) | (0.002,0.010,0.035) | (0.003,0.011,0.036) | (0.002,0.009,0.034) | (0.002,0.009,0.033) | (0.003,0.012,0.040) | |
| Flexibility and adaptability | (0.004,0.014,0.044) | (0.003,0.012,0.041) | (0.005,0.016,0.048) | (0.005,0.016,0.049) | (0.003,0.013,0.045) | (0.003,0.012,0.041) | (0.004,0.014,0.050) | (0.003,0.014,0.049) | (0.003,0.013,0.045) | |
| Technological cooperation | (0.004,0.014,0.043) | (0.004,0.015,0.046) | (0.004,0.013,0.042) | (0.004,0.014,0.044) | (0.003,0.012,0.042) | (0.002,0.010,0.037) | (0.002,0.009,0.038) | (0.002,0.010,0.039) | (0.003,0.012,0.043) | |
| Knowledge transfer | (0.002,0.006,0.019) | (0.002,0.006,0.020) | (0.002,0.006,0.019) | (0.002,0.006,0.018) | (0.001,0.005,0.018) | (0.001,0.005,0.016) | (0.001,0.004,0.016) | (0.001,0.004,0.017) | (0.001,0.005,0.018) | |
| Development an application of technology | (0.002,0.007,0.023) | (0.002,0.007,0.023) | (0.002,0.007,0.023) | (0.002,0.007,0.021) | (0.001,0.005,0.020) | (0.001,0.005,0.019) | (0.001,0.004,0.017) | (0.000,0.004,0.017) | (0.001,0.006,0.021) | |
| Overall productivity | (0.001,0.003,0.011) | (0.001,0.004,0.011) | (0.001,0.004,0.011) | (0.001,0.004,0.011) | (0.001,0.003,0.010) | (0.001,0.003,0.010) | (0.000,0.002,0.009) | (0.000,0.002,0.009) | (0.001,0.003,0.010) | |
| Compensation levels | (0.004,0.012,0.041) | (0.003,0.011,0.037) | (0.003,0.010,0.037) | (0.003,0.012,0.040) | (0.002,0.010,0.038) | (0.002,0.008,0.031) | (0.002,0.008,0.035) | (0.001,0.007,0.031) | (0.001,0.007,0.030) | |
| Working hours | (0.006,0.022,0.071) | (0.005,0.020,0.066) | (0.004,0.018,0.060) | (0.005,0.020,0.066) | (0.005,0.022,0.074) | (0.004,0.018,0.063) | (0.005,0.021,0.076) | (0.005,0.021,0.076) | (0.004,0.018,0.066) | |
| Total expenditure on R&D per capita | (0.033,0.093,0.233) | (0.042,0.113,0.266) | (0.031,0.091,0.232) | (0.030,0.089,0.230) | (0.021,0.078,0.223) | (0.035,0.102,0.257) | (0.021,0.080,0.236) | (0.015,0.069,0.214) | (0.022,0.074,0.211) | |
| Business expenditure on R&D per capita | (0.042,0.117,0.289) | (0.046,0.124,0.303) | (0.036,0.105,0.275) | (0.033,0.100,0.260) | (0.027,0.097,0.276) | (0.034,0.107,0.280) | (0.024,0.091,0.275) | (0.021,0.087,0.266) | (0.024,0.084,0.245) | |
| Total R&D personnel nationwide per capita | (0.010,0.027,0.068) | (0.010,0.028,0.071) | (0.011,0.029,0.072) | (0.007,0.022,0.059) | (0.007,0.023,.065) | (0.006,0.020,0.057) | (0.005,0.021,0.065) | (0.005,0.020,0.063) | (0.006,0.019,0.058) | |
| Total R&D personnel in business per capita | (0.012,0.033,0.081) | (0.011,0.032,0.080) | (0.010,0.029,0.076) | (0.010,0.028,0.074) | (0.007,0.025,0.074) | (0.007,0.023,0.067) | (0.007,0.024,0.076) | (0.006,0.023,0.073) | (0.007,0.023,0.067) | |
| Qualified engineers | (0.006,0.016,0.036) | (0.006,0.015,0.036) | (0.006,0.015,0.035) | (0.006,0.016,0.037) | (0.005,0.014,0.037) | (0.004,0.011,0.031) | (0.002,0.009,0.029) | (0.002,0.008,0.027) | (0.005,0.015,0.037) | |
| High-tech exports | (0.038,0.113,0.273) | (0.046,0.130,0.302) | (0.034,0.105,0.265) | (0.033,0.100,0.251) | (0.028,0.099,0.274) | (0.032,0.104,0.273) | (0.009,0.057,0.206) | (0.008,0.057,0.206) | (0.028,0.094,0.254) | |
| Basic research | (0.031,0.088,0.216) | (0.033,0.094,0.227) | (0.033,0.094,0.227 | (0.030,0.088,0.215) | (0.022,0.076,0.215) | (0.034,0.098,0.241) | (0.009,0.047,0.166) | (0.005,0.040,0.153) | (0.022,0.071,0.197) | |
| Scientific articles | (0.025,0.072,0.187) | (0.024,0.072,0.187 | (0.025,0.074,0.190) | (0.023,0.070,0.183) | (0.011,0.047,0.153) | (0.020,0.067,0.185) | (0.004,0.031,0.126) | (0.002,0.023,0.110) | (0.018,0.061,0.173) | |
| Patents granted to residents | (0.008,0.025,0.070) | (0.012,0.033,0.084) | (0.011,0.031,0.081) | (0.008,0.024,0.066) | (0.005,0.020,0.065) | (0.008,0.025,0.074) | (0.003,0.015,0.058) | (0.001,0.012,0.051) | (0.007,0.024,0.071) | |
| Securing patents abroad | (0.005,0.015,0.040) | (0.007,0.019,0.047) | (0.006,0.017,0.046) | (0.004,0.013,0.038) | (0.003,0.012,0.037) | (0.004,0.013,0.039) | (0.001,0.007,0.030) | (0.001,0.007,0.029) | (0.003,0.011,0.035) |
| Countries | Gap degree of | Satisfaction degree of | |||
|---|---|---|---|---|---|
| Singapore | 22.074 | 1.174 | 0.950 | 0.0505 | |
| South Korea | 22.021 | 1.237 | 0.947 | 0.0532 | |
| Taiwan | 22.088 | 1.163 | 0.950 | 0.0500 | |
| Hong Kong | 22.127 | 1.115 | 0.952 | 0.0480 | |
| Malaysia | 22.168 | 1.104 | 0.953 | 0.0474 | |
| China | 22.118 | 1.143 | 0.951 | 0.0491 | |
| Thailand | 22.283 | 0.984 | 0.958 | 0.0423 | |
| Philippines | 22.328 | 0.934 | 0.960 | 0.0401 | |
| India | 22.200 | 1.052 | 0.955 | 0.0452 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chou, Y.-C.; Yen, H.-Y.; Dang, V.T.; Sun, C.-C. Assessing the Human Resource in Science and Technology for Asian Countries: Application of Fuzzy AHP and Fuzzy TOPSIS. Symmetry 2019, 11, 251. https://doi.org/10.3390/sym11020251
Chou Y-C, Yen H-Y, Dang VT, Sun C-C. Assessing the Human Resource in Science and Technology for Asian Countries: Application of Fuzzy AHP and Fuzzy TOPSIS. Symmetry. 2019; 11(2):251. https://doi.org/10.3390/sym11020251
Chicago/Turabian StyleChou, Ying-Chyi, Hsin-Yi Yen, Van Thac Dang, and Chia-Chi Sun. 2019. "Assessing the Human Resource in Science and Technology for Asian Countries: Application of Fuzzy AHP and Fuzzy TOPSIS" Symmetry 11, no. 2: 251. https://doi.org/10.3390/sym11020251
APA StyleChou, Y.-C., Yen, H.-Y., Dang, V. T., & Sun, C.-C. (2019). Assessing the Human Resource in Science and Technology for Asian Countries: Application of Fuzzy AHP and Fuzzy TOPSIS. Symmetry, 11(2), 251. https://doi.org/10.3390/sym11020251




