1. Introduction
A graph invariant
f is a function from the set of all graphs into any commutative ring, such that
f has the same value for any two isomorphic graphs. Graph invariants can be used to check whether two graphs are not isomorphic. If a graph invariant
f satisfies the condition that
implies
G and
H are isomorphic, then
f is called a complete graph invariant. The problem of finding complete graph invariants is closely related to the graph isomorphism problem. Up to now, no complete graph invariant for general graphs has been found. However, some complete graph invariants have been identified for special cases and graph classes (see, for example, [
1]).
Graph polynomials are graph invariants whose values are polynomials, which have been developed for measuring the structural information of networks and for characterizing graphs [
2]. Noy [
3] surveyed results for determining graphs that can be characterized by graph polynomials. In a series of papers [
1,
4,
5,
6], Dehmer et al. studied highly discriminating descriptors to distinguish graphs (networks) based on graph polynomials. In [
5], it was found that the graph invariants based on the zeros of permanental polynomials are quite efficient in distinguishing graphs. Balasubramanian and Parthasarathy [
7,
8] introduced the bivariate permanent polynomial of a graph and conjectured that this graph polynomial is a complete graph invariant. In [
9], Liu gave counterexamples to the conjecture by a computer search.
In order to find almost complete graph invariants, we introduce a graph polynomial by employing graph matrices and the permanent of a square matrix. We will see that this graph polynomial turns out to be quite efficient when we use it to distinguish graphs (networks).
The permanent of an
matrix
M with entries
is defined by
where the sum is over all permutations
of
. Valiant [
10] proved that computing the permanent is #P-complete, even when restricted to (0,1)-matrices. The permanental polynomial of
M, denoted by
, is defined to be the permanent of the characteristic matrix of
M; that is,
where
is the identity matrix of size
n.
Let be a graph with adjacency matrix and degree matrix . The Laplacian matrix and signless Laplacian matrix of G are defined by and , respectively. The ordinary permanental polynomial of a graph G is defined as the permanental polynomial of the adjacency matrix of G (i.e., ). We call (respectively, ) the Laplacian (respectively, the signless Laplacian) permanental polynomial of G.
The permanental polynomial
of a graph
G was first studied in mathematics by Merris et al. [
11], and it was first studied in the chemical literature by Kasum et al. [
12]. It was found that the coefficients and roots of
encode the structural information of a (chemical) graph
G (see, e.g., [
13,
14]). Characterization of graphs by the permanental polynomial has been investigated, see [
15,
16,
17,
18,
19]. The Laplacian permanental polynomial of a graph was first considered by Merris et al. [
11], and the signless Laplacian permanental polynomial was first studied by Faria [
20]. For more on permanental polynomials of graphs, we refer the reader to the survey [
21].
We consider a bivariate graph polynomial of a graph
G on
n vertices, defined by
It is easy to see that generalizes some well-known permanental polynomials of a graph G. For example, the ordinary permanental polynomial of G is , the Laplacian permanental polynomial of G is , and the signless Laplacian permanental polynomial of G is . We call the generalized permanental polynomial of G.
We can write the generalized permanental polynomial
in the coefficient form
The general problem is to achieve a better understanding of the coefficients of . For any graph polynomial, it is interesting to determine its ability to characterize or distinguish graphs. A natural question is how well the generalized permanental polynomial distinguishes graphs.
The rest of the paper is organized as follows. In
Section 2, we obtain the combinatorial expressions for the first five coefficients
,
,
,
, and
of
, and we compute the first five coefficients of
for some specific graphs. In
Section 3, we compute the generalized permanental polynomials for all graphs on at most 10 vertices, and we count the numbers of such graphs for which there is another graph with the same generalized permanental polynomial. The presented data shows that the generalized permanental polynomial is quite efficient in distinguishing graphs. It may serve as a powerful tool for dealing with graph isomorphisms.
2. Coefficients
In
Section 2.1, we obtain a general relation between the generalized and the ordinary permanental polynomials of graphs. Explicit expressions for the first five coefficients of the generalized permanental polynomial are given in
Section 2.2. As an application, we obtain the explicit expressions for the first five coefficients of the generalized permanental polynomials of some specific graphs in
Section 2.3.
2.1. Relation between the Generalized and the Ordinary Permanental Polynomials
First, we present two properties of the permanent.
Lemma 1. Let A, B, and C be three matrices. If A, B, and C differ only in the rth row (or column), and the rth row (or column) of C is the sum of the rth rows (or columns) of A and B, then = .
Lemma 2. Let be an matrix. Then, for any ,where denotes the matrix obtained by deleting the ith row and jth column from M. Since Lemmas 1 and 2 can be easily verified using the definition of the permanent, the proofs are omitted.
We need the following notations. Let
G =
be a graph with vertex set
and edge set
. Let
be the degree of
in
G. The degree matrix
of
G is the diagonal matrix whose
th entry is
. Let
be
k distinct vertices of
G. Then
denotes the subgraph obtained by deleting vertices
from
G. We use
to denote the graph obtained from
G by attaching to the vertex
a loop of weight
. Similarly,
stands for the graph obtained by attaching to both
and
loops of weight
and
, respectively. Finally,
is the graph obtained by attaching a loop of weight
to vertex
for each
. The adjacency matrix
of
is defined as the
matrix
with
By Lemmas 1 and 2, expanding along the
rth column, we can obtain the recursion relation
For example, expanding along the first column of
, we have
By repeated application of (
1) for
, we have
Additional iterations can be made to take into account loops on additional vertices. For loops on all
n vertices, the expression becomes
Let
. We see that the generalized permanental polynomial
of
G is the permanental polynomial of
; that is,
. If the degree sequence of
G is
, then
is precisely the adjacency matrix of
. Hence, we obtain a relation between the generalized and ordinary permanental polynomials as an immediate consequence of (
2).
Theorem 1. Let G be a graph on n vertices. Then, Theorem 1 was inspired by Gutman’s method [
22] for obtaining a general relation between the Laplacian and the ordinary characteristic polynomials of graphs. From Theorem 1, one can easily give a coefficient formula between the generalized and the ordinary permanental polynomials.
Theorem 2. Suppose that and . Then, 2.2. The First Five Coefficients of
In what follows, we use and to denote respectively the number of triangles (i.e., cycles of length 3) and quadrangles (i.e., cycles of length 4) of G, and denotes the number of triangles containing the vertex v of G.
Liu and Zhang [
15] obtained combinatorial expressions for the first five coefficients of the permanental polynomial of a graph.
Lemma 3 ([
15])
. Let G be a graph with n vertices and m edges, and let be the degree sequence of G. Suppose that . Then, Theorem 3. Let G be a graph with n vertices and m edges, and let be the degree sequence of G. Suppose that . Then Proof. It is obvious that
. By Theorem 2 and Lemma 3, we have
By a straightforward calculation, we have
and
Substituting (
4) and (
5) into (
3), we obtain
This completes the proof. ☐
Since = and = , we immediately obtain the combinatorial expressions for the first five coefficients of and by Theorem 3.
Corollary 1. Let G be a graph with n vertices and m edges, and let be the degree sequence of G. Suppose that , then Corollary 2. Let G be a graph with n vertices and m edges, and let be the degree sequence of G. Suppose that . Then, 2.3. Examples
In this subsection, by applying Theorem 3, we obtain the first five coefficients of the generalized permanental polynomials of some specific graphs: Paths, cycles, complete graphs, complete bipartite graphs, star graphs, and wheel graphs.
Example 1. Let () be the path on n vertices. We see at once that = , and for each vertex v of . By Theorem 3, we have Example 2. Let () be the cycle on n vertices. We see at once that = , and for each vertex v of . By Theorem 3, we have Example 3. Let () be the complete graph on n vertices. It is easy to check that = = , = = , and = = for each vertex v of . By Theorem 3, we have Example 4. Let () be the complete bipartite graph with partition sets of sizes a and b. We see at once that , = = , and for each vertex v of . By Theorem 3, we have Example 5. Let () be the star graph with vertices and n edges. We see at once that = , and for each vertex v of . By Theorem 3, we have Example 6. Let () be the wheel graph with vertices and edges. It is obvious that = . Let be the hub (i.e., the vertex of degree n) of . We see that and for other vertices v of . By Theorem 3, we have 3. Numerical Results
In this section, by computer we enumerate the generalized permanental polynomials for all graphs on at most 10 vertices, and we count the numbers of such graphs for which there is another graph with the same generalized permanental polynomial.
Two graphs G and H are said to be generalized co-permanental if they have the same generalized permanental polynomial. If a graph H is generalized co-permanental but non-isomorphic to G, then H is called a generalized co-permanental mate of G.
In order to compute the generalized permanental polynomials of graphs, we, first of all, have to generate the graphs by computer. We use nauty and Traces [
23] to generate all graphs on at most 10 vertices. Next, the generalized permanental polynomials of these graphs are calculated by a Maple procedure. Finally, we count the numbers of generalized co-permanental graphs.
The results are summarized in
Table 1.
Table 1 lists, for
, the total number of graphs on
n vertices, the total number of distinct generalized permanental polynomials of such graphs, the number of such graphs with a generalized co-permanental mate, the fraction of such graphs with a generalized co-permanental mate, and the size of the largest family of generalized co-permanental graphs.
In
Table 1, we see that the smallest generalized co-permanental graphs, with respect to the order, contain 10 vertices. Even more striking is that out of 12,005,168 graphs with 10 vertices, only 106 graphs could not be discriminated by the generalized permanental polynomial.
From Table 1 in [
9], we see that the smallest graphs that cannot be distinguished by the bivariate permanent polynomial, introduced by Balasubramanian and Parthasarathy, contain 8 vertices. By comparing the present data of
Table 1 with that of Table 1 in [
9], we find that the generalized permanental polynomial is more efficient than the bivariate permanent polynomial when we use them to distinguish graphs. From Tables 2 and 3 in [
5], it is seen that the generalized permanental polynomial is more efficient than the graph invariants based on the zeros of permanental polynomials of graphs. Comparing the present data of
Table 1 with that of Table 1 in [
24], we see that the generalized permanental polynomial is also superior to the the generalized characteristic polynomial when distinguishing graphs. So, the generalized permanental polynomial is quite efficient in distinguishing graphs.
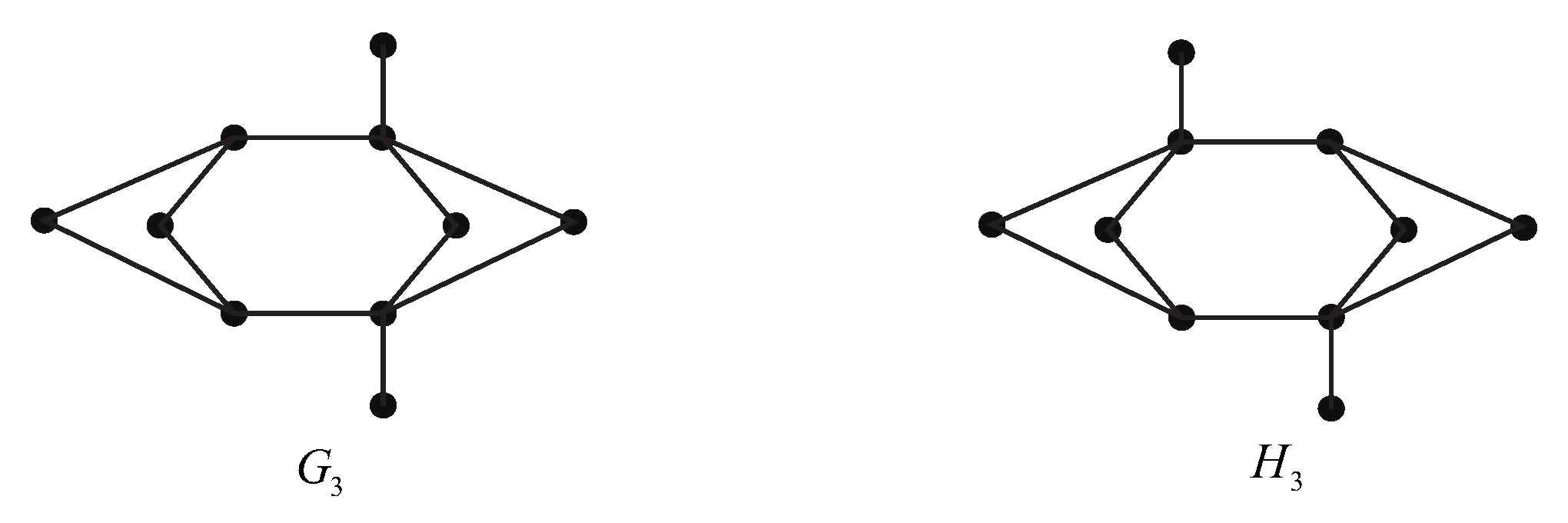
We enumerate all graphs on 10 vertices with a generalized co-permanental mate for each possible number of edges in
Appendix A. We see that the generalized co-permanental graphs
and
with 10 edges are disconnected (see
Figure 1), the generalized co-permanental graphs
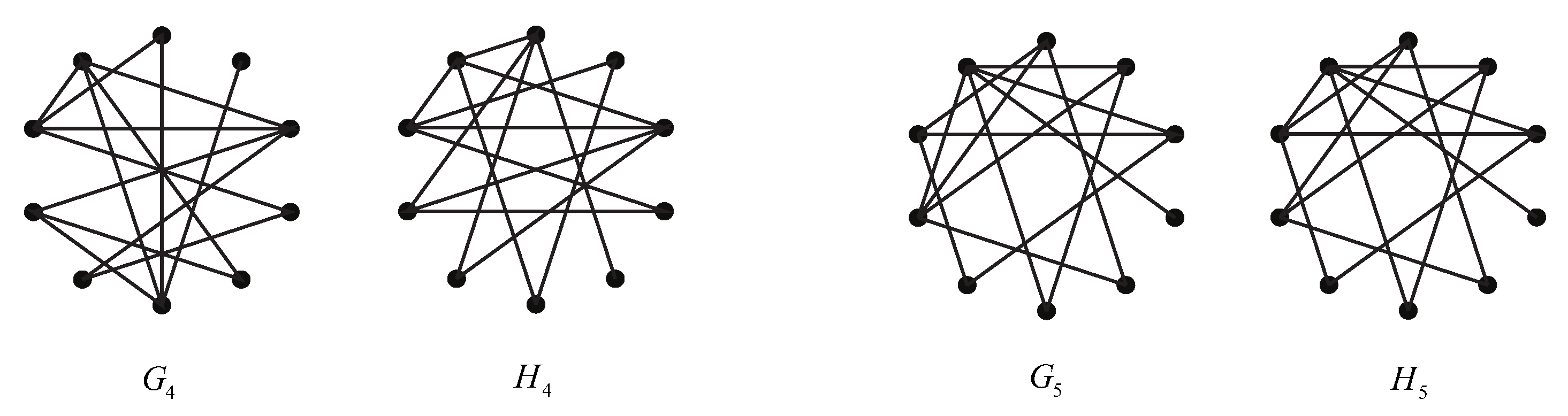
and
with 11 edges, and
and
with 12 edges are all bipartite (see
Figure 2 and
Figure 3), and two pairs
and
of generalized co-permanental graphs with 14 edges are all non-bipartite (see
Figure 4). The common generalized permanental polynomial of the smallest generalized co-permanental graphs
and
is