Nonclassical Symmetry Solutions for Non-Autonomous Reaction-Diffusion Equations
Abstract
:1. Introduction
2. Nonclassical Symmetries
2.1. Cubic
2.2.
2.2.1. and
2.2.2. and
2.2.3. and
3. Reduced Equations and Some Example Solutions
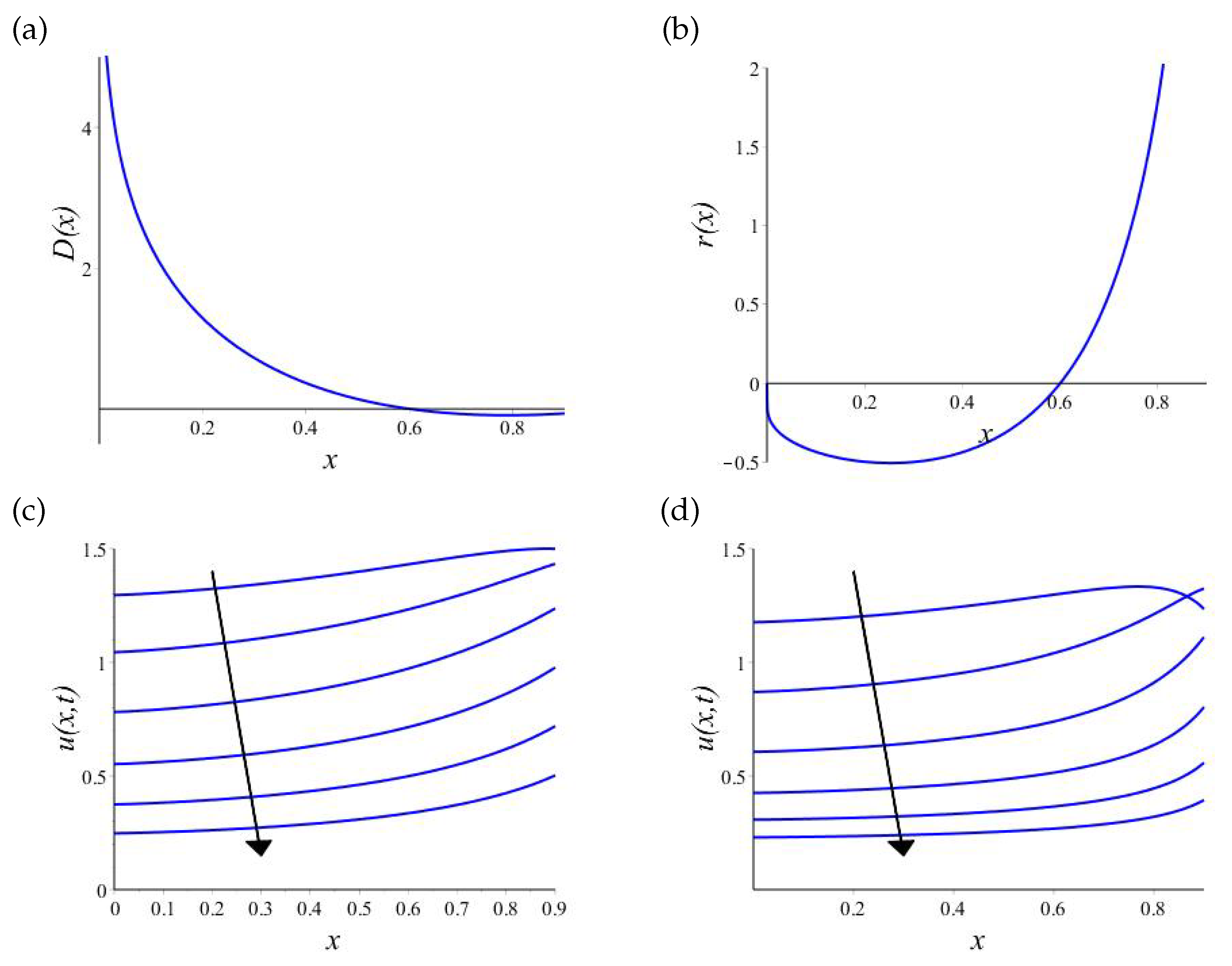
3.1. , ,
3.2. Arbitrary
3.2.1. Arbitrary, ,
3.2.2. Arbitrary, ,
3.2.3. Arbitrary, ,
4. Discussion and Final Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Aris, R. Mathematical Theory of Diffusion and Reaction in Permeable Catalysts I and II; Clarendon Press: Oxford, UK, 1975. [Google Scholar]
- Hill, J.M.; Smyth, N.F. On the mathematical analysis of hot-spots arising from microwave heating. Math. Eng. Ind. 1990, 2, 267–278. [Google Scholar]
- Fisher, R.A. The wave of advance of advantageous genes. Ann. Eugen. 1937, 7, 355–369. [Google Scholar] [CrossRef]
- Bradshaw-Hajek, B.H.; Edwards, M.P.; Broadbridge, P.; Williams, G.H. Nonclassical symmetry solutions for reaction-diffusion equations with explicit spatial dependence. Nonlinear Anal. Theor. 2007, 67, 2541–2552. [Google Scholar] [CrossRef]
- Scott, A.C. The electrophysics of a nerve fiber. Rev. Mod. Phys. 1975, 47, 487–533. [Google Scholar] [CrossRef]
- Simpson, M.J.; Landman, K.A.; Hughes, B.D.; Newgreen, D.F. Looking inside an invasion wave of cells using continuum models: Proliferation is the key. J. Theor. Biol. 2006, 243, 343–360. [Google Scholar] [CrossRef] [PubMed]
- Lane, D.C.; Murray, J.D.; Manoranjan, V.S. Analysis of wave phenomena in a morphogenetic mechanochemical model and an application to post-fertilization waves on eggs. Math. Med. Biol. 1987, 4, 309–331. [Google Scholar] [CrossRef]
- Bradshaw-Hajek, B.H.; Broadbridge, P. Analytic solutions for calcium ion fertilisation waves on the surface of eggs. Math. Med. Biol. 2019. accepted. [Google Scholar] [CrossRef] [PubMed]
- Cantrell, R.S.; Cosner, C. The effects of spatial heterogeneity in population dynamics. J. Math. Biol. 1991, 29, 315–338. [Google Scholar] [CrossRef]
- Benson, D.L.; Sherratt, J.A.; Maini, P.K. Diffusion driven instability in an inhomogeneous domain. Bull. Math. Biol. 1993, 55, 365–384. [Google Scholar] [CrossRef]
- Shigesada, N.; Kawasaki, K.; Teramoto, E. Spatial segregation of interacting species. J. Theor. Biol. 1979, 79, 83–99. [Google Scholar] [CrossRef]
- Pacala, S.W.; Roughgarden, J. Spatial heterogeneity and interspecific competition. Theor. Popul. Biol. 1982, 21, 92–113. [Google Scholar] [CrossRef]
- Hielscher, A.H.; Klose, A.D.; Hanson, K.M. Gradient-based iterative image reconstruction scheme for time-resolved optical tomography. IEEE Trans. Med. Imaging 1999, 18, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Zoppou, C.; Knight, J.H. Analytical solution of a spatially variable coefficient advection-diffusion equation in up to three dimensions. Appl. Math. Model. 1999, 23, 667–685. [Google Scholar] [CrossRef]
- Dorodnitsyn, V.A. Invariant solutions of the nonlinear heat equation with a source. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 1982, 22, 1393–1400. [Google Scholar]
- Galaktionov, V.A.; Dorodnitsyn, V.A.; Elenin, G.G.; Kurdyumov, S.P.; Samarskii, A.A. A quasilinear heat equation with a source: Peaking, localization, symmetry exact solutions, asymptotics, structures. J. Sov. Math. 1988, 41, 1222–1292. [Google Scholar] [CrossRef]
- Kametaka, Y. On the nonlinear diffusion equation of Kolmogorov-Petrovskii-Piskunov type. Osaka J. Math. 1976, 13, 11–66. [Google Scholar]
- McKean, H.P. Nagumo’s equation. Adv. Math. 1970, 4, 209–223. [Google Scholar] [CrossRef]
- Rinzel, J. Neutrally stable travelling wave solutions of nerve conduction equations. J. Math. Biol. 1975, 2, 205–217. [Google Scholar] [CrossRef]
- Carpenter, G.A. Periodic solutions of nerve impulse equations. J. Math. Anal. Appl. 1977, 58, 152–173. [Google Scholar] [CrossRef]
- Hastings, S. The existence of periodic solutions to Nagumo’s equations. Q. J. Math. 1974, 25, 369–378. [Google Scholar] [CrossRef]
- Conte, R. Universal invariance properties of Painlevé analysis and Bäcklund transformation in nonlinear partial differential equations. Phys. Lett. A 1988, 134, 100–104. [Google Scholar] [CrossRef]
- Chen, D.Y.; Gu, Y. Cole-Hopf quotient and exact solutions of the generalised Fitzhugh-Nagumo equations. Acta Math. Sci. 1999, 19, 7–14. [Google Scholar] [CrossRef]
- Kawahara, T.; Tanaka, M. Interactions of travelling fronts: An exact solution of a nonlinear diffusion equation. Phys. Lett. A 1983, 97, 311–314. [Google Scholar] [CrossRef]
- Arrigo, D.; Hill, J.M.; Broadbridge, P. Nonclassical symmetry reductions of the nonlinear diffusion equation with a nonlinear source. IMA J. Appl. Math. 1994, 52, 1–24. [Google Scholar] [CrossRef]
- Clarkson, P.A.; Mansfield, E.L. Symmetry reductions and exact solutions of a class of nonlinear heat equations. Physica D 1994, 70, 250–288. [Google Scholar] [CrossRef]
- Chen, Z.X.; Guo, B.Y. Analytic solutions of the Nagumo equation. IMA J. Appl. Math. 1992, 48, 107–115. [Google Scholar]
- Cherniha, R.; Serov, M. Symmetries, ansätze and exact solutions of nonlinear second-order evolution equations with convection terms. Eur. J. Appl. Math. 1998, 9, 527–542. [Google Scholar] [CrossRef]
- Cherniha, R. New Q-conditional symmetries and exact solutions of some reaction-diffusion-convection equations arising in mathematical biology. J. Math. Anal. Appl. 2007, 326, 783–799. [Google Scholar] [CrossRef]
- Cherniha, R.; Serov, M. Symmetries, ansätze and exact solutions of nonlinear second-order evolution equations with convection terms, II. Eur. J. Appl. Math. 2006, 17, 597–605. [Google Scholar] [CrossRef]
- Cherniha, R.; Serov, M.; Pliukhin, O. Nonlinear Reaction-Diffusion-Convection Equations: Lie and Conditional Symmetry, Exact Solutions and Their Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Joshi, N.; Morrison, T. New exact solutions of spatially and temporally varying reaction-diffusion equations. Anal. Appl. 2008, 6, 371–381. [Google Scholar] [CrossRef]
- Hashemi, M.S.; Nucci, M.C. Nonclassical symmetries for a class of reaction diffusion equations: the method of Heir-equations. J. Nonlinear Math. Phys. 2013, 20, 44–60. [Google Scholar] [CrossRef]
- Ivanova, N.M.; Sophocleous, C. On nonclassical symmetries of generalized Huxley equations. In Proceedings of the 5th International Workshop “Group Analysis of Differential Equations and Integrable Systems”, Protaras, Cyprus, 6–10 June 2010; pp. 91–98. [Google Scholar]
- Vaneeva, O.; Zhalij, A. Group classification of variable coefficient quasilinear reaction-diffusion equations. Publications de l Institut Mathematique-Beograd 2013, 94, 81–90. [Google Scholar] [CrossRef]
- Moitsheki, R.J.; Bradshaw-Hajek, B.H. Symmetry analysis of a heat conduction model for heat transfer in a longitudinal rectangular fin of a heterogeneous material. Commun. Nonlinear Sci. 2013, 18, 2374–2387. [Google Scholar] [CrossRef]
- Bradshaw-Hajek, B.H.; Moitsheki, R.J. Symmetry solutions for reaction-diffusion equations with spatially dependent diffusivity. Appl. Math. Comput. 2015, 254, 30–38. [Google Scholar] [CrossRef]
- Arrigo, D.J.; Hill, J.M. Nonclassical symmetries for nonlinear diffusion and absorption. Stud. Appl. Math. 1995, 94, 21–39. [Google Scholar] [CrossRef]
- Goard, J.M.; Broadbridge, P. Nonclassical symmetry analysis of nonlinear reaction-diffusion equations in two spatial dimensions. Nonlinear Anal. Theor. 1996, 26, 735–754. [Google Scholar] [CrossRef]
- Gilding, B.H.; Kersner, R. Travelling Waves in Nonlinear Diffusion-Convection Reaction; Birkhäuser: Basel, Switzerland, 2004. [Google Scholar]
- Vaneeva, O.O.; Popovych, R.O.; Sophocleous, C. Enhanced group analysis and exact solutions of variable coefficient semilinear diffusion equations with a power source. Acta Appl. Math. 2009, 106, 1–46. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Group to Differential Equations; AMS No 107; Springer: New York, NY, USA, 1982. [Google Scholar]
- Bluman, G.W.; Cole, J.D. The general similarity solution of the heat equation. J. Math. Mech. 1969, 18, 1025–1042. [Google Scholar]
- Zhdanov, R.Z.; Lahno, V.I. Conditional symmetry of a porous medium equation. Physica D 1998, 122, 178–186. [Google Scholar] [CrossRef]
- Broadbridge, P.; Bradshaw, B.H.; Fulford, G.R.; Aldis, G.K. Huxley and Fisher equations for gene propagation: An exact solution. ANZIAM J. 2002, 44, 11–20. [Google Scholar] [CrossRef]
- Bradshaw-Hajek, B.H.; Broadbridge, P. A robust cubic reaction-diffusion system for gene propagation. Math. Comput. Model. 2004, 39, 1151–1163. [Google Scholar] [CrossRef]
- Louw, K.; Moitsheki, R.J. Group-invariant solutions for the generalised Fisher type equation. Nat. Sci. 2015, 7, 613–624. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zaitsev, V.F. Handbook of Exact Solutions for Ordinary Differential Equations; Chapman and Hall/CRC: Boca/Raton, FL, USA, 2003. [Google Scholar]
- Broadbridge, P.; Bradshaw-Hajek, B.H. Exact solutions for logistic reaction-diffusion equations in biology. Z. Angew. Math. Phys. 2016, 67, 93. [Google Scholar] [CrossRef]
| Symmetry | Infinitesimals | ||
|---|---|---|---|
| 1 | n | ||
| 2(a) | n | ||
| arbitrary | |||
| 2(b) | c | ||
| arbitrary | |||
| 2(c) | c | ||
| arbitrary |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradshaw-Hajek, B.H. Nonclassical Symmetry Solutions for Non-Autonomous Reaction-Diffusion Equations. Symmetry 2019, 11, 208. https://doi.org/10.3390/sym11020208
Bradshaw-Hajek BH. Nonclassical Symmetry Solutions for Non-Autonomous Reaction-Diffusion Equations. Symmetry. 2019; 11(2):208. https://doi.org/10.3390/sym11020208
Chicago/Turabian StyleBradshaw-Hajek, Bronwyn H. 2019. "Nonclassical Symmetry Solutions for Non-Autonomous Reaction-Diffusion Equations" Symmetry 11, no. 2: 208. https://doi.org/10.3390/sym11020208
APA StyleBradshaw-Hajek, B. H. (2019). Nonclassical Symmetry Solutions for Non-Autonomous Reaction-Diffusion Equations. Symmetry, 11(2), 208. https://doi.org/10.3390/sym11020208





