Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions
Abstract
:1. Introduction
2. Problem Formulation
Physical Quantities of Interest
3. HAM Solution
4. Results and Discussion
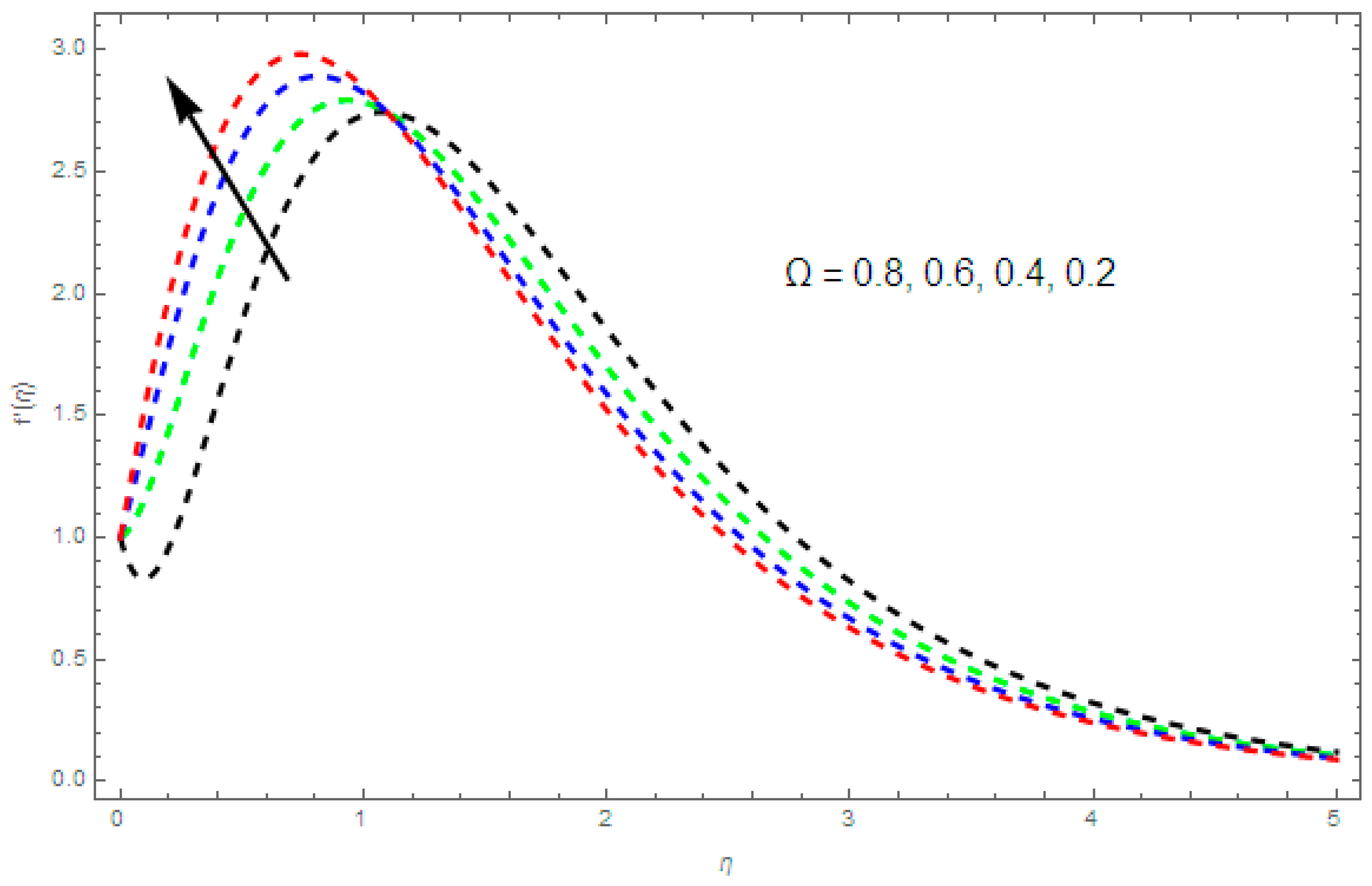
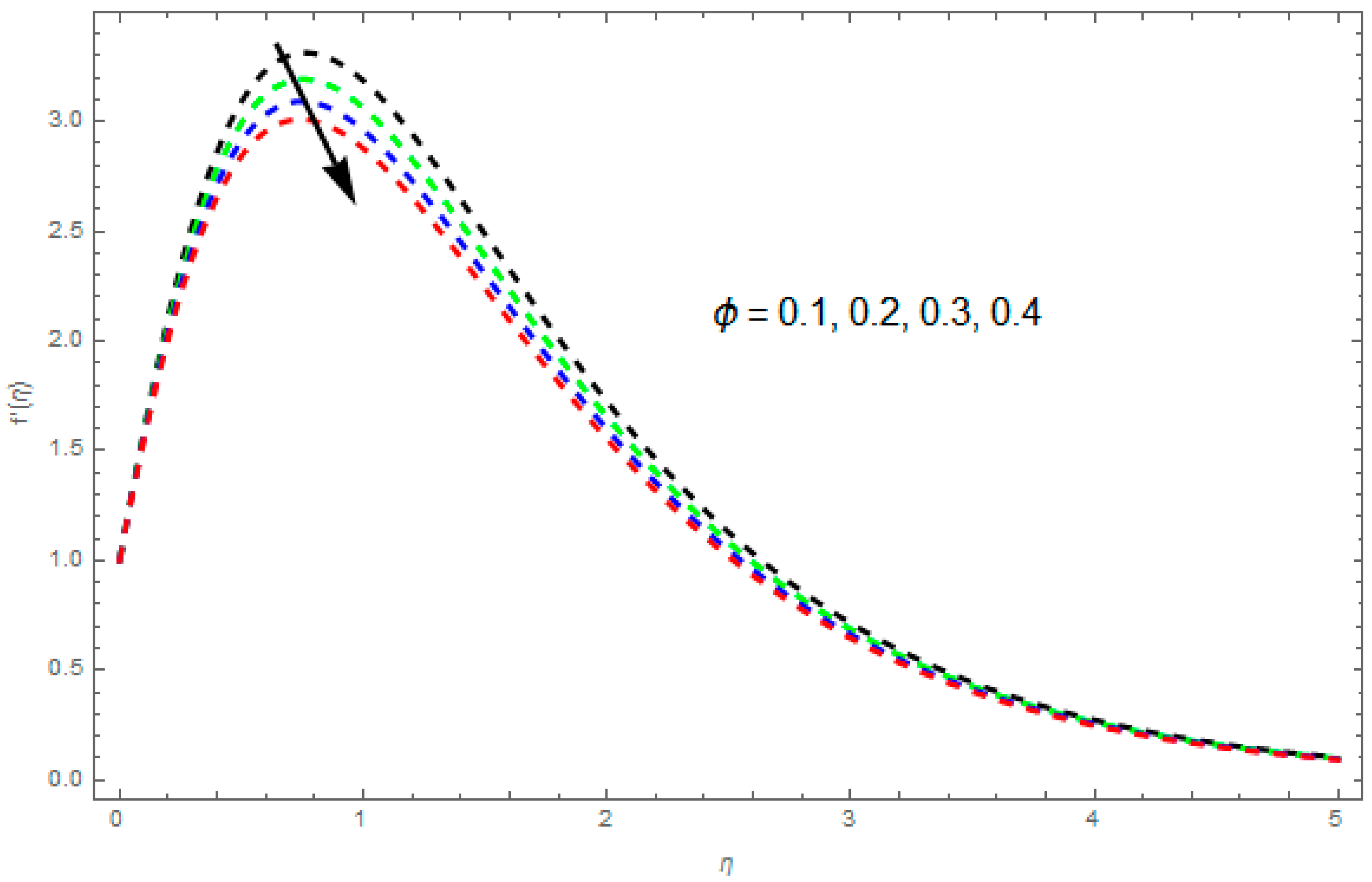
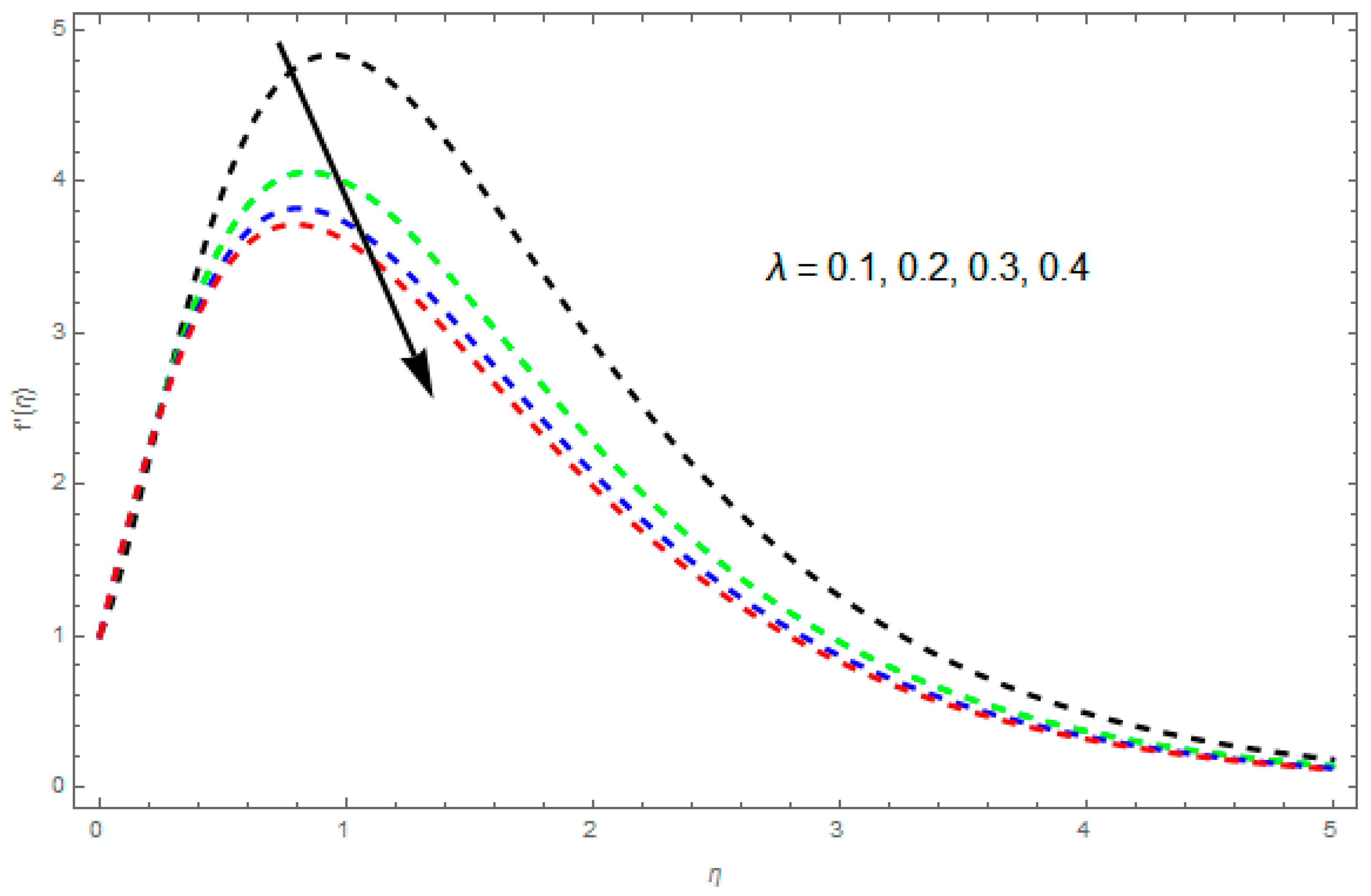
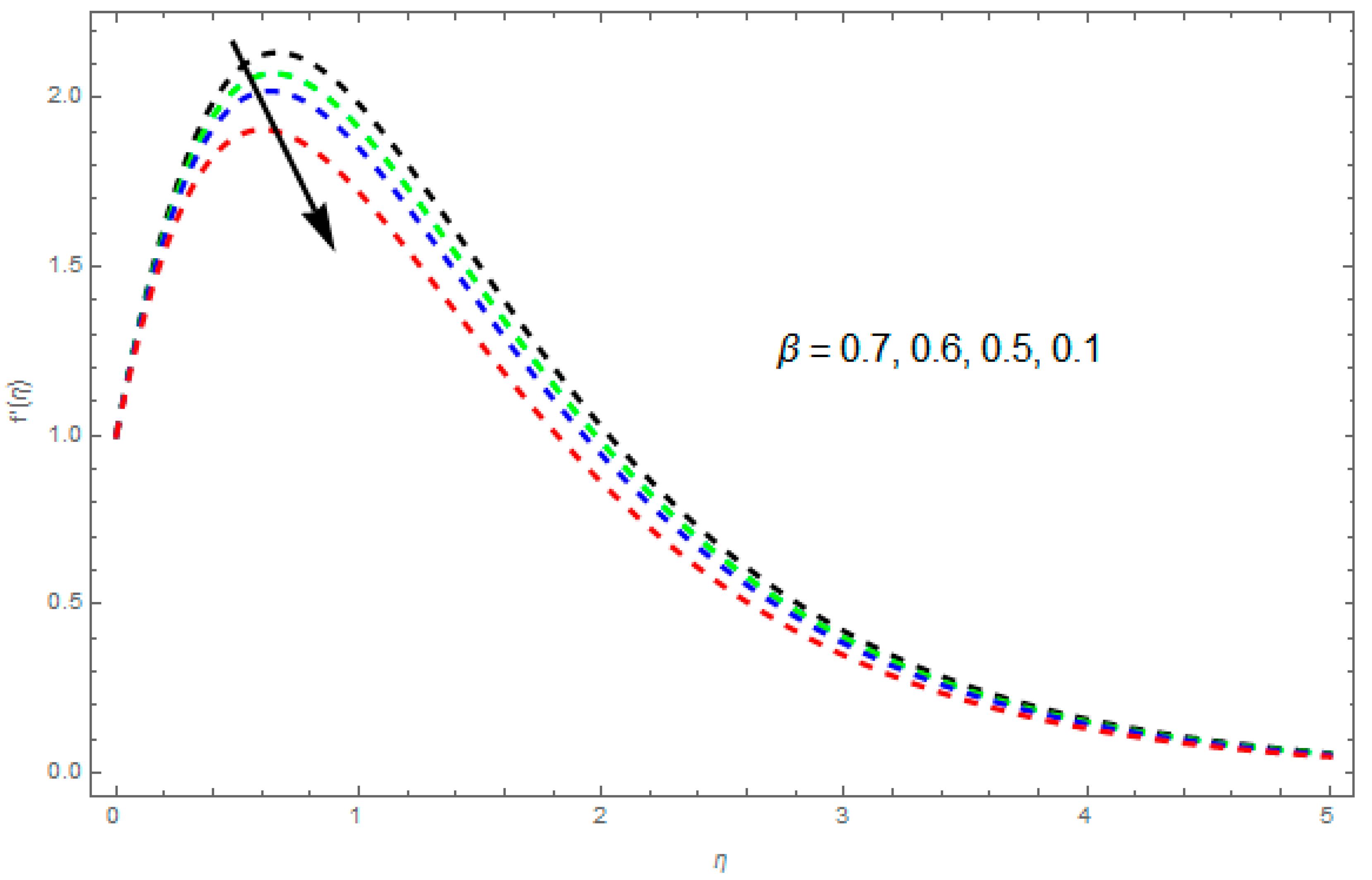
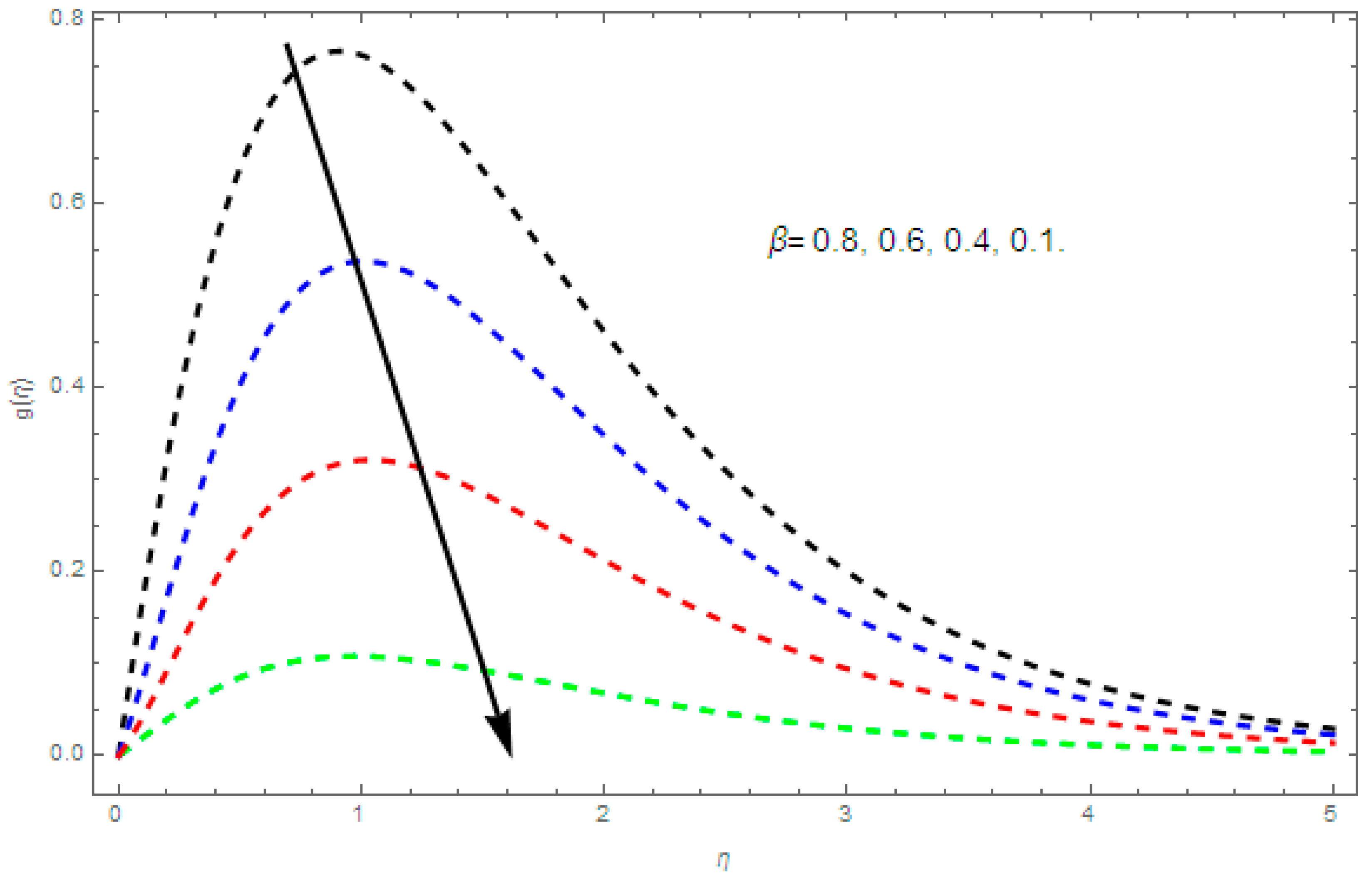
4.1. Velocity Profile and
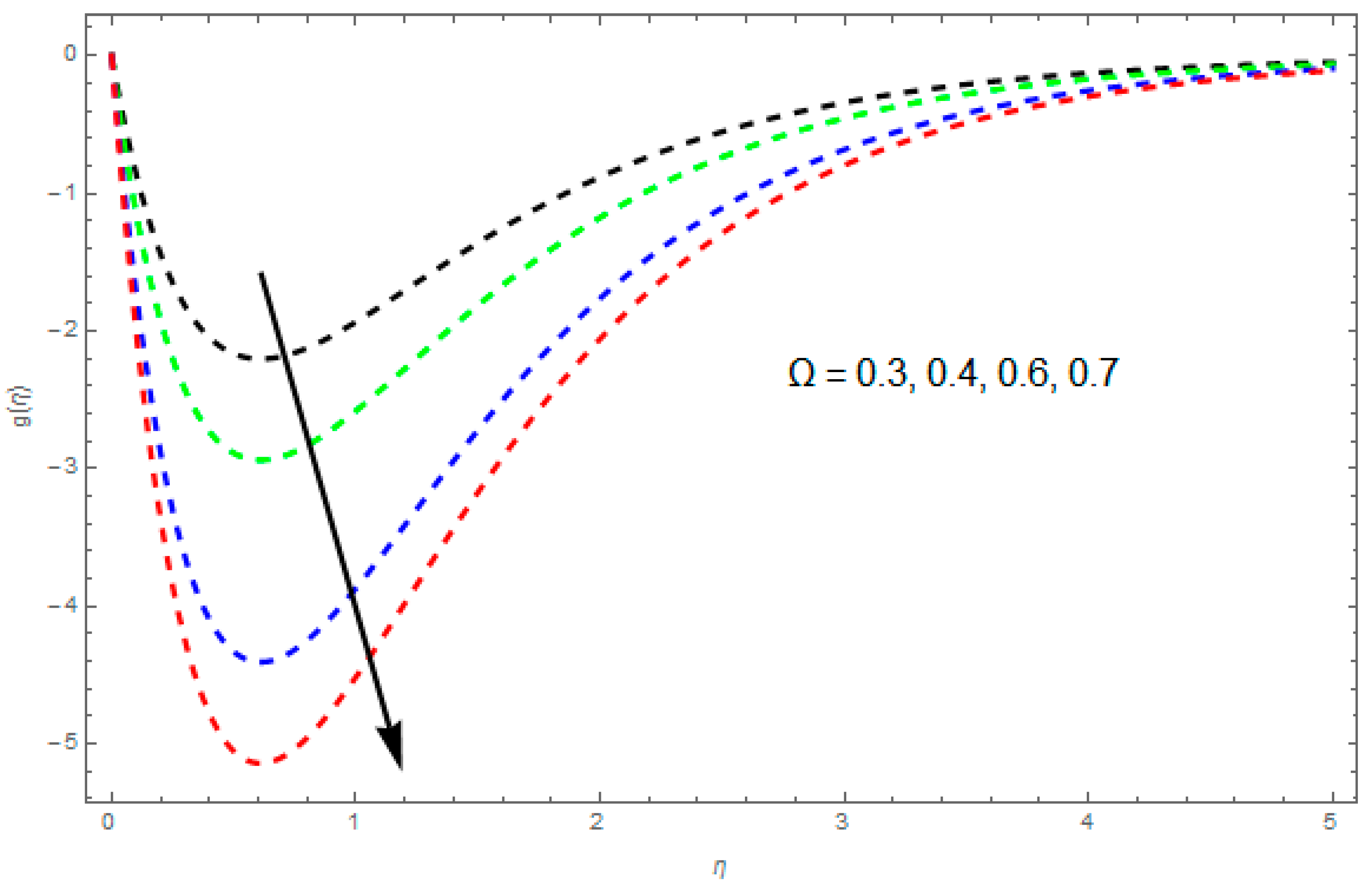
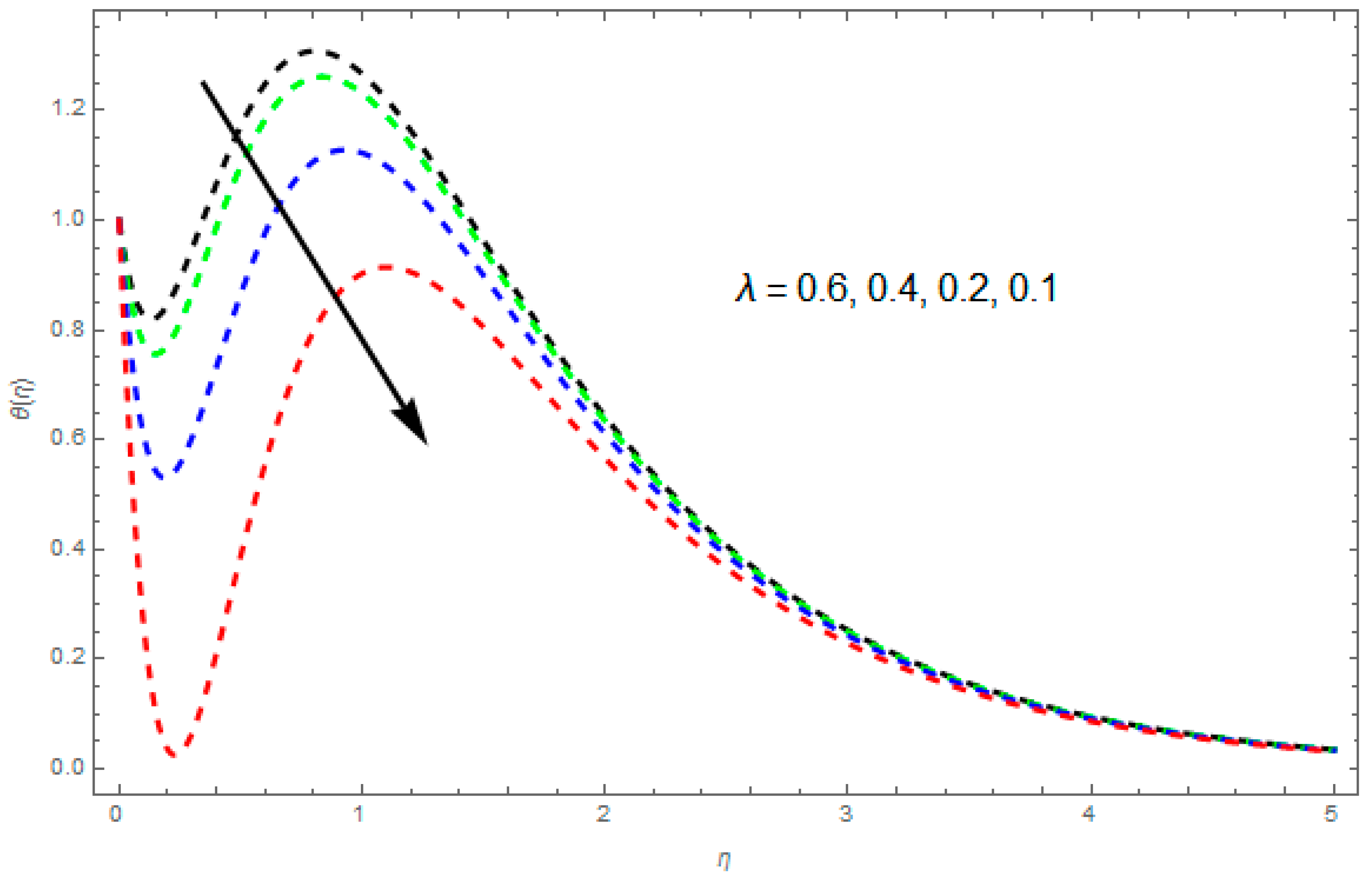
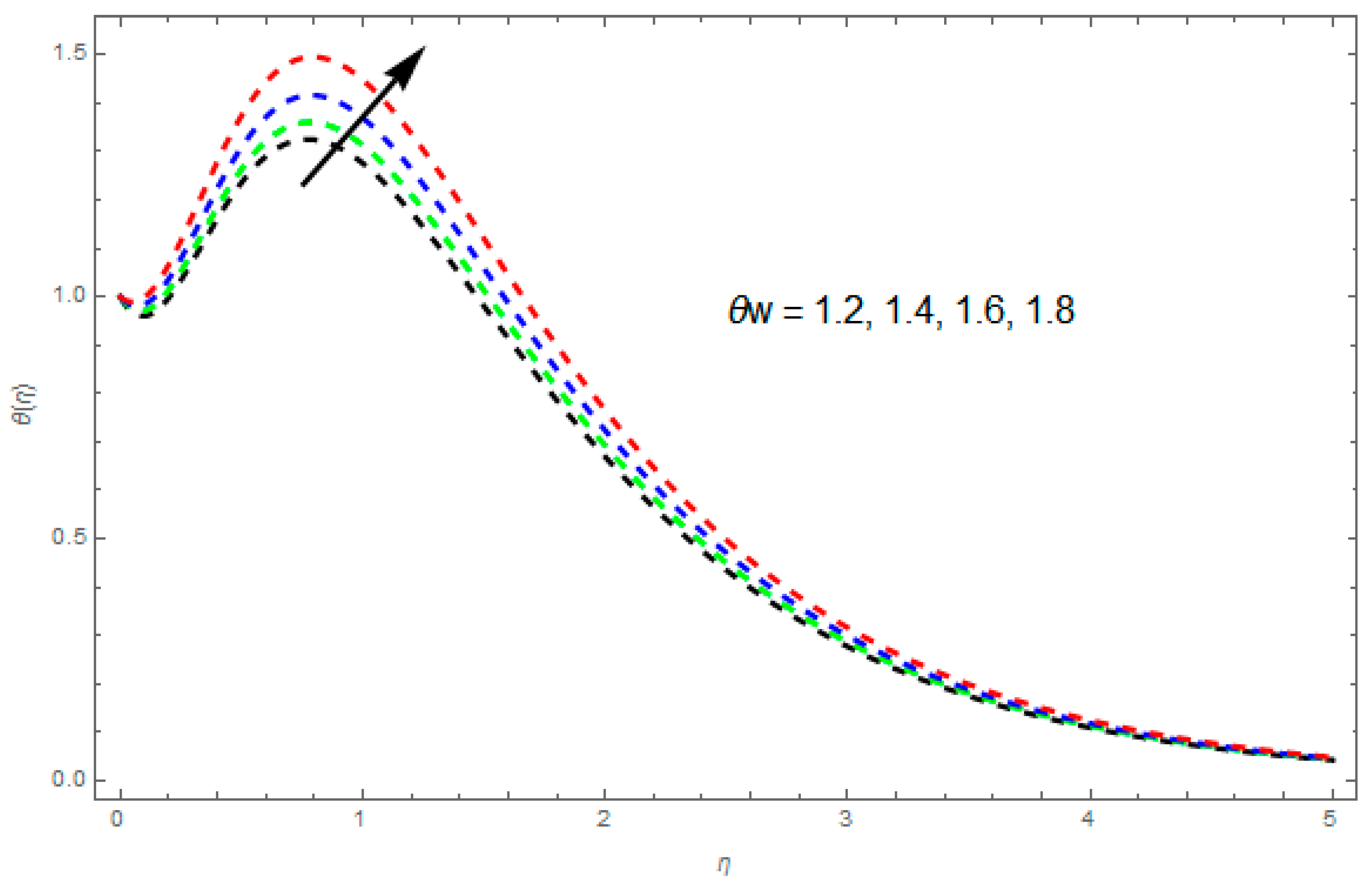
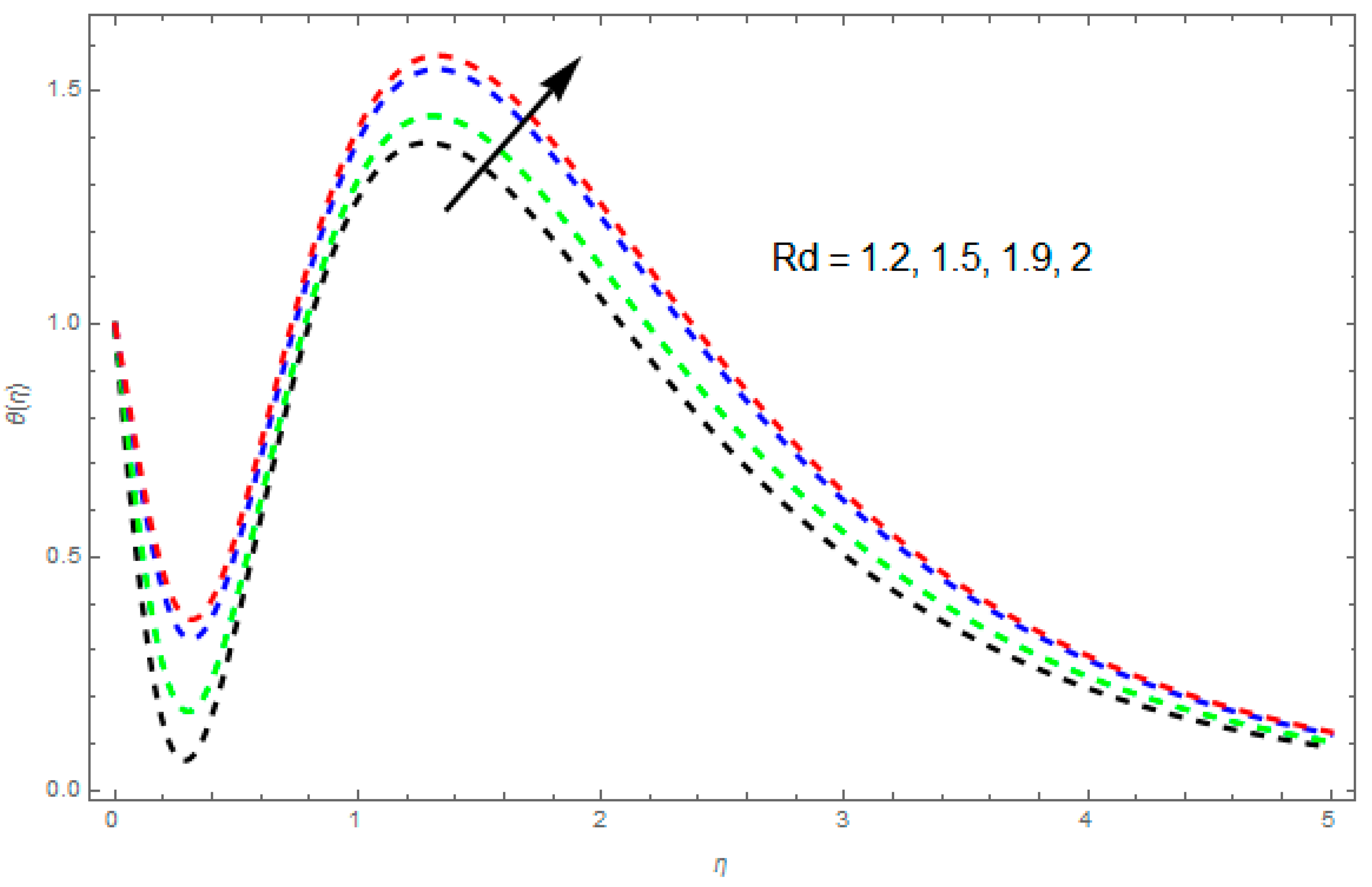
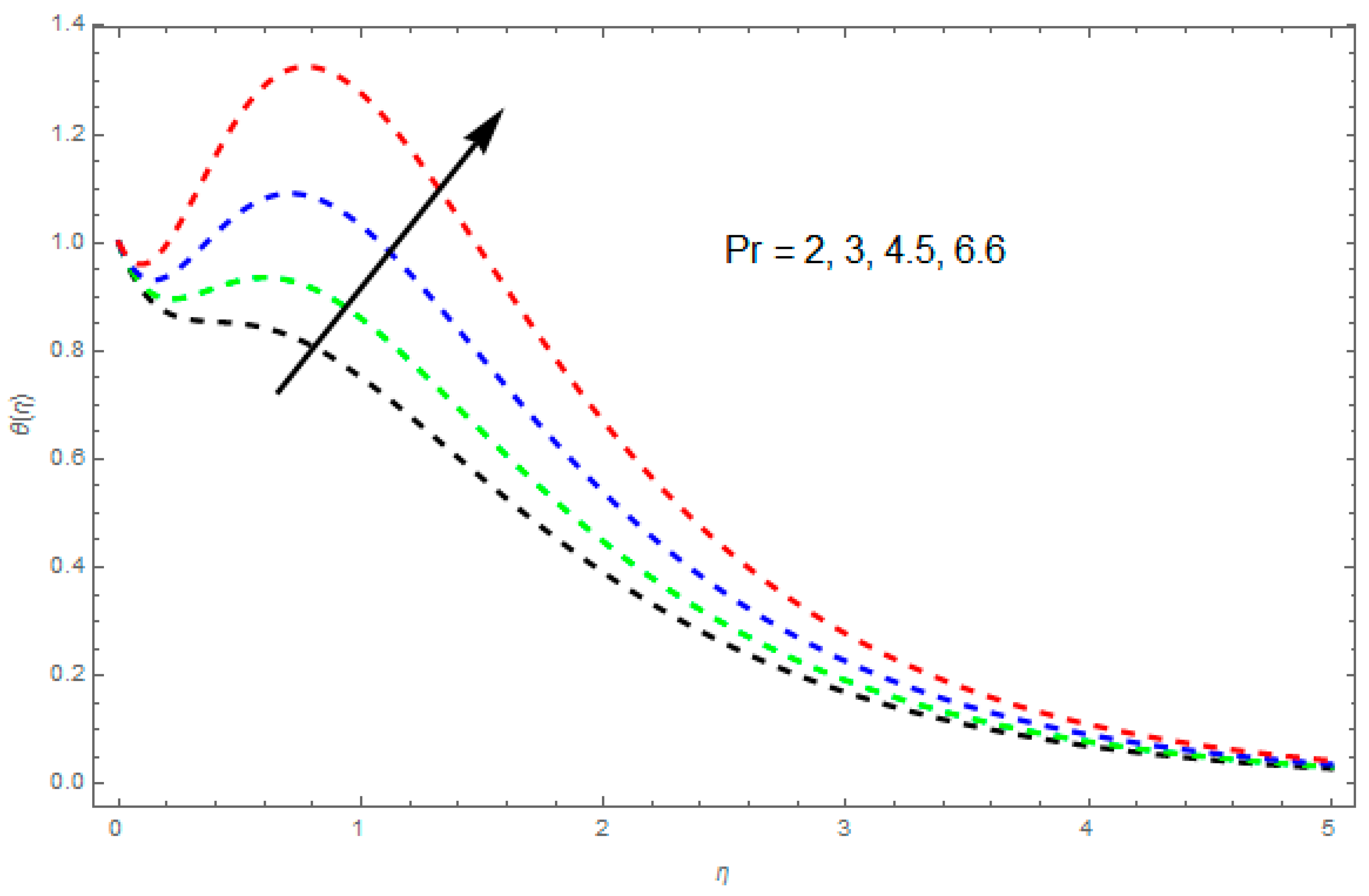
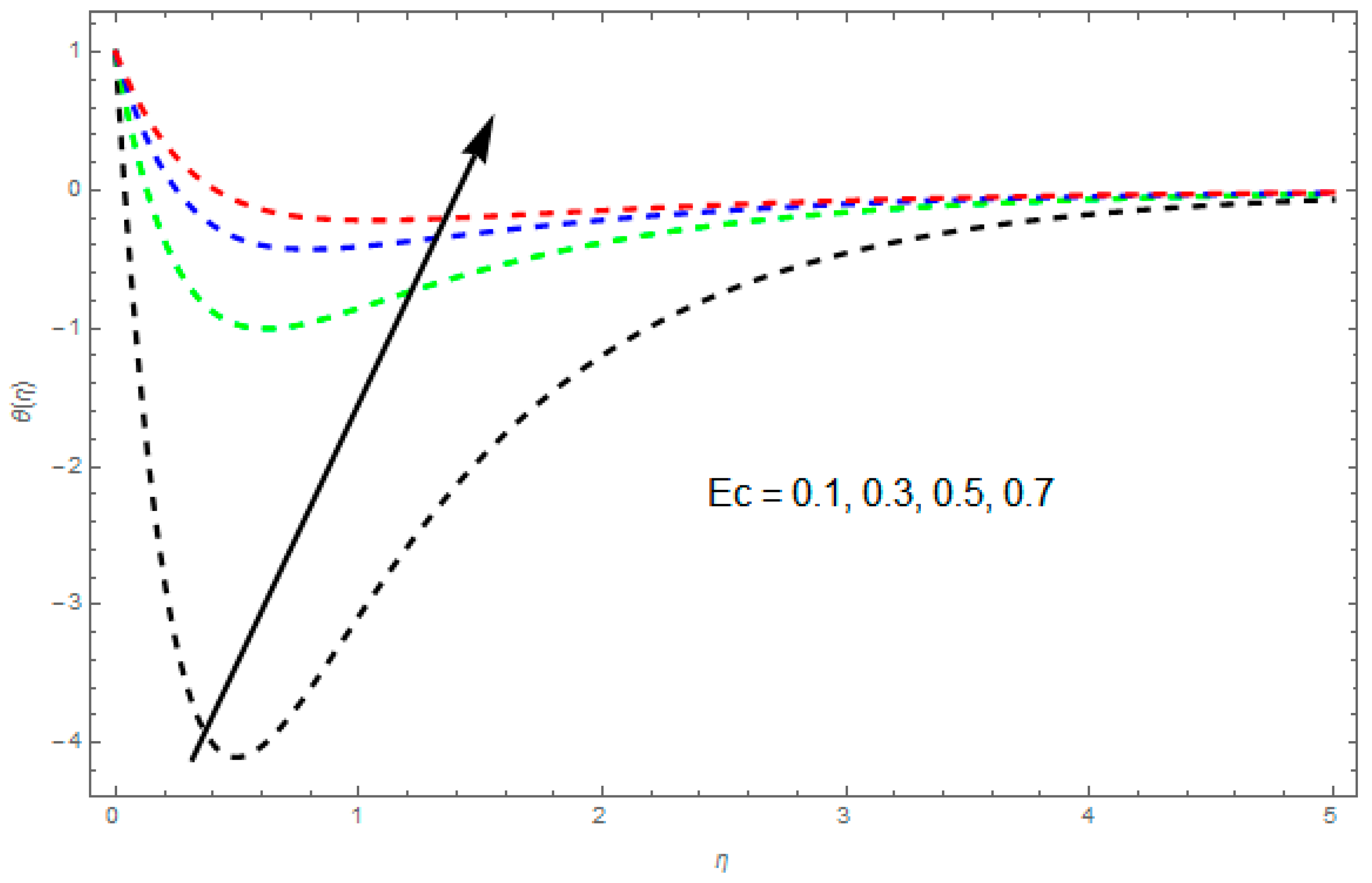
4.2. Temperature Profile
4.3. Table Discussion
5. Conclusions
- The thermal boundary layer thickness is reduced by a greater rotation rate parameter.
- Velocity and temperature profile decrease due to increases in the unsteadiness parameter.
- A greater increases the asset of frictional force within a fluid motion.
- The heat transfer rate rises for greater and values.
- The skin friction coefficient increases with increasing values of and .
- A greater value of and increases the heat flux, while a greater value of and decreases it.
- By enhancing , is reduced.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Khan, W.A. Buongiorno model for nanofluid Blasius flow with surface heat and mass fluxes. J. Thermophys. Heat Transf. 2013, 27, 134–141. [Google Scholar] [CrossRef]
- Mahdy, A.; Chamkha, A. Heat transfer and fluid flow of a non-Newtonian nano fluid over an unsteady contracting cylinder employing Buongiorno’smodel. Int. J. Numer. Method Heat Fluid Flow 2015, 25, 703–723. [Google Scholar] [CrossRef]
- Malvandi, A.; Moshizi, S.A.; Soltani, E.G.; Ganji, D.D. Modified Buongiorno’s model for fully developed mixed convection flow of nanofluids in a vertical annular pipe. Comput. Fluids 2014, 89, 124–132. [Google Scholar] [CrossRef]
- Hayat, T.; Ashraf, M.B.; Shehzad, S.A.; Abouelmaged, E.I. Three dimensional flow of Erying powell nanofluid over an exponentially stretching sheet. Int. J. Numer. Method Heat Fluid Flow 2015, 25, 333–357. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Lee, C.; Khan, Z.H. Numerical study of boundary layer flow and heat transfer of Oldroyed-B nanofluid towards a stretching sheet. PLoS ONE 2013, 8, e69811. [Google Scholar] [CrossRef] [PubMed]
- Rosmila, A.B.; Kandasamy, R.; Muhaimin, I. Lie symmetry groups transformation for MHD natural convection flow of nanofluid over linearly porous stretching sheet in presence of thermal stratification. Appl. Math. Mech. Engl. Ed. 2012, 33, 593–604. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD an temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. Series solution of unsteady Erying Powell nanofluid flow on a rotating cone. Indian J. Pure Appl. Phys. 2014, 52, 725–737. [Google Scholar]
- Abolbashari, M.H.; Freidoonimehr, N.; Rashidi, M.M. Analytical modeling of entropy generation for Casson nano-fluid flow induced by a stretching surface. Adv. Powder Technol. 2015, 6, 542–552. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Siginer, D.A.; Wang, H.P. Enhancing thermal conductivity of fluids with nanoparticle developments and applications of non-Newtonian flows. ASME N. Y. 1995, 66, 99–105. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. ASME J Heat Transf. 2005, 128, 240–250. [Google Scholar] [CrossRef]
- Kumar, K.G.; Rudraswamy, N.G.; Gireesha, B.J.; Krishnamurthy, M.R. Influence of nonlinear thermal radiation and viscous dissipation on three-dimensional flow of Jeffrey nanofluid over a stretching sheet in the presence of Joule heating. Nonlinear Eng. 2017, 6, 207–219. [Google Scholar]
- Rudraswamy, N.G.; Shehzad, S.A.; Kumar, K.G.; Gireesha, B.J. Numerical analysis of MHD three-dimensional Carreau nanoliquid flow over bidirectionally moving surface. J. Braz. Soc. Mech. Sci. Eng. 2017, 23, 5037–5047. [Google Scholar] [CrossRef]
- Gireesha, B.J.; Kumar, K.G.; Ramesh, G.K.; Prasannakumara, B.C. Nonlinear convective heat and mass transfer of Oldroyd-B nanofluid over a stretching sheet in the presence of uniform heat source/sink. Results Phys. 2018, 9, 1555–1563. [Google Scholar] [CrossRef]
- Kumar, K.G.; Gireesha, B.J.; Manjunatha, S.; Rudraswamy, N.G. Effect of nonlinear thermal radiation on double-diffusive mixed convection boundary layer flow of viscoelastic nanofluid over a stretching sheet. IJMME 2017, 12, 18. [Google Scholar]
- Nadeem, S.; Rehman, A.U.; Mehmood, R. Boundary layer flow of rotating two phase nanofluid over a stretching surface. Heat Transf. Asian Res. 2016, 45, 285–298. [Google Scholar] [CrossRef]
- Mabood, F.; Ibrahim, S.M.; Khan, W.A. Framing the features of Brownian motion and thermophoresis on radiative nanofluid flow past a rotating stretching sheet with magnetohydrodynamics. Results Phys. 2016, 6, 1015–1023. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Gul, T.; Bonyah, E.; Khan, M.A. The electrical MHD and hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. 2018, 9, 1201–1214. [Google Scholar] [CrossRef]
- Shah, Z.; Gul, T.; Khan, A.M.; Ali, I.; Islam, S. Effects of hall current on steady three dimensional non-newtonian nanofluid in a rotating frame with brownian motion and thermophoresis effects. J. Eng. Technol. 2017, 6, 280–296. [Google Scholar]
- Gireesha, B.J.; Ganesh, K.; Krishanamurthy, M.R.; Rudraswamy, N.G. Enhancement of heat transfer in an unsteady rotating flow for the aqueous suspensions of single wall nanotubes under nonlinear thermal radiation. Numer. Study 2018. [Google Scholar] [CrossRef]
- Ishaq, M.; Ali, G.; Shah, Z.; Islam, S.; Muhammad, S. Entropy Generation on Nanofluid Thin Film Flow of Eyring–Powell Fluid with Thermal Radiation and MHD Effect on an Unsteady Porous Stretching Sheet. Entropy 2018, 20, 412. [Google Scholar] [CrossRef]
- Sarit, K.D.; Stephen, U.S.; Choi Wenhua, Y.U.; Pradeep, T. Nanofluids Science and Technology; Wiley-Interscience: New Your, NY, USA, 2007; Volume 397. [Google Scholar]
- Wong, K.F.V.; Leon, O.D. Applications of nanofluids: Current and future. Adv. Mech. Eng. 2010, 2, 519659. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Haq, R.L.; Shafee, A.; Zhixiong, L. Heat transfer behavior of Nanoparticle enhanced PCM solidification through an enclosure with V shaped fins. Int. J. Heat Mass Transf. 2019, 130, 1322–1342. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Gerdroodbary, M.B.; Moradi, R.; Shafee, A.; Zhixiong, L. Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel. Comput. Methods Appl. Mech. Eng. 2019, 344, 1–12. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Mehryan, S.A.M.; Shafee, A.; Sheremet, M.A. Variable magnetic forces impact on Magnetizable hybrid nanofluid heat transfer through a circular cavity. J. Mol. Liquids 2019, 277, 388–396. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, D.; Cho, H.H.; Lee, J. The onset of double-diffusive nanofluid convection in a rotating porous medium layer with thermal conductivity and viscosity variation: A revised model. J. Porous Media 2016, 19, 31–46. [Google Scholar] [CrossRef]
- Yadav, D.; Nam, D.; Lee, J. The onset of transient Soret-driven MHD convection confined within a Hele-Shaw cell with nanoparticles suspension. J. Taiwan Inst. Chem. Eng. 2016, 58, 235–244. [Google Scholar] [CrossRef]
- Yadav, D.; Lee, J. The onset of MHD nanofluid convection with Hall current effect. Eur. Phys. J. Plus 2015, 130, 162–184. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C. Darcy-Forchheimer Flow of Radiative Carbon Nanotubes with Microstructure and Inertial Characteristics in the Rotating Frame. Case Stud. Therm. Eng. 2018, 12, 823–832. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Gul, T. Impact of thermal radiation on electrical mhd rotating flow of carbon nanotubes over a stretching sheet. AIP Adv. 2019, 9, 015115. [Google Scholar] [CrossRef]
- Shah, Z.; Dawar, A.; Islam, S.; Khan, I.; Ching, D.L.C.; Khan, Z.A. Cattaneo-Christov model for Electrical MagnetiteMicropoler Casson Ferrofluid over a stretching/shrinking sheet using effective thermal conductivity model. Case Stud. Therm. Eng. 2018. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Islam, S.; Idress, M.; Khan, W. Magnetohydrodynamic CNTs Casson Nanofl uid and Radiative heat transfer in a Rotating Channels. J. Phys. Res. Appl. 2018, 1, 017–032. [Google Scholar]
- Khan, A.S.; Nie, Y.; Shah, Z.; Dawar, A.; Khan, W.; Islam, S. Three-Dimensional Nanofluid Flow with Heat and Mass Transfer Analysis over a Linear Stretching Surface with Convective Boundary Conditions. Appl. Sci. 2018, 8, 2244. [Google Scholar] [CrossRef]
- Shah, Z.; Islam, S.; Ayaz, H.; Khan, S. Radiative Heat and Mass Transfer Analysis of Micropolar Nanofluid Flow of Casson Fluid between Two Rotating Parallel Plates with Effects of Hall Current. ASME J. Heat Transf. 2019, 141, 022401. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Khan, S.; Khan, W.; Khan, Z.A. Darcy–Forchheimer flow of micropolar nanofluid between two plates in the rotating frame with non-uniform heat generation/absorption. Adv. Mech. Eng. 2018, 10, 1687814018808850. [Google Scholar] [CrossRef]
- Shah, Z.; Bonyah, E.; Islam, S.; Khan, W.; Ishaq, M. Radiative MHD thin film flow of Williamson fluid over an unsteady permeable stretching. Heliyon 2018, 4, e00825. [Google Scholar] [CrossRef] [PubMed]
- Jawad, M.; Shah, Z.; Islam, S.; Islam, S.; Bonyah, E.; Khan, Z.A. Darcy-Forchheimer flow of MHD nanofluid thin film flow with Joule dissipation and Navier’s partial slip. J. Phys. Commun. 2018. [Google Scholar] [CrossRef]
- Khan, N.; Zuhra, S.; Shah, Z.; Bonyah, E.; Khan, W.; Islam, S. Slip flow of Eyring-Powell nanoliquid film containing graphene nanoparticles. AIP Adv. 2018, 8, 115302. [Google Scholar] [CrossRef]
- Hammed, K.; Haneef, M.; Shah, Z.; Islam, I.; Khan, W.; Asif, S.M. The Combined Magneto hydrodynamic and electric field effect on an unsteady Maxwell nanofluid Flow over a Stretching Surface under the Influence of Variable Heat and Thermal Radiation. Appl. Sci. 2018, 8, 160. [Google Scholar] [CrossRef]
- Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S. Unsteady squeezing flow of MHD CNTS nanofluid in rotating channels with Entropy generation and viscous Dissipation. Adv. Mech. Eng. 2019, 10, 1–18. [Google Scholar] [CrossRef]
- Khan, A.; Shah, Z.; Islam, S.; Dawar, A.; Bonyah, E.; Ullah, H.; Khan, Z.A. Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour andconvective non uniform heat source/sink in the rotating frame with microstructureand inertial characteristics. AIP Adv. 2018, 8, 125024. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Shah, Z.; Shafi, A.; Khan, I.; Itili, I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci. Rep. 2019. [CrossRef]
- Feroz, N.; Shah, Z.; Islam, S.; Alzahrani, E.O.; Khan, W. Entropy Generation of Carbon Nanotubes Flow in a Rotating Channel with Hall and Ion-Slip Effect Using Effective Thermal Conductivity Model. Entropy 2019, 21, 52. [Google Scholar] [CrossRef]
- Alharbi, S.O.; Dawar, A.; Shah, Z.; Khan, W.; Idrees, M.; Islam, S.; Khan, I. Entropy Generation in MHD Eyring–Powell Fluid Flow over an Unsteady Oscillatory Porous Stretching Surface under the Impact of Thermal Radiation and Heat Source/Sink. Appl. Sci. 2018, 8, 2588. [Google Scholar] [CrossRef]
- Liao, S.J. On Homotopy Analysis Method for Nonlinear Problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Nasir, N.; Shah, Z.; Islam, S.; Bonyah, E.; Gul, T. Darcy Forchheimer nanofluid thin film flow of SWCNTs and heat transfer analysis over an unsteady stretching sheet. AIP Adv. 2019, 9, 015223. [Google Scholar] [CrossRef]
- Tlili, I.; Khan, W.A.; Khan, I. Multiple slips effects on MHD SA-Al2O3 and SA-Cu non-Newtonian nanofluids flow over a stretching cylinder in porous medium with radiation and chemical reaction. Results Phys. 2018, 8, 213–221. [Google Scholar] [CrossRef]
- Khan, N.S.; Shah, Z.; Islam, S.; Khan, I.; Alkanhal, T.A.; Tlili, I. Entropy Generation in MHD Mixed Convection Non-Newtonian Second-Grade Nanoliquid Thin Film Flow through a Porous Medium with Chemical Reaction and Stratification. Entropy 2019, 21, 139. [Google Scholar] [CrossRef]
- Fiza, M.; Islam, S.; Ullah, H.; Shah, Z.; Chohan, F. An Asymptotic Method with Applications to Nonlinear Coupled Partial Differential Equations. Punjab Univ. J. Math. 2018, 50, 139–151. [Google Scholar]


| 0.1 | 0.3 | 0.5 | 0.4 | 0.4 | 1.80946 | 1.80946 |
| 0.3 | 2.36646 | 2.36646 | ||||
| 0.5 | 3.23183 | 3.23183 | ||||
| 0.1 | 0.1 | 1.80946 | 1.80946 | |||
| 0.3 | 1.83280 | 1.83280 | ||||
| 0.5 | 1.86280 | 1.86280 | ||||
| 0.1 | 0.1 | 1.80946 | 1.80946 | |||
| 0.3 | 1.81835 | 1.81835 | ||||
| 0.5 | 1.82867 | 1.82867 | ||||
| 0.1 | 0.1 | 1.80946 | 1.80946 | |||
| 0.3 | 1.82759 | 1.82759 | ||||
| 0.5 | 1.84571 | 1.84571 | ||||
| 0.1 | 0.1 | 1.80946 | 1.80946 | |||
| 0.3 | 1.79496 | 1.79496 | ||||
| 0.5 | 1.78530 | 1.78530 |
| 0.1 | 0.5 | 0.7 | 0.6 | 0.408170 |
| 0.3 | 0.452415 | |||
| 0.5 | 0.497617 | |||
| 0.1 | 0.1 | 0.408170 | ||
| 0.3 | 0.418514 | |||
| 0.5 | 0.429786 | |||
| 0.1 | 0.1 | 0.408170 | ||
| 0.3 | 0.401541 | |||
| 0.5 | 0.393572 | |||
| 0.1 | 0.1 | 0.408170 | ||
| 0.3 | 0.420824 | |||
| 0.5 | 0.430319 |
| Physical Properties | Base Fluid | Nanoparticles | |
|---|---|---|---|
| Water/Ethylene Glycol) | SWCNT | MWCNT | |
| = | 2,600 | 1,600 | |
| = | 425 | 796 | |
| = | 6,600 | 3,000 | |
| Diameter of CNTs | Thermal Conductivity of Nanofluids |
|---|---|
| 1.077 | |
| 1.078 | |
| 1.083 | |
| 1.085 | |
| 1.085 | |
| 1.087 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions. Symmetry 2019, 11, 207. https://doi.org/10.3390/sym11020207
Jawad M, Shah Z, Islam S, Majdoubi J, Tlili I, Khan W, Khan I. Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions. Symmetry. 2019; 11(2):207. https://doi.org/10.3390/sym11020207
Chicago/Turabian StyleJawad, Muhammad, Zahir Shah, Saeed Islam, Jihen Majdoubi, I. Tlili, Waris Khan, and Ilyas Khan. 2019. "Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions" Symmetry 11, no. 2: 207. https://doi.org/10.3390/sym11020207
APA StyleJawad, M., Shah, Z., Islam, S., Majdoubi, J., Tlili, I., Khan, W., & Khan, I. (2019). Impact of Nonlinear Thermal Radiation and the Viscous Dissipation Effect on the Unsteady Three-Dimensional Rotating Flow of Single-Wall Carbon Nanotubes with Aqueous Suspensions. Symmetry, 11(2), 207. https://doi.org/10.3390/sym11020207







