MHD Stagnation Point Flow of Nanofluid on a Plate with Anisotropic Slip
Abstract
:1. Introduction
2. Mathematical Formulation
3. Result and Discussion
4. Conclusions
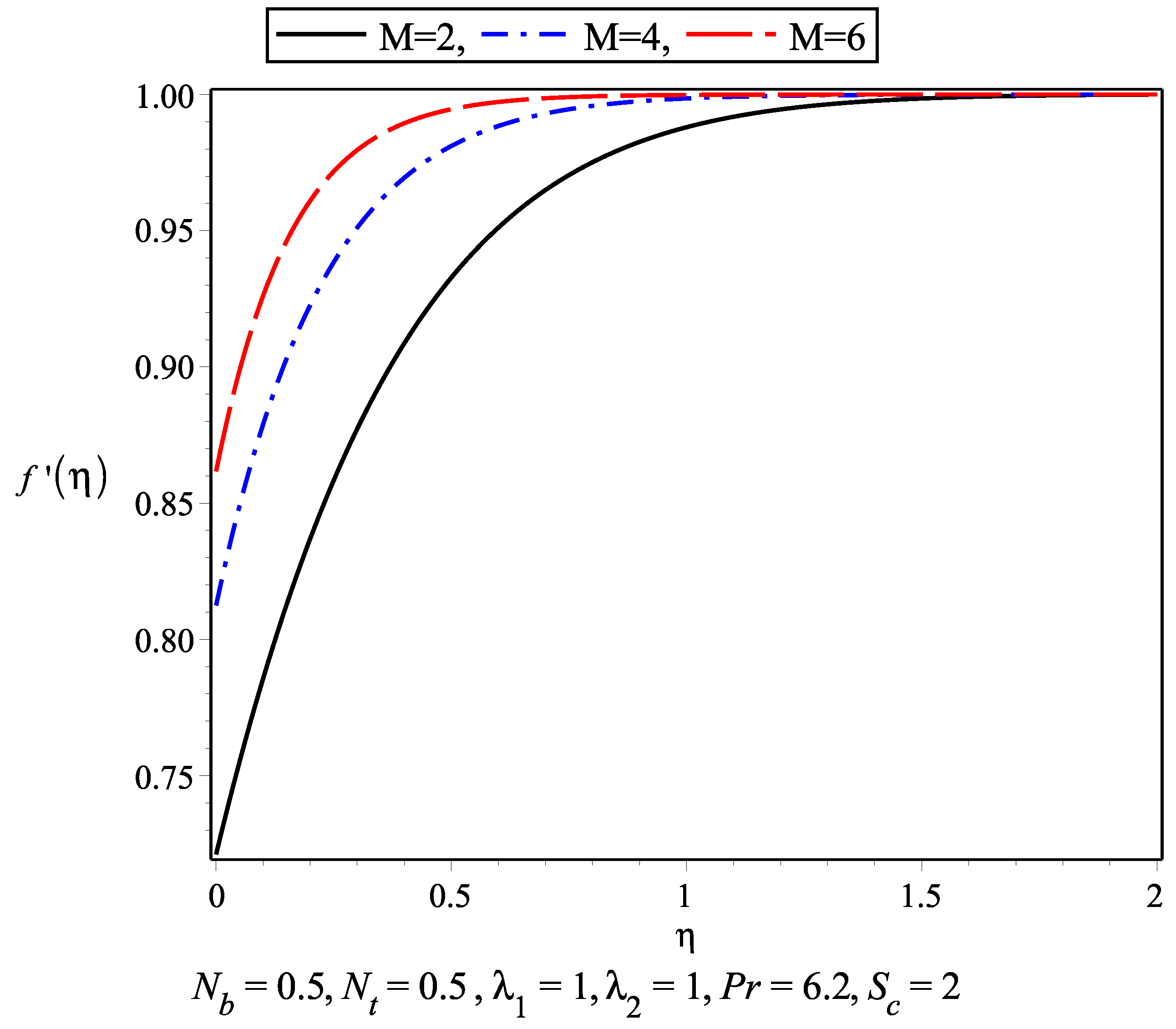
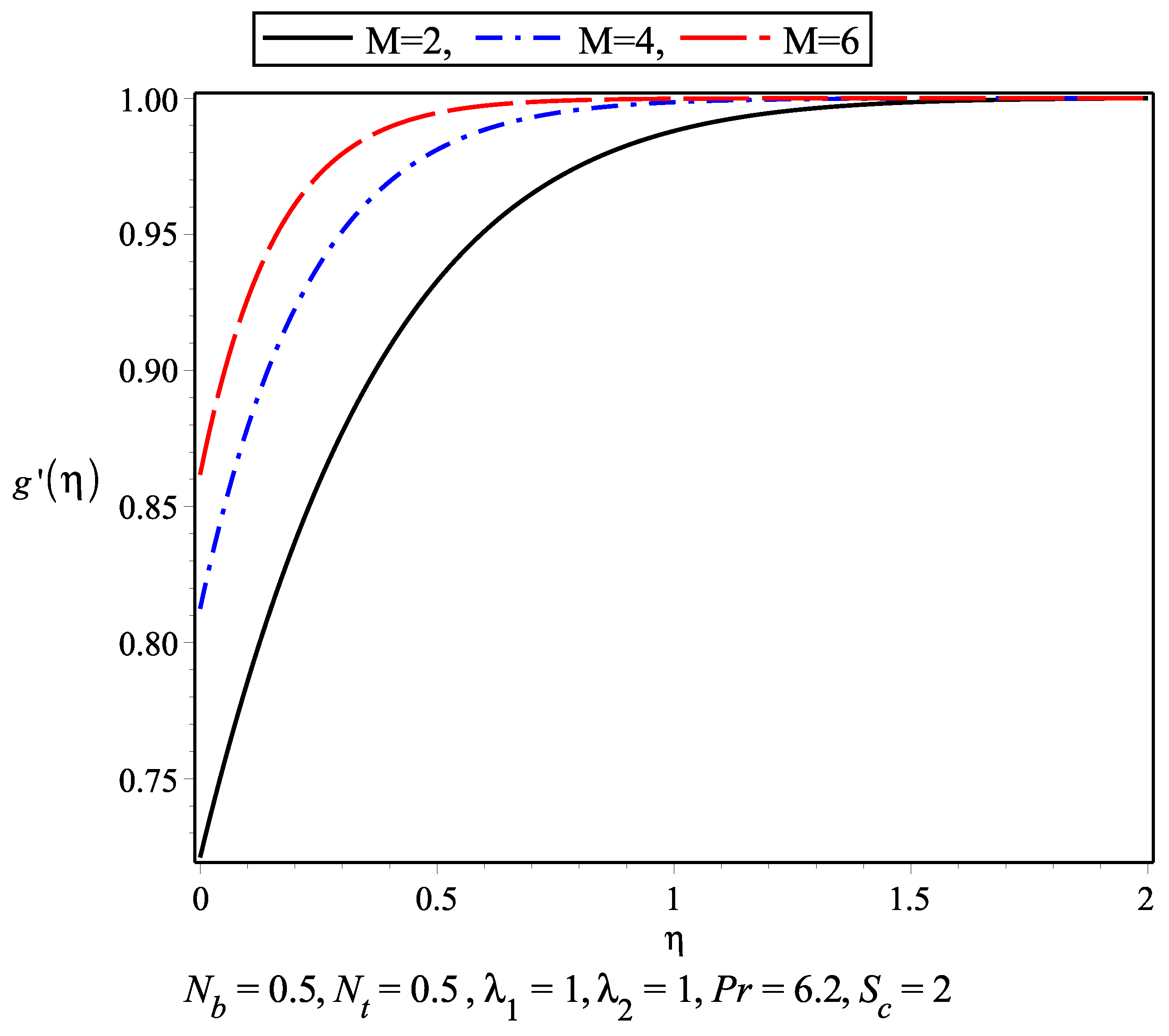
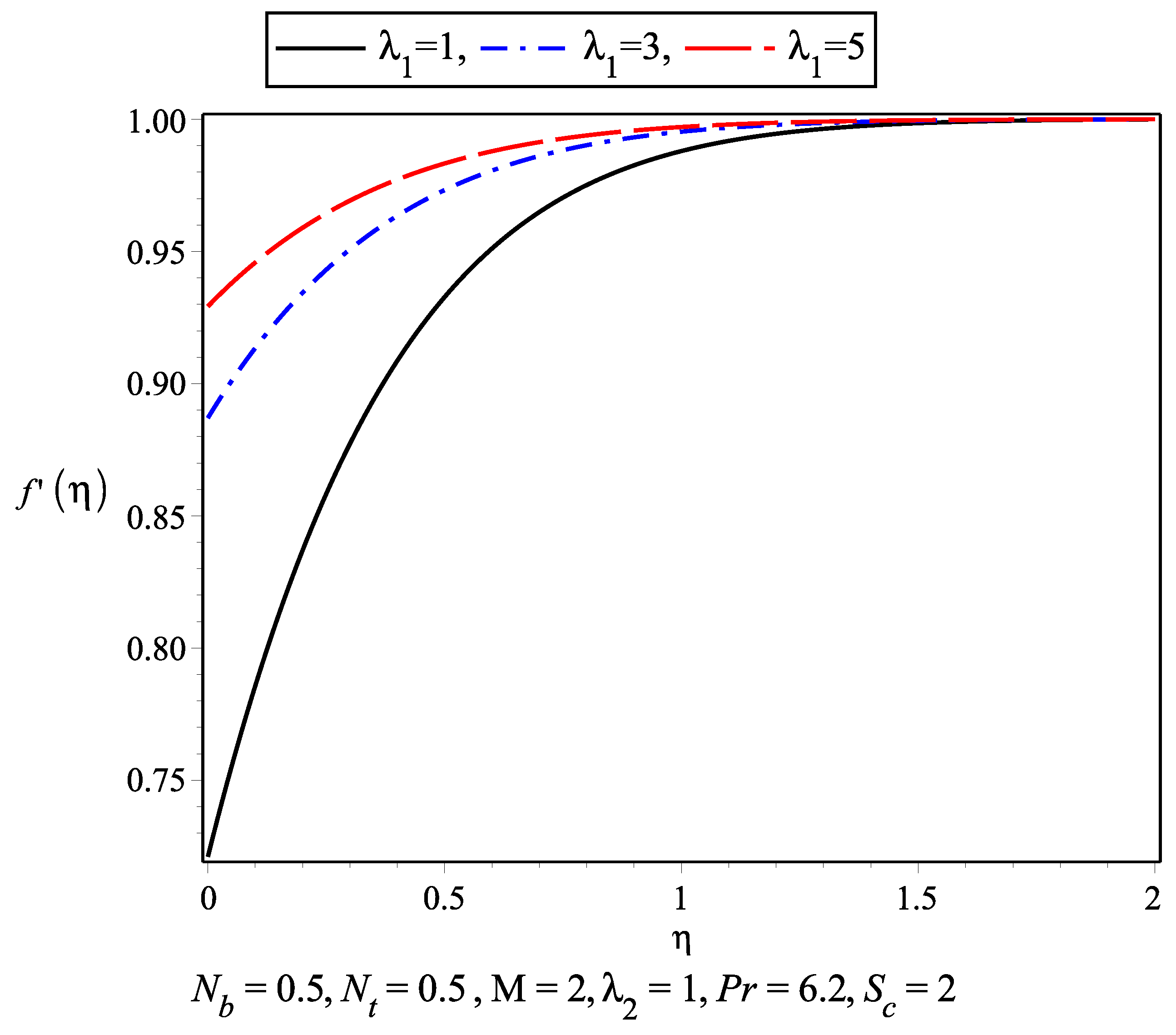
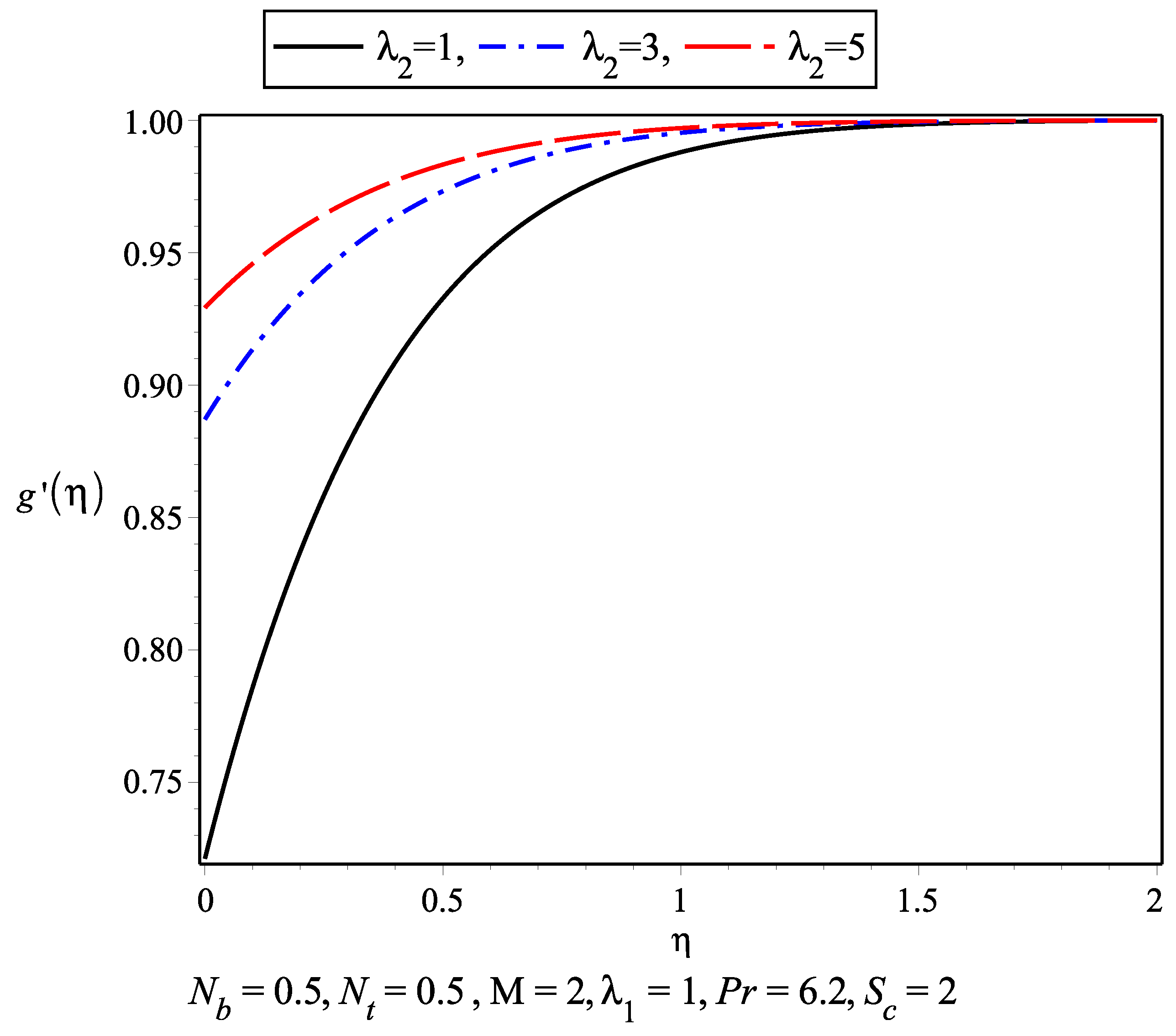
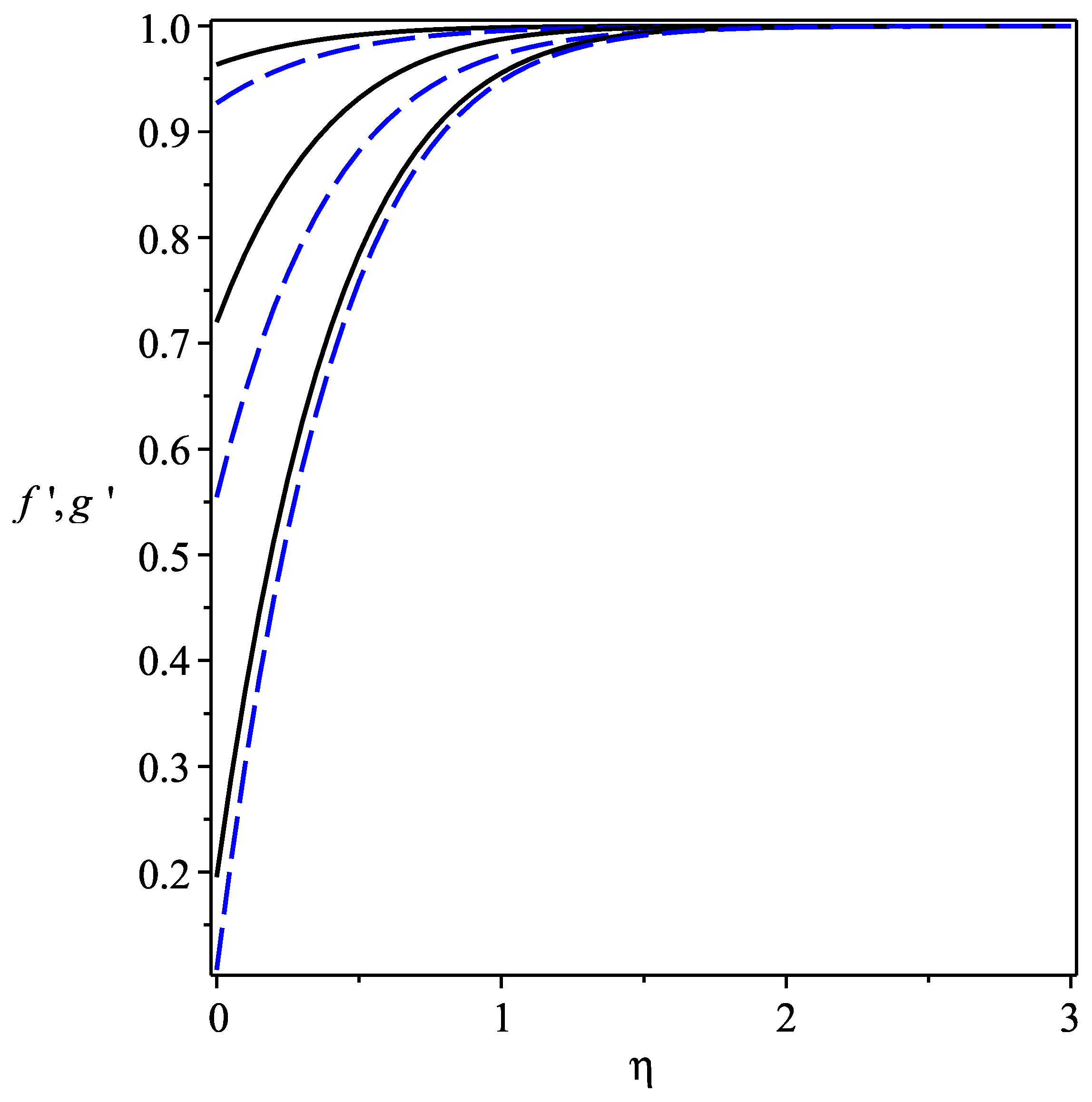
- An increase in the magnetic field M and slip parameter causes an increase in the velocity profile and decrease in the boundary layer thickness near the stagnation point.
- It is observed that in the absence of magnetic parameter M the boundary layer thickness is larger than while M is present.
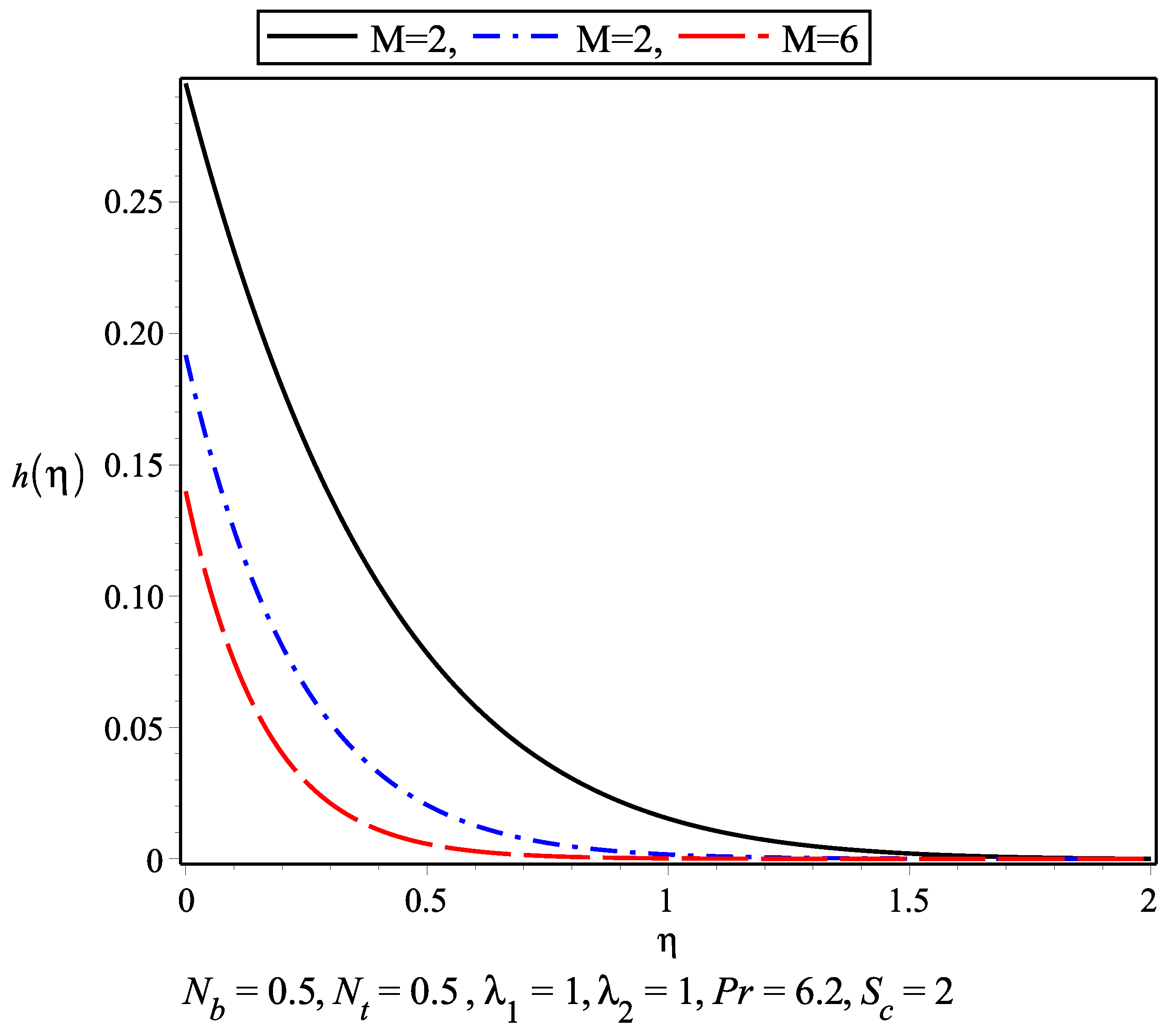
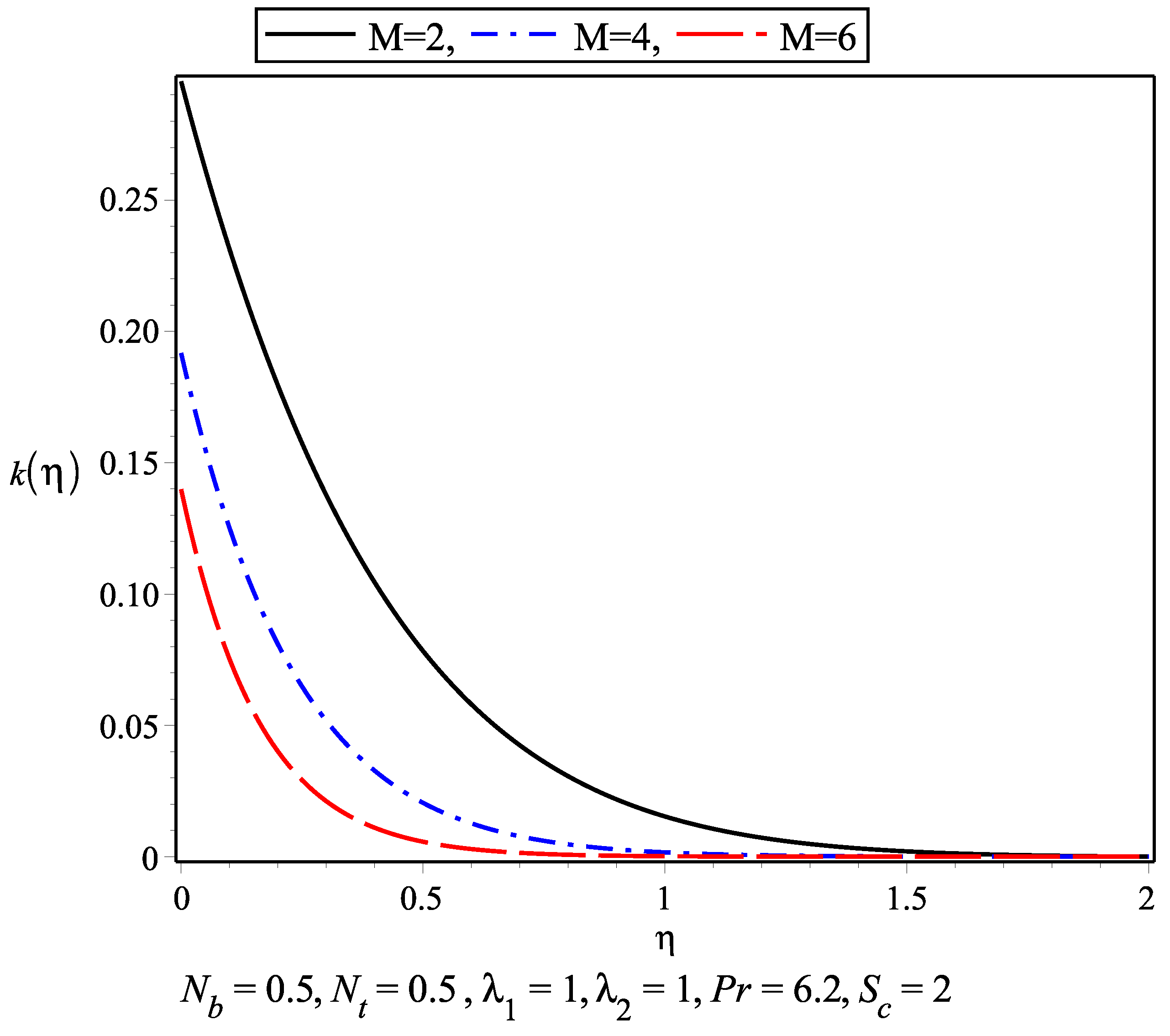
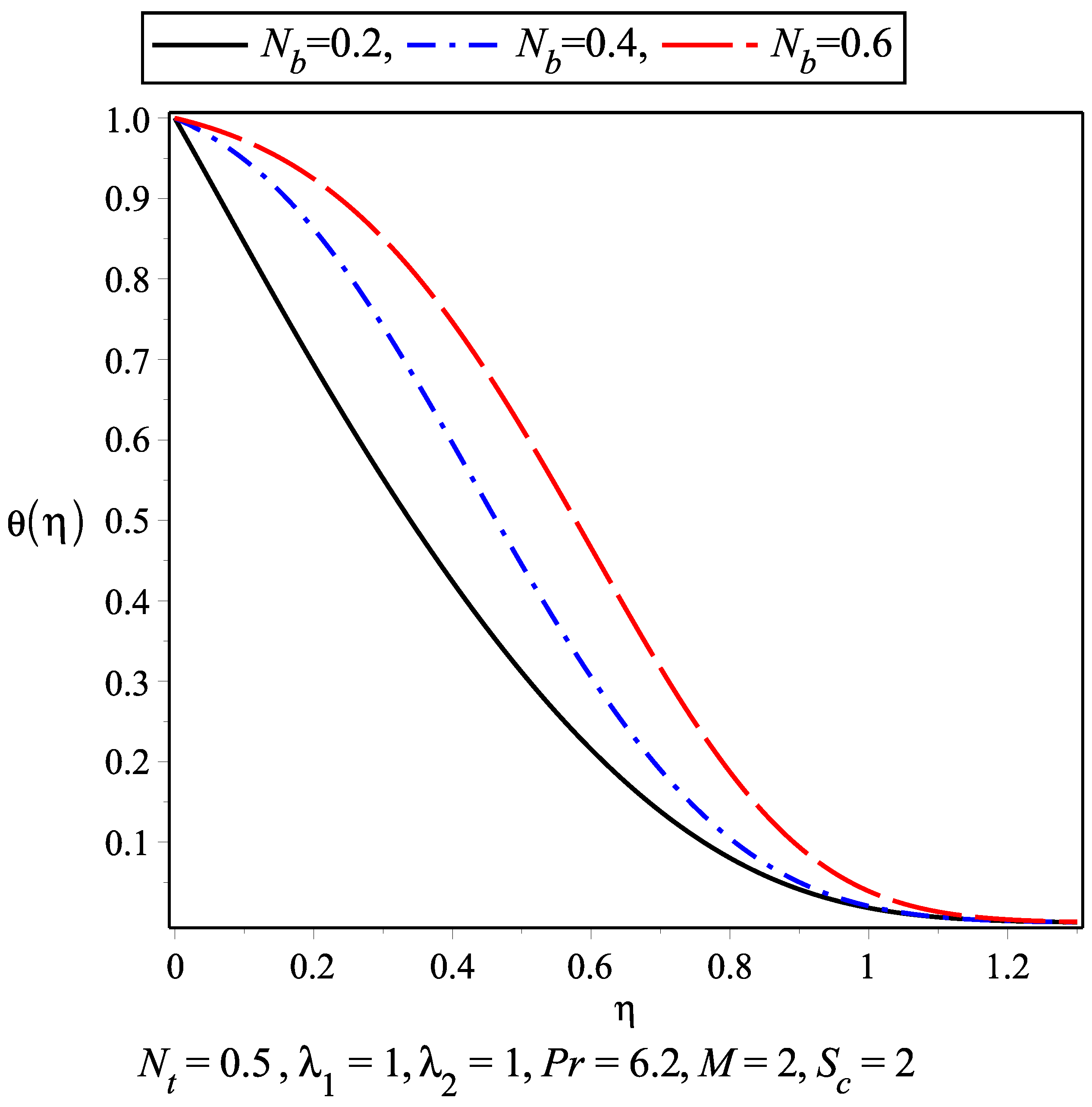
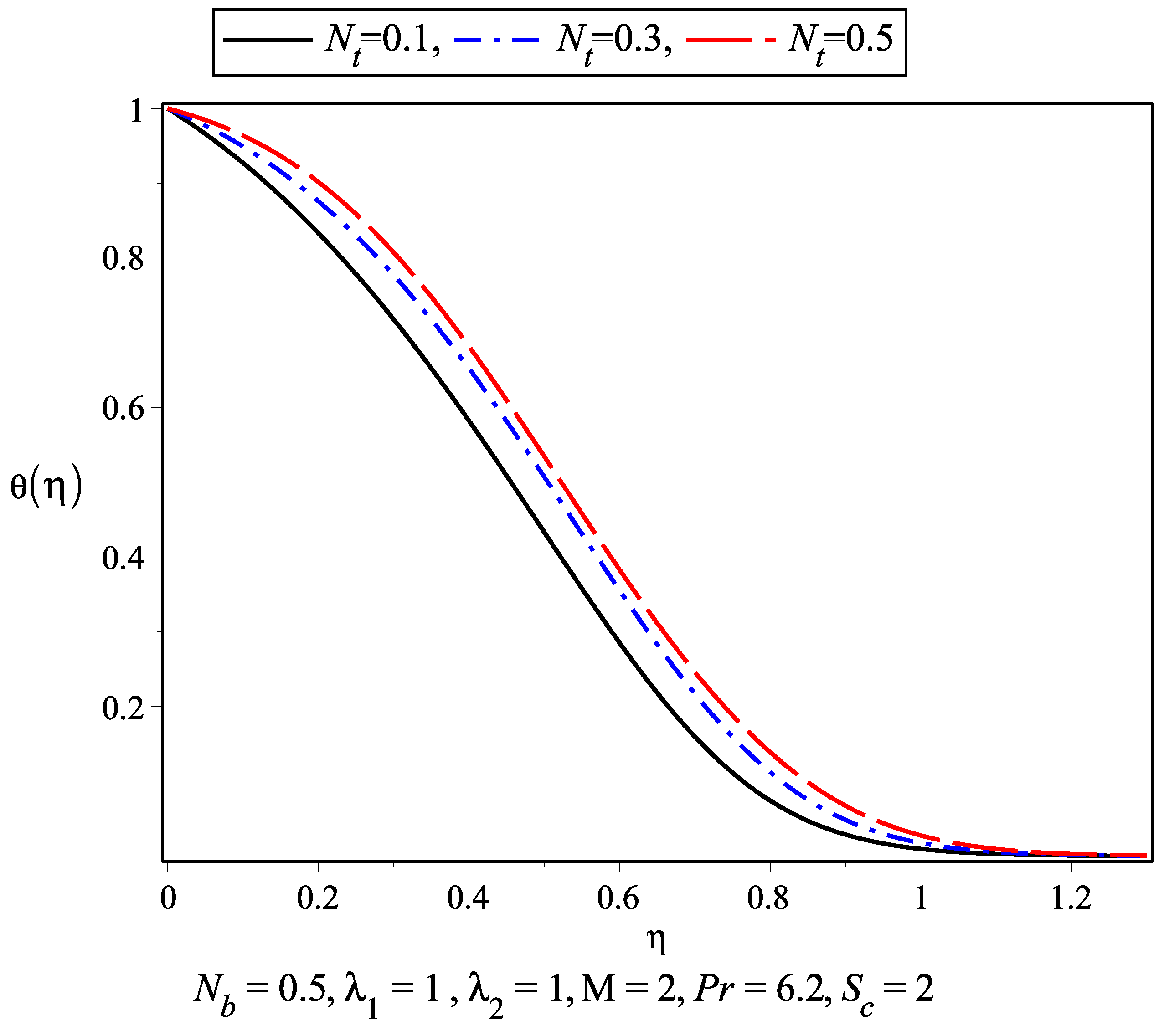
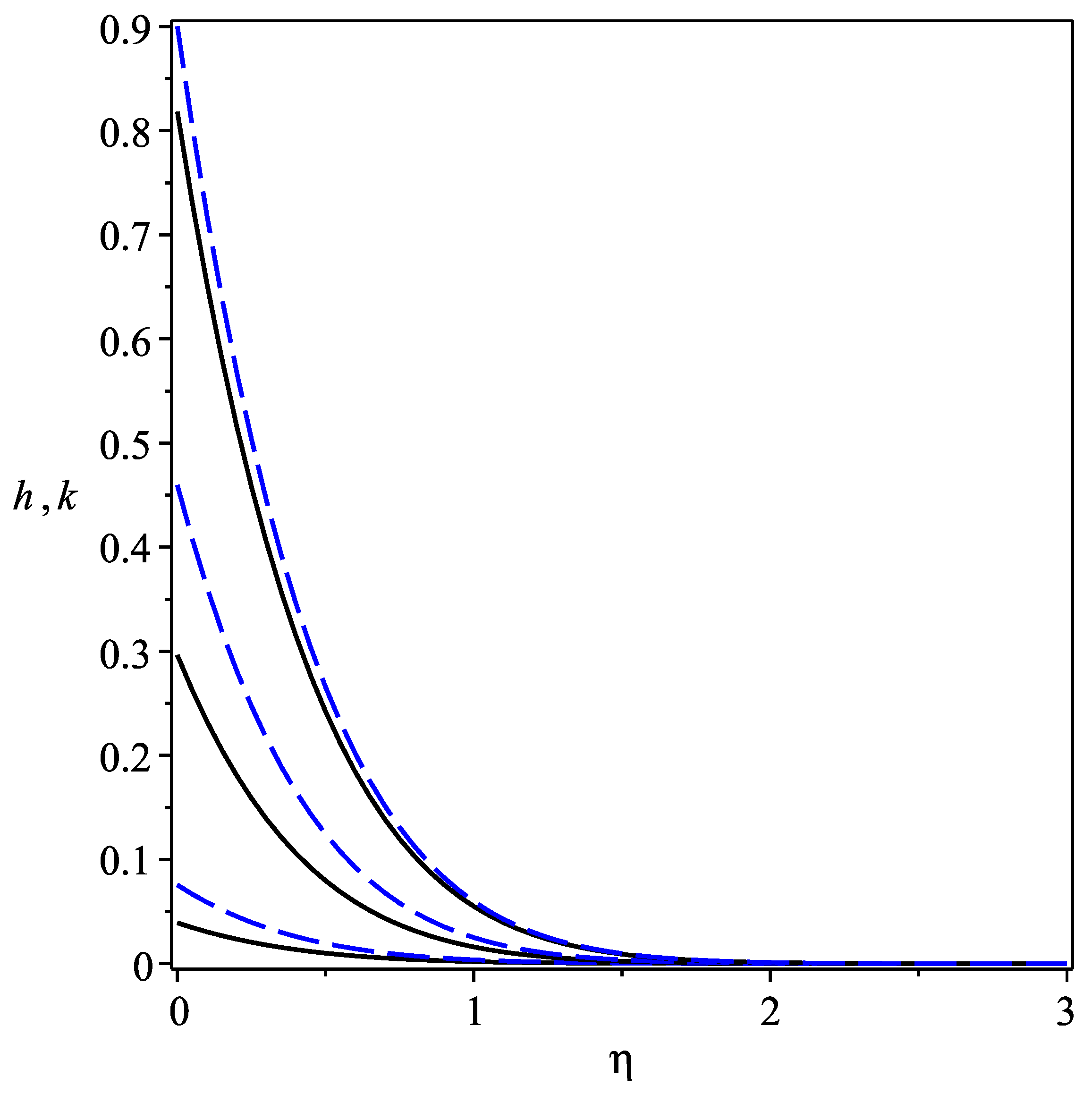
- The thermal boundary layer increases with an increase in the thermophoresis parameter and Brownian motion parameter . It is observed that the thermal boundary layer is achieved earlier compared to the momentum boundary layer.
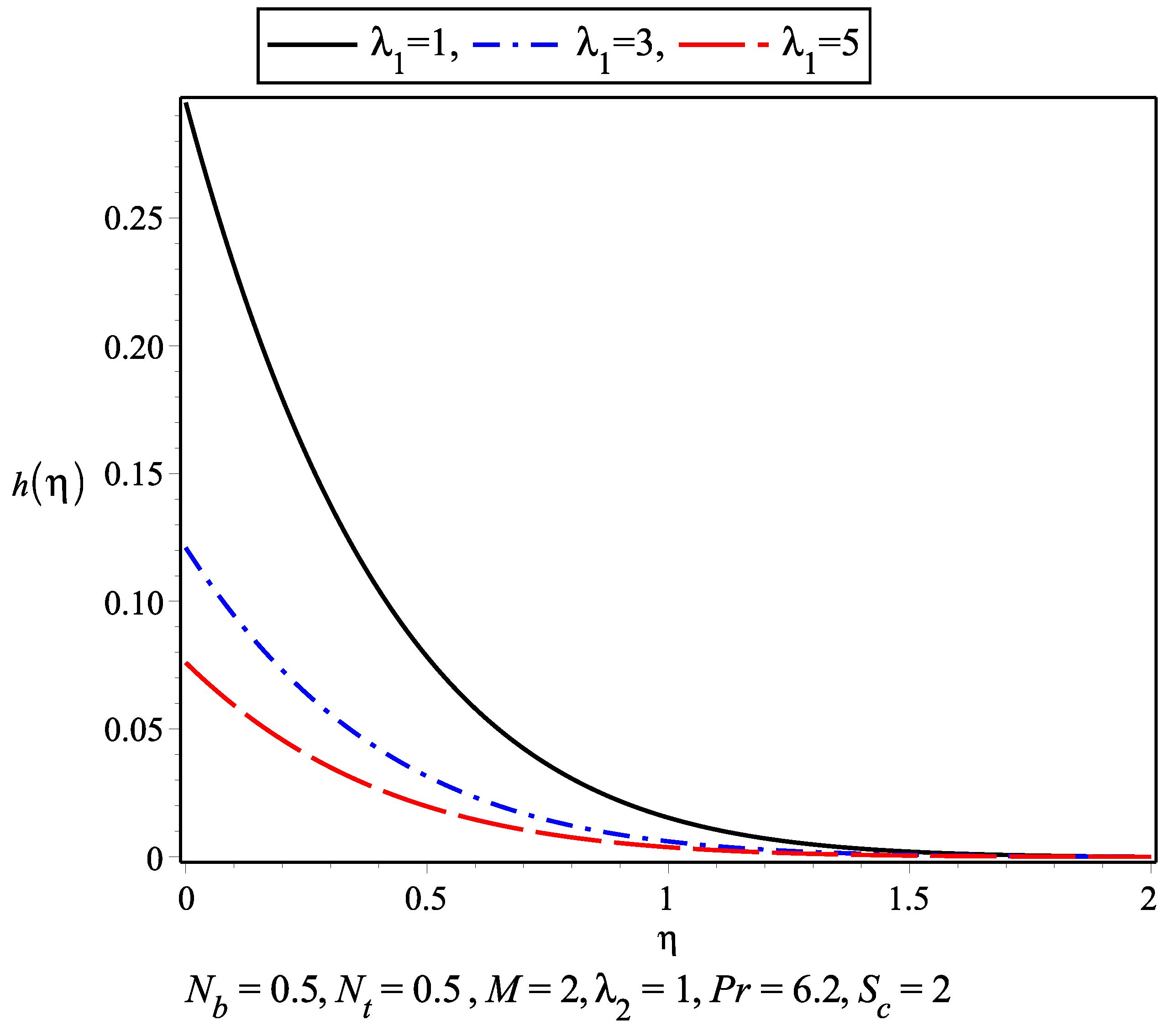
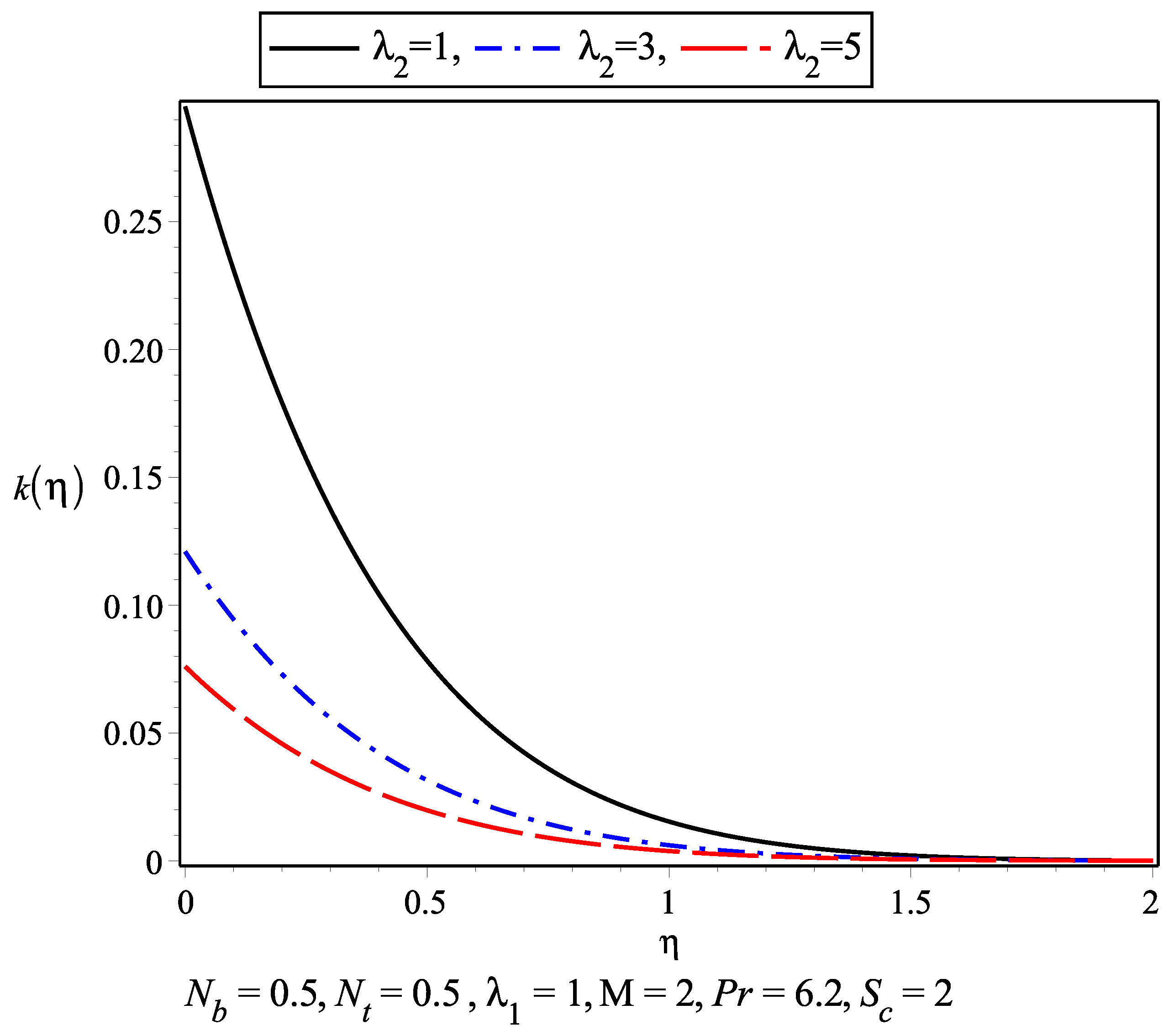
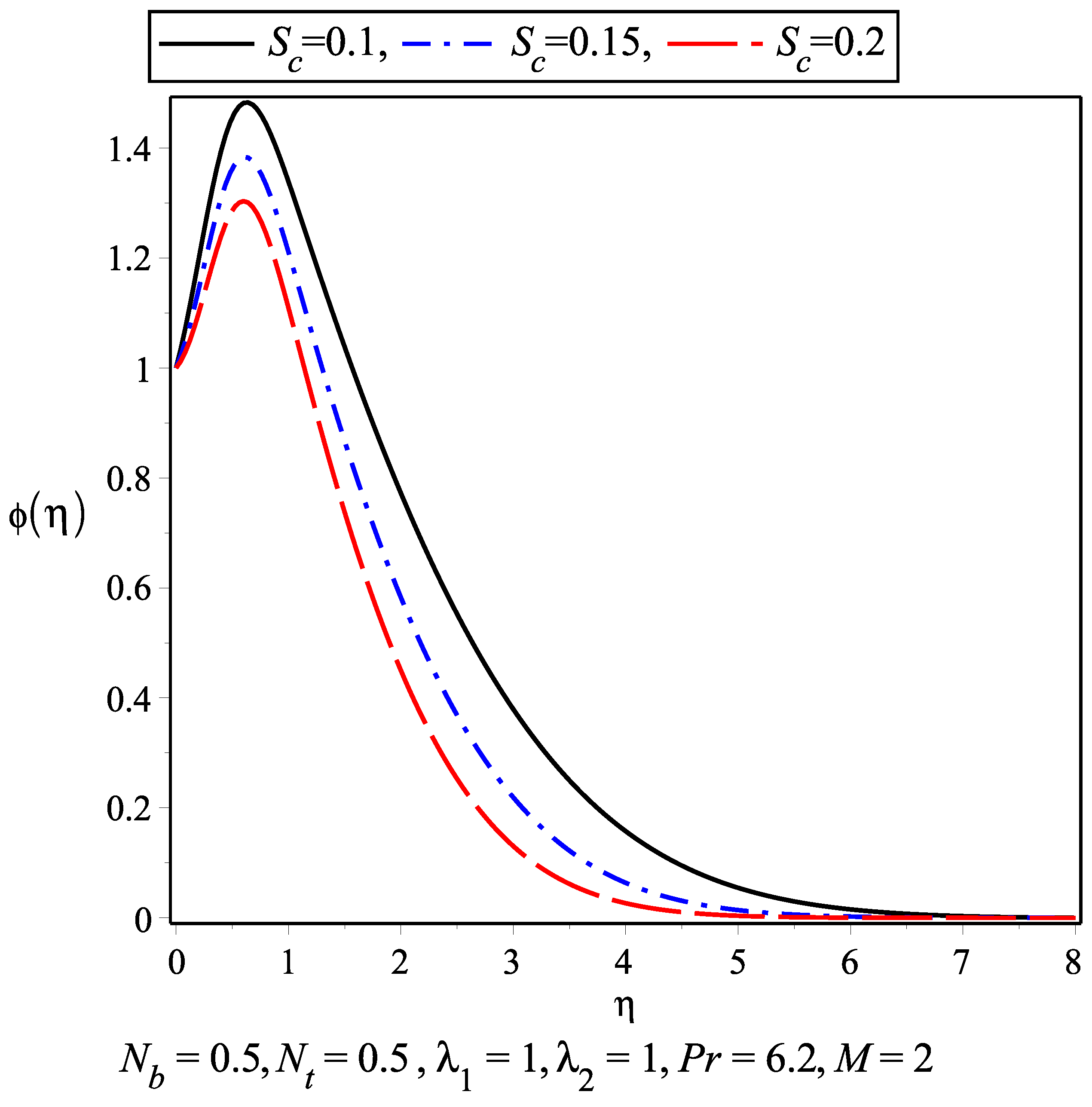
- It is observed that with the increase in and the nanoconcentration decreases and vice versa.
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| velocity Components | |
| kinematic viscosity | |
| slip coefficient | |
| T | temperature |
| thermal diffusivity | |
| C | volume of nano particles |
| heat capacity of fluid | |
| Brownian diffusion coefficient | |
| thermophoretic diffusion coefficient | |
| slip parameters | |
| thermophoresis parameter | |
| browning motion parameter | |
| skin friction coefficient | |
| local Nusselt number | |
| Sherwood number | |
| local Reynolds number | |
| Schmidt number | |
| prantle number | |
| ratio of slip parameters | |
| nano concentration | |
| M | magnetic parameter |
References
- Borrelli, A.; Giantesio, G.; Patria, M.C. Numerical simulations of three-dimensional MHD stagnation-point flow of a micropolar fluid. Comput. Math. Appl. 2013, 66, 472–489. [Google Scholar] [CrossRef]
- Lok, Y.Y.; Amin, N.; Pop, I. Non-orthogonal stagnation point flow towards a stretching shee. Int. J. Non Linear Mech. 2006, 41, 622–627. [Google Scholar] [CrossRef]
- Tilley, B.S.; Weidman, P.D. Oblique two-fluid stagnation-point flow. Eur. J. Mech. B Fluids 1998, 17, 205–217. [Google Scholar] [CrossRef]
- Grosan, T.; Pop, I.; Revnic, C.; Ingham, D.B. Magnetohydrodynamic oblique stagnation-point flow. Meccanica 2009, 44, 565. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow on a plate with anisotropic slip. Eur. J. Mech. B Fluids 2013, 38, 73–77. [Google Scholar] [CrossRef]
- Wang, C.Y. Off-centered stagnation flow towards a rotating disc. Int. J. Eng. Sci. 2008, 46, 391–396. [Google Scholar] [CrossRef]
- Wang, C.Y. Stagnation flow towards a shrinking sheet. Int. J. Non Linear Mech. 2008, 43, 377–382. [Google Scholar] [CrossRef]
- Nadeem, S.; Hussain, A.; Khan, M. HAM solutions for boundary layer flow in the region of the stagnation point towards a stretching sheet. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 475–481. [Google Scholar] [CrossRef]
- Ariel, P.D. Hiemenz flow in hydromagnetics. Acta Mech. 1994, 103, 31–43. [Google Scholar] [CrossRef]
- Raju, C.S.; Sandeep, N. Heat and mass transfer in MHD non-Newtonian bio-convection flow over a rotating cone/plate with cross diffusion. J. Mol. Liq. 2016, 215, 115–126. [Google Scholar] [CrossRef]
- Kleinstreuer, C.; Li, J.; Koo, J. Microfluidics of nano-drug delivery. Int. J. Heat Mass Trans. 2008, 51, 5590–5597. [Google Scholar] [CrossRef]
- Choi, S.U.S. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ. Fed 1995, 231, 99–106. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Nadeem, S.; Saleem, S. Analytical study of third grade fluid over a rotating vertical cone in the presence of nanoparticles. Int. J. Heat Mass Transf. 2015, 85, 1041–1048. [Google Scholar] [CrossRef]
- Bachok, N.; Ishak, A.; Nazar, R.; Pop, I. Flow and heat transfer at a general three-dimensional stagnation point in a nanofluid. Phys. B Condens. Matter 2010, 405, 4914–4918. [Google Scholar] [CrossRef]
- Ellahi, R.; Aziz, S.; Zeeshan, A. Non Newtonian nanofluids flow through a porous medium between two coaxial cylinders with heat transfer and variable viscosity. J. Porous Media 2013, 16, 205–216. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.; Javed, M.Y.; Ellahi, R. Effect of thermal radiation on nanofluid flow and heat transfer using two phase model. J. Magn. Magn. Mater. 2015, 374, 36–43. [Google Scholar] [CrossRef]
- Makinde, O.D.; Khan, W.A.; Khan, Z.H. Buoyancy effects on MHD stagnation point flow and heat transfer of a nanofluid past a convectively heated stretching/shrinking sheet. Int. J. Heat Mass Transf. 2013, 62, 526–533. [Google Scholar] [CrossRef]
- Junaid Ahmad Khan, M.; Mustafa, T.; Hayat, A.; Alsaedi, A. Three-dimensional flow of nanofluid over a non-linearly stretching sheet: An application to solar energy. Int. J. Heat Mass Transf. 2015, 86, 158–164. [Google Scholar] [CrossRef]
- Upadhya, M.; Mahesha, S.; Raju, C.S.K. Unsteady Flow of Carreau Fluid in a Suspension of Dust and Graphene Nanoparticles With Cattaneo–Christov Heat Flux. J. Heat Transf. 2018, 140, 092401. [Google Scholar] [CrossRef]
- Li, Z.; Sheikholeslami, M.; Ahmad Shafee, S.; Ali J Chamkha, S. Effect of dispersing nanoparticles on solidification process in existence of Lorenz forces in a permeable media. J. Mol. Liq. 2018, 266, 181–193. [Google Scholar] [CrossRef]
- Raju, C.S.K.; Saleem, S.; Mamatha, S.U. Iqtadar Hussain, Heat and mass transport phenomena of radiated slender body of three revolutions with saturated porous: Buongiorno’s model. Int. J. Therm. Sci. 2018, 132, 309–315. [Google Scholar] [CrossRef]
- Ram, P.; Kumar, A. Analysis of Heat Transfer and Lifting Force in a Ferro-Nanofluid Based Porous Inclined Slider Bearing with Slip Conditions. Nonlinear Eng. 2018. [Google Scholar] [CrossRef]
- Soomro, F.A.; Hammouch, Z. Heat transfer analysis of CuO-water enclosed in a partially heated rhombus with heated square obstacle. Int. J. Heat Mass Transf. 2018, 118, 773–784. [Google Scholar]
- Hayat, T.; Qayyum, S.; Alsaedi, A.; Ahmad, B. Results in Physics, Significant consequences of heat generation/absorption and homogeneous-heterogeneous reactions in second grade fluid due to rotating disk. Results Phys. 2018, 8, 223–230. [Google Scholar] [CrossRef]
- Hussain, S.; Aziz, A.; Aziz, T.; Khalique, C.M. Slip Flow and Heat Transfer of Nanofluids over a Porous Plate Embedded in a Porous Medium with Temperature Dependent Viscosity and Thermal Conductivity. Appl. Sci. 2016, 6, 376. [Google Scholar] [CrossRef]
- Anuar, N.; Bachok, N.; Pop, I. A Stability Analysis of Solutions in Boundary Layer Flow and Heat Transfer of Carbon Nanotubes over a Moving Plate with Slip Effect. Energies 2018, 11, 3243. [Google Scholar] [CrossRef]
- Fetecau, C.; Vieru, D.; Azhar, W.A. Natural Convection Flow of Fractional Nanofluids Over an Isothermal Vertical Plate with Thermal Radiation. Appl. Sci. 2017, 7, 247. [Google Scholar] [CrossRef]
- Khan, N.S.; Gul, T.; Islam, S.; Khan, I.; Alqahtani, A.M.; Alshomrani, A.S. Alqahtani and Ali Saleh Alshomrani, Magnetohydrodynamic Nanoliquid Thin Film Sprayed on a Stretching Cylinder with Heat Transfer. Appl. Sci. 2017, 7, 271. [Google Scholar] [CrossRef]

| , | ||||||
|---|---|---|---|---|---|---|
| 5.5 | 0.67084 | 1.47332 | 0.45477 | 1.58078 | 0.30641 | 1.77542 |
| 5.6 | 0.66527 | 1.47440 | 0.44833 | 1.58438 | 0.29987 | 1.78168 |
| 5.7 | 0.65976 | 1.47546 | 0.44197 | 1.58792 | 0.29346 | 1.78781 |
| 5.8 | 0.65431 | 1.47651 | 0.43570 | 1.59139 | 0.28716 | 1.79381 |
| 5.9 | 0.64890 | 1.47754 | 0.42950 | 1.59481 | 0.28098 | 1.79968 |
| 6.0 | 0.64355 | 1.47856 | 0.42343 | 1.59816 | 0.27492 | 1.80543 |
| 6.1 | 0.63826 | 1.47956 | 0.41742 | 1.60145 | 0.26897 | 1.81105 |
| 6.2 | 0.63302 | 1.48055 | 0.41150 | 1.60468 | 0.26314 | 1.81655 |
| 6.3 | 0.62784 | 1.48152 | 0.40566 | 1.60785 | 0.25742 | 1.82192 |
| 6.4 | 0.62272 | 1.48248 | 0.39992 | 1.61096 | 0.25181 | 1.82718 |
| 6.5 | 0.61766 | 1.48342 | 0.39425 | 1.61401 | 0.24631 | 1.83232 |
| 0.5 | 0.25129 | 1.78860 | 0.27363 | 1.85616 | 0.28527 | 1.88559 |
| 0.6 | 0.25465 | 1.79657 | 0.27603 | 1.86128 | 0.28698 | 1.88892 |
| 0.7 | 0.25737 | 1.80301 | 0.27791 | 1.86529 | 0.28829 | 1.89145 |
| 0.8 | 0.25962 | 1.80831 | 0.27943 | 1.86850 | 0.28933 | 1.89350 |
| 0.9 | 0.26152 | 1.81276 | 0.28068 | 1.87114 | 0.29018 | 1.89513 |
| 1.0 | 0.26314 | 1.81655 | 0.28172 | 1.87335 | 0.29087 | 1.89648 |
| 1.1 | 0.26453 | 1.81980 | 0.28261 | 1.87522 | 0.29146 | 1.89762 |
| 1.2 | 0.26575 | 1.82263 | 0.28337 | 1.87683 | 0.29196 | 1.89859 |
| 1.3 | 0.26682 | 1.82511 | 0.28403 | 1.87822 | 0.29239 | 1.89942 |
| 1.4 | 0.26776 | 1.82731 | 0.28461 | 1.87944 | 0.29277 | 1.90015 |
| 1.5 | 0.26861 | 1.82926 | 0.28513 | 1.88052 | 0.29310 | 1.90079 |
| , | |||
|---|---|---|---|
| 0.5 | 1.12177 | 1.36687 | 1.51354 |
| 0.6 | 1.00998 | 1.20285 | 1.31469 |
| 0.7 | 0.91823 | 1.07391 | 1..16200 |
| 0.8 | 0.84163 | 0.96991 | 1.04108 |
| 0.9 | 0.77675 | 0.88425 | 0.94294 |
| 1.0 | 0.72109 | 0.81248 | 0.86171 |
| 1.1 | 0.67283 | 0.75148 | 0.79336 |
| 1.2 | 0.63060 | 0.69899 | 0.73505 |
| 1.3 | 0.59334 | 0.65335 | 0.68473 |
| 1.4 | 0.56022 | 0.61330 | 0.64086 |
| 1.5 | 0.53059 | 0.57788 | 0.60227 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sadiq, M.A. MHD Stagnation Point Flow of Nanofluid on a Plate with Anisotropic Slip. Symmetry 2019, 11, 132. https://doi.org/10.3390/sym11020132
Sadiq MA. MHD Stagnation Point Flow of Nanofluid on a Plate with Anisotropic Slip. Symmetry. 2019; 11(2):132. https://doi.org/10.3390/sym11020132
Chicago/Turabian StyleSadiq, Muhammad Adil. 2019. "MHD Stagnation Point Flow of Nanofluid on a Plate with Anisotropic Slip" Symmetry 11, no. 2: 132. https://doi.org/10.3390/sym11020132
APA StyleSadiq, M. A. (2019). MHD Stagnation Point Flow of Nanofluid on a Plate with Anisotropic Slip. Symmetry, 11(2), 132. https://doi.org/10.3390/sym11020132




