A Continuous Coordinate System for the Plane by Triangular Symmetry
Abstract
:1. Introduction
2. Preliminaries
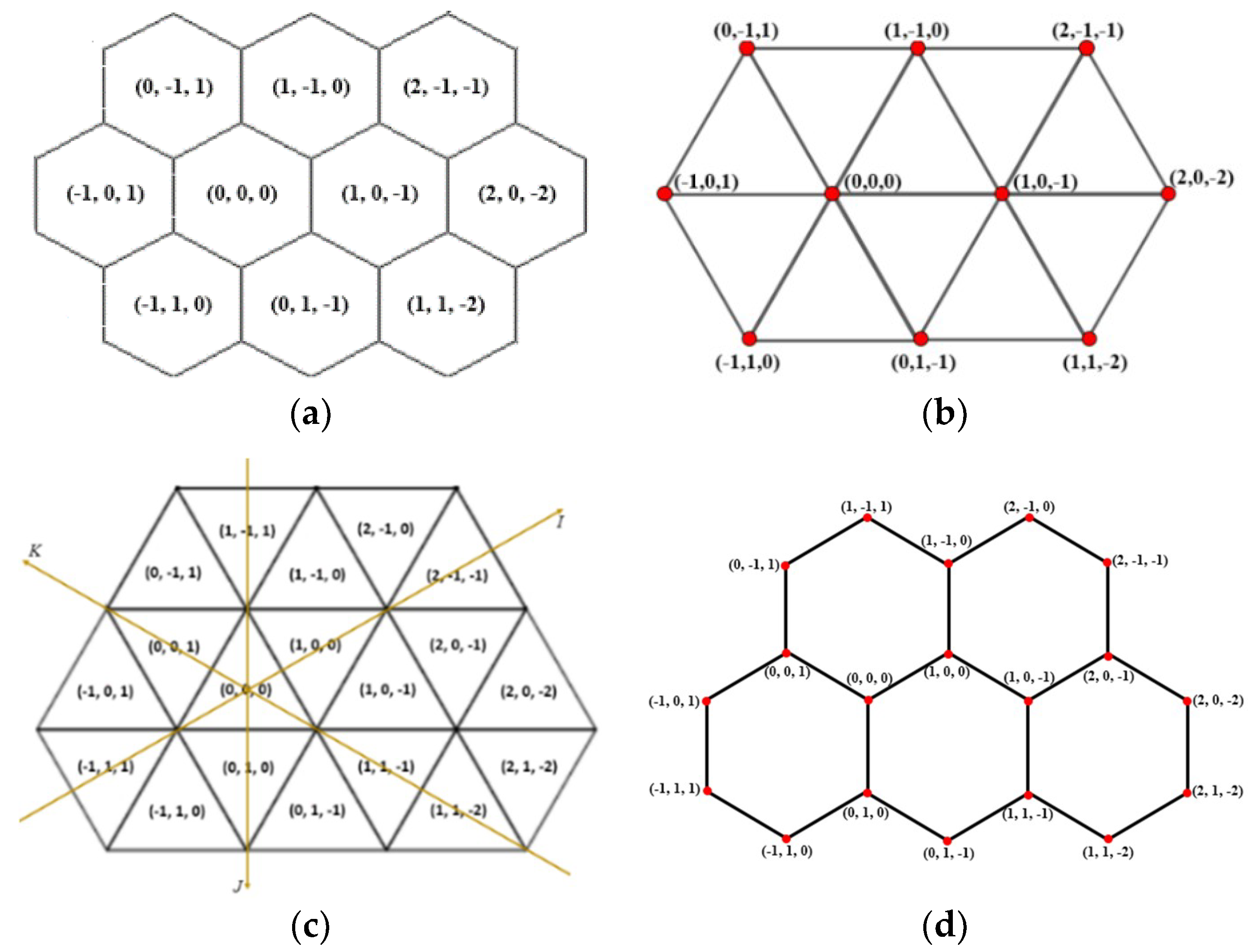
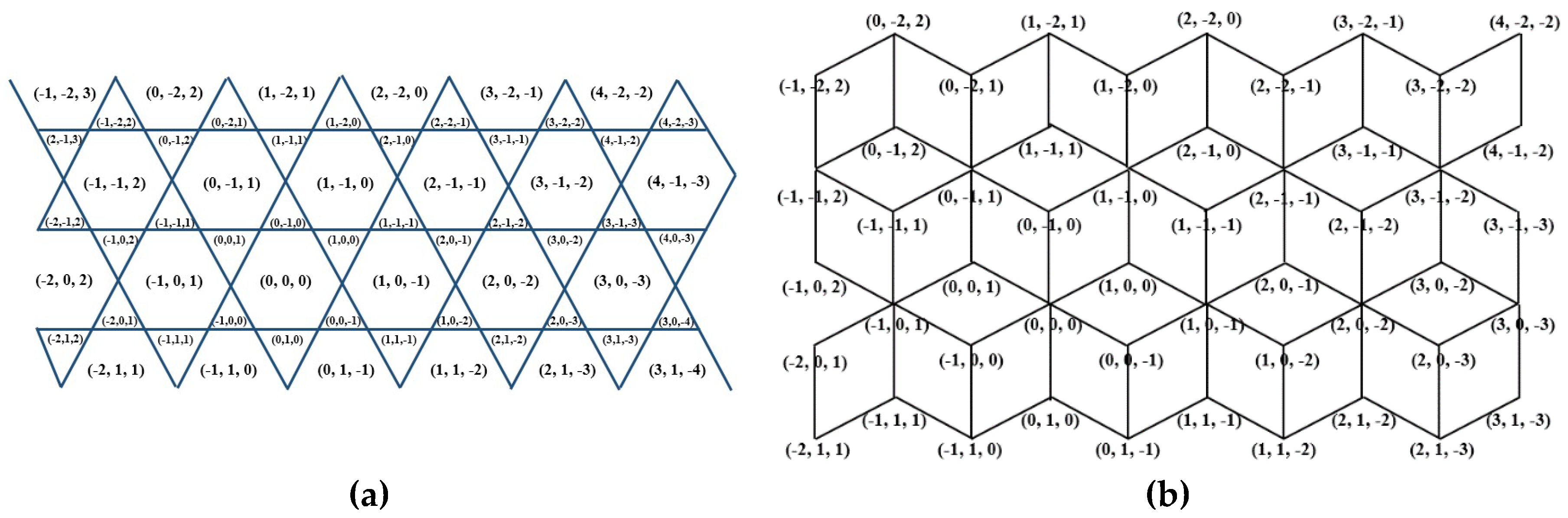
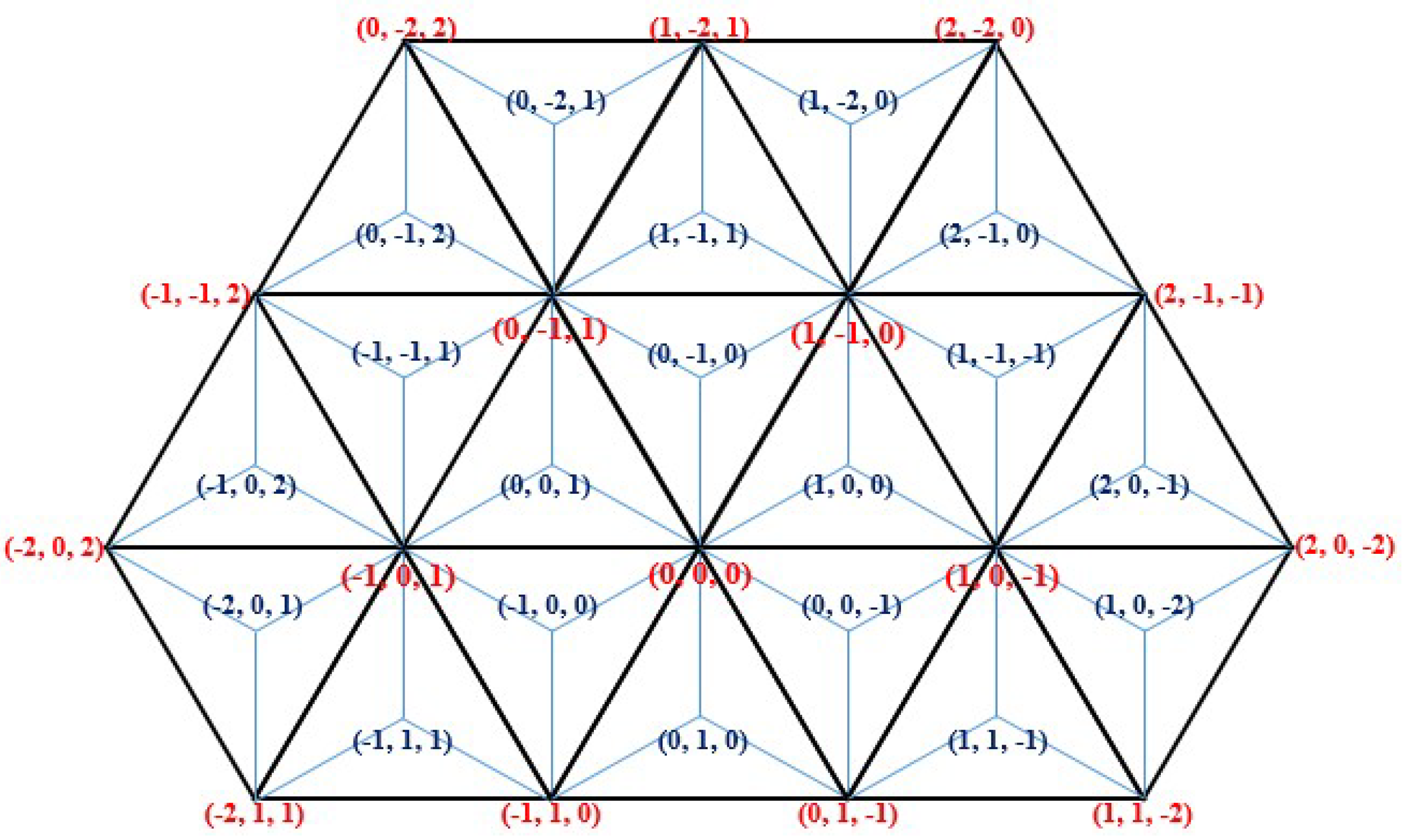
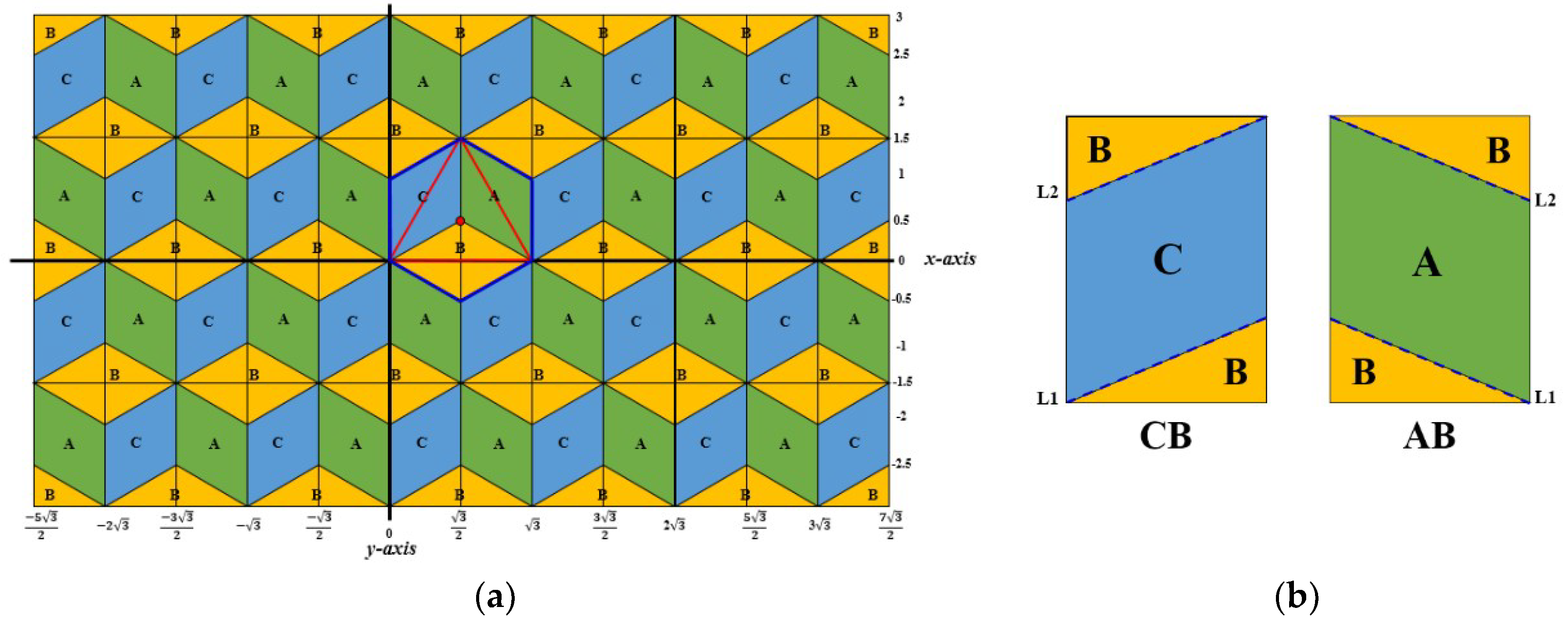
2.1. Discrete Triangular Coordinate System
2.2. The Barycentric Coordinate System (BCS)
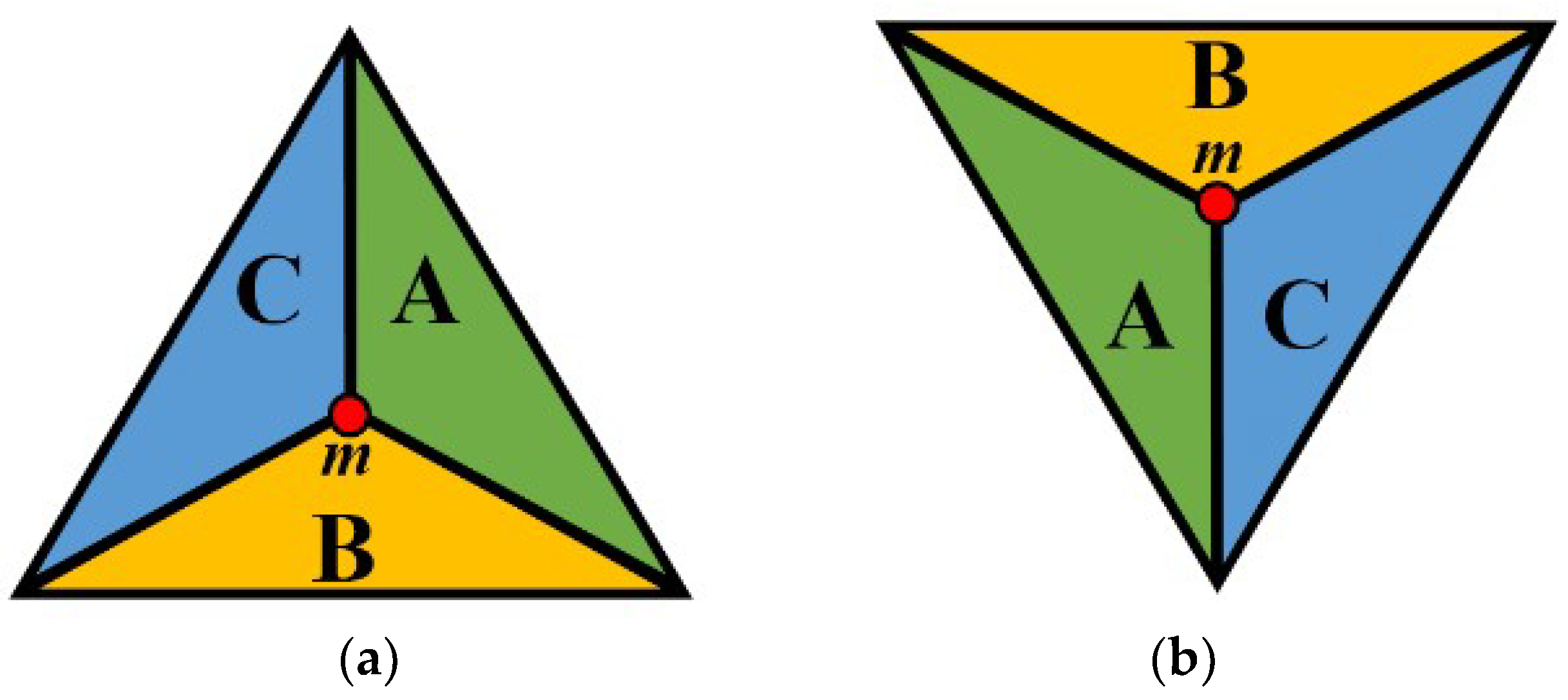
3. Continuous Coordinate System for Reflecting the Triangular Symmetry
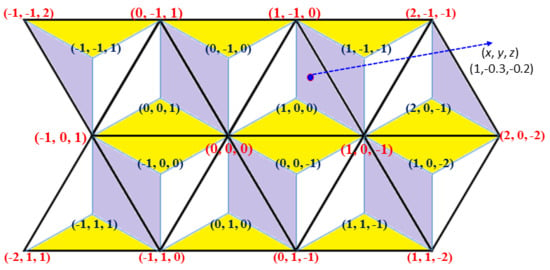
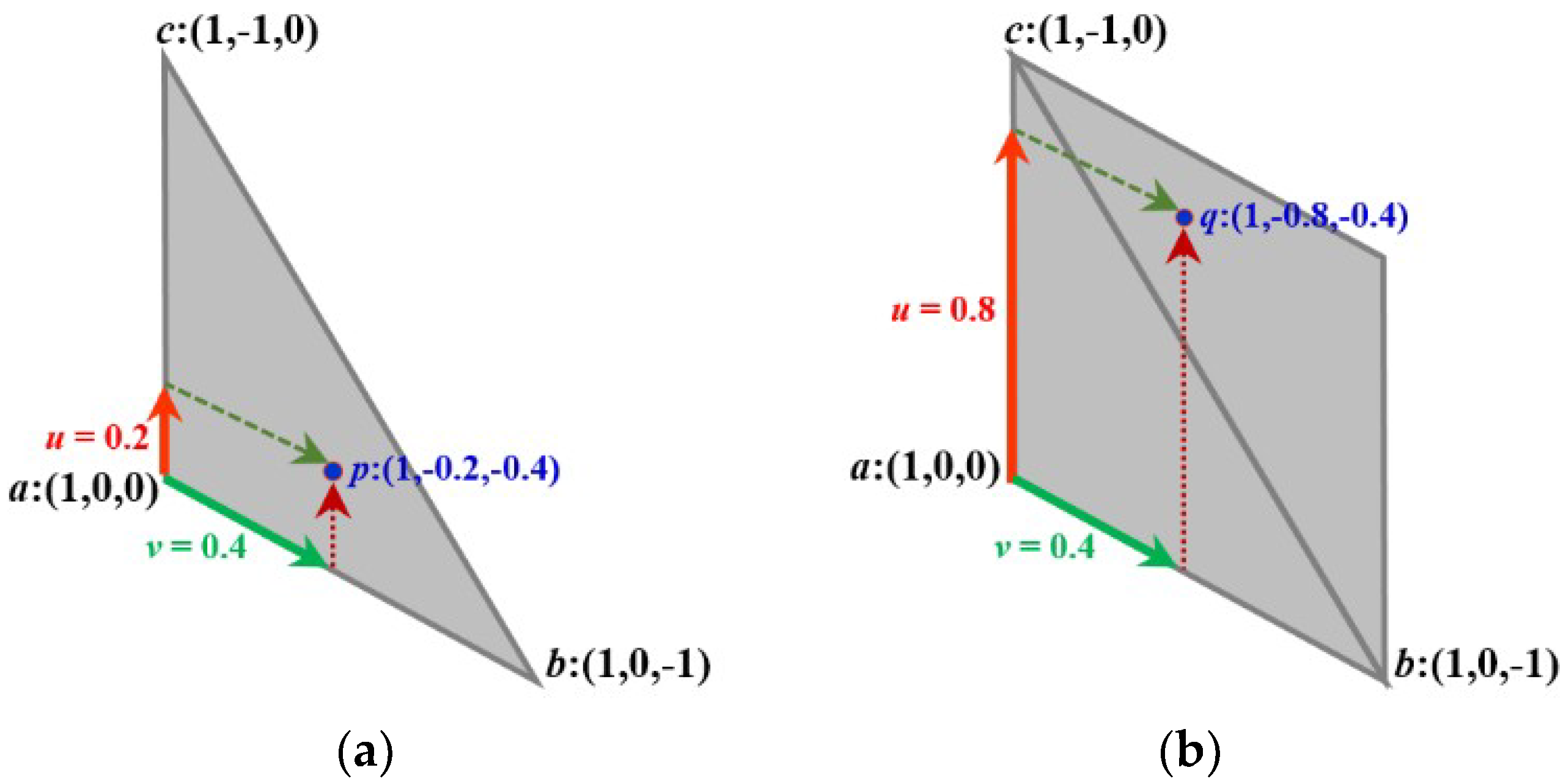
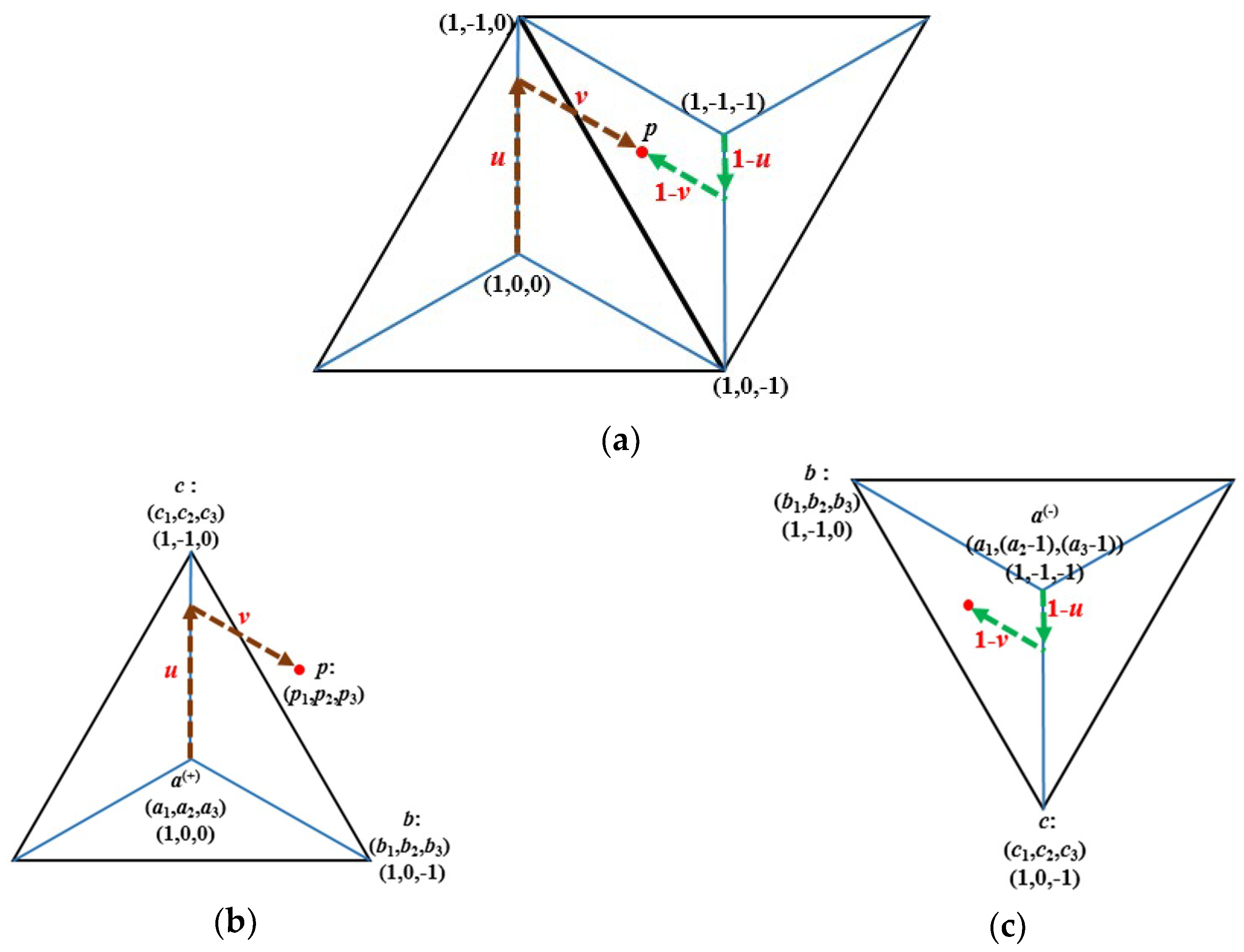
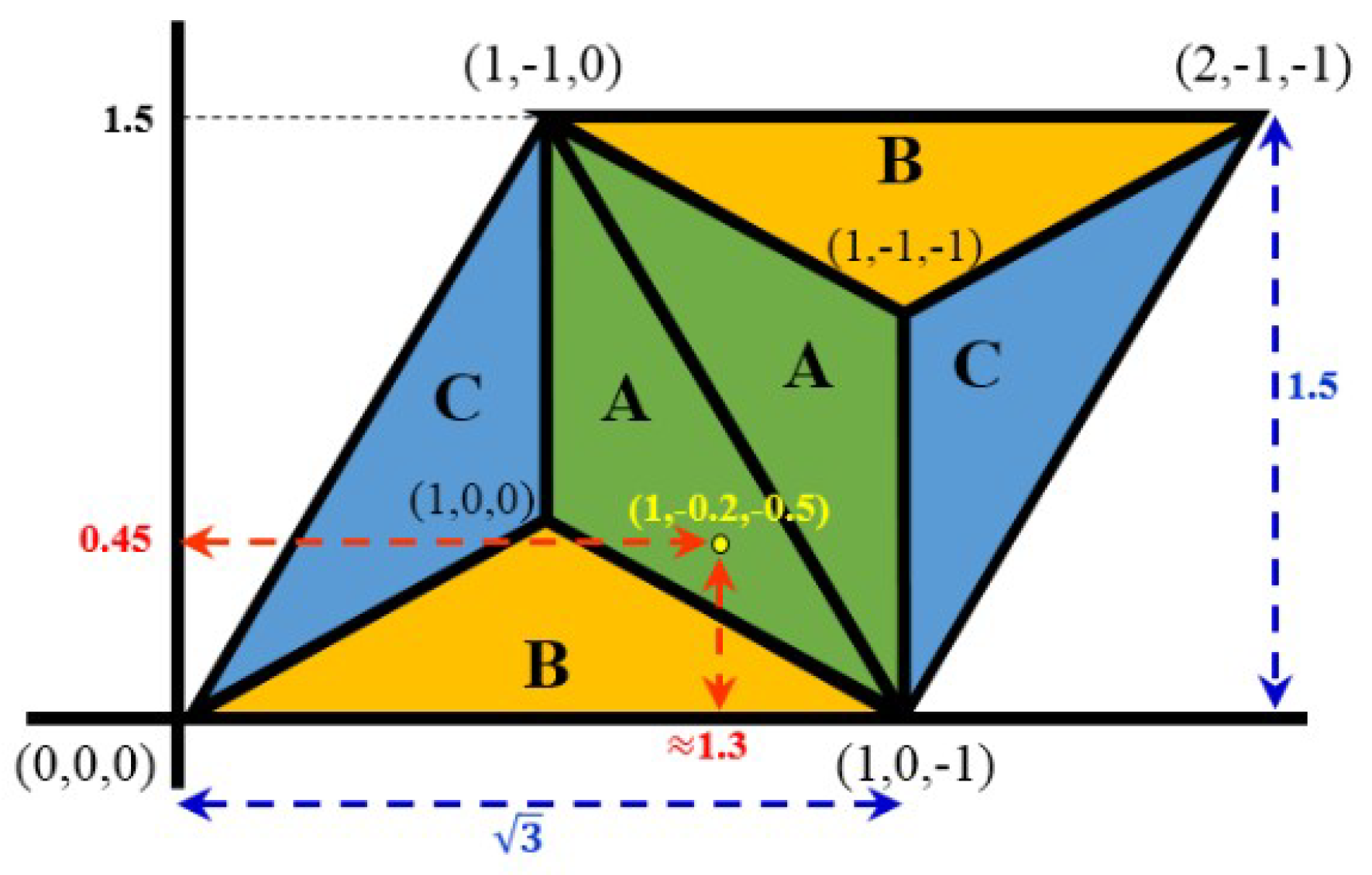
3.1. Converting Triplets to Cartesian Coordinates
3.2. Converting Cartesian Coordinates to Equivalent Triplets
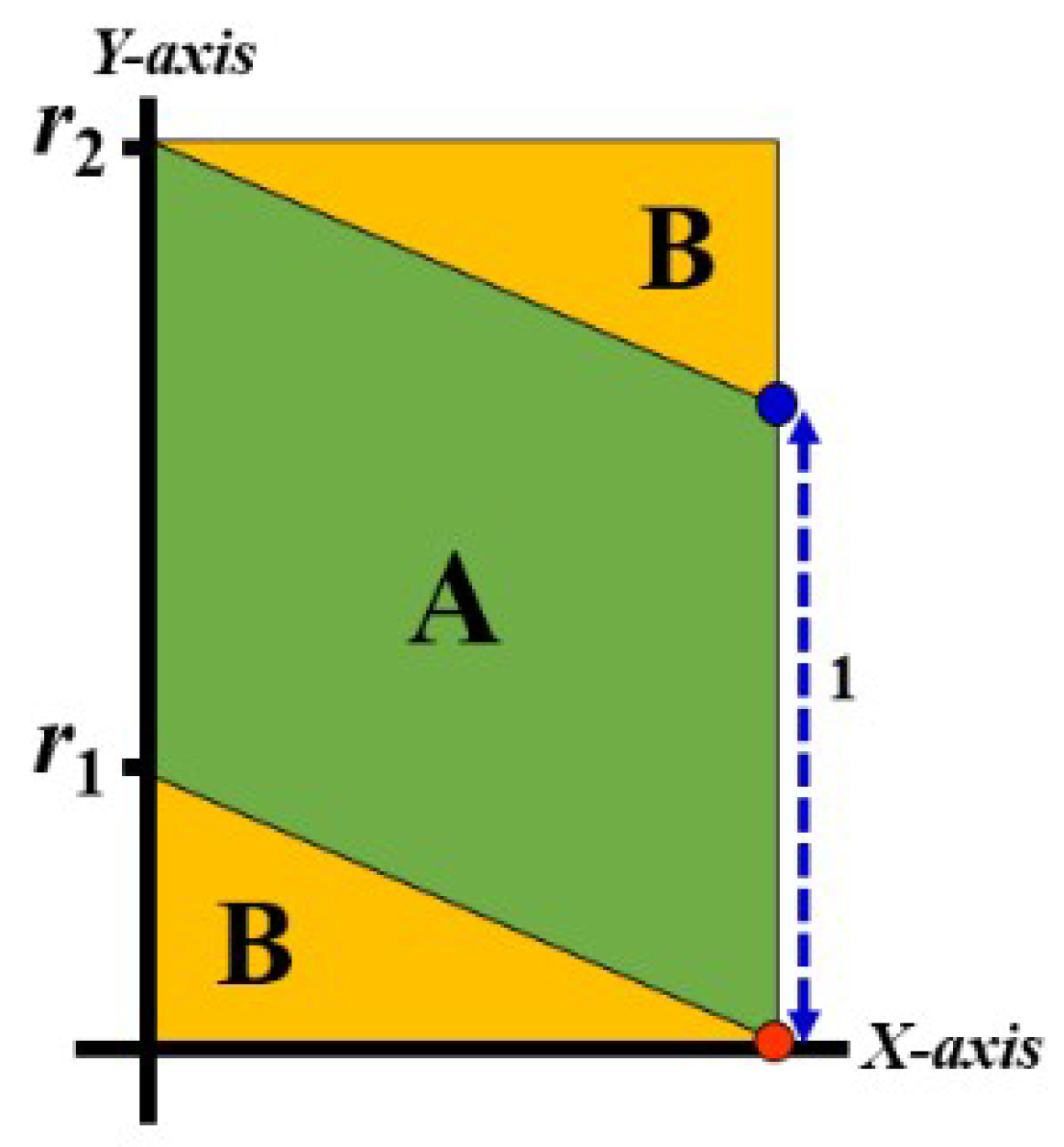
- Step 1
- Which quarter of the Cartesian plane is involved? Note that the 1st and 3rd quarters have the same structure, while the 2nd and 4th quarters have another one.
- Step 2
- Which rectangle is involved (AB or CB)?
- Step 3
- Which area is involved (A, B, or C)?
- IF ((x ≥ 0) AND (y ≥ 0)) OR ((x < 0) AND (y < 0))
- THEN “1st or 3rd quarter”
- ELSE “2nd or 4th quarter”
- IF ((int () mod 2 = 0) AND (int (y/1.5) mod 2) = 0) OR
- (int () mod 2 = 1) AND (int (y/1.5) mod 2) = 1))
- THEN “CB Rectangle is involved”
- ELSE “AB Rectangle is involved”
- int takes the integer part of the (decimal) number,
- mod is the modulus (or remainder, here after division by two).
- m is the slope of L1 and L2, which is a constant here, equal to ,
- r1 and r2 are the y-axis intercept with L1 and L2, respectively, where r2 = r1 + 1
- IF ((r1 − y) ≤ 0) AND ((r2 − y) ≥ 0)
- THEN “Area A is involved”
- ELSE “Area B is involved”
- Step 1
- The 1st or 3rd quarter is involved.
- Step 2
- It’s odd and even. Therefore, rectangle AB is involved.
- Step 3
- Area A is matched.
- (1)
- i == 1 + 0 = 1
- (2)
- k = 1 −−0.500.
- (3)
- j−y + 0.5 · 0.5 = −0.2
- (a)
- Converting from Continuous Coordinate System to CCS.
- Step 1
- It belongs to the 1st quarter.
- Step 2
- It belongs to rectangle CB.
- Step 3
- Area B is matched.
- (1)
- j = = 0
- (2)
- i =0.433 + 0.25 + 0 = 0.683
- (3)
- k =0.683 − 0.866 = −0.183
- (a)
- Converting from the Continuous Coordinate System to CCS.
- Step 1
- It belongs to the first quarter.
- Step 2
- It belongs to rectangle CB.
- Step 3
- Area C is matched.
- (1)
- k == 0 − 0 = 0
- (2)
- i =0.346 + 0 = 0.346
- (3)
- j =0.173 − 0.799 = −0.626
- (a)
- Converting from Continuous Coordinate System to CCS.
- Step 1
- It belongs to the first quarter.
- Step 2
- Based on Code 2, it belongs to rectangle CB (but, since it is a mid-point, then either rectangle AB or CB may be used).
- Step 3
- Area B is matched.
- (1)
- j == 0
- (2)
- i == 0.5 + 0.5 + 0 = 1
- (3)
- k == 1 − 1 = 0
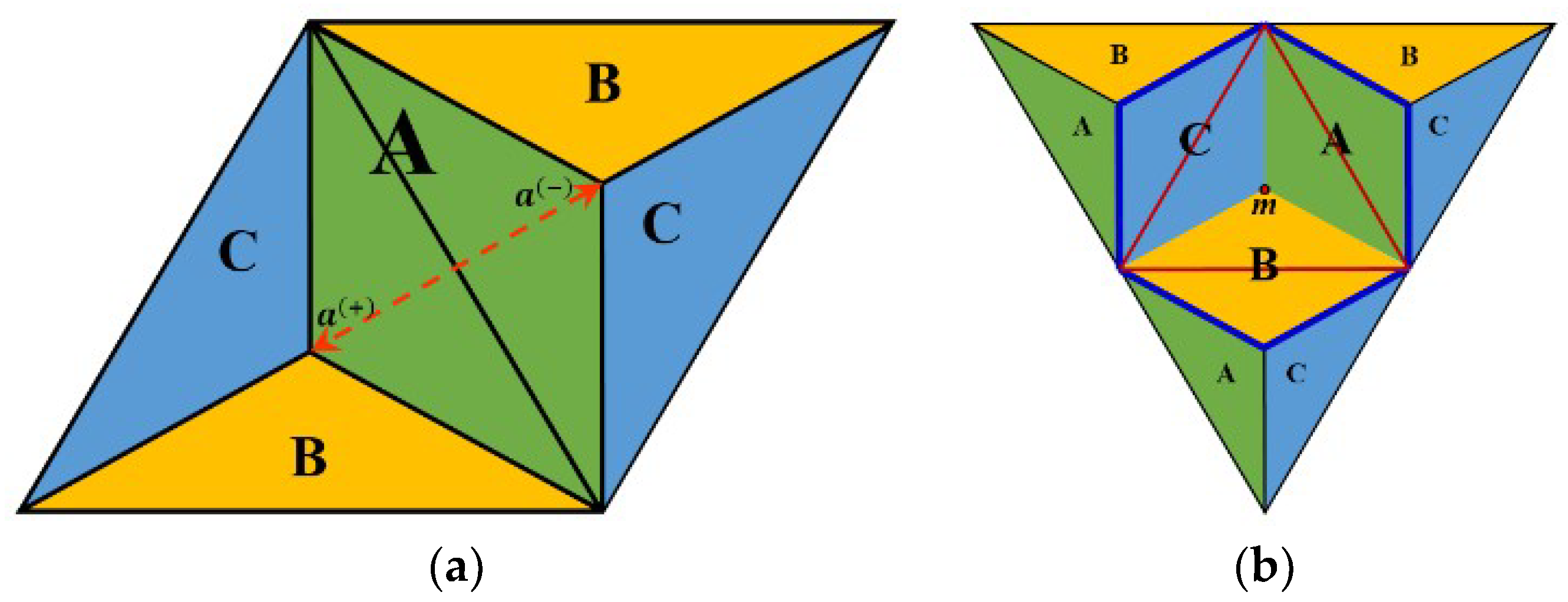
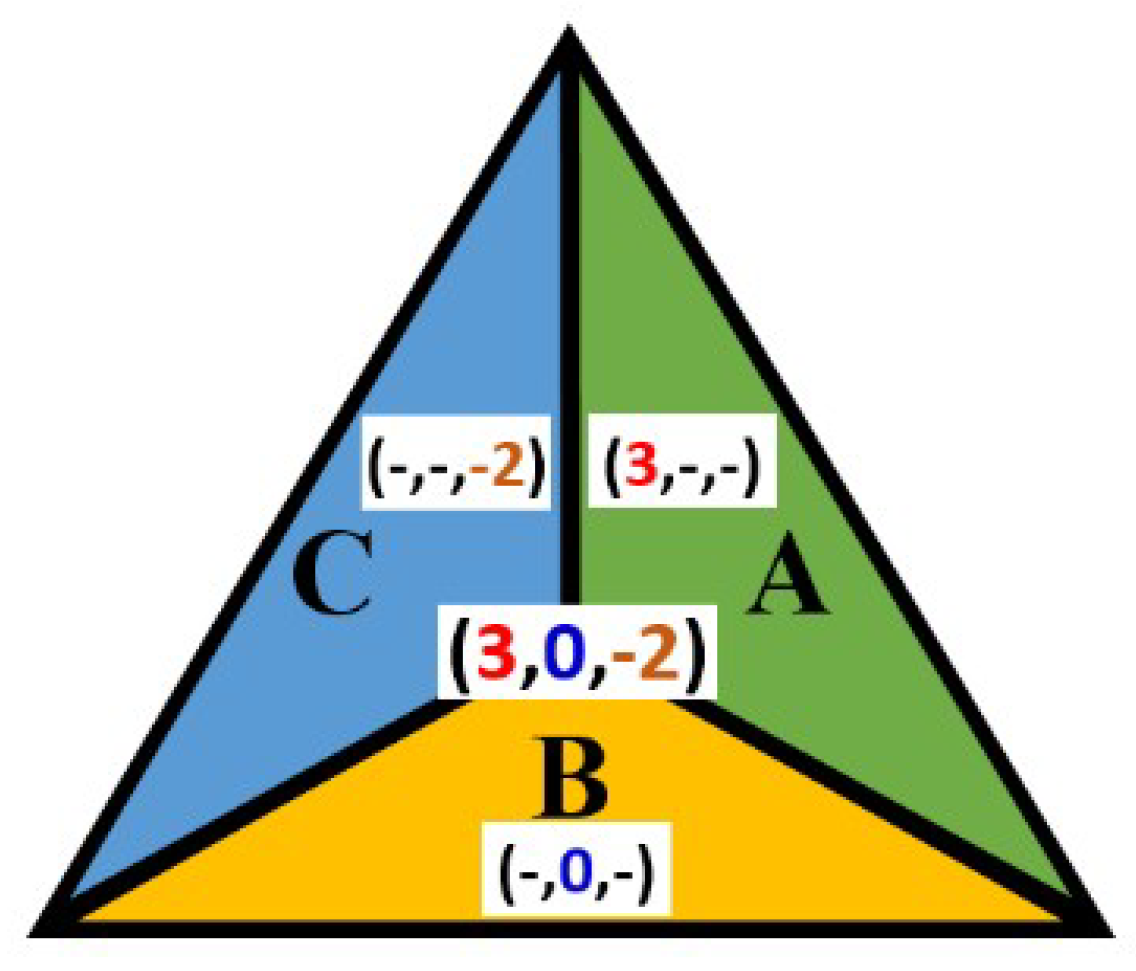
4. Properties of the Continuous Triangular Coordinate System
4.1. On the Triplets of a General Point
- equal to 1, then it indicates the positive midpoint (i.e., a(+));
- equal to −1, then it indicates the negative midpoint (i.e., a(−));
- equal to 0, then it indicates the point on the triangle’s edge;
- positive, then the point belongs to the positive triangle;
- negative, then the point belongs to the negative triangle.
4.2. Relation to Discrete Coordinate Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Coxeter, H.S.M. Introduction to Geometry, 2nd ed.; Wiley: New York, NY, USA, 1969. [Google Scholar]
- Middleton, L.; Sivaswamy, J. Hexagonal Image Processing—A Practical Approach; Springer: London, UK, 2005. [Google Scholar]
- Carr, D.B.; Olsen, A.R.; White, D. Hexagon mosaic maps for display of univariate and bivariate geographical data. Cartogr. Geograph. Inform. Syst. 1992, 19, 228–236. [Google Scholar] [CrossRef]
- Sahr, K. Hexagonal discrete global grid systems for geospatial computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Sakai, K.I. Studies on the competition in plants. VII. Effect on competition of a varying number of competing and non-competing individuals. J. Genet. 1957, 55, 227–234. [Google Scholar] [CrossRef]
- Birch, C.P.; Oom, S.P.; Beecham, J.A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology. Ecol. Model. 2007, 206, 347–359. [Google Scholar] [CrossRef]
- Her, I. A symmetrical coordinate frame on the hexagonal grid for computer graphics and vision. J. Mech. ASME 1993, 115, 447–449. [Google Scholar] [CrossRef]
- Her, I. Geometric Transformations on the Hexagonal Grid. IEEE Trans. Image Proc. 1995, 4, 1213–1222. [Google Scholar] [CrossRef] [PubMed]
- Luczak, E.; Rosenfeld, A. Distance on a hexagonal grid. IEEE Trans. Comput. 1976, 532–533. [Google Scholar] [CrossRef]
- Almansa, A. Sampling, Interpolation and Detection. Applications in Satellite Imaging. Ph.D. Thesis, École Normale Supérieure de Cachan-ENS Cachan, Cachan, France, 2002. [Google Scholar]
- Pluta, K.; Romon, P.; Kenmochi, Y.; Passat, N. Honeycomb geometry: Rigid motions on the hexagonal grid. In Proceedings of the International Conference on Discrete Geometry for Computer Imagery, Vienna, Austria, 19 September 2017; Springer: Cham, Switzerland, 2017. LNCS. Volume 10502, pp. 33–45. [Google Scholar]
- Nagy, B. Isometric transformations of the dual of the hexagonal lattice. In Proceedings of the 6th International Symposium on Image and Signal Processing and Analysis, Salzburg, Austria, 16–18 September 2009; pp. 432–437. [Google Scholar]
- Deutsch, E.S. Thinning algorithms on rectangular, hexagonal and triangular arrays. Commun. ACM 1972, 15, 827–837. [Google Scholar] [CrossRef]
- Bays, C. Cellular automata in the triangular tessellation. Complex Syst. 1994, 8, 127. [Google Scholar]
- Nagy, B. Finding shortest path with neighbourhood sequences in triangular grids. In Proceedings of the 2nd International Symposium, in Image and Signal Processing and Analysis, Pula, Croatia, 19–21 June 2001; pp. 55–60. [Google Scholar]
- Nagy, B. A symmetric coordinate frame for hexagonal networks. In Proceedings of the ACM Theoretical Computer Science-Information Society, Ljubljana, Slovenia, 11–15 October 2004; Volume 4, pp. 193–196. [Google Scholar]
- Nagy, B. Cellular topology and topological coordinate systems on the hexagonal and on the triangular grids. Ann. Math. Artif. Intel. 2015, 75, 117–134. [Google Scholar] [CrossRef]
- Nagy, B.; Lukic, T. Dense Projection Tomography on the Triangular Tiling. Fundam. Inform. 2016, 145, 125–141. [Google Scholar] [CrossRef]
- Nagy, B.; Valentina, E. Memetic algorithms for reconstruction of binary images on triangular grids with 3 and 6 projections. Appl. Soft Comput. 2017, 52, 549–565. [Google Scholar] [CrossRef]
- Kardos, P.; Palágyi, K. Topology preservation on the triangular grid. Ann. Math. Artif. Intell. 2015, 75, 53–68. [Google Scholar] [CrossRef]
- Abdalla, M.; Nagy, B. Dilation and Erosion on the Triangular Tessellation: An Independent Approach. IEEE Access 2018, 6, 23108–23119. [Google Scholar] [CrossRef]
- Nagy, B. Generalized triangular grids in digital geometry. Acta Math. Acad. Paedagog. Nyházi 2004, 20, 63–78. [Google Scholar]
- Skala, V. Barycentric coordinates computation in homogeneous coordinates. Comput. Graph. 2008, 32, 120–127. [Google Scholar] [CrossRef]
- Kovács, G.; Nagy, B.; Vizvári, B. Weighted Distances on the Trihexagonal Grid. In Proceedings of the International Conference on the Discrete Geometry for Computer Imagery, Vienna, Austria, 19 September 2017; Springer: Cham, Switzerland, 2017. LNCS. Volume 10502, pp. 82–93. [Google Scholar]
- Abuhmaidan, K.; Nagy, B. Non-bijective translations on the triangular plane. In Proceedings of the 2018 IEEE 16th World Symposium on Applied Machine Intelligence and Informatics (SAMI), Kosice, Slovakia, 7–10 February 2018; pp. 183–188. [Google Scholar]
| Coordinate Triplet | Area A | Area B | Area C |
|---|---|---|---|
| i | |||
| j | |||
| k |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nagy, B.; Abuhmaidan, K. A Continuous Coordinate System for the Plane by Triangular Symmetry. Symmetry 2019, 11, 191. https://doi.org/10.3390/sym11020191
Nagy B, Abuhmaidan K. A Continuous Coordinate System for the Plane by Triangular Symmetry. Symmetry. 2019; 11(2):191. https://doi.org/10.3390/sym11020191
Chicago/Turabian StyleNagy, Benedek, and Khaled Abuhmaidan. 2019. "A Continuous Coordinate System for the Plane by Triangular Symmetry" Symmetry 11, no. 2: 191. https://doi.org/10.3390/sym11020191
APA StyleNagy, B., & Abuhmaidan, K. (2019). A Continuous Coordinate System for the Plane by Triangular Symmetry. Symmetry, 11(2), 191. https://doi.org/10.3390/sym11020191