A Fuzzy Logic Algorithm for Optimizing the Investment Decisions within Companies

Abstract

As companies operate in a competitive environment, where the struggle for survival on the market is rather tough, the top management face new challenges to identify methods, and even techniques, which allows it to select from the market those assets that provide an optimal ratio between the acquisition cost and the economic performance. In this context, a fuzzy logic managerial decision tool for the assets acquisition is proposed with the paper. The algorithm has three main components: the matrix of the membership degree of the existing bids to asset selection criteria, using fuzzy triangular numbers; the vector of the global membership degree of the bids to the selection criteria and the maximum of the global membership degree as an inference operator for establishing the validated bids by the algorithm. Two scenarios of asset acquisition were tested. After simulations, it was determined that the proposed fuzzy logic managerial decision tool combines, with very good results, the acquisition cost of the assets with their economic performance.

1. Introduction

Companies operate in a competitive environment where the struggle for survival on the market is rather tough. They set out market survival strategies that start from cost control, product pricing policy and consumer relations so that companies can meet the quality and price requirements that consumers naturally have.

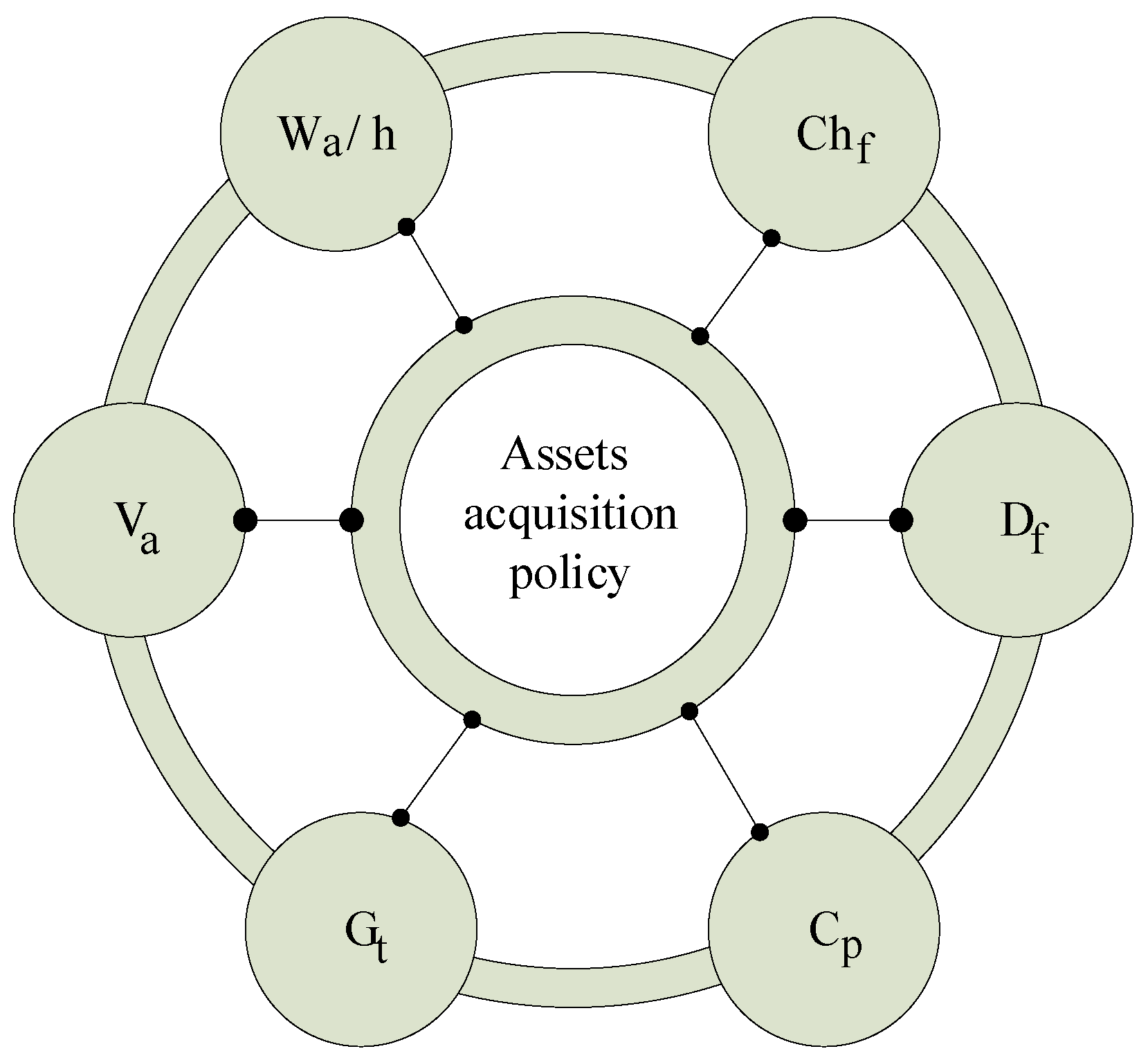
From the cost control policies that engender a large amount of financial resources that needs to be recovered within a limited timeframe is found the policy of acquiring the assets needed to conduct organic business. These assets, known as investment, no matter their form should be, have to be considered as a capital asset capable of generating an improvement in the company’s performance.

For this reason, asset purchasing policies are important in terms of acquisition costs and economic performance. Such economic performances can take different forms. For example, considering the productivity of an asset, we believe that this is important in modeling because, based on it, we will get the number of units of product per unit of time, and each unit of product is a win for the company. If we refer to the cost of operating the asset, it is also an important part of the modeling process as the cost of operating has a direct impact on the company’s financial result.

Also, it is clear that the policy of acquiring assets can no longer be regarded in classical financial theory as a capital immobilization that must be recovered within a certain period of time. According to modern financial theory, the asset acquisition policy is a complex operation (Figure 1—Where: $W_a/h$—the asset’s productivity; $C{h}_f$—the asset’s operating expenses; $D_f$—the asset’s useful life; $C_p$—the asset’s production capacity; $G_t$—the asset’s technical guarantee; $V_a$—the asset volume) which combines the immobilization of the company’s resources over a determined period of time with the advantages obtained from the economic performance of the asset, that together contribute to the financial sustainability of the company’s organic activity.

This way of redefining an asset acquisition policy makes top management face new challenges to identify methods and even techniques to select from to market those assets that provide an optimal ratio between the acquisition cost and the economic performance provided by the asset acquired in the company’s organic business.

From this perspective, the multicriterial fuzzy logic algorithm for optimizing the investment decision of companies proposed in the present paper provides solutions to problems usually faced by a company’s top management in the decision-making process of asset selection:

• Ensures the ratio optimization between the cost of acquiring an asset and its economic performance;
• Ensures the comparability of the criteria for the acquisition of an asset even when these criteria have different measurement units or can be judged through ratings;
• Ensures the transition from crisp sets used for the quantification of asset acquisition criteria to fuzzy sets, characterized by membership degrees, so that each acquisition criterion $\left(C_i\right)$ will have a membership degree $\mu \left(C_i\right)\in \left[0;1\right]$;
• When there are multiple offers on the market for the acquisition of assets, the algorithm allows the selection of the offer that best combines the cost of the asset with its economic performance;
• Ensures the selection of an asset or portfolio of assets based on the company’s asset purchase policy, and the acquisition criteria considered to be a priority. This feature is provided by the fuzzy logic multi-criteria algorithm using the adjustment coefficients described in this paper.

Unlike other methods found in the literature, such as the score method, which consists in awarding scores (based on the professional judgment of the decision maker) for the acquiring criteria of the asset, followed by hierarchizing the existing bids on the market according to these scores, the multicriterial fuzzy logic algorithm presented in this paper eliminates this inconvenience. The scores attributed to the acquisition criteria do not lead to the best results for asset purchases. Some of these drawbacks of the scores are presented below:

• They are based on professional judgment;
• Does not ensure comparability between asset acquisition criteria;
• The determined score functions do not generate the best combination of the asset cost and its economic performance.

The multi-criteria fuzzy logic algorithm is essentially based on determining the membership functions for each asset acquisition criterion (thus eliminating scores from the scores method), then by applying the “and” inference fuzzy operator; the offers available on the market for the acquisition assets being ranked according to the highest affiliate function value [1].

The multi-criteria fuzzy logic algorithm is thus a new instrument in the literature, functioning as a decision-making tool, based on scientific acquisition criteria of assets, with which the optimal combination between the cost of assets purchasing and its economic performances is assured, as mentioned.

In all this context, the purpose of this paper is to develop a modern and innovative management tool based on the artificial intelligence technique and the use of systems with fuzzy logic for companies to substantiate investment decisions in assets purchased from the market. The innovative management tool created must meet the real asset investment needs of the companies, e.g., to provide the best combination of asset immobilization and asset performance. In addition, artificial intelligence through systems with fuzzy logic solves a series of limitations of classical methods of substantiating investment decisions in companies’ assets. These limitations have been set out in the paper.

As for the identification of the issues that are part of the company’s investment decision system, it can be underlined that the investment decisions in companies’ assets are the most complex decisions both considering the time horizon and the impact. For this reason, these investments have to take into account a series of company’s constraints (including those of a budgetary nature) as well as the requirements resulting from its core business in terms by: increasing turnover, increasing labor productivity, customer quality and price requirements, etc.

Nevertheless, a series of elements strictly connected to the complex requirements of the selection process of the market assets to which they belong should be considered in terms of:

• The multitude and complexity of the selection criteria for assets to be purchased from the market;
• Lack of homogeneity in the content of the selection criteria;
• The possibility to provide metrics for measuring selection criteria in the form of linguistic variables;
• The existence of decision-shaping techniques based on the selection of market assets in line with company acquisition strategies.

Considering all of the above, we aim to create a modern and innovative management tool which will be able to solve the three major categories of problems: company’s constraints due to the limited nature of resources, the requirements of the core business of companies and the requirements of the selection process of the assets on the free market. The solution of these problems can be found through fuzzy logic systems as they are able to provide fuzzy modeling of non-homogeneous selection criteria as diverse, quantified content using linguistic variables as well as substantiating multi-criterial, diversified and complex decisions aimed at to provide capital immobilization that will generate an impact in terms of the company’s economic performance.

2. State of the Art

The scientific world has become recently more and more interested in computational intelligence techniques, among the most used being neural networks, genetic algorithms, support vector machine, fuzzy sets, and grey systems. Computational intelligence is useful in decision-making, as it allows an exhaustive and exploratory data analysis, using decision systems and intelligent algorithms. Over the time it has been proven that it can be successfully used for optimizing investment decisions, as they manage uncertainty, irreversibility and complexity. Among all these techniques, this study uses fuzzy sets due to the incontestable advantages generated by them, well recognized by the researchers all around the world in various areas, such as: computer science, engineering, mathematics, automation control systems, operations research, management science, business economics, environmental sciences ecology, telecommunications, imaging science photographic technology, science technology, or robotics. Currently, according to the WoS database being published 53.220 ISI articles using this technique.

In the computer science area, Ghorabaee et al. [1] proposed a quantitative approach, using MILP (Mixed Integer Linear Programming) models, that address various decision making challenges within the IT security process of an organization, that optimize the security of IT systems. Schilling [2] studied the influence of big data and analytics on adopting decisions in the health IT market. The results showed that using big data and analytics the companies can indicate the optimal pricing strategies. Wu et al. [3] used game theory models for important strategy decisions in the area of investment building projects, in order to find optimal prices of real estate according to opportunities of paying the bills and the optimal financial strategy in the situation of economic crisis.

In the area of business economics, Kurakova and Khomyak [4] studied the vagueness from discounting cash flows, proposing capital budgeting techniques using discounted fuzzy for cash flows, in order to select the investment alternatives. Kahraman et al. [5] studied the potential applications of the fuzzy logic in insurance.

Shapiro and Koissi [6] propose a hybrid model for investments that incorporate a fuzzy moving average strategy, in which the fuzzy logic rule is used to determine the strength of trading signals and the trading volume, and a genetic algorithm to identify an optimal fuzzy logic rule set and utilize crude oil futures prices from the New York Mercantile Exchange. Liu et al. [7] published an article in which the annual cost of a company was minimized using fuzzy inventory model. The fuzzy pay-off method was used by Sarkar and Mahapatra [8] to form a fuzzy pay-off distribution for an investment that is compatible with the requirements set by the circumstances surrounding giga-investments. The “Technique for Order Preference by Similarity to Ideal Solution” was used for city investment project rankings by Collan et al. [9]. In their paper, a fuzzy technique is proposed for order preferences, based on the similarity to an ideal solution.

Walczak and Rutkowska [10] built a model that involves the mixture of randomness and fuzziness, such as stochastic returns with fuzzy information, for portfolio optimization. Qin [11] proposed a model which innovated the multicriteria decision making (MCDM) problems, by solving the cognitive limitations and the factors that can deviate rational decisions. They applied this model on the estate investment area, obtaining significant results. Ma et al. [12] built a hybrid model for stock market forecasting and portfolio selection based on ARX, grey system and RS (rough-set) theories, while Huang and Jane [13] purposed a combination of the fuzzy analytic hierarchy process (AHP) with the portfolio selection problem. AHP is also used in Lesniak et al. [14] research for supporting contractors’ bidding decision.

Tiryaki and Ahlatcioglu [15] proposed a novel method for comparing two interval-valued intuitionist fuzzy numbers by introducing the membership uncertainty index and the hesitation uncertainty index. This was used to multi-attribute decision making with incomplete attribute weight information. Krohling and Pacheco [16] used an improved accuracy function for interval-valued intuitionistic fuzzy sets and applied it to multi-attribute group decision making. Joshi and Kumar [17] developed a fuzzy analytic hierarchy process method for tackling the uncertainty and imprecision associated with MCDM problems. This method was tested in a power plant, showing where the predictive maintenance strategy is the most suitable.

Wang et al. [18] solved the problem of long term investment in the telecommunication industry that affect the strategic positioning of the companies in the sector, by using combined fuzzy MCDM approach. The MCDM approach was also used by Onut et al. [19], in a fuzzy model with direct application in investment projects assessment. Wang and Zhang [20] proposed recently a new method for MCDM problem solving using an optimistic multi-granulation intuitionistic fuzzy rough set model, while Luo and Liang [21] created a novel similarity measure for interval-valued intuitionistic fuzzy set.

A fuzzy decision algorithm is proposed by Dimova et al. [22] to select the most suitable advanced manufacturing system; and Ertugrul and Tolga [23] built an application of fuzzy analytic network process along with fuzzy cost analysis for selecting R&D projects and solving the problem of the option’s qualitative attributes. Mohanty [24] focused also on the project selection problem, proposing AHP and fuzzy TOPSIS methods for oil-fields development.

Amiri [25] published an integrated decision making approach for ERP system selection, using a quality function deployment (QFD), a fuzzy linear regression and zero-one goal programming. For multi-criteria decision making, Hu et. al. [26] utilised a method based on possibility degree of interval type-2 fuzzy number. Karsak and Ozogul [27] modeled the supply chain (SC) uncertainties by fuzzy sets and develop a possibilist SC configuration model for new products with unreliable or unavailable SC statistical data.

Wang and Shu [28] aimed to study MCGDM problems in which the criterion values are hesitant fuzzy elements, and the weight information about both the decision makers and the criteria is unknown. Schilling [2] developed a fuzzy group decision making model which was applied based on compatibility with multiplicative trapezoidal fuzzy preference relations.

Fuzzy logic was used by Zhang [29] to assess commercial viability of technology start-up businesses in a government venture capital, while Shen and Tzeng [30] developed a fuzzy inference-enhanced VC-DRSA model for technical analysis of the investment. Other researches have been conducted in the area of: knowledge management performance measurement of small and medium enterprises [31], social behavior modeling [32], measuring customer loyalty [33], e-commerce [34], MADM (multi-attribute decision-making) [35,36,37,38,39,40,41], material selection [42], risk assessment [43], medical diagnosis [44], mobile robots [45], investment selection [46] and forecasting [47].

Considering the actual state of the art, we can underline that the methods and algorithms developed over the time are useful for giving a solution to the company’s decision-making problems when it acquires assets from the market that are needed to conduct current business. Some of these methods are based on the assignment of scores, noted as $\left(p_k\right)$, to the selection criteria, $\left(c_j\right),$ of assets, so that the decision-making problem for asset selection is based on identifying those asset classes that satisfy the max condition $max\left({{\displaystyle \sum }}_{j=1}^n{c}_j\times p_j\right)$.

Regardless of the type of algorithm or asset selection methods, they present several limitations, most often related to: comparability and modeling of different selection criteria as content, limitations of algorithm/criteria application when the number of selection criteria of assets and limitations on the selection of assets when they are part of a portfolio of assets each with specific selection criteria.

The multicriterial algorithm with fuzzy logic for substantiating companies’ investment decisions presents, when compared to the exiting state of the art, several novelty elements, such as:

• It is the first decision management tool in the literature to use artificial intelligence techniques over state-of-the-art methods/algorithms based on simple mathematical models. As we all know, these techniques are not always characterized by flexibility, adaptability or efficiency and are not well suited to the company’s needs;
• Modeling the asset selection decision is based on triangular fuzzy numbers. Considering the market selection criteria used in practice, it can be underlined that they are modeled by fuzzy logic, which allows for fuzzy modeling of those criteria that have the linguistic values as the sole alternative for quantification;
• It contains innovative components of the algorithm based on artificial intelligence, which refers to: the matrix of the degree of belonging, the global degree of belonging vector and the inference operator of the maximum of the global degree of belonging;
• It is a flexible managerial tool for companies that allows the selection of assets in portfolios, but also the adaptation of asset selection strategy to the real needs of the company;
• It effectively combines criteria for the selection of assets on the market with different content, such as asset-backed assets with selection criteria that take into account their economic performance;
• It solves extremely complex problems for substantiating the multi-criteria decisions underlying the selection of asset portfolios, regardless of the number and content of asset selection criteria.

3. The Development of the Fuzzy Logic Algorithm

3.1. The Fuzzy Logic Multi-Criteria Algorithm Premises

The fuzzy logic multi-criteria algorithm is designed to allow companies to identify those categories of assets $({\mathrm{A}}_{\mathrm{i}})$ on the market that best fit the correlation between the asset price and its economic performance. Thus, the fuzzy logic algorithm has been built starting from the following premises:

• P1: The company intends to purchase the assets A₁, A₂, .... A_n, with i = $\overline{1,\mathrm{n}}$ from the market, in order to improve its economic performance. These assets are required for investment activity and are purchased within the range of available funding sources.
• P2: For each asset A_i, i = $\overline{1,\mathrm{n}}$, the company sets acquisition criteria C_j with j = $\overline{1,\mathrm{m}},$ according to its purpose, so that each asset A_i, i = $\overline{1,\mathrm{n}}$, will have the associated criteria C_j, j = $\overline{1,\mathrm{m}},$ of the form:

  $$\begin{array}{ccc}{\mathrm{A}}_1=\mathrm{f}({\mathrm{C}}_{\mathrm{j}11}& {\mathrm{C}}_{\mathrm{j}12}\dots \dots \dots .& {\mathrm{C}}_{\mathrm{j}1\mathrm{m}})\\ {\mathrm{A}}_2=\mathrm{f}({\mathrm{C}}_{\mathrm{j}21}& {\mathrm{C}}_{\mathrm{j}22}\dots \dots \dots .& {\mathrm{C}}_{\mathrm{j}2\mathrm{m}})\\ \hfill \dots .& \hfill \dots .& \dots .\\ {\mathrm{A}}_{\mathrm{n}}=\mathrm{f}({\mathrm{C}}_{\mathrm{ji}1}& {\mathrm{C}}_{\mathrm{ji}2}\dots \dots \dots .& {\mathrm{C}}_{\mathrm{jim}})\end{array}$$

  (1)
• P3: There are offers (${\mathrm{O}}_{\mathrm{ki}})$ on the market for acquiring the assets $({\mathrm{A}}_{\mathrm{i}})\mathrm{with}\mathrm{i}=\overline{1,\mathrm{n}}$ that meet the purchase criteria C_j, $\mathrm{j}=\overline{1,\mathrm{m}}$ of the form:

  $$\left|\begin{array}{c}{\mathrm{A}}_1\\ {\mathrm{A}}_2\\ \dots \\ {\mathrm{A}}_{\mathrm{n}}\end{array}\right|\to \left|\begin{array}{cccc}{\mathrm{c}}_{11}& {\mathrm{c}}_{12}& \dots & {\mathrm{c}}_{1\mathrm{m}}\\ {\mathrm{c}}_{21}& {\mathrm{c}}_{22}& \dots & {\mathrm{c}}_{2\mathrm{m}}\\ \dots & \dots & \dots & \dots \\ {\mathrm{c}}_{\mathrm{k}1}& {\mathrm{c}}_{\mathrm{k}2}& \dots & {\mathrm{c}}_{\mathrm{km}}\end{array}\right|\to \left|\begin{array}{cccc}{\mathrm{O}}_{11}& {\mathrm{O}}_{12}& \dots & {\mathrm{O}}_{1\mathrm{m}}\\ {\mathrm{O}}_{21}& {\mathrm{O}}_{22}& \dots & {\mathrm{O}}_{2\mathrm{m}}\\ \dots & \dots & \dots & \dots \\ {\mathrm{O}}_{\mathrm{k}1}& {\mathrm{O}}_{\mathrm{k}2}& \dots & {\mathrm{O}}_{\mathrm{km}}\end{array}\right|$$

  (2)

  where: A_i—assets; C_j—acquisition criteria; ${\mathrm{O}}_{\mathrm{ki}}$—the offers existing on the market
  Each offer on the market meets the purchase criteria C_j, $\mathrm{j}=\overline{1,\mathrm{m}}$, otherwise the offer is rejected, namely:

  $$\begin{array}{l}{\mathrm{O}}_{11}\in \left\{{\mathrm{c}}_{11},{\mathrm{c}}_{12},\dots ,{\mathrm{c}}_{1\mathrm{n}}\right\};\\ {\mathrm{O}}_{22}\in \left\{{\mathrm{c}}_{21},{\mathrm{c}}_{22},\dots ,{\mathrm{c}}_{2\mathrm{n}}\right\};{\mathrm{O}}_{\mathrm{ki}}\in \left\{{\mathrm{c}}_{\mathrm{k}1},{\mathrm{c}}_{\mathrm{k}2},\dots ,{\mathrm{c}}_{\mathrm{kn}}\right\};\end{array}$$

  (3)
  For each asset A_i, i = $\overline{1,\mathrm{n}}$ is satisfied the condition ${\mathrm{O}}_{\mathrm{ki}}$ ≥ 2: there are at least two eligible offers, on the contrary the existing of only an eligible offer on the market, would make the problem irrelevant.
• P4: For each acquisition criterion ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ with $\mathrm{i},\mathrm{j}=\overline{1,\mathrm{n},\mathrm{m}}$, the decision maker sets a ${\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ considered the maximum accepted level for each criterion, and a ${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ considered the level below which the company rejects any existing offer on the market. Any acquisition criterion respects the following inequality:

  $${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$$

  (4)
• P5: The global membership degree of an offer ${\mathsf{\mu }}_{\mathrm{g}}\left({\mathrm{O}}_{\mathrm{ji}}\right)$ substantiates the company’s investment decision. Any offer with a global membership degree ${\mathsf{\mu }}_{\mathrm{g}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)$ below 0.5 is considered to be an offer that deviates from the company’s objectives, to identify an optimal ratio between the cost of asset acquisition and the economic performance.

3.2. The Content of the Fuzzy Logic Multi-Criteria Algorithm

Let O be the set of existing market offers that meet the assumptions of the proposed algorithm, each offer ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ with $\mathrm{i}=\overline{1,\mathrm{n}}$ and $\mathrm{k}=\overline{1,\mathrm{l}}$ fitting in the acquisition criteria ${\mathrm{C}}_{\mathrm{j}}$ with $\mathrm{j}=\overline{1,\mathrm{m}}$ and every offer ${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$.

The number of offers on the market that meet the above conditions will be of the form: O: {${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right)$, ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right)$,…, ${\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_{\mathrm{n}}$};

For each asset, ${\mathrm{A}}_{\mathrm{i}}$, i = $\overline{1,\mathrm{n}}$, there are at least two offers ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ > 2, k = $\overline{1,\mathrm{l}}$ and each offer respects the above-mentioned conditions for the acquisition criteria.

In the matrix form for each asset ${\mathrm{A}}_{\mathrm{i}}$, i = $\overline{1,\mathrm{n}}$ there will be the offers ${\mathrm{O}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ on the market, of the form:

$${\mathrm{A}}_1:\left(\begin{array}{c}{\mathrm{A}}_1\\ {\mathrm{A}}_2\\ \dots \\ {\mathrm{A}}_{\mathrm{n}}\end{array}\right)=\left(\begin{array}{cccc}{\mathrm{O}}_1\left({\mathrm{A}}_1\right)& {\mathrm{O}}_2\left({\mathrm{A}}_1\right)& \dots & {\mathrm{O}}_{\mathrm{l}}\left({\mathrm{A}}_1\right)\\ {\mathrm{O}}_1\left({\mathrm{A}}_2\right)& {\mathrm{O}}_2\left({\mathrm{A}}_2\right)& \dots & {\mathrm{O}}_{\mathrm{l}}\left({\mathrm{A}}_2\right)\\ \dots & \dots & \dots & \dots \\ {\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{n}}\right)& {\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{n}}\right)& \dots & {\mathrm{O}}_{\mathrm{l}}\left({\mathrm{A}}_{\mathrm{n}}\right)\end{array}\right)$$

(5)

Definition 1.

We define the vague sets corresponding to the criteria ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ with j = $\overline{1,\mathrm{m}}$ for the selection (acquisition) of assets ${\mathrm{A}}_{\mathrm{i}},$ using the offers ${\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_{\mathrm{i}})$ and the membership degree of the offers to the acquisition criterion ${\mathsf{\mu }}_{\mathrm{Cj}}({\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_{\mathrm{i}}))$:

$${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right):({\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_{\mathrm{i}}),{\mathsf{\mu }}_{\mathrm{Cj}}({\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_{\mathrm{i}}))$$

(6)

For each selection criterion ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ with $\mathrm{j}=\overline{1,\mathrm{m}}$ the accepted range is determined according to the assumption no. 4. Each selection criterion has the minimum-maximum pair defined.

$${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)\le {\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$$

(7)

Each acquisition criterion is defined by the crisp sets, because ${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)$, ${\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ $\in$ R. The fuzzy sets defined as this allow the comparison of the offers with each other and also allow the selection of the offers that best fit the asset selection criteria.

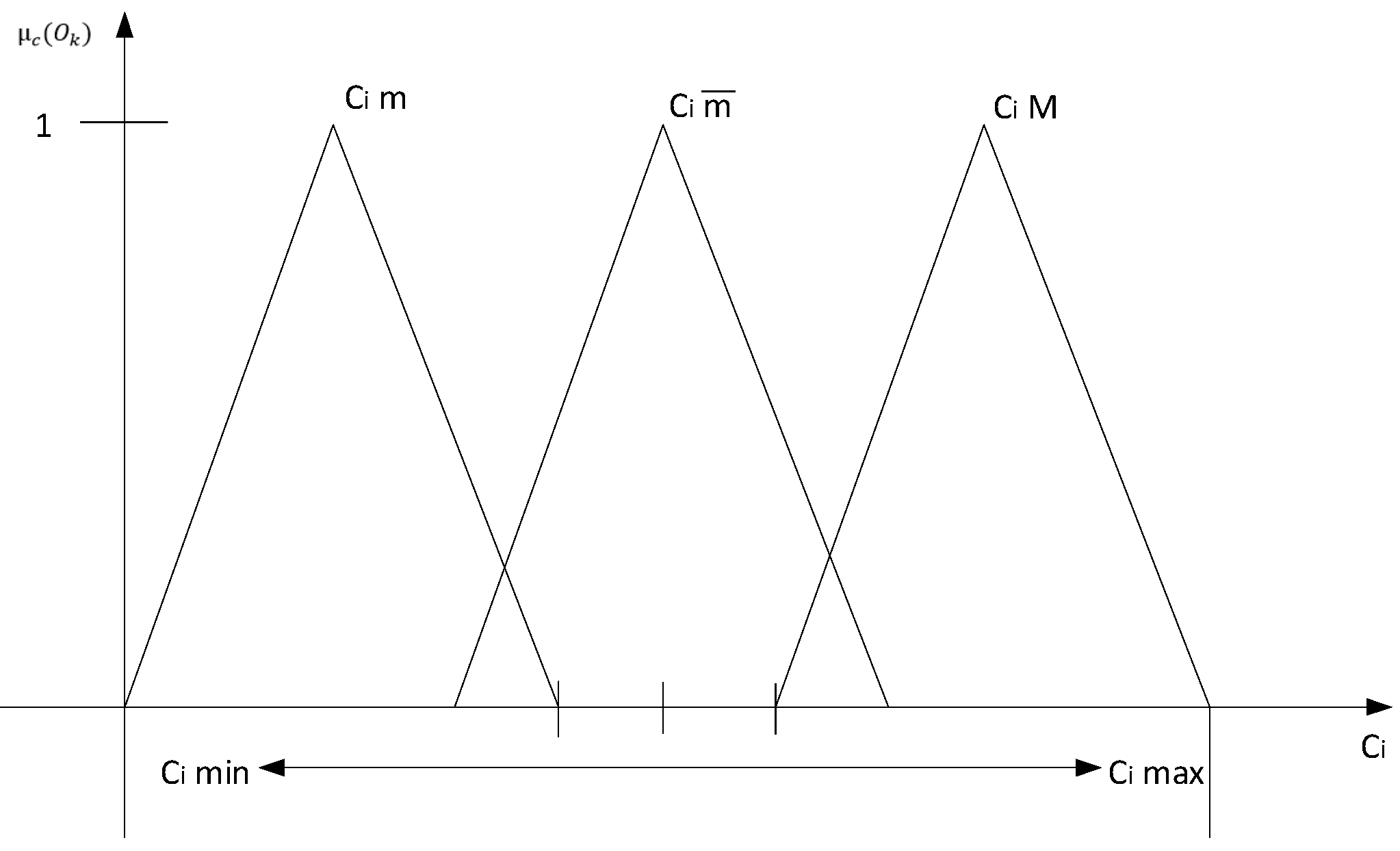
Definition 2.

Let be ${\mathrm{C}}_{\mathrm{jmin}}\left({\mathrm{A}}_{\mathrm{i}}\right)$, ${\mathrm{C}}_{\mathrm{jmax}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ $\in$. The fuzzy triangle number is a fuzzy subset of $\left({\mathrm{A}}_{\mathrm{i}}\right)$ of the form ${\mathsf{\mu }}_{\mathrm{cj}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)):\mathrm{O}\to \left[0,1\right]$ if its membership function is of the form:

• For minimum criteria:

  $${\mathsf{\mu }}_{\mathrm{cjmin}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))=\{\begin{array}{c}1 {\mathrm{if}\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)={\mathrm{C}}_{\mathrm{jmax}}\\ 1-\frac{{\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)-{\mathrm{C}}_{\mathrm{jmax}}}{{\mathrm{C}}_{\mathrm{jmin}}}{\mathrm{if}\mathrm{C}}_{\mathrm{jmax}}\le {\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\le {\mathrm{C}}_{\mathrm{jmax}}+{\mathrm{C}}_{\mathrm{jmin}}\\ 0 {\mathrm{if}\mathrm{V}}_{\mathrm{i}}\left({\mathrm{Ok}}_{\mathrm{i}}\right)\ge {\mathrm{C}}_{\mathrm{jmax}}+{\mathrm{C}}_{\mathrm{jmin}}\end{array}$$

  (8)

  where ${\mathrm{V}}_{\mathrm{i}}=$ the ${\mathrm{assets}\mathrm{A}}_{\mathrm{i}}$ market value generated by the offer ${\mathrm{O}}_{\mathrm{ki}}$
• For maximum criteria:

  $${\mathsf{\mu }}_{\mathrm{cjmax}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))=\{\begin{array}{c}1 {\mathrm{if}\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)={\mathrm{C}}_{\mathrm{jmax}}\\ 1-\frac{{\mathrm{C}}_{\mathrm{jmax}}-{\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)}{{\mathrm{C}}_{\mathrm{jmin}}}{\mathrm{if}\mathrm{C}}_{\mathrm{jmax}}-{\mathrm{C}}_{\mathrm{jmin}}\le {\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)<{\mathrm{C}}_{\mathrm{jmax}}\\ 0 {\mathrm{if}\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\le {\mathrm{C}}_{\mathrm{jmax}}-{\mathrm{V}}_{\mathrm{i}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\end{array}$$

  (9)

  where ${\mathrm{V}}_{\mathrm{i}}=$ the ${\mathrm{assets}\mathrm{A}}_{\mathrm{i}}$ market value generated by the offer ${\mathrm{O}}_{\mathrm{ki}}$.

The membership functions defined above have an important role in the algorithm, as they lead to the identification of the assets that best fit the selection criteria set by the companies. Thus, for each offer $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)),$ will be determined the membership degree ${\mathsf{\mu }}_{\mathrm{cj}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))$ of an offer to the selection criteria ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$.

Higher membership degrees will reflect that existing offers on the market comply with the selection criteria. Also, with the help of the fuzzy triangular number, each asset selection criteria can be appreciated by the linguistic terms specific to fuzzy sets (see Figure 2). For example, the price of an asset may be considered “high”, “medium” or “small” if it falls within a certain range of values.

For each offer ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ we determine the membership degree of the offer to the corresponding vague set, respectively the selection criterion ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right),$ obtaining for each asset a matrix equation of the form:

$${\mathrm{A}}_{\mathrm{i}}:\left(\begin{array}{c}{\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\\ {\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\\ ⋮\\ {\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\end{array}\right)=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ {\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))& {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\end{array}\right)$$

(10)

Definition 3.

We define the global membership degree ${\mathsf{\mu }}_{\mathrm{g}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)$ of an offer to the selection criteria ${\mathrm{C}}_{\mathrm{J}}\left({\mathrm{A}}_{\mathrm{i}}\right),$ the lowest value of the membership degrees determined for each offer and for each selection criterion, after a relation of the form:

$${\mathsf{\mu }}_{\mathrm{g}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=\min \left\{{\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)),{\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right),\dots ,{\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\right\}$$

(11)

On the basis of the previous matrix equation we determine the global membership degree ${\mathsf{\mu }}_{\mathrm{g}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)$ of each offer $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ to the asset selection criteria, in order to determine which of the offers best match the acquisition criteria set by the company.

Thus, the matrix equation of the form:

$${\mathrm{A}}_{\mathrm{i}}:\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ {\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))& {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\end{array}\right)=\left(\begin{array}{c}\min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ \min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮\\ \min {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))\end{array}\right)$$

(12)

If the value of the global membership degree of an offer ${\mathsf{\mu }}_{\mathrm{g}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)$ ≤ 0.5 it can be mentioned that the offer is far from the selection criteria, so it is recommended that the selection procedure to be resumed or the offer to be rejected.

In conclusion, the global membership degree ${\mathsf{\mu }}_{\mathrm{g}}\left({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)\right)$ determines the extent to which each offer ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ simultaneously meets all asset selection criteria so as to achieve an optimal value between the price of the asset and its performance economic.

The final step of the fuzzy logic multi-criteria algorithm consists in establishing the offer ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ with the highest degree $\max ({\mathsf{\mu }}_{\mathrm{g}}\left({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)\right),$ the offer that best meets the selection criteria of company based on the matrix Equation:

$${\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_{\mathrm{i}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right):\max \left(\begin{array}{c}\min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ \min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮\\ \min {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))\end{array}\right)$$

(13)

The offer with the highest global membership degree $({\mathsf{\mu }}_{\mathrm{g}}\left({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)\right)$ is considered the result of the fuzzy logic multi-criteria algorithm to substantiate the optimal investment decision. The higher the global membership degree is, the better the selection criteria are satisfied and the investment decision of the company will be the one for which the highest values of the global membership degree are recorded.

Proposition 1.

The ranking coefficients for the selection criteria (${\mathrm{a}}_{\mathrm{i}}),\mathrm{i}=\overline{1,\mathrm{n}}$ are used in situations when the company intends that certain criteria to be considered as priority over other criteria. For example, if a company considers the price of an asset as a priority over its productivity, then it will assign a higher value of the hierarchy coefficients for the price than for asset productivity. The ranking coefficients for the selection criteria (${\mathrm{a}}_{\mathrm{i}}),\mathrm{i}=\overline{1,\mathrm{n}}$ meet three cumulative conditions:

a) 

(${\mathrm{a}}_{\mathrm{i}}),\mathrm{i}=\overline{1,\mathrm{n}}$, cu ${\mathrm{a}}_{\mathrm{i}}\in \mathrm{R}$;

b) 

${{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}}=1$;

c) 

${\mathrm{a}}_{\mathrm{i}}:\mathrm{R}\to \left[0,1\right]$

The ranking/hierarchy coefficients assigned to the asset selection criteria are entered into the membership degree matrix, resulting the adjusted matrix, as follows:

$${\mathrm{A}}_{\mathrm{i}}:\left(\begin{array}{c}{\mathrm{Ok}}_1\\ {\mathrm{Ok}}_2\\ ⋮\\ {\mathrm{Ok}}_{\mathrm{i}}\end{array}\right)=\left(\begin{array}{cccc}{\mathrm{a}}_1{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathrm{a}}_2{\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ {\mathrm{a}}_1{\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathrm{a}}_2{\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathrm{a}}_1{\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))& {\mathrm{a}}_2{\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))& \cdots & {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))\end{array}\right)$$

(14)

This way the adjusted global membership degree is obtained (${\mathsf{\mu }}_{\mathrm{gai}}\left({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)\right)$ that is established with the help of the column vector:

$$({\mathsf{\mu }}_{\mathrm{gai}}\left({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)\right):\max \left(\begin{array}{c}\min {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{Ok}}_1\right)\\ \min {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{Ok}}_2\right)\\ ⋮\\ \min {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{Ok}}_2\right)\end{array}\right)$$

(15)

The offer with the highest global adjusted membership degree is considered the best choice that fuses the company’s asset acquisition policy with the selection criteria it formulates.

$${\mathrm{A}}_{\mathrm{i}}:\max \left(\begin{array}{ccc}{\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{Ok}}_1\right)& {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{Ok}}_2\right)& \cdots {\mathrm{a}}_{\mathrm{i}}{\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{Ok}}_{\mathrm{i}}\right)\end{array}\right)$$

(16)

The ranking coefficients (${\mathrm{a}}_{\mathrm{i}}),\mathrm{i}=\overline{1,\mathrm{n}}$ of the selection criteria are used by companies to substantiate asset acquisition strategies when the ratio between the asset purchase price and the economic performance is aimed at economic criteria to the detriment of technical criteria or vice versa. In case the company intends to acquire a chain of assets of the form ${\mathrm{A}}_1,{\mathrm{A}}_2,\dots ,{\mathrm{A}}_{\mathrm{n}}$, for each of these assets, the matrix of the membership degree of the existing offers on the market to the selection criteria shall be established as follows:

$$\begin{gathered} {\mathrm{A}}_1:\left(\begin{array}{c}{\mathrm{O}}_1\left({\mathrm{A}}_1\right)\\ {\mathrm{O}}_2\left({\mathrm{A}}_1\right)\\ ⋮\\ {\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right)\end{array}\right)=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_1\right)\right)& {\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_1\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_1\right)\right)\\ {\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_1\right)\right)& {\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_1\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_1\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right))& {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right)\right)\end{array}\right) \\ {\mathrm{A}}_2:\left(\begin{array}{c}{\mathrm{O}}_1\left({\mathrm{A}}_2\right)\\ {\mathrm{O}}_2\left({\mathrm{A}}_2\right)\\ ⋮\\ {\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right)\end{array}\right)=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_2\right)\right)& {\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_2\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_2\right)\right)\\ {\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_2\right)\right)& {\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_2\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_2\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right))& {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right)\right)\end{array}\right) \\ {\mathrm{A}}_{\mathrm{i}}:\left(\begin{array}{c}{\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\\ {\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\\ ⋮\\ {\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\end{array}\right)=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{c}}_{11}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{12}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ {\mathsf{\mu }\mathrm{c}}_{21}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& {\mathsf{\mu }\mathrm{c}}_{22}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{2\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮& ⋮& ⋮& ⋮\\ {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}1}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))& {\mathsf{\mu }\mathrm{c}}_{\mathrm{k}2}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)& \cdots & {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}\left({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\end{array}\right) \end{gathered}$$

(17)

For each of these assets that are the subject of the acquisition process, the global membership degree of each offer ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ to the asset selection criteria ${\mathrm{C}}_{\mathrm{j}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ is determined by obtaining the column vectors of the form:

$$\begin{gathered} {\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_1({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right):\max \left(\begin{array}{c}\min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_1\right)\right)\\ \min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_1\right)\right)\\ ⋮\\ \min {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right))\end{array}\right) \\ {\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_2({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right):\max \left(\begin{array}{c}\min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_2\right)\right)\\ \min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_2\right)\right)\\ ⋮\\ \min {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right))\end{array}\right) \\ {\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_{\mathrm{i}}({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right):\max \left(\begin{array}{c}\min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_1\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ \min {\mathsf{\mu }\mathrm{c}}_{1\mathrm{i}}\left({\mathrm{O}}_2\left({\mathrm{A}}_{\mathrm{i}}\right)\right)\\ ⋮\\ \min {\mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))\end{array}\right) \end{gathered}$$

(18)

The selection of assets will be based on the highest value of the global membership degree to the selection criteria, as a result of the values recorded using the column vector:

$${\mathrm{A}}_1:{\max \mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right)),{\mathrm{A}}_2:{\max \mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right)),\dots ,{\mathrm{A}}_{\mathrm{i}}:{\max \mathsf{\mu }\mathrm{c}}_{\mathrm{ki}}({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))$$

(19)

Thus, the asset chain selected with fuzzy logic multi-criteria algorithm will ensure the companies that all assets purchased best meet the selection criteria formulated for each asset. The fuzzy logic multi-criteria algorithm is thus one of the first tools of management, made using fuzzy techniques that underpin the company’s decisions regarding the acquisition of assets. The algorithm performs as it has been possible to observe, the optimal combination of immobilizing financial resources in the acquisition of assets of a company and its technical and economic parameters such as asset productivity, technical warranties, or operating expenses that lead in long-term to positive or negative cash-flows.

4. Simulation of the Fuzzy Logic Multi-Criteria Algorithm

For testing the fuzzy logic multi-criteria algorithm were considered two situations met in a production company from Northwestern part of Romania, namely:

4.1. First Scenario

The purchase of an asset (A₁) needed for the current activity of a company, for which the following information was known: six asset acquisition criteria, grouped into two categories, namely: economic criteria (asset price) and technical criteria (asset productivity, asset guarantee, operating costs, production capacity and quality of the products obtained), as well as five offers available on the market. Following the implementation of fuzzy logic multi-criteria algorithm, the following results were obtained:

The matrix of the membership degree for the criteria ${\mathrm{C}}_{\mathrm{i}}\left({\mathrm{A}}_{\mathrm{i}}\right)$, $\left({\mathrm{A}}_{\mathrm{i}}\in {\mathrm{m}}_{\mathrm{i}}\times {\mathrm{n}}_{\mathrm{i}}\right)$ of each qualified offer. An offer is considered qualified if it falls within the minimum and maximum selection criteria. The offer number 5 does not meet the criterion C₃ (the operating cost), so that this offer has been removed from the algorithm. The first result of the algorithm is the matrix of the membership degree of the offers ${\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)$ to the corresponding selection criterion ${\mathrm{C}}_{\mathrm{i}}\left({\mathrm{A}}_{\mathrm{i}}\right)$.

$${\mathrm{A}}_1=\left(\begin{array}{cccccc}{\mathsf{\mu }\mathrm{C}}_1\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_3\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_4\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_5\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_6\left({\mathrm{O}}_{\mathrm{k}}\right)\\ 0.5& 0.5& 0.83& 0.5& 0.5& 1\\ 0.8& 0& 0.5& 0& 0.2& 0.75\\ 0.86& 0.2& 0.2& 0.8& 0.6& 0.5\\ 0.8& 0.7& 1& 1& 0.8& 0.75\end{array}\right)$$

The column vector for the global membership degree corresponding to offers $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right)),$ is as follows:

$${\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_1({\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.5\\ 0\\ 0.2\\ 0.7\end{array}\right)$$

The offer $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))$ considered to be the most convenient for the company policy of acquiring assets, obtained by applying the inference operator “or” (maximum value) is the offer (O₄), for which ${\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_1({\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)=0.7$ has the higher value and has following features presented in

Table 1. The technical-economic parameters of the offer O₄, established as the winning offer after testing the fuzzy logic multi-criteria algorithm.

Name of Acquisition Criterion	Criterion	Unit of Measurement	Planned Indicator Value	Indicative Accepted Value	Winning Offer Features
Asset purchase value	${\mathrm{C}}_1$	1000 * Euro	20,000	15,000	16,000
Assets productivity	${\mathrm{C}}_2$	Pieces/hour	25	15	22
Operating costs	${\mathrm{C}}_3$	Euro/month	5000	3500	3500
Technical guarantee of the asset	${\mathrm{C}}_4$	Year	3	2	3
Asset production capacity	${\mathrm{C}}_5$	Thousands pieces/month	1000	500	900
Quality of products obtained	${\mathrm{C}}_6$	Qualitative	Very good	Average	Good

.

The offer O₄, being the winning offer after applying the algorithm, falls within the category of offers that best fit the selection criteria formulated by the company. The global membership degree has the value of 0.7 for the $({\mathrm{O}}_4\left({\mathrm{A}}_1\right))$ and the highest value for each offer. The global membership degree provides information on how the offers best fit the selection criteria formulated by the company. A higher value of the degree indicates that all the technical and economic criteria of an offer fit “well” into the restrictions set for each offer.

When the company applies a policy of acquiring assets in which the amount of resources used to buy the asset and the asset productivity are priority, some coefficients are assigned to the asset selection criteria. In this respect, the column vector of the hierarchy coefficients corresponding to the selection criteria has the following form:

$$\left(\begin{array}{c}\mathrm{C}1\\ \mathrm{C}2\\ \mathrm{C}3\\ \mathrm{C}4\\ \mathrm{C}5\\ \mathrm{C}6\end{array}\right)=\left(\begin{array}{c}0.4\\ 0.2\\ 0.15\\ 0.05\\ 0.15\\ 0.05\end{array}\right)$$

For this policy of acquiring the asset (A₁), after applying the fuzzy logic multi-criteria algorithm, the following results are obtained:

The matrix of the adjusted membership degree for the criteria ${\mathrm{C}}_{\mathrm{i}}\left({\mathrm{A}}_{\mathrm{i}}\right)$, $\left({\mathrm{A}}_1\in {\mathrm{m}}_{\mathrm{i}}\times {\mathrm{n}}_{\mathrm{i}}\right)$

$${\mathrm{A}}_1=\left(\begin{array}{cccccc}{\mathsf{\mu }\mathrm{aC}}_1\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_3\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_4\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_5\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_6\left({\mathrm{O}}_{\mathrm{k}}\right)\\ 0.2& 0.1& 0.125& 0.025& 0.075& 0.05\\ 0.32& 0& 0.075& 0& 0.03& 0.0375\\ 0.344& 0.04& 0.03& 0.04& 0.03& 0.025\\ 0.32& 0.14& 0.15& 0.05& 0.12& 0.0\end{array}\right)$$

The adjusted column vector for the fuzzy inference operator “and” corresponding to the offers $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))$ is as follows:

$${\mathsf{\mu }}_{\mathrm{ga}}{\mathrm{A}}_1({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.025\\ 0\\ 0.025\\ 0\end{array}\right)$$

The offer $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_{\mathrm{i}}\right))$ is considered the most convenient for the company policy of acquiring asset, which focuses on the amount of resources used to buy the asset and the asset productivity, with the help of the prioritization coefficients is the offer $\left({\mathrm{O}}_3\left({\mathrm{A}}_{\mathrm{i}}\right)\right)$ that has the highest value of the global membership degree ${\mathsf{\mu }}_{\mathrm{ga}}{\mathrm{A}}_1({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=0.025,$ as offer number 1, but has the lowest acquisition price. In this case, in order to declare an offer as being the winner one was used as ranking criterion the acquisition value of the asset.

For offer O₃ the best combination between highest value of the global membership degree is recorded, respectively 0.025, which implies that the technical and economic parameters of this offer best fit in the company’s selection criteria and between the acquisition value of the asset.

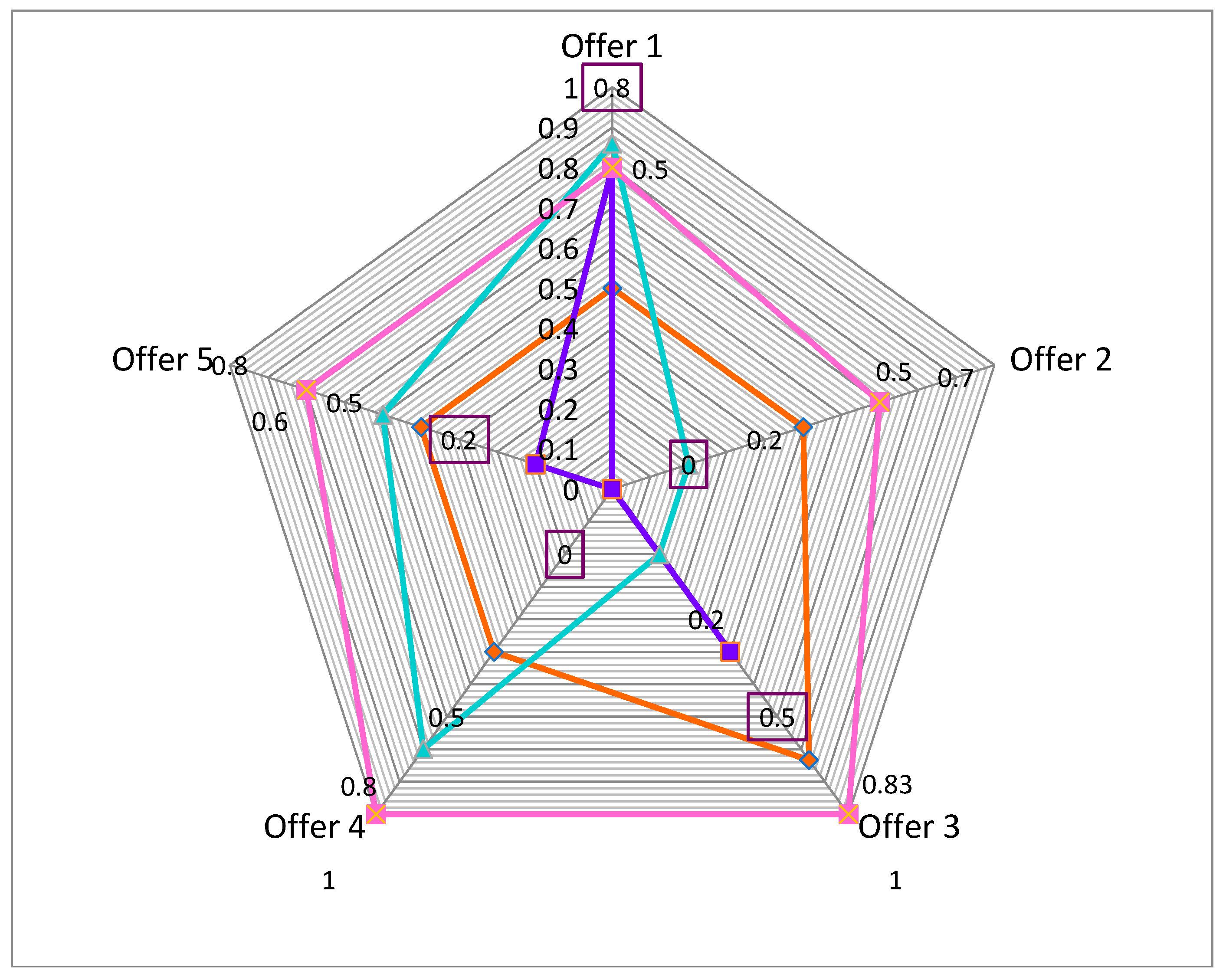
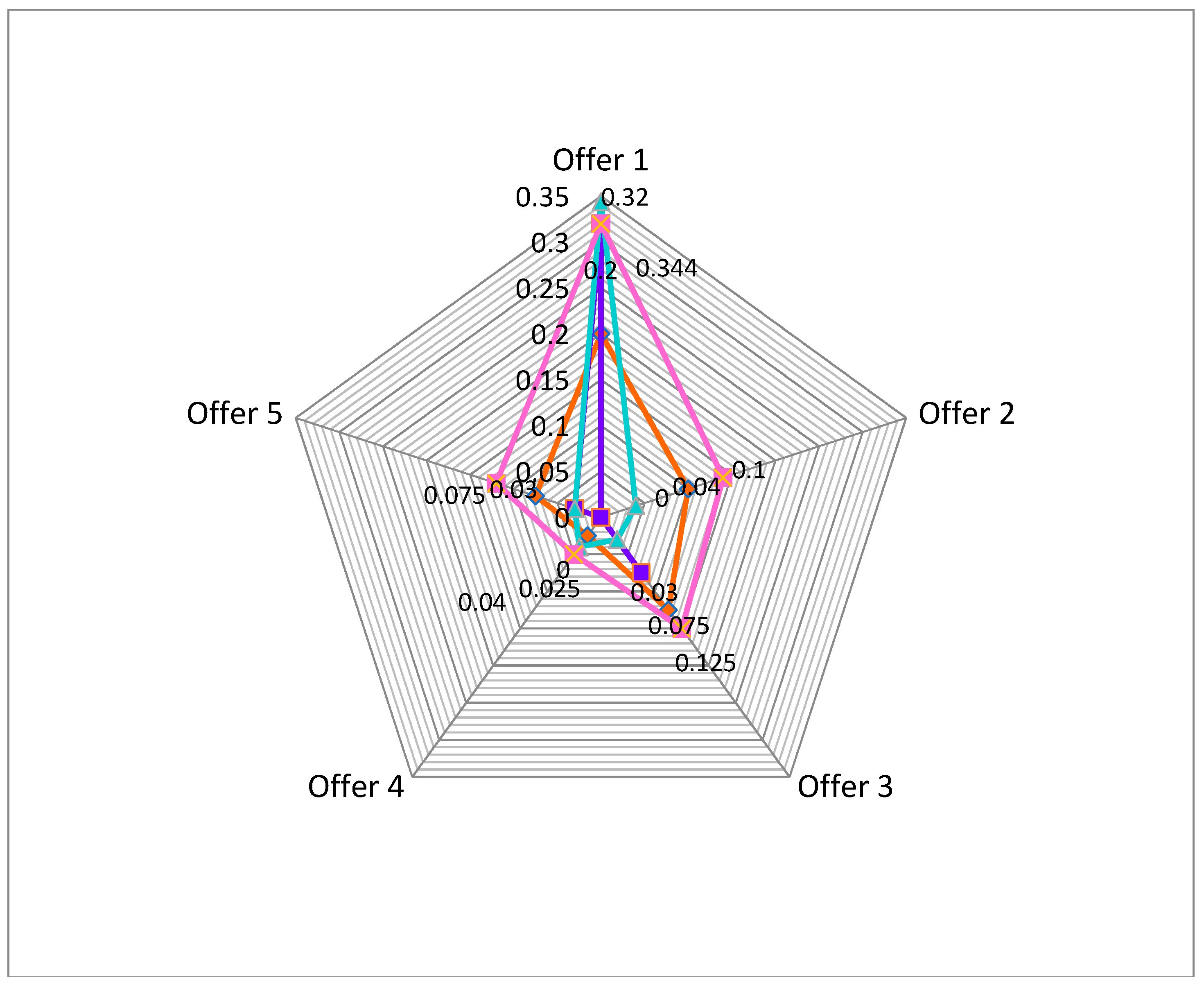
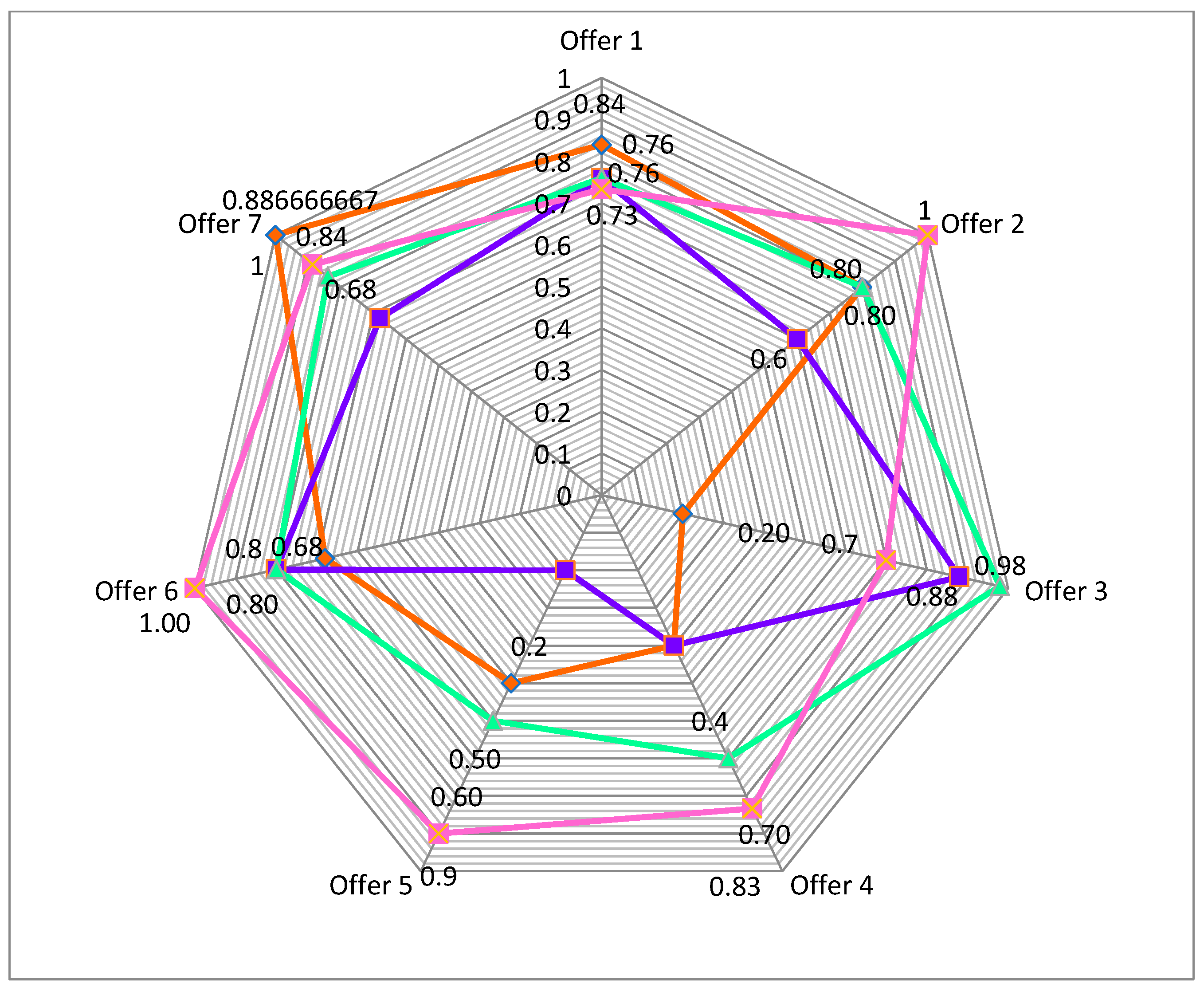
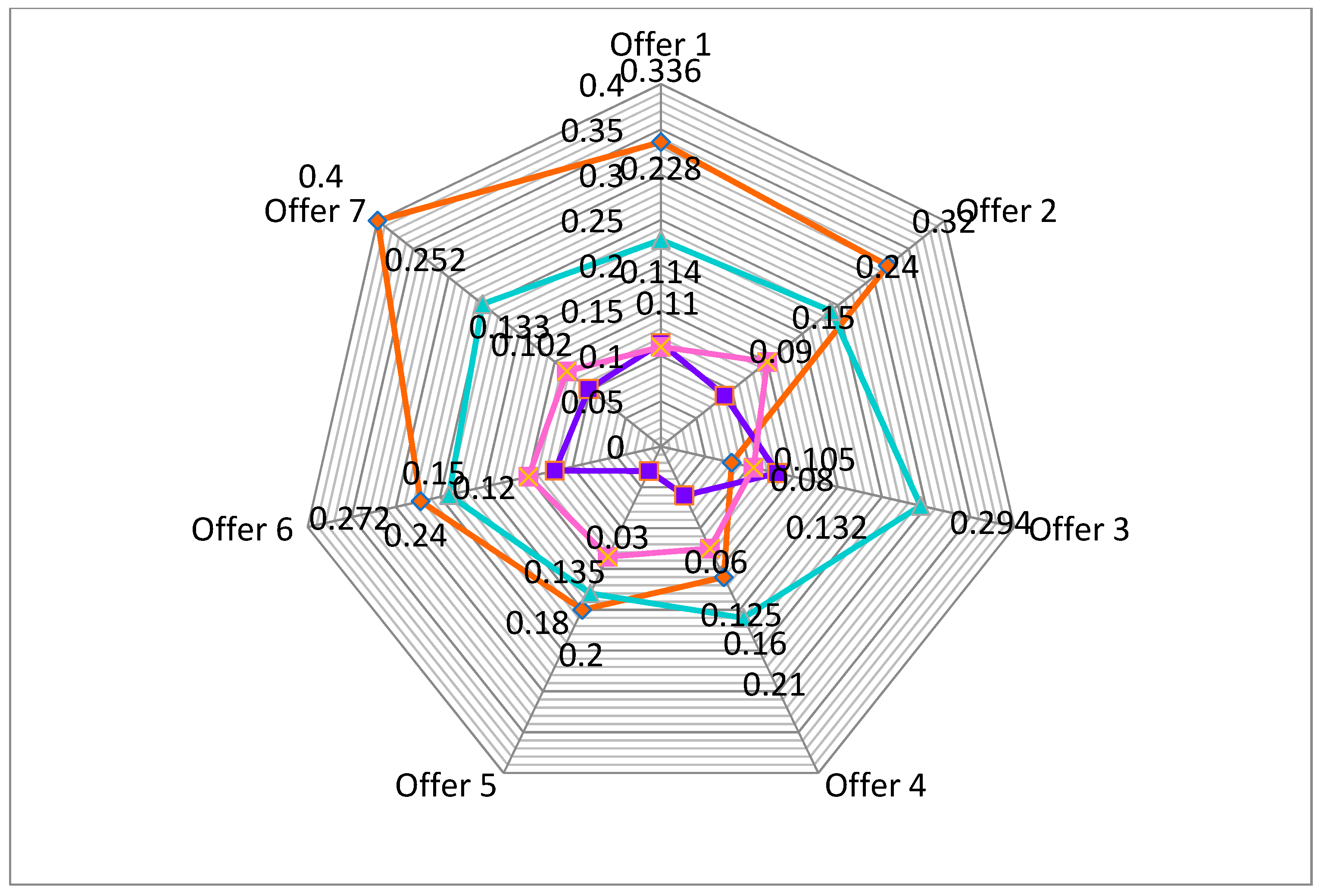
In order to test the fuzzy logic multi-criteria algorithm, the following issues have been tracked: the evolutions of the acquisition values of the asset, the asset productivity, the asset operating costs, the asset technical guarantee, as well as the asset production capacity, as can be seen in the following pictures. Also, the values of the limits accepted by the company as values under which any offer is considered disqualified have been analyzed, as it is shown in Figure 3 and Figure 4.

From the analysis of Figure 3 we can see that the offer that has the highest values for the membership degree in the first case is $({\mathrm{O}}_4)$, resulting also from the application of the fuzzy logic algorithm presented previously. Under these circumstances $({\mathrm{O}}_4)$ will be selected by the company management.

Also, when the company applies some coefficients to the asset selection criteria, the winning offer is $({\mathrm{O}}_3)$, as it is shown in Figure 4, resulting also from the application of the fuzzy logic algorithm presented previously. Under these circumstances $({\mathrm{O}}_3)$ will be selected by the company management.

4.2. Second Scenario

The acquisition of a portfolio of two assets denoted P (A₁, A₂) needed for the current activity of a company, for which the following information is known: for asset (A₁) are maintained the same data, while for the asset (A₂), the information provided are related to: the asset purchase value (1000 * Euro), the asset productivity (pieces/hour), the operating cost (Euro/month) and the maintenance cost (Euro/month).

In order to purchase the asset A₂, the company obtained seven offers from the market, each of them with its technical-economic parameters. Following the implementation of the fuzzy logic algorithm the results that were obtained are:

The matrix of the membership degree for the criteria C_i (A_i), related to A₁ and A₂, (${\mathrm{A}}_1,{\mathrm{A}}_2\in {\mathrm{m}}_{\mathrm{i}}\times {\mathrm{n}}_{\mathrm{i}})$ of each qualified offer.

$${\mathrm{A}}_1=\left(\begin{array}{cccccc}{\mathsf{\mu }\mathrm{C}}_1\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_3\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_4\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_5\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_6\left({\mathrm{O}}_{\mathrm{k}}\right)\\ 0.5& 0.5& 0.83& 0.5& 0.5& 1\\ 0.8& 0& 0.5& 0& 0.2& 0.75\\ 0.86& 0.2& 0.2& 0.8& 0.6& 0.5\\ 0.8& 0.7& 1& 1& 0.8& 0.75\end{array}\right)$$

$${\mathrm{A}}_2=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{C}}_1\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_3\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{C}}_4\left({\mathrm{O}}_{\mathrm{k}}\right)\\ 0.84& 0.76& 0.76& 0.73\\ 0.8& 0.6& 0.80& 1.00\\ 0.2& 0.88& 0.98& 0.70\\ 0.4& 0.4& 0.70& 0.83\\ 0.50& 0.2& 0.60& 0.90\\ 0.68& 0.8& 0.80& 1.00\\ 1& 0.68& 0.84& 0.886667\end{array}\right)$$

The column vector for the asset’s global membership degree to the selection criteria for the two assets $({\mathrm{A}}_1ș{\mathrm{i}\mathrm{A}}_2),$ corresponding to $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right))$ and $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right))$ is:

$${\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_1({\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.5\\ 0\\ 0.2\\ 0.7\end{array}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathsf{\mu }}_{\mathrm{g}}{\mathrm{A}}_2({\mathrm{C}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.73\\ 0.60\\ 0.20\\ 0.40\\ 0.20\\ 0.68\\ 0.68\end{array}\right)$$

The offers $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right))$ and $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_2\right))$ considered the most convenient for the acquiring assets policy of the company, obtained by applying the inference operator “or” is represented by $({\mathrm{O}}_4({\mathrm{A}}_1))$ whose characteristics were previously presented and by $({\mathrm{O}}_1\left({\mathrm{A}}_2\right))$ that has the features in

Table 2. The technical-economic parameters of the offer O₁, for asset A₂ established by applying the algorithm.

Name of Acquisition Criterion	Criterion	Unit of Measurement	Planned Indicator Value	Indicative Accepted Value	Winning Offer Features
Asset purchase value	$C_1$	1000 * Euro	7500	5000	5400
Assets productivity	$C_2$	Pieces/hour	100	75	94
Operating costs	$C_3$	Euro/month	10,000	5000	6200
The maintenance cost	$C_4$	Euro/month	3000	1500	2600

.

When the company applies a policy of acquiring assets in which the amount of resources used to buy the asset and the asset operating cost are priorities, the column vector of the adjusted coefficients has the following form:

$${\mathrm{A}}_1:\left(\begin{array}{c}\mathrm{C}1\\ \mathrm{C}2\\ \mathrm{C}3\\ \mathrm{C}4\\ \mathrm{C}5\\ \mathrm{C}6\end{array}\right)=\left(\begin{array}{c}0.4\\ 0.2\\ 0.15\\ 0.05\\ 0.15\\ 0.05\end{array}\right)\mathrm{and}\mathrm{A}2\text{:}\left(\begin{array}{c}\mathrm{C}1\\ \mathrm{C}2\\ \mathrm{C}3\\ \mathrm{C}4\end{array}\right)=\left(\begin{array}{c}0.4\\ 0.15\\ 0.3\\ 0.15\end{array}\right)$$

For the asset (A₁), the adjustment coefficients for the asset acquisition policy remain the same as those presented under the first situation. These asset acquisition policies for (A₁) and (A₂), after applying the fuzzy logic algorithm lead to the following results:

The matrix of the adjusted global membership degree for the criteria C_i (A_i), (${\mathrm{A}}_{\mathrm{i}}\in {\mathrm{m}}_{\mathrm{i}}\times {\mathrm{n}}_{\mathrm{i}})$ for A₁ and A₂ is:

$${\mathrm{A}}_1=\left(\begin{array}{cccccc}{\mathsf{\mu }\mathrm{aC}}_1\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_2\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_3\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_4\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_5\left({\mathrm{O}}_{\mathrm{k}}\right)& {\mathsf{\mu }\mathrm{aC}}_6\left({\mathrm{O}}_{\mathrm{k}}\right)\\ 0.2& 0.1& 0.125& 0.025& 0.075& 0.05\\ 0.32& 0& 0.075& 0& 0.03& 0.0375\\ 0.344& 0.04& 0.03& 0.04& 0.03& 0.025\\ 0.32& 0.14& 0.15& 0.05& 0.12& 0.0\end{array}\right)$$

$${\mathrm{A}}_2=\left(\begin{array}{cccc}{\mathsf{\mu }\mathrm{aC}}_1\left({\mathrm{O}}_{\mathrm{i}}\right)& {\mathsf{\mu }\mathrm{aC}}_2\left({\mathrm{O}}_{\mathrm{i}}\right)& {\mathsf{\mu }\mathrm{aC}}_3\left({\mathrm{O}}_{\mathrm{i}}\right)& {\mathsf{\mu }\mathrm{aC}}_4\left({\mathrm{O}}_{\mathrm{i}}\right)\\ 0.336& 0.114& 0.228& 0.11\\ 0.32& 0.09& 0.24& 0.15\\ 0.08& 0.132& 0.294& 0.105\\ 0.16& 0.06& 0.21& 0.125\\ 0.2& 0.03& 0.18& 0.135\\ 0.272& 0.12& 0.24& 0.15\\ 0.4& 0.102& 0.252& 0.133\end{array}\right)$$

The adjusted column vectors for the global membership degree of the existing offers on the market, computed for both assets ${\mathrm{A}}_1,{\mathrm{A}}_2$ corresponding to $({\mathrm{O}}_{\mathrm{k}}\left({\mathrm{A}}_1\right))$ and $({\mathrm{O}}_{\mathrm{k}}({\mathrm{A}}_2$)) are:

$${\mathsf{\mu }}_{\mathrm{ga}}{\mathrm{A}}_1({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.025\\ 0\\ 0.025\\ 0\end{array}\right)\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{\mathsf{\mu }}_{\mathrm{ga}}{\mathrm{A}}_2({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=\left(\begin{array}{c}0.11\\ 0.09\\ 0.08\\ 0.06\\ 0.03\\ 0.12\\ 0.102\end{array}\right)$$

The offer $({\mathrm{O}}_3\left({\mathrm{A}}_1\right))$ for the asset $\left({\mathrm{A}}_1\right)$ is considered the most convenient for the asset acquisition policy, because has the highest value of the global membership degree ${\mathsf{\mu }}_{\mathrm{ga}}{\mathrm{A}}_1({\mathrm{C}}_{\mathrm{j}}\left({\mathrm{O}}_{\mathrm{k}}\right)=0.025,$ as offer number 1, but has the lowest acquisition price. The offer $({\mathrm{O}}_6\left({\mathrm{A}}_2\right))$ for the asset $({\mathrm{A}}_2)$ is considered the most convenient for the asset acquisition policy. See Figure 5 and Figure 6.

This tracks the link between the acquisition cost and the productivity for $\left({\mathrm{A}}_1\right)$ and the link between the acquisition cost and the maintaining cost for $({\mathrm{A}}_2).$ The correlations are obtained by applying the global membership degree of the offers to the acquisition criteria. The features of the two offers were previously presented.

The application of the multi-criteria fuzzy logic algorithm for the acquisition of “n” assets requires that for each asset, the algorithm has to be applied, so that by determining the global membership degree of offers to the asset selection criteria to be computed the value of the immobilized capital in the batch of assets the company is about to acquire. The winning offers provide the best combination of asset cost and asset performance.

5. Conclusions

The fuzzy logic multi-criteria algorithm, therefore, has some basic components without which it cannot be implemented. This category includes:

• The matrix of membership degrees $\left({\mu }_{C_i}\right)$ of the market offers to the asset selection criteria, which analyzes the extent to which the existing offers on the market correspond to the criteria for the selection of the assets. The fuzzy triangular numbers formed have their membership function and allow the appreciation of the selection criteria in linguistic terms. The higher the membership degree of an existing offer on the market to a criterion, the better the offer. The lower the membership degree of an offer to a criterion, the worse is the offer.
• The column vector of the global membership degree determines the hierarchy of existing offers on the market, according to the membership degree of the offers to all selection criteria. The higher the degree of compatibility of an offer with the selection criteria is, the more attractive the offer is for the company.
• Establishing the highest global membership degree used for identifying the best offer that suits to all criteria for the selection of assets on the market, including the situations where the company is about to acquire a chain of assets.

The algorithm has been tested for two situations. A first situation relates to the acquisition of an asset for which six selection criteria are fixed and five offers are identified on the market. For each selection criterion, a maximum and minimum value was set. Any offer that does not fall within these limits is considered ineligible, or the offer is disqualified. Within these intervals the fuzzy triangular numbers were defined through which the offers of membership degrees to the selection criteria were subsequently established. The elements of the membership matrix were determined and the offer with the highest membership degree for all the criteria was considered the winning one.

The algorithm was tested for the case when the company develops an asset acquisition strategy, in which the price criterion and the productivity criterion are considered priorities. The results of the simulation led to the same conclusion, namely that the initial offer has the highest adjusted membership degree. The analysis of the offers portfolio showed that the algorithm works adequately with significant results in substantiating asset acquisition decisions.

The second situation concerns the acquisition of a portfolio of two assets. For asset (A₁) the same criteria and data are maintained (six selection criteria and five offers), while for the asset (A₂), the information provided are related to: the asset purchase value (1000 * Euro), the asset productivity (pieces/hour), the operating cost (Euro/month) and the maintenance cost (Euro/month): four selection criteria and seven offers. For each of these selection criteria a maximum and a minimum threshold were determined, respectively the matrix and the vector of the global membership degree. For each asset the algorithm steps were performed, so the validated offers were identified.

The fuzzy logic multi-criteria algorithm becomes a tool that provides for any company, regardless of the number of assets acquired and the number of selection criteria, the most convenient combination of assets cost and their economic and technical performance.

Testing the algorithm has demonstrated that it meets the requirements of the company to select offers from the market, even if a set of assets with multiple selection criteria is acquired.