Matching Model of Dual Mass Flywheel and Power Transmission Based on the Structural Sensitivity Analysis Method

Abstract

As a new torsional vibration absorber, the dual mass flywheel (DMF) contains a symmetric structure in which the damping element is a pair of springs symmetrically distributed along the circumference direction. Through reasonable matching parameters, the DMF functions in isolating torsional vibrations caused by the engine from the transmission system. Our work aims to solve the accuracy of matching models between the DMF and power transmission system. The critical structural parameters of each order modal are treated consecutively by two methods: Absolute sensitivity (e.g., under the idle condition and driving condition), and relative sensitivity. The operation achieves a separation of the parameters and diagnosis of the relationship between these parameters and the natural frequency in the system. In addition, the natural frequency range is determined based upon the area of the resonance speed. As a result, the matching model is established based on the sensitivity analysis method and the natural frequency range, which means the moment of inertia distribution (its coefficient should be used as one structural parameter in relative sensitivity analysis) and the torsional stiffness in multiple stages can be observed under the combined values. The effectiveness of the matching model is verified by experiments of a real vehicle test under the idling condition and driving condition. It is concluded that the analysis study can be applied to solve the parameters matching accuracy among certain multi-degree-of-freedom dynamic models.

1. Introduction

As the automobile power output and transmission are linked, dynamic characteristics of power transmissions are an important factor in ride safety, fuel economy, and NVH (noise, vibration, and harshness) performance of vehicles. It is recognized that vibrations and noises are the most important indicators to evaluate the vehicle NVH performance [1]. Vehicle vibration noises can be caused by the power source, aerodynamics, tires, transmission system, and uneven loads and so on. Among them, power source vibration noises account for more than one half of vibration noises [2,3]. In fact, torsional vibration is the main source of the vibration noises of power transmission. There are several ways to suppress torsional vibration of the power transmission. The traditional way uses the elastic element to change the natural frequency to avoid the resonance zone and the damping element to attenuate the vibration amplitude [4]. Traditionally, we used a driven plate type clutch torsional vibration damper. However, due to its space structure constrains, the damping performance is not satisfactory.

DMF (Dual Mass Flywheel) is a new kind of vehicle torsional damper, which not only has the function of the single mass flywheel, but also a driven plate type clutch torsional vibration damper [5]. Due to its construction on reasonable inertia distribution and torsional stiffness, DMF can make the resonance rotating speed lower than the idling speed through power transmission, thus attenuating torsional vibrations under driving conditions [6]. Indeed, DMF has been widely used both in traditional ICE (internal combustion engine) vehicles and HEVs (hybrid electric vehicle), providing a more efficient damping performance. Figure 1 shows a schematic diagram of the power transmission with the DMF, which consists of a primary flywheel assembly, and a secondary flywheel assembly and a damper. Figure 2 shows a schematic diagram of the DMF, which consists of a primary flywheel assembly, a secondary flywheel assembly, and a damper. The primary flywheel assembly includes a starting gear ring, a signal ring, a cover, and a primary flywheel. The secondary flywheel assembly comprises a flange, a seal disc, and a secondary flywheel. The damper is composed of springs and damping elements. DMFs can be divided into several types according to the structure and the form of the springs, in which the circumferential arc spring dual mass flywheel (DMF-CS) is the most widely used type. As shown in Figure 1, the primary assembly and the crankshaft are connected by bolts. In addition, the clutch and the AT (automatic transmission) can be connected by the secondary assembly. Thus, power from the engine can be initially transmitted to the primary assembly, and then to the secondary assembly by compression of the flange into the arc springs. In the end, the power reaches the power transmission, leading to the car’s driving.

Despite recent advances in the DMF’s experiments, simulations, structure innovations, and performance comparisons, little is known about the matching method between the DMF and power transmission. Some studies by Hartmut [7], Zeng [8], and Maffiodo [9] suggested that the excellent damping performance of DMF is associated with idling and low speed conditions by simulating characteristics of a power transmission with DMF and reviewing the angular accelerations and displacements between the output of the engine and the input of the gearbox under idling, sliding, and accelerating conditions. Others [10] found that although the angular acceleration of the crankshaft increased with the DMF, the corresponding dynamic load of the crankshaft decreased as the inertia was reduced. Kang, Kauh, and Ha [11] proposed the development of the displacement measuring system for the DMF based on the principle of the linear variable differential transformer (LVDT), which was used for installation in a real vehicle. Liupeng He [12] suggested a method for estimating the instantaneous engine torque of vehicles with conventional combustion engines and the DMF to obtain better control of engines equipped with a DMF. Peter and Robert [13] experimentally studied the dynamic change rules of the torsional stiffness and damping of the DMF. Li [14] and Wang [15] studied the natural torsion characteristic of DMF, and proposed the result that the natural frequency would be the minimum when the inertia ratio of the primary and secondary flywheel was 1:1. Yadav, Birari, et al. created a two-degree freedom dynamic model without a transmission system in the design of a crankshaft torsional vibration damper, and they found that the torsional vibration of the engine was attenuated when the natural frequency of the torsional vibration damper was equal to the first natural frequency of the engine, but this also introduced two new resonating frequencies to the original system [16]. Shangguan, Liu, and Rakheja proposed that the reduction of the torsional stiffness of a clutch was the most effective way to reduce gear rattle, and the torsional stiffness of a clutch at the first stage was determined by considering the excitation frequency of an engine at idle [17].

Structural sensitivity can reflect the gradient of the structural parameters to the response of the system. It is accepted that structural sensitivity will facilitate the optimization of the dynamic characteristics by modifying the structural parameters. Yue, et al. [18] studied the design parameters of a quarter wave tuner through sensitivity analysis by using acoustic simulations of the orifice noise of an intake system. Moreover, others [19] presented an explicit time-domain method for sensitivity analysis of structural responses under non-stationary random excitations and a new and more concise time-domain explicit expression of response sensitivity was derived using the direct differentiation method (DDM) based on time-domain explicit expressions of dynamic responses. A well-defined vibration mode [20,21] was used in the properties of a new micro machined tuning fork gyroscope (TFG) with an anchored diamond coupling mechanism to calculate Eigen sensitivities and establish exact formulae to connect the natural frequency sensitivity with the modal strain or kinetic energy, and determine the sensitivity to all stiffness and inertia parameters by the modal energy distribution.

The literature [7,8,9,10,11,12,13,14,15] shows that DMF can greatly improve the dynamic load of the crankshaft and can effectively isolate the torsional vibration caused by the engine at idling speed and in the low speed region. Moreover, the inertias of the primary and secondary flywheel assembly and the multi-stage torsional stiffness have a great influence on the characteristics of the power transmission. Therefore, the structural parameters of the DMF may be a decisive factor of the damping effect when the value reasonably matches the power transmission. It can be concluded from the literature [16,17] that the vibration reduction principle and the structure of a crankshaft torsional vibration damper are completely different from that of the DMF, which has only two structural parameters, and a torsional vibration damper of the clutch driven disk has only one structural parameter (torsional stiffness). Therefore, the matching model of the DMF and power transmission is different from that of a crankshaft torsional vibration damper and a torsional vibration damper of a clutch driven disk. Studies have shown that the sensitivity analysis method can be widely used in mechanical dynamical analysis and can also directly reflect the relationship between the structural parameters and the dynamic response of the system [18,19,20,21].

The literature shows the data of the main structural parameters of the DMF, including the inertias of the primary and secondary flywheel assemblies as well as the multi-stage torsional stiffness. Additionally, the sum of inertia of the primary and the secondary flywheel assembly is equal to the moment of inertia of the single mass flywheel, indicating the moment of inertia of the dual mass flywheel is a constant for a certain type of engine. The inertias of the primary and secondary flywheel assembly and the multi-stage torsional stiffness need to be reasonably determined in the process of matching, which suggests the matching problem between DMF and the power transmission is actually a multivariable matching problem. The literature recommends that sensitivity analysis is suitable for multivariable matching problems. This paper achieves the matching of DMF and the power transmission by integration of the sensitivity analysis method and the vibration reduction theories. Firstly, we demonstrated the modal analysis of the power transmission with the DMF. According to the analysis results, the absolute sensitivity analysis method was used to determine the main structural parameters, and the relative sensitivity analysis was used for the mathematical relationship between the main structural parameters and the natural frequencies of the system. Through the relative sensitivity analysis, the inertias of the primary and secondary flywheel assemblies can be combined as one structural parameter because of the constraint relation of the moment of inertia of the dual mass flywheel, namely the inertia ratio of them. The parameter should directly reflect the influence of the change of the inertias on the natural frequency of the system. Secondly, the range of the natural frequencies of the system was determined according to the vibration attenuation theories. Finally, the matching data between the DMF and the power transmission were predicted by using the above mathematical relationship and the range of natural frequencies.

2. Structural Sensitivity Analysis Method of Automobile Power Transmission

Sensitivity is widely used with different meanings in different areas. The meanings of sensitivity can be summarized as the gradient of a structural parameter or a variable to the system response or a solution of a function [16]. As a multivariable function, $f\left(x_i\right)$, with regard to $x_i\left(i=1,2\dots ,n\right)$, the sensitivity of $f\left(x_i\right)$ related to $x_i$ can be expressed as:

$$S_{ab}\left(f/x_i\right)=\underset{\Delta x_i\to 0}{lim}\frac{\Delta f}{\Delta x_i}=\frac{\partial f}{\partial x_i}$$

(1)

where $S_{ab}$ is the absolute sensitivity, of which the value denotes the influence of the variable, $x_i$, on $f\left(x_i\right)$. If we change the numerator and denominator of Equation (1) into the change rates of $f\left(x_i\right)$ and $x_i$, shown in Equation (2), $S_{rt}$ is the relative sensitivity, of which the value denotes the relation between the change rates of $f\left(x_i\right)$ and $x_i$:

$$S_{rt}\left(f/x_i\right)=\underset{\Delta x_i\to 0}{lim}\frac{\frac{\Delta f}{f}}{\frac{\Delta x_i}{x_i}}=\frac{\frac{\partial f}{f}}{\frac{\partial x_i}{x_i}}=\frac{x_i}{f}\frac{\partial f}{\partial x_i}$$

(2)

The structural sensitivity analysis method can be regarded as the application of the sensitivity analysis method in mechanical dynamics. Using this method, we can evaluate the influence of the change of system structural parameters on the system dynamic response. The dynamic characteristics of the power transmission generally cover amplitude-frequency and phase-frequency characteristics. Normally, DMF change the natural frequency of the power transmission by matching inertias and decreasing stiffness to avoid the resonance zone. Therefore, the structural sensitivity analysis can only involve the gradients of the system’s natural frequencies to the inertias and stiffness under free vibration.

With rotational motion, the dynamic model of automobile power transmission is a torsional vibration model. The dynamic equation without damping is given by:

$$\left(\left[K\right]-{\omega }_i^2\left[J\right]\right){\left\{\theta \right\}}_i=0$$

(3)

where $\left[K\right]$ and $\left[J\right]$ are the torsional stiffness matrix and inertia matrix, respectively, ${\omega }_i$ is the i^th order natural frequency, and ${\left\{\theta \right\}}_i$ is the i^th order modal shape. Structural damping and viscous damping still exist in the actual model; however, damping elements have little influence on the natural frequency of the system because of a small damping coefficient [4,22]. Furthermore, viscous friction and coulomb friction can cause a DMF to assume the hysteresis nonlinearity; however, the nonlinear model needs to be identified by the modified Bouc-Wen model combined with experimental data [23]. That is, the nonlinear model must be determined after a DMF is manufactured. Some studies [23] showed that the real natural frequency is approximately equal to the real natural frequency of the system without damping at low rotational speed. Therefore, the dynamic Equation (3) can be used to analyze the model in the process of matching.

2.1. Sensitivity of Natural Frequencies of Torsional Vibration to Torsional Stiffness

Both $\left[K\right]$ and $\left[J\right]$ are the real symmetric matrix. To simplify the calculation, Equation (3) is pre-multiplied by ${\theta }_i^T$ to obtain Equation (4):

$${\left\{\theta \right\}}_i^T\left(\left[K\right]-{\omega }_i^2\left[J\right]\right){\left\{\theta \right\}}_i=0$$

(4)

$${\left\{\theta \right\}}_i^T\left[J\right]{\left\{\theta \right\}}_i=M_i$$

(5)

where $M_i$ is the modal mass under the i^th order. Let the absolute and relative sensitivities of ${\omega }_i$ to the torsional stiffness of the j^th unit be $S_{ab}\left({\omega }_i/K_j\right)$ and $S_{rt}\left({\omega }_i/K_j\right)$, respectively. Referring to Equations (1) and (2), the partial derivative with respect to $K_j$ in Equation (4) is operated to obtain Equation (6). Thus, $S_{ab}\left({\omega }_i/K_j\right)$ and $S_{rt}\left({\omega }_i/K_j\right)$ can be derived as:

$${\theta }_i^T\left(\frac{\partial \left[K\right]}{\partial K_j}-2{\omega }_i\frac{\partial {\omega }_i}{\partial K_j}\left[J\right]-\frac{{\omega }_i^2\partial \left[J\right]}{\partial K_j}\right){\theta }_i=0$$

(6)

$$S_{ab}\left({\omega }_i/K_j\right)=\frac{\partial {\omega }_i}{\partial K_j}=\frac{{\theta }_i^T\frac{\partial \left[K\right]}{\partial K_j}{\theta }_i}{2{\omega }_i{M}_i}$$

(7)

$$S_{rt}\left({\omega }_i/K_j\right)=\frac{\partial {\omega }_i/{\omega }_i}{\partial K_j/K_i}=\frac{{\theta }_i^T\frac{\partial \left[K\right]}{\partial K_j}{\theta }_i}{2{\omega }_i{M}_i}\frac{K_j}{{\omega }_i}$$

(8)

$\left[K\right]$ is expressed as Equation (9), so $\frac{\partial \left[K\right]}{\partial K_j}$ can be obtained as Equation (10) when $j<n-1$ and $\frac{\partial \left[K\right]}{\partial K_j}$ can be given by Equation (11) when $j=n-1$. Where $n$ is the degree of freedom of the system.

$$\left[K\right]=\left[\begin{array}{cccccccc}{K}_1& -K_1& & & & & & \\ -K_1& K_1+K_2& -K_2& & & & 0& \\ & -K_2& K_2+K_3& -K_3& & & & \\ & & \ddots & \ddots & \ddots & & & \\ & & & -K_{i-1}& K_{j-1}+K_j& -K_j& & \\ & & & & \ddots & \ddots & \ddots & \\ & 0& & & & -K_{n-2}& K_{n-2}+K_{n-1}& -K_{n-1}\\ & & & & & & -K_{n-1}& K_{n-1}\end{array}\right]$$

(9)

$$\frac{\partial \left[K\right]}{\partial K_j}=\left[\begin{array}{cccccccc}0& & & & & & & \\ & & & & & & 0& \\ & & & & & & & \\ & & \ddots & \ddots & \ddots & & & \\ & & & & 1& -1& & \\ & & & & \ddots & \ddots & \ddots & \\ & 0& & & & & & \\ & & & & & & & 0\end{array}\right]$$

(10)

$$\frac{\partial \left[K\right]}{\partial K_j}=\left[\begin{array}{cccccccc}0& & & & & & & \\ & & & & & & 0& \\ & & & & & & & \\ & & \ddots & \ddots & \ddots & & & \\ & & & & & & & \\ & & & & \ddots & \ddots & \ddots & \\ & 0& & & & & & \\ & & & & & & -1& 1\end{array}\right]$$

(11)

Combining Equations (7), (8), (10), and (11), $S_{ab}\left({\omega }_i/k_j\right)$ and $S_{rt}\left({\omega }_i/k_j\right)$ are given by:

$$S_{ab}\left({\omega }_i/K_j\right)=\frac{{\left[{\left({\theta }_i\right)}_j-{\left({\theta }_i\right)}_{j+1}\right]}^2}{2{\omega }_i{M}_i}$$

(12)

$$S_{rt}\left({\omega }_i/K_j\right)=\frac{{\left[{\left({\theta }_i\right)}_j-{\left({\theta }_i\right)}_{j+1}\right]}^2}{2{\omega }_i{M}_i}\frac{K_j}{{\omega }_i}$$

(13)

2.2. Sensitivity of Natural Frequencies of Torsional Vibration to Inertias

Let the absolute sensitivity and relative sensitivity of the i^th natural frequency, ${\omega }_i$ to the torsional stiffness of the j^th unit be $S_{ab}\left({\omega }_i/J_j\right)$ and $S_{rt}\left({\omega }_i/J_j\right)$. By seeking the partial derivative with respect to $J_j$ in Equation (4), Equation (14) can be obtained as:

$${\theta }_i^T\left(\frac{\partial \left[K\right]}{\partial J_j}-2{\omega }_i\frac{\partial {\omega }_i}{\partial J_j}\left[J\right]-\frac{{\omega }_i^2\partial \left[J\right]}{\partial J_j}\right){\theta }_i=0$$

(14)

Therefore, the absolute and relative sensitivities can be calculated by:

$$S_{ab}\left({\omega }_i/J_j\right)=\frac{\partial {\omega }_i}{\partial J_j}=-\frac{{\omega }_i{\theta }_i^T\frac{\partial \left[J\right]}{\partial J_j}{\theta }_i}{2M_i}$$

(15)

$$S_{rt}\left({\omega }_i/J_j\right)=\frac{\partial {\omega }_i/{\omega }_i}{\partial J_j/J_j}=-\frac{J_j{\theta }_i^T\frac{\partial \left[J\right]}{\partial J_j}{\theta }_i}{2M_i}$$

(16)

$\left[J\right]$ is expressed as Equation (17), thus $\frac{\partial \left[J\right]}{\partial J_j}$ is expressed as Equation (18):

$$\left[J\right]=\left[\begin{array}{cccccc}{J}_1& & & & & \\ & J_2& & & 0& \\ & & \ddots & & & \\ & & & J_j& & \\ & 0& & & \ddots & \\ & & & & & J_n\end{array}\right]$$

(17)

$$\frac{\partial \left[J\right]}{\partial J_j}=\left[\begin{array}{cccccc}0& & & & & \\ & 0& & & 0& \\ & & \ddots & & & \\ & & & 1& & \\ & 0& & & \ddots & \\ & & & & & 0\end{array}\right]$$

(18)

Combining Equations (15), (16), and (18), $S_{ab}\left({\omega }_i/J_j\right)$ and $S_{rt}\left({\omega }_i/J_j\right)$ are obtained as:

$$S_{ab}\left({\omega }_i/J_j\right)=-\frac{{\omega }_i{[{({\theta }_i)}_j]}^2}{2M_i}$$

(19)

$$S_{rt}\left({\omega }_i/J_j\right)=-\frac{J_j{[{({\theta }_i)}_j]}^2}{2M_i}$$

(20)

3. Matching Model of DMF and the Power Transmission Based on the Structural Sensitivity Analysis Method

Comparative analysis between the DMF and clutch suggested that the DMF can effectively attenuate the torsional vibrations under the idling condition and in the low engine speed zone (1200–3000 r/min) and exhibit a similar damping performance to the clutch in the high engine speed region (above 3000 r/min) [8]. The goals of this study were to describe the reasonable inertia distributions of the primary and secondary flywheels and multi-stage torsional stiffness, and to identify a potential association of a matching DMF and power transmission in terms of avoiding resonances under the idling condition and low speed zone. Only the first order torsional vibration will occur in the power transmission system under the idling condition and the modal vibrations of the system in the low speed zone under driving conditions are usually much more complicated, which are determined by the absolute structural sensitivity analysis method in the low speed zone. The natural frequency ranges of each mode can be established based on the resonance speed zone and then the matching model is created based on the natural frequency ranges and the relative structural sensitivity analysis method. The steps of building a matching model are shown in Figure 3.

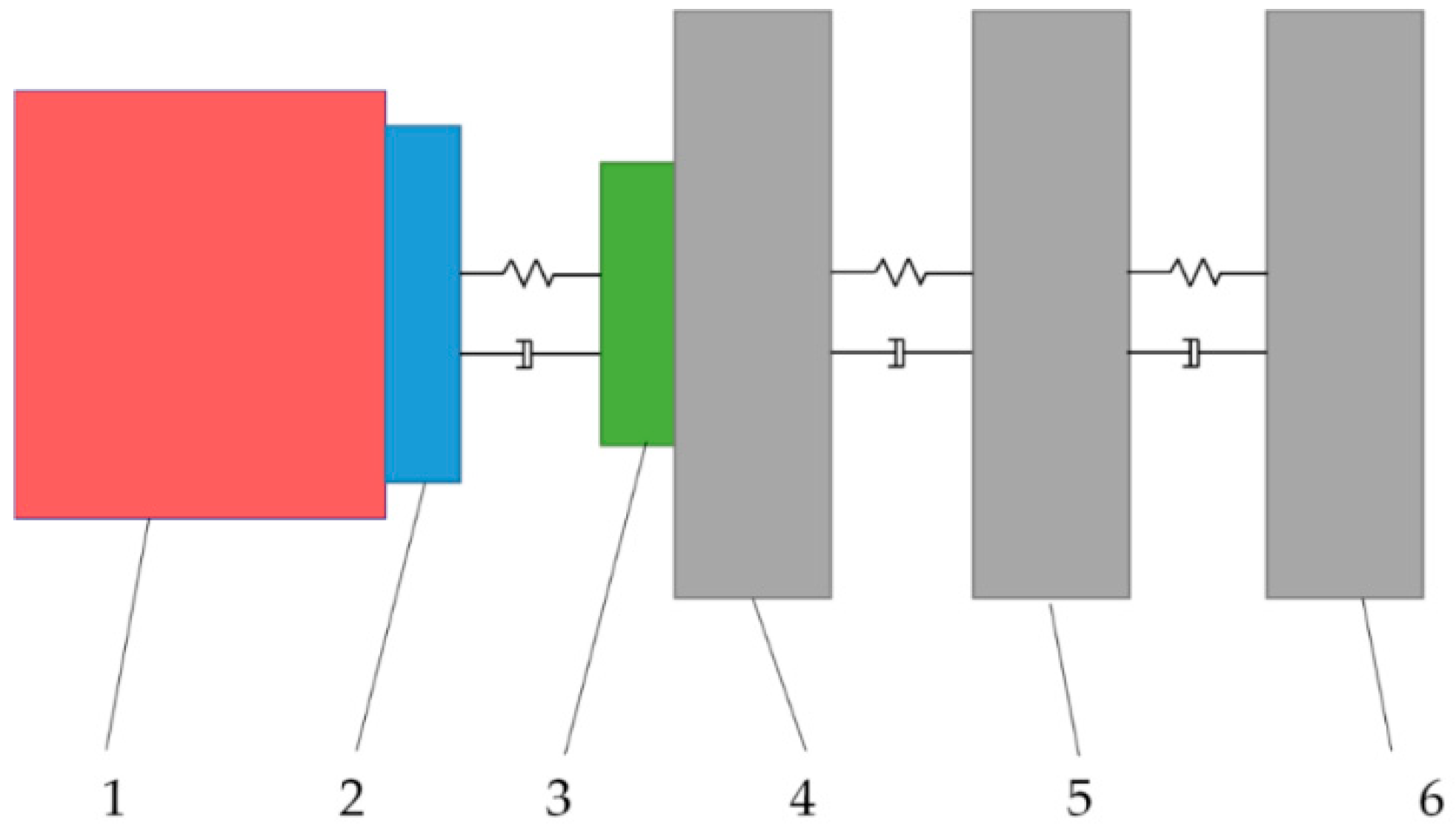
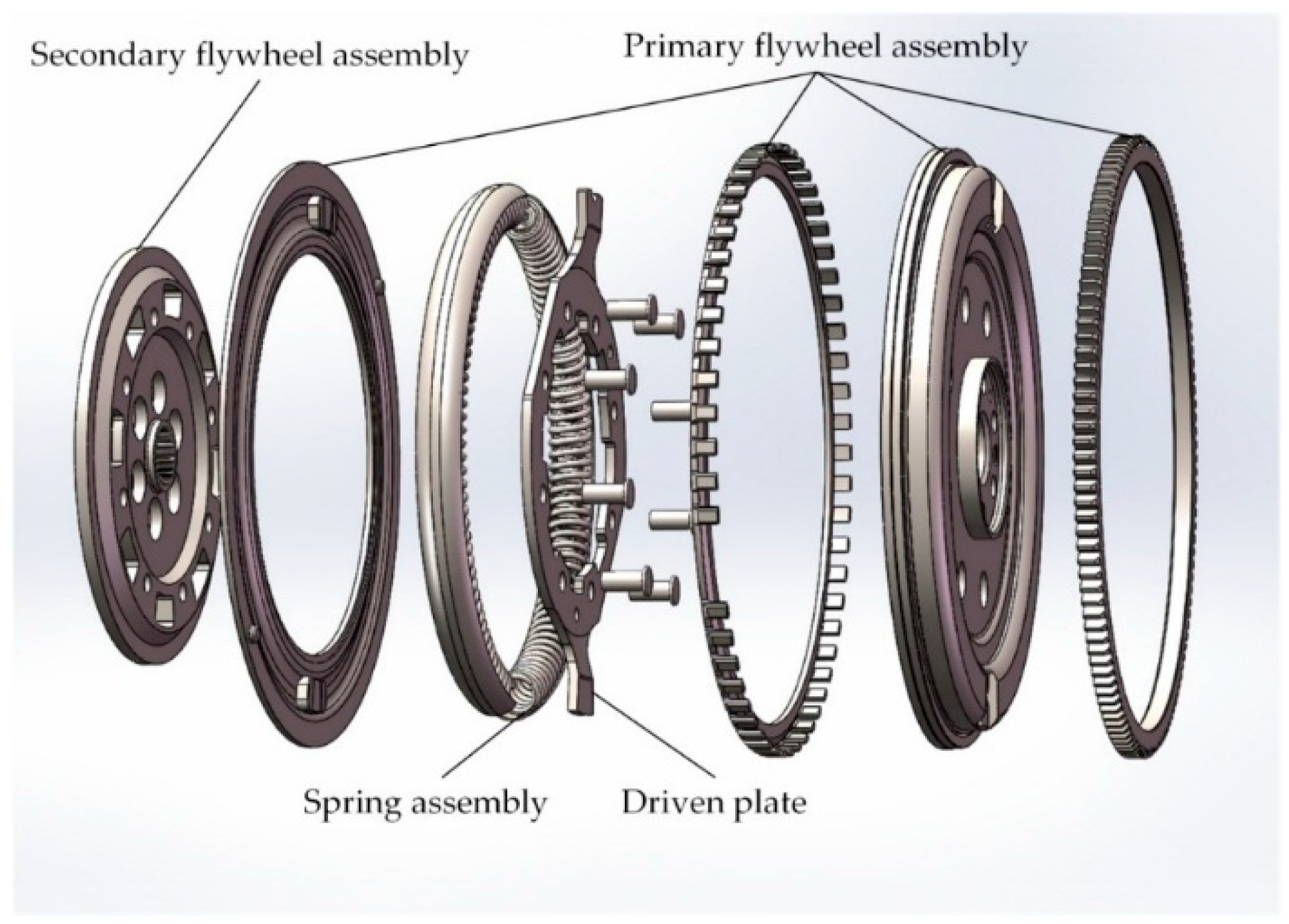
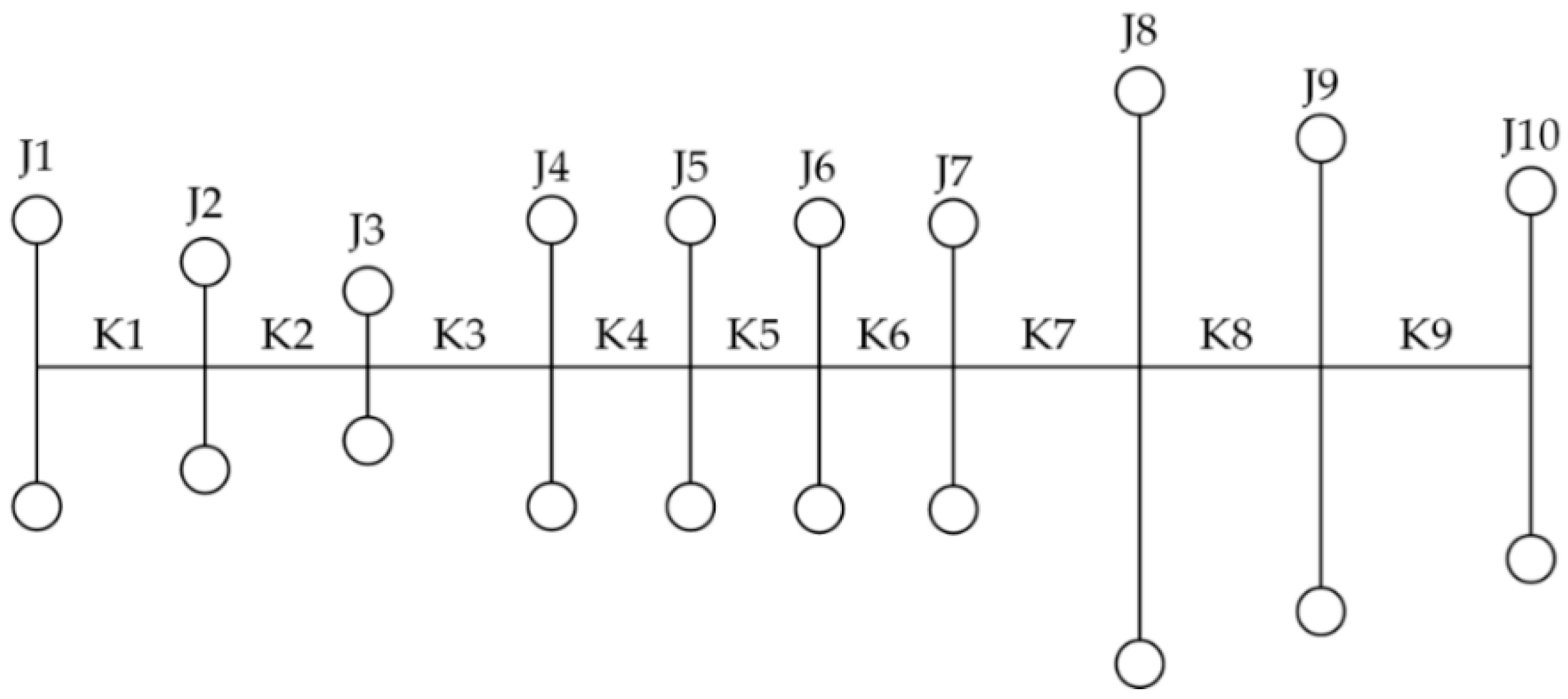
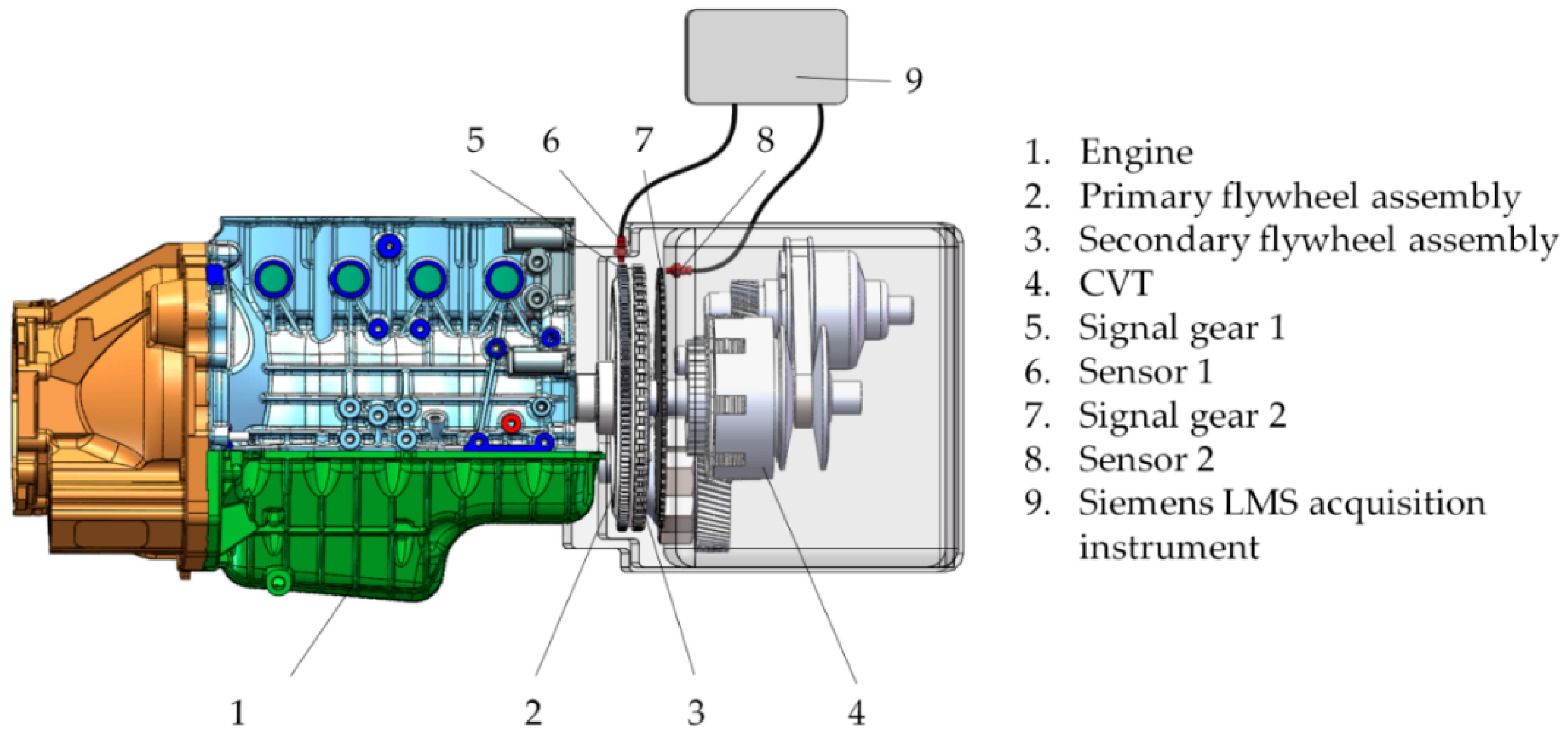
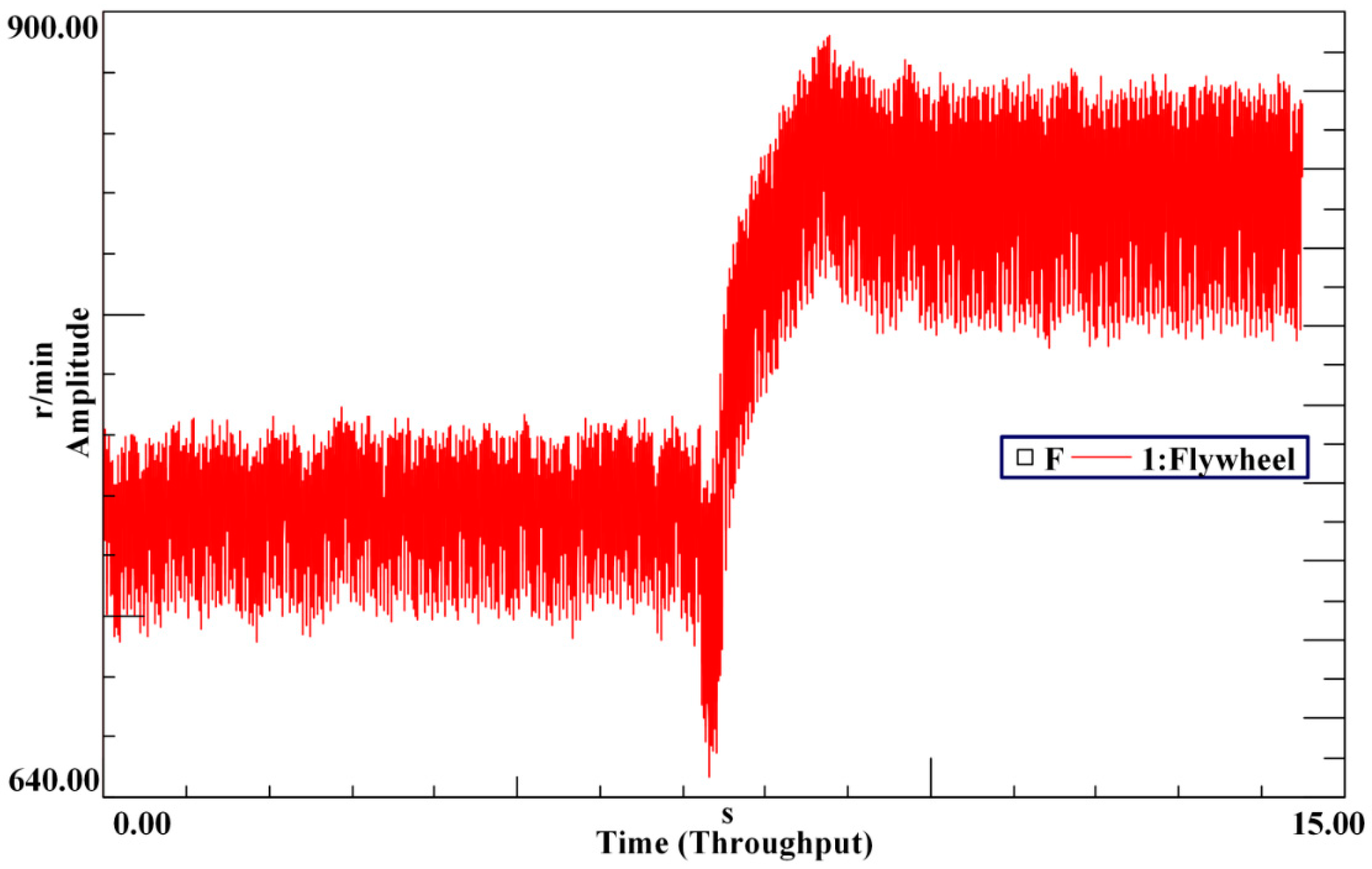
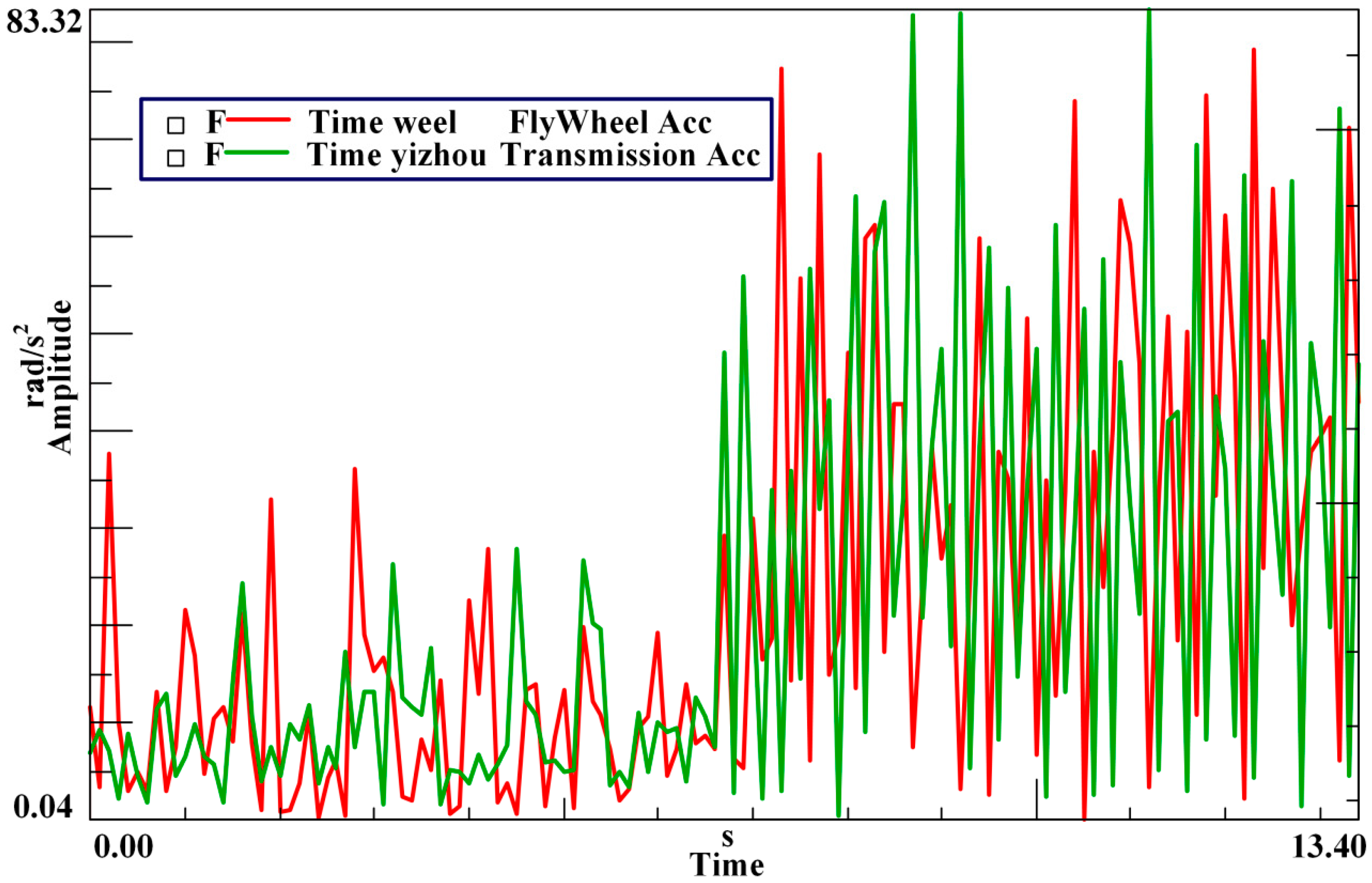
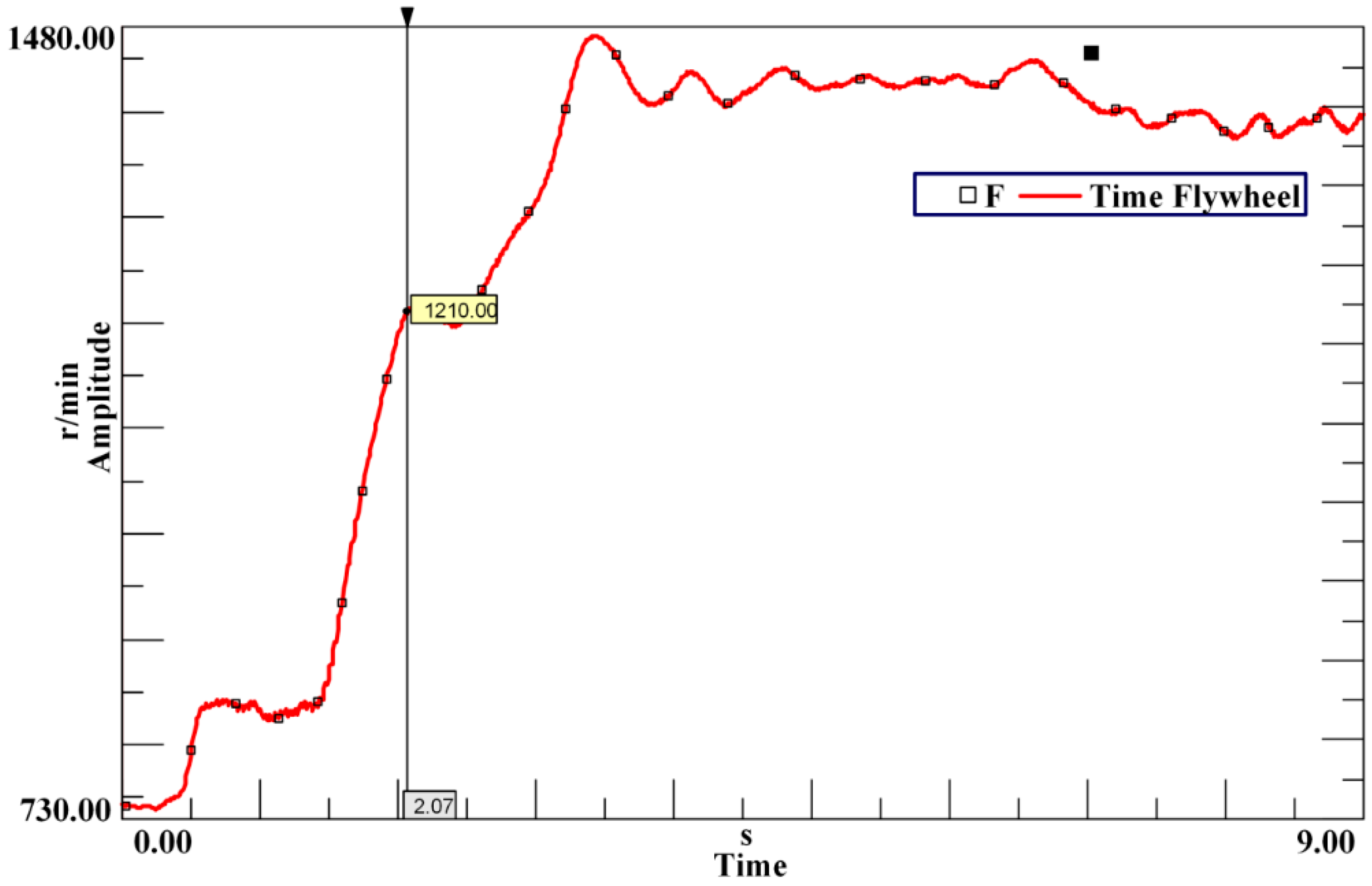
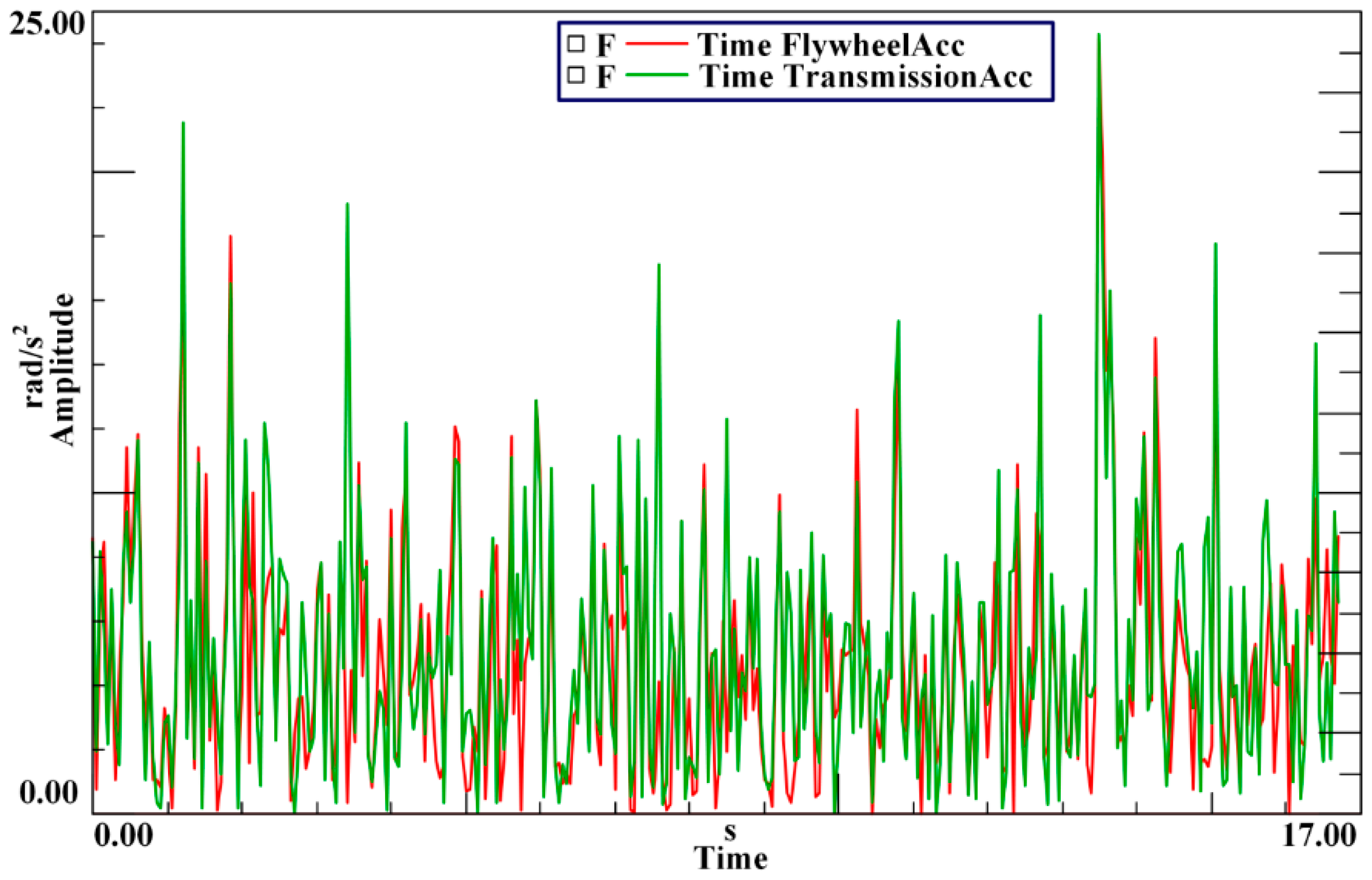
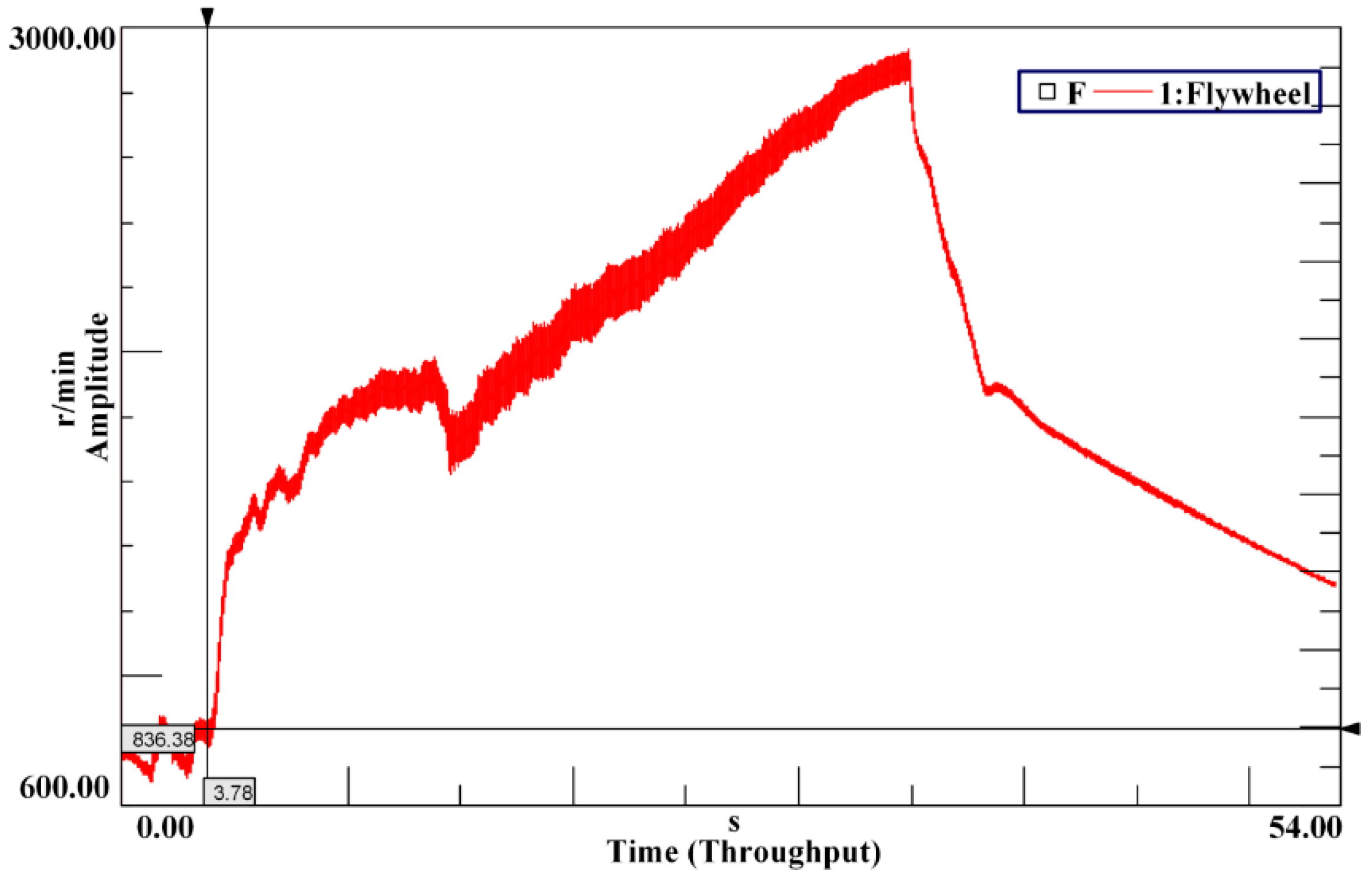
3.1. Matching Model of Inertia and Torsional Stiffness of the DMF under the Idling Condition

The rotational speed of the engine under the idling condition is relatively low, usually around 800 r/min. For four stroke engines, the first order modal resonance under the 0.5th, 1st, 1.5th, and 2nd harmonic excitations will occur in this range of speed. In theory, the DMF can reduce the 1st natural frequency of the idling condition to be lower than the frequency corresponding to the idling speed by adjustment the inertias of the primary and secondary flywheels and torsional stiffness. However, in practice, many factors may influence the matching of the inertias of the DMF, such as the installation space, the dynamic load bearing capacity of the engine crankshaft, and the transmission shifting impact. Since the change interval of the inertias is limited, the natural frequency under the idling condition may be higher than the frequency corresponding to the idling speed. Therefore, two situations should be considered:

(1)

When the 1st order modal resonance speed of the power transmission is lower than the idling speed, the 0.5th and 1st harmonic resonances should be avoided. In this case, we should compare the vector sums of the relative amplitudes of the 0.5th and the 1st harmonic orders to determine the main harmonic excitations that should be avoided.

(2)

When the 1st order modal resonance speed of the power transmission is higher than the idling speed, the 1st, 1.5th, and 2nd harmonic resonances should be avoided. Under the idling condition, since nodes of the 1st order modal shape will not exist in the engine blocks, the main harmonic order will be the 2nd one for four-cylinder engines. In this instance, the 2nd order harmonic torsional vibration should be avoided.

Let the 1st order natural frequency be f, the resonance and the idling speed be $n_1$ and $n_2$, respectively, the harmonic order be I, and the resonance speed zone be $Z_n$, where $n_1=i·n_2=60f$. According to vibration attenuation theories, the resonance speed zone, $Z_n$, will be from $0.8·n_1$ to $1.2·n_1$, that is, $Z_n= \left(0.8, 1.2\right)·n_1$ [20]. We will discuss the two cases respectively.

(1) $n_1<n_2$, $i=0.5, 1$. In this case, f should meet the following requirements:

$$60f<\frac{i{n}_2}{1.2}$$

(21)

$$60f>\frac{i{n}_2}{0.8}$$

(22)

For the 0.5th order harmonic excitation, the natural frequency is relatively low. Two situations will occur when using Equation (21) to design the natural frequency. Firstly, the torsional stiffness at the idling condition is so low that the torsional stiffness at driving conditions will be exclusively high. Thus, resonances will occur under driving conditions. Secondly, the engine starts at an instant speed of about 200 r/min, which will cause start-up resonance and difficulties in starting. Therefore, only Equation (22) will be available.

For the 1st order harmonic excitation, the 1.5th and 2nd order resonances will occur when using Equation (22) to design the natural frequency. Therefore, only Equation (21) will be available in this situation.

In a word, the natural frequency under the idling condition will be:

$$\frac{0.5n_2}{0.8}<60f<\frac{n_2}{1.2}$$

(23)

At the 1st mode, when the vector sum of the relative amplitude of the 0.5th harmonic is larger than that of the 1st harmonic, it is assumed that the resonance speed zone is $Z_n=\left(x, 1.2\right)·n_1$. Thus, $x$ should satisfy Equation (24):

$$\frac{0.5n_2}{x}<\frac{n_2}{1.2}$$

(24)

According to Equation (24), that is, $0.6<x<0.8$, so $x$ can be valued at 0.7. Therefore, $f$ can be calculated by:

$$\frac{0.5n_2}{0.7}<60f<\frac{n_2}{1.2}$$

(25)

At the 1st mode, when the vector sum of the relative amplitude of the 1st harmonic is larger than that of the 0.5th harmonic, it is assumed that the resonance speed zone is $Z_n=\left(0.8, x\right)·n_1$. Thus, $x$ should satisfy Equation (26):

$$\frac{0.5n_2}{0.8}<\frac{n_2}{x}$$

(26)

According to Equation (26), that is, $1.2<x<1.6$, so $x$ can be valued at $\sqrt{2}$. Therefore, $x$ can be calculated by:

$$\frac{0.5n_2}{0.8}<60f<\frac{n_2}{\sqrt{2}}$$

(27)

(2) $n_1> n_2$, $i=1, 1.5, 2$.

Similarly, for each order harmonic excitation, $f$ should also satisfy Equations (21) and (22), which can be expressed as:

$$\{\begin{array}{c}\frac{n_2}{0.8}<60f<\frac{1.5n_2}{1.2}\\ \frac{1.5n_2}{0.8}<60f<\frac{2n_2}{1.2}\end{array}$$

(28)

In fact, $f$ cannot satisfy Equation (28). Under such a circumstance, resonances under the 1st and 2nd order harmonic excitations can only be considered. Furthermore, since the 2nd order harmonic is the main one for the four-cylinder engine, $f$ should firstly satisfy Equation (29), and then satisfy the Equation (30):

$$\frac{n_2}{0.8}<60f<\frac{2n_2}{\sqrt{2}}$$

(29)

$$\frac{n_2}{0.8}<60f<\frac{2n_2}{1.2}$$

(30)

In summary, the 1st order natural frequency should be lower than the frequency corresponding to the idling speed as much as possible. Otherwise, the 1.5th order resonance will not be avoided. It is assumed that the inertias of the primary and secondary flywheel assembly are $J_1$ and $J_2$, respectively, and the inertia of the single mass flywheel matched to the engine is $J_3$. $J_3$ is provide by the engine manufacturer, and will usually be within a certain range; that is, $J_3\in \left(J_x,J_y\right)$. Thus, $J_1+J_2\in \left(J_x,J_y\right)$. Furthermore, the inertia ratio of the primary and secondary flywheel assembly can be obtained by the constraints of the inertias, the masses, and the installation spaces of the primary and secondary flywheel assembly. The inertia ratio can be expressed as $\lambda$ and $\lambda \in \left(a,b\right)$. With initial conditions, the initial values of $J_1$ and $J_2$ can be determined by:

$$\lambda =\frac{a+b}{2}{J}_1+J_2=\frac{J_x+J_y}{2}$$

(31)

$$J_1=\frac{\lambda \left(J_x+J_y\right)}{2\left(\lambda +1\right)}{J}_2=\frac{J_x+J_y}{2\left(\lambda +1\right)}$$

(32)

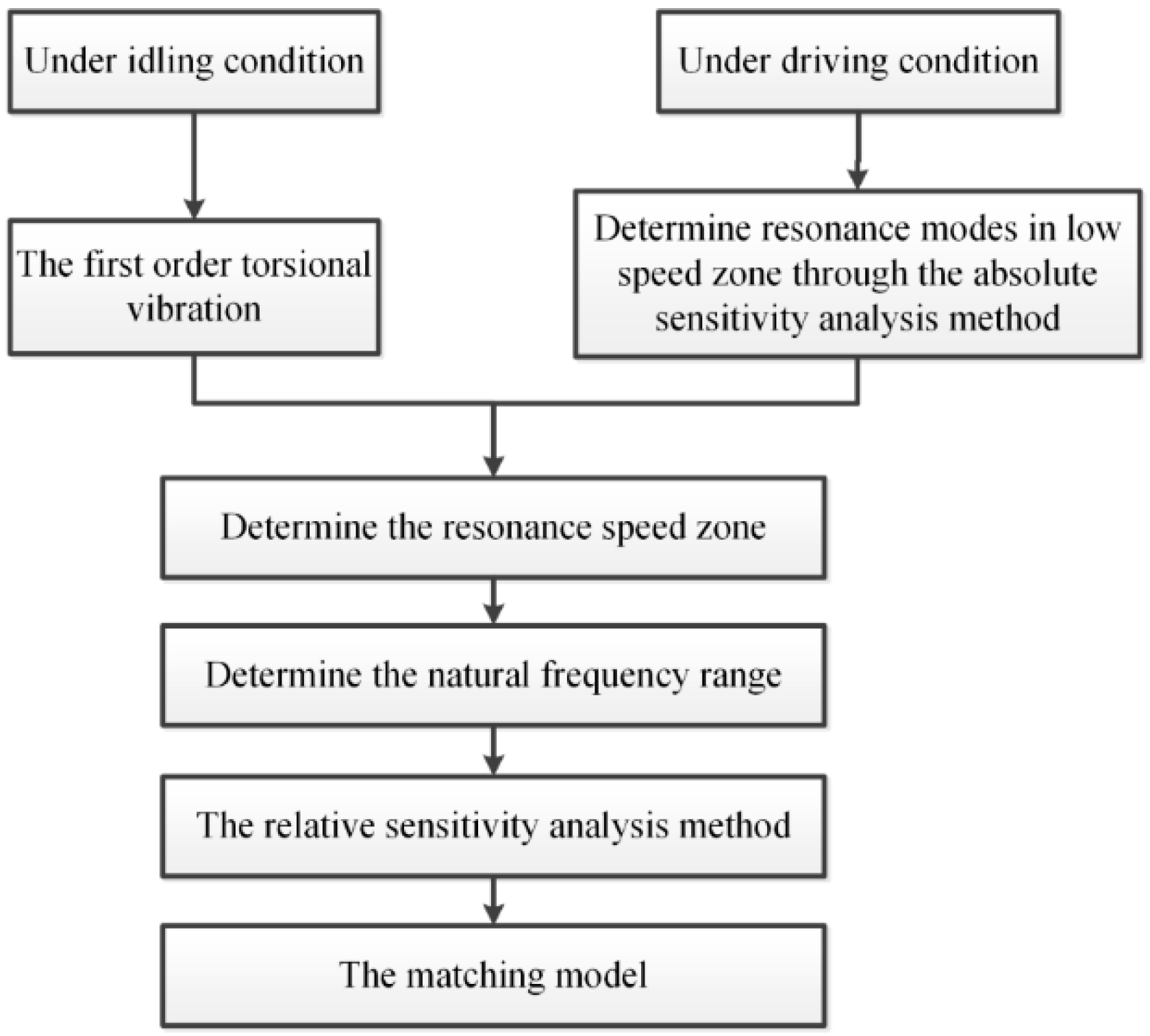
Let the torsional stiffness of DMF at the idling stage be $K_1$. Based on the initial conditions of the moment inertias of the primary and secondary flywheel assembly and the torsional stiffness at the idling stage, combined with the value range of the 1st order resonance and the analysis method of structural sensitivity, the matching of $J_1$, $J_2$, and $K_1$ to the power transmission follows the procedure outlined in Figure 4.

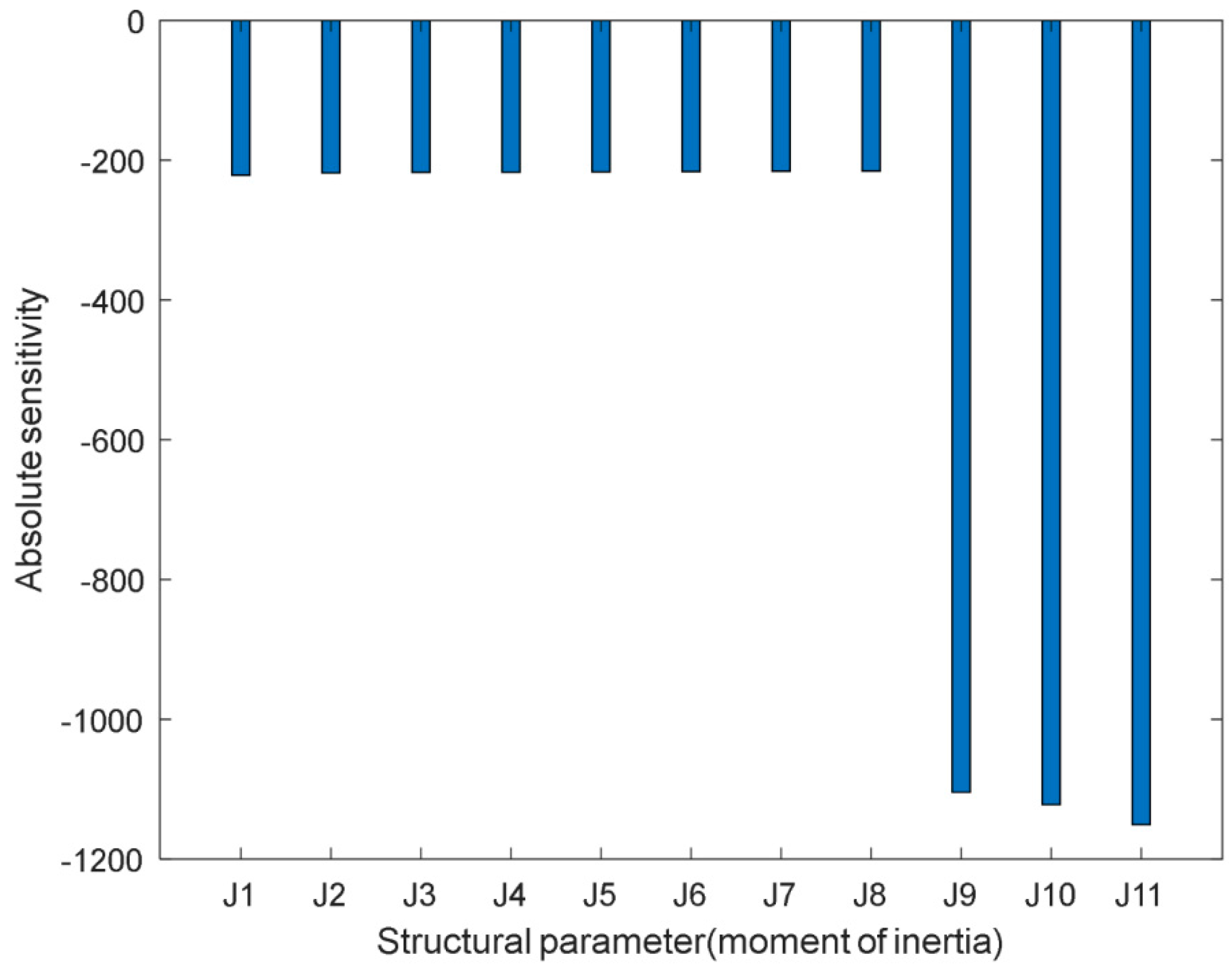
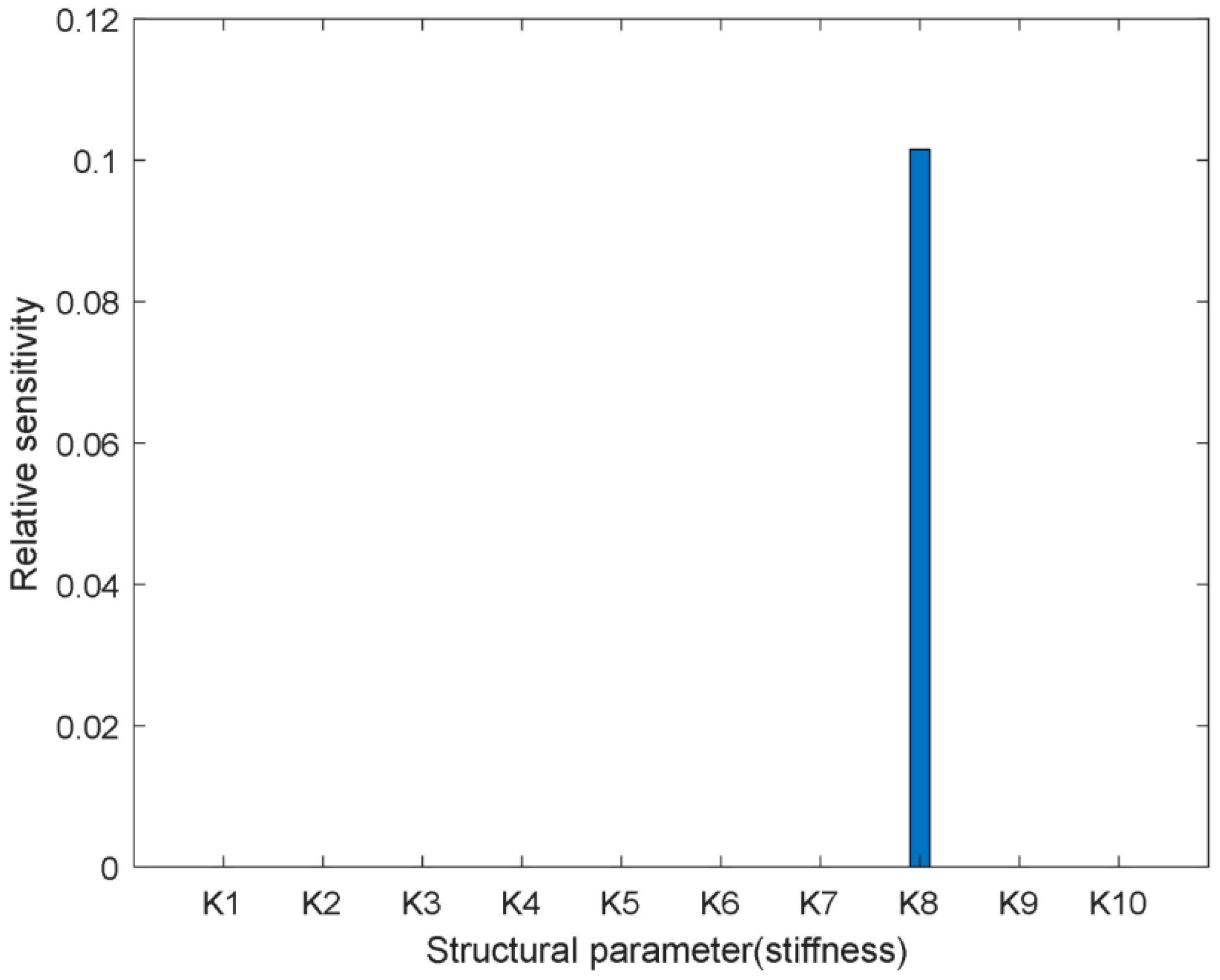
In Figure 4, $S_{ab}\left({\omega }_1/J_1\right)$ and $S_{ab}\left({\omega }_1/J_2\right)$ denote the absolute sensitivities of the 1st order natural frequency to the moment of inertias of the primary and secondary flywheel assembly, respectively, and $S_{rt}\left({\omega }_1/\lambda \right)$ denotes the relative sensitivity of the 1st order natural frequency to the inertia ratio. Meanwhile, $S_{ab}\left({\omega }_1/K_1\right)$ and $S_{rt}\left({\omega }_1/K_1\right)$ are the absolute and relative sensitivities of the 1st order natural frequency to the torsional stiffness at the idling stage, respectively. If both $S_{ab}\left({\omega }_1/J_1\right)$ and $S_{ab}\left({\omega }_1/J_2\right)$ are not significant, $J_1$ and $J_2$ will not be the main structural parameters affecting the 1st order natural frequency. Thus, $K_1$ should be the crucial structural parameter to tune the natural frequency. On the other hand, if $S_{ab}\left({\omega }_1/K_1\right)$ is not the largest sensitivity, $J_1$ and $J_2$ will be the key structural parameters to adjust the natural frequency. In addition, if all the three sensitivities are significant, $K_1$, $J_1$, and $J_2$ will be the key parameters to adjust the natural frequency. In the matching process, because of the constraints of the primary and secondary flywheel assembly, any change of the moment of inertia of the flywheel assembly will cause the change of the other. Thus, the moment of inertia ratio, $\lambda$, should be used instead of $J_1$ and $J_2$ as the structural parameter to conduct the calculations when analyzing the gradient relationship between the change of the primary and secondary flywheel assembly and that of the natural frequency. Therefore, Equation (16) involving $\lambda$ can be rewritten as:

$$S_{rt}\left({\omega }_i/\lambda \right)=\frac{\partial {\omega }_i/{\omega }_i}{\partial \lambda /\lambda }=-\frac{\lambda {\theta }_i^T\frac{\partial \left[J\right]}{\partial \lambda }{\theta }_i}{2M_i}$$

(33)

Let the j^th and $\left(j+1\right)$^th units be the primary flywheel assembly and secondary flywheel assembly, respectively, then:

$$\left[J\right]=\left[\begin{array}{cccccc}{J}_1& & & & & \\ & J_2& & & 0& \\ & & \ddots & & & \\ & & & \frac{\lambda \left(J_x+J_y\right)}{2\left(\lambda +1\right)}& & \\ \begin{array}{c}\\ \end{array}& \begin{array}{c}0\\ \end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}\frac{J_x+J_y}{2\left(\lambda +1\right)}\\ \ddots \end{array}& \begin{array}{c}\\ \end{array}\\ & & & & & J_n\end{array}\right]$$

(34)

$$\frac{\partial \left[J\right]}{\partial J_j}==\left[\begin{array}{cccccc}0& & & & & \\ & & & & 0& \\ & & \ddots & & & \\ & & & \frac{\left(J_x+J_y\right)}{2{(\lambda +1)}^2}& & \\ \begin{array}{c}\\ \end{array}& \begin{array}{c}0\\ \end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}\\ \end{array}& \begin{array}{c}-\frac{J_x+J_y}{2{(\lambda +1)}^2}\\ \ddots \end{array}& \begin{array}{c}\\ \end{array}\\ & & & & & 0\end{array}\right]$$

(35)

Substituting Equation (35) into Equation (33), it can be rewritten as:

$$S_{rt}\left({\omega }_i/\lambda \right)=-\frac{\lambda }{2M_i}\frac{J_x+J_y}{2{(\lambda +1)}^2}\left[{({\theta }_i)}_j{}^2-{({\theta }_i)}_{j+1}{}^2\right]$$

(36)

According to $S_{rt}\left({\omega }_1/K_1\right)$ and $S_{rt}\left({\omega }_1/\lambda \right)$, the mathematical relationships between the 1st order natural frequency and $\lambda$, $K_1$ can be respectively established as:

$$\Delta \lambda =\frac{\Delta {\omega }_1/{\omega }_1}{S_{rt}\left({\omega }_1/\lambda \right)}\lambda$$

(37)

$$\Delta K_1=\frac{\Delta {\omega }_1/{\omega }_1}{S_{rt}\left({\omega }_i/K_1\right)}{K}_1$$

(38)

where $\Delta \lambda$ is the variation based on the initial value of λ, $\Delta {\omega }_1$ is the variation of the 1st order natural frequency, ${\omega }_1$, based on the initial conditions, and $\Delta K_1$ is the variation based on the initial value of $K_1$. Thus $J_1$, $J_2$, and $K_1$ are obtained as:

$$J_1=\frac{\left(\lambda +\mathsf{\Delta }\lambda \right)\left(J_x+J_y\right)}{2\left(\lambda +\mathsf{\Delta }\lambda +1\right)}{J}_2=\frac{J_x+J_y}{2\left(\lambda +\mathsf{\Delta }\lambda +1\right)}$$

(39)

$$K_1=K_1+\mathsf{\Delta }{K}_1$$

(40)

$\Delta {\omega }_1$ can be determined by the difference between the actual value and the value range of ${\omega }_1$. Then, the range of $\lambda$ and $K_1$ can be determined by Equations (39) and (40). In this process, $Max\left(S_{rt}\left(\frac{{\omega }_1}{K_1}\right),S_{rt}\left({\omega }_1/\lambda \right)\right)$ should be the structural parameter to be adjusted firstly. When it cannot meet the requirement, another structural parameter should be adjusted.

3.2. Matching Model of Inertia and Torsional Stiffness of the DMF under the Driving Condition

Under driving conditions, the torsional stiffness of the DMF at the driving stage that is $K_2$ can both transfer the engine power and adjust the system natural frequency. Let the operating angle of DMF at $K_1$ and $K_2$ be ${\theta }_1$ and ${\theta }_2$, respectively. Generally, the total torsion angle of the DMF springs being $\theta$ is about 65°–70° [5], thus, ${\theta }_1+{\theta }_2=\theta$. ${\theta }_1$ can be primarily valued as:

$${\theta }_1=\frac{T_1}{K_1}$$

(41)

where $T_1$ is the moment of inertia of the power transmission under the idling condition, which is related to the inertias of the secondary flywheel assembly, the clutch and the input shaft of the transmission, and the angular accelerations of the starting motor. Accordingly, $K_2$ can be primarily calculated as:

$$K_2=\frac{\xi T_{max}}{\theta -{\theta }_1}$$

(42)

where $T_{max}$ is the maximum torque from the engine, and $\xi$ is the torque backup coefficient, which is related to the real car.

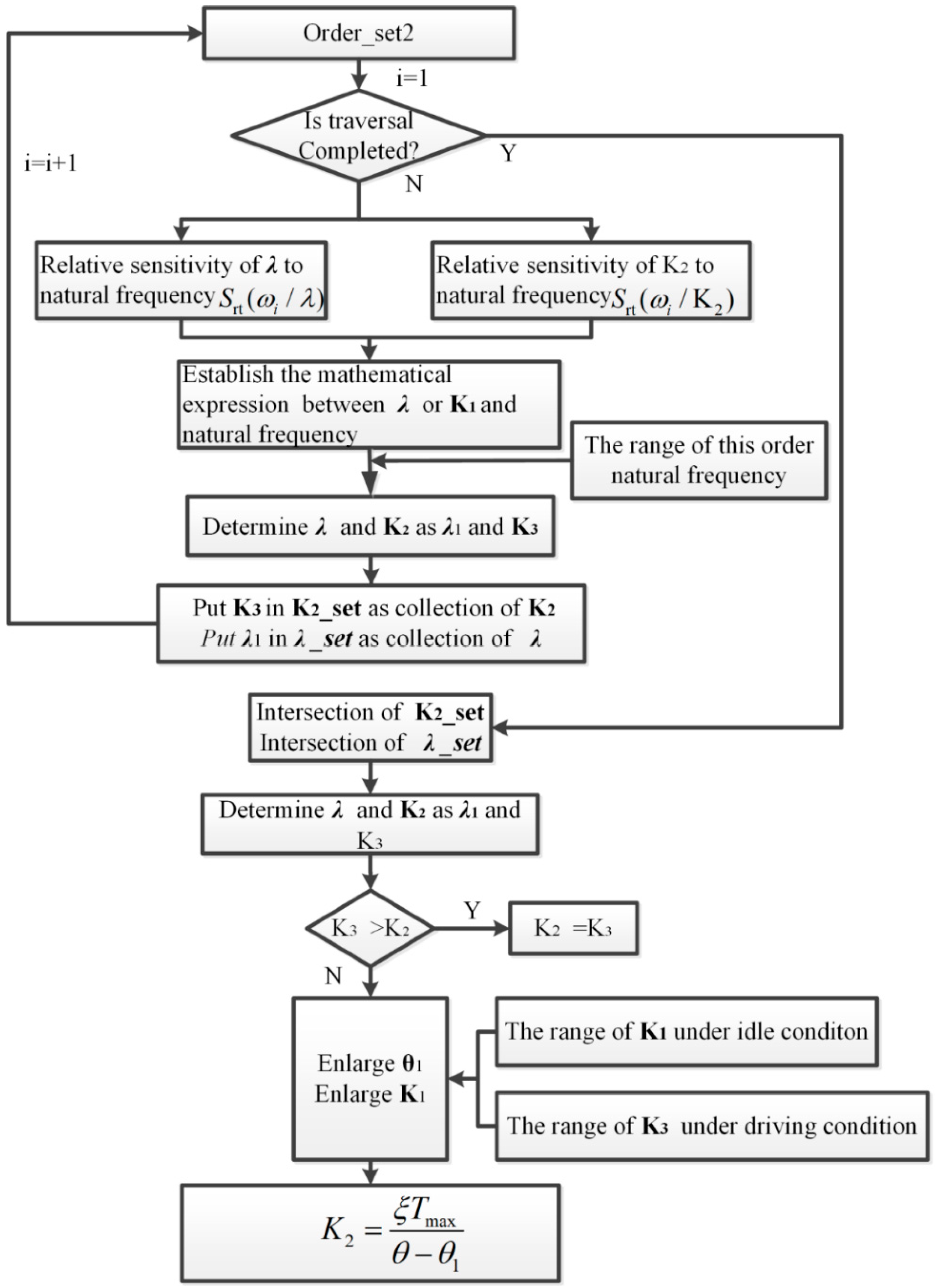
Figure 5 shows the matching process of the structural parameters of the DMF using the structural sensitivity analysis method. Taking $J_1$, $J_2$, and $K_2$ as initial conditions, the torsional vibration model of the system can be established firstly. Then, modal analysis will be conducted to determine whether the resonance speed is in the low speed region. If the resonance speed deviates from the low speed region, $J_1$, $J_2$, $K_1$, and $K_2$ will be the final structural parameters of DMF. Whereas, if the resonance speed is in the low speed region, we should firstly obtain the order set of resonances, which is order_set1. Then, the absolute sensitivities of $J_1$, $J_2$, and $K_2$ to the natural frequency are analyzed for each order in order_set1 to obtain order_set2 associated with $J_1$, $J_2$, and $K_2$. Finally, the structural sensitivities of $K_2$ and $\lambda$ are analyzed in order_set2, and their values are matched.

In this process, for the orders of resonance, the ranges of the natural frequency can be determined by Equations (21) and (22). Meanwhile, the relative sensitivities of $K_2$ and $\lambda$ to each order natural frequency can be calculated. Then, referring to Equations (39) and (40), the ranges of $K_2$ and $\lambda$ can be determined and stored in the K₂_set and λ_set, respectively. After traversing order_set2, the intersection of all values in the λ_ set and K₂_set will be obtained, and the values of $K_2$ and $\lambda$ will be determined accordingly. After the above calculations under driving conditions, $K_2$ will change to be $K_3$. If $K_3>K_2$, we value the torsional stiffness of the DMF at the driving stage as $K_3$; that is $K_2=K_3$. If $K_3<K_2$, $K_3$ cannot meet the requirement of torque transmission. Therefore, in this case, the intersection of the ranges of $K_1$ and $K_3$ under the idling condition should be determined firstly. In this intersection, by increasing $K_1$ and its operating angle, ${\theta }_1$, $K_2$ will finally be determined according to Equation (42).

4. Matching Example and Real Vehicle Test of DMF

4.1. Matching Example of the DMF Based on the Structural Sensitivity Analysis Method

Taking a car matching a CVT (continuously variable transmission) as an example, the undamped torsional vibration models under idling and driving conditions are shown in Figure 6 and Figure 7, respectively, where $J_i$ denotes the moment of inertia and $K_i$ denotes the torsional stiffness linking the two lumped masses. The structural parameters of the power transmission are listed in

Table 1. Structural parameters of the power transmission.

Names of Elements	Inertia	Value of Inertia (kg·m2)	Torsional Stiffness	Value of Torsional Stiffness (N·m/rad)
Driven part of rubber damper	J1	4.795 × 10−3	K1	14,320.0
Driving part of rubber damper	J2	2.038 × 10−3	K2	74,636.1
Accessories	J3	9.74 × 10−5	K3	356,080.5
Cylinder 1	J4	4.669 × 10−3	K4	358,856.9
Cylinder 2	J5	4.712 × 10−3	K5	360,638.8
Cylinder 3	J6	4.712 × 10−3	K6	359,640
Cylinder 4	J7	4.686 × 10−3	K7	1,871,080
Primary flywheel assembly	J8	0.08	K8	160.43; 733.39
Secondary flywheel assembly	J9	0.012	K9	98,731.62
Input shaft of CVT	J10	7.312 × 10−3	K10	48,483.78
Driving cone of CVT	J11	0.0268368

, where the units of the moment of inertia and torsion stiffness are kg·m² and N·m/rad, respectively.

The idling speed and maximum torque of the engine of this car are 750 r/min and 225 N·m, respectively. According to the technical parameters provided by the vehicle factory, the range of the total inertia of the DMF is 0.08–0.11 kg·m², where the inertia of the primary flywheel assembly is not less than 0.075 kg·m², and the secondary flywheel assembly quality should be less than 5 kg. Furthermore, $\xi =1.33$, thus $4.2<\lambda <9$.

The car has been fitted with a DMF. The inertias of the primary and secondary flywheel assembly are 0.08 kg·m² and 0.012 kg·m², respectively, and the torsional stiffness at the idling stage and driving stage is 160.43 N·m/rad (${\theta }_1=45.25 °$) and 733.39 N·m/rad (${\theta }_2=15 °$), respectively. In addition, the hollow travel angle is 4.75 °, and the total torsional stiffness is 65 °, that is, $\theta =65 °$.

Based on the above data, the simulation model is established by using Adams software. Figure 8 and Figure 9 are the simulation models of the automotive power transmission system with the DMF under idle and driving conditions, respectively. The simulation models created by Adams software usually consist of bodies, connectors, and forces, where bodies represent centralized mass units and constraints on each body are implemented by connectors, and the force transfer between bodies is achieved by torsion springs in forces.

The modal analysis is carried out according to the above simulation models, and the natural frequencies under idling and driving conditions are listed in

Table 2. Natural frequencies under the idling condition (Hz).

f1	f2	f3	f4	f5	f6	f7	f8	f9
15.8	239.8	603.8	742	1053	1731	2481	3602	10,667

and

Table 3. System natural frequency under the driving condition (Hz).

f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
22.5	239.8	300	603.8	821.79	1053	1731	2481	3602	10,667

.

It is shown that the 1st order natural frequency is 15.8 Hz under the idling condition and the corresponding resonance speed will be 940 r/min under the idling condition, which can meet the requirement of Equation (29). The 1st order natural frequency is 22.5 Hz under the driving condition and the corresponding resonance speed is 1350 r/min under the driving condition, which means that resonance will occur in the low speed region. Therefore, the structural parameters of the original DMF needed to be modified.

The calculation flow of sensitivity is shown in Figure 10, where n is the degree of freedom of the system, and i stands for the i^th order and j represents the j^th unit. According to this calculation flow, the program of m file is coded by using MATLAB, and the corresponding program code is shown in Appendix A. The absolute sensitivities of the 1st order natural frequency to the inertias and torsional stiffness can be obtained based on the torsional vibration model under the driving condition, as shown in

Table 4. The absolute sensitivities of the 1st order natural frequency to inertias under the driving condition.

J1	J2	J3	J4	J5	J6	J7	J8	J9	J10	J11
−221.583	−218.24	−217.333	−217.14	−216.821	−216.376	−215.803	−215.668	−1104.44	−1122.1	−1150.73

and

Table 5. The absolute sensitivities of the 1st order natural frequency to torsional stiffness under the driving condition.

K1	K2	K3	K4	K5	K6	K7	K8	K9	K10
5.62 × 10−7	4.18 × 10−8	1.89 × 10−9	5.18 × 10−9	1.01 × 10−8	1.68 × 10−8	9.29 × 10−10	0.101543	3.1 × 10−6	7.97 × 10−6

and Figure 11 and Figure 12.

For inertias, the absolute sensitivities show that the inertias of the secondary flywheel assembly and the CVT component have the greatest influence on the 1st order natural frequency under the driving condition and the natural frequency will decrease with the increase of inertias. For the torsional stiffness, the torsional stiffness of the DMF at the driving stage has the greatest influence on the 1st order natural frequency and the natural frequency will increase with the increase of the torsional stiffness. Since the structural parameters of the CVT cannot be modified, the key structural parameters will be the inertia ratio of the primary and secondary flywheel assembly $\left(\lambda \right)$ and the torsional stiffness of the DMF under the driving condition $\left(K_8\right)$.

The relative sensitivities of the 1st order natural frequency to the torsional stiffness driving condition are shown in

Table 6. The relative sensitivities of the 1st order natural frequency to torsional stiffness under the driving condition.

K1	K2	K3	K4	K5	K6	K7	K8	K9	K10
5.35 × 10−5	2.08 × 10−5	4.47 × 10−6	1.24 × 10−5	2.42 × 10−5	4.03 × 10−5	1.16 × 10−5	0.495229	0.002033	0.00257

and Figure 13, where $S_{rt}\left({\omega }_1/K_8\right)=0.495$, and it can be calculated that $S_{rt}\left({\omega }_1/\lambda \right)=0.062$ according to Equation (36). Combined with Equations (37) and (38), Figure 4, Figure 5, and the initial conditions, the matching results can be obtained, which are $J_8=0.077$ kg·m², $J_9=0.018$ kg·m², $K_8=257.8$ N·m/rad (${\theta }_1=54.25 °$) (the torsion stiffness under idling condition), $K_8=710.5$ N·m/rad (${\theta }_2=6 °$) (the torsion stiffness under driving condition), ${\theta }_0=4.75 °$ (the hollow travel angle), and $\theta =65 °$ (the total torsion angle). The rematching DMF is shown as Figure 14.

After rematching, the natural frequencies of the power transmission under idling and driving conditions are obtained as shown in

Table 7. Natural frequencies under the idling condition (Hz).

f1	f2	f3	f4	f5	f6	f7	f8	f9
18.8	240.1	605.1	713.4	1053.6	1731.9	2481.7	3604.7	10,667.8

and

Table 8. Natural frequencies under the driving condition (Hz).

f1	f2	f3	f4	f5	f6	f7	f8	f9	f10
15	240.1	282.9	605.1	801.7	1053.6	1731.9	2481.7	3604.7	10,667.8

. The 1st order natural frequency is 18.8 Hz and the corresponding resonance speed is 1128 r/min under the idling condition, which can meet the requirement of Equation (29). Furthermore, the 1st order natural frequency under the driving condition is 15 Hz and the corresponding resonance speed is 900 r/min under the driving condition, which can avoid resonances in the low speed region.

4.2. Real Vehicle Test

Real vehicle tests were carried out for the power transmissions matching the DMFs before and after optimization, as shown in Figure 15 and Figure 16. As is shown in Figure 16, two electromagnetic speed sensors of which the model number is ONOSOKKI-MP-910 were mounted on the housing of the transmission. Furthermore, the arrangement details of these two sensors are shown in Figure 17, where sensor 1 is pointed to signal gear 1 on the primary flywheel of the DMF and sensor 2 is pointed to signal gear 2 on the input shaft of the transmission. As is shown in Figure 18, with the rotation of the gear, the clearance between the gear and the sensor will also change due to the different distances between the addendum and the dedendum of the gear and the sensor, which will cause a variation of the magnetic flux of the coil in the sensor, thus the output signal of the sensor is similar to a sinusoidal wave. Let the rotating speed of the gear be $\omega$ (r/min), the number of teeth of the gear be Z, and the frequency of the signal be f(Hz), so $\omega$ will be:

$$\omega =\frac{f}{Z}\times 60$$

(43)

In this experiment, the signal wires of these two rotating speed sensors were connected with a Siemens data acquisition instrument, LMS SCADAS302VB. The collected data were processed by Siemens LMS Test.Lab 15A, and the tracking settings for the two signal channels are shown in Figure 19, where the number of teeth of signal gear 1 (as shown in Figure 17) is 133 and the number of teeth of signal gear 2 (as shown in Figure 17) is 60. In Figure 20, tacho1 and tacho2 are the rotating speed signal channel of the primary flywheel and the rotating speed signal channel of the input shaft of the transmission, respectively.

Speed signals were collected under idling and driving conditions and the angular acceleration of the primary flywheel and the transmission input were analyzed. For the engine mounted with the original DMF, under the idling condition, the engine speed starts at around 750 r/min, as shown in Figure 21, in which the red curve represents the engine speed. Figure 22 shows the angular acceleration, in which the red and green curves respectively present the angular acceleration of the primary flywheel and the transmission input, where the maximum angular acceleration of the transmission input is about 83 $\mathrm{rad}/{\mathrm{s}}^2$. Under the driving condition, the range of the engine speed is 750 r/min–1500 r/min, as shown in Figure 23, in which the red curve represents the engine speed in the time-domain. Figure 24 shows the angular acceleration, in which the red and green curves respectively present the angular acceleration of the primary flywheel and the transmission input, where the maximum angular acceleration of the transmission input is about 203 $\mathrm{rad}/{\mathrm{s}}^2$ around 1210 r/min.

For the rematching DMF, the engine speed was around 750 r/min under the idling condition, as shown in Figure 25, in which the red curve represents the engine speed. Figure 26 shows the angular acceleration under the idling condition, in which the red and green curves respectively present the angular acceleration of the primary flywheel and the transmission input, where the maximum angular acceleration of the transmission input is about 25 $\mathrm{rad}/{\mathrm{s}}^2$. Under the driving condition, the range of the engine speed is 750 r/min–2500 r/min, as shown in Figure 27, in which the red curve represents the engine speed in the time-domain. Figure 28 shows the angular acceleration, in which the red and green curves respectively present the angular acceleration of the primary flywheel and the transmission input, where the maximum angular acceleration of the transmission input is 184 $\mathrm{rad}/{\mathrm{s}}^2$ around 836 r/min.

Theoretical calculation results and the experimental results of the engine with the original DMF and rematching DMF are compared as shown in

Table 9. Comparative analysis of the results.

Items	Under Idling Condition		Under Driving Conditon
	Original DMF	Rematching DMF	Original DMF	Rematching DMF
The maximum angular acceleration (rad/s2)	83	25	203	184
Measured resonance speed (r/min)			1210	836
Theoretical resonance speed (r/min)	940	1128	1350	900

. Under the idling condition, the theoretical value of the first order resonance speed of the system is 940 r/min with the original DMF and 1128 r/min with the rematching DMF, however, there is no change in terms of the engine speed, remaining around 750 r/min under the idling condition. Thus, the resonance speed appears unmeasured. Figure 25 shows that the resonance speed under the idling condition occurs around 750 r/min; Figure 26 shows that the resonance speed under the idling condition remains around 750 r/min and the maximum angular acceleration of the transmission input is decreased as the torsional stiffness of the DMF at the idling stage rises, suggesting an acceptance of the theoretical calculation result.

Under the driving condition, the actual measurement result of the first order resonance speed of the engine with the original DMF is 1210 r/min, and then the theoretical calculation of the resonance speed is 1350 r/min based on the undamped torsional vibration model; that is, the error is about 11%. Moreover, the actual measurement result of the first order resonance speed of the engine with the rematching DMF is 836 r/min and the theoretical calculation of the resonance speed is 900 r/min based on the undamped torsional vibration model; that is, the error is about 7%, which means the theoretical model can be used to analyze the modal in the process of matching.

Under the idling condition, the angular acceleration of the transmission input is not damped compared with that of the primary flywheel because the resonance speed is higher than the idling speed for the engine with the rematching DMF. Nevertheless, the maximum angular acceleration of the transmission input decreases from 83 $\mathrm{rad}/{\mathrm{s}}^2$ to 25 $\mathrm{rad}/{\mathrm{s}}^2$. Under the driving condition, the maximum angular acceleration of the transmission input decreases from 203 $\mathrm{rad}/{\mathrm{s}}^2$ to 184 $\mathrm{rad}/{\mathrm{s}}^2$ for the engine with the rematching DMF. Moreover, the resonance speed is reduced from 1210 r/min to 836 r/min for the engine with the rematching DMF under the driving condition, avoiding the resonance at the low speed region. Obviously, the damping performance of the rematching DMF is better than the original DMF, thus these results confirm the validity of the matching model.

5. Conclusions

This study addressed the matching model of the DMF and the power transmission by integration of the sensitivity analysis method and the vibration reduction theories. Based on the mathematical meaning of sensitivity, the structural sensitivity analysis method for an automobile power transmission system was obtained. Furthermore, considering the constraints of the inertia of the primary and secondary flywheel assembly, the inertia ratio of them was taken as one structural parameter completing a successful sensitivity analysis. The main function of the DMF is to attenuate torsional vibration from the engine and hence the resonance speed zones were defined in light of the vibration reduction theories and their working characteristics. The matching model of the DMF and the power transmission was established based on the resonance speed zones and the structural sensitivity analysis method. The matching model was applied to modify the structural parameters of the DMF of a certain vehicle and then the effectiveness of the matching model was verified by experiments of a real vehicle test under the idling condition and driving condition. The main conclusions in this research are summarized as follows:

(1)

The absolute structural sensitivity can effectively isolate key structural parameters of the vibration modal at each stage and the resultant parameters can be quantitatively revised by the relative structural sensitivity. Under the driving condition, the inertia of the secondary flywheel assembly and torsional stiffness of DMF have a significant influence on the 1st order natural frequency of automotive power transmission. The inertia of the secondary flywheel assembly is inversely proportional to the 1st order natural frequency. In contrast, the torsional stiffness is positively proportional to the 1st order and the inertia ratio of the primary and secondary assembly is positively associated to the 1st order.

(2)

Given that the resonance speed is higher than the idle speed under the idling condition, the 1st order natural frequency of the system should be increased through enhancement of the torsional stiffness of the DMF at the idling stage to decrease the angular acceleration amplitude of the input shaft of the transmission. In contrast, the 1st order natural frequency of the system should be decreased through reduction of the torsional stiffness of the DMF at the idling stage to attenuate the angular acceleration amplitude of the input shaft of the transmission.

(3)

Under the driving condition, the 1st order natural frequency of the system should be decreased by reduction of the inertia ratio and the torsional stiffness of the DMF at the driving stage, which appears to protect resonances in low speed zones and attenuates the angular acceleration amplitude of the input shaft of the transmission.

(4)

Given that the torsional stiffness at the driving stage cannot meet the requirements of the matching model, the operation range of the torsional stiffness at the idling stage should be enlarged to make it work under driving conditions.

As the matching model proposed in this paper can achieve reasonable matching between structural parameters of the DMF and power transmission system, it is useful to make a transmission system that is insulated from torsional vibrations caused by the engine. The matching model can also be applied in structural parameters matching of other types of shock absorber in vehicle systems and other mechanical systems after adjusting the resonance frequency ranges and vibration model according to the actual operating conditions of the system.

The matching model can be used to preliminarily determine the main structural parameters of the DMF, however, these were not further optimized according to the dynamic non-linear characteristics of the DMF, so in future study, we will combine the dynamic non-linearity model of the DMF with the linear matching model to further optimize the structural parameters in order to obtain a better damping performance.