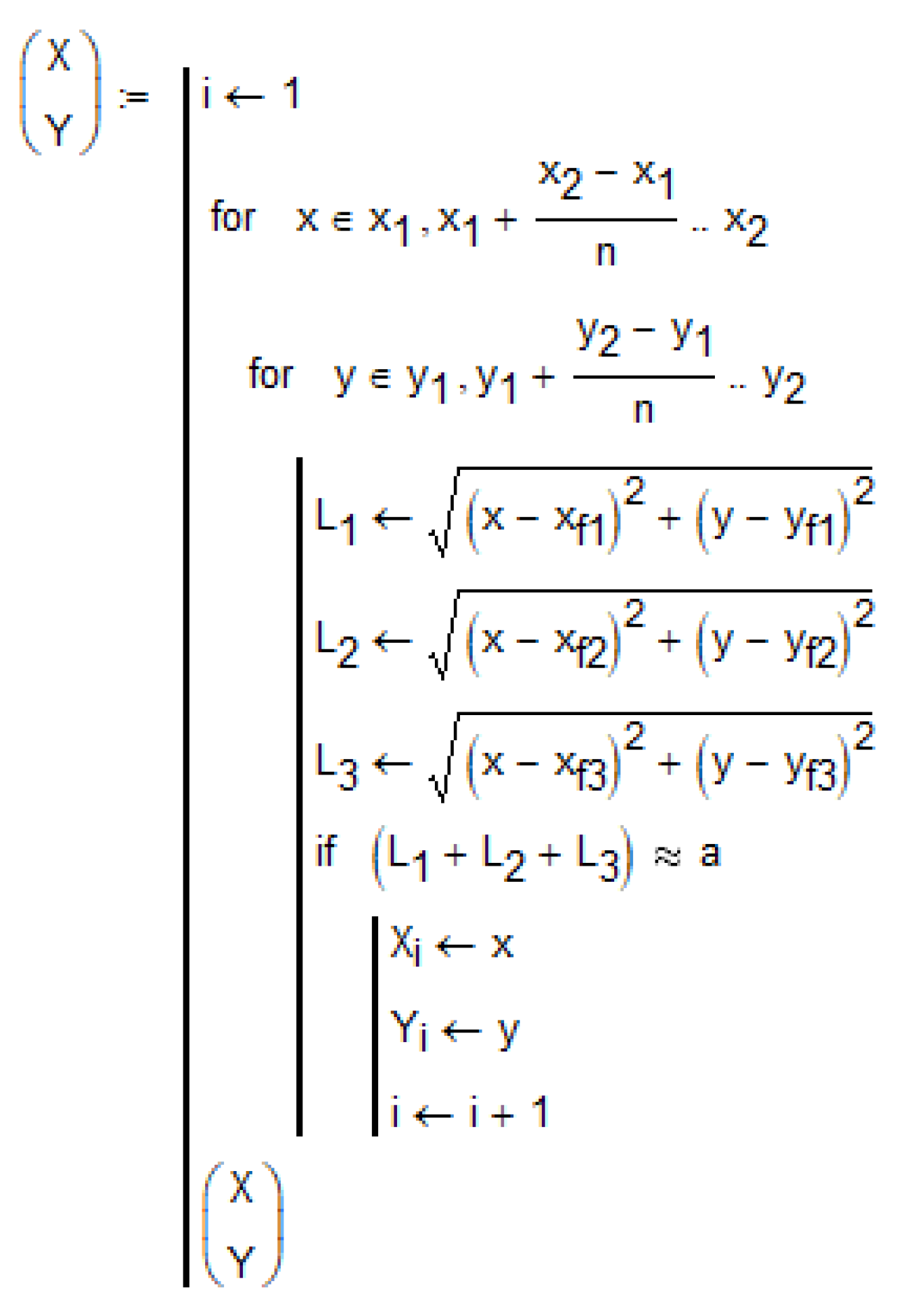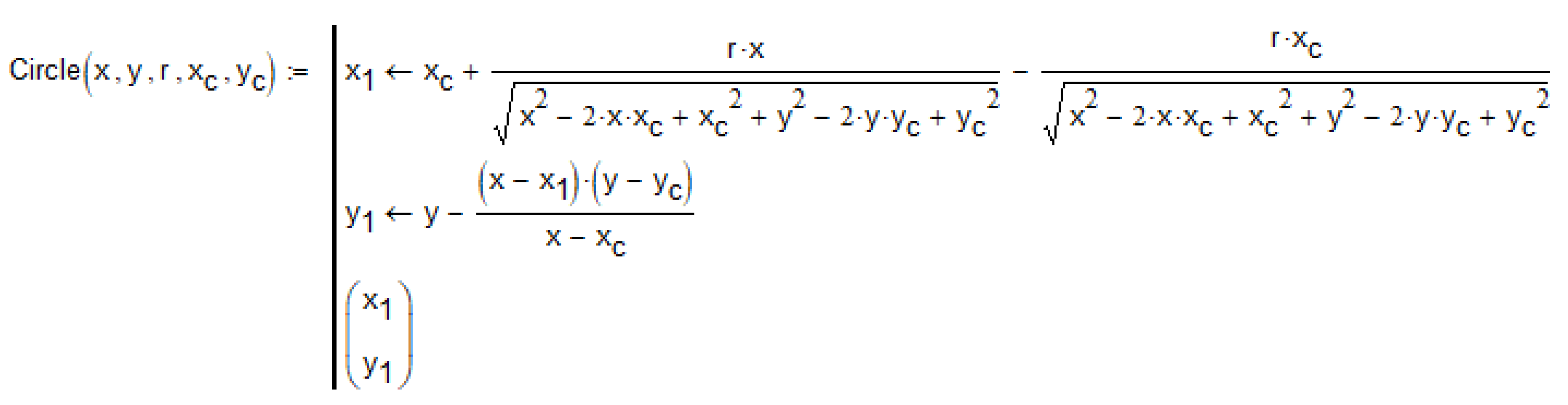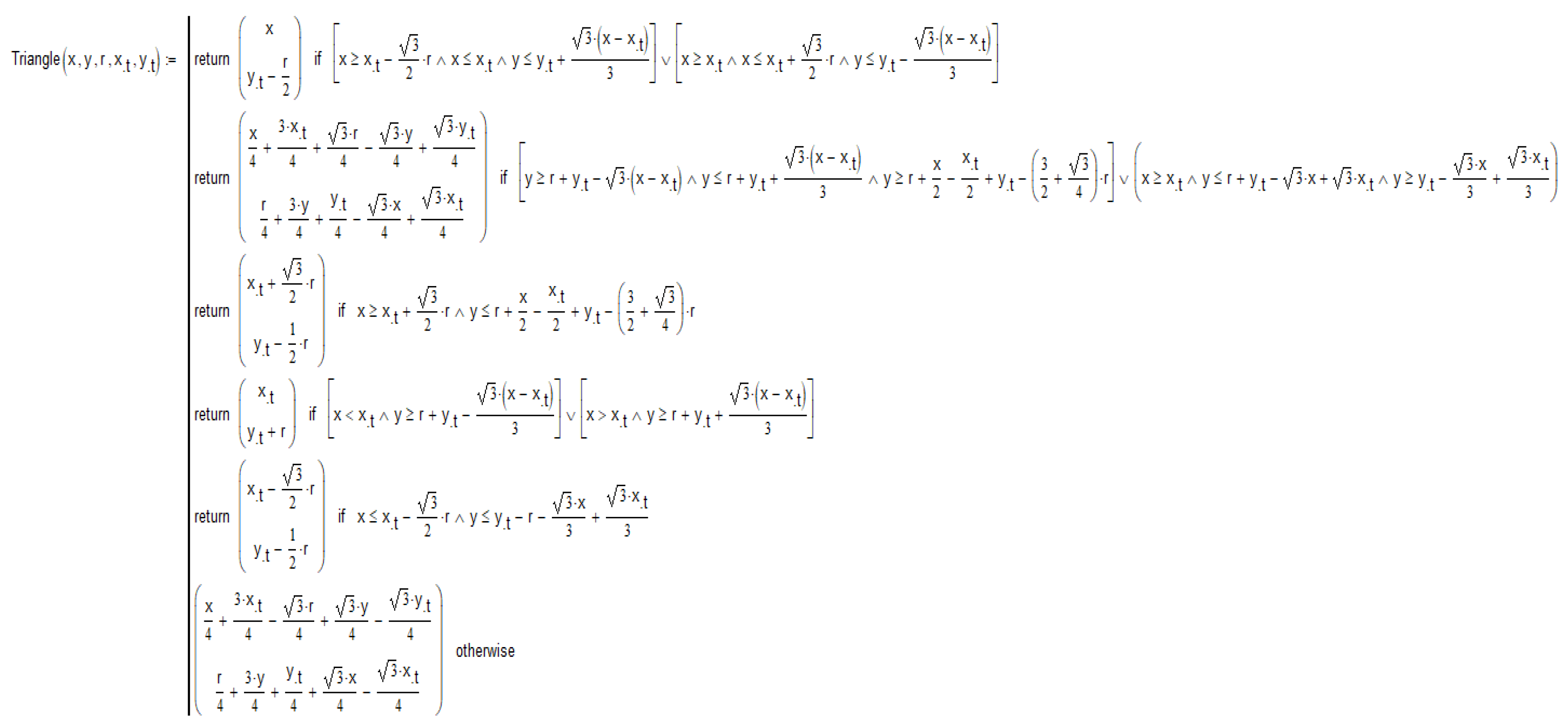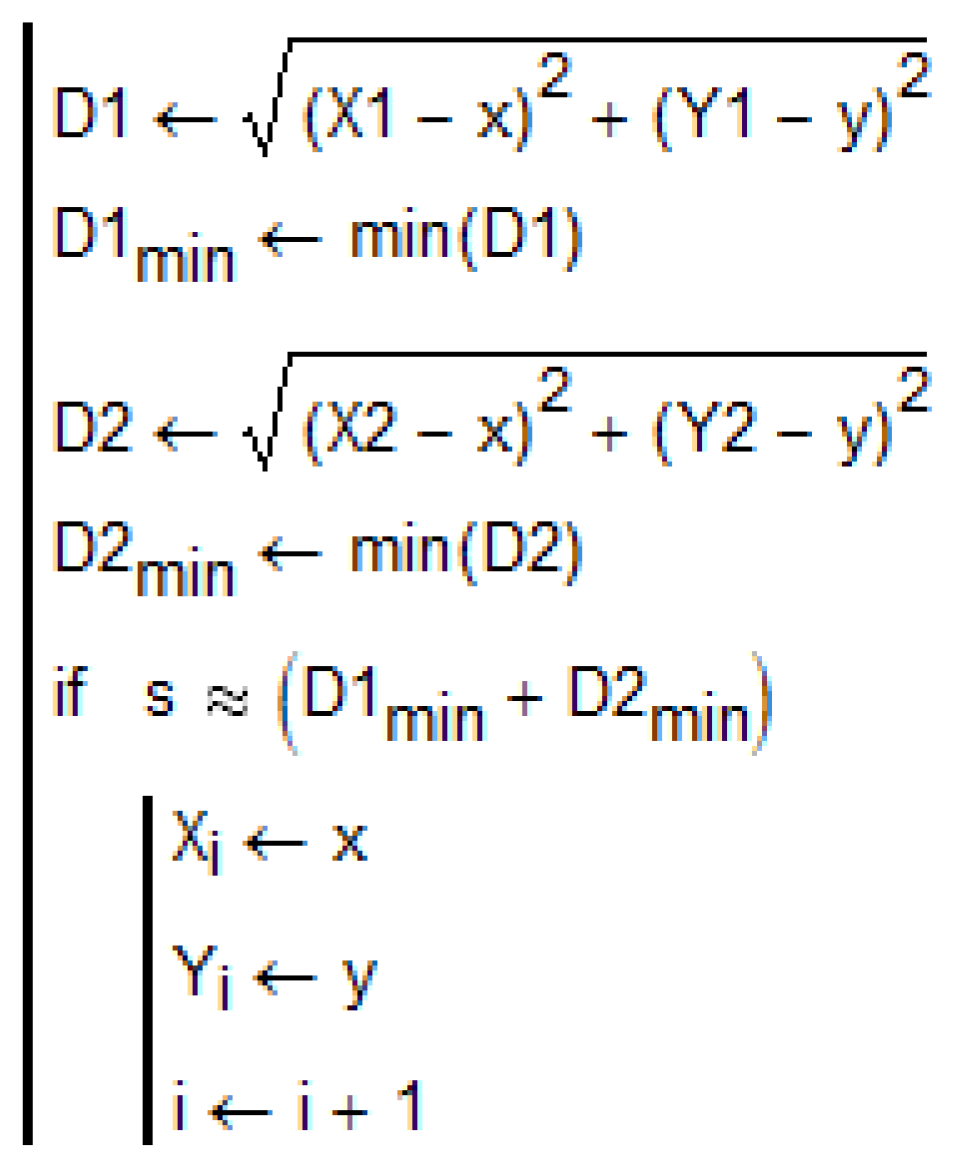Author Contributions
Conceptualization, V.O.; methodology, V.O.; software, M.N.; validation, V.O., M.N.; formal analysis, E.B., W.R.; investigation, V.O.; resources, E.B.; writing—original draft preparation, V.O., M.N., E.B., W.R.; writing—review and editing, M.N., E.B., W.R.; visualization, V.O, M.N., E.B., W.R.; supervision, W.R.
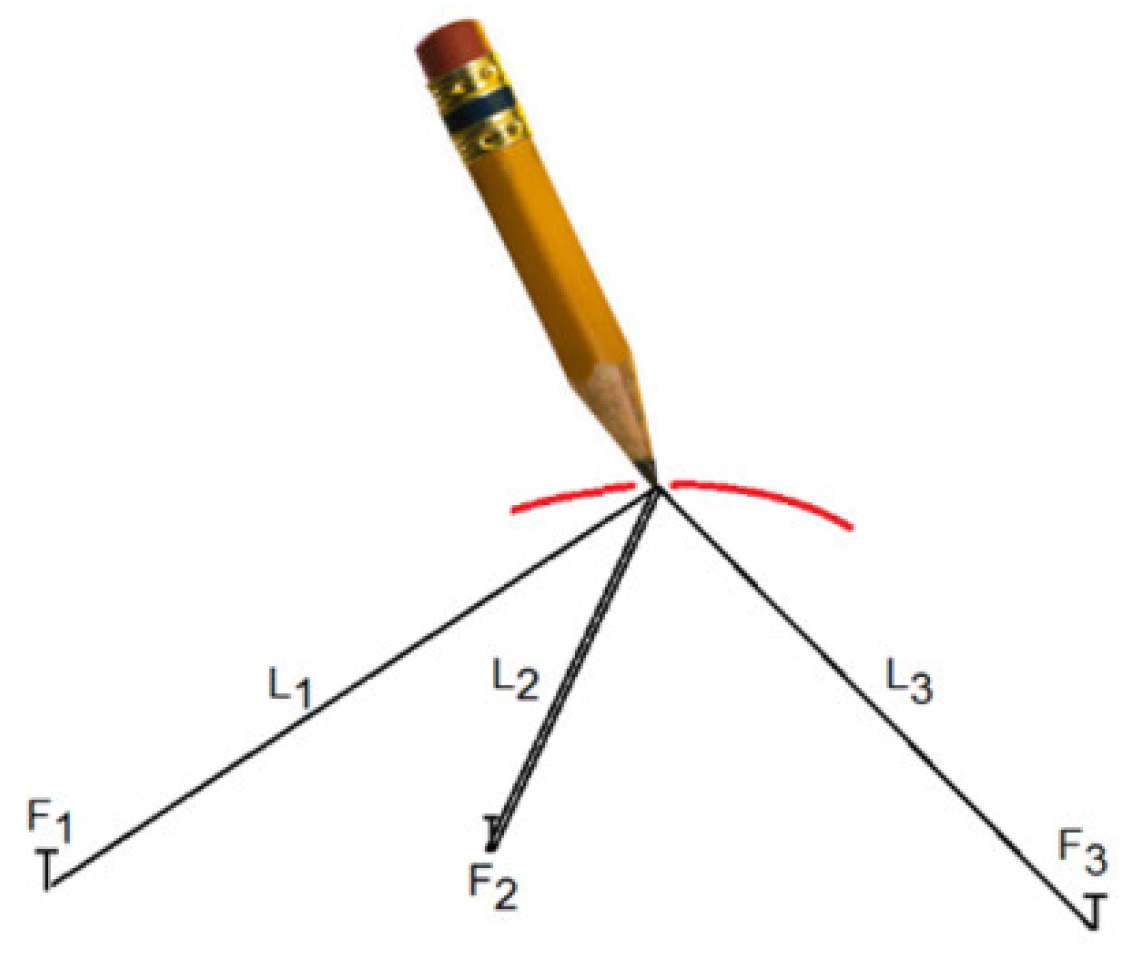
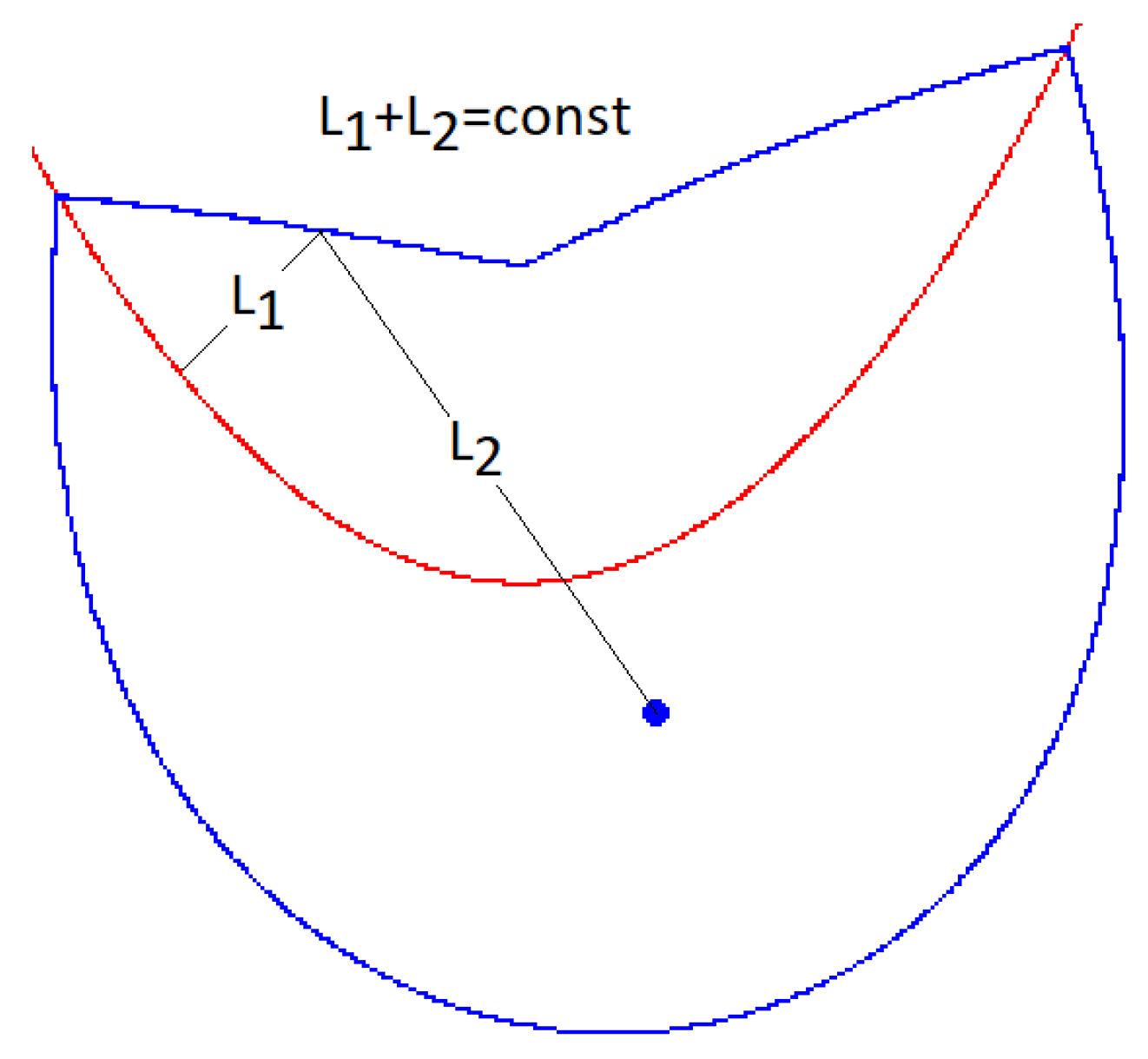
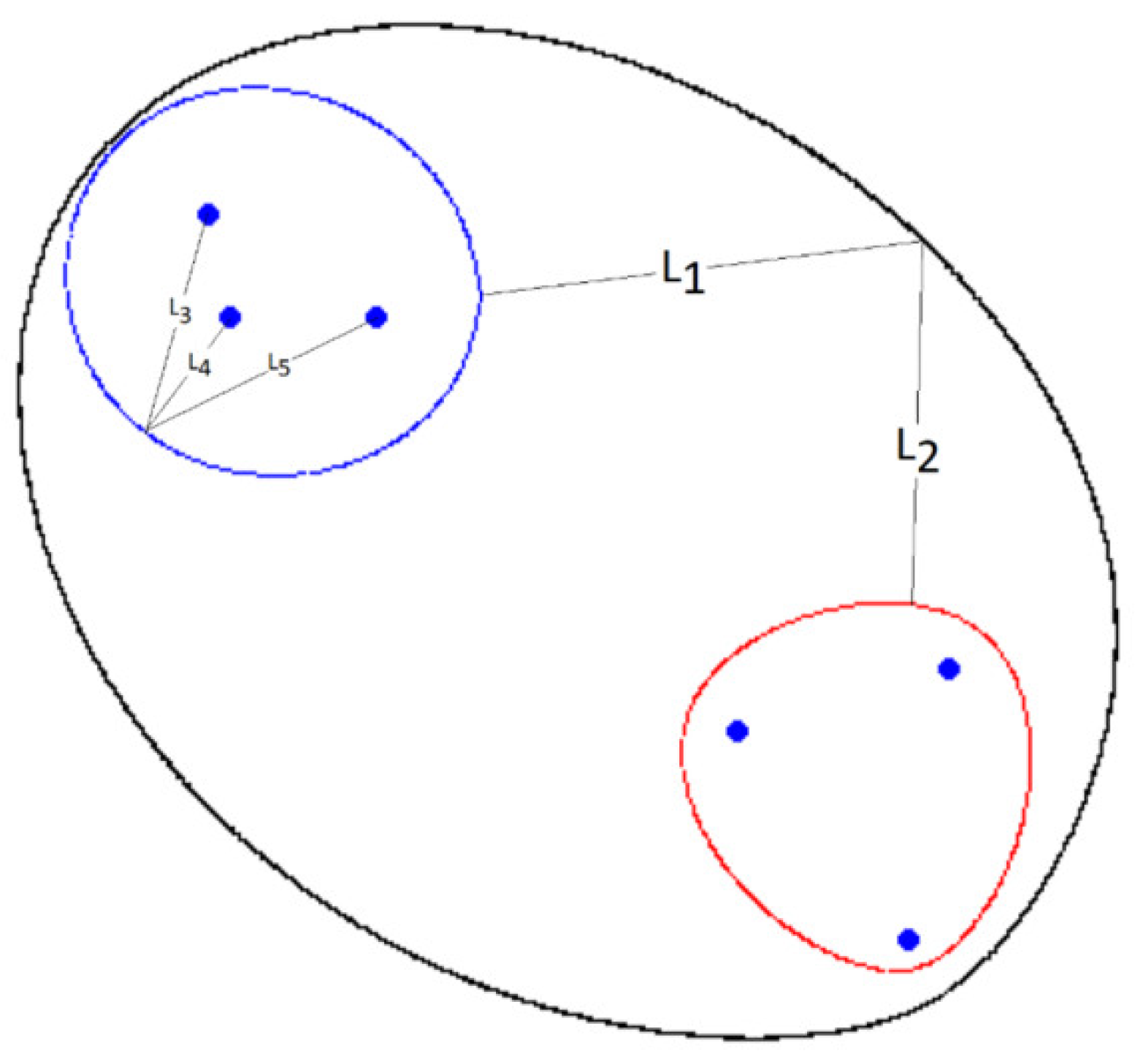
Figure 1.
Drawing a three-foci ellipse, L1 + 2L2 + L3 = const.
Figure 1.
Drawing a three-foci ellipse, L1 + 2L2 + L3 = const.
Figure 2.
Sketch of a porcelain plate with two blue three-foci ellipses of Tschirnhaus.
Figure 2.
Sketch of a porcelain plate with two blue three-foci ellipses of Tschirnhaus.
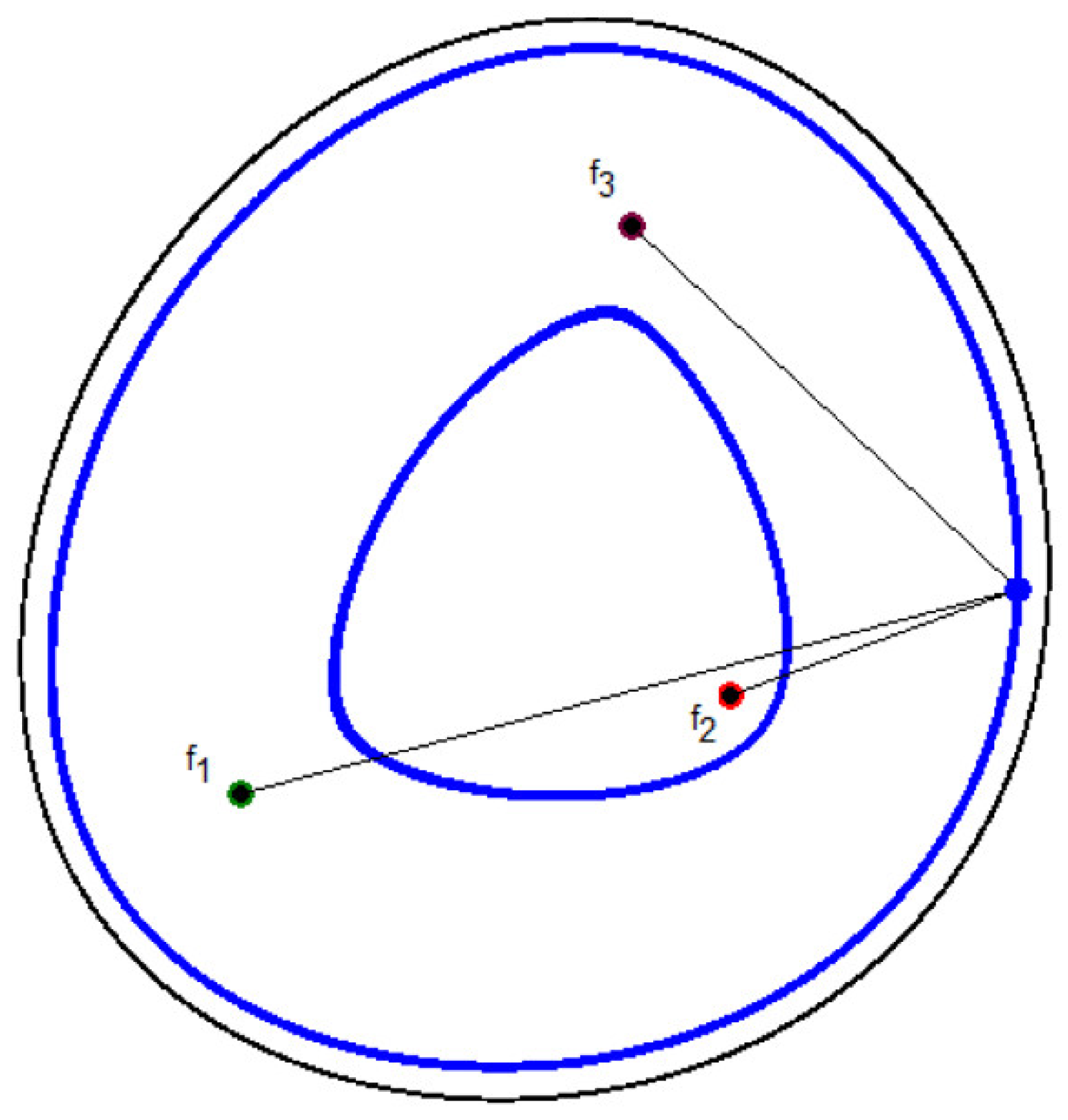
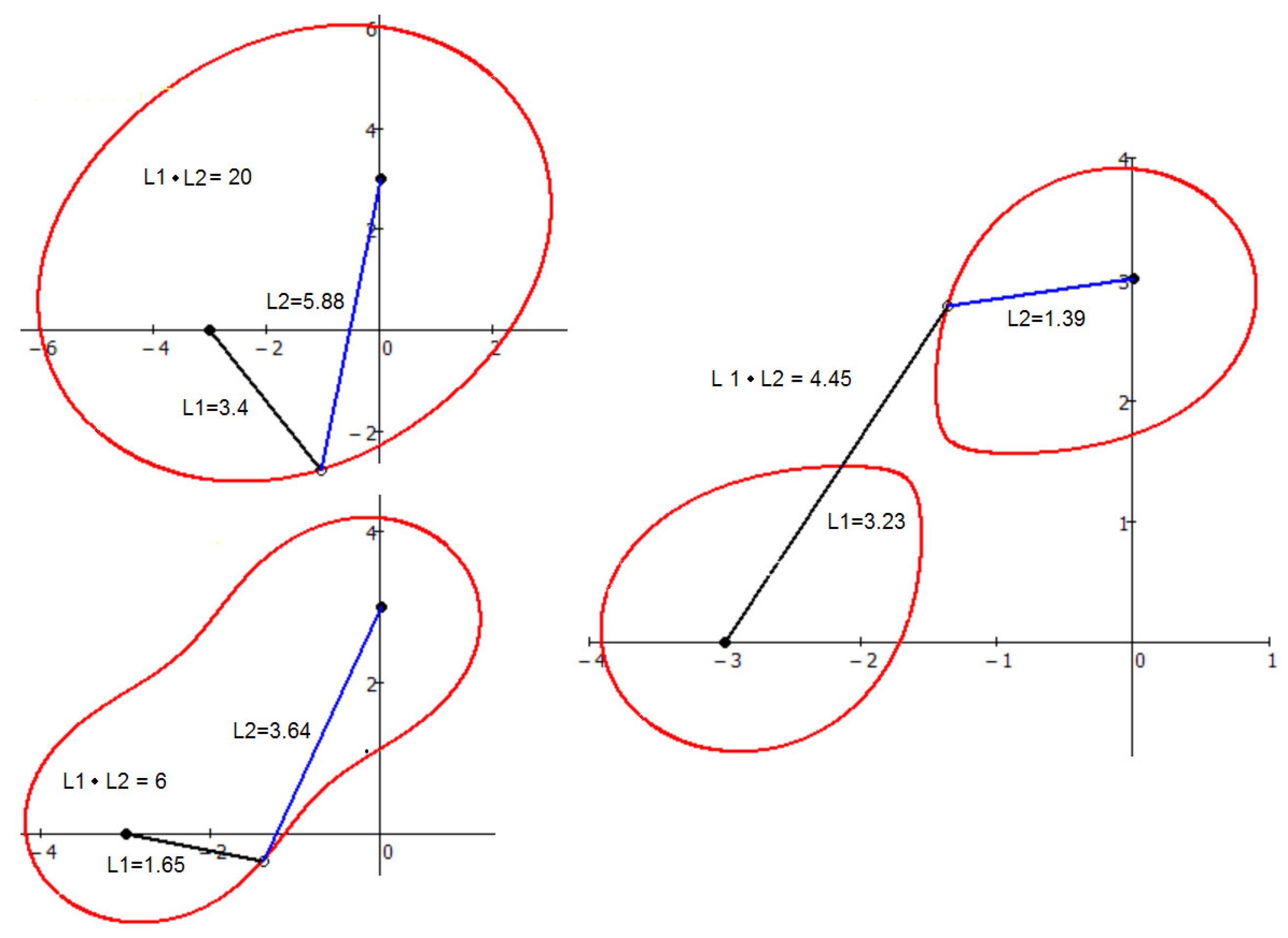
Figure 3.
New Three-foci ellipse Lc + Ls + Lt = 1.80 m.
Figure 3.
New Three-foci ellipse Lc + Ls + Lt = 1.80 m.
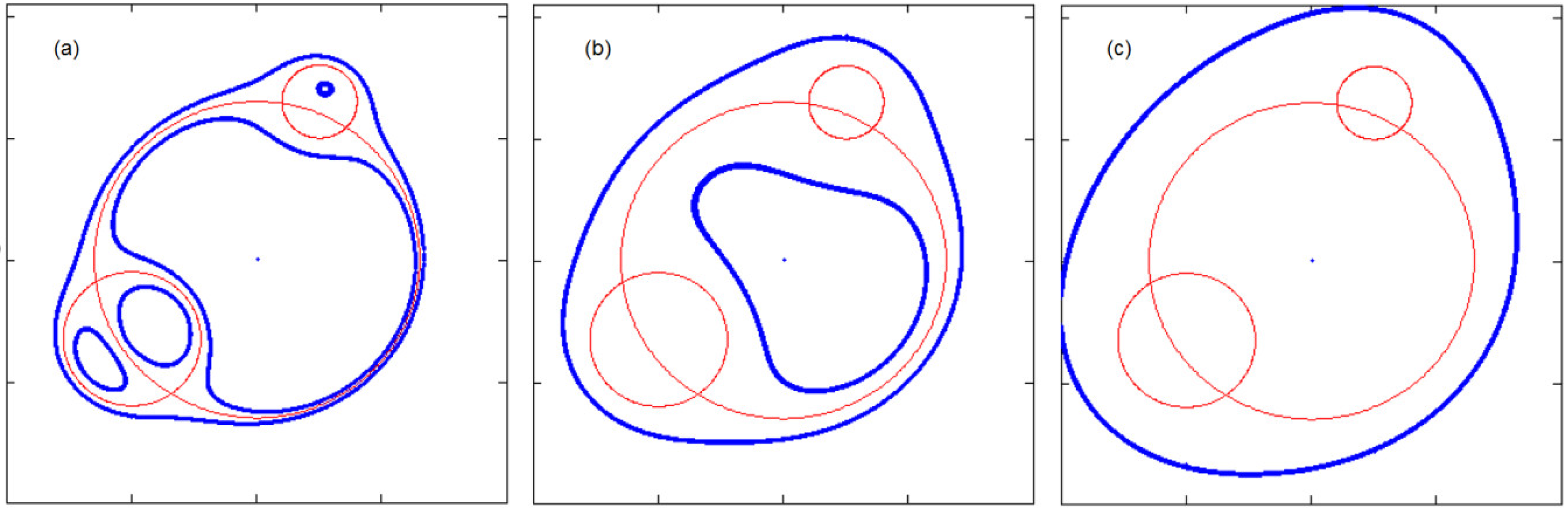
Figure 4.
Sketch of a porcelain plate with modified ellipses of Tschirnhaus (different blue ovals correspond to different values of the sum Lcircle1 + Lcircle2 + Lcircle3).
Figure 4.
Sketch of a porcelain plate with modified ellipses of Tschirnhaus (different blue ovals correspond to different values of the sum Lcircle1 + Lcircle2 + Lcircle3).
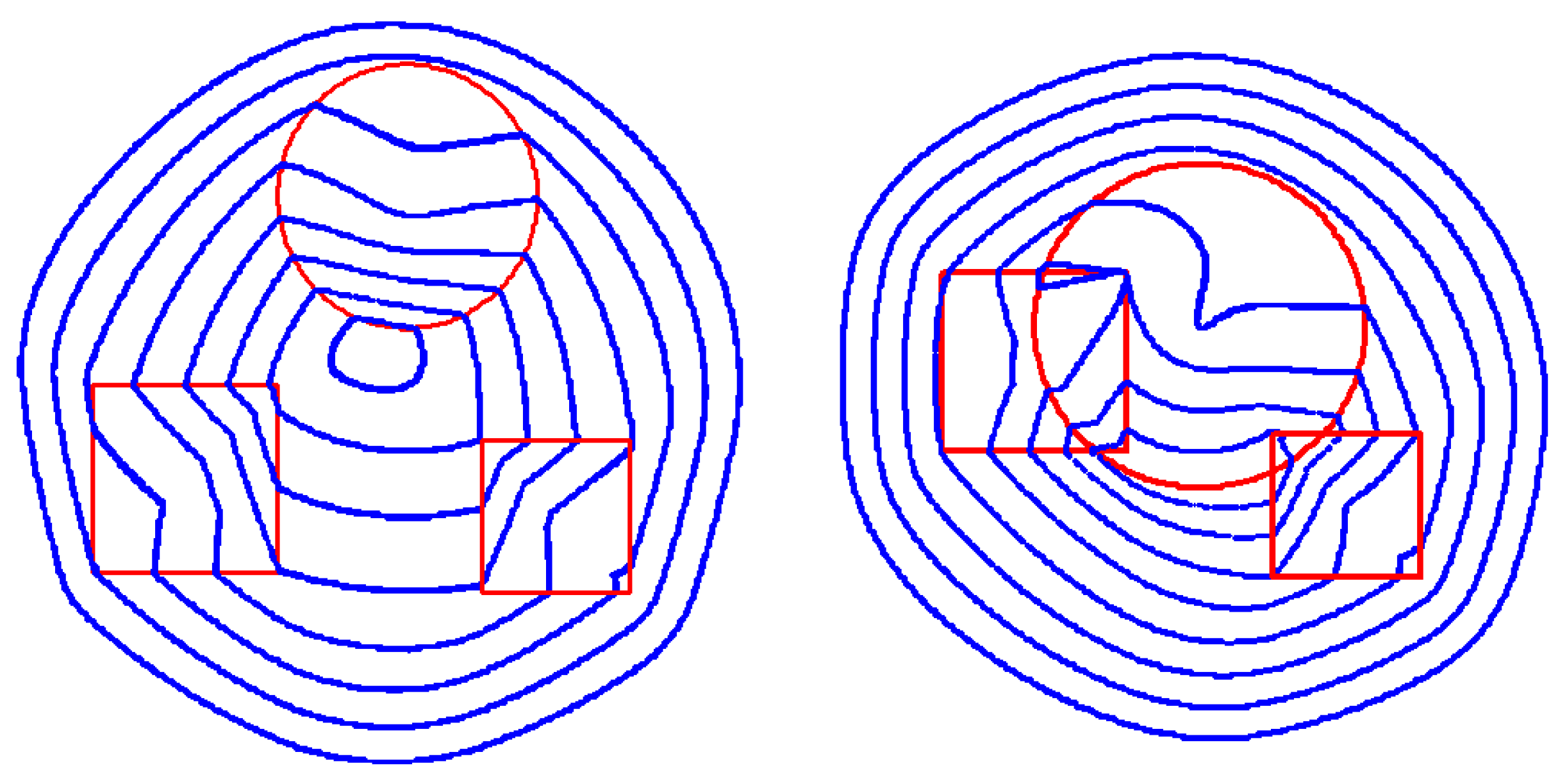
Figure 5.
Sketches of the drawing of two porcelain plates obtained with a circle and two squares as “foci” (different blue ovals correspond to different values of the sum Lcircle + Lsquate1 + L squate2).
Figure 5.
Sketches of the drawing of two porcelain plates obtained with a circle and two squares as “foci” (different blue ovals correspond to different values of the sum Lcircle + Lsquate1 + L squate2).
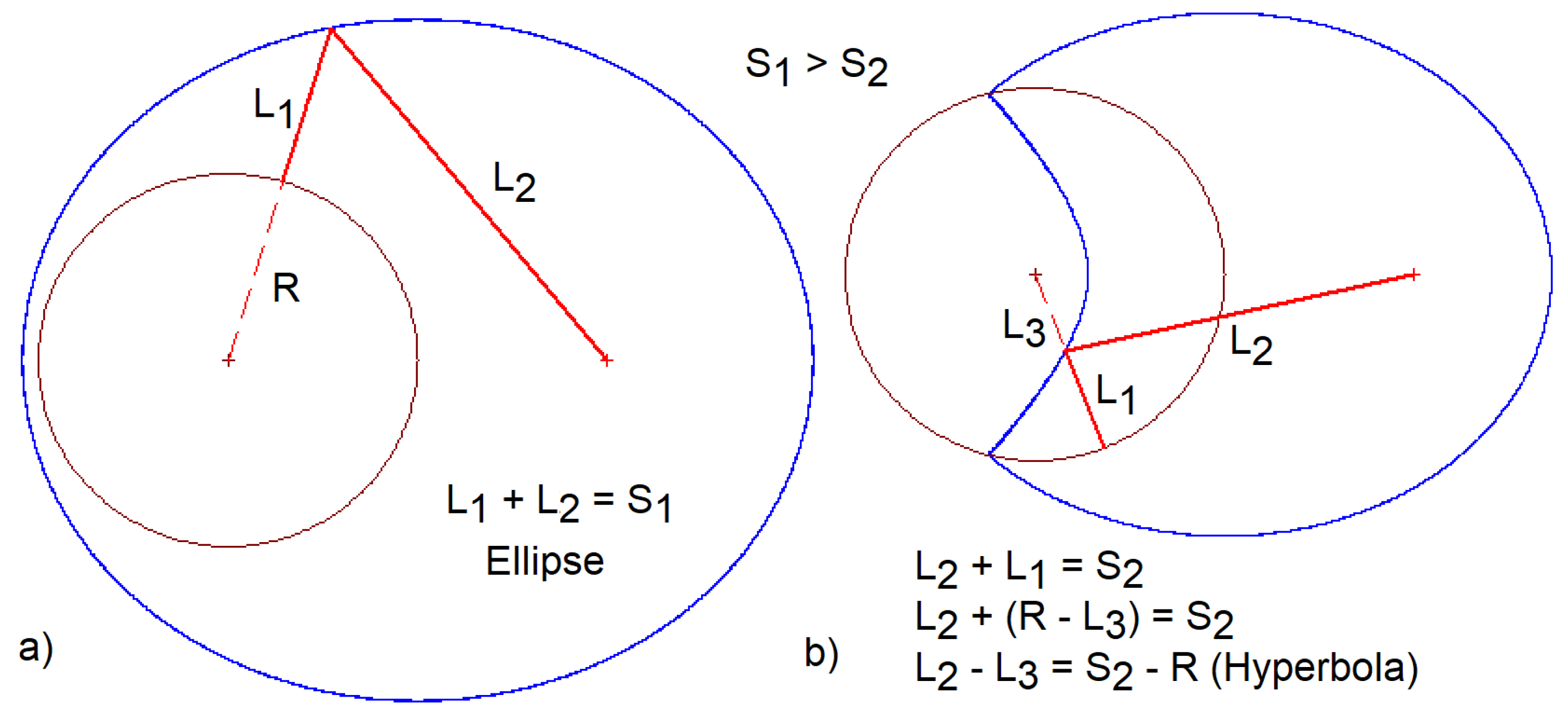
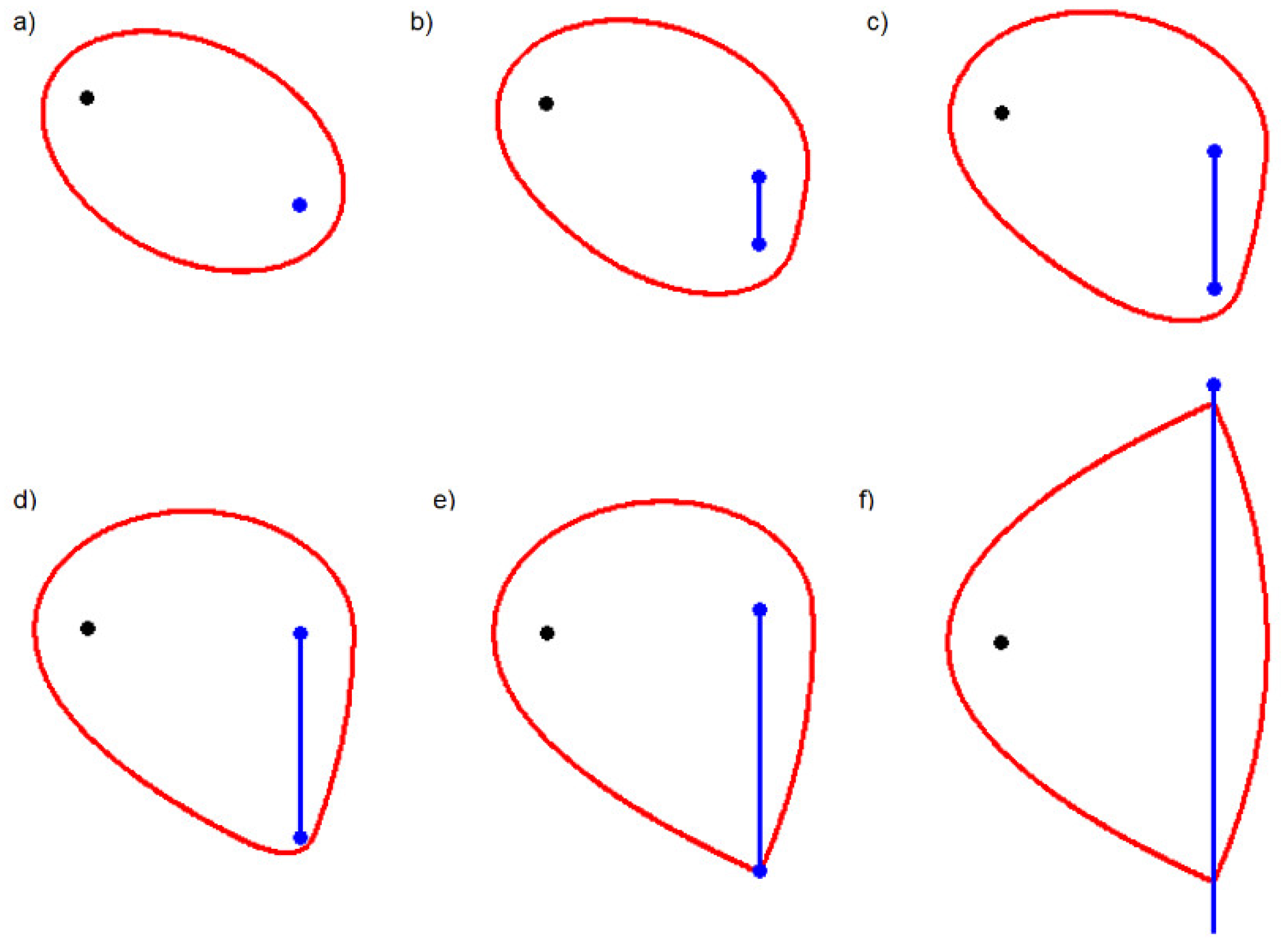
Figure 6.
An Ellipse (a - the blue oval) and an elliptic-hyperbolic oval (b - the blue oval); the brown circle is the second focus, the first focus is a point.
Figure 6.
An Ellipse (a - the blue oval) and an elliptic-hyperbolic oval (b - the blue oval); the brown circle is the second focus, the first focus is a point.
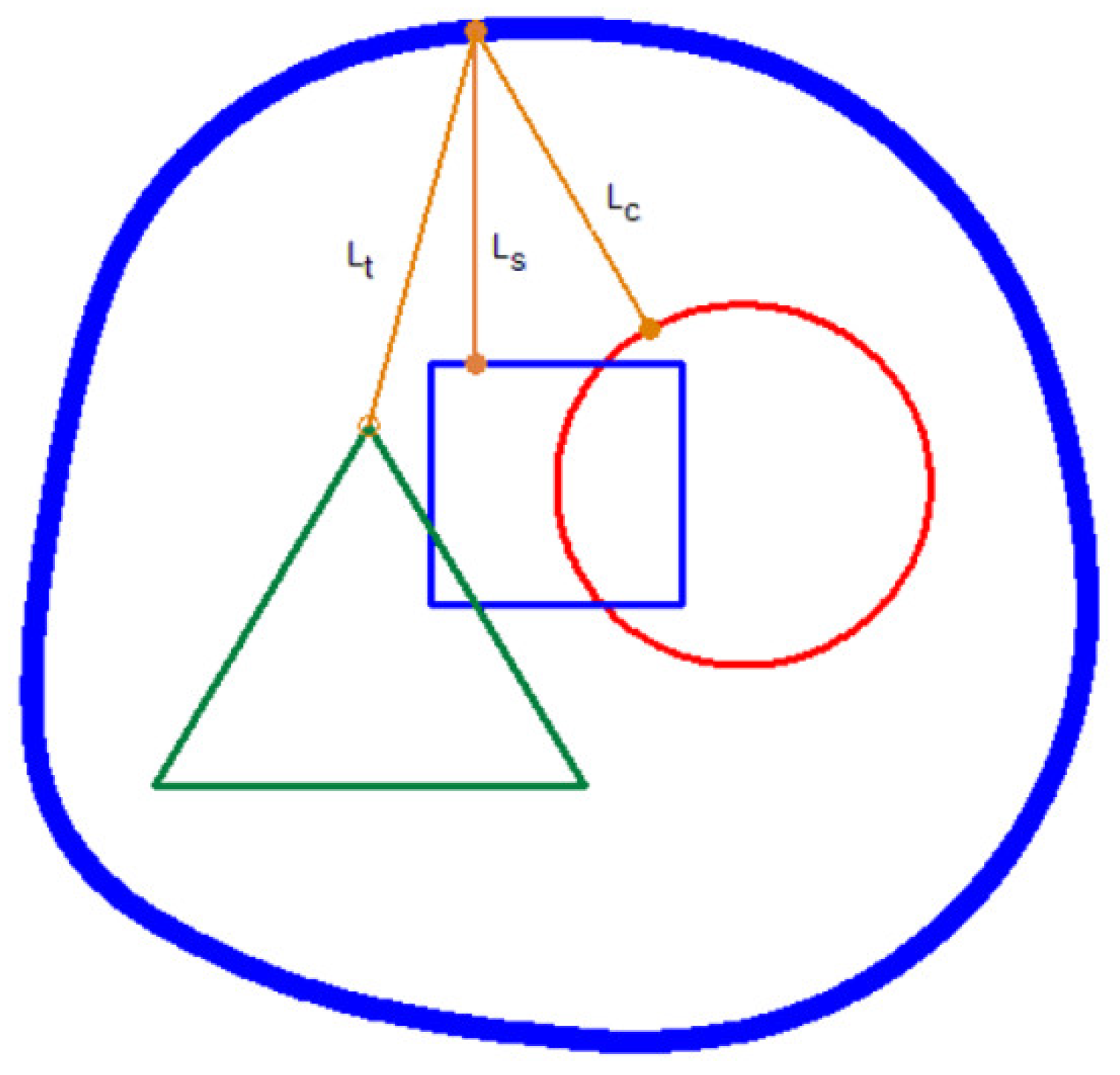
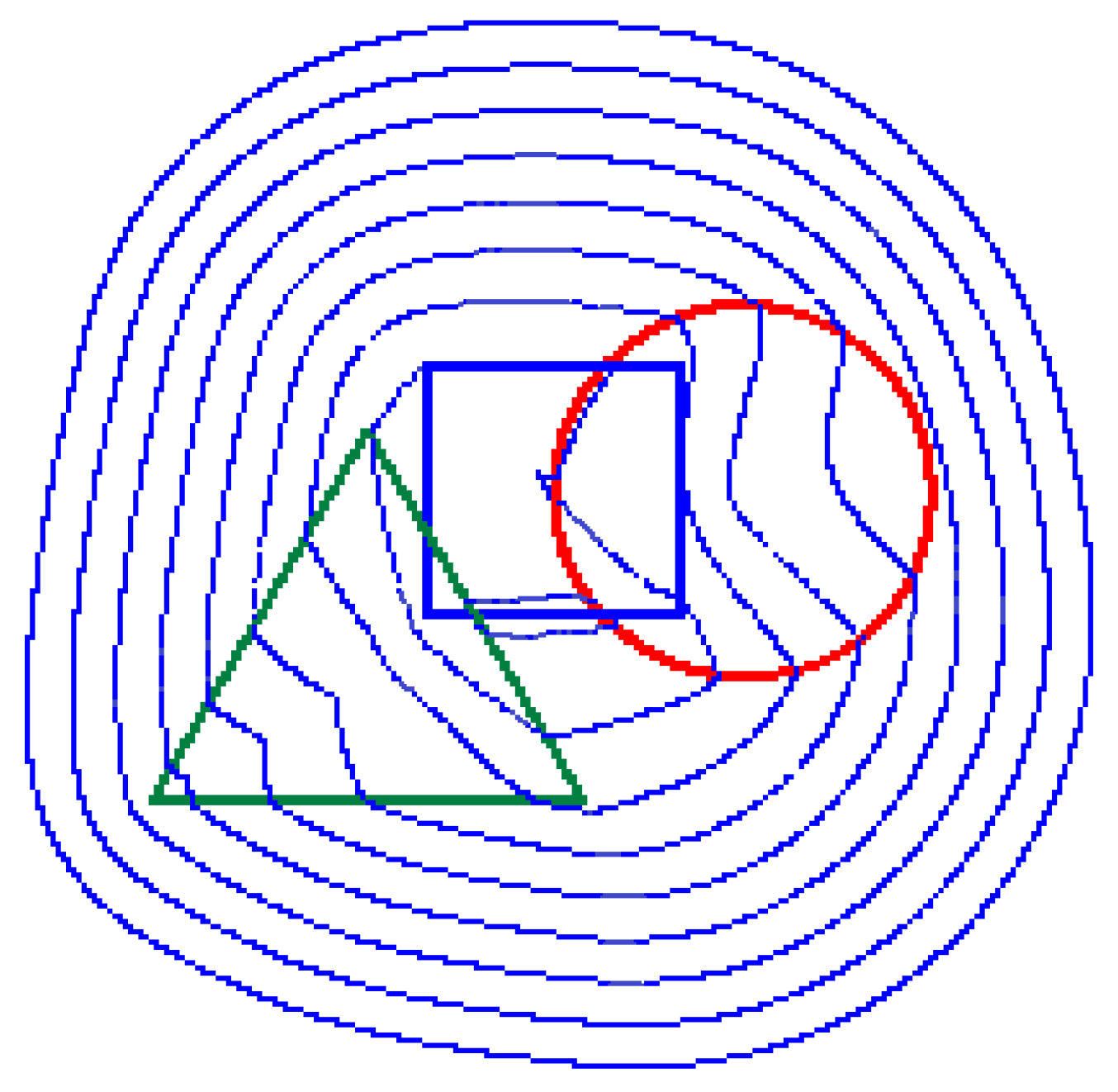
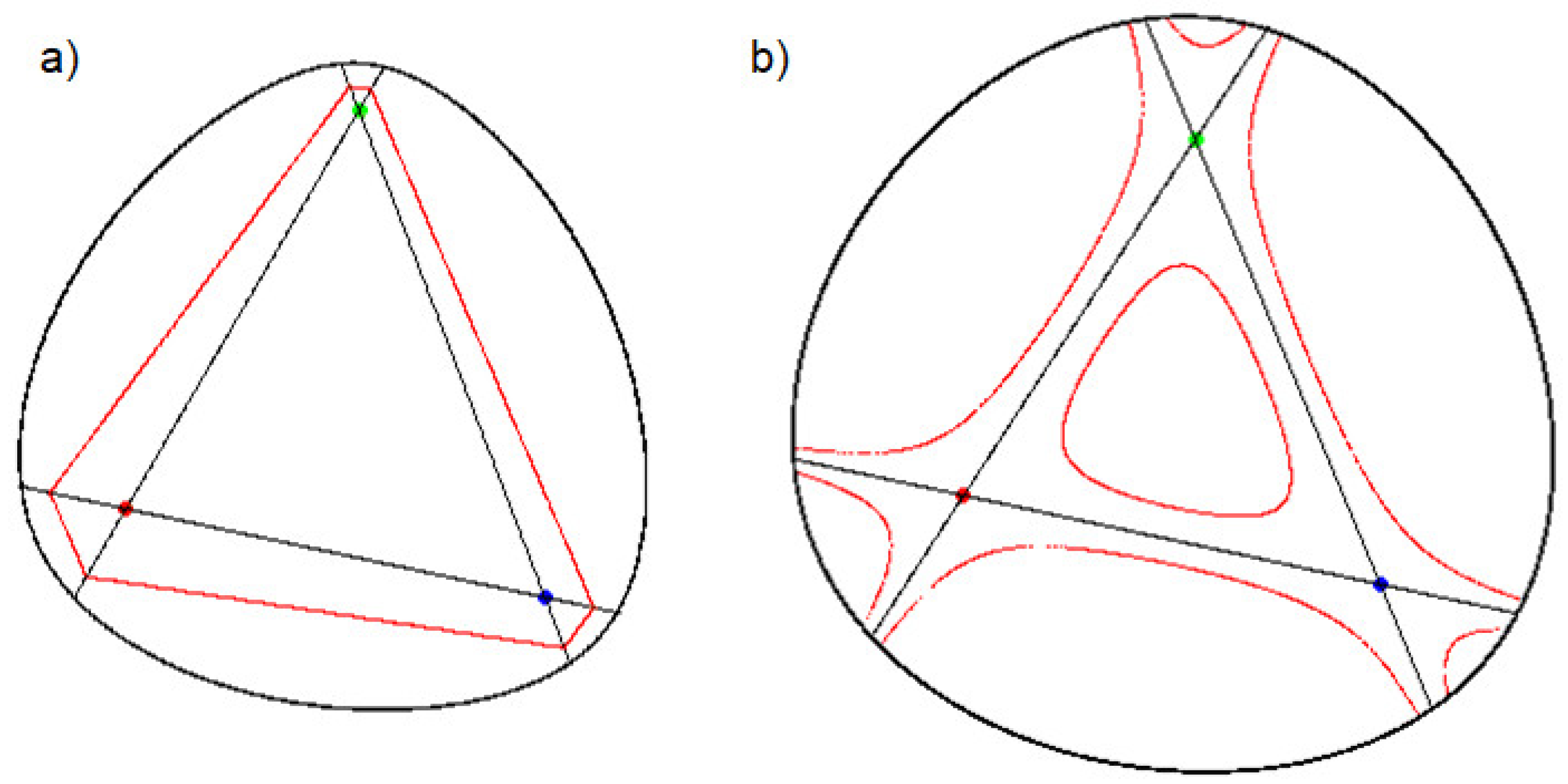
Figure 7.
Another sketch of a Tschirnhaus plate; the green triangle is a first focus, the dark blue square is the second focus, the red circle is a third focus; blue ovals have different sum Lc + Ls + Lt.
Figure 7.
Another sketch of a Tschirnhaus plate; the green triangle is a first focus, the dark blue square is the second focus, the red circle is a third focus; blue ovals have different sum Lc + Ls + Lt.
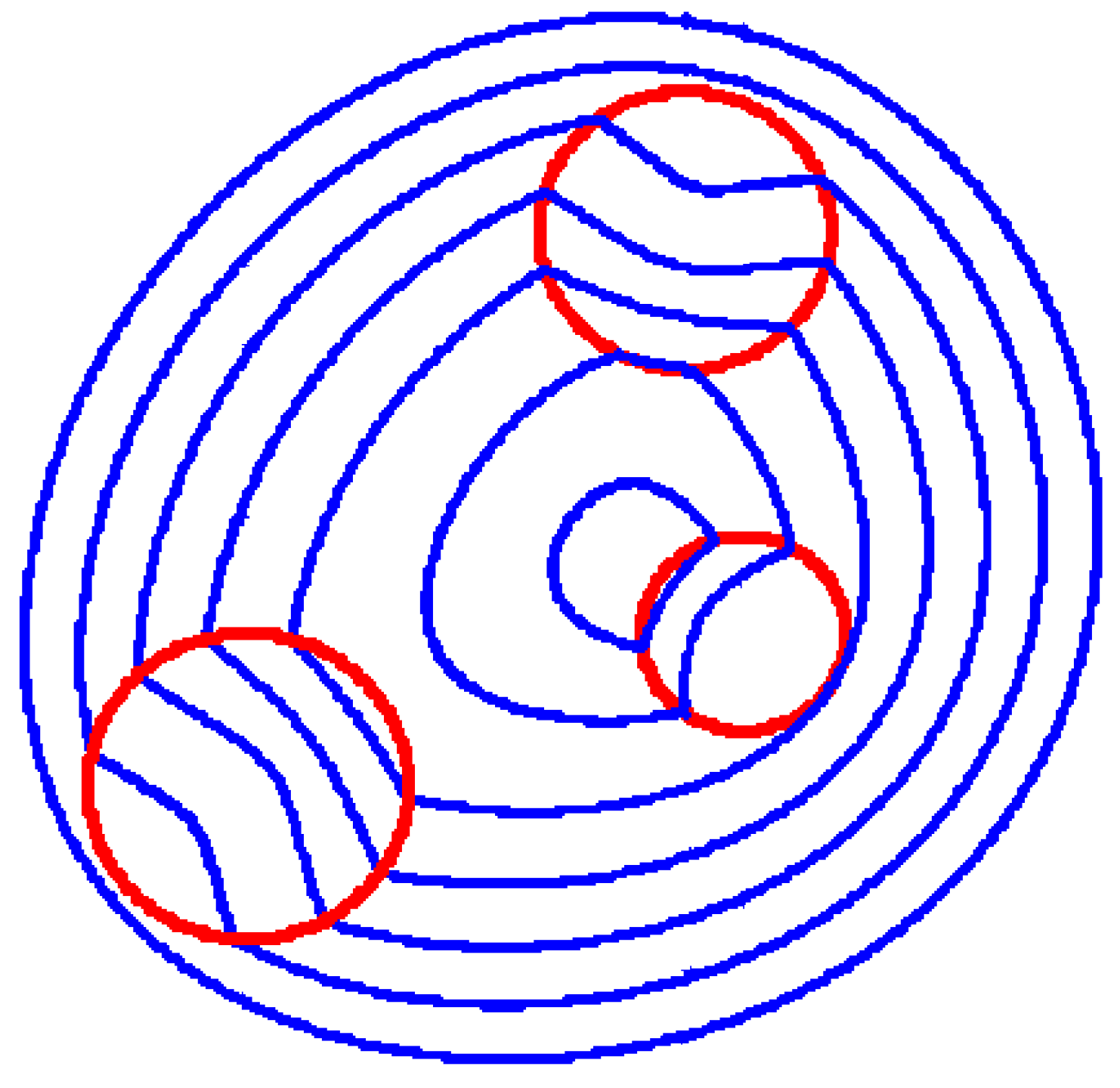
Figure 8.
Frames of the drawing animation on a Tschirnhaus plate at (Lc + Ls + Lt = S): (a) S = 1.920 m; (b) S = 1.360 m; (c) S = 0.910 m; (d) S = 0.620 m; (e) S = 0.330 m (the green triangle is a first focus, the blue square is the second focus and the red circle is a third focus).
Figure 8.
Frames of the drawing animation on a Tschirnhaus plate at (Lc + Ls + Lt = S): (a) S = 1.920 m; (b) S = 1.360 m; (c) S = 0.910 m; (d) S = 0.620 m; (e) S = 0.330 m (the green triangle is a first focus, the blue square is the second focus and the red circle is a third focus).
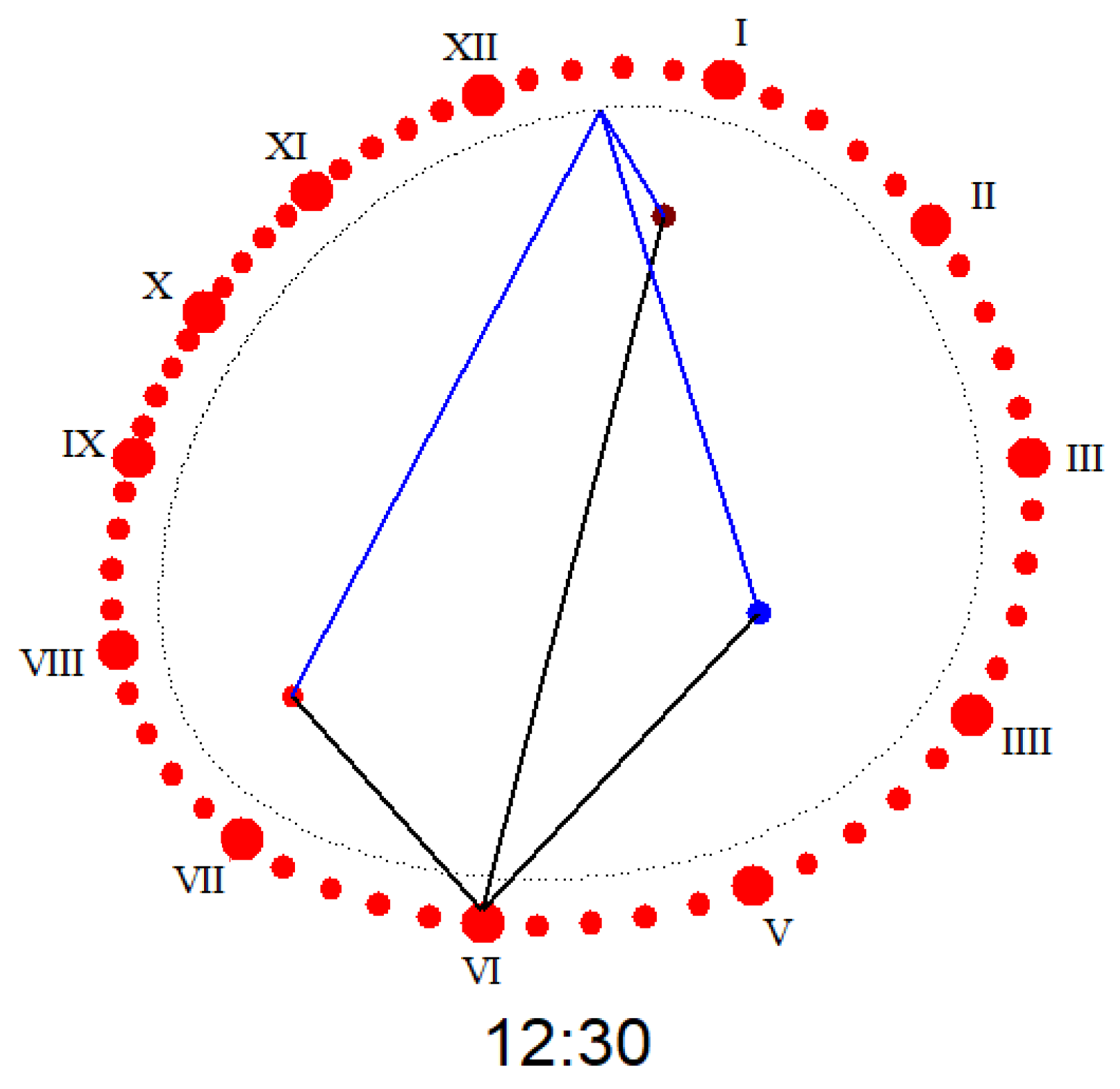
Figure 9.
Watch with an elliptical three-focal dial (blue lines are the hours hand and black lines are for the minutes hand).
Figure 9.
Watch with an elliptical three-focal dial (blue lines are the hours hand and black lines are for the minutes hand).
Figure 10.
Profile of the vase in the form of a parabola (red curve), a directrix (bottom black straight line), a focus (top ball), and a vertical bar connecting all parts.
Figure 10.
Profile of the vase in the form of a parabola (red curve), a directrix (bottom black straight line), a focus (top ball), and a vertical bar connecting all parts.
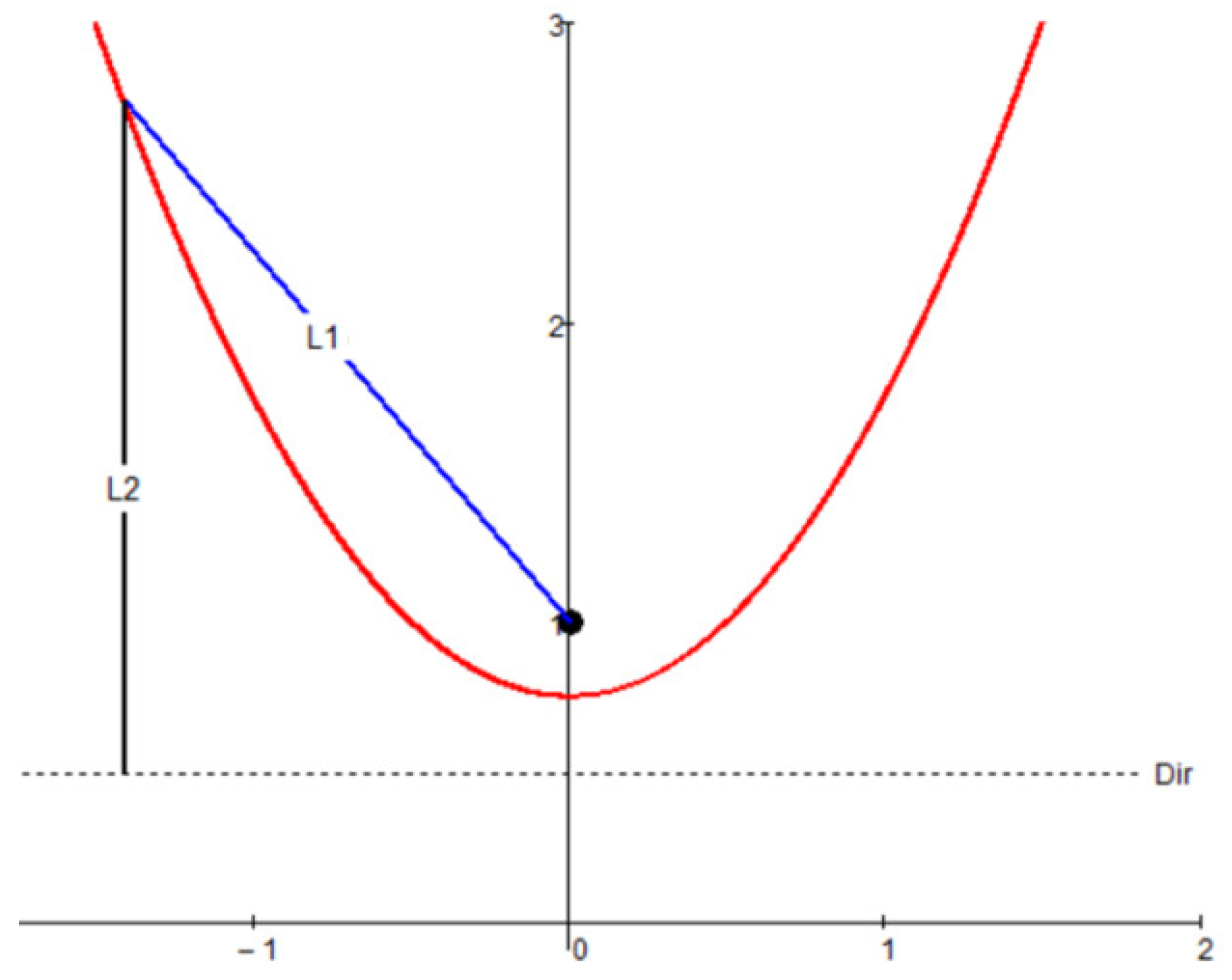
Figure 11.
Parabola with a focus and a directrix (Dir) L1 = L2 = 2.235 (the red line is the parabola, the black point is the focus and the dashed line is the directory).
Figure 11.
Parabola with a focus and a directrix (Dir) L1 = L2 = 2.235 (the red line is the parabola, the black point is the focus and the dashed line is the directory).
Figure 12.
Frames of the animation of the parabola with a circular focus (the red lines are the parabolas, the black circles are the foci and the blue lines are the directories).
Figure 12.
Frames of the animation of the parabola with a circular focus (the red lines are the parabolas, the black circles are the foci and the blue lines are the directories).
Figure 13.
Profile of a vase for flowers made in the form of a single-sheeted hyperboloid.
Figure 13.
Profile of a vase for flowers made in the form of a single-sheeted hyperboloid.
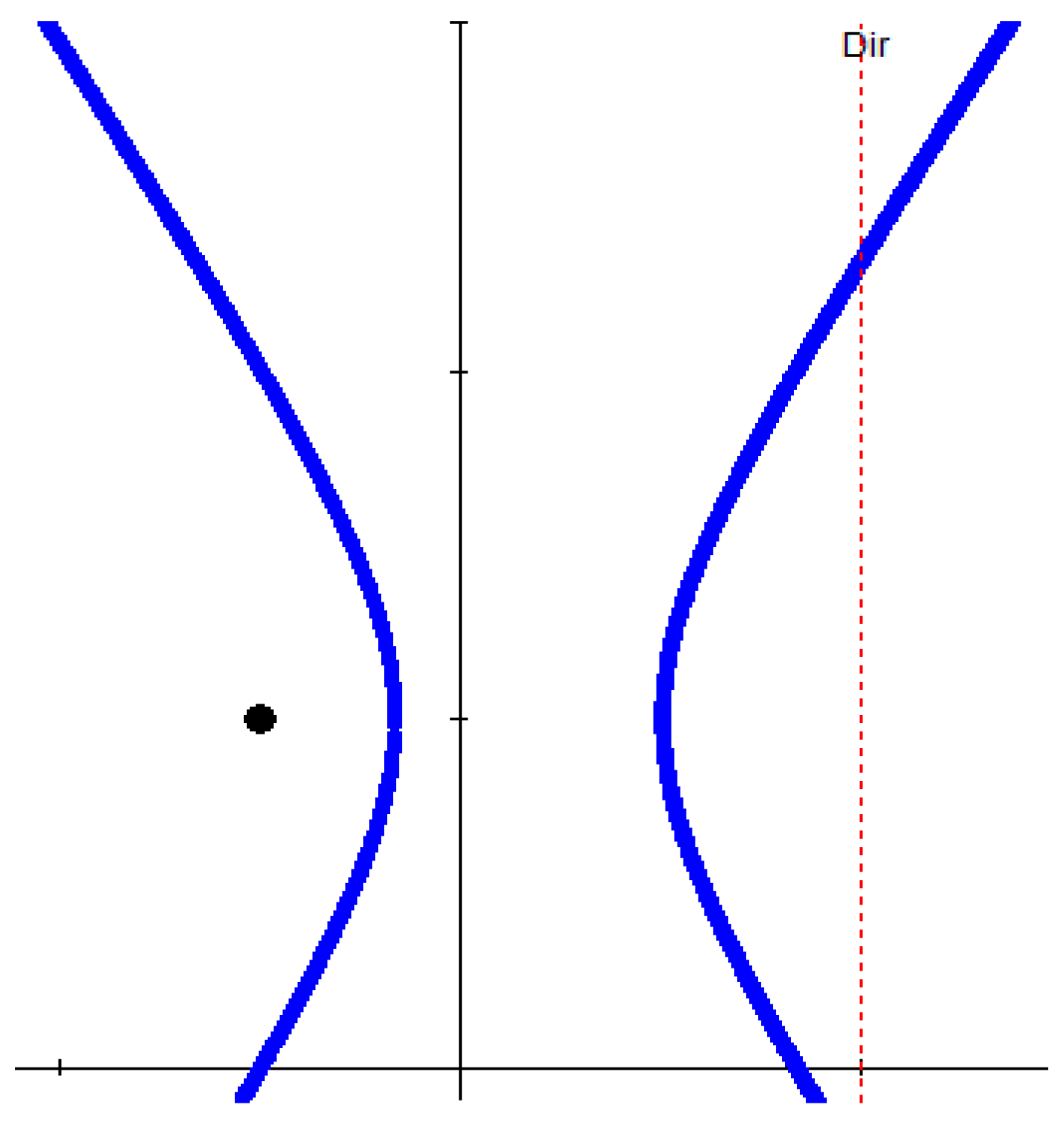
Figure 14.
Hyperbola with two circular foci |L1 −L2| = a, a = 1.7 m, r = 0.5 m, r1 = 0.7 m (the red circles are the foci, the blue curves is two blanch of the hyperbola).
Figure 14.
Hyperbola with two circular foci |L1 −L2| = a, a = 1.7 m, r = 0.5 m, r1 = 0.7 m (the red circles are the foci, the blue curves is two blanch of the hyperbola).
Figure 15.
Hyperbola with two square foci |L1 − L2| = a, a = 0.940 m (the red squares are the foci, the blue curves is two blanch of the hyperbola).
Figure 15.
Hyperbola with two square foci |L1 − L2| = a, a = 0.940 m (the red squares are the foci, the blue curves is two blanch of the hyperbola).
Figure 16.
Ovals of Cassini (red ovals).
Figure 16.
Ovals of Cassini (red ovals).
Figure 17.
Three frames of animation of the three-foci (L1·L2·L3 = a) blue Cassini oval with red circles in the role of foci: (a) a = 0.073 m3; (b) a = 0.317 m3; (c) a = 1.003 m3.
Figure 17.
Three frames of animation of the three-foci (L1·L2·L3 = a) blue Cassini oval with red circles in the role of foci: (a) a = 0.073 m3; (b) a = 0.317 m3; (c) a = 1.003 m3.
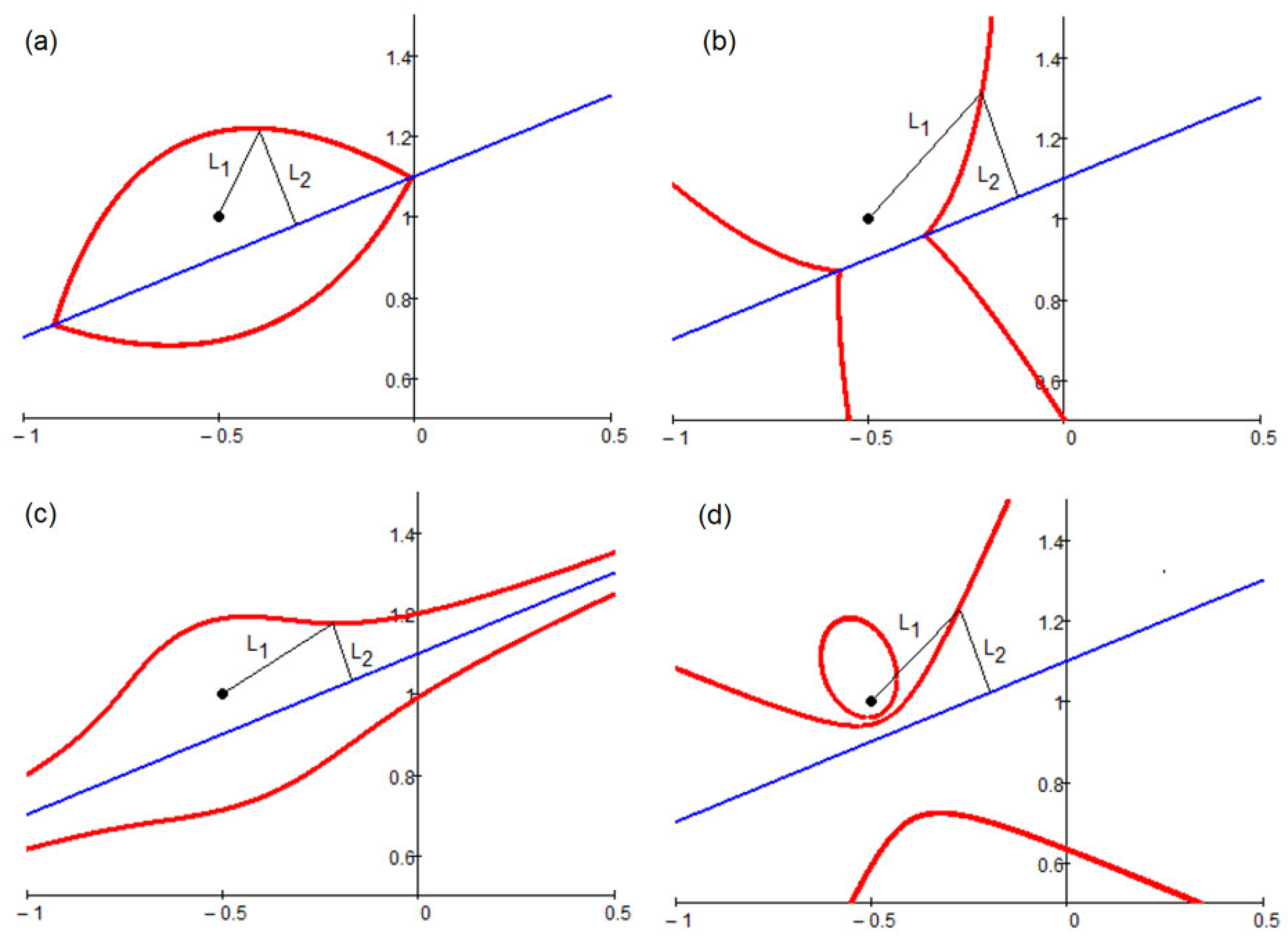
Figure 18.
Extended ellipse, hyperbola, Cassini oval and Apollonius circle (red ovals and curves): (a) L1 + L2 = s, s = 0.5 m; (b) |L1 + L2| = s, s = 0.15 m; (c) L1·L2 = s, s = 0.05 m2; (d) L1/L2 = s or L2/L1 = s s = 0.7 (blue lines are the first focus and the black points are the second focus).
Figure 18.
Extended ellipse, hyperbola, Cassini oval and Apollonius circle (red ovals and curves): (a) L1 + L2 = s, s = 0.5 m; (b) |L1 + L2| = s, s = 0.15 m; (c) L1·L2 = s, s = 0.05 m2; (d) L1/L2 = s or L2/L1 = s s = 0.7 (blue lines are the first focus and the black points are the second focus).
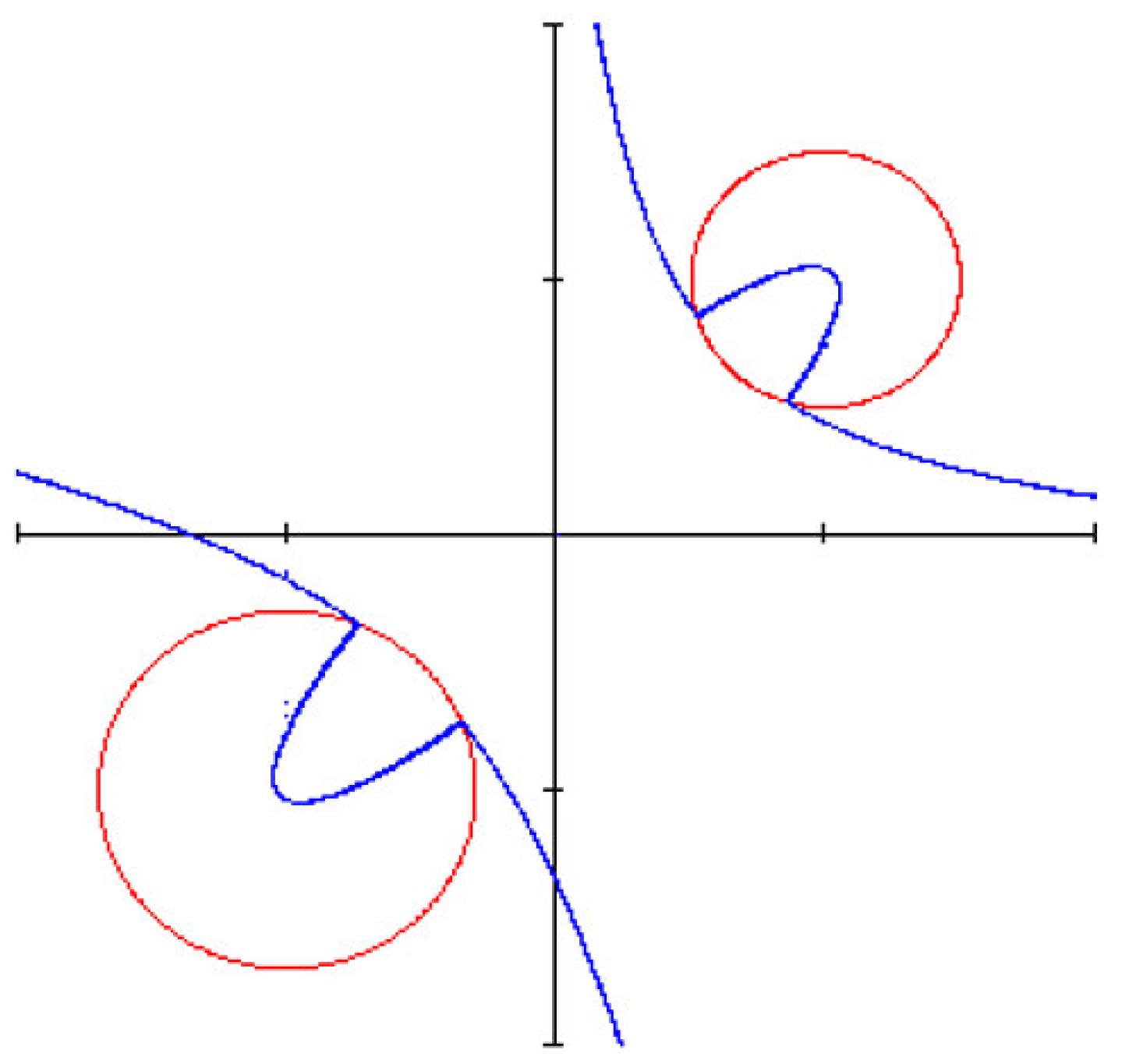
Figure 19.
An ellipse with two foci given by a point and a parabola.
Figure 19.
An ellipse with two foci given by a point and a parabola.
Figure 20.
An ellipse with a focus changing from a point to a line segment.
Figure 20.
An ellipse with a focus changing from a point to a line segment.
Figure 21.
Sketches of the Tschirnhaus plates with a: (a) Constant sum or (b) product of distances from a point to three straight lines.
Figure 21.
Sketches of the Tschirnhaus plates with a: (a) Constant sum or (b) product of distances from a point to three straight lines.
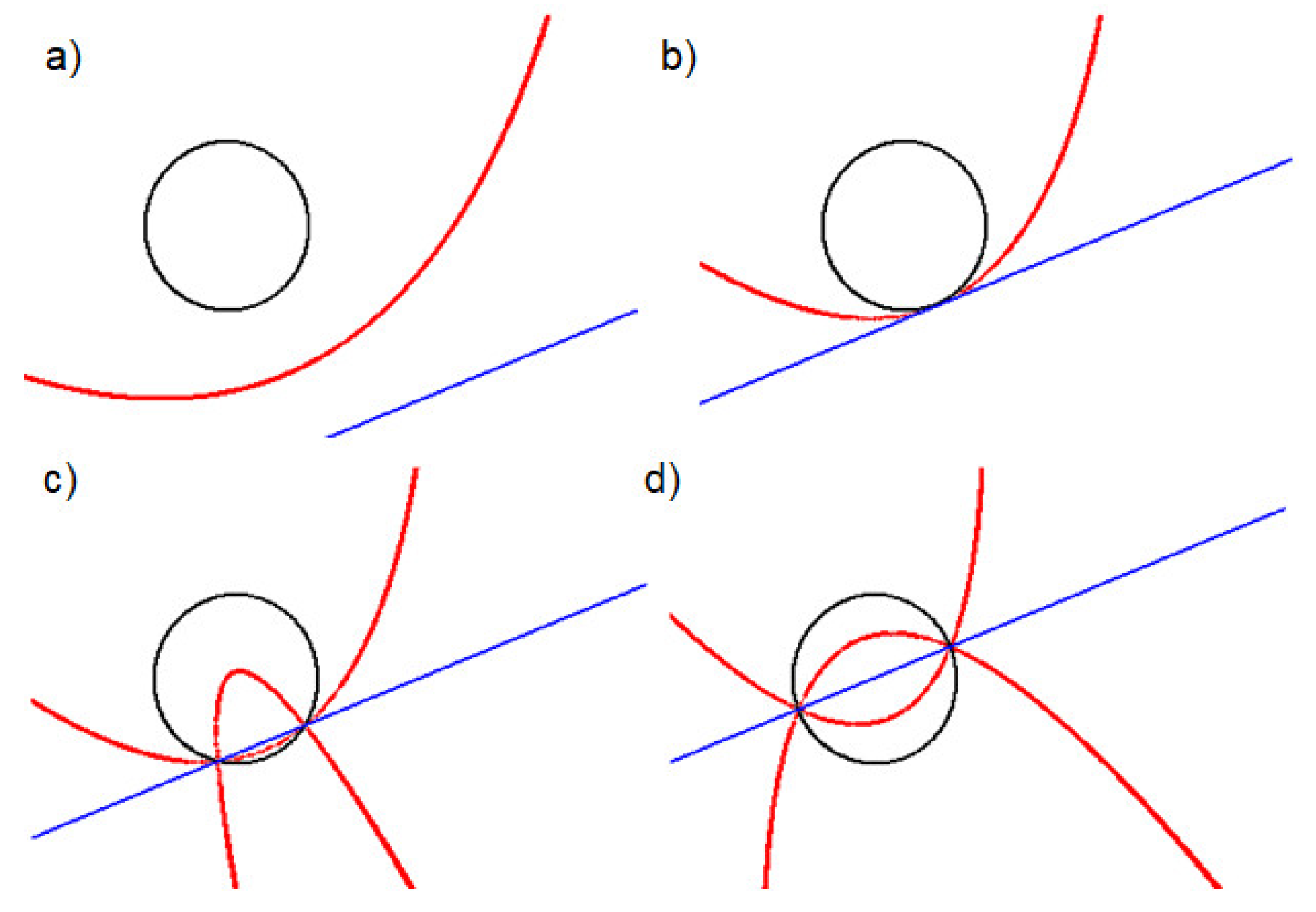
Figure 22.
Curves of different orders: (a) 2; (b) 3; (c) 4; (d) 5; (e) 6; (f) 7; (h) 13; (i) 16; (j) 17.
Figure 22.
Curves of different orders: (a) 2; (b) 3; (c) 4; (d) 5; (e) 6; (f) 7; (h) 13; (i) 16; (j) 17.
Figure 23.
Scanning a flat area for drawing a Tschirnhaus three-foci ellipse.
Figure 23.
Scanning a flat area for drawing a Tschirnhaus three-foci ellipse.
Figure 24.
A Mathcad function that returns the coordinates of a point on the circumference of a circle with radius r and centre at the point (xc, yc) closest to a given point with the coordinates (x, y).
Figure 24.
A Mathcad function that returns the coordinates of a point on the circumference of a circle with radius r and centre at the point (xc, yc) closest to a given point with the coordinates (x, y).
Figure 25.
A Mathcad function that returns the coordinates of a point on the contour of a square with a “radius” r (half the length of the side of the square) and centred at the point (xs, ys) closest to the given point with the coordinates (x, y).
Figure 25.
A Mathcad function that returns the coordinates of a point on the contour of a square with a “radius” r (half the length of the side of the square) and centred at the point (xs, ys) closest to the given point with the coordinates (x, y).
Figure 26.
A Mathcad function that returns the coordinates of a point on the contour of an equilateral triangle with a “radius” r (the distance from the center of the triangle to its vertex) and centered at the point (xt, yt) closest to the given point with coordinates (x, y).
Figure 26.
A Mathcad function that returns the coordinates of a point on the contour of an equilateral triangle with a “radius” r (the distance from the center of the triangle to its vertex) and centered at the point (xt, yt) closest to the given point with coordinates (x, y).
Figure 27.
The procedure for forming the super-ellipse shown in
Figure 28.
Figure 27.
The procedure for forming the super-ellipse shown in
Figure 28.
Figure 28.
Super-ellipse with “elliptical” foci, L1 + L2 = const, L3 + L3 + L5 = const.
Figure 28.
Super-ellipse with “elliptical” foci, L1 + L2 = const, L3 + L3 + L5 = const.
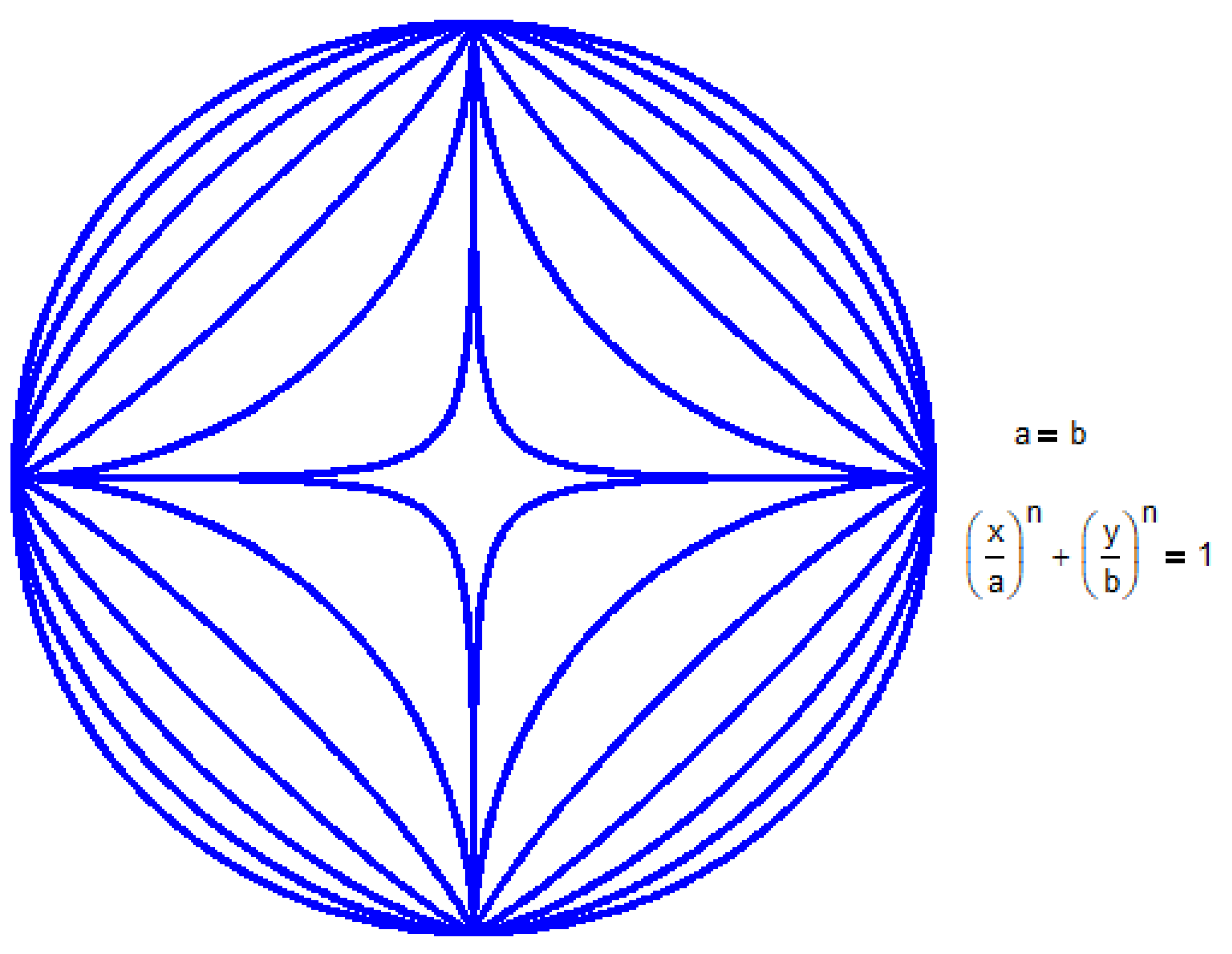
Figure 29.
Lame round plate.
Figure 29.
Lame round plate.
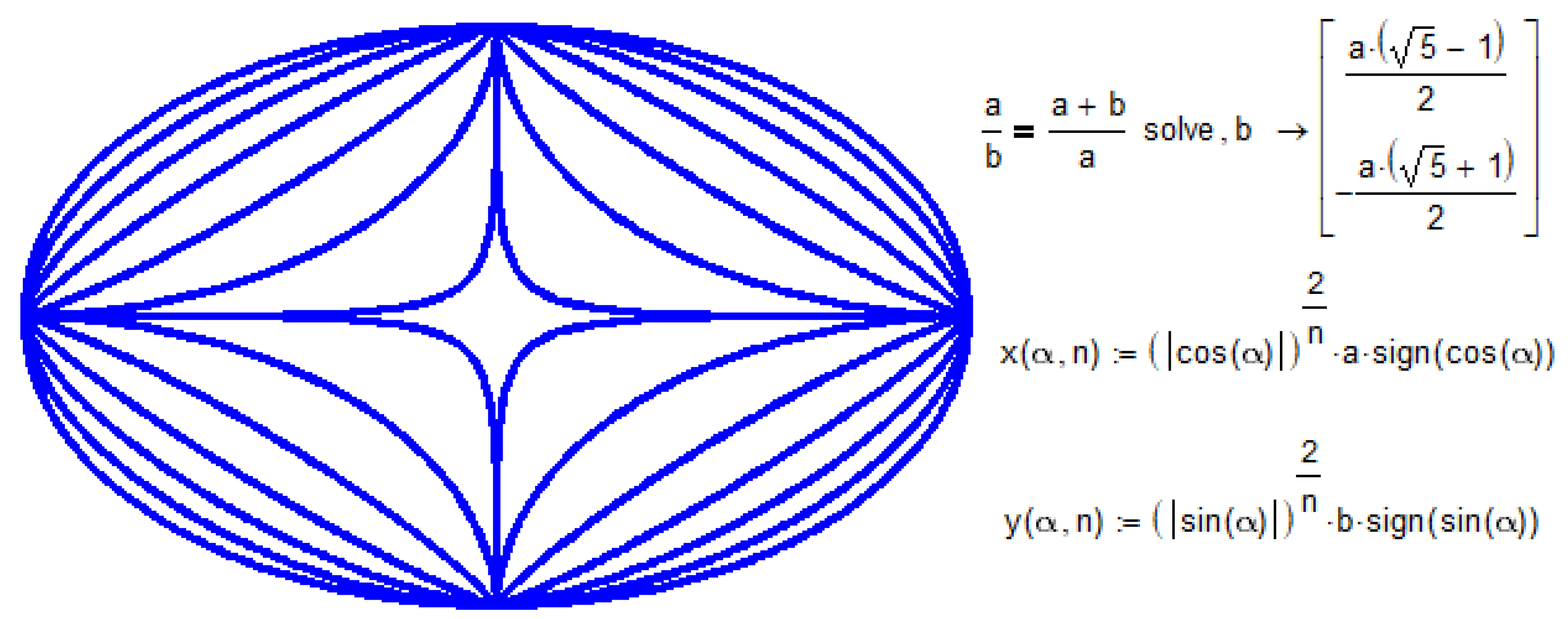
Figure 30.
Lame Oval plate with golden section proportion.
Figure 30.
Lame Oval plate with golden section proportion.