Optimal Control of Nonsmooth Production Systems with Deteriorating Items, Stock-Dependent Demand, with or without Backorders
Abstract
:1. Introduction
- System dependent parameters: Taking into account the effect of the system parameters on an inventory system can lead to an improvement of its performance. The dependence of the demand rate on the stock is, without doubt, the dependence that received the most attention, and the literature on this topic is abundant. Among the most recent references we cite [9,10,11,12,13].
- Items backorders: In many real-life situations, demand is not met on time and shortages occur, the condition that exists when the inventory on hand is not sufficient to cover needs. Shortages are undesirable because they are quite expensive. However, in certain situations, management may find it desirable from a cost point of view not only to allow shortages but to plan for them. This specific shortage is called a backorder. After the exhaustion of inventory, we allow a period of time over which backorders accumulate to some level. When allowing backorders, we have, in addition to the usual costs, the additional cost of backordering. For more works on item backorders, we refer the reader to [18,20,21].
2. Model without Backorders
- Case 1:
- on some subset S of . This means that the firm has to produce the exact total amount corresponding to the amount consumed plus the amount lost due to deterioration. In this case on S and is obviously constant on S andTo get an explicit form of and , we integrated the previous differential equation. Then, we used Equation (9) to derive an explicit form of the Lagrange multiplier function . We pointed out that if the obtained function was not nonnegative, then we did not accept the solutions stated in Equation (10).
- Case 2:
- for . The firm should produce more than the total amount corresponding to the amount consumed plus the amount lost due to deterioration, in order to avoid a shortage situation. In this case, on , and so the necessary conditions in Equations (3), (8) and (9) becomeandCombining the state equation with these equations yields the following second order differential equation:andThese equations are enough to determine the optimal solution of problem . To be able to push the derivations any further, one needs to have an explicit form for the functions involved. For illustration purposes, let us assume the following forms for the cost ratesand for the exogenous functionsHere K, h, , and are positive constants. For these functions the necessary conditions for to be an optimal solution of problem becomewithandThis is a two-point boundary value problem () that we solved in the next proposition.
- 1.
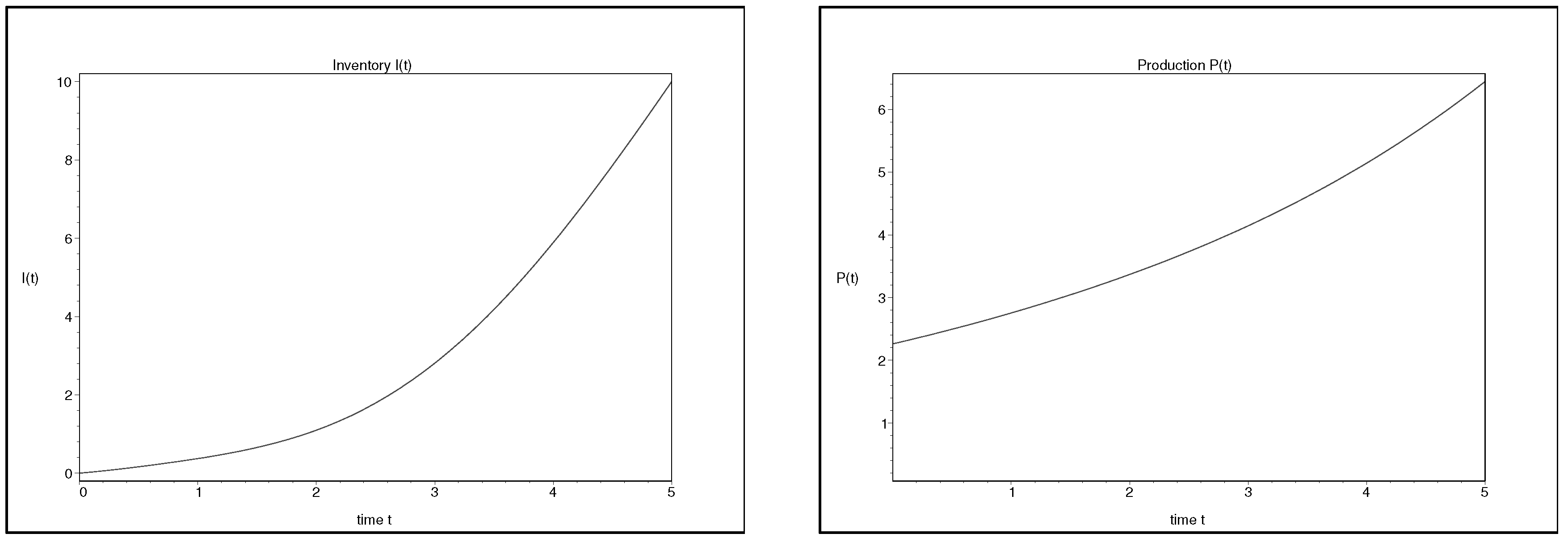
- We illustrated the results obtained by considering a production system with the following characteristics: planning horizon of length , initial and terminal inventory levels, , , unit costs and discount factor , and , respectively. The demand rate is such that and the deterioration rate is such that .The optimal control and state are displayed in Figure 1.The optimal objective function value is .
- 2.
- To assess the effect of the deterioration rate on the value of the optimal objective function, we set and varied the value of from to , and we kept all the other parameters as in Example (1). As shown by Table 1, the resulting optimal cost increases as increases.
- 3.
- Next, we studied the effect of the discount factor on the value of the optimal objective function, we set and varied the value of ρ from 0 to , and we keep all the other parameters as in Example (1). As shown by Table 2, the resulting optimal cost increases as ρ increases.
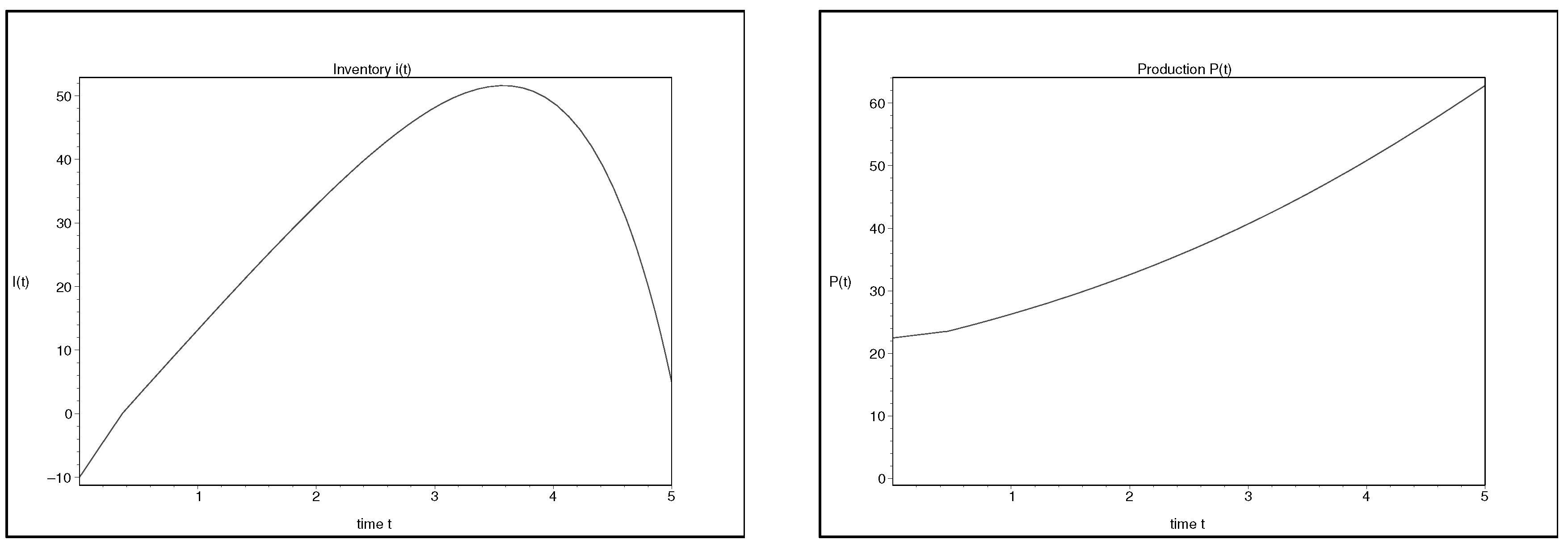
3. Model with Backorders Allowed
| Regime 1 | : | . |
| Regime 2 | : | . |
| Regime 3 | : | . |
- Scenario 1. Regime 2 arises on intervals: For simplicity we assumed that there was only one subinterval on which . In this scenario, there are four cases; , and .
- Case 1. In this case we proceed as follows:
- Case 2.. This case is unlikely to happen in practice, but if it does, then we proceed as follows:
- Scenario 2. Regime 2 does not arise on intervals: As in the previous scenario, we again had to consider the four cases; , and .
- Case 1. For simplicity we assumed that there is only one point with . In this case we proceed as follows:
- Step 1.
- Step 2.
- Step 3. The optimal level is the one with the smallest objective function value.
- Case 2.. This case is unlikely to happen in practice, but if it does, then we proceed as in case 1.
- Case 3.. In this case we solved the differential Equation (24) with the boundary conditions and .
- Case 4.. In this case we solved the differential Equation (22) with the boundary conditions and .
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Simon, H.A. On the application of servomechanism theory in the study of production control. Econometrica 1952, 20, 247–268. [Google Scholar] [CrossRef]
- Salama, Y. Optimal control of a simple manufacturing system with restarting costs. Oper. Res. Lett. 2000, 26, 9–16. [Google Scholar] [CrossRef]
- Riddalls, C.E.; Bennett, S. The optimal control of batched production and its effect on demand amplification. Int. J. Prod. Econ. 2001, 72, 159–168. [Google Scholar] [CrossRef]
- Zhang, Q.; Yin, G.G.; Boukas, E.-K. Optimal control of a marketing-production system. IEEE Trans. Autom. Control 2001, 46, 416–427. [Google Scholar] [CrossRef]
- Khmelnitsky, E.; Gerchak, Y. Optimal control approach to production systems with inventory-level-dependent demand. IEEE Trans. Autom. Control 2002, 47, 289–292. [Google Scholar] [CrossRef]
- Kiesmüller, G.P. Optimal control of a one product recovery system with lead times. Int. J. Prod. Econ. 2003, 81–82, 333–340. [Google Scholar] [CrossRef]
- Dobos, I. Optimal production-inventory strategies for a HMMS-type reverse logistics system. Int. J. Prod. Econ. 2003, 81–82, 351–360. [Google Scholar] [CrossRef]
- Hedjar, R.; Bounkhel, M.; Tadj, L. Predictive control of periodic-review production inventory systems with deteriorating items. Top 2004, 12, 193–208. [Google Scholar] [CrossRef]
- Haijema, R. A new class of stock-level dependent ordering policies for perishables with a short maximum shelf life. Int. J. Prod. Econ. 2013, 143, 434–439. [Google Scholar] [CrossRef]
- Panda, S.; Saha, S.; Goyal, S.K. Dilemma of rented warehouse and shelf for inventory systems with displayed stock level dependent demand. Econ. Model. 2013, 32, 452–462. [Google Scholar] [CrossRef]
- Yogender, S.; Prerna, M.; Kuldeep, C. Optimal production policy for multi-product with inventory-level-dependent demand in segmented market. Yugoslav J. Oper. Res. 2013, 23, 237–247. [Google Scholar]
- Lu, L.; Zhang, J.; Tang, W. Optimal dynamic pricing and replenishment policy for perishable items with inventory-level-dependent demand. Int. J. Syst. Sci. 2016, 47, 1480–1494. [Google Scholar] [CrossRef]
- Singh, D.; Singh, S.R. Review of Literature and Survey of the Developed Inventory Models. Int. J. Math. Appl. 2018, 6, 673–685. [Google Scholar]
- Goyal, S.K.; Giri, B.C. Recent trends in modeling of deteriorating inventory. Eur. J. Oper. Res. 2001, 134, 1–16. [Google Scholar] [CrossRef]
- Naddor, E. Inventory Systems; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Alfares, H.K.; Ghaithan, A.M. EOQ and EPQ Production-Inventory Models with Variable Holding Cost: State-of-the-Art Review. Arab. J. Sci. Eng. 2018, 1–19. [Google Scholar] [CrossRef]
- Paknejad, J.; Nasri, F.; Affisco, J.F. Shape of power yield distribution: impact on EOQ model with nonlinear holding cost and random quality. Int. J. Manag. Sci. Eng. Manag. 2018, 13, 237–244. [Google Scholar] [CrossRef]
- San-José, L.A.; Sicilia, J.; Gonzàlez-de-la-Rosa, M.; Febles-Acosta, J. An economic order quantity model with nonlinear holding cost, partial backlogging and ramp-type demand. Eng. Optim. 2018, 50, 1164–1177. [Google Scholar] [CrossRef]
- Tripathi, R.P. Deterministic inventory models with nonlinear time-dependent and stock-dependent holding cost under non-increasing time-sensitive demand. Int. J. Econ. Bus. Res. 2018, 16, 326–336. [Google Scholar] [CrossRef]
- Paknejad, J.; Nasri, F.; Affisco, J.F. Yield improvement and yield variability reduction in an EOQ model with planned shortages and random yield. Comput. Ind. Eng. 2015, 88, 386–394. [Google Scholar] [CrossRef]
- Aslani, A.; Taleizadeh, A.A.; Zanoni, S. An EOQ model with partial backordering with regard to random yield: Two strategies to improve mean and variance of yield. Comput. Ind. Eng. 2017, 112, 379–390. [Google Scholar] [CrossRef]
- Sethi, S.P.; Thompson, G.L. Optimal Control Theory: Applications to Management Science and Economics, 2nd ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E.F. The Mathematical Theory of Optimal Processes; John Wiley and Sons: New York, NY, USA, 1962. [Google Scholar]
- Hartel, R.F.; Sethi, S.P. Optimal control problems with differential inclusions: Sufficiency conditions and an application to a production inventory model. Optim. Control Appl. Methods 1984, 5, 289–307. [Google Scholar] [CrossRef]
| 0.0005 | 0.001 | 0.002 | 0.004 | 0.008 | 0.016 | 0.032 | 0.064 | 0.128 | 0.256 | |
| J | 490.49 | 491.19 | 492.61 | 495.45 | 501.15 | 512.64 | 536.02 | 584.22 | 685.60 | 902.52 |
| 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 | 0.1 | |
| J | 216.67 | 664.06 | 664.36 | 664.86 | 665.55 | 666.42 | 667.48 | 668.71 | 670.11 | 671.68 | 673.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bounkhel, M.; Tadj, L.; Benhadid, Y.; Hedjar, R. Optimal Control of Nonsmooth Production Systems with Deteriorating Items, Stock-Dependent Demand, with or without Backorders. Symmetry 2019, 11, 183. https://doi.org/10.3390/sym11020183
Bounkhel M, Tadj L, Benhadid Y, Hedjar R. Optimal Control of Nonsmooth Production Systems with Deteriorating Items, Stock-Dependent Demand, with or without Backorders. Symmetry. 2019; 11(2):183. https://doi.org/10.3390/sym11020183
Chicago/Turabian StyleBounkhel, Messaoud, Lotfi Tadj, Yacine Benhadid, and Ramdane Hedjar. 2019. "Optimal Control of Nonsmooth Production Systems with Deteriorating Items, Stock-Dependent Demand, with or without Backorders" Symmetry 11, no. 2: 183. https://doi.org/10.3390/sym11020183
APA StyleBounkhel, M., Tadj, L., Benhadid, Y., & Hedjar, R. (2019). Optimal Control of Nonsmooth Production Systems with Deteriorating Items, Stock-Dependent Demand, with or without Backorders. Symmetry, 11(2), 183. https://doi.org/10.3390/sym11020183





