Group Decision Making Based on Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operators
Abstract
:1. Introduction
2. Preliminaries
Triangular Neutrosophic Cubic Fuzzy Number
3. Some Einstein Operations on TNCFNs
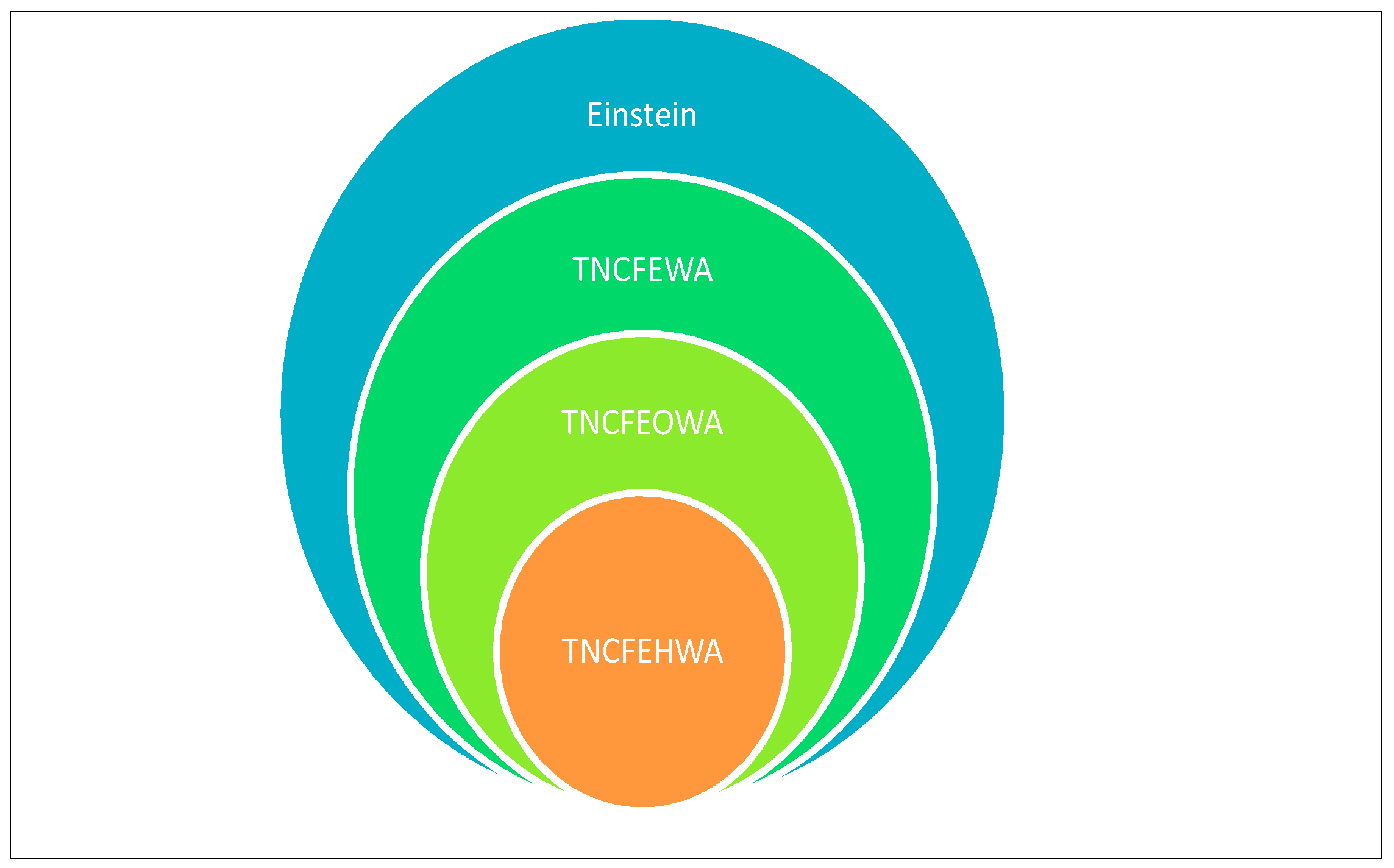
4. Triangular Neutrosophic Cubic Fuzzy Averaging Operators Based on Einstein Operations
4.1. Triangular Neutrosophic Cubic Fuzzy Einstein Weighted Averaging Operator
4.2. Triangular Neutrosophic Cubic Fuzzy Einstein Ordered Weighted Averaging Operator
4.3. Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operator
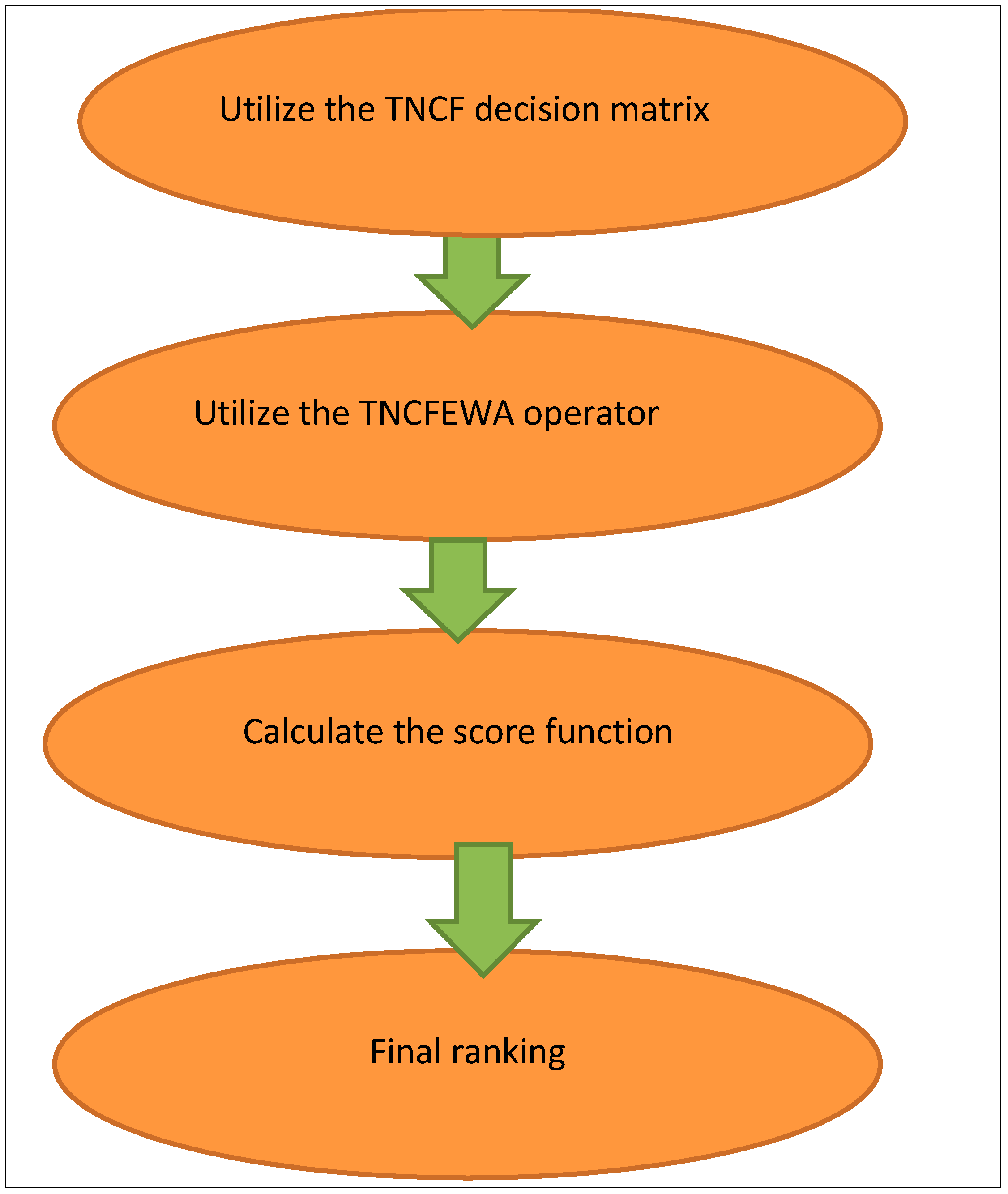
5. An Approach to MADM with TNCF Data
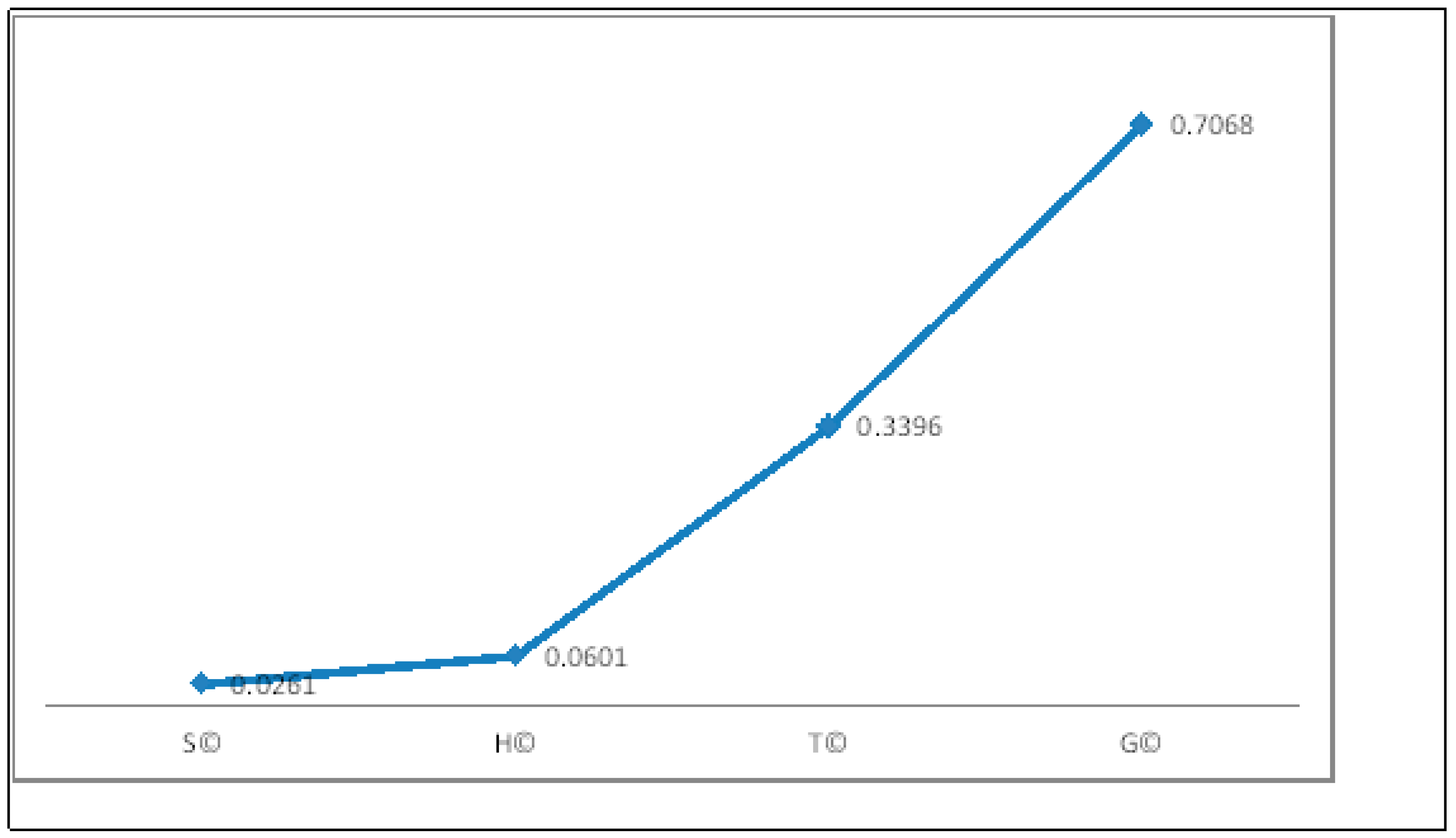
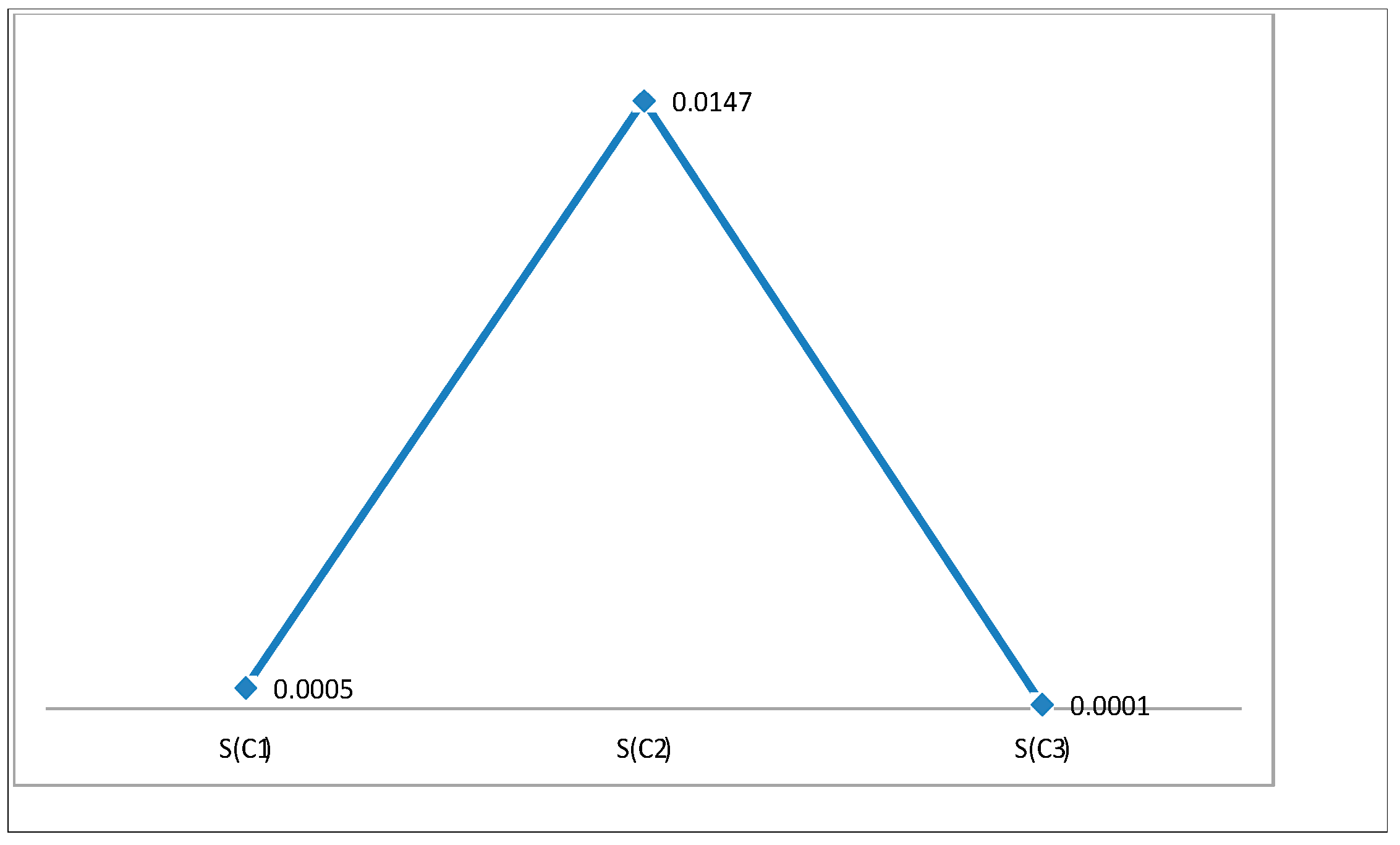
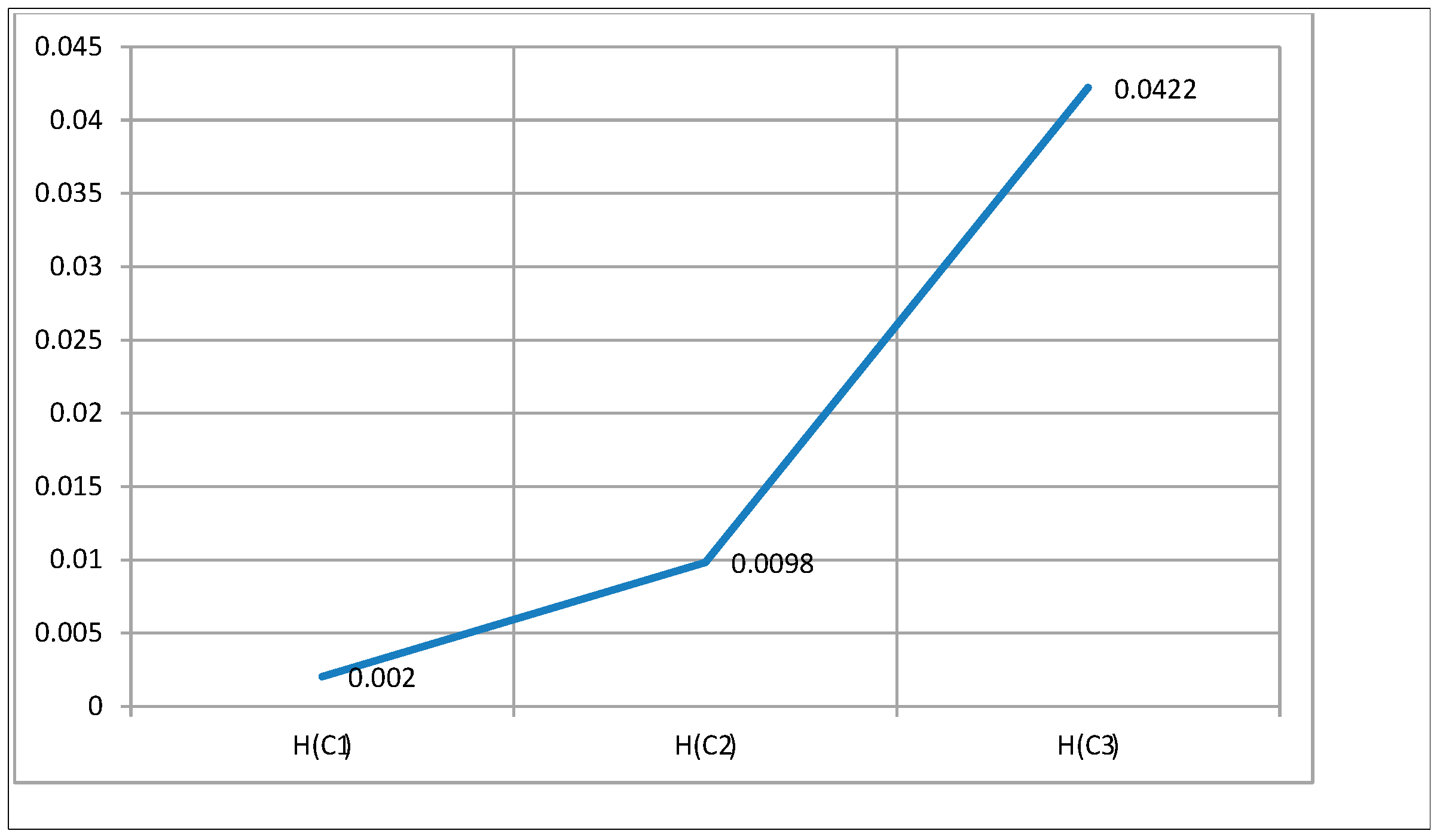
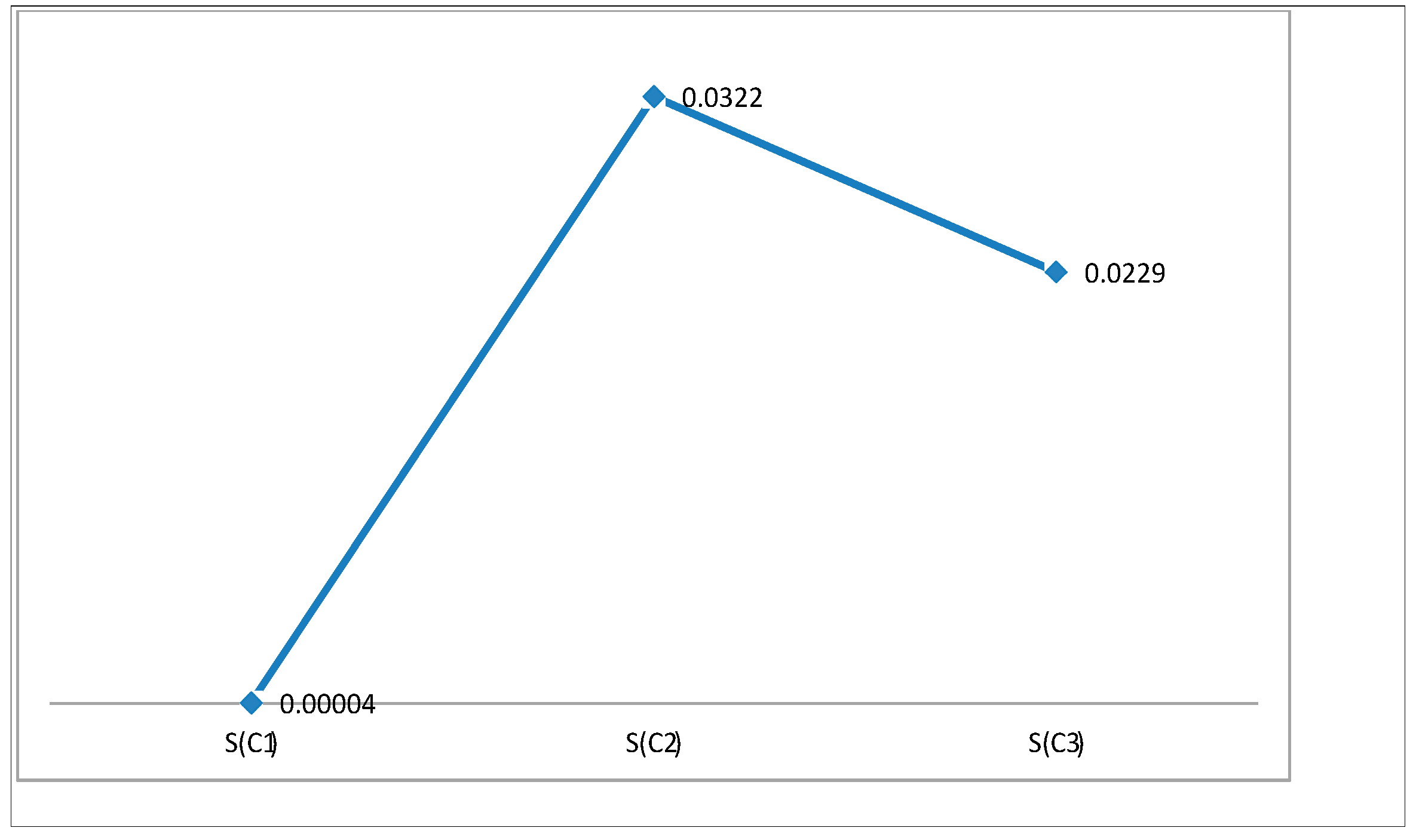
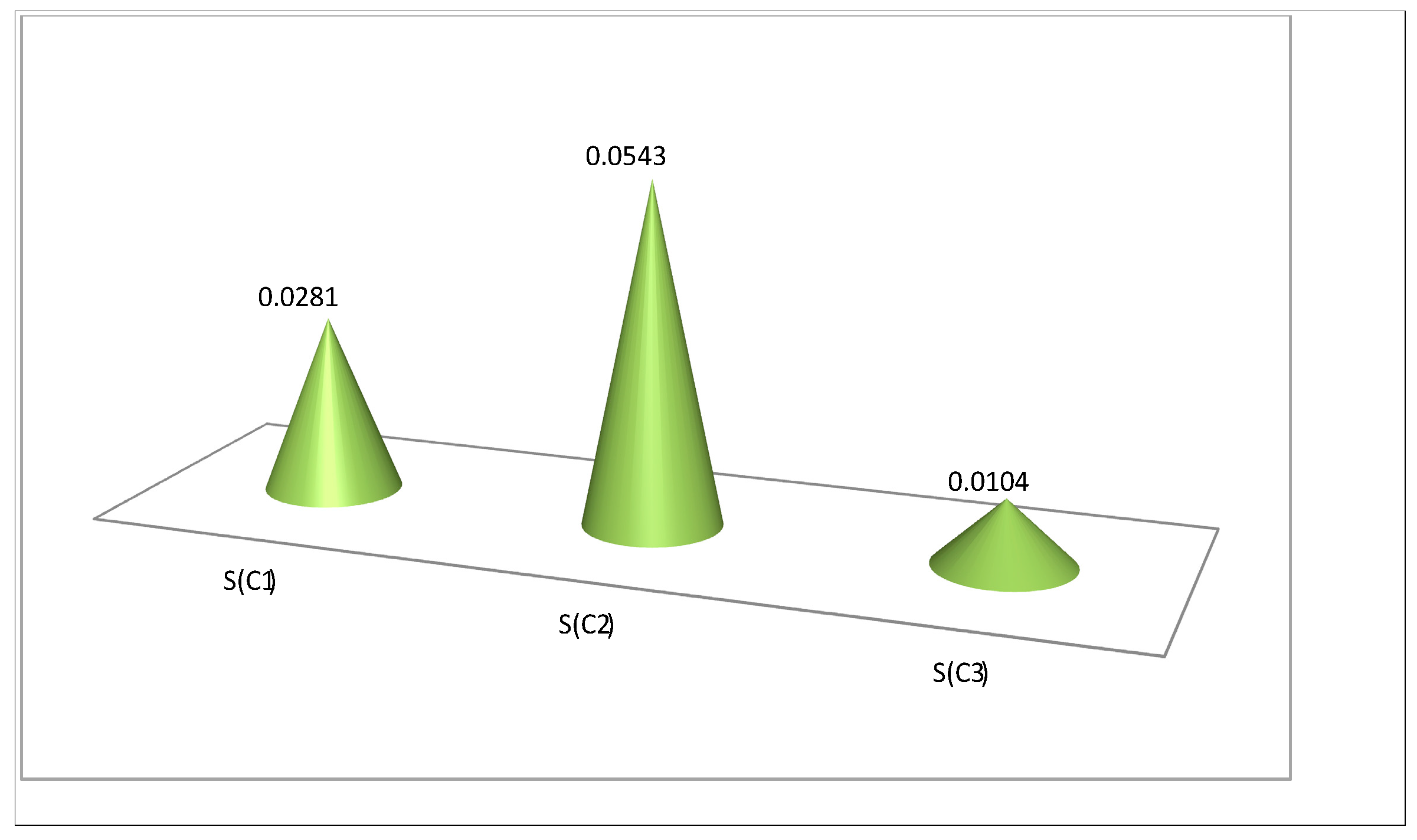
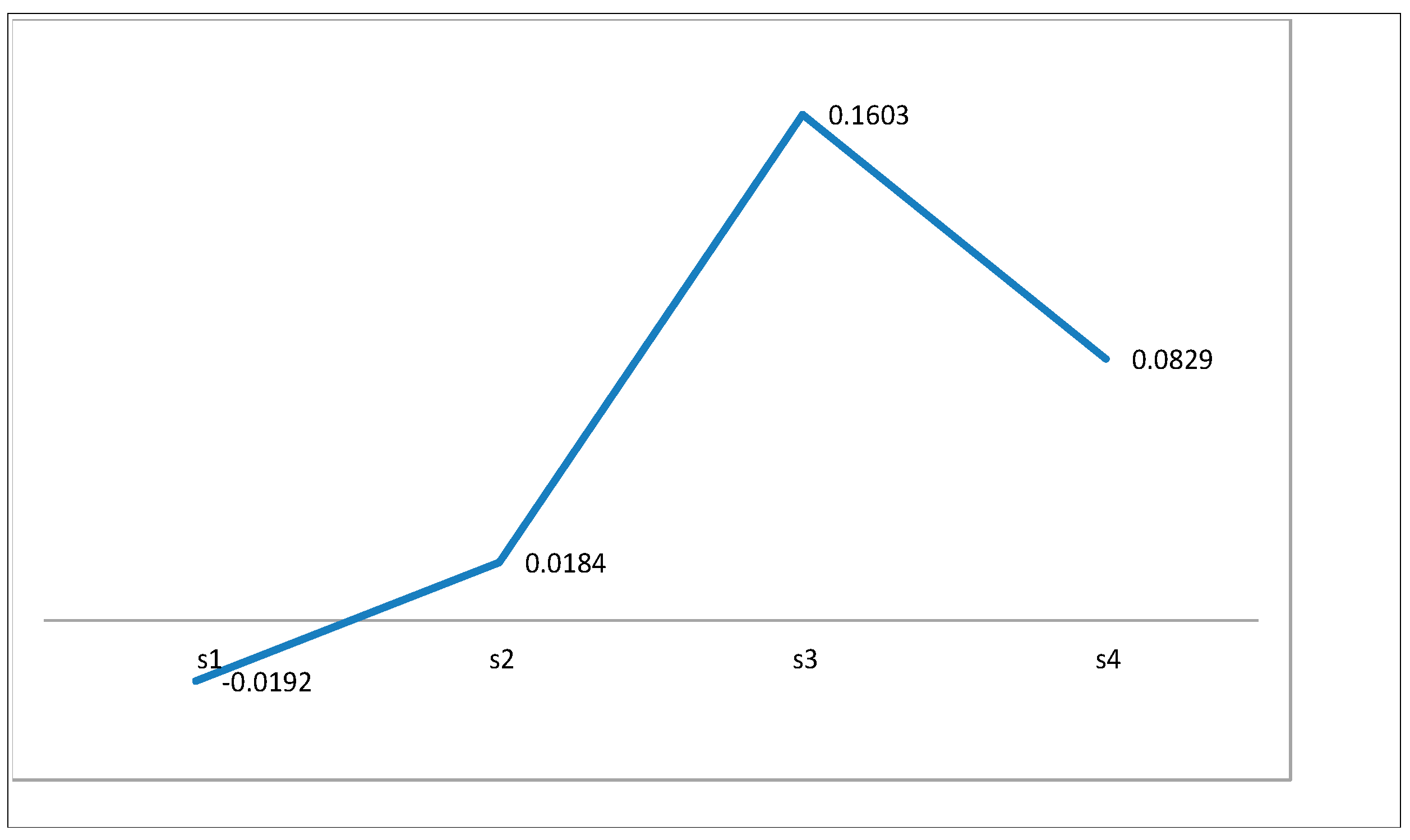
6. Numerical Application
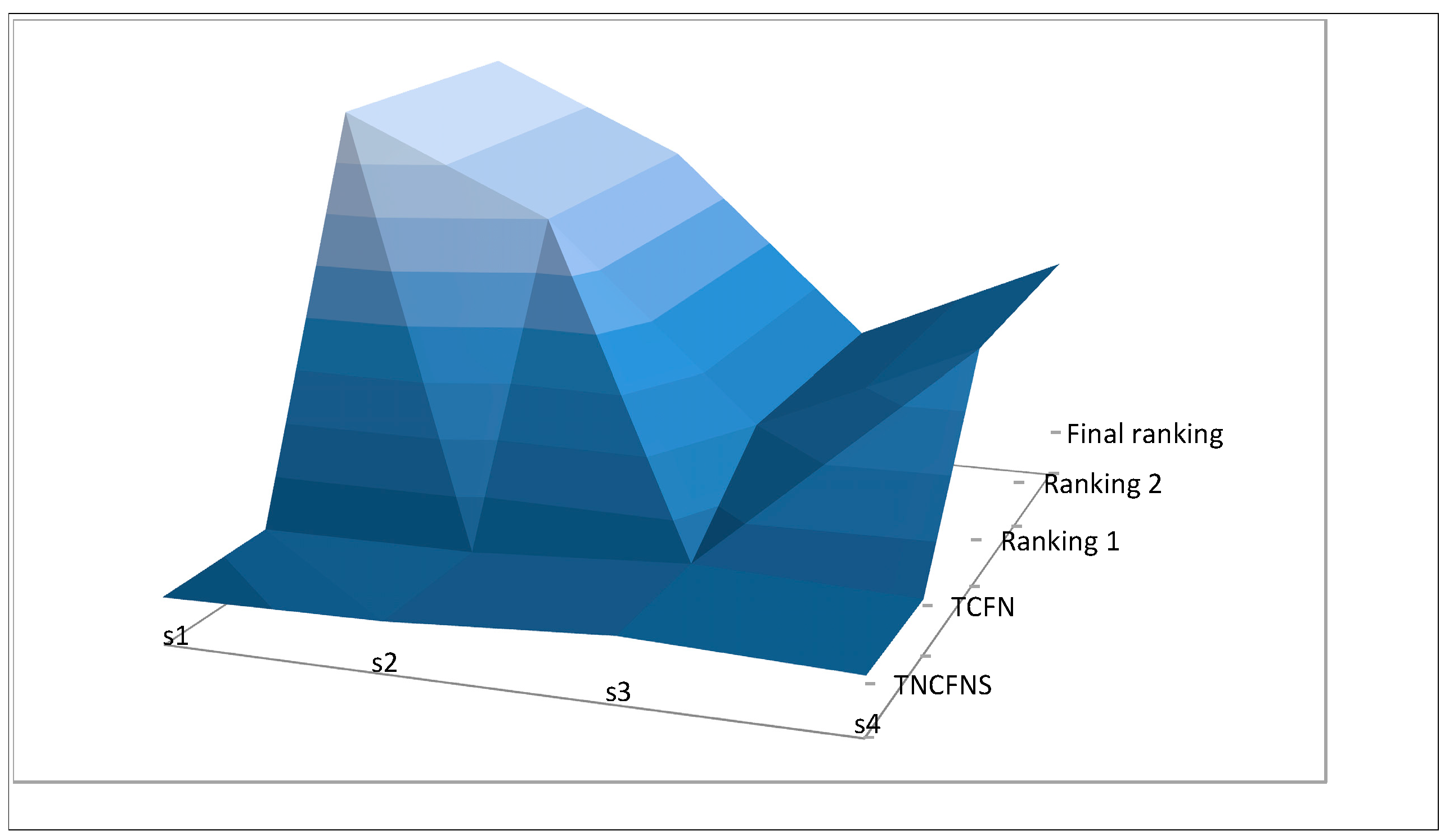
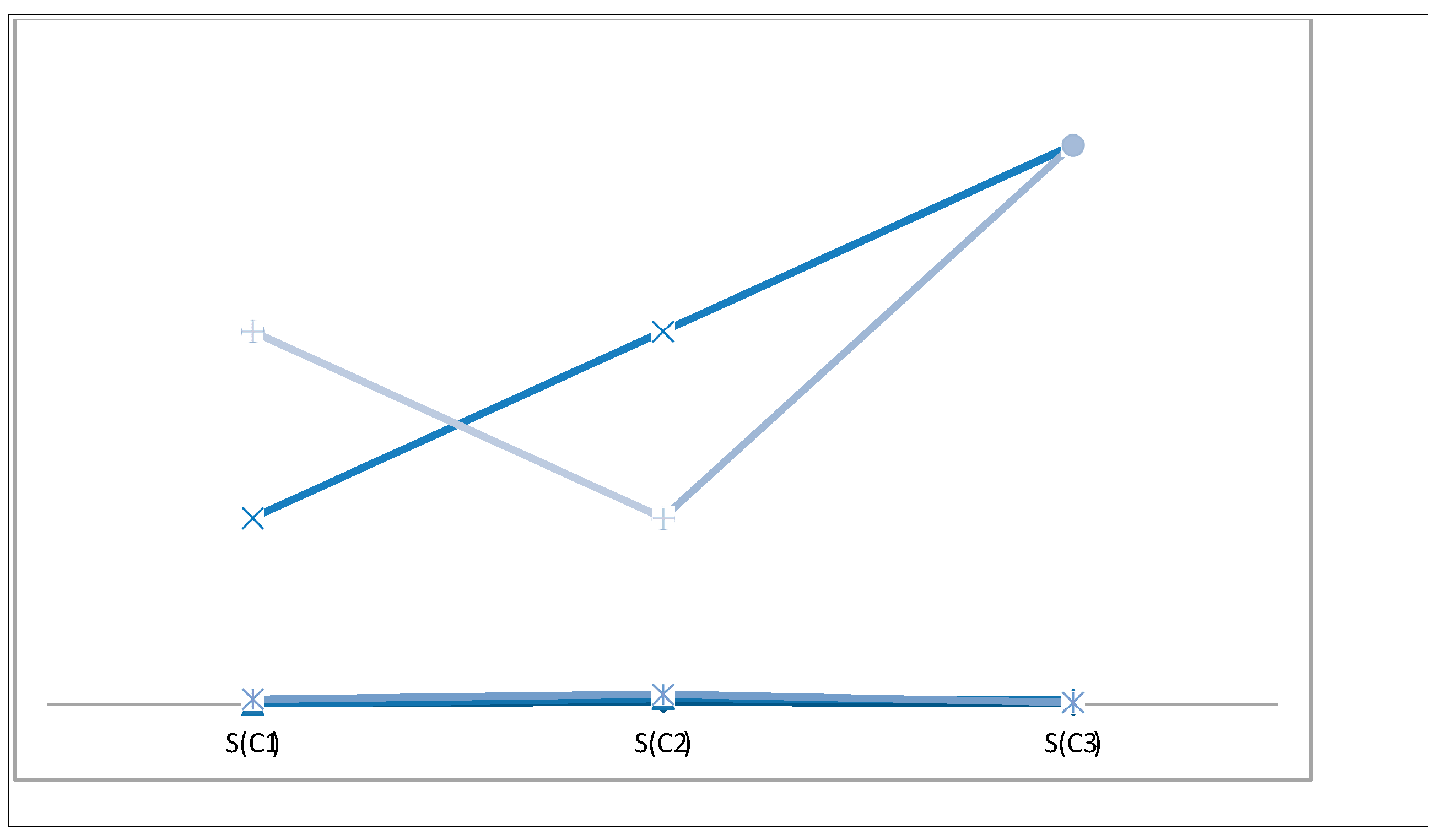
7. Comparsion Analysis
A Comparison Analysis with the Existing MCDM Method Triangular Cubic Fuzzy Number
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A. Proof of Proposition 1
Appendix B. Proof of Theorem 1
References
- Atanassov, K.T. Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. New Operations Defined Over the Intuitionistic Fuzzy Sets. Fuzzy Sets Syst. 1994, 61, 137–142. [Google Scholar] [CrossRef]
- Bustince, H.; Burillo, P. Structures on intuitionistic fuzzy relations. Fuzzy Sets Syst. 1996, 78, 293–303. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. On the relationship between some extensions of fuzzy set theory. Fuzzy Sets Syst. 2003, 133, 227–235. [Google Scholar] [CrossRef]
- Deschrijver, G.; Kerre, E.E. On the position of intuitionistic fuzzy set theory in the framework of theories modelling imprecision. Inf. Sci. 2007, 177, 1860–1866. [Google Scholar] [CrossRef]
- Jun, Y.B.; Kim, C.S.; Yang, K.O. Annals of Fuzzy Mathematics and Informatics. Cubic Sets 2011, 4, 83–98. [Google Scholar]
- Muhiuddin, G.; Feng, F.; Jun, Y.B. Subalgebras of BCK/BCI-Algebras Based on Cubic Soft Sets. Sci. World J. 2014, 2014, 458638. [Google Scholar] [CrossRef]
- Turksen, I.B. Interval valued fuzzy sets based on normal forms. Fuzzy Sets Syst. 1986, 20, 191–210. [Google Scholar] [CrossRef]
- Xu, Z.S. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gener. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z.S.; Cai, X. Recent advances in intuitionistic fuzzy information aggregation. Fuzzy Optim. Decis. Mak. 2010, 9, 359–381. [Google Scholar] [CrossRef]
- Liu, H.W.; Wang, G.-J. Multi-criteria decision-making methods based on intuitionistic fuzzy sets. Eur. J. Oper. Res. 2007, 179, 220–233. [Google Scholar] [CrossRef]
- Zeng, S.Z.; Su, W.H. Intuitionistic fuzzy ordered weighted distance operator. Knowl.-Based Syst. 2011, 24, 1224–1232. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inform. Contr. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. Outline of a new approach to analysis of complex systems and decision processes interval-valued fuzzy sets. IEEE Trans. Syst. Man Cybern. 1973, 3, 28–44. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.L.; Gong, Z.-T. Aggregating of Interval-valued Intuitionistic Uncertain Linguistic Variables based on Archimedean t-norm and It Applications in Group Decision Makings. J. Comput. Anal. Appl. 2018, 24, 874–885. [Google Scholar]
- Zhao, X.; Lin, R.; Wei, G. Hesitant triangular fuzzy information aggregation based on Einstein operations and their application to multiple attribute decision making. Expert Syst. Appl. 2014, 41, 1086–1094. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Dynamic intuitionistic fuzzy multi-attribute decision making. Int. J. Approx. Reason. 2008, 48, 246–262. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophic set—A generalization of the intuitionistic fuzzy set. In Proceedings of the 2006 IEEE International Conference on Granular Computing, Atlanta, GA, USA, 10–12 May 2006; pp. 38–42. [Google Scholar]
- Smarandache, F. A geometric interpretation of the neutrosophic set—A generalization of the intuitionistic fuzzy set. In Proceedings of the 20011 IEEE International Conference on Granular Computing (GrC), Kaohsiung, Taiwan, 8–10 November 2011; pp. 602–606. [Google Scholar]
- Fahmi, A.; Abdullah, S.; Amin, F.; Ali, A. Weighted average rating (WAR) method for solving group decision making problem using triangular cubic fuzzy hybrid aggregation (TCFHA). Punjab Univ. J. Math. 2018, 50, 23–34. [Google Scholar]
- Fahmi, A.; Amin, F.; Smarandache, F.; Khan, M.; Hassan, N. Triangular Cubic Hesitant Fuzzy Einstein Hybrid Weighted Averaging Operator and Its Application to Decision Making. Symmetry 2018, 10, 658. [Google Scholar] [CrossRef]
- Beg, I.; Rashid, T. Group decision making using intuitionistic hesitant fuzzy sets. Int. J. Fuzzy Log. Intell. Syst. 2014, 14, 181–187. [Google Scholar] [CrossRef]
- Grzegorzewski, P. On Separability of Fuzzy Relations. Int. J. Fuzzy Log. Intell. Syst. 2017, 17, 137–144. [Google Scholar] [CrossRef]
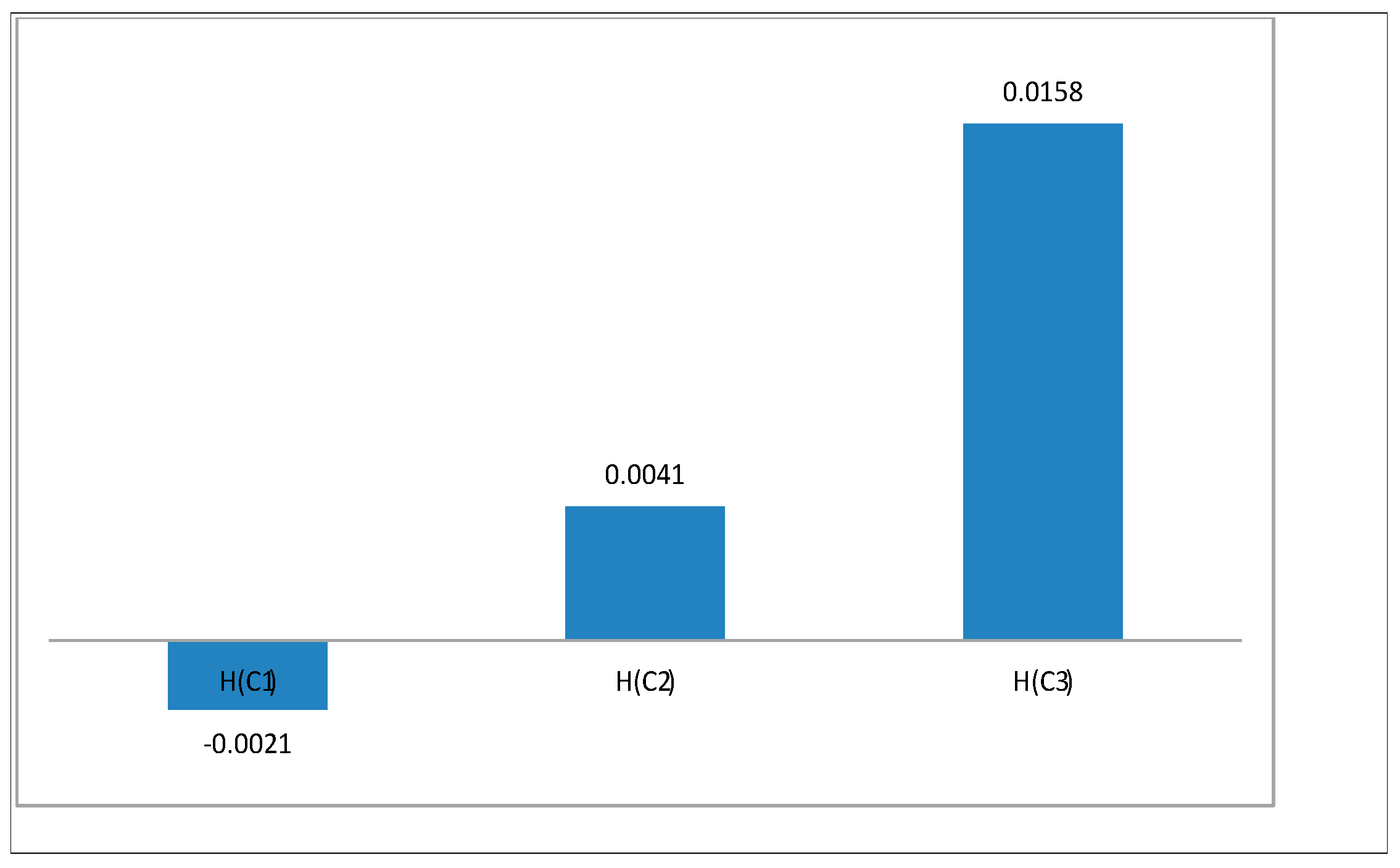
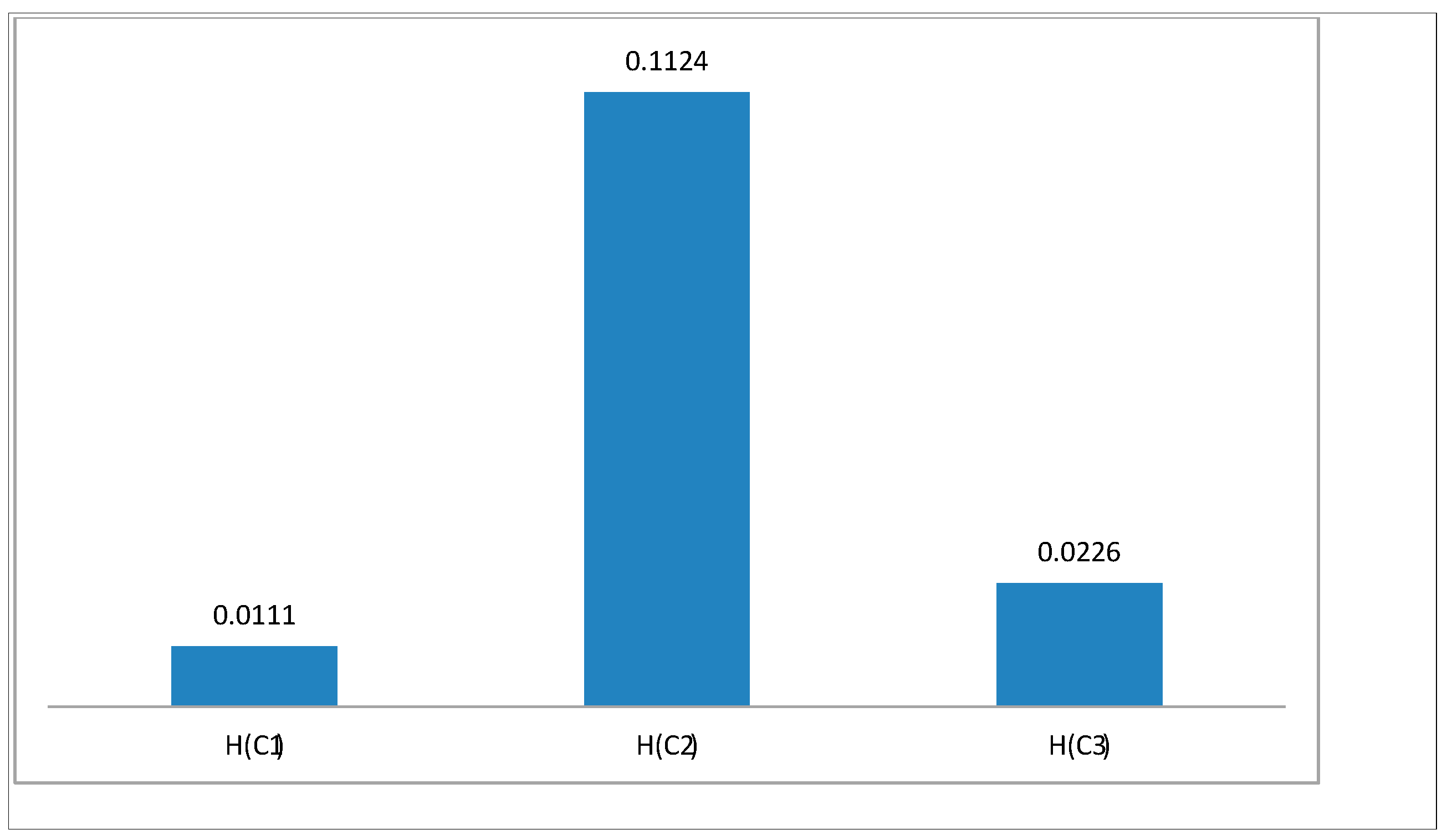
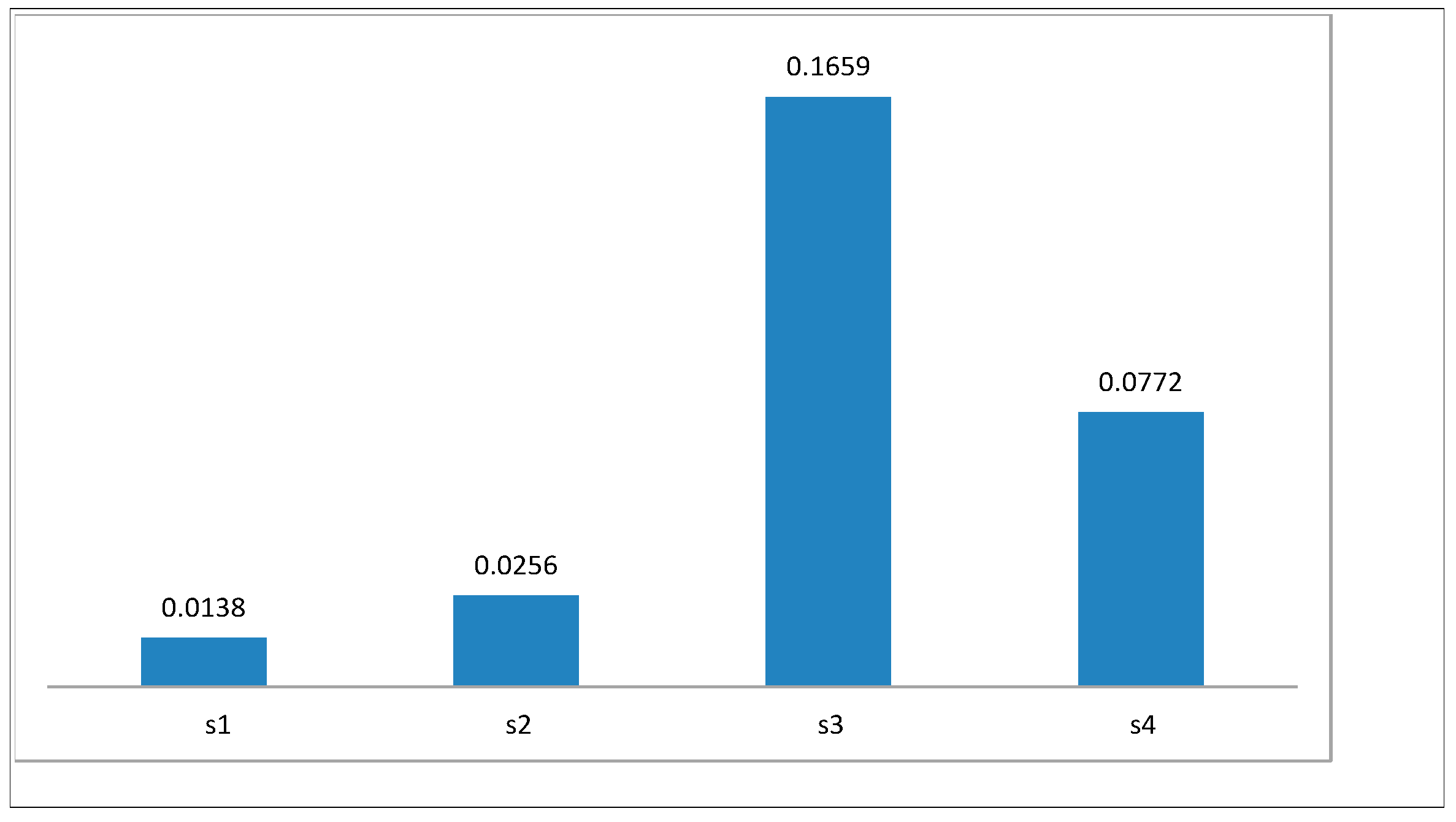
| Reference 21 | Reference 22 | Current Paper |
|---|---|---|
| Defines a new extension of the triangular cubic fuzzy number by using a cubic set. | Defines a new extension of the triangular cubic hesitant fuzzy number by using a cubic set. | Defines a new extension of the triangular neutrosophic cubic fuzzy number by using a neutrosophic set. |
| Introduced the triangular cubic fuzzy number, operational laws, and their score and accuracy functions. | Introduced the triangular cubic hesitant fuzzy number, operational laws, and their score, accuracy functions, membership uncertainty index and hesitation index. | Introduced the triangular cubic fuzzy number, operational laws, and their score and accuracy functions, membership uncertainty index and hesitation index. |
| Introduced the triangular cubic fuzzy hybrid aggregation operator. | Introduced three Einstein aggregation operators, such as the triangular cubic fuzzy hybrid aggregation operator, and the TCHFEWA, TCHFEOWA and TCHFEHWA operators | Introduced three Einstein aggregation operators, such as the triangular neutrosophic cubic fuzzy hybrid aggregation operator, and the TNCFEWA, TNCFEOWA and TNCFEHWA operators |
| Method | Ranking |
|---|---|
| TNCFNs | |
| TCFN [21] |
| Score function Ranking |
|---|
| TNCFEWA operator |
| TNCFEOWA operator |
| TNCFEHWA operator |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fahmi, A.; Amin, F.; Khan, M.; Smarandache, F. Group Decision Making Based on Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operators. Symmetry 2019, 11, 180. https://doi.org/10.3390/sym11020180
Fahmi A, Amin F, Khan M, Smarandache F. Group Decision Making Based on Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operators. Symmetry. 2019; 11(2):180. https://doi.org/10.3390/sym11020180
Chicago/Turabian StyleFahmi, Aliya, Fazli Amin, Madad Khan, and Florentin Smarandache. 2019. "Group Decision Making Based on Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operators" Symmetry 11, no. 2: 180. https://doi.org/10.3390/sym11020180
APA StyleFahmi, A., Amin, F., Khan, M., & Smarandache, F. (2019). Group Decision Making Based on Triangular Neutrosophic Cubic Fuzzy Einstein Hybrid Weighted Averaging Operators. Symmetry, 11(2), 180. https://doi.org/10.3390/sym11020180






