Neutrosophic Compound Orthogonal Neural Network and Its Applications in Neutrosophic Function Approximation
Abstract
:1. Introduction
2. Basic Concepts and Operations of NsNs
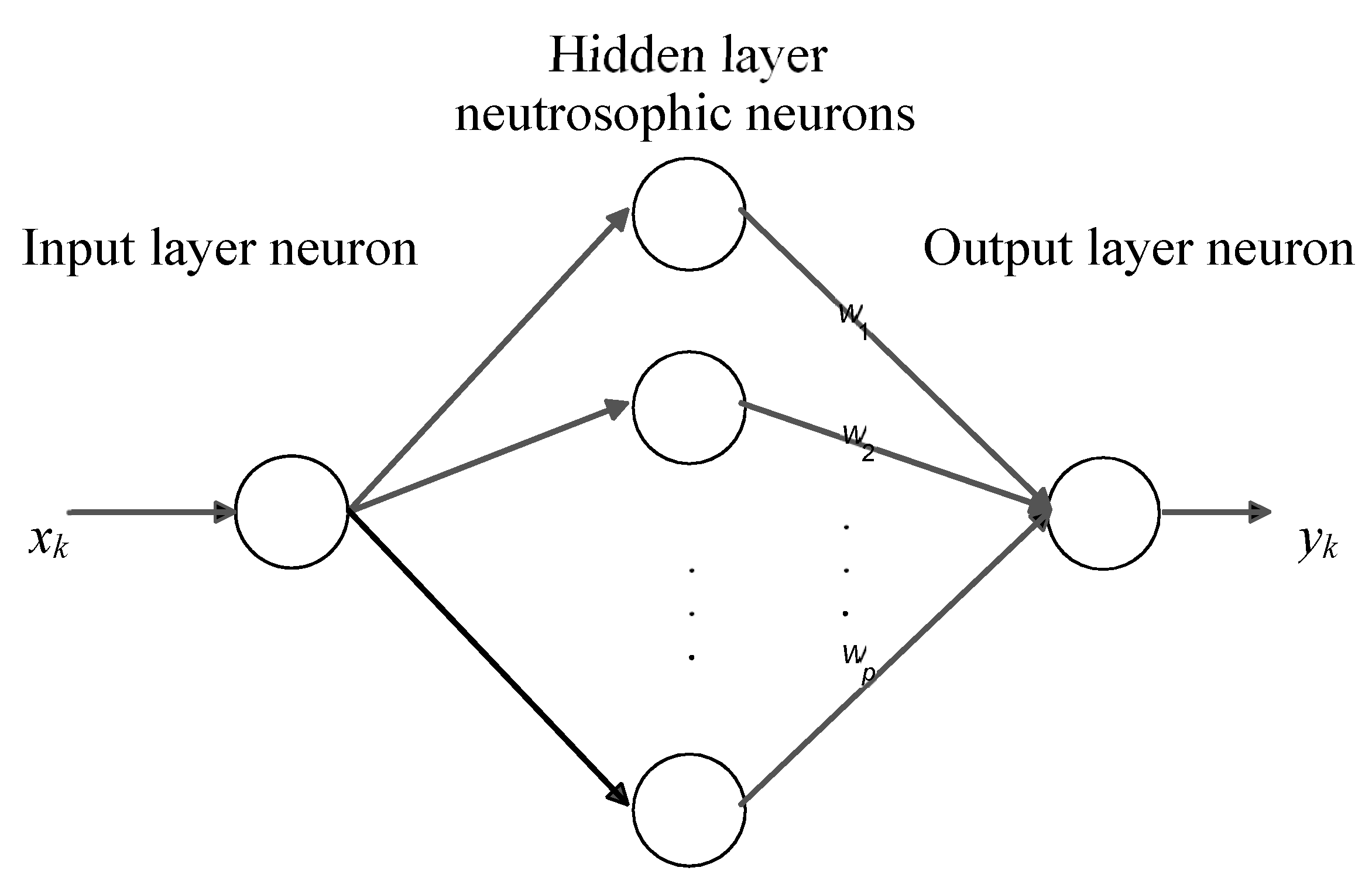
3. NCONN with NsNs
4. NsN Nonlinear Function Approximation Applied by the Proposed NCONN
5. Actual Example on the Approximation of the JRC NsNs Based on the Proposed NCONN
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baker, M.R.; Patil, R.B. Universal approximation theorem for interval neural networks. Reliab. Comput. 1998, 4, 235–239. [Google Scholar] [CrossRef]
- Beheshti, M.; Berrached, A.; Korvin, A.D.; Hu, C.; Sirisaengtaksin, O. On interval weighted three-layer neural networks. In Proceedings of the 31st Annual Simulation Symposium, Boston, MA, USA, 5–9 April 1998; pp. 188–195. [Google Scholar]
- Rossi, F.; Conan-Guez, B. Multi-layer perceptron on interval data. Classification, clustering, and data analysis. In Studies in Classification, Data Analysis, and Knowledge Organization; Springer: Berlin, Germany, 2002; pp. 427–434. [Google Scholar]
- Patiño-Escarcina, R.E.; Callejas Bedregal, B.R.; Lyra, A. Interval computing in neural networks: One layer interval neural networks. In Intelligent Information Technology. Lecture Notes in Computer Science; Das, G., Gulati, V.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3356, pp. 68–75. [Google Scholar]
- Lu, J.; Xue, S.; Zhang, X.; Han, Y. A neural network-based interval pattern matcher. Information 2015, 6, 388–398. [Google Scholar] [CrossRef]
- Piotr, A.; Kowalski, P.K. Interval probabilistic neural network. Neural Comput. Appl. 2017, 28, 817–834. [Google Scholar]
- Specht, D.F. Probabilistic neural networks. Neural Netw. 1990, 3, 109–118. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy: Neutrosophic Probability, Set, and Logic; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Measure, Neutrosophic Integral, and Neutrosophic Probability; Sitech & Education Publisher: Craiova, Columbus, 2013. [Google Scholar]
- Smarandache, F. Introduction to Neutrosophic Statistics; Sitech & Education Publishing: Columbus, OH, USA, 2014. [Google Scholar]
- Ye, J. A multicriteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Uluçay, V.; Sahin, M.; Dey, A.; Dhar, M.; Tan, R.P.; Bahnasse, A.; et al. Neutrosophic sets: An overview. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Publishing House: Brussels, Belgium, 2018; Volume II, pp. 403–434. [Google Scholar]
- Broumi, S.; Bakali, A.; Talea, M.; Smarandache, F.; Vladareanu, L. Computation of shortest path problem in a network with SV-trapezoidal neutrosophic numbers. In Proceedings of the 2016 International Conference on Advanced Mechatronic Systems, Melbourne, Australia, 30 November–3 December 2016; pp. 417–422. [Google Scholar]
- Gal, I.A.; Bucur, D.; Vladareanu, L. DSmT decision-making algorithms for finding grasping configurations of robot dexterous hands. Symmetry 2018, 10, 198. [Google Scholar] [CrossRef]
- Ye, J. Multiple-attribute group decision-making method under a neutrosophic number environment. J. Intell. Syst. 2016, 25, 377–386. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ye, J. A projection model of neutrosophic numbers for multiple attribute decision making of clay-brick selection. Neutrosophic Sets Syst. 2016, 12, 139–142. [Google Scholar]
- Ye, J. Bidirectional projection method for multiple attribute group decision making with neutrosophic numbers. Neural Comput. Appl. 2017, 28, 1021–1029. [Google Scholar] [CrossRef]
- Kong, L.W.; Wu, Y.F.; Ye, J. Misfire fault diagnosis method of gasoline engines using the cosine similarity measure of neutrosophic numbers. Neutrosophic Sets Syst. 2015, 8, 43–46. [Google Scholar]
- Ye, J. Fault diagnoses of steam turbine using the exponential similarity measure of neutrosophic numbers. J. Intell. Fuzzy Syst. 2016, 30, 1927–1934. [Google Scholar] [CrossRef]
- Jiang, W.Z.; Ye, J. Optimal design of truss structures using a neutrosophic number optimization model under an indeterminate environment. Neutrosophic Sets Syst. 2016, 14, 93–975. [Google Scholar]
- Ye, J. Neutrosophic number linear programming method and its application under neutrosophic number environments. Soft Comput. 2018, 22, 4639–4646. [Google Scholar] [CrossRef]
- Ye, J. An improved neutrosophic number optimization method for optimal design of truss structures. New Math. Nat. Comput. 2018, 14, 295–305. [Google Scholar] [CrossRef]
- Ye, J.; Cui, W.H.; Lu, Z.K. Neutrosophic number nonlinear programming problems and their general solution methods under neutrosophic number environments. Axioms 2018, 7, 13. [Google Scholar] [CrossRef]
- Ye, J.; Chen, J.Q.; Yong, R.; Du, S.G. Expression and analysis of joint roughness coefficient using neutrosophic number functions. Information 2017, 8, 69. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ye, J.; Du, S.G. Scale effect and anisotropy analyzed for neutrosophic numbers of rock joint roughness coefficient based on neutrosophic statistics. Symmetry 2017, 9, 208. [Google Scholar] [CrossRef]
- Chen, J.Q.; Ye, J.; Du, S.G.; Yong, R. Expressions of rock joint roughness coefficient using neutrosophic interval statistical numbers. Symmetry 2017, 9, 123. [Google Scholar] [CrossRef]
- Ye, J.; Yong, R.; Liang, Q.F.; Huang, M.; Du, S.G. Neutrosophic functions of the joint roughness coefficient (JRC) and the shear strength: A case study from the pyroclastic rock mass in Shaoxing City, China. Math. Probl. Eng. 2016, 4825709. [Google Scholar] [CrossRef]
- Vlădăreanu, V.; Dumitrache, I.; Vlădăreanu, L.; Sacală, I.S.; Tonţ, G.; Moisescu, M.A. Versatile intelligent portable robot control platform based on cyber physical systems principles. Stud. Inform. Control 2015, 24, 409–418. [Google Scholar] [CrossRef]
| NCONN Structure | α | λ | The Number of the Specified Learning Iteration | |
|---|---|---|---|---|
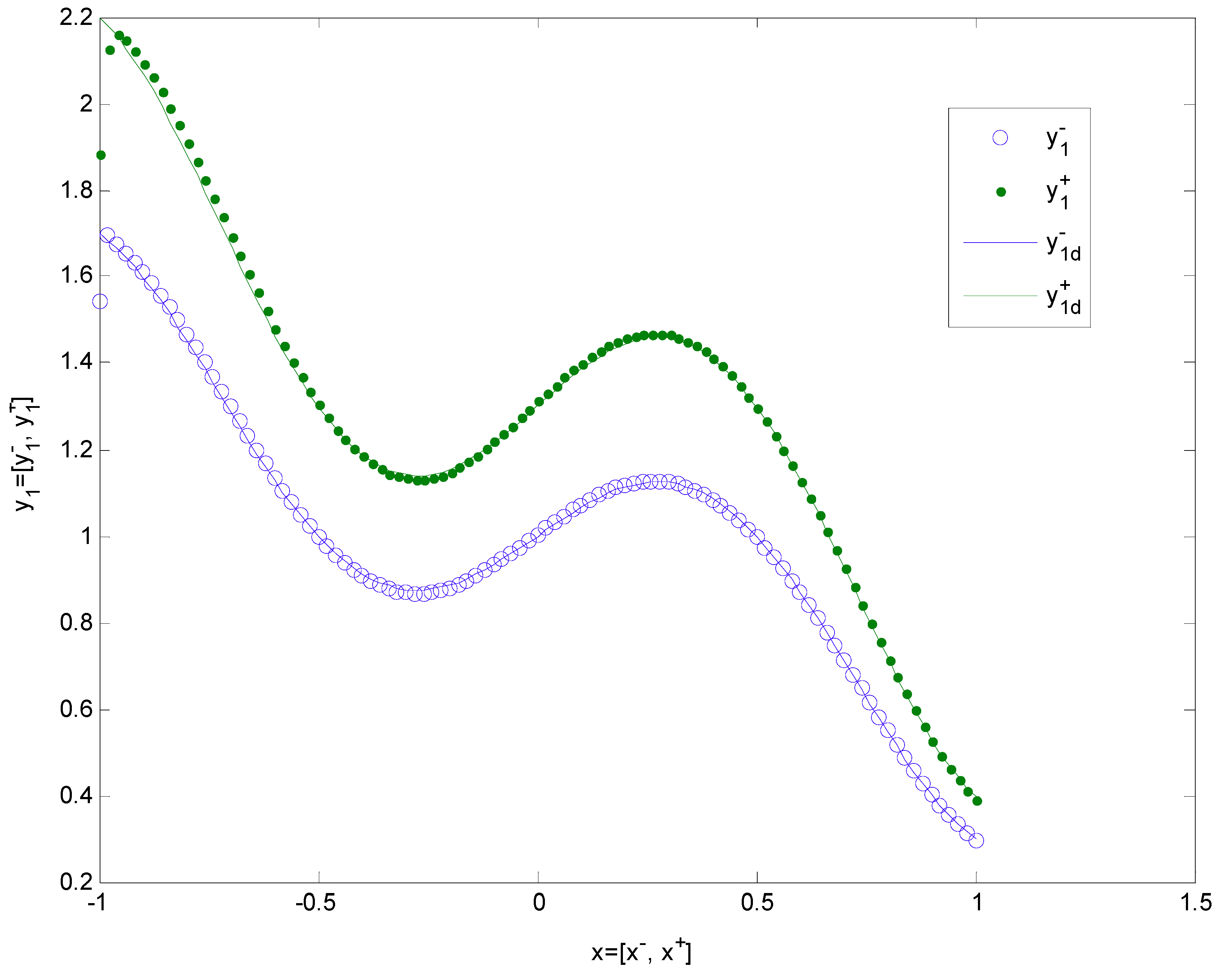
| 1 × 8 × 1 | 2.5 | 0.25 | 20 | [3.2941, 8.5088] |
| NCONN Structure | α | λ | The Number of the Specified Learning Iteration | |
|---|---|---|---|---|
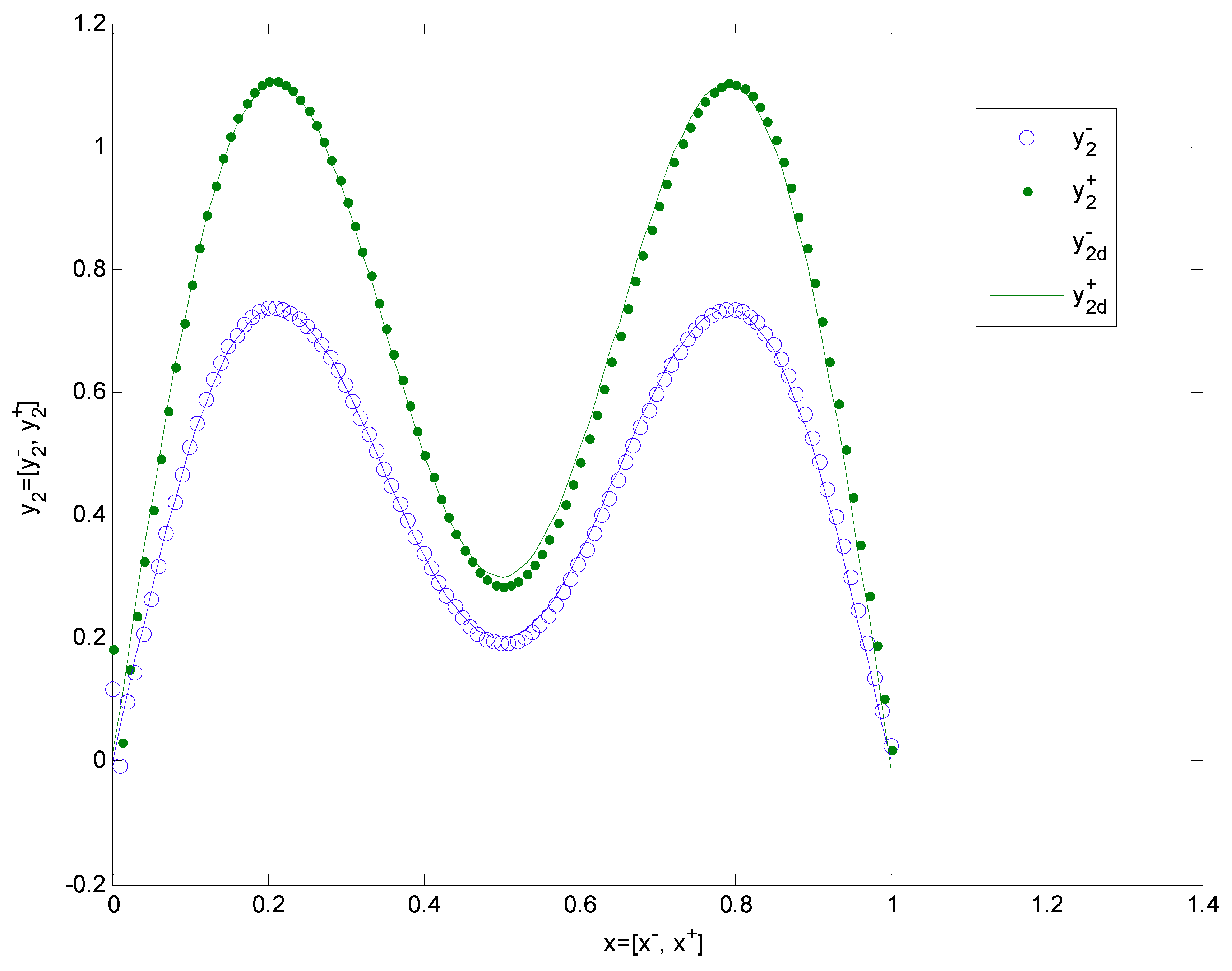
| 1 × 8 × 1 | 8 | 0.3 | 20 | [0.5525, 1.1261] |
| Sample Length L (cm) | xk | JRC | yk |
|---|---|---|---|
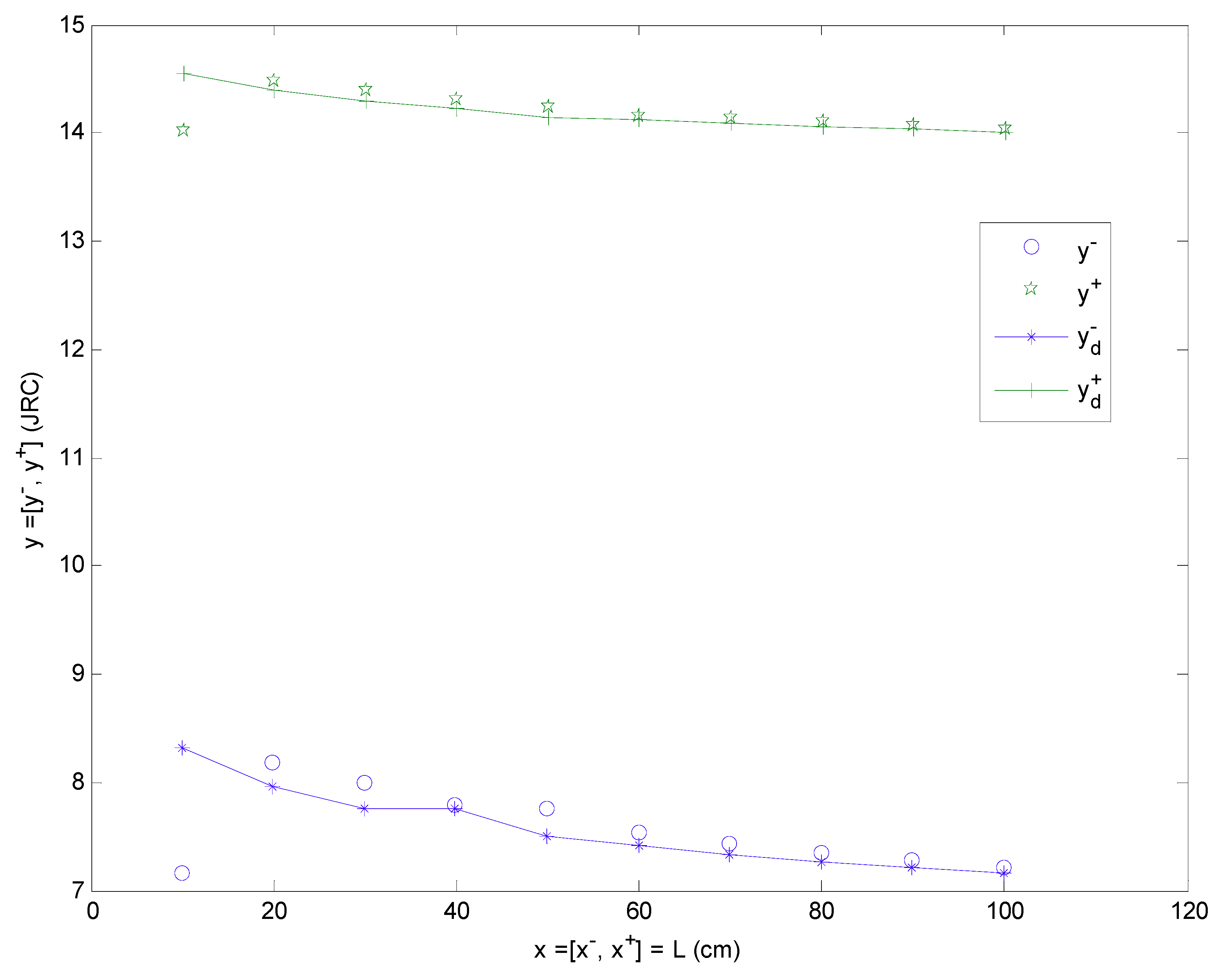
| 9.8 + 0.4I | [9.8, 10.2] | 8.321 + 6.231I | [8.321, 14.552] |
| 19.8 + 0.4I | [19.8, 20.2] | 7.970 + 6.419I | [7.970, 14.389] |
| 29.8 + 0.4I | [29.8, 30.2] | 7.765 + 6.529I | [7.765, 14.294] |
| 39.8 + 0.4I | [39.8, 40.2] | 7.762 + 6.464I | [7.762, 14.226] |
| 49.8 + 0.4I | [49.8, 50.2] | 7.507 + 6.64I | [7.507, 14.147] |
| 59.8 + 0.4I | [59.8, 60.2] | 7.417 + 6.714I | [7.417, 14.131] |
| 69.8 + 0.4I | [69.8, 70.2] | 7.337 + 6.758I | [7.337, 14.095] |
| 79.8 + 0.4I | [79.8, 80.2] | 7.269 + 6.794I | [7.269, 14.063] |
| 89.8 + 0.4I | [89.8, 90.2] | 7.210 + 6.826I | [7.210, 14.036] |
| 99.8 + 0.4I | [99.8, 100.2] | 7.156 + 6.855I | [7.156, 14.011] |
| NCONN Structure | α | λ | The Number of the Specified Learning Iteration | |
|---|---|---|---|---|
| 1 × 8 × 1 | 8 | 0.11 | 5 | [3.2715, 22.3275] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, J.; Cui, W. Neutrosophic Compound Orthogonal Neural Network and Its Applications in Neutrosophic Function Approximation. Symmetry 2019, 11, 147. https://doi.org/10.3390/sym11020147
Ye J, Cui W. Neutrosophic Compound Orthogonal Neural Network and Its Applications in Neutrosophic Function Approximation. Symmetry. 2019; 11(2):147. https://doi.org/10.3390/sym11020147
Chicago/Turabian StyleYe, Jun, and Wenhua Cui. 2019. "Neutrosophic Compound Orthogonal Neural Network and Its Applications in Neutrosophic Function Approximation" Symmetry 11, no. 2: 147. https://doi.org/10.3390/sym11020147
APA StyleYe, J., & Cui, W. (2019). Neutrosophic Compound Orthogonal Neural Network and Its Applications in Neutrosophic Function Approximation. Symmetry, 11(2), 147. https://doi.org/10.3390/sym11020147





