1. Introduction
Consider a system of
N molecules, modeled as identical spherical particles, enclosed in a bounded region
of
. At any given instant (or in an equilibrium configuration), the total potential energy of the molecular array is given by:
where
is the intermolecular potential energy with
the standard Euclidean or two-vector norm, and
are the positions of the particles. More general energy potentials have been considered of which (
1) is a special case (cf. [
1,
2]), or those based on the eigenvalues of adjacency matrices like in [
3]. The problem of minimizing (
1) subject to certain type of global or local conditions have been studied extensively (see e.g., [
4,
5,
6] and the references there in). In these models either the array is infinite, with some local repeating structure, or finite but with
. In this paper, none of these conditions are required but we expect that our results can be extrapolated to such more general scenarios. Also, we do not commit to any particular intermolecular potential
(but give examples for instance for Lennard–Jones type potentials) so that our results are applicable to any such smooth potential.
The particular problems that we consider in this paper are those of characterizing the minimum energy configurations of (
1) in the case of three particles (
) arranged in a triangle and that of four particles (
) in a tetrahedral array. The minimization problem is subject to the constraint of fixed area for the triangular array and of fixed volume in the tetrahedral case. We are particularly interested on the dependence of the minimizing states on the parameter of area or volume in the constraint. Both problems have the particularity that they can be formulated in terms of the intermolecular distances only, that is, without specifying the coordinates corresponding to the positions of the particles, thus substantially reducing the number of unknowns in each problem.
The motivation to study these problems comes from the following phenomena observed both in laboratory experiments and molecular dynamics simulations (see e.g., [
7,
8]). As the density of a fluid is progressively lowered (keeping the temperature constant), there is a certain “critical” density such that if the density of the fluid is lower than this critical value, then bubbles or regions with very low density appear within the fluid. This phenomenon is usually called “cavitation” and it has been extensively studied as well in solids. (See for instance [
9,
10] for discussions and further references.) When using discrete models of materials like (
1), distinguishing between regions of low vs. high density, or whether bubbles or holes have form within the array, is not obvious since one is dealing essentially with a set of points. (See for instance [
11,
12] for the use of Voronoi polyhedra to study such arrays.) Thus, to study this phenomenon within this discrete model, one is naturally led to study or characterize the stability of homogeneous energy minimizing configurations of such an array, as the density of the array changes. The problems considered in this paper are the simplest problems within such a model. Our main contribution is on the application of global bifurcation theory (as opposed to just local) to study the set of equilibrium configurations for (
1) under the stated constraints. In particular, to give specific conditions in terms of the intermolecular potential
for the existence of nontrivial states.
In
Section 3 we consider the problem of three particles. By Heron’s formula for the area of a triangle, any three numbers (representing the intermolecular distances) that yield a positive value for the area formula, represent a triangle. In this case, we show that the functional (
1) subject to the constraint of fixed area
A, has for any value of
A, a critical point representing an equilateral triangle. Moreover, in Theorem 2 we give a necessary and sufficient condition (cf. (
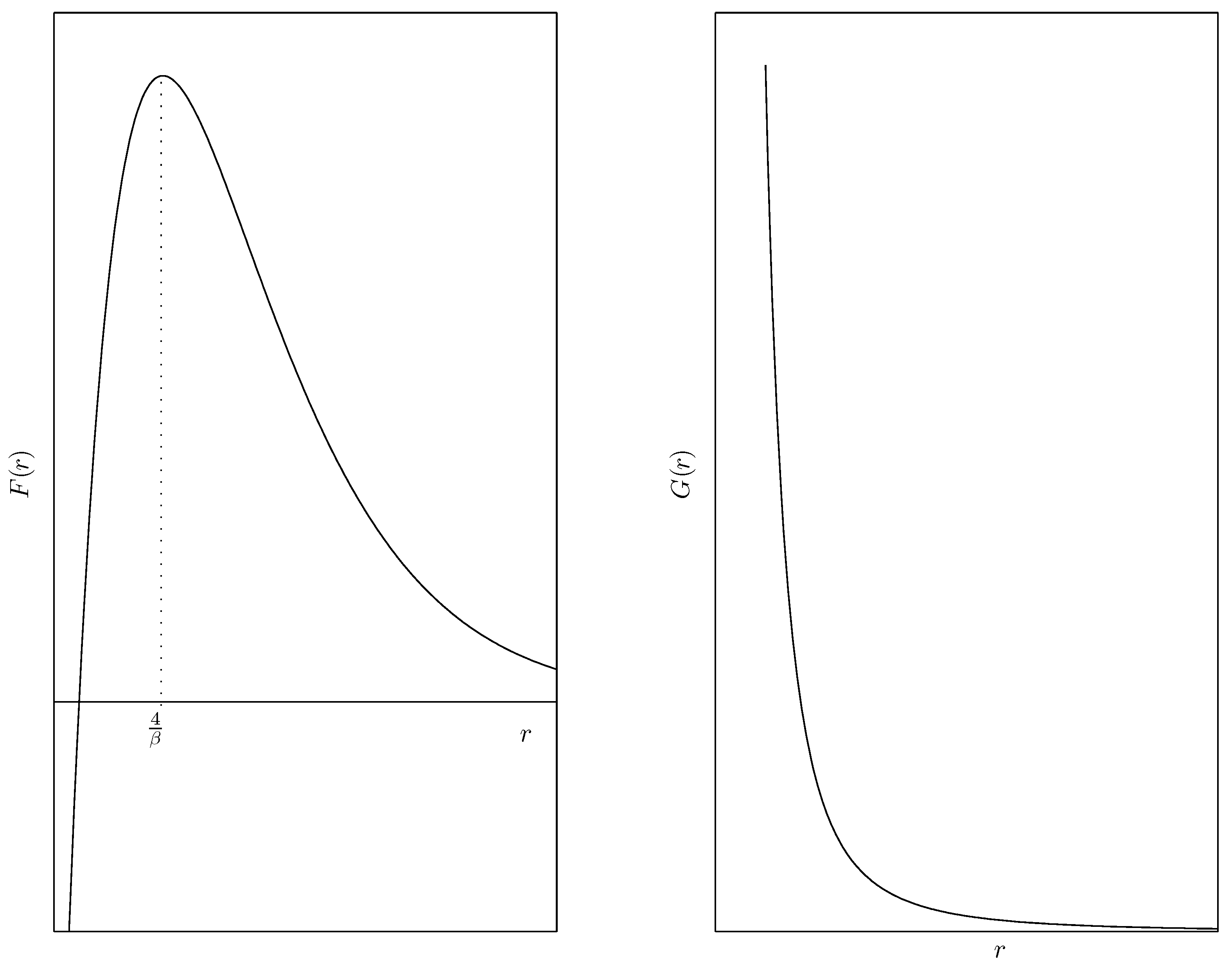
22)), in terms of the intermolecular potential, for this equilibrium point to be a (local) minimizer of the energy functional. This condition leads to a set of values
for the area parameter
A for which the equilateral triangle is a stable configuration. We give examples of how this set looks for various intermolecular potentials including the classical Lennard–Jones [
13] and Buckingham [
14] potentials, and those that model hard and soft springs including the usual Hooke’s law.
Next in
Section 3.2 we turn to the question of whether there exists other (not equilateral) equilibrium configurations for those values of the area parameter
A for which the equilateral triangle becomes unstable, that is, when it ceases to be a local minimizer. To answer this question, we treat the system of equations characterizing the equilibrium points (cf. (
13)) as a bifurcation problem with the parameter
A as a bifurcation parameter, and the set of equilateral equilibrium configurations as the trivial solution branch. We find that the necessary condition for bifurcation from the trivial branch for this system occurs exactly at the boundary points of the set
given by the stability condition (
22). To check the sufficiency condition for bifurcation, one must consider the linearization of the system (
13) about the trivial branch at a boundary point
of
. However, since the kernel of this linearization is two-dimensional we cannot immediately apply the usual or standard results from bifurcation theory (cf. [
15,
16,
17,
18]). Because of the symmetries present in this problem (cf (
32)), we can apply bifurcation equivariant theory (cf. [
16,
19]) to construct a suitable reduced problem corresponding to isosceles triangular equilibrium configurations. The linearization of the reduced problem at the point where
has now a one-dimensional kernel and provided that a certain transversality condition is satisfied (cf. (
34)), we can show that there are three branches corresponding to isosceles triangles bifurcating from the trivial branch at the point where
. Since the stability of these bifurcating branches can only be determined numerically (because one must linearize about an unknown solution), in
Section 5 we construct numerically the bifurcation diagrams, with their respective stability patterns, for instances of the Lennard–Jones and Buckingham potentials. These examples show that the primary bifurcations off the trivial branch are of trans-critical type, and that at least for the Lennard–Jones potential, there are secondary bifurcations corresponding to stable scalene triangles. Moreover, there are intervals of values of the area parameter, for which there exists multiple stable states of the system for each value of
A in such an interval.
In
Section 4 we consider an array of four molecules in a tetrahedron. The general treatment in this case is similar to the three particle case but with two main differences. First the characterization of when six numbers (representing the lengths of the sides of the tetrahedron) determine a tetrahedron, is given in terms of the Cayley-Menger determinant and the triangle inequalities of one of its faces (cf. [
20]). The next complication arises from the fact that the tetrahedron has 24 symmetries as compared to only six for the triangle! To deal with this many possibilities, once again we make use of the basic techniques of equivariant theory to get suitable reduced problems to work with. As the Cayley–Menger determinant is proportional to the volume of the corresponding tetrahedron, the volume constraint in our problem is basically that of setting this determinant to a given value
V for the volume. In this case we show in
Section 4.1 that the functional (
1) subject to the constraint of fixed volume
V, has for any value of
V a critical point representing a regular or equilateral tetrahedron. Moreover, in Theorem 4 we give necessary and sufficient conditions (cf. (
43)), in terms of the intermolecular potential, for this equilibrium point to be a (local) minimizer of the energy functional. As for the triangular case, these conditions determine a set of values
for the volume parameter
V for which the equilateral tetrahedron is a stable configuration.
In
Section 4.2 we consider the question of the existence of non-equilateral equilibrium configurations. The equilibrium configurations in this case are given as solutions to a nonlinear system of seven equations in eight unknowns (cf. (
40)). We treat this system as a bifurcation problem with the parameter
V as a bifurcation parameter, and the set of equilateral tetrahedrons as the trivial solution branch. The necessary condition for bifurcation from the trivial branch for this system occurs exactly at the boundary points of the set
given by the stability conditions (
43). At a boundary point
of
there are two possibilities: the kernel of the linearization has dimension two or three. Using some of the machinery of equivariance theory as in [
16], we can construct suitable reduced problems in each of these two cases, which enables us to establish the existence of non-equilateral equilibrium configurations and to get a full description of the symmetries of the bifurcating branches (cf. Theorems 5–7). As in the triangular case, the stability of this bifurcating branches can only be established numerically because one must linearize about the unknown bifurcating branch.
Notation: We let denote the n dimensional space of column vectors with elements denoted by , ,⋯ The inner product of is denoted either by or , where the superscript “t” denotes transpose. We denote the set of matrices by . For , we let and . For a function , we denote its Fréchet derivative by which is given by the matrix of partial derivatives of the components of . If the variables in are given by , then denotes the derivative of with respect to the vector of variables , i.e., the matrix of the partial derivatives of the components of with respect to the variables corresponding to .
2. Equivariant Bifurcation from a Simple Eigenvalue
In this section, we provide an overview on some of the basic results on bifurcation theory from a simple eigenvalue for mappings between finite dimensional spaces, where the maps possess certain symmetries. The literature on this subject is extensive but we refer to [
6,
15,
17] for details on the material presented in this section and further developments like for instance, the infinite dimensional case.
Let
where
is an open subset of
, be a
function, and consider the problem of characterizing the solution set of:
We assume that there exists a (known) smooth function
such that:
The set
is called the
trivial branch of solutions of (
2). We say that
is a
bifurcation point off the trivial branch
, if every neighborhood of
contains solutions of (
2) not in
. If we let
then by the Implicit Function Theorem, a necessary for
to be a bifurcation point is that
must be singular, a condition well known to be not sufficient.
In many applications of bifurcation theory and for the problems considered in this paper, the mapping
possesses symmetries due to the geometry of the underlying physical problem. The use of these symmetries in the analysis is useful for example to deal with problems in which
. Thus, we assume that for a proper subgroup
of
, characterizing the symmetries in the problem, the mapping
satisfies:
Let
and define the
isotropy subgroup of
at
by
and the
–
fixed point set by
Clearly .
Let
be a linear map that projects onto
that is
and
. With
, we define
by:
An easy calculation now gives that
We assume that
for all
A, so that
It follows now that
is given by:
Clearly
. The
-
reduced problem is now given by:
An important property relating (
2) and (
7) is that
is a solution of (
2) if and only if
is a solution of (
7). The following result provides the required sufficient conditions for
to be a bifurcation point of the
-reduced problem.
Theorem 1 (Equivariant Bifurcation Theorem [
19]).
Assume that for there exists that defines a proper isotropy subgroup such that:Then there exists a branch of nontrivial solutions of bifurcating from the trivial branch at the point where and such that either:
- 1.
is unbounded in ;
- 2.
the closure of intersects the boundary of ;
- 3.
intersects at a point where .
The proof of this theorem is basically an application of a result from Krasnoselski [
18] that uses the homotopy invariance of the topological degree. The three alternatives in the statement of the theorem are usually referred to as the Crandall and Rabinowitz alternatives. The local version of this result (cf. [
6]) that is, without the Crandall and Rabinowitz alternatives, can be obtained via the Lyapunov–Schmidt reduction method. A useful consequence of this reduction is an approximate formula for the bifurcating branch in a neighborhood of the bifurcation point. Let
, where
, so that
. Now if we define
(here the zero superscripts mean evaluated at
), then the bifurcating branch have the following asymptotic expansion (cf. [
16]):
where
4. Four Particles in a Tetrahedron
We now consider the case of four particles arranged in a tetrahedron
T. Let
a,
b,
c,
A,
B,
C be the distances between the particles where
denote the lengths of the edges joining a vertex of
T,
A the length of the edge opposite to
a,
B the length of the edge opposite to
b, and
C the length of the edge opposite to
c. The six-tuple
generates a tetrahedron ([
20]) if and only if
where
is given by the Cayley–Menger determinant:
If we let
denote the set of positive real numbers, then we define
Please note that is open in . Moreover, any regular tetrahedron in which , is contained in .
If generates a tetrahedron, then so does where and
R permutes and with the same permutation of three elements;
Q is any permutation of in which the base of the tetrahedron is changed to another face. For example, corresponds to reorienting the tetrahedron so that the base is given by .
Since there are six permutations of the type
R and four of the type
Q, we get that there are 24 permutations of the form
. These 24 permutations form a subgroup
of the group of permutations of six letters. Also, it is easy to show that
As the Cayley–Menger determinant is directly proportional to the square of the volume of the tetrahedron (cf. (
39)), this identity simply states that the volume of the tetrahedron remains the same after rotations of the base and independent of which face we use as the base.
The total energy of the system of four particles is given now by:
where the intermolecular potential
is as before. For any
we consider the constrained minimization problem:
The constraint here specifies that the tetrahedron determined by
has volume
V (cf. [
20]). The first-order necessary conditions for a solution of this problem are given by (Since the inequality constraints in the definition of the set
are strict (non-active), the multipliers corresponding to these constraints are zero.): confirm.
which is now a nonlinear system for the seven unknowns
in terms of the parameter
V.
4.1. Existence and Stability of Trivial States
Expanding the determinant in (
36) and computing its partial derivatives, we get that
Since
, the system (
40) when evaluated at the regular tetrahedron
, reduces to
Thus, we have the following result.
Lemma 2. For any the system (40) has the solution where and We now examine the stability of the trivial state (
41). A lengthy but otherwise elementary calculation shows that
where
Since
, we need examine the structure of
on the subspace of
given by
We have now the following result:
Theorem 4. Let be twice continuously differentiable function. Then the matrix (42) is positive definite over if and only if and , which in turn are equivalent to Thus, the regular tetrahedron is a relative minimizer for the problem (39) for those values of V for which conditions (43) hold. Proof. It is easy to check that
where
The matrix corresponding to the quadratic form of
restricted to
is now given by
. The eigenvalues of
are:
Since the product of the last two of these eigenvalues is
, and
, we can conclude now that they are all positive if and only if
and
. Thus,
restricted to
is positive definite provided these two conditions hold, which in turn implies that
is a relative minimizer for problem (
39). That
and
are equivalent to (
43) follows from the definitions of
and
. □
Example 4. For the Lennard–Jones potential (23) we have that: For simplicity, we assume . We now have two cases:
- 1.
Assume that . Then the second condition in (43) is automatically satisfied and the first condition holds if and only if , where is determined from the condition (cf. (41)):from which it follows that: Thus, in this case the regular tetrahedron is a (local) solution of (39) if and only if . - 2.
If , then the second condition in (43) holds if and only if , where is determined from the condition:from which it follows that: Since , it follows that . Thus, in this case the regular tetrahedron is a (local) solution of (39) if and only if .
Example 5. For the Buckingham (25), we have that Please note that the first condition in (43) holds for an interval of volume values under the conditions (27) in Example 2. The analysis now becomes rather complicated and we just describe it qualitatively. If , then the second condition in (43) would hold as well for values of V in an interval of the form provided some condition similar to (27) holds. Depending as to whether or not the intersection is non-empty, we might get stable regular tetrahedrons. On the other hand, if , then the second condition in (43) would hold as well for values of V in an interval of the form and again the existence of trivial states will depend on whether the corresponding intersection is non-empty. Example 6. For the potential (29)Please note that the stability conditions (43) holds when independent of the value of V! That is, the regular tetrahedron is a relative minimizer for the problem (39) for all values of V. In the case , since the functional (38) is convex, this state is a global minimizer. On the other hand, if , the first condition in (43) holds if and the second condition if where Since we get that conditions (43) hold both for . For either one or both conditions fail. 4.2. Existence and Stability of Nontrivial States
Let
be given by the left-hand side of (
40):
where
. We have now that
It follows from (
37) that
with similar relations for the total energy
E. It follows now from (
45a) that
where
Thus, the system (
40) remains the same, up to reordering of the equations, when
is replaced by
.
We now begin the analysis of the existence of solutions of the system (
40) bifurcating from the trivial branch:
If we evaluate (
44) at the trivial state
, then this matrix reduces to:
where
and
is given by (
42). The matrix (
47) has two eigenvalues which are nonzero for every value of
, with the remaining eigenvalues given by:
with algebraic and geometric multiplicity three, and corresponding eigenvectors:
with algebraic and geometric multiplicity two, and corresponding eigenvectors:
Remark 1. Please note that the expressions for these eigenvalues are the ones that appear in Theorem 4 characterizing the stability of the trivial state . Thus, the trivial state can change stability exactly when one of these two eigenvalues becomes zero.
To deal with these kernels with dimension greater than one, we proceed as in the previous section by considering a suitable reduced problem in each case. These reductions are determined by the symmetries present in this problem which are embodied in (
46).
4.2.1. The Eigenvalue
Let us take the eigenvector
of the eigenvalue
above. (The analysis for the other two eigenvectors is similar.) By inspection it is easy to get that the isotropy subgroup
of
at
is given by:
The
-
fixed point set is now given by:
The projection
has matrix representation:
and the
reduced problem is now:
Since
, it follows that
is a branch of solutions for the
reduced problem. Also, since
we have that
is given by:
It easy to check now that
is a simple eigenvalue of
restricted to
with corresponding eigenvector
that is
We now have the result for the existence of bifurcating branches for the reduced problem. We omit the proof as it is similar to that of Theorem 3.
Theorem 5. Let and assume that . Then the system (40) has a branch of nontrivial solutions in bifurcating from the trivial branch at the point where , where is given by (50). Remark 2. It follows from (46) that there are two additional branches of nontrivial solutions of the system (40) of the forms: We now consider the case of the eigenvector
of
. This eigenvector is obtained by adding the three eigenvectors in (
48). By inspection, the isotropy subgroup
of
at
is given by those permutations in
that permute the symbols
and
in
with the same permutation. (Thus,
has six elements.) The
–fixed point set is now given by:
The projection
has matrix representation:
It follows now that for the reduced problem, is a simple eigenvalue with corresponding eigenvector . The proof of the following result is as that of Theorem 3.
Theorem 6. Let and assume that . Then the system (40) has a branch of nontrivial solutions in bifurcating from the trivial branch at the point where , where is given by (51). Remark 3. By applying all the transformations in , it follows from (46) that there are three additional branches of solutions of the system (40) of the forms: Thus, combining both theorems, we get that there are seven branches of nontrivial solutions bifurcating from the trivial branch at the value of where and .
4.2.2. The Eigenvalue
We now consider the case of the eigenvector
of
. This eigenvector is obtained by adding the eigenvectors in (
49). By inspection, the isotropy subgroup
of
at
is given by
with
–fixed point set given by:
The projection
has matrix representation:
It follows now that for the -reduced problem, is a simple eigenvalue with corresponding eigenvector . The proof of the following result is as that of Theorem 3.
Theorem 7. Let and assume that . Then the system (40) has a branch of nontrivial solutions in bifurcating from the trivial branch at the point where , where is given by (52). Remark 4. By applying all the transformations in , it follows from (46) that there are two additional branches of solutions of the system (40) of the forms: 5. Numerical Examples
In this section, we present some numerical examples illustrating the results of the previous sections. For simplicity we limit ourselves to the three particle problem. The examples show that the structure of the bifurcation diagrams is quite rich and complex. To construct the pictures in this section, we use the results of Theorem 3, in particular the symmetries given by (
32), together with various numerical techniques to get full or detailed descriptions of the corresponding bifurcation diagram.
To compute approximations of the bifurcating solutions predicted by Theorem 3, one employs a predictor-corrector continuation method (cf. [
24,
25]). The bifurcation points off the trivial branch can be determined, by Theorem 3, from the solutions of the equation
(cf. (
17), (
33)). Secondary bifurcation points off nontrivial branches can be detected by monitoring the sign of a certain determinant. Once a sign change in this determinant is detected, the bifurcation point can be computed by a bisection or secant type iteration. After detection and computation of a bifurcation point, then one can use formulas (
8)–(
10) to get an approximate point on the solution curve from which the continuation of the bifurcating branch can proceed.
Any trivial or nontrivial computed solution
will be called
stable, if the matrix
(cf. (
31)) is positive definite when restricted to the tangent space at
of the constraint of fixed area. Otherwise the point
will be called
unstable. We recall that the tangent space at
of the constraint of fixed area is given by
Please note that since this space depends on the point , then except for the trivial branch where the solution is known explicitly, the stability of a solution can only be determined numerically.
In our first example we consider the Lennard–Jones potential (
23) with
,
,
, and
. (We obtained similar results for other values of
like those for argon in which
Å
.) From equation (
24) we get that the bifurcation point off the trivial branch is given approximately by
. For the case of Theorem 3 in which
, we show in
Figure 2 a close-up of the bifurcating branch near this bifurcation point, for the projection onto the
A–
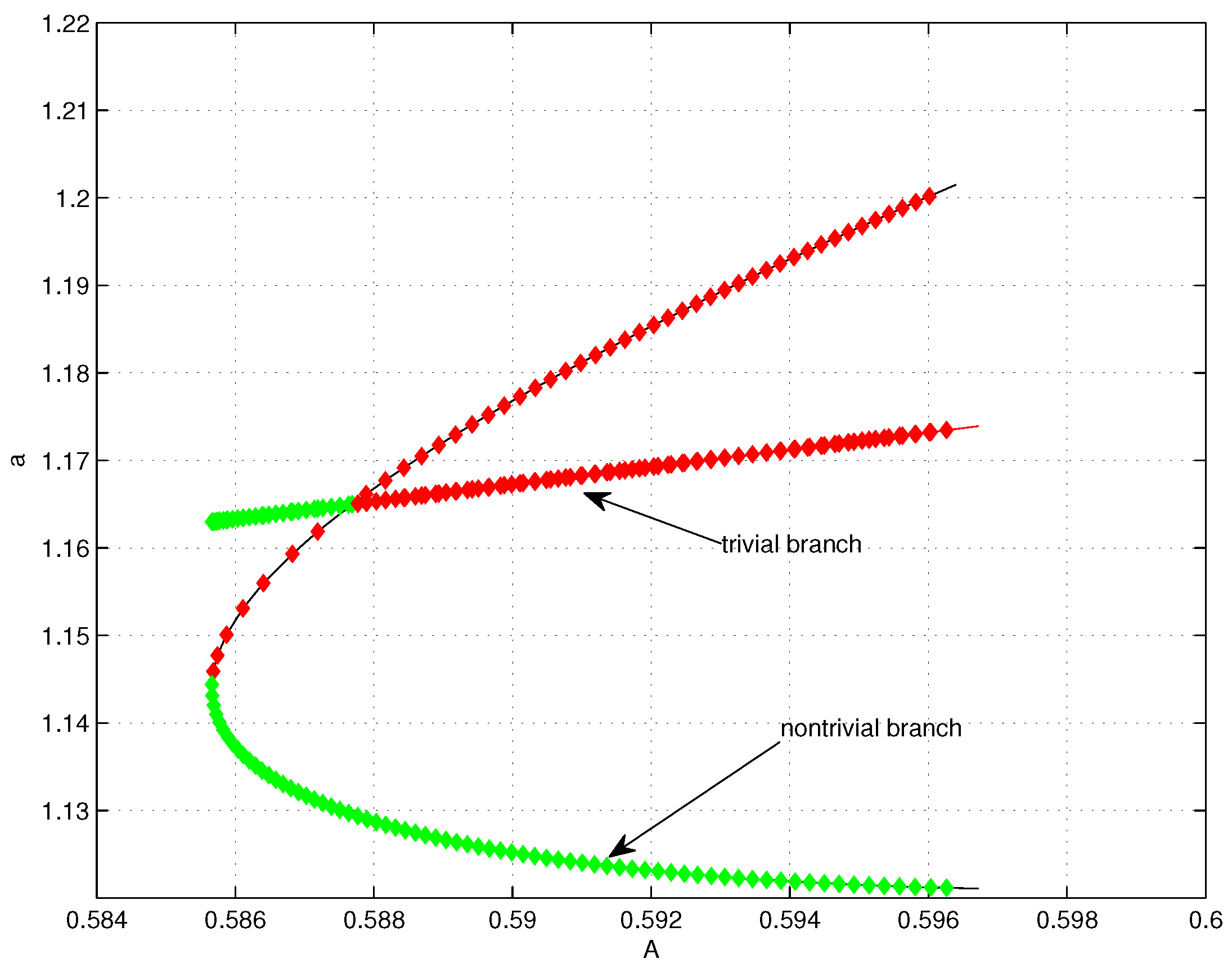
a plane. In this figure and the others, the color red indicates unstable solutions while the stable ones are marked in green. Please note that the bifurcation is of the trans-critical type. It is interesting to note that for an interval of values of the parameter
A to the left of
in the figure (approximately
), there are multiple states (trivial and nontrivial) which are stable, the trivial one with an energy less than the nontrivial state in this case. In
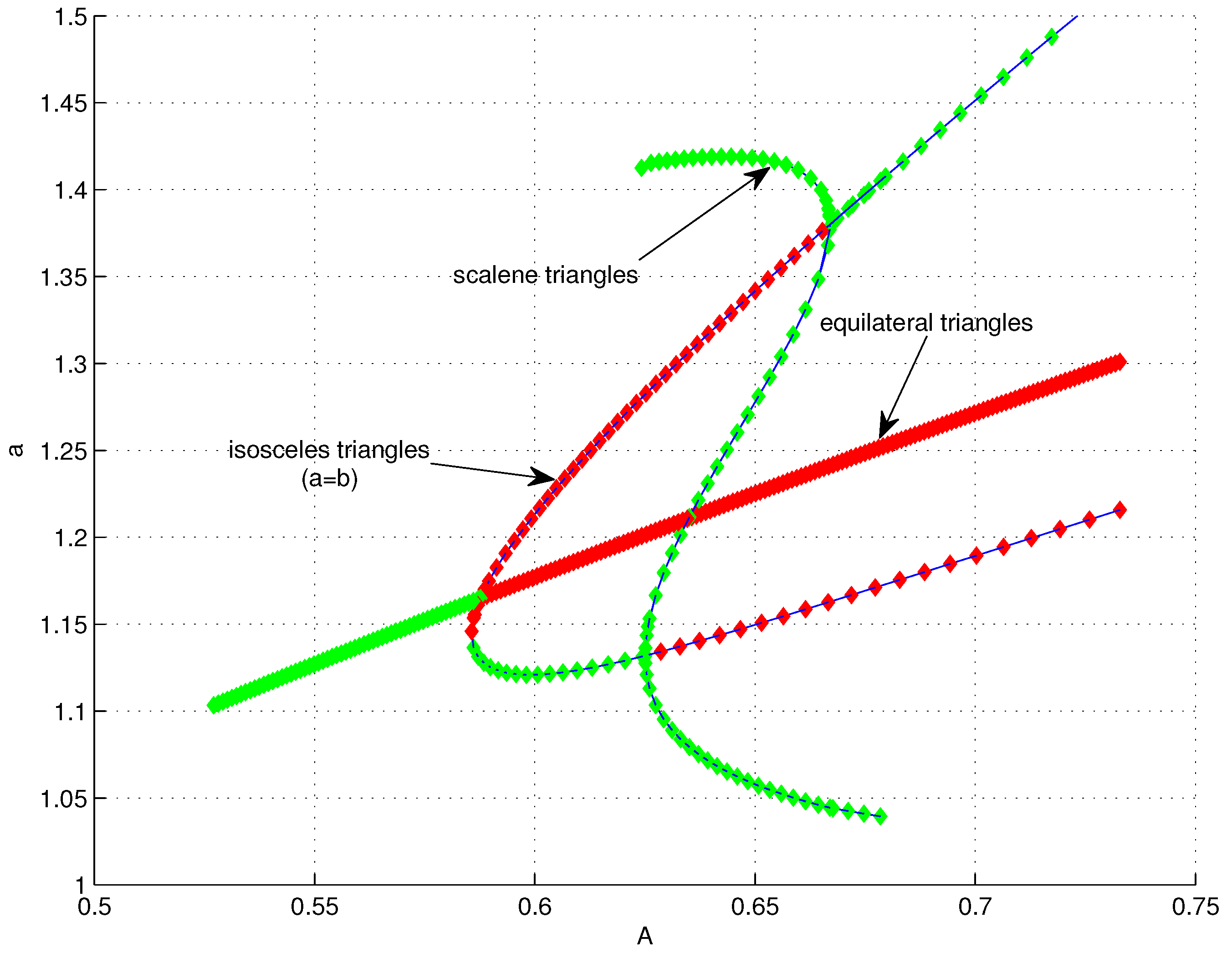
Figure 3 we look at the same branches of solutions, again the projection onto the
A–
a plane, but for a larger interval of values of
A. We now discover that there are two secondary bifurcation points (In
Figure 3 there are bifurcations only corresponding to the values of
,
and
. The apparent crossing of a branch of scalene triangles and the trivial branch is just an artifact of the projection onto the
A–
a plane.) at approximately
and
, and once again we have multiple stable states (with different symmetries) existing for an interval of values of the parameter
A. The branches of solutions bifurcating at these values of
A correspond to stable scalene triangles. Once a branch of solutions is computed, we can use the symmetries (
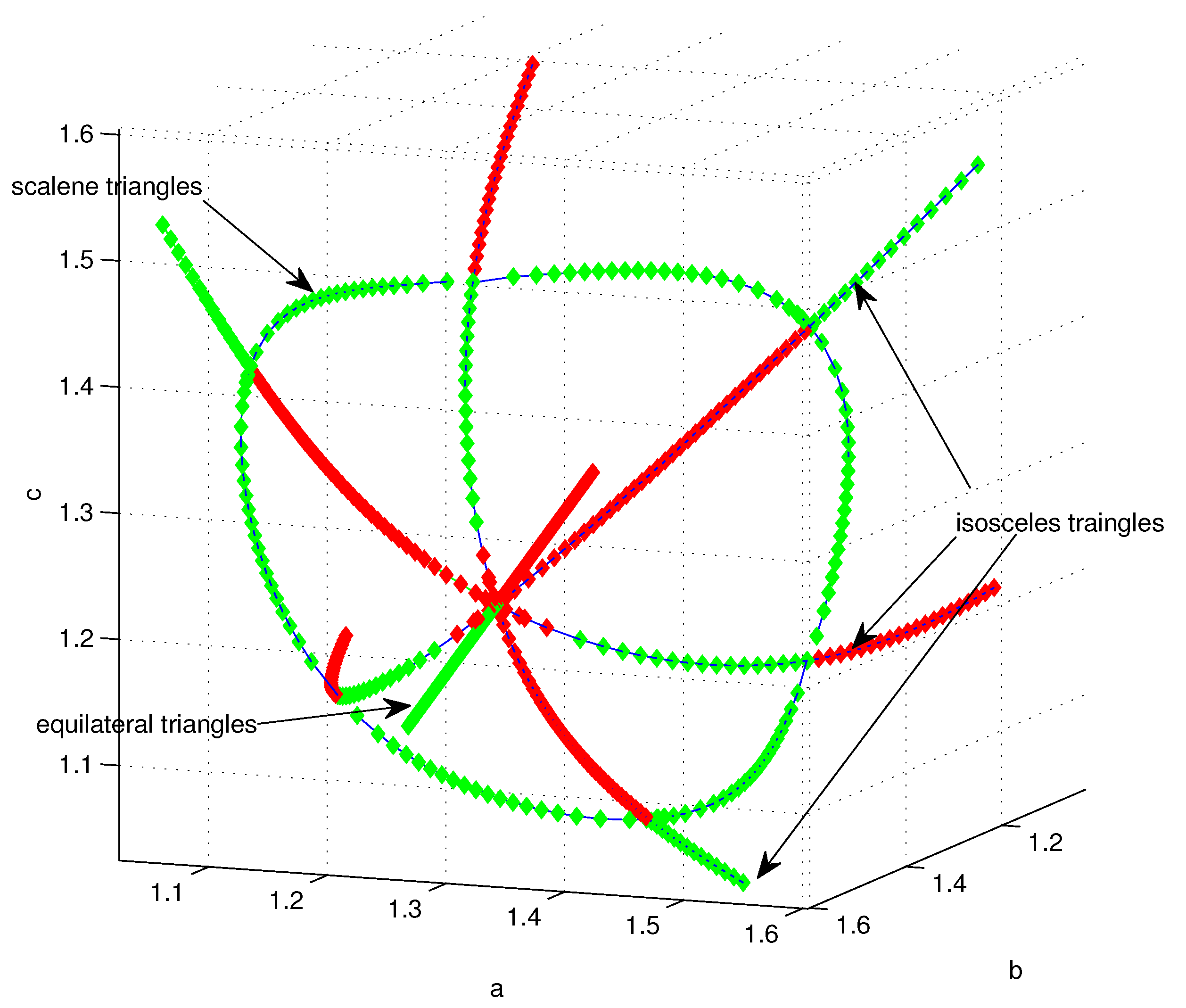
32) to generate other branches of solutions. In
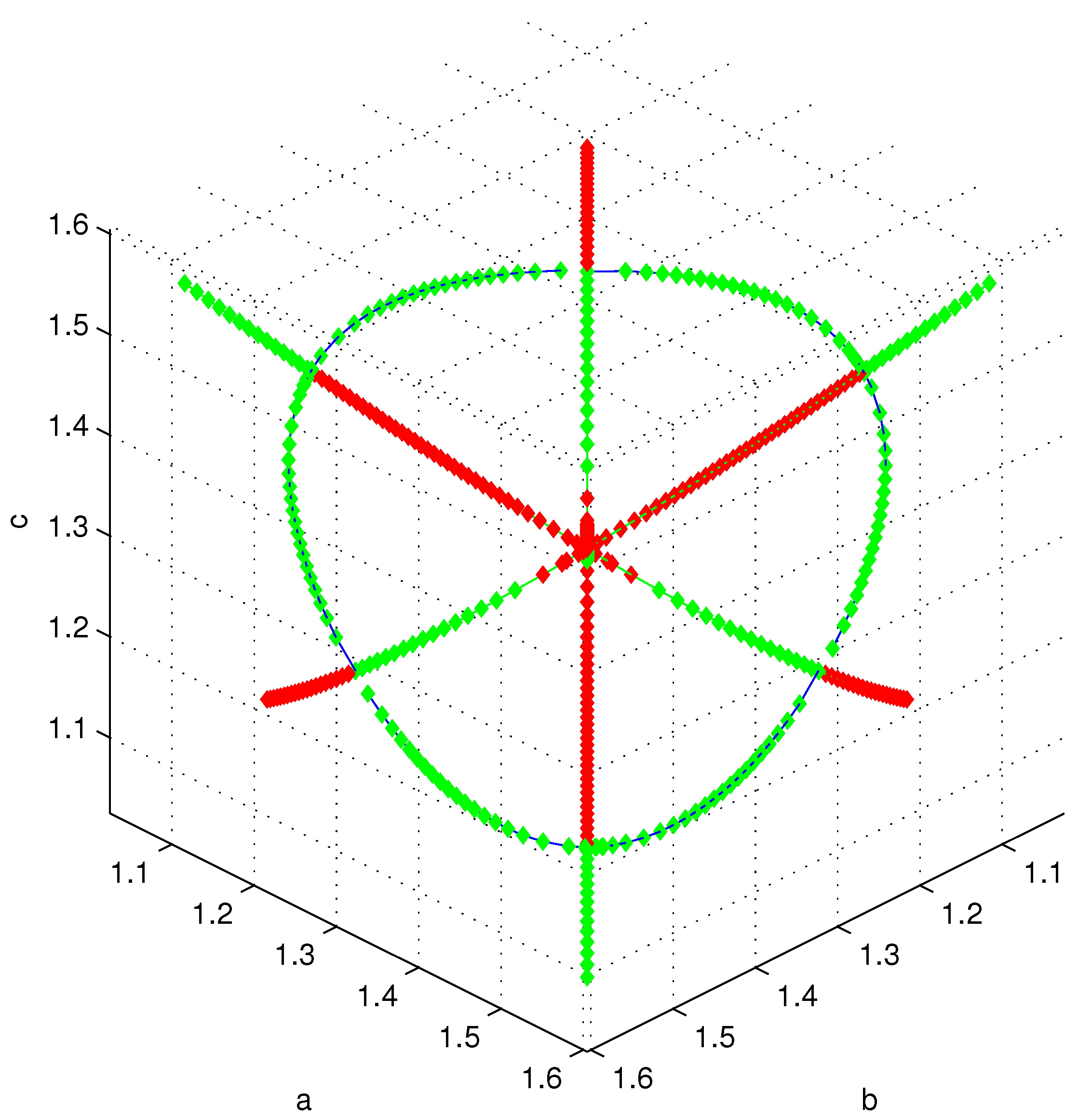
Figure 4 we show all the solutions obtained via this process, projected to the
space (no
A dependence).
Figure 5 show the same set of solution but with the branch or axis of trivial solutions coming out of the page. The figures clearly show the variety of solutions (stable and unstable) for the problem (
12) as well as the rather complexity of the corresponding solution set.
For our next numerical example, we consider the Buckingham potential (
25) with parameter values
and
, which satisfy (
27). In this case, we have two bifurcation points off the trivial branch (which correspond to solutions of
) at approximately
and
. The trivial branch is stable for
and unstable otherwise. Both bifurcations are into isosceles triangles, and both are of trans-critical type but with different stability patterns. In
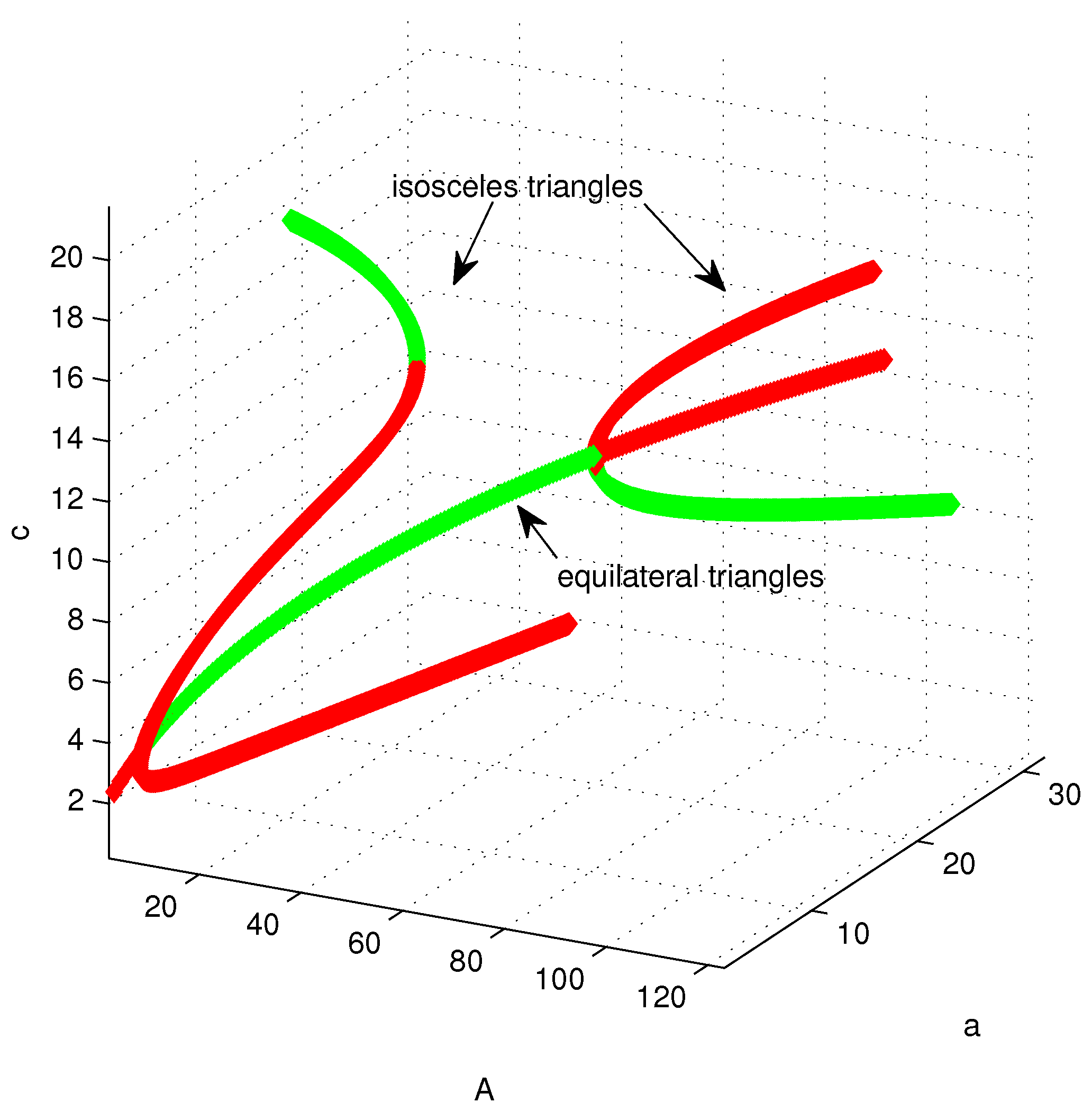
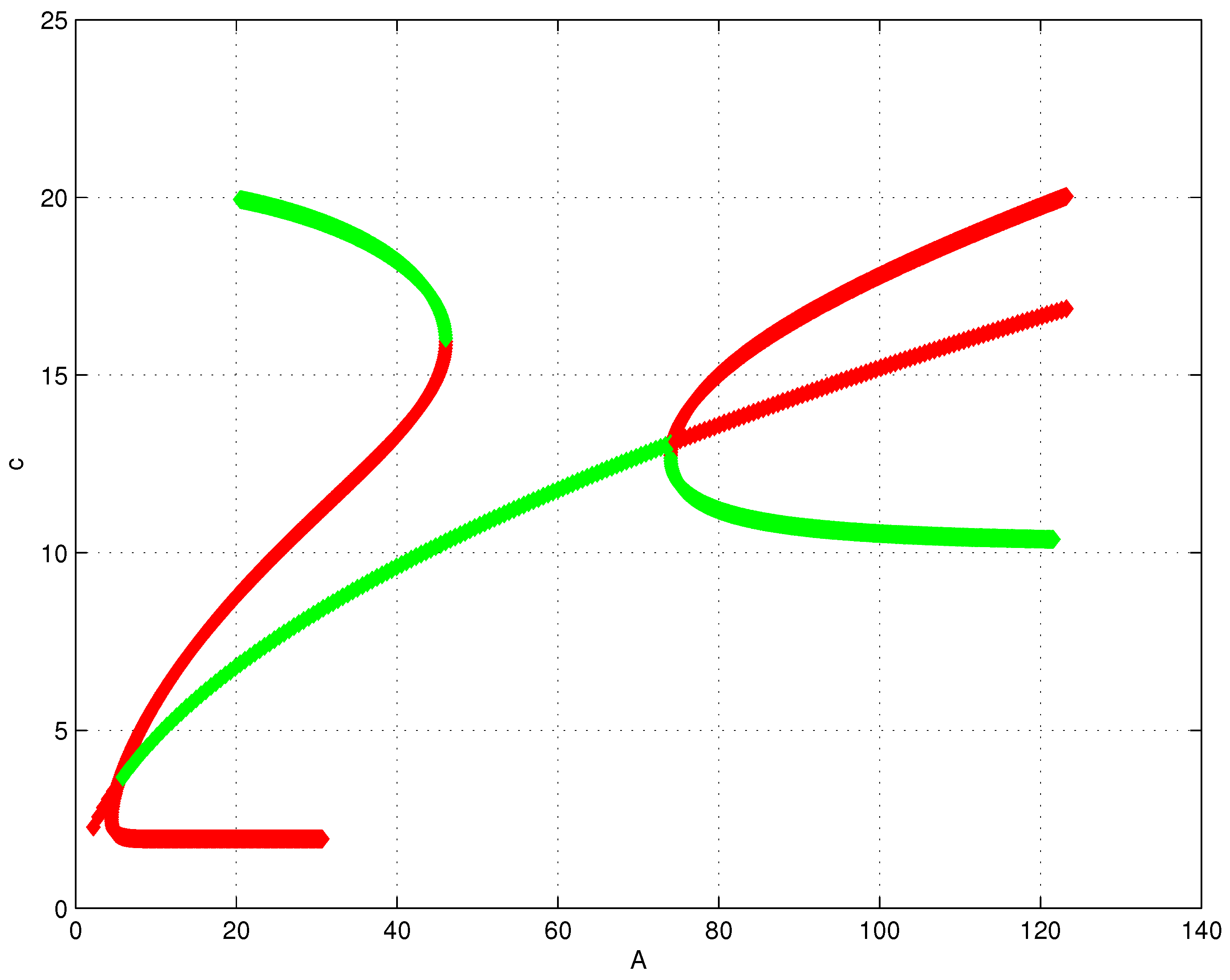
Figure 6 we show the solution set for the case
. The plot shows the dependence of the
a and
c components on the area parameter
A. In
Figure 7 we show the projection of this set onto the
c vs.
A plane where one can appreciate somewhat better the stability patterns at each bifurcation point, and that there is a turning point for
on the branch bifurcating from
. Please note that once again we have multiple stable states existing for an interval of values of the parameter
A. No secondary bifurcations were detected in this case.