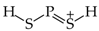Abstract
The geometry-based HOMA (Harmonic Oscillator Model of Aromaticity) descriptor, based on the reference compounds of different delocalizations of n- and π-electrons, can be applied to molecules possessing analogous bonds, e.g., only CC, only CN, only CO, etc. For compounds with different heteroatoms and a different number of CC, CX, XX, and XY bonds, its application leads to some discrepancies. For this reason, the structural descriptor was modified and the HOMED (Harmonic Oscillator Model of Electron Delocalization) index defined. In 2010, the HOMED index was parameterized for compounds with C, N and O atoms. For parametrization, the reference molecules of similar delocalizations of n- and π-electrons were employed. In this paper, the HOMED index was extended to compounds containing the CP, CS, NN, NP, PP, NO, NS, PO, and PS bonds. For geometrical optimization of all reference molecules and of all investigated heterocompounds, the same quantum–chemical method {B3LYP/6-311+G(d,p)} was used to eliminate errors of the HOMED estimation. For some tautomeric systems, the Gn methods were also employed to confirm tautomeric preferences. The extended HOMED index was applied to five-membered heterocycles, simple furan and thiophene, and their N and P derivatives as well as for tautomeric pyrrole and phosphole and their N and P derivatives. The effects of additional heteroatom(s) in the ring on the HOMED values for furan are parallel to those for thiophene. For pyrroles, aromaticity dictates the tautomeric preferences. An additional N atom in the ring only slightly affects the HOMED values for the favored and well delocalized NH tautomers. Significant changes take place for their rare CH forms. When intramolecular proton-transfer is considered for phosphole and its P derivatives, the PH tautomers seem to be favored only for 1,2,3-triphosphole/1,2,5-triphosphole and for 1,2,3,5-tetraphosphole. For other phospholes, the CH forms have smaller Gibbs energies than the PH isomers. For phosphazoles, the labile proton in the favored form is linked to the N atom. The PH forms have smaller HOMED indices than the NH tautomers but higher than the CH ones.
1. Introduction
For a quantitative description of aromaticity in homo- and heteroaromatic compounds, Kruszewski and Krygowski proposed in 1972–1974 the Harmonic Oscillator Model of Aromaticity (HOMA) index [1,2,3,4]. This criterion of aromatic character is directly based on molecular structures (bond lengths) of π-electron systems. Twenty years later, taking into account the concept of resonance coordinate proposed by Jug and Koester [5], Krygowski reformulated the original HOMA index [6]. Although a use of the reformulated HOMA index (rHOMA) to different cyclic and acyclic, less or more delocalized heteroatomic systems leads to some unexpected results [7,8,9,10,11,12], it is continuously used for the analyses of π-electron delocalization in heterocompounds [13,14,15,16,17,18,19]. The greatest discrepancies in rHOMA can be distinguished for five-membered heterocycles containing N, P, O, S and Se atoms, e.g., pyrrole, phosphole, furan, thiophene, selenophene, and their derivatives [7,8,12,13]. The rHOMA values are completely different. They are very low (<0.3) for furan and phosphole, suggesting that these compounds are not aromatic, while they are very high (>0.7) for pyrrole, thiophene and selenophene, confirming that they display an aromatic character [12]. Note that the original HOMA procedure predicts the values close to unity for pyrrole, furan and thiophene [4].
Looking for a more appropriate structural descriptor of electron delocalization in any conjugated heterocompound, we returned to the original HOMA idea. In 2006, a new parametrization was signaled for HOMA [20]. To distinguish the reformulated HOMA index that can be used for hydrocarbons and also for some heteroaromatic π-electron molecules, a name ‘Harmonic Oscillator Model of Electron Delocalization’ and an abbreviation ‘HOMED’ was suggested for the new parameter [20]. However, it can also be named HOMA. In 2010, the HOMED index was parametrized for molecules with C, N and O atoms [21]. This index describes π-electron delocalization in conjugated cyclic and acyclic homo- and heterosystems [21,22,23,24]. It properly measures electron delocalization in aromatic systems, medium π-π and n-π conjugated compounds, as well as weak σ-π hyperconjugated molecules. In 2012, the HOHMED (Harmonic Oscillator Model of Heterocyclic Electron Delocalization) descriptor was applied to 16 heterocompounds [25]. For parametrization, authors took the idea of the original HOMA [1,2,3,4] and HOMED indices [21] and the statistical experimental bond lengths for C–C, C–X, X–Y, C=C, C=X, and X=Y. Both the HOMED and HOHMED procedures predict the values close to unity (>0.65) for furan, oxazole, pyrrole, imidazole, etc. [12,21,25].
In the literature, one can also find other structural as well as electronic, energetic, magnetic, and spectroscopic descriptors of aromaticity [7,8,12,13,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55]. Note that geometry-based indices can be applied for entire conjugated systems and also for selected fragment(s) in these systems [12,21]. Since the same resonance phenomenon operates in aromatic compounds and in other cyclic and acyclic homo- and hetero-conjugated systems [56,57,58,59,60], various parameters quantitatively describing π-electron delocalization in a series of weakly, moderately and strongly conjugated compounds can be mutually interrelated [34,45,46,47,48,49,50,52,53,54,55]. However, the situation is more complex, and a hypothesis of the multidimensional character of aromaticity has been formulated [7,12]. Nevertheless, in some cases, a lack of general correlations between various descriptors of aromaticity needs some explanation. Recently [12,21], it has been signaled that values of various descriptors depend on the reference systems. Hence, it is necessary to analyze first the similarities and differences for descriptors based on the same property, and in the case of a lack of correlation between them, it is important to clarify the reason(s).
In this paper, the HOMED index was extended to π-electron heterocompounds possessing the CP, CS, NN, NP, PP, NO, NS, PO, and PS bonds. For investigations, the same quantum–chemical method {B3LYP/6-311+G(d,p) [61,62,63,64]} was employed as previously described for π-electron molecules with C, N and O atoms [21]. The procedures and parametrizations of the HOMED descriptor were compared to those of the rHOMA index, and some similarities and differences were analyzed. This analysis gives the possibility to indicate the most important discrepancies between the rHOMA and HOMED values for compounds containing various numbers of CC, CX, XX, and XY bonds and to explain their reasons. It also makes it possible to formulate some limits of rHOMA application. The extended HOMED index was employed to five-membered heterocycles, simple furan, thiophene, and their N- and P-derivatives as well as tautomeric pyrrole, phosphole, their N- and P-derivatives, and phosphazoles. The effects of additional heteroatom(s) in the ring on the HOMED values were discussed. Tautomeric conversions for azoles, phospholes and phosphazoles were analyzed. For selected tautomeric systems, the Gn levels of theory [65] were also applied to confirm the stability of favored tautomers. The effects of planarity and aromaticity of the ring on tautomeric equilibria were considered.
2. Methodology
Geometries of the simplest molecules applied for the reference bond lengths Rs, Rd and Ro in the HOMED procedure as well as the geometries of simple and tautomeric five-membered heterocycles were optimized using the B3LYP functional [61,62,63] and the 6-311+G(d,p) basis set [64] as described previously [21,66]. The optimized structures are energy minima possessing positive vibrational frequencies. An application of other methods (HF and MP2) and the other basis sets {6-31G(d), 6-31G(d,p), 6-31+G(d,p), 6-31++G(d,p), 6-311++G(d,p), 6-311+G(3df,2p), 6-311++(3df,2p), cc-pVTZ, and aug-cc-pVTZ} does not influence the HOMED values when the same level of theory is applied for the investigated and reference compounds [21]. For example, using various levels of theory, the HOMED values estimated for propene (CH3–CH=CH2) are close to 0.26–0.27, 0.31–0.32, and 0.32–0.33, at the HF, MP2, and B3LYP levels, respectively. For tautomeric azoles, phospholes and phosphazoles, zero point energies, electronic energies, and additionally enthalpies, entropies, and Gibbs energies at 298.15 K were estimated for each tautomeric form using the same functional and the same basis set {B3LYP/6-311+G(d,p)} as those applied for geometry optimization. For phospholes, calculations were also carried out using the Gn methods [65]. For geometric optimization and for thermochemical quantities estimation, the Gaussian 03 program [67] was used.
3. Results and Discussion
3.1. HOMED Procedure
The procedures of structural descriptors, HOMED [21], original HOMA [1,2,3,4], and reformulated HOMA [6] are analogous. The HOMED and HOMA indices can be estimated according to Equation (1), where α are the normalization constants for CC, CX, XX, and XY bonds (X, Y = N, P, O, S, etc.); Ro are the appropriate optimum CC, CX, XX, and XY bond lengths for completely delocalized compounds with only CC, only CX, only XX, and only XY bonds; Rx are the experimental or calculated bond lengths in a studied system; and n is the number of CC, CX, XX, and/or XY bonds taken into account. In the original HOMA procedure, the normalization α constant for aromatic hydrocarbons is equal to 98.89 [1,2,3]. This value is a consequence of the following condition: HOMA = 0 for the structure of benzene, proposed by Kekulé, with hypothetical pure C–C and pure C=C bonds. For aromatic benzene, HOMA = 1. The same factor of 98.89 was employed for conjugated heterocycles [4]. Considering the harmonic oscillator method of optimization, the optimum bond lengths in HOMA could be calculated using Equation (2), where Rs and Rd are the single and double bond lengths, respectively, in selected reference compounds, and ω (assumed to be close to 2 for different types of bonds) is the ratio of stretching force constants for pure double and pure single bonds [1,2,3,4,6].
HOMA or HOMED = 1 − {α(CC)Σ[Ro(CC) − Rx(CC)]2 + α(CX)Σ[Ro(CX) − Rx(CX)]2 + α(XX)Σ[Ro(XX) − Rx(XX)]2 + α(XY)Σ[Ro(XY) − Rx(XY)]2}/n
Ro = (Rs + ωRd)/(1 + ω)
α = 2[(Ro − Rs)2 + (Ro − Rd)2]−1
α = (2i + 1)[(i + 1) (Ro − Rs)2 + i(Ro − Rd)2]−1
α = (2i +1)[i(Ro − Rs)2 + (i +1)(Ro − Rd)2]−1
In the reformulated HOMA procedure [6], the normalization α constants are not the same for the CC, CX, XX, and XY bonds. They can be calculated using Equation (3). This equation can also be applied in the HOMED procedure [21] for molecules possessing an even number of bonds (2i). However, equations (4) and (5) can be employed for molecules with an odd number of bonds (2i + 1), i.e., i double bonds and (i + 1) single bonds, and (i + 1) double bonds and i single bonds, respectively. Equations (3)–(5) fulfill the following condition: rHOMA = 1 and HOMED = 1 for completely delocalized compounds with Rx = Ro, like for original HOMA. For molecules possessing the calculated single and double bond lengths close to Rs and Rd, respectively, rHOMA and HOMED indices are close to zero [6,21]. Since differently delocalized molecules were taken for the reference bond lengths in both descriptors, zero in the rHOMA and HOMED scales does not correspond to the same molecule (see subchapters 3.2 and 3.3).
3.2. HOMED Parametrization
Based on parametrization of the original HOMA index [1,2,3,4], the simplest compounds of analogous delocalization of n- and π-electrons were chosen for Rs, Rd and Ro in the HOMED procedure [21]. Their formulae and selected bond lengths are given in Table 1. This choice leads to the normalization α constant (α2i and α2i + 1) values for the CC, CX, XX, and XY bonds between 40 and 100 (Table 2). The α values in HOMED are not larger than the factor of 98.89 proposed in the original HOMA procedure [1,2,3,4].

Table 1.
The reference molecules and the DFT-calculated Rs, Rd, and Ro bond lengths (in Å) applied in the HOMED procedure.

Table 2.
Comparison of the normalization constants (α) for CC, CX, XX, and XY bonds applied in the rHOMA and HOMED procedures.
The reference compounds possessing different delocalizations of n- and π-electrons and applied for the Rs and Rd bond lengths in the rHOMA procedure [6] cause considerably greater variations in the normalization α constant values than those in original HOMA and HOMED. For example, the choice of 1,3-butadiene (CH2=CH–CH=CH2, moderately delocalized by π-π conjugation) for Rs(CC) and Rd(CC) gives a very high α(CC) value (257.7). Consequently, some cyclic and acyclic hydrocarbons, less delocalized than butadiene, display the negative rHOMA values, even close to −10 [21,68,69]. Originally, Krygowski claimed that rHOMA varies from unity to zero [6], like original HOMA [1,2,3,4]. However, in the light of recent results for hydrocarbons, this assumption has been modified, and now rHOMA can vary from unity to −∞ [12].
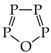
The use of monomeric formic acid (HO−CH=O, moderately delocalized by n-π conjugation) for the reference C−O and C=O bond lengths also gives an exceptionally high α(CO) value (157.38). Its application together with the extreme α(CC) value for O-containing heterocompounds can only explain why the rHOMA values are close to zero [7,8,12,13,21]. In some cases, the rHOMA indices for compounds containing C and O atoms are even negative [21,23]. The reference molecules chosen for CP (CH3–P=CH2), NN {(CH3)2N–N=C(CH3)2 and CH3–N=N–CH3}, and NO (CH3–O–N=O) bonds are not analogously delocalized. Consequently, their α values in the rHOMA procedure differ from 57.21 (for NO) to 130.33 (for NN).
Quite a different situation occurs for the reference C−N and C=N bond lengths. In this case, the application of the simplest molecules (CH3–NH2 and CH2=NH) in the rHOMA procedure, analogously as in the original HOMA and HOMED indices, explains both the low α(CN) value (93.52) and the large rHOMA indices (>0.7) for cyclic azines and azoles [7,8,12,13,21]. The same is true for the reference C−S and C=S bond lengths for which the simplest molecules (CH3–S–CH3 and CH2=S) used in rHOMA are not very different from those (CH3–SH and CH2=S) employed in HOMED. Consequently, the α(CS) value is also low (94.09) and the rHOMA indices are also large (>0.7) for thiophene and thioazoles [7,8,12,21]. For less delocalized N and/or S compounds, rHOMA is close to zero [21].
The other discrepancy in the HOMA and HOMED parametrization results from the use of different methods for Ro calculation. This parameter can be estimated from Equation (2) in the original and reformulated HOMA procedure, whereas in the HOMED procedure, Ro corresponds to the intrinsic bond length of the fully delocalized system optimized by using the same theoretical method {B3LYP/6-311+G(d,p)} as that applied for the reference molecules (Table 1). The differences between the reference Ro bond lengths slightly affect the HOMA and HOMED values for heterocycles.
The use of the experimental (X-ray) and computational {DFT(B3LYP)/6-311+G(d,p)} reference Rs and Rd bond lengths in the original HOMA and HOMED procedures, respectively, is an additional difference between the two descriptors. It should be mentioned here that the application of the HOMA procedure to experimental and computational structures of investigated heterocompounds does not lead to the same HOMA values. For some derivatives (e.g., furan and oxazoles), differences are even larger than 0.2 units [12]. For this reason, it is important to use the same method for determination of the reference (Rs, Rd, and Ro) and running (Rx) bond lengths [21,68]. The use of the same method for all bond lengths gives the possibility to minimize errors in the structural-descriptor estimation (<0.05 for HOMED) [21].
3.3. Differences in the HOMED and rHOMA Scales
Since the reference molecules used for Rs and Rd in the rHOMA procedure are differently delocalized, the normalization α constants vary from ca. 60 to 260 [6,7,8,12,13,14]. Consequently, the rHOMA and HOMED scales are not analogous (Figure 1) [21,22,23]. For completely delocalized π-electron compounds, e.g., benzene and its heteroanalogs, rHOMA = 1 and HOMED = 1 [6,7,8,12,13,14,20,21,69,70]. However, rHOMA and HOMED have different values for Kekulé benzene (cyclohexatriene) with pure C–C and C=C bonds. When we assume that the C–C and C=C bond lengths in cyclohexatriene are equal to those in 1,3-butadiene (reference compound chosen in the rHOMA procedure), rHOMA = 0 [6,7,8], while HOMED = 0.694 [21,22]. When we take the C–C and C=C bond lengths in Kekulé benzene to be equal to those in ethane and ethene, respectively (reference compounds in the HOMA and HOMED procedures), HOMED = 0, while rHOMA = −2.023 [21,22].

Figure 1.
Comparison of the HOMED and rHOMA scales for π-electron delocalized compounds possessing CC, CN, CP, CO, CS, or NN bonds.
Lack of analogy in the HOMED and rHOMA scales also takes place for heterocompounds possessing CP, CO, or NN bonds for which the selected reference molecules are also differently delocalized, and zero in the HOMED and rHOMA scales does not correspond to the same heterocompound. The two geometry-based indices do not have the identical values for the reference molecules employed in the rHOMA procedure for CO and CP bonds. For example, rHOMA = 0 and HOMED = 0.569 for monomeric formic acid, HO–CH=O (n-π conjugated) is used for CO bonds. For H2C=P–CH3 (σ-π hiperconjugated) applied for CP bonds, rHOMA = 0 and HOMED = 0.059. There are also some differences for triazine HN=N–NH2 (n-π conjugated), for which rHOMA = 0.699 and HOMED = 0.720, indicating that zero in both scales for π-electron systems with NN bonds can refer to various molecules.
For compounds containing CN bonds, the situation is quite different. For hypothetical 1,3,5-triazine with pure C−N and C=N bonds (aza derivative of Kekulé benzene), rHOMA = 0 and HOMED = 0. In this case, the same reference compounds, methylamine and methylimine, were used for C−N and C=N bonds, respectively. Very similar values of both descriptors can also be observed for compounds containing CS bonds. In this case, almost analogously delocalized molecules were used for the reference Rs and Rd bonds, CH3–S–CH3 and CH2=S in rHOMA, and CH3–SH and CH2=S in HOMED.
3.4. From Linear Tendencies to Scatter Plots Between rHOMA and HOMED Indices
All discrepancies between the rHOMA and HOMED parametrizations discussed above affect the rHOMA vs. HOMED relations for simple π-electron compounds containing heteroatoms. They cannot be ignored even for long series, because the relation between the two parameters strongly depends not only on the type of atoms present in heterocompounds but also on their number. The rHOMA and HOMED indices are almost parallel for compounds containing only one type of bond, e.g., only CC, only CX, or only XY. Figure 2a shows linear tendencies between the rHOMA and HOMED indices estimated for three series of cyclic and acyclic π-electron compounds considered in our previous article [21] such as hydrocarbons containing only CC bonds, heterocompounds containing only CN bonds, and derivatives containing only CO bonds. The slopes of regression lines are different for each series because the normalization α constants for CC, CN and CO bonds are not the same in the rHOMA and HOMED procedures (Table 2). Generally, the slopes of regression lines are close to 1, 2 and 3 for the series ‘CN’, ‘CO’ and ‘CC’, similar to the α(rHOMA)/α(HOMED) ratio for the CN, CO and CC bonds. Some deviations of points from the linear relationships in Figure 2a are a consequence of slightly different values for Ro in rHOMA and HOMED.
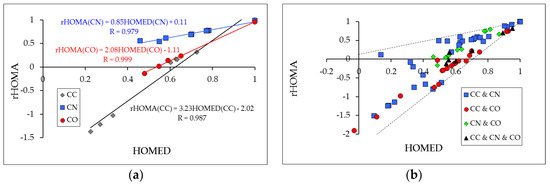
Figure 2.
Linear tendencies between the rHOMA and HOMED indices estimated for three series of compounds containing only CC, only CN, and only CO bonds (a) and scatter plots between the rHOMA and HOMED indices estimated for four series of compounds containing only CC and CN, only CC and CO, only CN and CO, and only CC, CN, and CO bonds (b). The rHOMA and HOMED values are taken from Ref. [21].
On the basis of these linear tendencies found for compounds possessing only one type of bond and regarding their different slopes, we can conclude that the character of the rHOMA vs. HOMED plots for conjugated heterocompounds containing various CC, CX, and XY bonds can be different. They can be almost linear, parabolic, or scatter. For example, a scatter plot exists for a series of cyclic and acyclic conjugated heterosystems containing a different number of CC and CN bonds (Figure 2b). The points are placed between the lines corresponding to the two series of compounds containing only CN and only CC bonds. The great difference between the slopes of the ‘CC’ and ‘CN’ lines leads to a large scatter plot for a series of conjugated systems containing CC and CN bonds. For three other series of compounds (‘CC & CO’, ‘CN & CO’, and ‘CC & CN & CO‘), their data points are not so scattered as those for the ‘CC & CN’ series, and in some cases the rHOMA vs. HOMED relations can be considered as linear. Nevertheless, the data points for series ‘CC & CO’, ‘CN & CO’, and ‘CC & CN & CO’, are placed between the lines found for the corresponding series of compounds possessing only one type of bond. The rHOMA and HOMED values for all heterocompounds considered in Figure 2 were taken from Ref. [21].
Even for isomers of the same compound possessing the same number of CC, CX, and XY bonds, the relation between the rHOMA and HOMED indices cannot be linear. For example, bicyclic purine contains five C atoms and four N atoms. It also possesses one labile proton that can be moved between nine conjugated sites according to amine–enamine and amine–imine tautomeric conversions. Nine tautomers are thus possible for bicyclic purine. All of them contain the same number of CC and CN bonds in the imidazole and pyrimidine rings and also in the entire purine molecule. However, the rHOMA vs. HOMED plots, found for the imidazole and pyrimidine rings and bicyclic purine, are analogous to that presented in Figure 2b for the series ‘CC & CN’ [71].
Pyrimidine bases (uracil, cytosine, and isocytosine) possess the same number of CC and CN bonds in the pyrimidine ring and two different groups (–NH2/=NH and/or –OH/=O) at 2- and 4-positions. They contain two labile protons that can be moved between five conjugated sites according to different types of prototropic conversions (amide-iminol, amine-imine, enamine-imine, and/or keto-enol). All possible rearrangements lead to nine prototropic tautomers, which are analogous for pyrimidine bases [23,72,73]. For tautomers with the –OH and =NH substituents, additional isomerism takes place, rotational isomerism for –OH and geometrical isomerism for =NH. Hence, 18 isomers can be distinguished for uracil [72] and 21 isomers are possible for cytosine [73] and isocytosine [23]. Only for aromatic isomers with structural descriptors larger than 0.7 (Figure 3), the rHOMA vs. HOMED relations seem to be linear for the six-membered ring (rHOMA6 vs. HOMED6) and for the complete molecule including exo substituents (rHOMA8 vs. HOMED8). For medium (π-π and n-π cross conjugated) and weak (π-π, n-π, and σ-π cross conjugated) delocalized isomers, variations of the rHOMA values are larger than those of the HOMED ones. This leads to non-linear rHOMA vs. HOMED relations for isocytosine, cytosine and uracil isomers. The relations seem to have a parabolic character. The points for pyrimidine bases are placed between two lines corresponding to compounds containing only CC and only CN bonds.
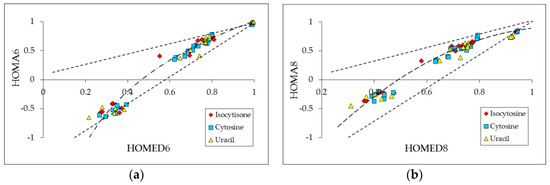
Figure 3.
Plots between the rHOMA and HOMED indices estimated for isocytosine, cytosine and uracil: for the six-membered ring (a) and for the complete molecule of pyrimidine base (b). Data taken from Ref. [23].
Figure 2 and Figure 3 confirm the most important discrepancies between the two structural indices observed for heterocompounds. The choice of the reference compounds with different delocalizations of n- and π-electrons for the C–C and C=C, C–X and C=X, X–X and X=X, X–Y and X=Y bonds can be considered as the main reason for differences between the rHOMA and HOMED values, and consequently, non-linear rHOMA vs. HOMED relations found for heterocompounds [21,22,23,71,72,73]. Although the HOMA idea is based on the theory of resonance and equalization of bond lengths in completely delocalized π-electron systems, the rHOMA parametrization seems to be inappropriate for compounds containing heteroatoms. The rHOMA parametrization can be considered as one of the principal reasons of artificial relations between rHOMA and other descriptors of aromaticity. The rHOMA index can be applied for non-tautomeric compounds containing only CC, only CX, only XX, or only XY bonds, e.g., hydrocarbons [69,70].
The choice of the experimental Rs and Rd bond lengths for the rHOMA parametrization, and the rHOMA application to the theoretical structures of π-electron systems is a secondary factor that causes significant differences between rHOMAs even for the same compound optimized at different levels of theory. These discrepancies have been confirmed by Andrzejak et al. [68], who compared the rHOMA indices for hydrocarbons studied by using different theoretical methods for optimization of their geometries. In the case of the HOMED procedure, when the same method is applied for the calculation of Rs, Rd, Ro in the reference compounds and Rx in the investigated π-electron systems, computational errors cancel out. Consequently, differences between the HOMED values are lower than 0.05 [21,74].
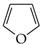
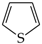
3.5. HOMED Application to Furan, Thiophene and Their N- and P-Derivatives
Furan and thiophene belong to the family of simple five-membered heterocycles that display an aromatic character [4,21,25,26,36,37,38,39,40,41,42,43,44,55,56,57]. Similar to benzene, they possess six delocalized electrons, four π-electrons and two n-electrons in the ring, and fulfill the Hűckel rule (4n + 2). Both compounds have planar structures. Hence, their geometric descriptors should not be very different than those of benzene. The presence of additional N (or P) atoms in the ring can cause similar effects. Lone pairs of electrons at additional N (or P) atoms are outside of the ring and do not participate in delocalization of the six ring electrons.
However, the rHOMA values reported for furan are between 0.0 and 0.3 and those for thiophene are between 0.7 and 0.9 [12]. Additional N atoms increase the rHOMA indices for furan derivatives (even to 0.7 for 2,5-diazafuran [75]), while they vary very little for thiophene. These variations do not describe well the N-effects on electron delocalization in furan and thiophene derivatives observed for other descriptors of aromaticity. For example, linear relationships (Figure 4) exist between the magnetic descriptors and nucleus-independent chemical shift {NICS(1)} indices, and between the energetic parameters and aromatic stabilization energy (ASE) indices, both being estimated earlier for N-derivatives of furan and thiophene [75]. The correlation coefficients (0.961 and 0.977, respectively) are close to unity. The slopes of these lines (0.792 and 0.721, respectively) are also not very different from unity.
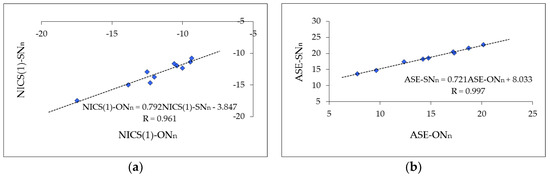
Figure 4.
Linear relations between magnetic NICS(1) indices (a) and between energetic ASE indices (b) estimated for N derivatives of furan and thiophene. NICS(1) and ASE are taken from Ref. [75]. NICS(1)-ONn and ASE-ONn correspond to furan and its N-derivatives and NICS(1)-SNn and ASE-SNn refer to thiophene and its N derivatives.
The situation seems to be analogous for the HOMED indices. Preliminary HOMED estimations made in 2010 for furan (0.749) and oxazole (0.702) [21] showed evidently that the HOMED procedure, based on the original HOMA one, gives a values typical for five-membered aromatic systems. For this reason, the HOMED index has been extended here to π-electron compounds containing CS, NN, NO, NS, CP, PO, and PS bonds, and applied to isolated furan and thiophene and their derivatives substituted at 2-, 3-, 2,3-, 2,4-, 2,5-, 3,4-, 2,3,4-, 2,3,5-, and 2,3,4,5-positions by N or P atoms. The estimated HOMED indices for furans and thiophenes are listed in Table 3. Generally, some linear tendencies exist between the HOMED values estimated for furan and thiophene and their N and P derivatives (Figure 5). Effects of N and P atoms in furan are analogous to those in thiophene. The slopes of regression lines (1.003 and 0.282 for N and P effects, respectively) are only different.

Table 3.
Structures of N and P derivatives of furan and thiophene and their HOMED indices estimated for the DFT structures.
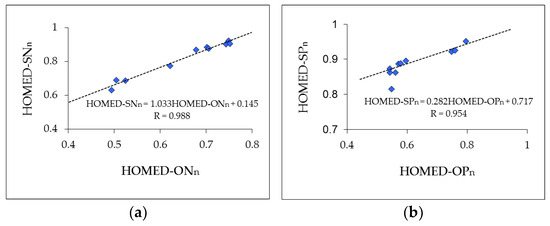
Figure 5.
Linear relations between the structural HOMED indices for N derivatives (a) and P derivatives (b) of furan and thiophene. HOMED-ONn and HOMED-OPn correspond to furans and HOMED-SNn and HOMED-SPn refer to thiophenes. Data are taken from Table 3.
Derivatives of furan possess lower HOMED values than those of thiophene. This is in good agreement with the structural chemistry on heterocyclic compounds that furan is less aromatic than thiophene. Furan and thiophene also have lower HOMED values than benzene (1.000 by definition). Heteroatoms O and S are more electronegative than C atom, consequently, electron delocalization in benzene is stronger than that in furan and thiophene. Moreover, in benzene, six electrons are π-π conjugated, while in furan and thiophene four π-electrons are cross conjugated with n-electrons. According to the rules of resonance theory [56,57], we can propose many Lewis structures without separation of the charge for the resonance hybrid of benzene, while for those of furan and thiophene we can write many Lewis structures with separation of the charge. Contribution of the later structures in the resonance hybrid of five-membered heterocycles is usually smaller than that of the former ones, for which some localization of π-electrons takes place.
3.6. HOMED Application to Tautomeric Azoles and Phospholes
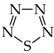
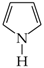
It is well recognized that pyrrole and its N derivatives exhibit prototropic tautomerism [9,21,22,57,76,77,78,79,80,81,82,83,84,85,86,87,88]. The labile proton can move from one site to the other according to 1,3- or 1,5-shift. Since proton transfer takes place between conjugated sites, it is always accompanied by a rearrangement of π-electrons. Hence, prototropic tautomers are never zwitterions. For azoles, five tautomers are possible with the labile proton at N (NH tautomers) or C atom (CH tautomers). Analogous proton transfer (Scheme 1) and analogous five tautomers (PH and CH) can be considered for phosphole and its P derivatives [89]. Depending on the position of additional N atoms in azoles and P atom in phospholes, some tautomers have the same structures. For example, tautomers with the labile proton at C2 and C3 possess the same structures as those with the labile proton at C5 and C4, respectively, for pyrrole and phosphole.
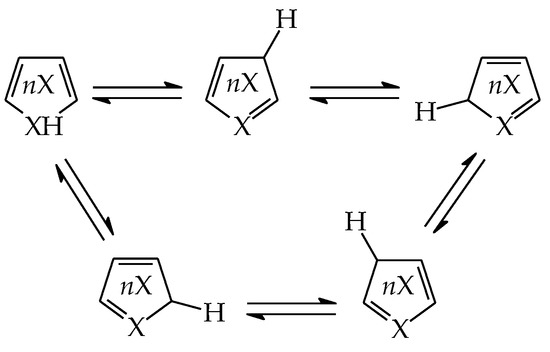
Scheme 1.
Proton transfer for five prototropic tautomers of azoles and phospholes (X = N or P).
The NH tautomers of azoles have planar structures. Four π- and two n-electrons (4n + 2) are well delocalized in the five-membered ring. In the literature, their aromatic character has been quantitatively proved by various geometric, energetic and magnetic indices of aromaticity [7,8,9,12,21,25,26,27,28,29,30,31,32,75,83,90,91,92]. The rare CH tautomers possess C-sp3 atom in the ring. They are not planar [58,59,62]. The rearrangement of the labile proton from N to C atom also changes the position of n-electrons which are outside the ring in the CH tautomers and, consequently, they are not conjugated with four π-electrons of the ring. The CH tautomers do not fulfill the Hűckel rule. They are not aromatic like cyclopenta-1,3-diene for which π-electrons of the diene-part are cross conjugated with σ-electrons of the >CH2 fragment.
The structural HOMED indices (Table 4) determined here for azoles confirm the general trend of their aromaticity. The HOMED values are exceptionally large (≥0.9) for the well delocalized and planar NH tautomers, whereas they are very low (≤0.4) for the rare CH forms with C-sp3 atom. The CH tautomer of tautomeric 2,3,4-triazapyrrole/2,3,5-triazapyrrole is not stable at the DFT level. Its five-membered ring opens during structure optimization. The calculated relative Gibbs energies of the CH tautomers (ΔG ≥ 15 kcal·mol−1) are in good agreement with earlier observations. The CH isomers can be neglected for neutral azoles which prefer the planar NH forms. Interestingly, the relative Gibbs energies estimated for the NH and CH tautomers of azoles are almost parallel to the structural HOMED indices.

Table 4.
Structures of azoles, their DFT-calculated relative Gibbs energies (ΔG in kcal·mol−1) and HOMED indices estimated for DFT structures.
Figure 6 shows that some simple linear relationship can be distinguished for azoles between the HOMED descriptors that measure the delocalization of n- and π-electrons and relative Gibbs energies (ΔG) that refer to tautomeric conversions. Analogous linear tendencies between energetic and geometric parameters of NH and CH tautomers have been reported for other tautomeric heterocompounds possessing CC and CN bonds, e.g., 2- and 4-aminopyridines, 2- and 4-aminopyrimidines, purine and adenine [22,71,93,94,95,96]. In the case of compounds containing additional CO bonds, such as 2- and 4-hydroxypyridines, 2- and 4-hydroxypyrimidines, and pyrimidine bases (uracil, cytosine and isocytosine), the relations between the HOMED and ΔG values are more complex [23,72,73,97].
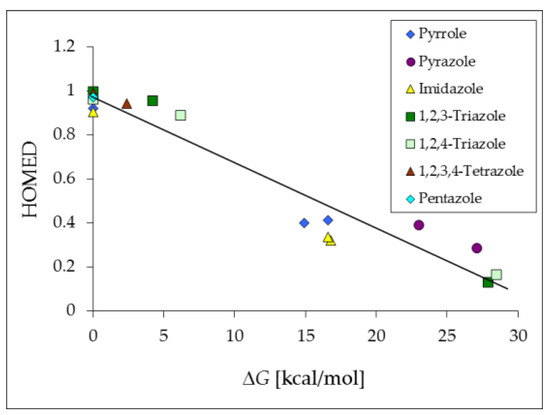
Figure 6.
Plot between the relative Gibbs energies (ΔG) and HOMED indices for possible tautomers of azoles. Data taken from Table 4.
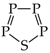
Phospholes with a PH group (except P5H) are not planar compounds [30,32,89,98,99,100,101,102,103,104,105,106,107,108,109,110,111]. Phosphorus with H atom in five-membered phospholes is pyramidal, and the bond-angles sum about P is smaller than 360°. Hence, the electron lone pair of PH cannot interact with the ring π-electrons. Various types of aromaticity descriptors estimated for phosphole and for its P derivatives have smaller values than those for azoles [30,98,99,100,101,102,103,104]. However, planar mono-, di-, tri-, and tetra-phospholes (transition states—first order saddle points) and also planar P5H display an aromatic character analogous to that of the corresponding azoles [99,100,101,102,103]. Note that P substitution in phospholes reduces the pyramidal character of phosphorus, and P-substituted phosphole becomes aromatic [98,103,104,112,113,114].
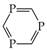
DFT calculations performed here for phosphole and its P derivatives confirm the literature data. Only P5H has a planar structure. Other phospholes contain the pyramidal PH group. Generally, the HOMED values estimated for the PH tautomers of phospholes (Table 5) are smaller than those for the NH tautomers of azoles (Table 4). A different situation occurs for the CH forms. Their HOMED values for phospholes are higher than those for azoles. Consequently, there is no simple relation between the structural descriptors of phospholes and azoles (Figure 7).

Table 5.
Structures of phospholes, their DFT-calculated relative Gibbs energies (ΔG in kcal·mol−1), and HOMED indices estimated for DFT-structures.
Note that the PH tautomers can be detected only in the tautomeric mixtures of 1,2,3-triphosphole/1,2,5-triphosphole and 1,2,3,4-tetraphosphole/1,2,3,5-tetraphosphole. Their relative Gibbs energies are close to zero. Additional calculations performed at the Gn levels prove that the CH tautomers are favored for other P derivatives (except for the derivative with five P atoms) (Table 5). The tautomeric preferences for phospholes are different from those for azoles. Delocalization of n- and π-electrons does not determine the tautomeric preferences for phospholes.
3.7. HOMED Application to Tautomeric Phosphazoles
Monophosphapyrroles display prototropic tautomerism similar to azoles and phospholes. The labile proton can be transferred from N site to P or C atom according to a 1,3- or 1,5-shift. Five tautomers can be distinguished for phosphazoles with the labile proton at N (NH tautomers), P (PH tautomers), or C atom (CH tautomers). Intramolecular proton transfer reactions for phosphazoles (Scheme 2) are analogous to those for azoles and phospholes (Scheme 1).
Scheme 2.
Proton transfer for five prototropic tautomers of monophosphapyrroles.
The tautomeric mixture of monophosphapyrroles consists of five tautomers: one NH, one PH, and three different CH forms. DFT calculations performed here for 2- and 3-phosphapyrroles prove that the NH tautomers are favored. They are planar and aromatic. Their HOMED values are larger than 0.8 (Table 6). However, orders of energetic stabilities for the non-planar PH and CH tautomers are different. For 2-phosphapyrrole, the PH tautomer has smaller Gibbs energy than the CH forms (by 3–5 kcal·mol−1), whereas for 3-phosphapyrrole the reverse situation takes place. Two CH tautomers (C2H and C4H) are more stable than the PH form, and one CH isomer (C5H) has similar stability to the PH one.

Table 6.
Structures of phosphapyrroles, their DFT-calculated relative Gibbs energies (ΔG in kcal·mol−1), and HOMED indices estimated for DFT structures.
In the case of monophosphadiazoles studied earlier by Ozimiński [115], the planar and well delocalized NH forms are also favored in the tautomeric mixture, and the non-planar PH and CH forms possess smaller Gibbs energies than the NH ones (by more than 25 kcal·mol−1 at the MP2/cc-pVTZ level). Generally, phosphazoles prefer a pyrrole-like structure. Note that there is no linear relationship between the structural and energetic descriptors for phosphazoles.
4. Conclusions
The HOMED index, based on the reference compounds of similar delocalizations of n- and π-electrons and on the bond lengths determined using the same DFT method for the reference molecules and investigated π-electron systems, has been extended to heterocompounds containing CS, CP, NN, NP, NO, NS, PP, PO, and PS bonds and applied to simple and tautomeric five-membered heterocycles. The HOMED indices correctly measure the delocalization of n- and π-electrons in completely, moderately, as well as partially delocalized heterosystems. The HOMA index reformulated in 1993 by Krygowski cannot be applied for compounds containing heteroatoms (N, P, O, and/ or S).
For the planar and aromatic simple molecules containing the Hűckel number (4n + 2) of delocalized n- and π-electrons in the five-membered ring, the HOMED values are larger than 0.5. Furan and its N- and P-derivatives possess smaller HOMED values than analogous thiophenes. Tautomeric azoles and phosphazoles prefer the pyrrole-like structures (NH forms) that are also planar and aromatic (HOMED close to unity). The non-aromatic and non-planar CH tautomers (with C-sp3 in the ring) have the lowest structural descriptors for azoles, phospholes and phosphazoles. The values of their structural descriptors are lower than 0.5. Tautomers with the pyramidal PH group in phospholes and phosphazoles are moderately delocalized and have smaller HOMED values than the planar PH forms.
Additional N or P atom(s) included in the molecule affect the HOMED indices of furan in an analogous way to those of thiophene (Figure 5). The parallelism of changes for electron delocalization in simple five-membered heterocycles is also proved by the energetic (ASE) and magnetic (NICS) descriptors of aromaticity (Figure 4). However, in the case of tautomeric azoles and phospholes, the relation between structural indices seems to be more complex (Figure 7).
The linear tendencies can be observed between the relative Gibbs energies and HOMED values estimated for the NH and CH forms of azoles (Figure 6). These simple relations indicate that aromaticity affects the isomeric preferences for N-containing heterocycles. For phospholes and phosphazoles, the relations between two phenomena, prototropic tautomerism (described by relative Gibbs energies) and delocalizations of n- and π-electrons (determined by HOMED) are not so simple for azoles. Aromaticity cannot be considered as the principal factor that determines the structure of the favored tautomer in phospholes.
Funding
This research received no external funding.
Acknowledgments
I thank Hideo Ando from Department of Physics, Faculty of Science, Yamagata University (Japan) for valuable comment on the HOMED parametrization.
Conflicts of Interest
The author declare no conflict of interest.
References
- Kruszewski, J.; Krygowski, T.M. Harmonic oscillator approach to the definition of aromaticity. Bull. Acad. Pol. Sci. Chim. 1972, 20, 907–915. [Google Scholar]
- Kruszewski, J.; Krygowski, T.M. Definition of aromaticity basing on the harmonic oscillator model. Tetrahedron Lett. 1972, 3839–3842. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Kruszewski, J. Bond reactivity index (BRI) in terms of simple harmonic oscillator theory. Bull. Acad. Pol. Sci. Chim. 1973, 21, 409–412. [Google Scholar]
- Krygowski, T.M.; Kruszewski, J. Aromaticity of thiophene, pyrrole and furan in terms of aromaticity indices and Hammett σ constants. Bull. Acad. Pol. Sci. Chim. 1974, 22, 871–876. [Google Scholar]
- Jug, K.; Koester, A. Influence of σ and π electrons on aromaticity. J. Am. Chem. Soc. 1990, 112, 6772–6777. [Google Scholar] [CrossRef]
- Krygowski, T.M. Crystallographic studies of inter- and intramolecular interactions reflected in aromatic character of π-electron systems. J. Chem. Inform. Comput. Sci. 1993, 33, 70–78. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Cyrański, M.K. Structural aspects of aromaticity. Chem. Rev. 2001, 101, 1385–1419. [Google Scholar] [CrossRef]
- Cyrański, M.K. Energetic aspects of cyclic pi-electron delocalization: Evaluation of the methods of estimating aromatic stabilization energies. Chem. Rev. 2005, 105, 3773–3811. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kosińska, W.; Ośmiałowski, B.; Gawinecki, R. Tautomeric equilibria in relation to pi-electron delocalization. Chem. Rev. 2005, 105, 3561–3612. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Krygowski, T.M.; Zachara, J.E.; Ośmiałowski, B.; Gawinecki, R. Tautomeric equilibria, H-bonding and π-electron delocalization in o-nitrosophenol. A B3LYP/ 6-311+G(2df,2p) study. J. Phys. Org. Chem. 2005, 18, 892–897. [Google Scholar] [CrossRef]
- Ośmiałowski, B.; Raczyńska, E.D.; Krygowski, T.M. Tautomeric equilibria and pi electron delocalization for some monohydroxyarenes–Quantum chemical studies. J. Org. Chem. 2006, 71, 3727–3736. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Szatyłowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Paluszak, M. Aromaticity from the viewpoint of molecular geometry: Application to planar systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Szatyłowicz, H. Aromaticity: What does it mean? ChemTexts 2015, 1, 12:1–12:10. [Google Scholar] [CrossRef] [PubMed]
- Szatyłowicz, H.; Stasyuk, O.A.; Krygowski, T.M. Calculating the aromaticity of heterocycles. Adv. Heterocycl. Chem. 2016, 120, 301–327. [Google Scholar] [CrossRef]
- Stasyuk, O.A.; Szatyłowicz, H.; Krygowski, T.M. Effect of the H-bonding on aromaticity of purine tautomers. J. Org. Chem. 2012, 77, 4035–4045. [Google Scholar] [CrossRef] [PubMed]
- Stasyuk, O.A.; Szatyłowicz, H.; Krygowski, T.M. Effect of H-bonding and complexation with metal ions on the pi-electron structure of adenine tautomers. Org. Biomol. Chem. 2014, 12, 456–466. [Google Scholar] [CrossRef] [PubMed]
- Stasyuk, O.A.; Szatyłowicz, H.; Krygowski, T.M. Metal complexation and H-bonding effects on electronic structure of cytosines studied in the gas phase. Croat. Chem. Acta 2014, 87, 335–342. [Google Scholar] [CrossRef]
- Stasyuk, O.A.; Szatyłowicz, H.; Krygowski, T.M. Tautomerisation of thymine acts against the Hűckel 4N + 2 rule. The effect of metal ions and H-bond complexations on the electronic structure of thymine. Org. Biomol. Chem. 2014, 12, 6476–6483. [Google Scholar] [CrossRef] [PubMed]
- Stasyuk, O.A.; Szatyłowicz, H.; Krygowski, T.M. Aromaticity of H-bonded and metal complexes of guanine tautomers. Struct. Chem. 2016, 27, 111–118. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Krygowski, T.M.; Duczmal, K.; Hallmann, M. On geometry-based HOMED (a measure of hyperconjugation, n-π, and π-π conjugation) and HOMA index (a measure of aromaticity). In Proceedings of the XVIII International Conference on Physical Organic Chemistry, Warsaw, Poland, 20–25 August 2006; p. 31. [Google Scholar]
- Raczyńska, E.D.; Hallmann, M.; Kolczyńska, K.; Stępniewski, T.M. On the harmonic oscillator model of electron delocalization (HOMED) index and its application to heteroatomic π-electron systems. Symmetry 2010, 2, 1485–1509. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Makowski, M.; Hallmann, M.; Kamińska, B. Geometric and energetic consequences of prototropy for adenine and its structural models—A review. RSC Adv. 2015, 5, 36587–36604. [Google Scholar] [CrossRef]
- Raczyńska, E. Quantum-chemical studies on the favored and rare isomers of isocytosine. Comput. Theor. Chem. 2017, 1121, 58–67. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Michalec, P.; Zalewski, M. Exceptionally high proton and lithium cation gas-phase basicity of the anti-diabetic drug metformin. J. Phys. Chem. A 2017, 121, 8706–8718. [Google Scholar] [CrossRef] [PubMed]
- Frizzo, C.P.; Martins, M.A.P. Aromaticity in heterocycles: New HOMA index parametrization. Struct. Chem. 2012, 23, 375–380. [Google Scholar] [CrossRef]
- Bird, C.W. A new aromaticity index and its application to five-membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to six-membered ring heterocycles. Tetrahedron 1986, 42, 89–92. [Google Scholar] [CrossRef]
- Bird, C.W. The application of a new aromaticity index to some bicyclic heterocycles. Tetrahedron 1987, 43, 4725–4730. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 4. The status of phosphorus and arsenic as heteroatoms. Tetrahedron 1990, 46, 5697–5702. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 5. A unified aromaticity index. Tetrahedron 1992, 48, 335–340. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 6. The effect of molecular distortion on aromaticity. Tetrahedron 1992, 48, 1675–1682. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 7. Some quantitative aspects of the tautomerism of hydroxy- and mercaptoazines. Tetrahedron 1992, 48, 7857–7862. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 8. The influence of N-oxide formation on heterocyclic Aromaticity. Tetrahedron 1993, 49, 8441–8448. [Google Scholar] [CrossRef]
- Bird, C.W. The relation of classical and magnetic criteria of aromaticity. Tetrahedron 1996, 52, 9945–9952. [Google Scholar] [CrossRef]
- Bird, C.W. Heteroaromaticity. 10. The direct calculation of resonance energies of azines and azoles from molecular dimentions. Tetrahedron 1997, 53, 13111–13118. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Barczyński, P.; Musumurra, G.; Pisano, D.; Szafran, M. Aromaticity as a quantitative concept. 1. A statistical demonstration of the orthogonality of ‘classical’ and ‘magnetic’ aromaticity in five- and six-membered heterocycles. J. Am. Chem. Soc. 1989, 11, 7–15. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Jug, K.; Oniciu, D.C. Quantitative measures of aromaticity for mono-, bi-, and tricyclic penta- and hexaatomic heteroaromatic ring systems and their interrelations. Chem. Rev. 2001, 101, 1421–1450. [Google Scholar] [CrossRef] [PubMed]
- Balaban, A.T.; Oniciu, D.C.; Katritzky, A.R. Aromaticity as a cornestone of heterocyclic chemistry. Chem. Rev. 2004, 104, 2777–2812. [Google Scholar] [CrossRef]
- Minkin, V.I.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity. Electronic and Structural Aspects; John Wiley & Sons, Inc.: New York, NY, USA, 1994; ISBN 0471593826. [Google Scholar]
- Schleyer, P.v.R.; Maerker, C.; Dransfield, A.; Jiao, H.; van Eikema Hommes, N.J.R. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Jiao, H. What is aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.v.R. Nucleus-independent chemical shifts (NICS) as aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef]
- Poater, J.; Duran, M.; Solà, M.; Silvi, B. Theoretical evaluation of electron delocalization in aromatic molecules by means of atoms in molecules (AIM) and electron localization function (ELF) topological approaches. Chem. Rev. 2005, 105, 3911–3947. [Google Scholar] [CrossRef]
- Feixas, F.; Matito, E.; Poater, J.; Solà, M. On the performance of some aromaticity indices: A critical assessment using a test set. J. Comput. Chem. 2008, 29, 1543–1554. [Google Scholar] [CrossRef] [PubMed]
- D’Auria, M. A new proposal for the estimation of the aromatic character. Lett. Org. Chem. 2013, 10, 277–282. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—II. Lett. Org. Chem. 2014, 11, 250–258. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—III. Lett. Org. Chem. 2014, 11, 731–735. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—IV. Lett. Org. Chem. 2014, 11, 657–663. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—V. Lett. Org. Chem. 2015, 12, 233–236. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—VI. Lett. Org. Chem. 2015, 12, 482–490. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—VII. Lett. Org. Chem. 2015, 12, 402–406. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—VIII. Lett. Org. Chem. 2015, 12, 549–559. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—IX. Lett. Org. Chem. 2016, 13, 33–43. [Google Scholar] [CrossRef]
- D’Auria, M. A new index for the estimation of the aromatic character—X. Lett. Org. Chem. 2016, 13, 368–373. [Google Scholar] [CrossRef]
- D’Auria, M. An approach to the aromaticity based on the energy of the occupied π orbitals. Curr. Org. Chem. 2016, 20, 971–983. [Google Scholar] [CrossRef]
- Wheland, G.W. The Theory of Resonance and Its Application to Organic Chemistry; John Wiley and Sons, Inc.: New York, NY, USA, 1955. [Google Scholar]
- Pauling, L. The Nature of the Chemical Bond, 3rd ed.; Cornell University Press: Ithaca, NY, USA, 1960; ISBN 0801403332. [Google Scholar]
- Glendening, E.D.; Weinhold, F. Natural resonance theory: I. General formalism. J. Comput. Chem. 1998, 19, 593–609. [Google Scholar] [CrossRef]
- Glendening, E.D.; Weinhold, F. Natural resonance theory: II. Natural bond order and valency. J. Comput. Chem. 1998, 19, 610–627. [Google Scholar] [CrossRef]
- Glendening, E.D.; Badenhoop, J.K.; Weinhold, F. Natural resonance theory: III. Chemical applications. J. Comput. Chem. 1998, 19, 628–646. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989; ISBN 0-19-504279-4. [Google Scholar]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. 1988, B37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. 1988, A38, 3098–3100. [Google Scholar] [CrossRef]
- Jensen, F. Introduction to Computational Chemistry, 3rd ed.; John Wiley & Sons: New York, NY, USA, 2017; ISBN 978-1-118-82599-0. [Google Scholar]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gn theory. WIREs Comput. Mol. Sci. 2011, 1, 810–825. [Google Scholar] [CrossRef]
- Raczyńska, E.D. On the Basicity and π-Electron Delocalization of ‘Hexaazabenzene’ N6—Quantum-Chemical Studies. Comput. Theor. Chem. 2011, 971, 38–41. [Google Scholar] [CrossRef]
- Firsch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian-03, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Andrzejak, M.; Kubisiak, P.; Zborowski, K.K. Avoiding pitfalls of a theoretical approach: The harmonic oscillator measure of aromaticity index from quantum chemistry calculations. Struct. Chem. 2013, 24, 1171–1184. [Google Scholar] [CrossRef]
- Ostrowski, S.; Dobrowolski, J.C. What does the HOMA index really measure? RSC Adv. 2014, 4, 44158–44161. [Google Scholar] [CrossRef]
- Dobrowolski, J.C.; Ostrowski, S. On the HOMA index of some acyclic and conducting systems. RSC Adv. 2015, 5, 9467–9471. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kamińska, B. Variations of the tautomeric preferences and π-electron delocalization for the neutral and redox forms of purine when proceeding from the gas phase (DFT) to water (PCM). J. Mol. Model. 2013, 19, 3947–3960. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Zientara, K.; Stępniewski, T.M.; Kolczyńska, K. Stability, polarity, intramolecular interactions and π-electron delocalization for all eighteen tautomers-rotamers of uracil. DFT studies in the gas phase. Collect. Czech. Chem. Commun. 2009, 74, 57–72. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Sapuła, M.; Zientara-Rytter, K.; Kolczyńska, K.; Stępniewski, T.M.; Hallmann, M. DFT Studies on the favored and rare tautomers of neutral and redox cytosine. Struct. Chem. 2016, 27, 133–143. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Juras, W. Effects of ionization and proton-transfer on bond length alternation in favored and rare isomers of isocytosine. Comput. Theor. Chem. 2019, 1148, 16–26. [Google Scholar] [CrossRef]
- Cyrański, M.K.; Krygowski, T.M.; Katritzky, A.R.; Schleyer, P.v.R. To what extent can aromaticity be defined uniquely? J. Org. Chem. 2002, 67, 1333–1338. [Google Scholar] [CrossRef]
- Elguero, J.; Marzin, C.; Katritzky, A.R.; Linda, P. The Tautomerism of Heterocycles, Advances in Heterocyclic Chemistry; Supplement 1; Academic Press: New York, NY, USA, 1976; ISBN 9780120206513. [Google Scholar]
- Minkin, V.I.; Garnovskii, A.D.; Elguero, J.; Katritzky, A.R.; Denisko, O.V. The tautomerism of heterocycles: Five-membered rings with two or more heteroatoms. Adv. Heterocycl. Chem. 2000, 76, 157–323. [Google Scholar] [CrossRef]
- Trifonov, R.E.; Alkorta, I.; Ostrovskii, V.A.; Elguero, J. A theoretical study of the tautomerism and ionization of 5-substituted NH-tetrazoles. J. Mol. Struct. (Theochem) 2004, 668, 123–132. [Google Scholar] [CrossRef]
- de la Hoz, A.; Sanchez-Migallon, A.; Mateo, A.C.; Prieto, P.; Infantes, L.; Elguero, J. The unusual transformation of an aromatic 1H-imidazole into a non-aromatic 2H-imidazole. Struct. Chem. 2005, 16, 485–490. [Google Scholar] [CrossRef]
- Alkorta, I.; Elguero, J.; Liebman, J.F. The annular tautomerism of imidazoles and pyrazoles: The possible existence of nonaromatic forms. Struct. Chem. 2006, 17, 439–444. [Google Scholar] [CrossRef]
- Raczyńska, E.D. Semiempirical (AM1) studies of gas-phase basicity and acidity of simple cyclic nitrogen compounds: Imidazole, 1-, 2- and 4(5)-methylimidazoles. Structural effects: Isomerism and tautomerism. Polish J. Chem. 1996, 70, 795–808. [Google Scholar]
- Raczyńska, E.D. Application of semiempirical method (AM1) to the study of tautomeric equilibria in the gas phase for simple compounds containing the amidine group: 4(5)-substituted imidazoles. Anal. Chim. Acta 1997, 348, 431–441. [Google Scholar] [CrossRef]
- Raczyńska, E.D. Quantum-chemical studies of the consequences of one-electron oxidation and one-electron reduction for imidazole in the gas phase and water. Comput. Theor. Chem. 2012, 993, 73–79. [Google Scholar] [CrossRef]
- Luque, F.J.; López-Bes, J.M.; Cemeli, J.; Aroztegui, M. Orozco, M. Solvent effects on tautomerism equilibria in heterocycles. Theor. Chem. Acc. 1997, 96, 105–113. [Google Scholar] [CrossRef]
- Kurzepa, M.; Dobrowolski, J.C.; Mazurek, A.P. Theoretical studies on tautomerism and IR spectra of C-5 substituted imidazole. J. Mol. Struct. 2001, 565–566, 107–113. [Google Scholar] [CrossRef]
- Jarończyk, M.; Dobrowolski, J.C.; Mazurek, A.P. Theoretical studies on tautomerism and IR spectra of pyrazole derivatives. J. Mol. Struct. (Theochem) 2004, 673, 17–28. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C.; Mazurek, A.P. DFT studies on tautomerism of C5-substituted 1,2,3-triazoles. J. Mol. Struct. 2003, 652–653, 697–704. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C.; Mazurek, A.P. DFT studies on tautomerism of C5-substituted 1,2,4-triazoles. J. Mol. Struct. (Theochem) 2004, 680, 107–115. [Google Scholar] [CrossRef]
- Ozimiński, W.P.; Dobrowolski, J.C. On the tautomerism, planarity, and vibrations of phospholes. Chem. Phys. 2005, 313, 123–132. [Google Scholar] [CrossRef]
- Cyrański, M.K.; Schleyer, P.v.R.; Krygowski, T.M.; Jiao, H.; Hohleicher, G. Facts and artifacts about aromatic stability estimation. Tetrahedron 2003, 59, 1657–1665. [Google Scholar] [CrossRef]
- Ramsden, C.A. The influence of aza-substitution on azole aromaticity. Tetrahedron 2010, 66, 2695–2699. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Oziminski, W.; Ramsden, C.A. Sigma-and pi-electron structure of aza-azoles. J. Mol. Model. 2011, 17, 1427–1433. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Stępniewski, T.M.; Kolczyńska, K. DFT studies on one-electron oxidation and one-electron reduction for 2- and 4-amiopyridines. J. Mol. Model. 2012, 18, 4367–4380. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D. Effects of positive and negative ionization for 2-aminopyrimidine in the gas phase and in water solution. Comput. Theoret. Chem. 2014, 1031, 56–63. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Kolczyńska, K.; Stępniewski, T.M. Consequences of one-electron oxidation and one-electron reduction for 4-aminopyrimidine—DFT studies. J. Mol. Model. 2012, 18, 3523–3533. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Kolczyńska, K.; Stępniewski, T.M.; Kamińska, B. On relation between prototropy and electron delocalization for neutral and redox adenine—DFT studies. Comput. Theor. Chem. 2013, 1022, 35–44. [Google Scholar] [CrossRef]
- Raczyńska, E.D. Electron delocalization and relative stabilities for the favored and rare tautomers of hydroxyazines in the gas phase—A comparison with aminoazines. Comput. Theor. Chem. 2014, 1042, 8–15. [Google Scholar] [CrossRef]
- Nyulászi, L. Effects of substituents on the aromatization of phosphole. J. Phys. Chem. 1995, 99, 586–591. [Google Scholar] [CrossRef]
- Nyulászi, L. Pentaphosphole: An aromatic ring with a planar σ3-phosphorus. Inorg. Chem. 1996, 35, 4690–4693. [Google Scholar] [CrossRef]
- Nyulászi, L. Toward a planar σ3-phosphorus. J. Phys. Chem. 1996, 100, 6194–6198. [Google Scholar] [CrossRef]
- Glukhovtsev, M.N.; Dransfeld, A.; Schleyer, P.v.R. Why pentaphosphole, P5H, is planar in contrast to phosphole, (CH)4PH? J. Phys. Chem. 1996, 100, 13447–13454. [Google Scholar] [CrossRef]
- Dransfeld, A.; Nyulászi, L.; Schleyer, P.v.R. The aromaticity of polyphosphaphospholes decreases with the pyramidality of the tricoordinate phosphorus. Inorg. Chem. 1998, 37, 4413–4420. [Google Scholar] [CrossRef] [PubMed]
- Nyulászi, L. Aromatic compounds with planar tricoordinate phosphorus. Tetrahedron 2000, 56, 79–84. [Google Scholar] [CrossRef]
- Nyulászi, L. Aromaticity of phosphorus heterocycles. Chem. Rev. 2001, 101, 1229–1246. [Google Scholar] [CrossRef] [PubMed]
- Nyulászi, L.; Hollóczki, O.; Lescop, C.; Hissler, M.; Réau, R. An aromatic–antiaromatic switch in P-heteroles. A small change in delocalisation makes a big reactivity difference. Org. Biomol. Chem. 2006, 4, 996–998. [Google Scholar] [CrossRef]
- Pelloni, S.; Lazzeretti, P. Magnetotropicity of phosphole and its arsenic analogue. Theor. Chem. Acc. 2007, 118, 89–97. [Google Scholar] [CrossRef]
- Chesnut, D.B.; Quin, L.D. The important role of the phosphorus lone pair in phosphole aromaticity. Heteroatom Chem. 2007, 18, 754–758. [Google Scholar] [CrossRef]
- Wang, L.; Wang, H.J.; Dong, W.B.; Ge, Q.Y.; Lin, L. Using three major criteria to evaluate aromaticity of five-member C-containing rings and their Si-, N-, and P-substituted aromatic heterocyclics. Struct. Chem. 2007, 18, 25–31. [Google Scholar] [CrossRef]
- Vessally, E. Aromatic stability energy studies on five-membered heterocyclic C4H4M (M = O, S, Se, Te, NH, PH, AsH AND SbH): DFT calculations. J. Struct. Chem. 2008, 49, 979–985. [Google Scholar] [CrossRef]
- Josa, D.; Peña-Gallego, A.; Rodríguez-Otero, J.; Cabaleiro-Lago, E. A MP2 and DFT study of the aromatic character of polyphosphaphospholes. Is the pyramidality the only factor to take into consideration? J. Mol. Model. 2011, 17, 1267–1272. [Google Scholar] [CrossRef] [PubMed]
- Zagidullin, A.A.; Bezkishko, I.A.; Miluykov, V.A.; Sinyashin, O.G. Phospholes—Development and recent advances. Mendeleev Commun. 2013, 23, 117–130. [Google Scholar] [CrossRef]
- Quin, L.D.; Keglevich, G.; Ionkin, A.S.; Kalgutkar, R.; Szalontai, G. Phospholes with reduced pyramidal character from steric crowding. I. Synthesis and NMR characterization of 1-(2,4-di-tert-butyl-6-methyl)phenyl-3-methylphosphole. J. Org. Chem. 1996, 61, 7801–7807. [Google Scholar] [CrossRef]
- Nyulászi, L.; Keglevich, G.; Quin, L.D. Phospholes with reduced pyramidal character from steric crowding. II. Photoelectron spectral evidence for electron delocalization in 1-(2,4-di-tert-butyl-6-methylphenyl)-3-methylphosphole. J. Org. Chem. 1966, 61, 7808–7812. [Google Scholar] [CrossRef]
- Keglevich, G.; Quin, L.D.; Böcskei, Z.; Keserű, G.M.; Kalgutkar, R.; Lahti, P.M. Phospholes with reduced pyramidal character from steric crowding. III. NMR and X-ray diffraction studies on 1-(2,4,6-tri-isopropylphenyl)-3-methylphosphole. J. Organomet. Chem. 1997, 532, 109–116. [Google Scholar] [CrossRef]
- Ozimiński, W. Tautomeric equilibria and aromaticity of phosphodiazoles: An ab initio study. Comput. Theor. Chem. 2012, 980, 92–100. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).