1. Introduction
One late-March morning in 1918, a high-pitched whistle pierced the streets of Paris, followed promptly by an explosion. This came as a surprise to many Parisians, literally “out of the blue” [
1]. While they were used by that stage of World War I to explosions following the thunders of artillery, or the rickety humming of a biplane on a bomb run, this shelling was relatively stealthy, having little to no forewarning in the way of sound effects. This led to the widespread belief among the shelled citizenry that they were targeted by a high-flying Zeppelin air-ship [
1,
2].
However, these projectiles were shot some 120 km away by “The Paris gun” (also referred to as “Big Bertha”) [
1,
2], a behemoth of artillery setup deployed on a hill near Crépy, a town under German occupation since the German offensive of 1914, all through the war until the final stages in the fall of 1918. This piece of artillery was a modern member of the old and respected family of Superguns: Guns of unusual characteristics, be it a huge bore, a much heavier payload, extremely high muzzle velocity, etc. [
2].
351 shells hit Paris, killing 256 and wounding 620. However, this did not affect the course of the war. What was the discovery that allowed the Germans to increase the range of shells four times than the best contemporary guns? This discovery was accidental [
2,
3]. The German artillerymen noticed that when the cannon muzzle was tilted at a large angle, the shells traveled far more than expected—40 km instead of 20 km. When the shell was fired, the high-altitude trajectory reached a thin layer of different atmospheric resistance, before it hit the ground again. This formidable cannon was a strategic rather than a tactical weapon, it was intended to sow fear and panic in the heart of Parisians. The accuracy of the cannon was quite low, making it possible to attack Paris, but with little precision [
1,
2,
3].
Physics textbooks would have us believe that the optimal firing angle for achieving maximal distance is 45 degrees. This is due to the decoupling of the horizontal and vertical components of the projectile movement neglecting air resistance [
4]. In practice, when considering the air drag, the projectile trajectory is much more complex, spawning a rich branch of physics and engineering called exterior ballistics [
4,
5]. This branch deals with the movement of projectiles after leaving the barrel, and accounts for the variety of forces exerted on and dynamics affecting the shell or shot. For instance, a shell usually moves through a spiral or coil etched or drilled in the gun bore to give it a spiraling movement [
6,
7]. This is done (among other reasons) to average out the irregularities of the shell along the longitudinal dimension and stabilize its flight. There are additional factors, such as the shape of the shell, the angle of attack, wind, and the influence of Coriolis’ force [
6,
7,
8,
9,
10]. The purpose of this work is to examine the effect of the atmosphere on a long-range shell [
4,
5,
6,
11].
2. Accounting for Air Resistance
The naïve ballistic equations state that the horizontal and vertical components of the movement are decoupled, thus we have
One can set the initial coordinates
to vanish, and by a process of substitution get the trajectory equation.
which is a manifestly symmetric trajectory, regardless of the firing angle. This symmetry is sourced by the conservation of energy on both axes and the conservation of momentum on the horizontal axis. Both of which are postulated symmetries in physics in general.
Classically then, the firing range is given by:
Which has a maxima at and it is strictly quadratic in the muzzle velocity .
However, when considering air resistance, the picture is somewhat more complicated [
1,
2,
3,
11]. The drag force term, which encapsulates the resistance of the air (or any sufficiently non-viscous medium for that matter) to the projectile traversing through it is given in our case by
where
is the air density,
is the projectile velocity,
the cross-section of the projectile along its movement direction, and
is some scale-less shape dependent coefficient empirically measured, which is aptly called the “drag coefficient” and it may depend on the projectile velocity [
11,
12]. This drag force, is independent of location, as it is sourced by velocity, which, in phase space, is independent of the coordinate. This independence is also reflected in the process of developing the Euler-Lagrange formalism, for instance, where as a rule kinetic energy is a function of velocity alone, and potential terms are function of coordinates. Thus, the drag force, by breaking momentum and energy conservation, actually breaks the symmetries of the system. For circular bodies, the value of C is 0.5 and it can be as much as 2 for bodies of irregular shape. In fact, the square velocity model best describes the motion of most of the globular bodies we know from everyday life, accounting for air resistance.
In general, the air resistance for a body in motion depends on several factors: the direction of the body’s velocity, its size, body’s rotation, air characteristics, and the force of the wind. For small bodies moving at low speeds, the friction force (drag force) is proportional to the speed, and for high velocities, the friction force
is proportional to the speed square and can be written as above [
11,
12,
13].
For this case then, the ballistic equations in the
x and the
y directions are written:
These equations are coupled by virtue of
, thus even the decoupling between x and y is lost and the symmetry between the first and second half of the trajectory is broken.
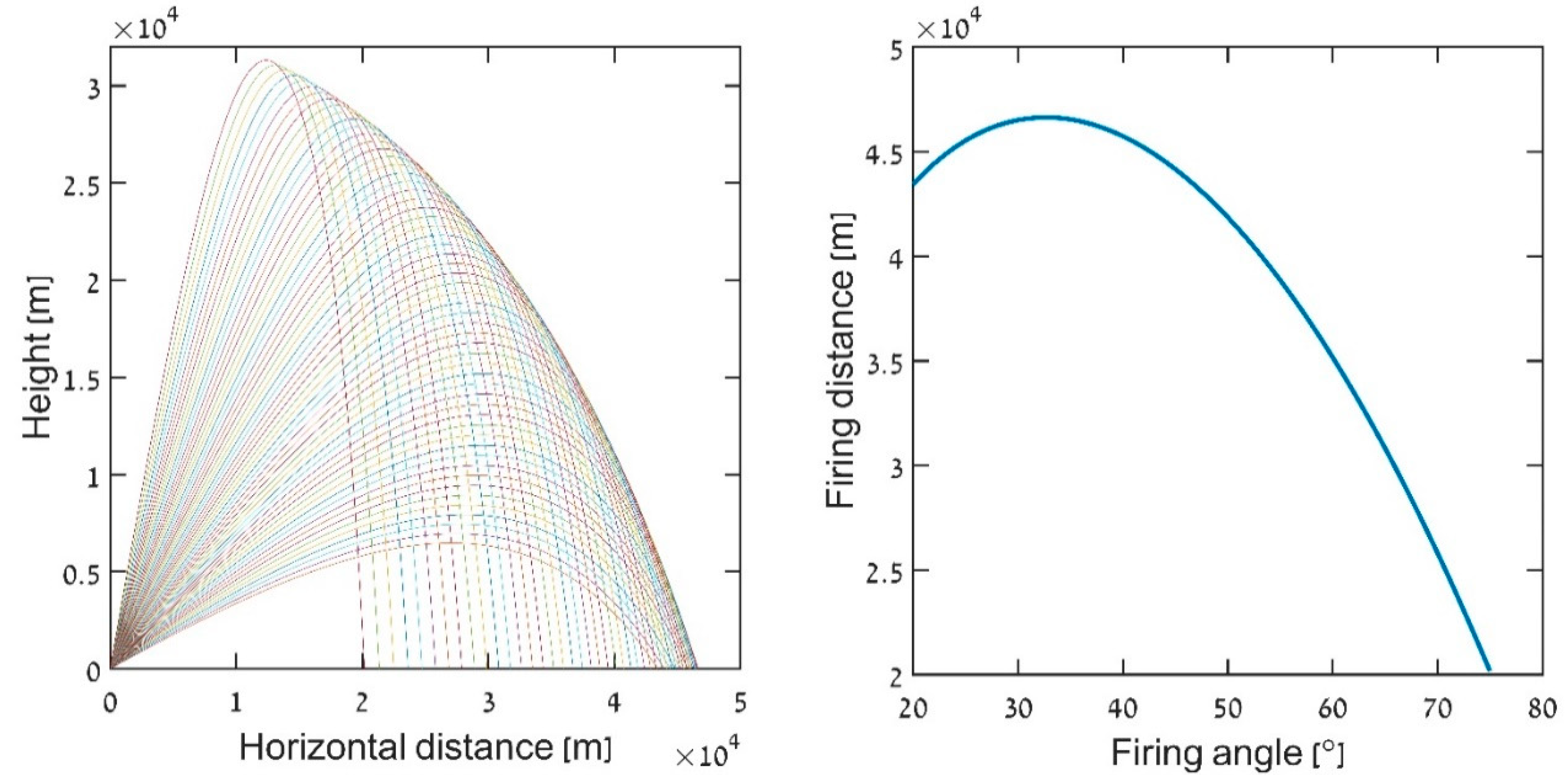
Figure 1 shows the result of studying trajectories that account for a fixed air density
. It is easy to see that, even in this simplest of cases, the optimal angle is different than the textbook 45-degree angle [
13,
14,
15].
German artillery thus found that air friction cannot be neglected in realistic ballistic movement estimations.
The previous section discussed the ballistic equations, adjusted for air resistance. In order to develop a density profile for the atmosphere we can turn first to classical mechanics, and then to thermodynamics [
13,
14,
15].
Atmospheric or Barometric—Choose Your Flavor
Classical mechanics, along with the ideal gas law, provides us with a naïve treatment of the earth’s atmosphere. We look at a virtual box, with the vertical dimensions enclosing the area
and height
, like
Figure 2:
The pressure gradient times
is the force exerted on the gas enclosed in the cube by neighboring cells, and the gas itself experiences a total gravitational force of
, where
is the density of the gas,
is the total volume of the cube, and
is earth’s gravitational acceleration constant. We assume that the cube of gas is in mechanical and thermal equilibrium, thus:
where T is temperature and
V is volume and is constant. Specifying the forces, one gets
We now use the connection
to find that
which yields the following solution:
Notice however that this equation is valid only where the temperature
is height independent. Wherever
, we have to take that into account:
Taking the leading order approximation of
as:
where
is the lapse coefficient that starts at the height of
, we get:
Accordingly, if we go for the simplest of atmospheric profiles, we get a fixed temperature and an exponential decay of air density as we go up. However, experimental evidence indicates that the density profile is better described by the second equation [
12,
13].
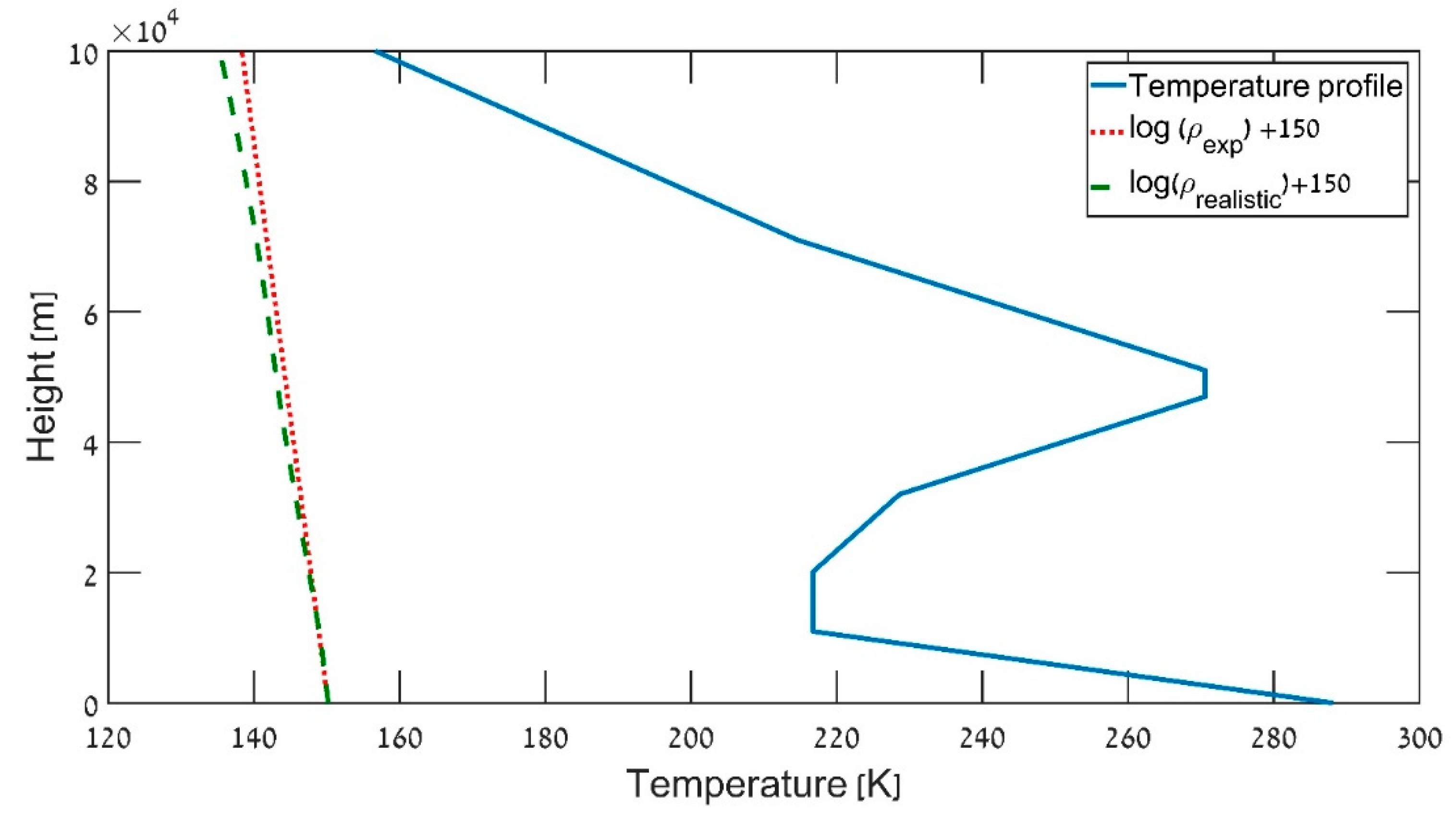
As can be seen in
Figure 3, the density profile as a function of altitude for the exponential description is very close to the first order derivation result, i.e., the so-called barometric equation; this suggests that the ballistic results change very little when we use the barometric equation, rather than the atmospheric one (
Table 1).
Figure 2 also contains the linear atmospheric temperature profile [
6,
7].
We factored the different profiles for several elevation angle trajectories to study the differences in trajectory due to air density profile effects. The baseline data we used for the simulations are the following parameters:
Where for each analysis we set most parameters to be constant, and change one, to examine the effect on trajectory or other derived quantities. The simulation code is fairly simple. We use an adaptive step Runga–Kutta differential equation solver to numerically solve the amended equations of motion that include drag force. At each time step, we calculate the air density according to the barometric or atmospheric equations and insert this into the drag force expression. By setting the air density to zero, we can also recover the naïve equations of motion. Some granularity in results usually occur, not due to the differential equation solver, as this yields a smooth function. Rather, the granularity is due to the steps in parameter that are examined. Time and resource considerations limit our step size in the examined parameter values.
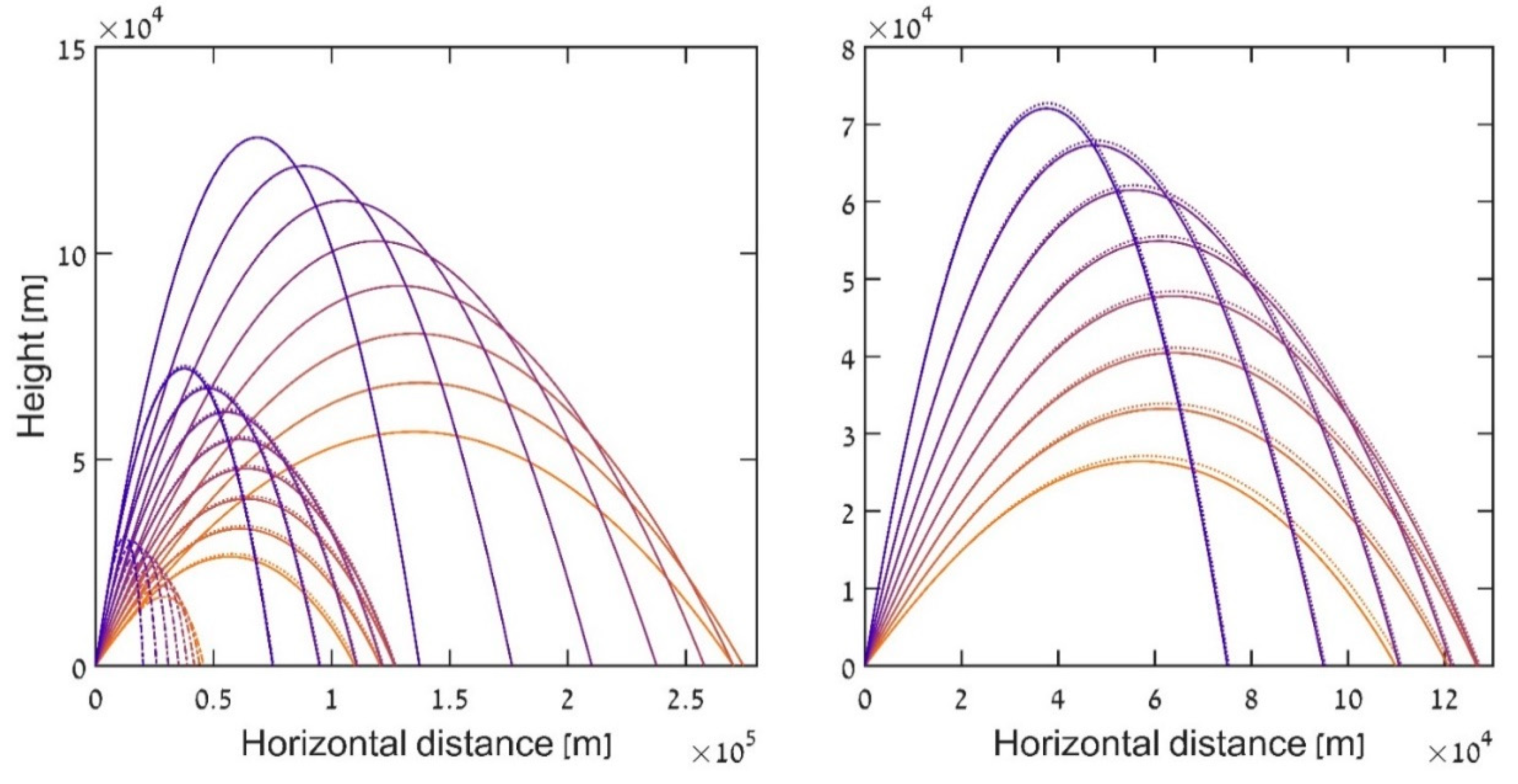
We see that, as suggested before, the difference in maximal firing distance yielded from using the more realistic barometric equation, is only slightly different from using the more approximated exponential air density profile.
Figure 4 shows the four flavors discussed: Ballistic motion in vacuum, Ballistic motion in a constant air density, and lastly, the exponential and barometric air density profiles [
7,
8].
3. So Which Angle Is Best?
We set out to find which angle is preferred, using the specifications of the “Paris gun”. The optimal angle for firing distance should no doubt depend on the ground temperature, even in the simplest exponential case. However, using the temperature profile of the atmosphere makes the temperature dependence even more pronounced [
6,
7,
8,
9]. Additionally, the muzzle velocity should play a major role in finding the optimal angle, since presumably higher velocity means the ability to reach low density regions and traverse there with modest energy losses. We first looked at the optimal angle with a ground temperature of 288.15 K, and found the optimal angle to be
, with a whooping firing distance of 128 km.
Figure 5 displays the results of our numerical simulation for the initial conditions corresponding to the “Paris Gun”, which are given in the above
Table 1.
Ground temperature should be a major factor in firing distance, this is due to the effects of temperature on density via the ideal gas law [
13,
14]. However, we have not studied the effects of ground temperature on atmospheric strata and the “breathing” effect of strata is well documented. We have found (
Figure 6) that indeed the temperature plays a key role, and that the optimal angle is approximately linear to ground temperature.
In order to examine the effects of crossing different strata on the optimal angle, a more direct approach was called for. We hence studied the effects of muzzle velocity on the optimal angle. The assumption is, when the velocity is sufficient high, the projectile will cross over to a different regime of air density [
8,
9]. In that case, the optimal angle should not change a lot until a cross over to the next regime takes place.
Figure 7 shows just that; we see an approximate quadratic behavior of the angle as a function of muzzle velocity, until some threshold is crossed. We then see a constant-like behavior.
where
are all positive coefficients. They have the combined effect of shifting the quadratic function from being symmetric around the vertical axis.
The projectile mass should also play some role, as it affects the energy balance. More mass means smaller in-flight deceleration, relatively less energy loss to drag and thus should result in better distance. We would expect then, that the heavier the projectile, the closer we get to reverting to the ideal 45 degree angle optimal trajectory [
4,
6,
7,
8]. This is evident in
Figure 8, where the simulated data is well fitted by a
function, with the constant being
as suspected. It is easy to make the mistake of approximating the results by a quadratic function, however this misses the high mass limit.
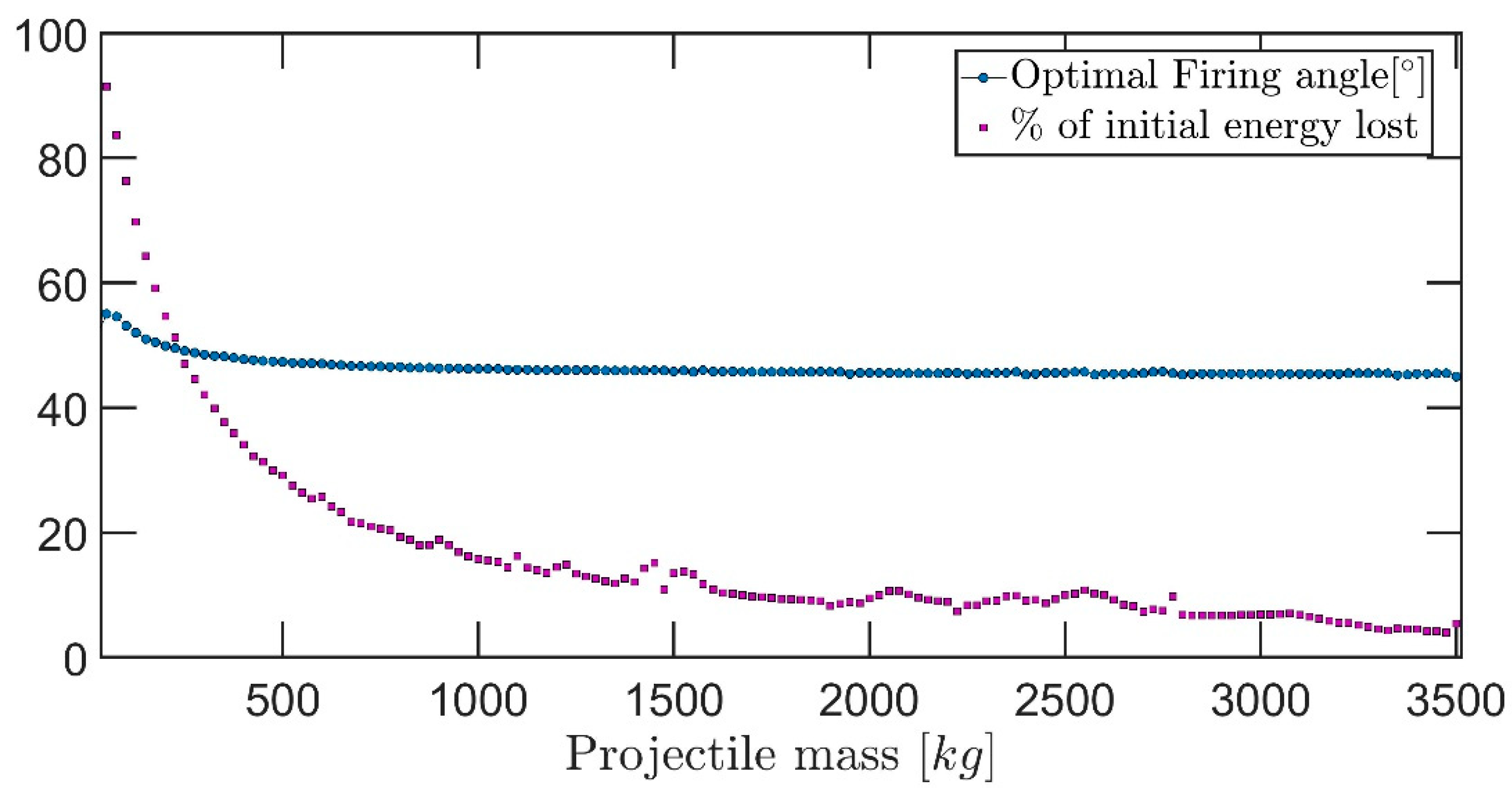
Yet another interesting aspect of this problem is the energy leakage as a function of projectile mass. As hinted before, inspecting the overall energy loss over the ballistic trajectory should lead to a better understanding of the mass dependence.
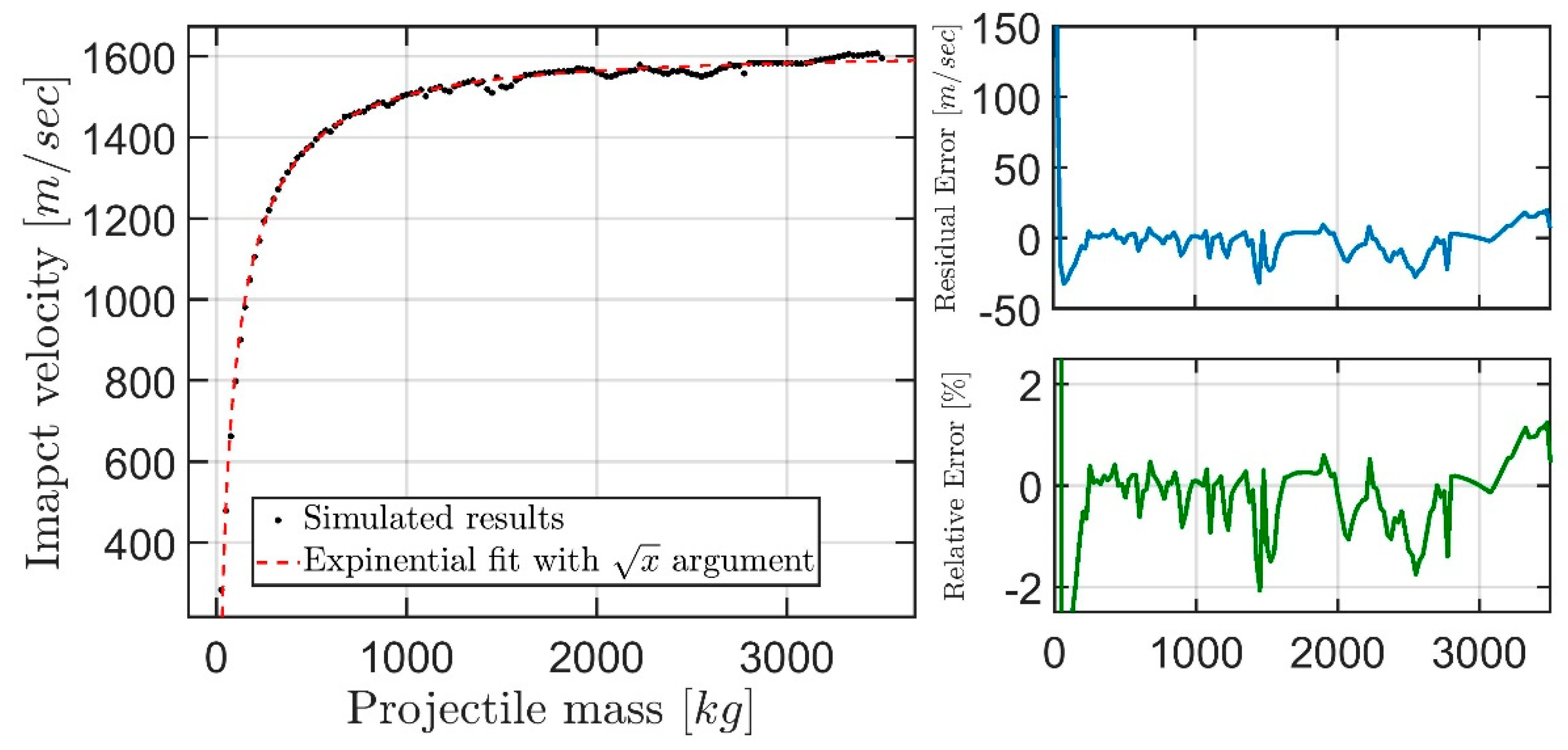
Figure 9 presents the optimal angle vs. mass along with the percentage lot of initial energy. An in-depth analysis of the impact velocity shows a good fit is presented by an exponential fit where the argument is the square root of the mass. This makes sense due to the drag being proportional to the velocity squared, whereas the energy term is linear with respect to mass.
Figure 10 shows these, as well as the relative error between fit and simulated results.
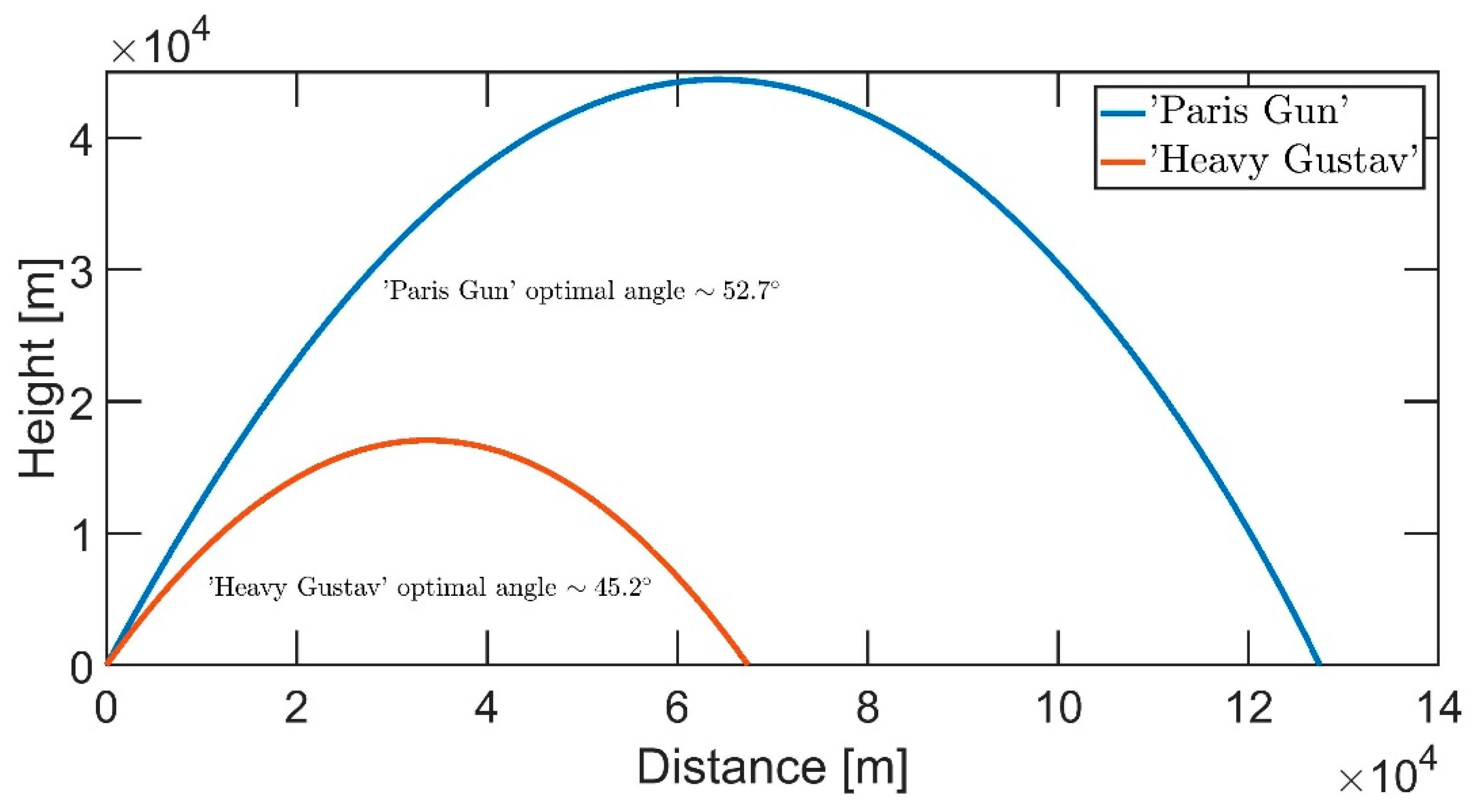
At this point it might be beneficial to mentioned yet another member of the illustrious “super gun” family, the ‘Schwerer Gustav’ (Eng. ‘Heavy Gustav’), which was more than five times heavier than the 256 ton ‘Paris Gun’. The engineers of the Heavy Gustav have basically made the projectiles so heavy that drag became an almost non-issue.
Figure 11 compares the two super guns in terms of optimal degree and firing range, we can immediately see that the Heavy Gustav was not as long-ranged as the Paris Gun, and the optimal firing angle is closer to the textbook
. However, due to the heavier payload (45–67 times heavier), drag and other effects should be greatly reduced. Consequently, the accuracy should be greatly increased.
4. Conclusions
The wartime employment of “super-guns”, while not a new idea, gives us the opportunity to delve deeper into some advanced ballistic ideas. As an example, we looked into the “Paris gun”, which, by classroom physics alone, should have reached a staggering firing distance of ~250 km. However, if one takes the simplified notion of fixed air density, the distance is greatly suppressed, even to the point of being largely ineffective. A good approximation to the actual range lies somewhere in the middle of the two extremes. This is given by using the air density profile function, be it the more accurate so-called barometric equation, or the more rudimentary exponential profile. This was our first motivation, but we have looked deeper into the effects of projectile mass, ground temperature, etc. We claim that these concepts can and should be incorporated in the basic toolbox of ballistic physics, and not relegated off-handedly to the obscure regions of ballistic engineering. Some effects are overlooked in this analysis, such as the dependence of the drag coefficient on shell velocity. Also, there are atmospheric effects not discussed herein that may have a large effect on trajectories and hence optimal firing angles, etc. We have found that even the simplest of complications that include air density, shifts the optimal angle from the schoolbook’s 45-degree angle, ground temperature plays a major role. While the optimal angle changes by a mere two degrees in response to a huge change in ground temperature, the maximal distance is largely affected. Muzzle velocity is perhaps the most influential variable, when working within a sensible projectile mass range. Finally, the optimal angle behaves as expected in the large mass limit, where energy losses due to drag become negligible and the optimal angle converges to a 45 degree angle.