Power Spectrum and Diffusion of the Amari Neural Field
Abstract
1. Introduction
2. Amari Equation
3. Linearized Amari Equation
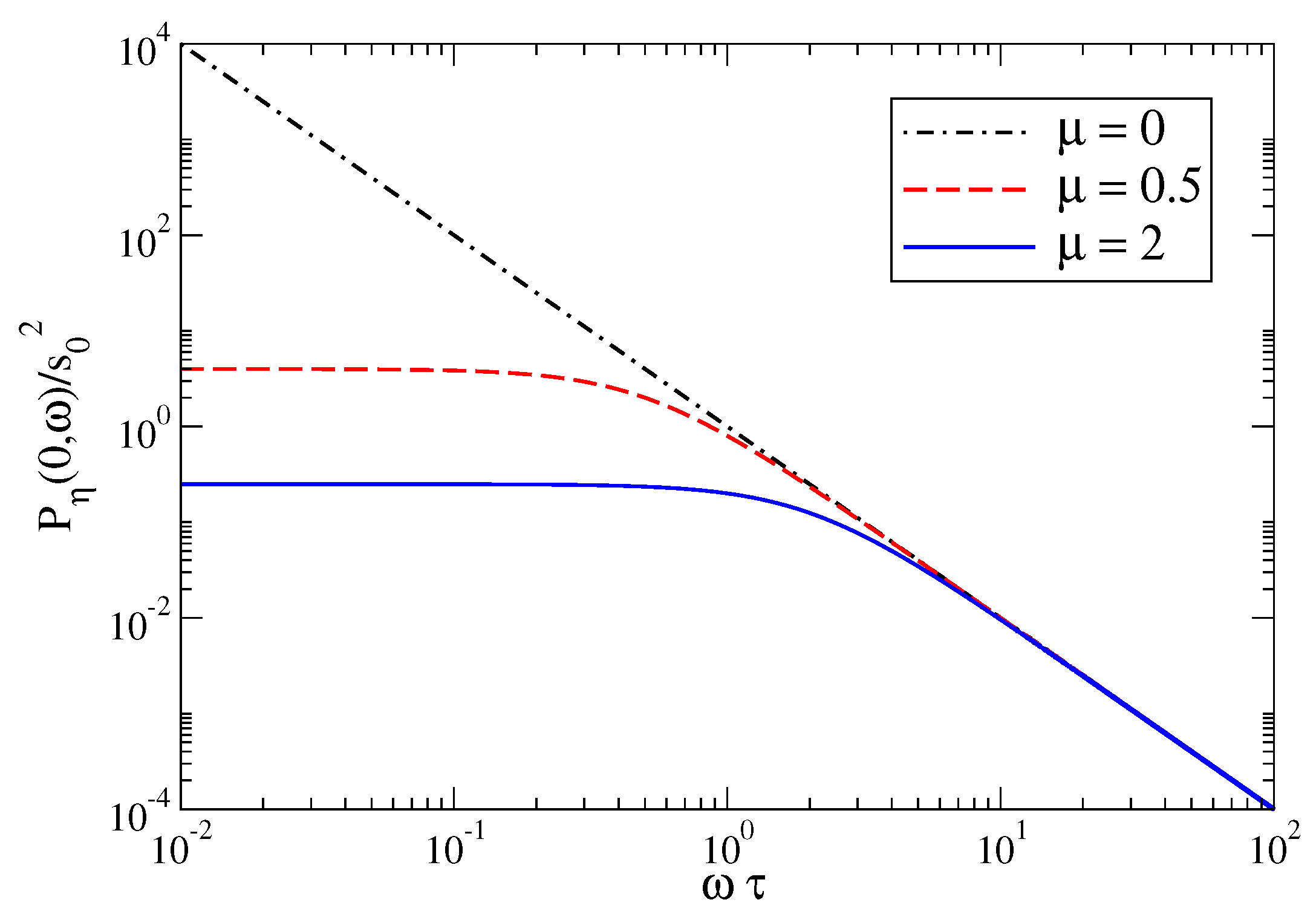
3.1. Power Spectrum of the Linearized Amari Equation
3.2. Diffusion Equation From the Linearized Amari Equation
4. Reaction-Diffusion From the Amari Equation with Weak Nonlinearity
Dissipation and Neural Action
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Bresloff, P.C. Spatiotemporal dynamics of continuum neural fields. J. Phys. A 2012, 45. [Google Scholar] [CrossRef]
- Coombes, S.; Graben, P.B.; Rotthast, R.; Wright, J. (Eds.) Neural Fields: Theory and Applications; Springer: Heidelberg, Germany, 2014. [Google Scholar]
- Wilson, H.R.; Cowan, J.D. Excitatory and Inhibitory Interactions in Localized Populations of Model Neurons. Biophys. J. 1972, 12, 1–24. [Google Scholar] [CrossRef]
- Nunez, P.L. The brain wave equation: A model for the EEG. Math. Biosci. 1974, 21, 279–297. [Google Scholar] [CrossRef]
- Amari, S. Dynamics of excitation patterns in lateral-inhibitory neural fields. Biol. Cyber. 1977, 27, 77–87. [Google Scholar] [CrossRef]
- Buice, M.A.; Cowan, J.D. Statistical mechanics of the neocortex. Prog. Biophys. Mol. Biol. 2009, 99, 53–86. [Google Scholar] [CrossRef] [PubMed]
- Buice, M.A.; Cowan, J.D. Field-theoretic approach to fluctuation effects in neural networks. Phys. Rev. E 2007, 75, 051919. [Google Scholar] [CrossRef] [PubMed]
- Freeman, W.J.; Rogers, L.J.; Holmes, M.D.; Silbergeld, D.L.; Cowan, J.D. Field-theoretic approach to fluctuation effects in neural networks. J. Neurosci. Meth. 2000, 95, 111–121. [Google Scholar] [CrossRef]
- Rowe, D.L.; Robinson, P.A.; Rennie, C.J. Estimation of neurophysiological parameters from the waking EEG using a biophysical model of brain dynamics. J. Theor. Biol. 2004, 231, 413–433. [Google Scholar] [CrossRef] [PubMed]
- Robinson, P.A.; Rennie, C.J.; Rowe, D.L.; O’Connor, S.C.; Gordon, E. Multiscale brain modelling. Philos. Trans. R. Soc. B 2004, 360. [Google Scholar] [CrossRef] [PubMed]
- Stein, E.; Shakarchi, R. Fourier Analysis: An Introduction; Princeton University Press: Princeton, NJ, USA, 2003. [Google Scholar]
- Jirsa, V.K.; Haken, H. A derivation of a macroscopic field theory of the brain from the quasi-microscopic neural dynamics. Phys. D Nonlinear Phenomena 1997, 99, 503–526. [Google Scholar] [CrossRef]
- Sobolev, S.L.; Dawson, E.R.; Broadbent, T.A.A. Partial Differential Equations of Mathematical Physics; Dover: London, UK, 1989. [Google Scholar]
- Bateman, H. On Dissipative Systems and Related Variational Principles. Phys. Rev. 1931, 38, 815–819. [Google Scholar] [CrossRef]
- Celeghini, E.; Rasetti, M.; Vitiello, G. Quantum dissipation. Ann. Phys. 1992, 215, 156–170. [Google Scholar] [CrossRef]
- Gribov, V. A reggeon diagram technique. Sov. Phys. JEPT 1968, 26, 414–423. [Google Scholar]
- Cardy, J.; Sugar, R.J. Directed percolation and Reggeon field theory. Phys. A 1980, 13, L423. [Google Scholar] [CrossRef]
- Pettersen, K.H.; Linden, H.; Tetzlaff, T.; Einevoll, T. Power Laws from Linear Neuronal Cable Theory: Power Spectral Densities of the Soma Potential, Soma Membrane Current and Single-Neuron Contribution to the EEG. PLoS Comput. Biol. 2014, 10, e1003928. [Google Scholar] [CrossRef] [PubMed]
- Jirsa, V. Neural field dynamics with local and global connectivity and time delay. Philos. Trans. R. Soc. A 2009, 367, 1131. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salasnich, L. Power Spectrum and Diffusion of the Amari Neural Field. Symmetry 2019, 11, 134. https://doi.org/10.3390/sym11020134
Salasnich L. Power Spectrum and Diffusion of the Amari Neural Field. Symmetry. 2019; 11(2):134. https://doi.org/10.3390/sym11020134
Chicago/Turabian StyleSalasnich, Luca. 2019. "Power Spectrum and Diffusion of the Amari Neural Field" Symmetry 11, no. 2: 134. https://doi.org/10.3390/sym11020134
APA StyleSalasnich, L. (2019). Power Spectrum and Diffusion of the Amari Neural Field. Symmetry, 11(2), 134. https://doi.org/10.3390/sym11020134




